Computationally Efficient Solution of a 2D Diffusive Wave Equation Used for Flood Inundation Problems
Abstract
1. Introduction
2. Methods
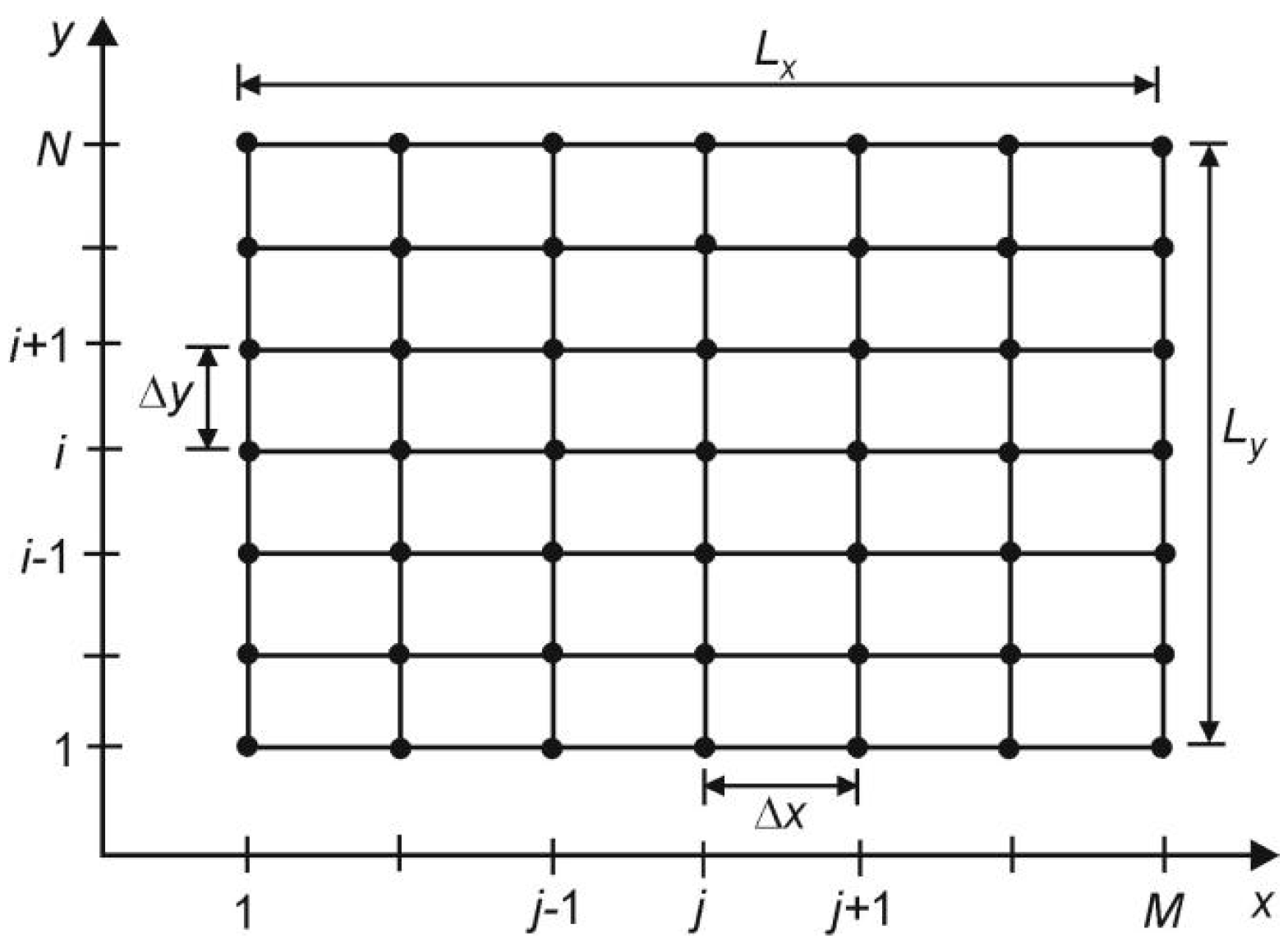
2.1. Decomposition of the 2D Equation with the Splitting Method
2.2. Solution of the 1D Equation Using the FDM Explicit Scheme
- when the water depth is negative or zero, h ≤ 0,
- or when the water stage derivative takes a very small value, ∂H/∂s < ε, where ε represents the assumed tolerance, usually ranging from 10−6 to 10−9.
2.3. Solution of the 1D Equation Using Modified FEM with the Implicit Scheme
- for node j = 1
- for each internal node j = 2, 3, …, M − 1
- for node j = Mwhere ω is the weighting parameter ranging from 0 to 1, and is the nodal value of the averaged diffusion coefficient calculated by Equation (8). Equation (17) written for each node gives a system of ODE, which can be expressed using the matrix notation.where H = [H1,…,Hj−1,Hj,Hj+1,…,HM]T is the column vector of water stage nodal values, A is a tridiagonal constant matrix of size M × M, B is a tridiagonal matrix of size M × M with elements dependent on the solution vector, and G is the column vector representing the fluxes through the ends of the elements.
2.4. Solution of the System of Algebraic Equations
2.4.1. Solution of the Nonlinear System
2.4.2. Solution of the Linear System
- for row j = 1:
- for rows j = 2, 3, …, M − 1:
- for row j = M:
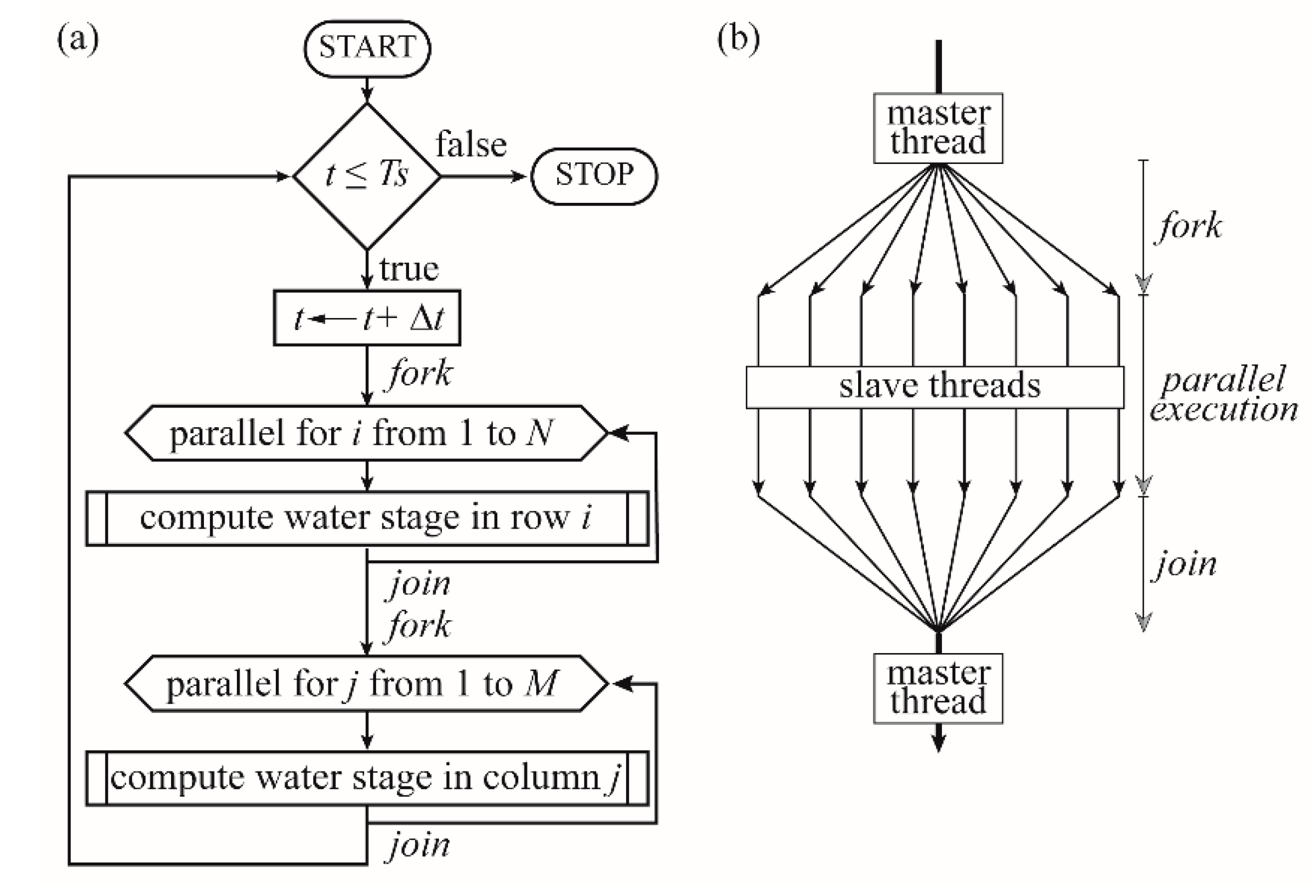
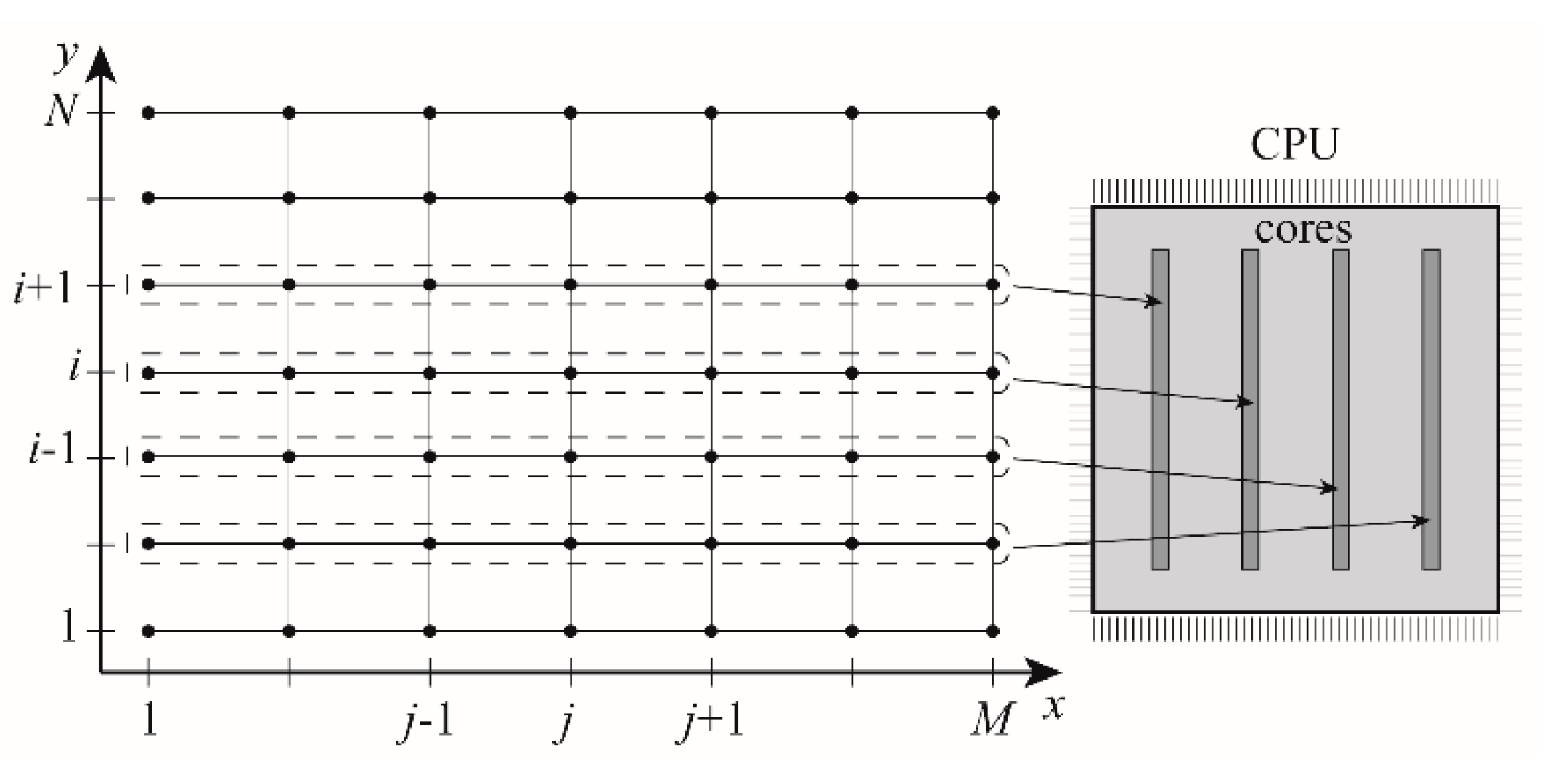
2.5. Parallelization and Solver Implementation
- (1)
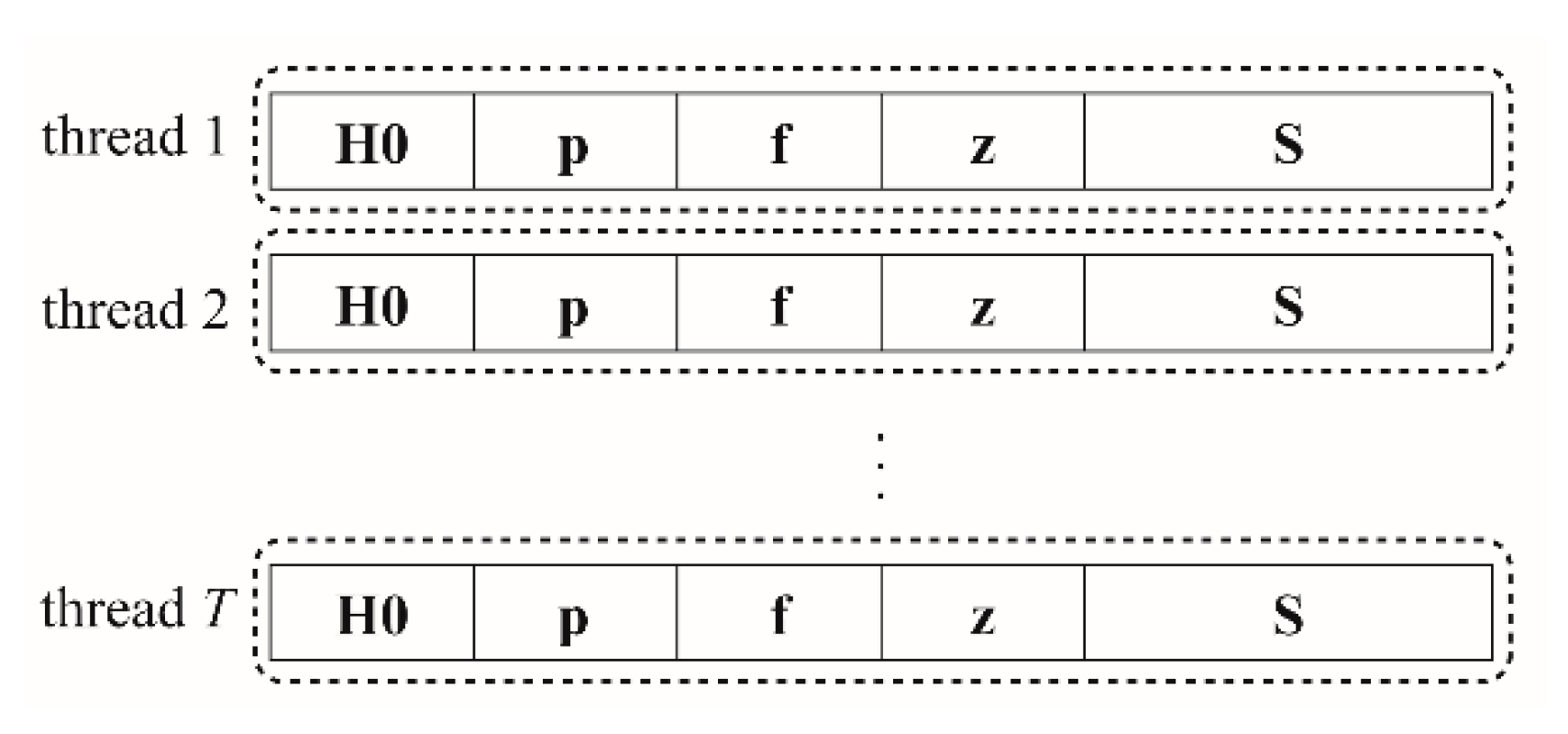
- Bottom height values for the considered row or column are copied from the shared bottom variable Z and stored in the private variable z,
- (2)
- Water stage values from the previous computation step for the considered row or column are copied from the shared water stage variable H and written in the private variable H0,
- (3)
- Private variable S is used to create and then temporarily store the matrix ,
- (4)
- Product is stored in the private variable p,
- (5)
- Private variable S is used to create and store matrix ,
- (6)
- Vector is created and stored in the private variable f,
- (7)
- System (23) is solved and the solution result is written in the variable f,
- (8)
- Water stage vector is updated and stored in H0,
- (9)
- If the required solution accuracy is obtained, go to step 10, if not, return to step 5,
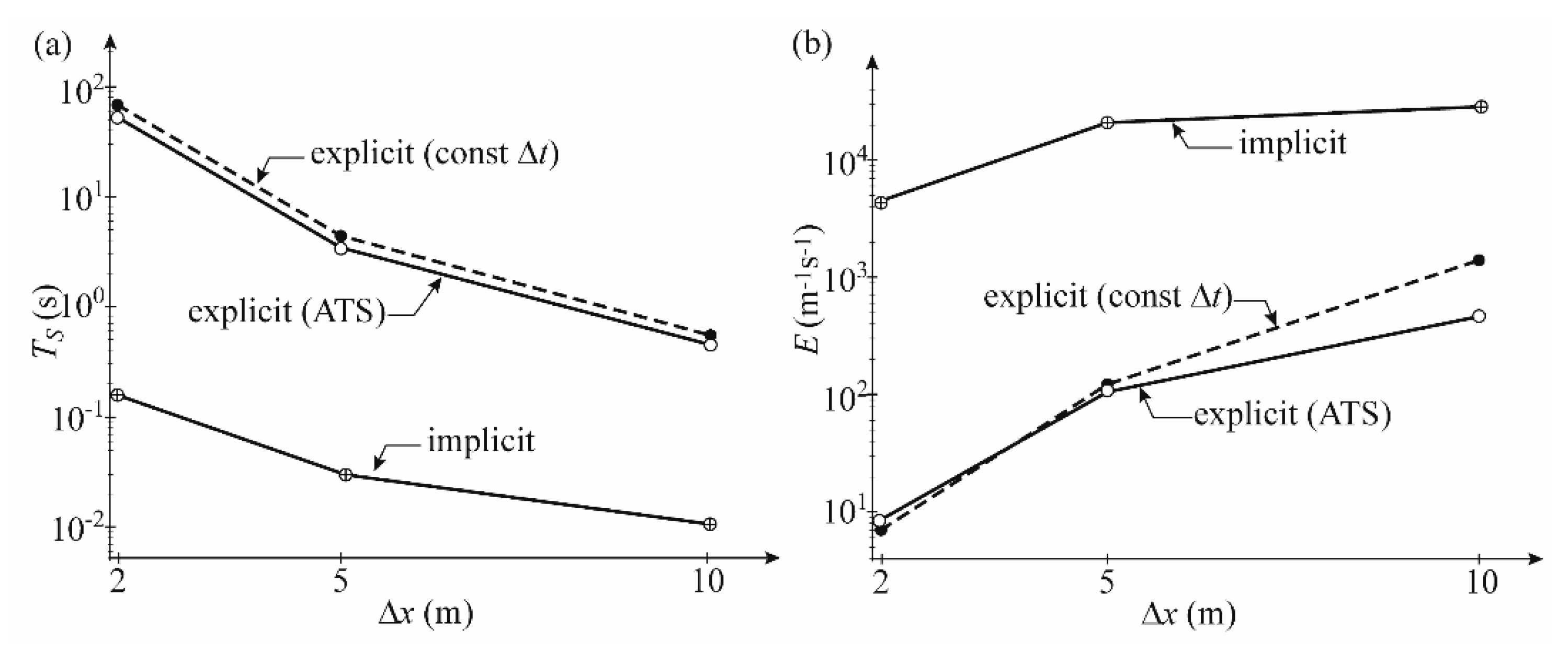
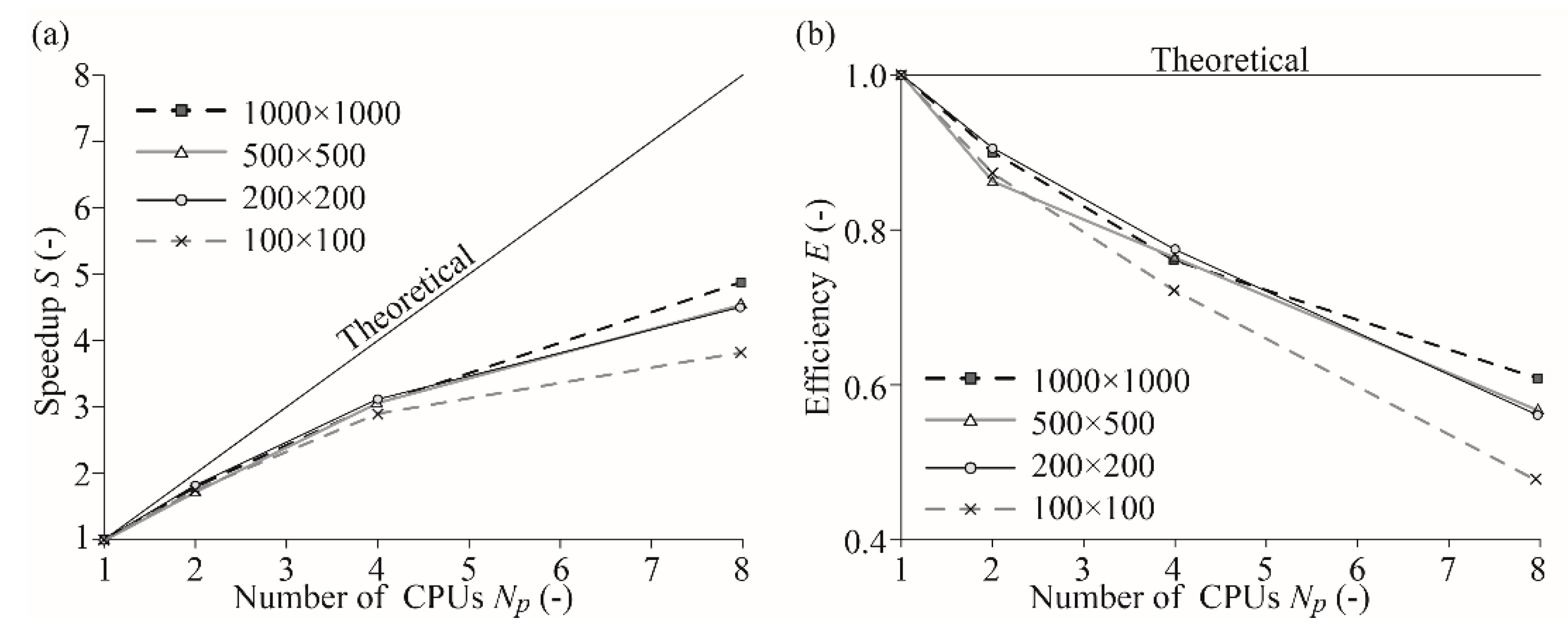
2.6. Measure of Efficiency
3. Results
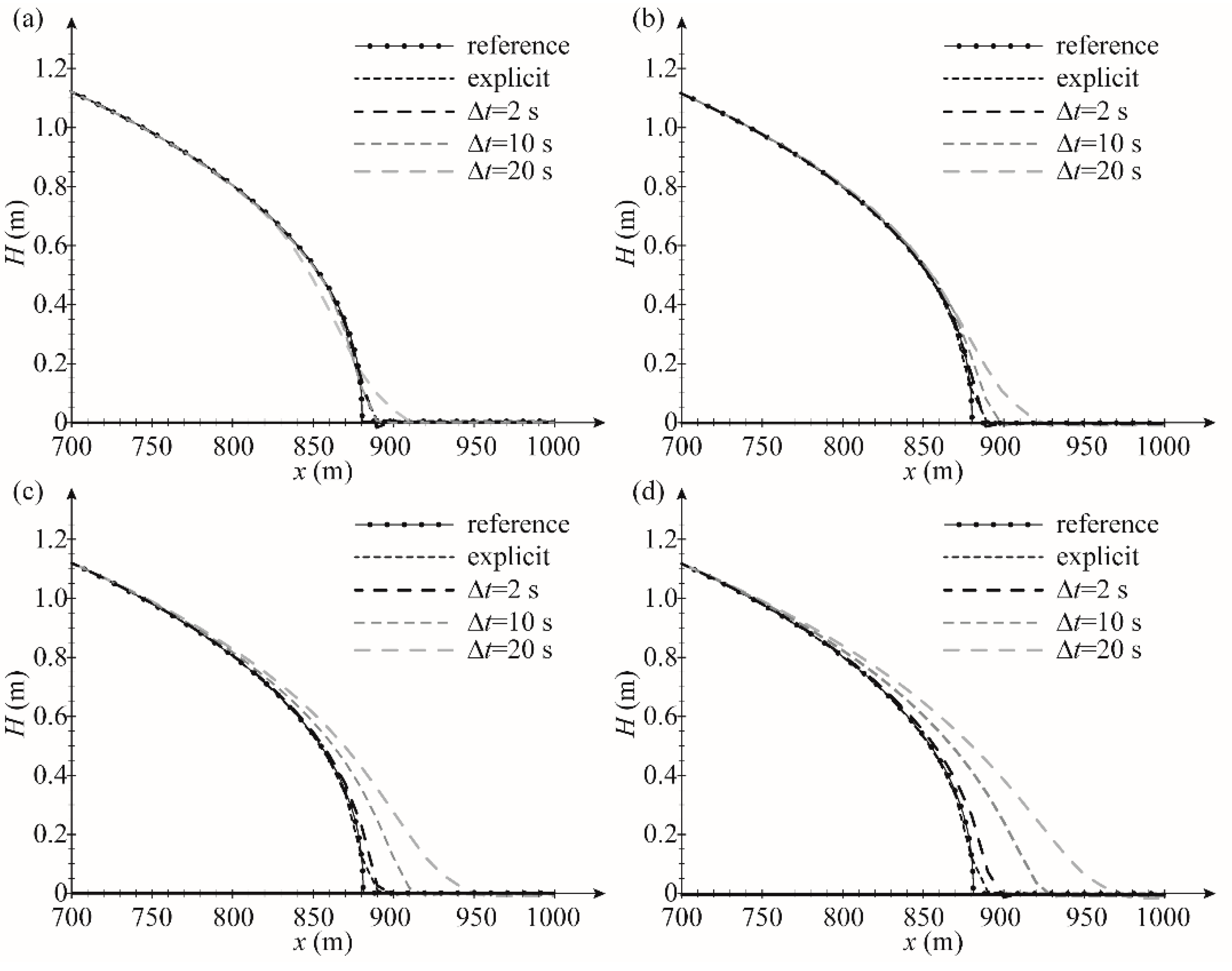
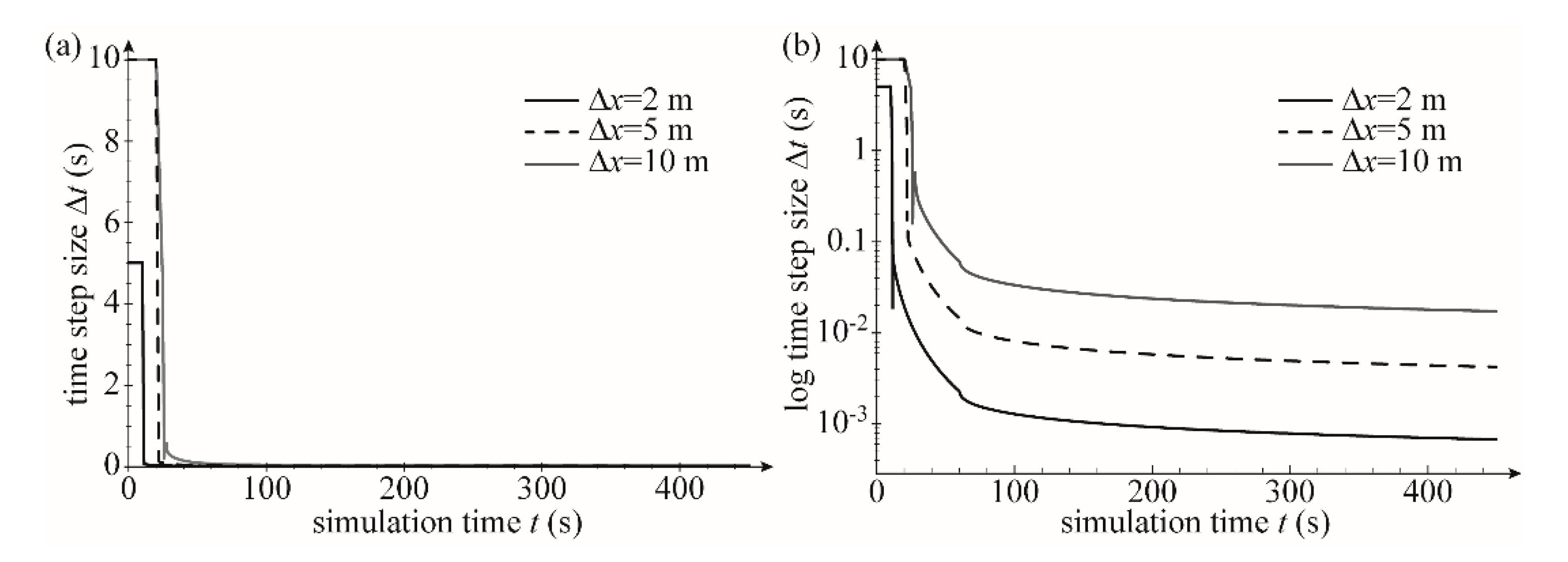
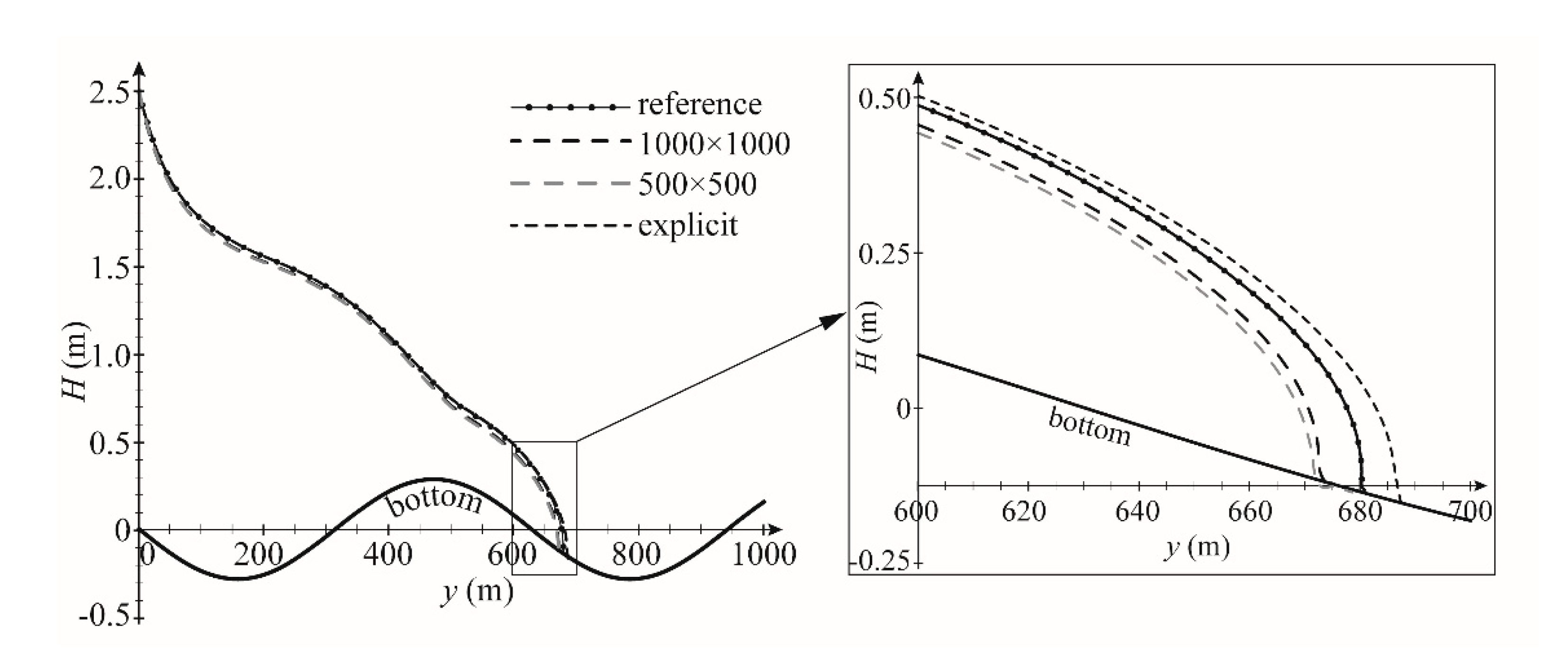
3.1. One-Dimensional Flow, Horizontal Plane Wetting Test
- (1)
- Tolerance for the iterative process of the solution of the system of nonlinear equations: δ = 0.001 m,
- (2)
- Threshold for the water stage derivative in Equation (9a) ∂H/∂s = ∂H/∂x: ε = 10−9,
- (3)
- Maximum number of iterations in a simulation step is 50.
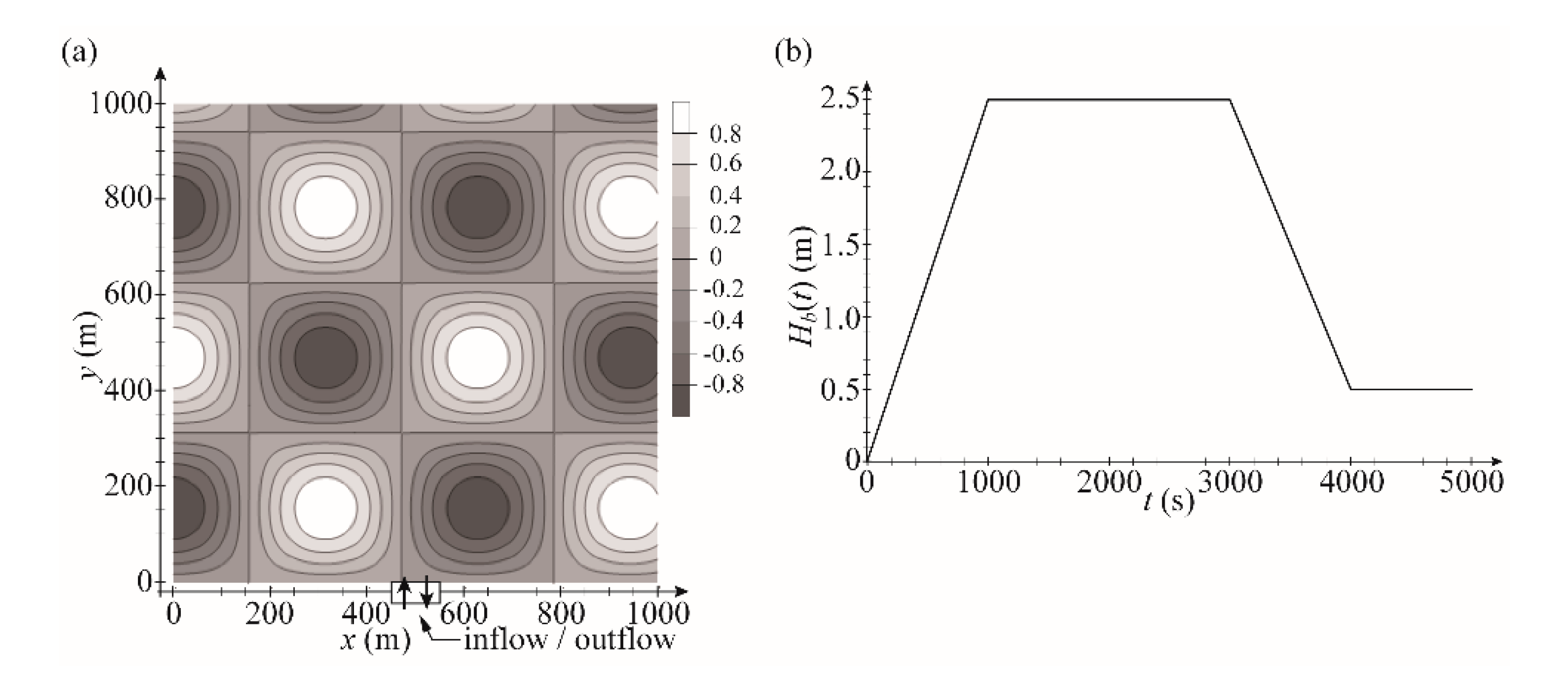
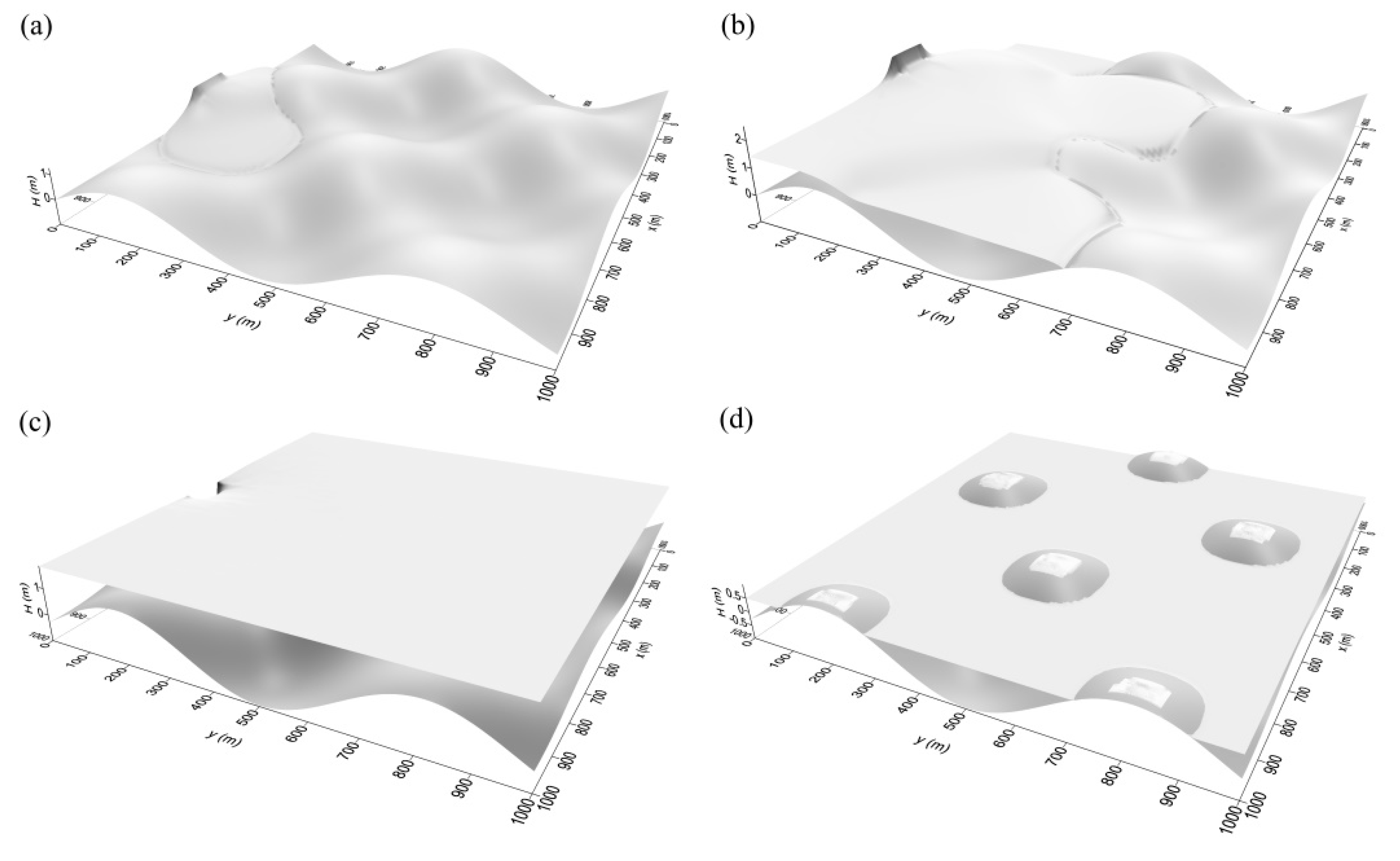
3.2. Two-Dimensional Flow, Parallel Computation for the Wetting-Drying Test
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Heniche, M.; Secretan, Y.; Boudreau, P.; Leclerc, M. A two-dimensional finite drying-wetting shallow water model for rivers and estuaries. Adv. Water Resour. 2000, 23, 359–372. [Google Scholar] [CrossRef]
- Horritt, M.S. Evaluating wetting and drying algorithms for finite element models of shallow water flow. Int. J. Numer. Methods Eng. 2002, 55, 835–851. [Google Scholar] [CrossRef]
- Begnudelli, L.; Sanders, B.F. Unstructured grid finite-volume algorithm for shallow-water flow and scalar transport with wetting and drying. J. Hydraul. Eng. ASCE 2006, 132, 371–384. [Google Scholar] [CrossRef]
- Liang, Q.; Borthwick, A.G.L. Adaptive quadtree simulation of shallow flow with wet-dry fronts over complex topography. Comput. Fluids 2009, 38, 221–234. [Google Scholar] [CrossRef]
- Szydłowski, M.; Kolerski, T.; Zima, P. Impact of the Artificial Strait in the Vistula Spit on the Hydrodynamics of the Vistula Lagoon (Baltic Sea). Water 2019, 11, 990. [Google Scholar] [CrossRef]
- Tan, W.Y. Shallow Water Hydrodynamics; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Song, L.; Zhou, J.; Guo, J.; Zou, Q.; Liu, Y. A robust well-balanced finite volume model for shallow water flows with wetting and drying over irregular terrain. Adv. Water Resour. 2011, 34, 1915–1932. [Google Scholar] [CrossRef]
- Vacondio, R.; Palù, A.D.; Mignosa, P. GPU-enhanced Finite Volume Shallow Water solver for fast flood simulations. Environ. Modell. Softw. 2014, 57, 60–75. [Google Scholar] [CrossRef]
- Oritz, P. Shallow water flows over flooding areas by a flux-corrected finite element method. J. Hydraul. Res. 2013, 52, 241–252. [Google Scholar] [CrossRef]
- Gourgue, O.; Comblen, R.; Lambrechts, J.; Kärnä, T.; Legat, V.; Deleersnijder, E. A flux-limiting wetting–drying method for finite-element shallow-water models, with application to the Scheldt Estuary. Adv. Water Resour. 2009, 32, 1726–1739. [Google Scholar] [CrossRef]
- Cimorelli, L.; Cozzolino, L.; Della Morte, R.; Pianese, D.; Singh, V.P. A new frequency domain analytical solution of a cascade of diffusive channels for flood routing. Water Resour. Res. 2015, 51, 2393–2411. [Google Scholar] [CrossRef]
- Cimorelli, L.; Cozzolino, L.; D’Aniello, A.; Pianese, D. Exact solution of the Linear Parabolic Approximation for flow-depth based diffusive flow routing. J. Hydrol. 2018, 563, 620–632. [Google Scholar] [CrossRef]
- Zhang, X.H.; Ishidaira, H.; Takeuchi, K.; Xu, Z.X.; Zhuang, X.W. An approach to inundation in large river basins using the triangle finite difference method. J. Environ. Inform. 2004, 3, 51–63. [Google Scholar] [CrossRef][Green Version]
- Prestininzi, P. Suitability of the diffusive model for dam break simulation application to a CADAM experiment. J. Hydrol. 2008, 361, 172–185. [Google Scholar] [CrossRef]
- Moussa, R.; Bocquillon, C. On the use of the diffusive wave for modeling extreme flood events with overbank flow in the floodplain. J. Hydrol. 2009, 374, 116–135. [Google Scholar] [CrossRef]
- Hromadka, T.V.; Yen, C.C. A diffusion hydrodynamic model (DHM). Adv. Water Resour. 1986, 9, 118–170. [Google Scholar] [CrossRef]
- Han, K.Y.; Lee, J.T.; Park, J.H. Flood inundation analysis resulting from levee-break. J. Hydraul. Res. 1998, 36, 747–759. [Google Scholar] [CrossRef]
- Lal, A.M. Weighted implicit finite-volume model for overland flow. J. Hydraul. Eng. ASCE 1998, 124, 941–950. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J. Experimental validation of two-dimensional depth-averaged models for forecasting rainfall-runoff from precipitation data in urban areas. J. Hydrol. 2010, 382, 88–102. [Google Scholar] [CrossRef]
- Di Giammarco, P.; Todini, E.; Lamberti, P. A conservative finite elements approach to overland flow: The control volume finite element formulation. J. Hydrol. 1996, 175, 267–291. [Google Scholar] [CrossRef]
- Arico, C.; Sinagra, M.; Begnudelli, L.; Tucciarelli, T. MAST-2D diffusive model for flood prediction on domains with triangular Delaunay unstructured meshes. Adv. Water Resour. 2011, 34, 1427–1449. [Google Scholar] [CrossRef]
- Szymkiewicz, R.; Gąsiorowski, D. Simulation of unsteady flow over floodplain using the diffusive wave equation and the modified finite element. J. Hydrol. 2012, 464–465, 165–167. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin, Germany, 1997. [Google Scholar]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, MA, USA, 2002. [Google Scholar] [CrossRef]
- Neal, J.C.; Fewtrell, T.J.; Bates, P.D.; Wright, N.G. A comparison of three parallelisation methods for 2D flood inundation models. Environ. Modell. Softw. 2010, 25, 398–411. [Google Scholar] [CrossRef]
- Yu, D. Parallelization of a two-dimensional flood inundation model based on domain decomposition. Environ. Modell. Softw. 2010, 25, 935–945. [Google Scholar] [CrossRef]
- Gąsiorowski, D. Analysis of floodplain inundation using 2D nonlinear diffusive wave equation solved with splitting technique. Acta Geophys. 2013, 61, 668–689. [Google Scholar] [CrossRef]
- Hsu, M.H.; Chen, S.H.; Chang, T.J. Inundation simulation for urban drainage basin with storm sewer system. J. Hydrol. 2000, 234, 21–37. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods. Recent advances and uncertainty analysis. Environ. Modell. Softw. 2017, 90, 210–216. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S.N. Urban fluvial flood modelling using a two-dimensional diffusion-wave treatment. part 1: Mesh resolution effects. Hydrol. Process. 2006, 20, 1541–1565. [Google Scholar] [CrossRef]
- Neal, J.; Fewtrell, T.; Trigg, M. Parallelisation of storage cell flood models using OpenMP. Environ. Modell. Softw. 2009, 24, 872–877. [Google Scholar] [CrossRef]
- Prestininzi, P.; Di Baldassarre, G.; Schumann, G.; Bates, P.D. Selecting the appropriate hydraulic model structure using low-resolution satellite imagery. Adv. Water Resour. 2011, 34, 38–46. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, A.S.; Schumann, A. A 2D parallel diffusive wave model for floodplain inundation with variable time step (P-DWave). J. Hydrol. 2014, 517, 250–259. [Google Scholar] [CrossRef]
- Hunter, N.M.; Horritt, M.S.; Bates, P.D.; Wilson, M.D.; Werner, G.F. An adaptive time step solution for raster-based storage cell modeling of floodplain inundation. Adv. Water Resour. 2005, 28, 975–991. [Google Scholar] [CrossRef]
- Bates, P.D.; Horrit, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modeling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Dal Palù, A.; Mignosa, P. A local time stepping algorithm for GPU-accelerated 2D shallow water models. Adv. Water Resour. 2018, 111, 274–288. [Google Scholar] [CrossRef]
- Feng, K.; Molz, F.J. A 2-D, diffusion based, wetland flow model. J. Hydrol. 1997, 196, 230–250. [Google Scholar] [CrossRef]
- Gąsiorowski, D.; Szymkiewicz, R. Mass and momentum conservation in the simplified flood routing models. J. Hydrol. 2007, 346, 51–58. [Google Scholar] [CrossRef]
- Gąsiorowski, D. Impact of diffusion coefficient averaging on solution accuracy of the 2D nonlinear diffusive wave equation for floodplain inundation. J. Hydrol. 2014, 517, 923–935. [Google Scholar] [CrossRef]
- Lal, A.M. Performance comparison of overland flow algorithms. J. Hydraul. Eng. ASCE 1998, 124, 342–349. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1991; Volume I. [Google Scholar]
- Szymkiewicz, R. Method to solve 1D unsteady transport and flow equations. J. Hydraul. Eng. ASCE 1995, 121, 396–403. [Google Scholar] [CrossRef]
- Szymkiewicz, R. Numerical Modeling in Open Channel Hydraulics; Water Science and Technology Library; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Dahlquist, G.; Bjorck, A. Numerical Methods; Prentice-Hall: Englewood Cliffs, NJ, USA, 1974. [Google Scholar]
- Lin, C.A.; Ecer, A.; Periaux, J.; Satofuka, N.; Fox, P. Parallel Computational Fluid Dynamics. In Development and Applications of Parallel Technology; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill Book Company: New York, NY, USA, 1959. [Google Scholar]
| Spatial Step Δx | Explicit | Implicit | |||||
|---|---|---|---|---|---|---|---|
| Time Step min/max Δt | RMSE | Time Step Δt | RMSE | ||||
| θ = 0.5 | θ = 0.6 | θ = 0.8 | θ = 1.0 | ||||
| (m) | (s) | (10−3 m) | (s) | (10−3 m) | (10−3 m) | (10−3 m) | (10−3 m) |
| 2 | 0.00067/2 | 2.09 | 2 | 1.43 | 5.45 | 12.66 | 18.64 |
| 5 | 0.00420/5 | 2.64 | 5 | 1.58 | 10.61 | 24.89 | 36.26 |
| 10 | 0.01690/10 | 4.73 | 10 | 3.55 | 18.70 | 41.55 | 59.77 |
| Spatial Step Δx | Constant Time Step | Adaptive Time Step (ATS) | Relative Effic. ΔE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Time Step Δt | RMSE | Comp. Time TS | Comp. Effic. EE | Time Step Min/Max Δt | RMSE | Comp. Time TS | Comp. Effic. EEA | ||
| (m) | (s) | (10−3 m) | (s) | (m−1s−1) | (s) | (10−3 m) | (s) | (m−1s−1) | (%) |
| 2 | 0.0006 | 2.05 | 67.89 | 7.2 | 0.0006/2 | 2.09 | 53.46 | 8.9 | 23.6 |
| 5 | 0.0042 | 1.92 | 4.35 | 119.9 | 0.0042/5 | 2.64 | 3.53 | 106.9 | −10.8 |
| 10 | 0.0169 | 1.31 | 0.55 | 1386.7 | 0.0169/10 | 4.73 | 0.45 | 469.0 | −66.2 |
| Spatial Step x | Explicit Adaptive Time Step (ATS) | Implicit | Relative Effic. ΔE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Time Step min/max t | RMSE | Comp. Time TS | Effic. EEA | Time Step Δt | RMSE | Comp. Time TS | Effic. EI | ||
| (m) | (s) | (10−3 m) | (s) | (m−1 s−1) | (s) | (10−3 m) | (s) | (m−1 s−1) | (%) |
| 2 | 0.0006/2 | 2.09 | 53.46 | 8.9 | 2 | 1.42 | 0.16 | 4386 | 49,105 |
| 5 | 0.0042/5 | 2.64 | 3.53 | 106.9 | 5 | 1.58 | 0.03 | 21,059 | 19,590 |
| 10 | 0.0169/10 | 4.73 | 0.45 | 469.0 | 10 | 3.55 | 0.01 | 28,158 | 5303 |
| No. Elements | Spatial Step Δx = Δy | Time Step Δt | RMSE | No. CPU Proc. | Comp. Time TS | Speed Up S | Parallel Effic. EP |
|---|---|---|---|---|---|---|---|
| (-) | (m) | (s) | (m) | (-) | (s) | (-) | (-) |
| 100 × 100 | 10 | 2.5 | 0.026 | 1 | 87.59 | 1.00 | 1.00 |
| 2 | 50.17 | 1.75 | 0.87 | ||||
| 4 | 30.35 | 2.89 | 0.72 | ||||
| 8 | 23.04 | 3.80 | 0.48 | ||||
| 200 × 200 | 5 | 1.25 | 0.036 | 1 | 627.99 | 1.00 | 1.00 |
| 2 | 346.80 | 1.81 | 0.91 | ||||
| 4 | 202.73 | 3.09 | 0.77 | ||||
| 8 | 140.17 | 4.48 | 0.56 | ||||
| 500 × 500 | 2 | 0.5 | 0.035 | 1 | 9047.14 | 1.00 | 1.00 |
| 2 | 5245.99 | 1.72 | 0.86 | ||||
| 4 | 2959.87 | 3.06 | 0.76 | ||||
| 8 | 1996.98 | 4.53 | 0.57 | ||||
| 1000 × 1000 | 1 | 0.25 | 0.027 | 1 | 73,267.80 | 1.00 | 1.00 |
| 2 | 40,659.70 | 1.80 | 0.90 | ||||
| 4 | 24,075.80 | 3.04 | 0.76 | ||||
| 8 | 15,064.30 | 4.86 | 0.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Artichowicz, W.; Gąsiorowski, D. Computationally Efficient Solution of a 2D Diffusive Wave Equation Used for Flood Inundation Problems. Water 2019, 11, 2195. https://doi.org/10.3390/w11102195
Artichowicz W, Gąsiorowski D. Computationally Efficient Solution of a 2D Diffusive Wave Equation Used for Flood Inundation Problems. Water. 2019; 11(10):2195. https://doi.org/10.3390/w11102195
Chicago/Turabian StyleArtichowicz, Wojciech, and Dariusz Gąsiorowski. 2019. "Computationally Efficient Solution of a 2D Diffusive Wave Equation Used for Flood Inundation Problems" Water 11, no. 10: 2195. https://doi.org/10.3390/w11102195
APA StyleArtichowicz, W., & Gąsiorowski, D. (2019). Computationally Efficient Solution of a 2D Diffusive Wave Equation Used for Flood Inundation Problems. Water, 11(10), 2195. https://doi.org/10.3390/w11102195





