Investigation of Trends, Temporal Changes in Intensity-Duration-Frequency (IDF) Curves and Extreme Rainfall Events Clustering at Regional Scale Using 5 min Rainfall Data
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
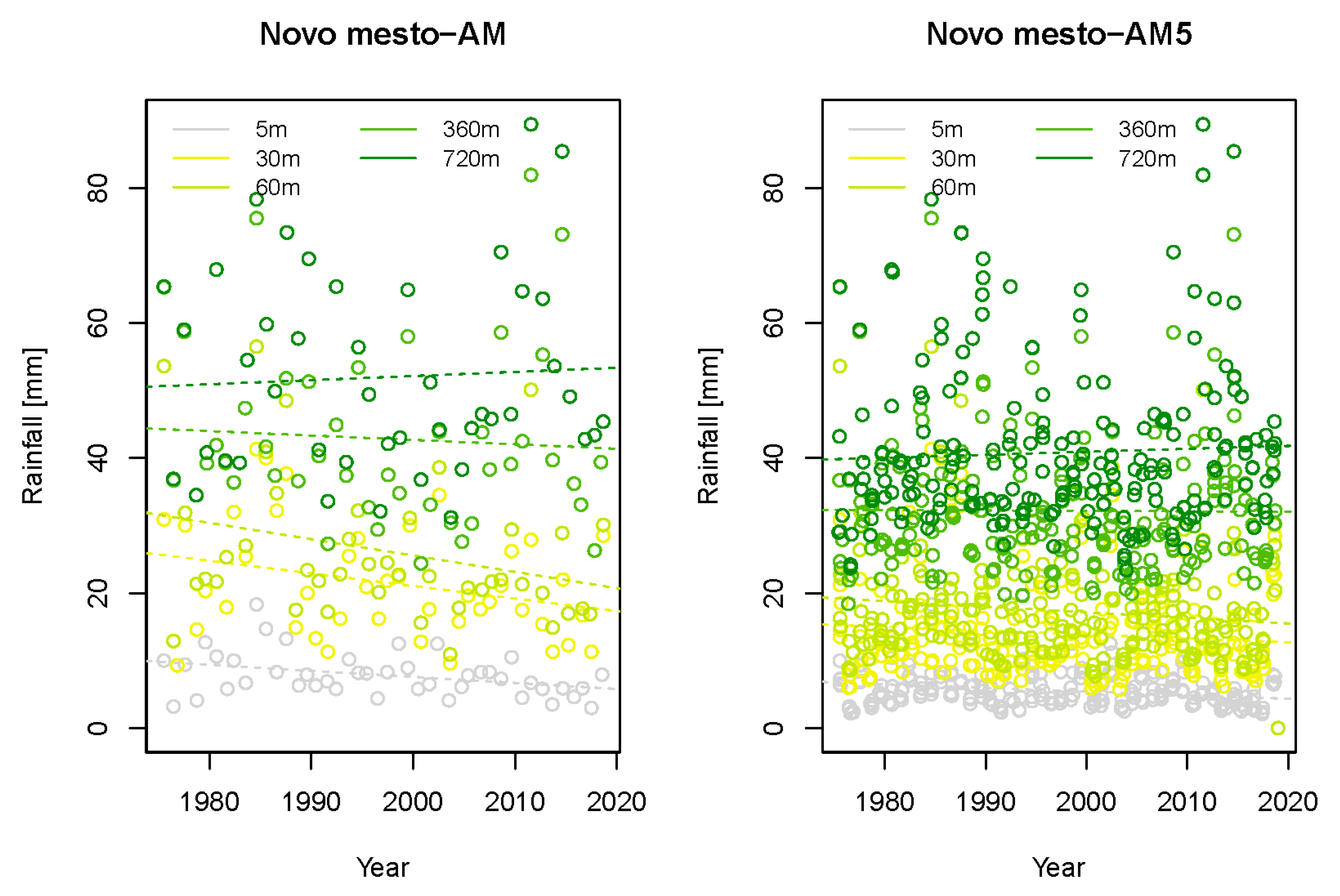
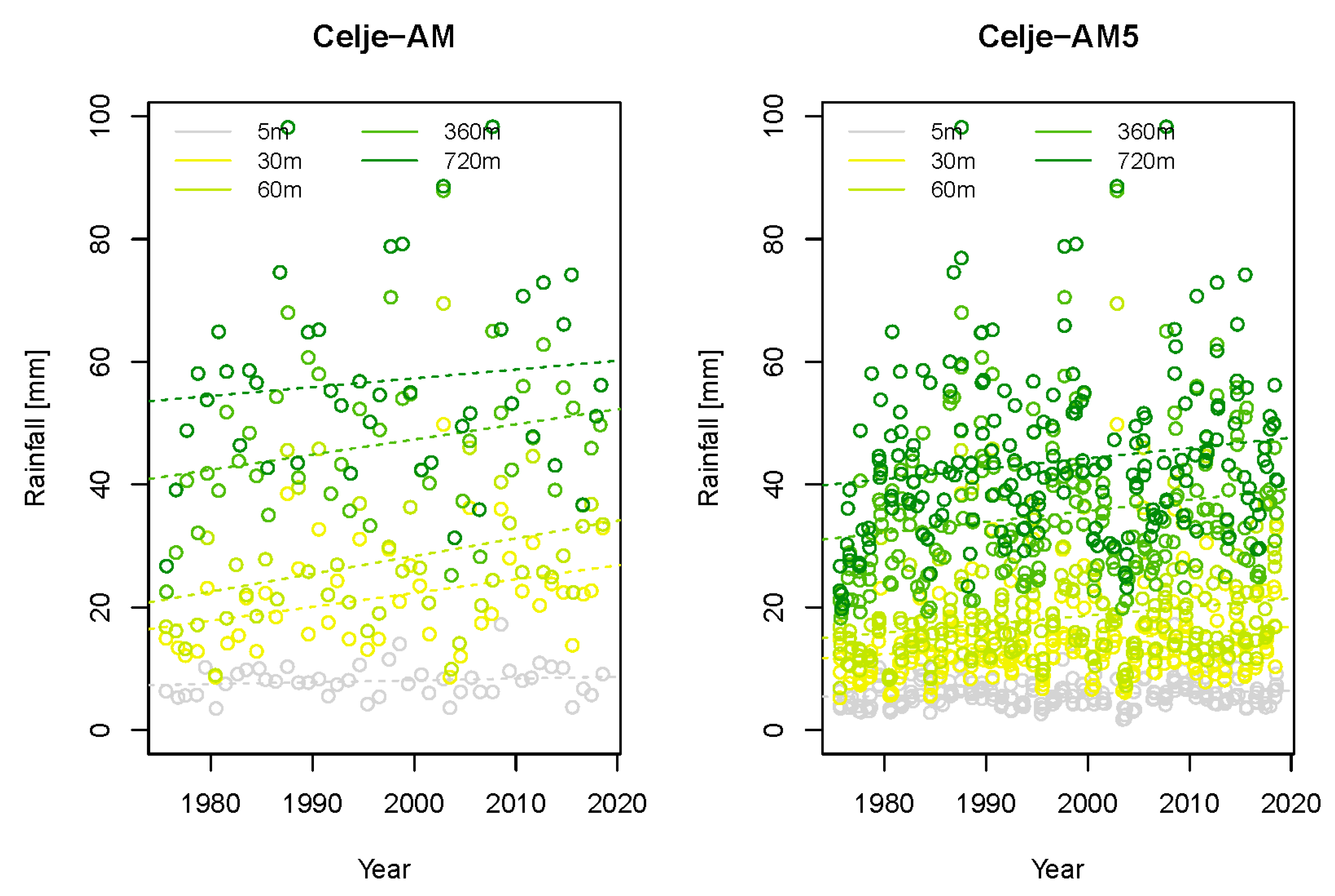
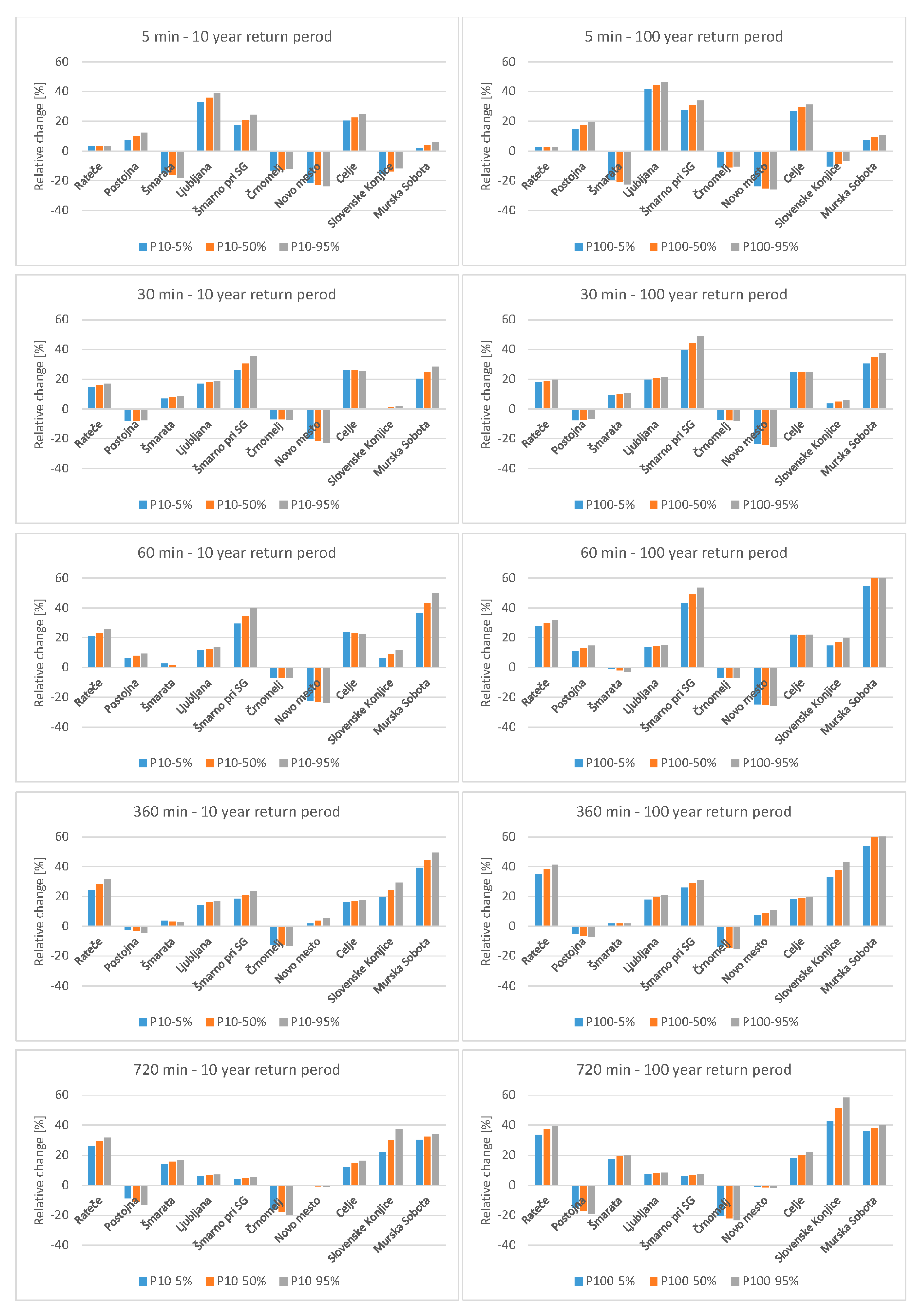
3.1. Trend Detection and Changes in IDF Curves
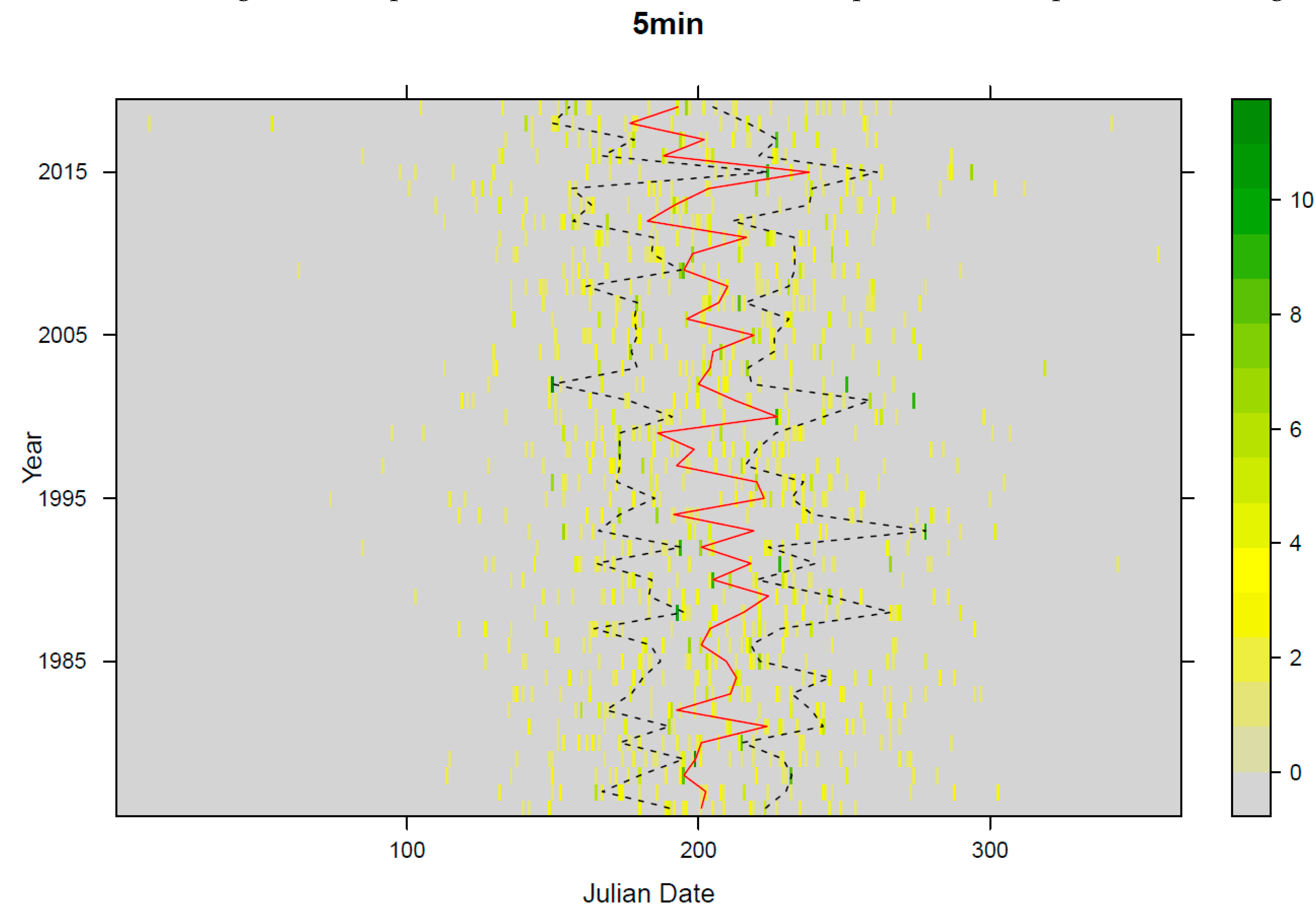
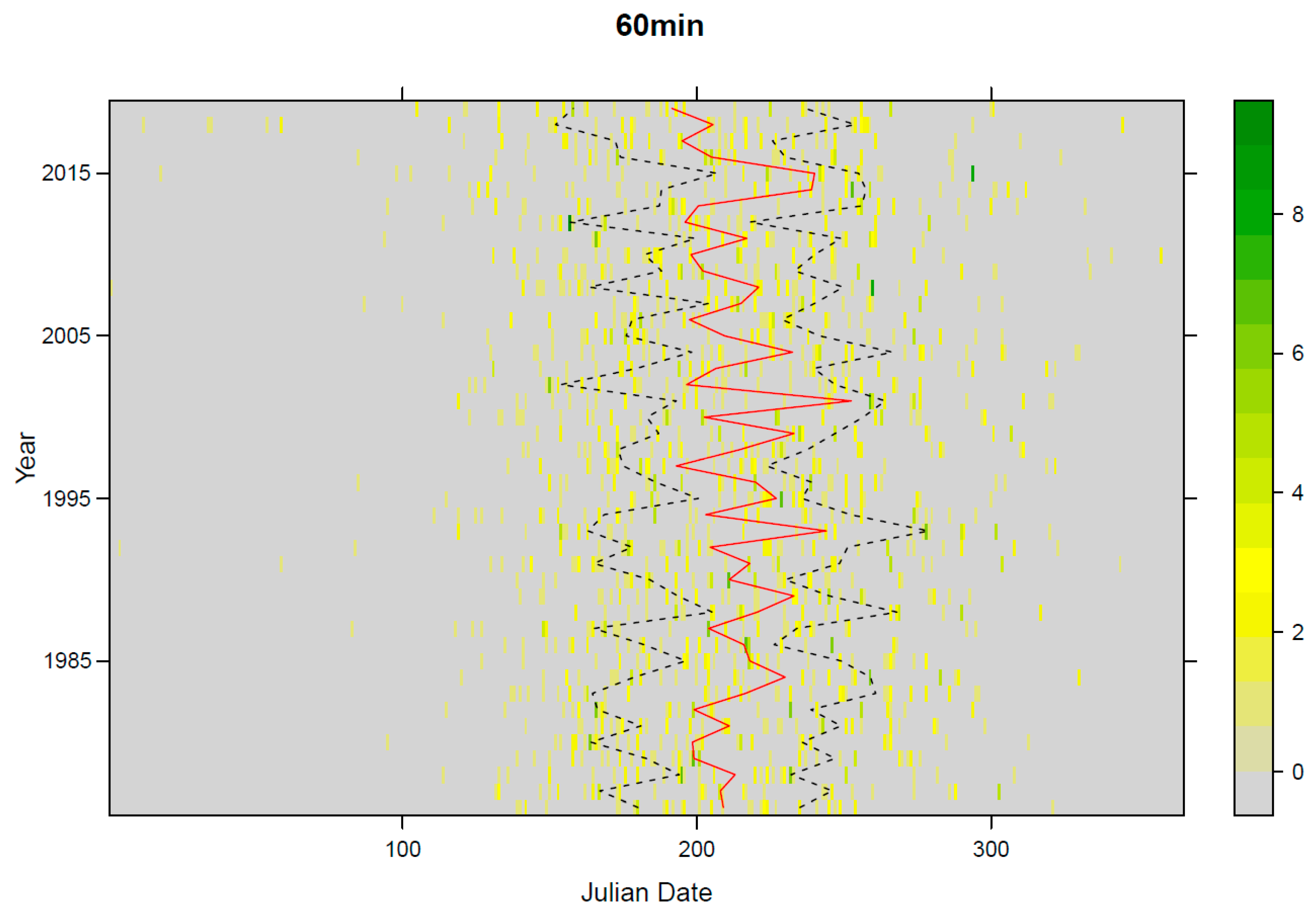
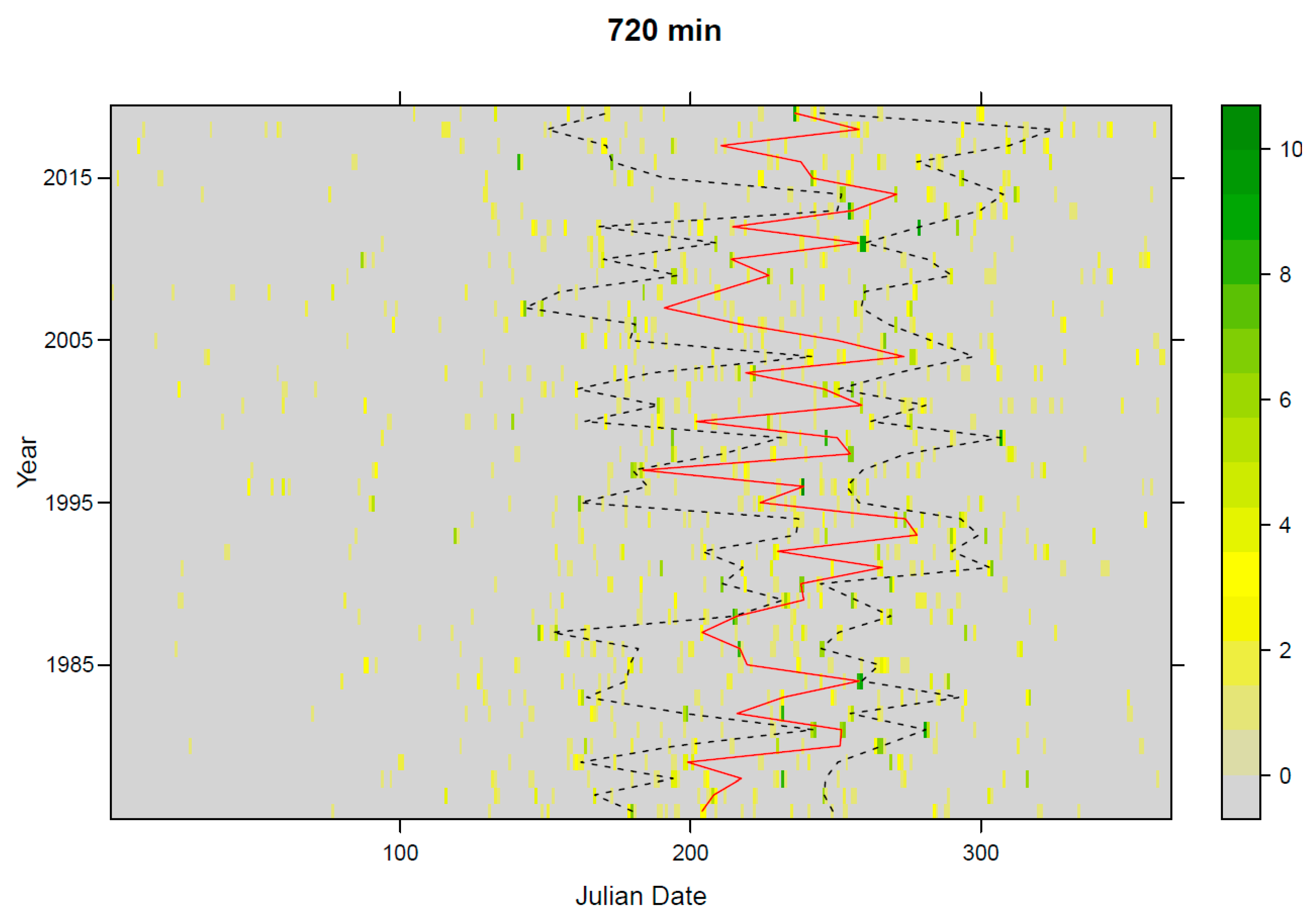
3.2. Clustering of Events
4. Conclusions
- All the statistically significant trends for the 5 min rainfall data are negative for the AM and AM5 samples. Among all statistically significant trends at the 5% level for all rainfall durations, around 65% and 55% of the trends are positive for the AM and AM5 samples, respectively. However, only a few detected trends were statistically significant. This means that according to the analyzed data, extreme rainfall events are not significantly more intense than they were in the past decades.
- For the AM and AM5 samples, there is no clear pattern in the calculated trends for all five rainfall durations, which means that no uniform trend could be determined. Moreover, calculated trends are also very site-specific, and no clear regional trend could be identified for all analyzed rainfall durations.
- The regional Mann-Kendall test results indicate that for the 5 min rainfall duration, the detected trend at the regional level is negative and statistically significant with the selected significance level of 0.05. For longer rainfall durations, trend results are positive, but not statistically significant with the selected significance level.
- The comparison of the results of the IDF analyses for two subsequent sub-samples (first and second 22 years) indicate that changes in the results are relatively consistent with the trend analysis. However, for more stations, we have detected an increase in the design rainfall values for the 1997–2018 period compared to the 1975–1996 period. The maximum change was up to 60%. The largest negative change did not exceed 30%.
- The median Julian date occurrence of the AM5 events for the 5 min data is mid-July, while for longer rainfall durations, it is mid-August.
- Longer rainfall duration extremes are shifting toward the (late) autumn period, while shorter rainfall durations are occurring a few days earlier compared to the past decades.
- The spread in the occurrence of the longer duration events is larger than it was in the past decades, which means that extreme longer duration events can now more frequently occur also in winter and spring periods compared to the past decades. However, the spread was only statistically significant for the 720 min duration for the AM5 case. For other cases, there are no significant differences between the past and present. Furthermore, similar analyses could also be carried out for longer duration events.
- Moreover, Mann-Whitney test results indicate that there is no statistically significant difference among four 11-year periods (i.e., mean number of occurrences for different Julian dates).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Courtey, L.G.; Wilby, R.L.; Hillier, J.K.; Slater, J. Intensity-duration-frequency curves at the global scale. Environ. Res. Lett. 2019, 14, 084045. [Google Scholar] [CrossRef]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T.R. Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3635–3650. [Google Scholar] [CrossRef]
- Ganguli, P.; Coulibaly, P. Does nonstationarity in rainfall require nonstationary intensity–duration–frequency curves? Hydrol. Earth Syst. Sci. 2017, 21, 6461–6483. [Google Scholar] [CrossRef]
- Soulis, E.D.; Sarhadi, A.; Tinel, M.; Suthar, M. Extreme precipitation time trends in Ontario, 1960–2010. Hydrol. Process. 2016, 30, 4090–4100. [Google Scholar] [CrossRef]
- Hernebring, C. 10-Årsregnets Återkomst förr och Nu—Regndata för Dimensionering/Kontrollberäkning av VA-System i Tätorter (in Swedish: Design Storms in Sweden—Before and Now. Rain Data for Design and Control of Urban Drainage Systems); VA-Forsk Report 2006¨C04; Svenskt Vatten: Stockholm, Sweden, 2006. [Google Scholar]
- Madsen, H.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S. Update of regional intensity–duration–frequency curves in Denmark: Tendency towards increased storm intensities. Atmos. Res. 2009, 92, 343–349. [Google Scholar] [CrossRef]
- Pashiardis, S. Compilation of Rainfall Curves in Cyprus; Meteorological Note No. 15; Meteorological Service, Ministry of Agriculture, Natural Resources and Environment: Nicosia, Cyprus, 2009.
- Ntegeka, V.; Willems, P. Trends and multidecadal oscillations in rainfall extremes, based on a more than 100-year time series of 10 min rainfall intensities at Uccle, Belgium. Water Resour. Res. 2008, 44, W07402. [Google Scholar] [CrossRef]
- Soro, G.E.; Noufe, D.; Bi, T.A.G.; Shorohou, B. Trend Analysis for Extreme Rainfall at Sub-Daily and Daily Timescales in Côte d’Ivoire. Climate 2016, 4, 37. [Google Scholar] [CrossRef]
- Mekis, A.; Vincent, L.A.; Shephard, M.W.; Zhang, X. Observed Trends in Severe Weather Conditions Based on Humidex, Wind Chill, and Heavy Rainfall Events in Canada for 1953–2012. Atmos. Ocean 2015, 53, 383–397. [Google Scholar] [CrossRef]
- Shephard, M.W.; Mekis, E.; Morris, R.J.; Feng, Y.; Zhang, X.; Kilcup, K.; Fleetwood, R. Trends in Canadian Short-Duration Extreme Rainfall: Including an Intensity–Duration–Frequency Perspective. Atmos. Ocean 2014, 52, 398–417. [Google Scholar] [CrossRef]
- Cannon, A.J.; Innocenti, S. Projected intensification of sub-daily and daily rainfall extremes in convection-permitting climate model simulations over North America: Implications for future intensity–duration–frequency curves. Nat. Hazards Earth Syst. Sci. 2019, 19, 421–440. [Google Scholar] [CrossRef]
- Dolšak, D.; Bezak, N.; Šraj, M. Temporal characteristics of rainfall events under three climate types in Slovenia. J. Hydrol. 2016, 541, 1395–1405. [Google Scholar] [CrossRef]
- De Luis, M.; Čufar, K.; Saz, M.A.; Longares, L.A.; Ceglar, A.; Kajfež-Bogataj, L. Trends in seasonal precipitation and temperature in Slovenia during 1951–2007. Reg. Environ. Chang. 2014, 14, 1801–1810. [Google Scholar] [CrossRef]
- Petek, M.; Mikoš, M.; Bezak, N. Rainfall erosivity in Slovenia: Sensitivity estimation and trend detection. Environ. Res. 2018, 167, 528–535. [Google Scholar] [CrossRef] [PubMed]
- Burn, D.H.; Elnur, M.A.H. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Douglas, E.M.; Vogel, R.M.; Kroll, C.N. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, S. Trend test and change-point detection for the annual discharge series of the Yangtze River at the Yichang hydrological station. Hydrol. Sci. J. 2004, 49, 99–112. [Google Scholar] [CrossRef]
- Bezak, N.; Brilly, M.; Šraj, M. Flood frequency analyses, statistical trends and seasonality analyses of discharge data: A case study of the Litija station on the Sava River. J. Flood Risk Manag. 2016, 9, 154–168. [Google Scholar] [CrossRef]
- Kendall, M.G. Multivariate Analysis; Griffin: London, UK, 1975. [Google Scholar]
- Helsel, D.R.; Frans, L.M. The regional Kendall test for trend. Environ. Sci. Technol. 2006, 40, 4066–4073. [Google Scholar] [CrossRef]
- Marchetto, A. Package Rkt. Available online: http://cran.r-project.org/web/packages/rkt/rkt.pdf (accessed on 30 August 2019).
- Maidment, D.R. Handbook of Hydrology; McGraw-Hill Education: New York, NY, USA, 1993. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Lmomco Package: Program, R. Available online: https://cran.r-project.org/web/packages/lmomco/lmomco.pdf (accessed on 30 August 2019).
- Meylan, P.; Favre, A.C.; Musy, A. Predictive Hydrology: A Frequency Analysis Approach; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Fagerland, M.W.; Sandvik, L. The Wilcoxon–Mann–Whitney test under scrutiny. Stat. Med. 2009, 28, 1487–1497. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Bonacci, O.; Roje-Bonacci, T. Analyses of the Zagreb Grič observatory air temperatures indices for the period 1881 to 2017. Acta Hydrotech. 2018, 31, 67–85. [Google Scholar] [CrossRef]
- Kitoh, A.; Endo, H. Changes in precipitation extremes projected by a 20-km mesh global atmospheric model. Weather Clim. Extrem. 2016, 11, 41–52. [Google Scholar] [CrossRef]
- Bezak, N.; Brilly, M.; Šraj, M. Comparison between the peaks-over-threshold method and the annual maximum method for flood frequency analysis. Hydrol. Sci. J. 2014, 59, 959–977. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.P.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing climate shifts timing of European floods. Science 2017, 357, 11. [Google Scholar] [CrossRef] [PubMed]
| Station | Latitude; Longitude | Altitude (m a.s.l.) | Mean Annual Precipitation (mm) |
|---|---|---|---|
| Rateče | 46°29′51″; 13°43′3″ | 864 | 1475 |
| Postojna | 45°45′59″; 14°11′51″ | 533 | 1588 |
| Šmarata | 45°41′20″; 14°28′23″ | 599 | 1421 |
| Ljubljana | 46°3′57″; 14°31′2″ | 299 | 1368 |
| Šmartno pri SG | 46°29′24″; 15°6′58″ | 445 | 1139 |
| Črnomelj | 45°33′37″; 15°9′3″ | 157 | 1257 |
| Novo mesto | 45°48′7″; 15°10′56″ | 220 | 1148 |
| Celje | 46°14′41″; 15°15′9″ | 244 | 1130 |
| Slovenske Konjice | 46°20′37″; 15°25′37″ | 330 | 1069 |
| Murska Sobota | 46°39′9″; 16°11′46″ | 188 | 806 |
| Station | 5 min | 30 min | 60 min | 360 min | 720 min |
|---|---|---|---|---|---|
| Rateče | 0.008 | 0.064 | 0.058 | 0.107 | 0.190 |
| Postojna | −0.126 | −0.132 | −0.434 | −0.044 | −0.028 |
| Šmarata | −0.0735 | 0.040 | 0.044 | 0.005 | 0.086 |
| Ljubljana | −0.009 | 0.048 | 0.022 | 0.074 | 0.065 |
| Šmartno pri SG | −0.020 | 0.072 | 0.082 | 0.098 | 0.052 |
| Črnomelj | −0.147 | −0.075 | −0.088 | −0.124 | −0.086 |
| Novo mesto | −0.247 * | −0.168 | −0.221 * | −0.085 | 0.036 |
| Celje | 0.106 | 0.252 ** | 0.254 ** | 0.180 | 0.059 |
| Slovenske Konjice | −0.325 | −0.103 | −0.086 | 0.015 | −0.012 |
| Murska Sobota | 0.012 | 0.132 | 0.172 | 0.290 ** | 0.292 ** |
| Station | 5 min | 30 min | 60 min | 360 min | 720 min |
|---|---|---|---|---|---|
| Rateče | −0.047 | 0.051 | 0.026 | 0.047 | 0.146 ** |
| Postojna | −0.227 * | −0.119 * | −0.121 * | 0.064 | 0.106 ** |
| Šmarata | −0.006 | 0.090 | 0.075 | 0.094 ** | 0.139 ** |
| Ljubljana | −0.096 * | 0.021 | 0.015 | −0.001 | 0.044 |
| Šmartno pri SG | −0.058 | 0.026 | 0.020 | 0.087 | 0.081 |
| Črnomelj | −0.025 | −0.045 | −0.037 | −0.031 | 0.035 |
| Novo mesto | −0.192 * | −0.078 * | −0.104 * | −0.033 | 0.030 |
| Celje | 0.071 | 0.141 ** | 0.154 ** | 0.143 ** | 0.109 ** |
| Slovenske Konjice | −0.212 * | −0.113 * | −0.085 | −0.022 | −0.042 |
| Murska Sobota | 0.027 | 0.164 ** | 0.147 ** | 0.194 ** | 0.263 ** |
| AM5 (n = 220 Events) | AM (n = 44 Events) | |||||
|---|---|---|---|---|---|---|
| Rainfall Duration | 25% | 50% | 75% | 25% | 50% | 75% |
| 5 min | −11.4 | −8.1 | −7.1 | −11.7 | −5.3 | −6.3 |
| 30 min | −6.9 | −4.7 | −4.5 | −7.0 | 0.6 | 0.9 |
| 60 min | −0.6 | −3.1 | −2.5 | −9.1 | −0.3 | 12.7 |
| 360 min | 6.4 | 14.2 | 21.8 | −13.6 | 3.3 | 8.9 |
| 720 min | −6.4 | 14.7 | 40.4 | −9.6 | 2.9 | 4.6 |
| AM5 (n = 220 Events) | AM (n = 44 Events) | |||||
|---|---|---|---|---|---|---|
| Rainfall Duration | 25% | 50% | 75% | 25% | 50% | 75% |
| 5 min | 182 | 209 | 236 | 186 | 206 | 231 |
| 30 min | 180 | 211 | 240 | 186 | 206 | 230 |
| 60 min | 180 | 214 | 246 | 191 | 214 | 231 |
| 360 min | 186 | 226 | 255 | 214 | 233 | 257 |
| 720 min | 195 | 226 | 256 | 213 | 238 | 264 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bezak, N.; Mikoš, M. Investigation of Trends, Temporal Changes in Intensity-Duration-Frequency (IDF) Curves and Extreme Rainfall Events Clustering at Regional Scale Using 5 min Rainfall Data. Water 2019, 11, 2167. https://doi.org/10.3390/w11102167
Bezak N, Mikoš M. Investigation of Trends, Temporal Changes in Intensity-Duration-Frequency (IDF) Curves and Extreme Rainfall Events Clustering at Regional Scale Using 5 min Rainfall Data. Water. 2019; 11(10):2167. https://doi.org/10.3390/w11102167
Chicago/Turabian StyleBezak, Nejc, and Matjaž Mikoš. 2019. "Investigation of Trends, Temporal Changes in Intensity-Duration-Frequency (IDF) Curves and Extreme Rainfall Events Clustering at Regional Scale Using 5 min Rainfall Data" Water 11, no. 10: 2167. https://doi.org/10.3390/w11102167
APA StyleBezak, N., & Mikoš, M. (2019). Investigation of Trends, Temporal Changes in Intensity-Duration-Frequency (IDF) Curves and Extreme Rainfall Events Clustering at Regional Scale Using 5 min Rainfall Data. Water, 11(10), 2167. https://doi.org/10.3390/w11102167






