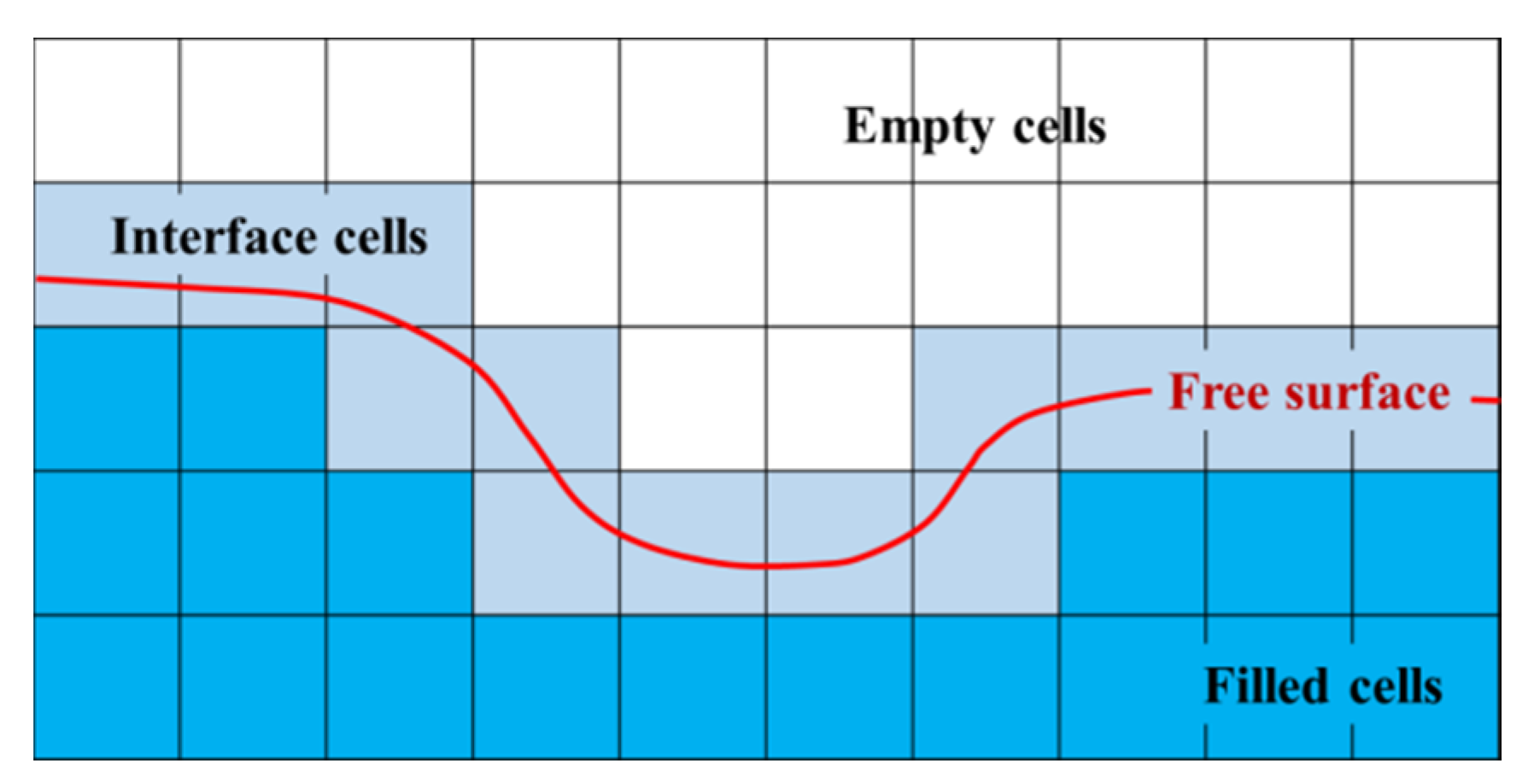
1. Introduction
Water fluctuation phenomena such as waves and tiding exist widely in nature. Water wave dynamics on large scales is one of the research focuses of hydraulic projects, such as the surges generated by landslides [
1], water-level fluctuations in surge chambers [
2], and flood discharge of spillways [
3]. The above phenomena are large-scale free-surface (LS-FS) flows with the following features: (1) the viscosity and density ratios of the two phases are large; (2) the movements of the interface between the two phases are dominated by the phase with larger density and viscosity; (3) the capillary effects on flows can be neglected. These hydraulic problems are quite complex, and they are vital to the safe operation and stability of the hydraulic projects. Therefore, an intensive study on effective and efficient simulation of LS-FS flows is necessary.
At present, the general methods for studying LS-FS flows are mainly two-dimensional (2-D) numerical models, especially shallow water equations for simulating planar flows. 2-D numerical simulations have been one of the most important tools to analyze LS-FS flows, such as flows in rivers, reservoirs, or ocean [
4,
5]. However, the above 2-D numerical models cannot analyze vertical velocity variation, and they cannot be used to simulate the breaking down, merging, and expanding of water surface, which greatly limits the applications of 2-D models in the field of hydraulic projects. Therefore, the free surface flows with obvious three-dimensional (3-D) features should be simulated by 3-D methods. Traditionally, 3-D numerical methods developed for free-surface flows are mainly based on gas–liquid two-phase flow models [
6], interface tracking models (common approaches include Volume of fluid (VOF) [
7], level set [
8], phase field [
9]), and interface capturing models (including moving mesh approach [
10], marker and cell (MAC) method [
11], and particle-in-cell approach [
12]). However, simulating LS-FS flows, particularly those in the area of hydraulic projects, requires a remarkable amount of computing resources, while it is challenging to maintain the stability and accuracy of the simulation.
The single phase free surface lattice Boltzmann (SPFS-LB) model was originally proposed by Thürey in 2003 [
13]. The SPFS-LB model is more suitable to simulate 3-D LS-FS flows in comparison with traditional 3-D numerical models in which both gas and fluid are simulated to properly reflect the interface boundary conditions [
13,
14]. The SPFS-LB model only simulates the water flows, without consideration of air influence, so the consumption of computation resources is low. In addition, this model is on the basis of lattice Boltzmann (LB) method, which has the advantages of a simple algorithm, good parallelism, easily programing, and simple implementation of boundary conditions [
15].
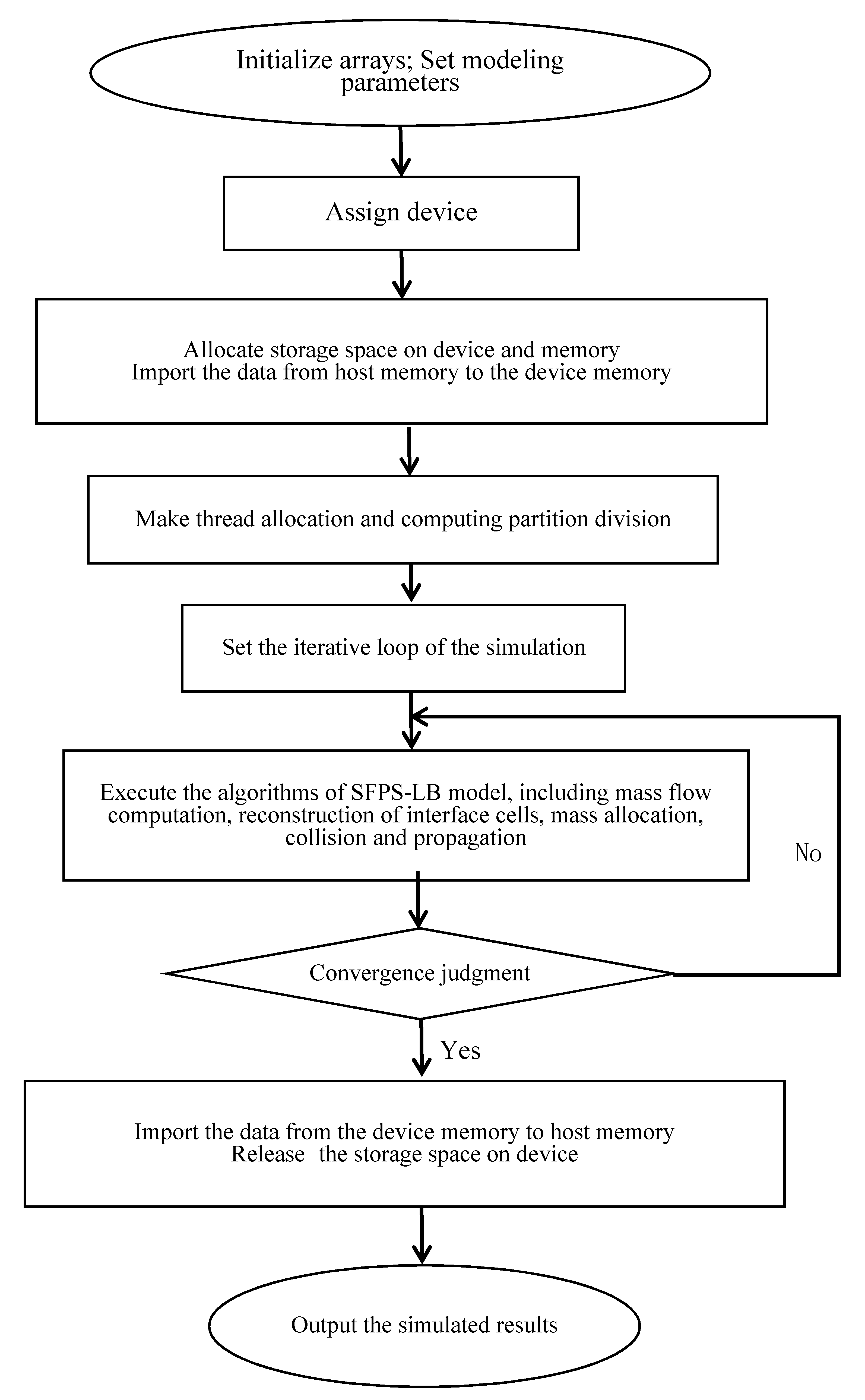
The design of graphic processing units (GPUs) consists of a high-speed super-long pipeline and massively parallel processing in hardware, and its frame is naturally consistent with features of the LB algorithm. At present, the accelerated computing research of GPU-based LB methods has made certain progress. In reference [
16], the implementation of the LB method for shallow water flows on a GPU unit can realize billions of lattice updates per second, which is hundreds of times higher than that on a single CPU core. However, there are rare research reports on simulating large-scale 3-D wave movements by the SPFS-LB model in hydraulic projects using GPUs; therefore, this paper investigates this field.
In this paper, the SPFS-LB model is coupled with the large-eddy simulation (LES) method for analyzing the LS-FS flows, and the method is implemented on a GPU. Firstly, the coupling model is used to simulate sudden whole dam-break flow, partial dam-break flow, and dam-break flow over a triangular step. To validate the accuracy of the proposed model in simulating large-scale free surface flows, the simulated water surface profiles, velocity distribution, and the process of waves are compared with the reference data. The SPFS-LB model is applied to analyze the flood discharge of an arch dam for demonstrating its capability for simulating practical flow problems. In the
Appendix A, the algorithm is implemented on a GPU to realize efficient computation. Eventually, our work shows that this new method can simulate LS-FS flows in actual project problems accurately and efficiently.
3. Testing and Discussion
In this section, the SPFS-LB model is used to simulate whole and partial dam-break waves. Through comparative analysis between the simulated results and the reference data, it turns out that the present model can simulate the large-scale free surface effectively. The 3D SPFS-LB model can reflect more abundant hydrodynamic information compared with the traditional 1D or 2D methods. If not otherwise stated, the acceleration of gravity, water density, and viscosity are set as , , and , respectively.
3.1. Sudden Whole Dam-Break Flow
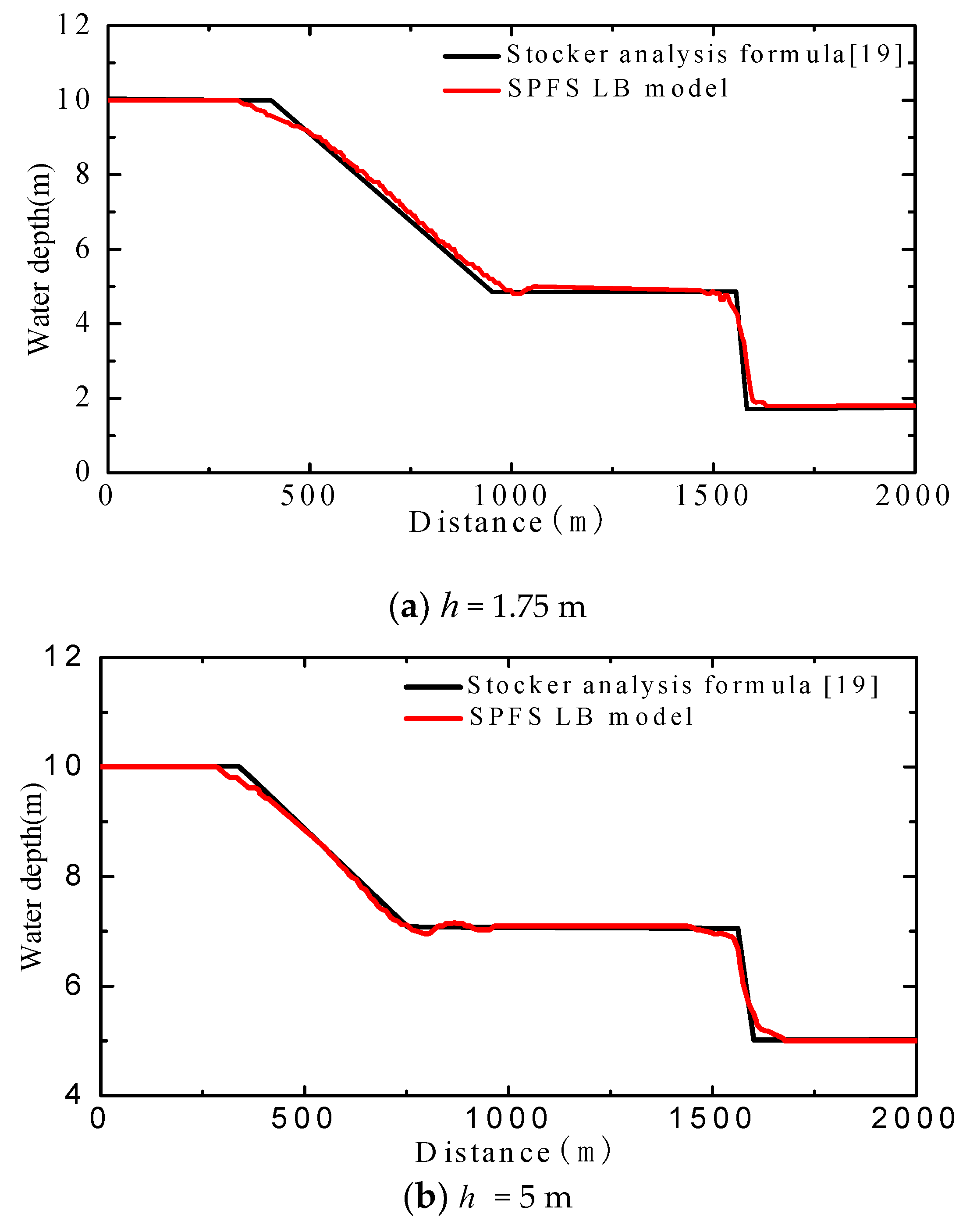
The sudden whole dam-break flow is a classic test case with an analytical solution, and it is simulated to make a comparison between the numerical results and the analytical results. It is assumed that a horizontal river channel is 2000 m long with equivalent width and a perfectly smooth bottom. The dam is located in the middle of the channel, and the water depth of upstream reservoir is
H = 10 m. The water surface profile of the dam-break wave is simulated with the downstream water depth of
h = 5 m and 1.75 m, and compared with the analytical values [
19]. The simulations are conducted on a uniform lattice 10,000 × 50 (Δ
x = 0.2 m). The left side, right side, and bottom of the computational domain are treated as nonslip wall boundary conditions.
Figure 2 indicates that the simulated water surface profile based on the SPFS-LB model agrees well with the computed results obtained from the analysis formula of reference (60 s after dam failure) [
19], especially in the horizontal section of approximately stable zone and the descending section of the single fluctuation zone. The comparison reveals that the SPFS-LB model can provide good capture capability for dam-break waves, and can compute the propagation velocity and evolution state of dam-break waves accurately. As for the sudden change of wave surfaces (for instance, comparison of the surfaces at the distance of 385 m, 965 m, and 1555 m in
Figure 3a), the simulated result is slightly different from the reference, which means the present method is deficient in capturing shock waves. In the field of hydraulic projects, the purposes of studies are to determine the height and the velocity of surges instead of shock waves, so the accurate simulation of shock waves is not so important.
3.2. Partial Dam-Break Flow
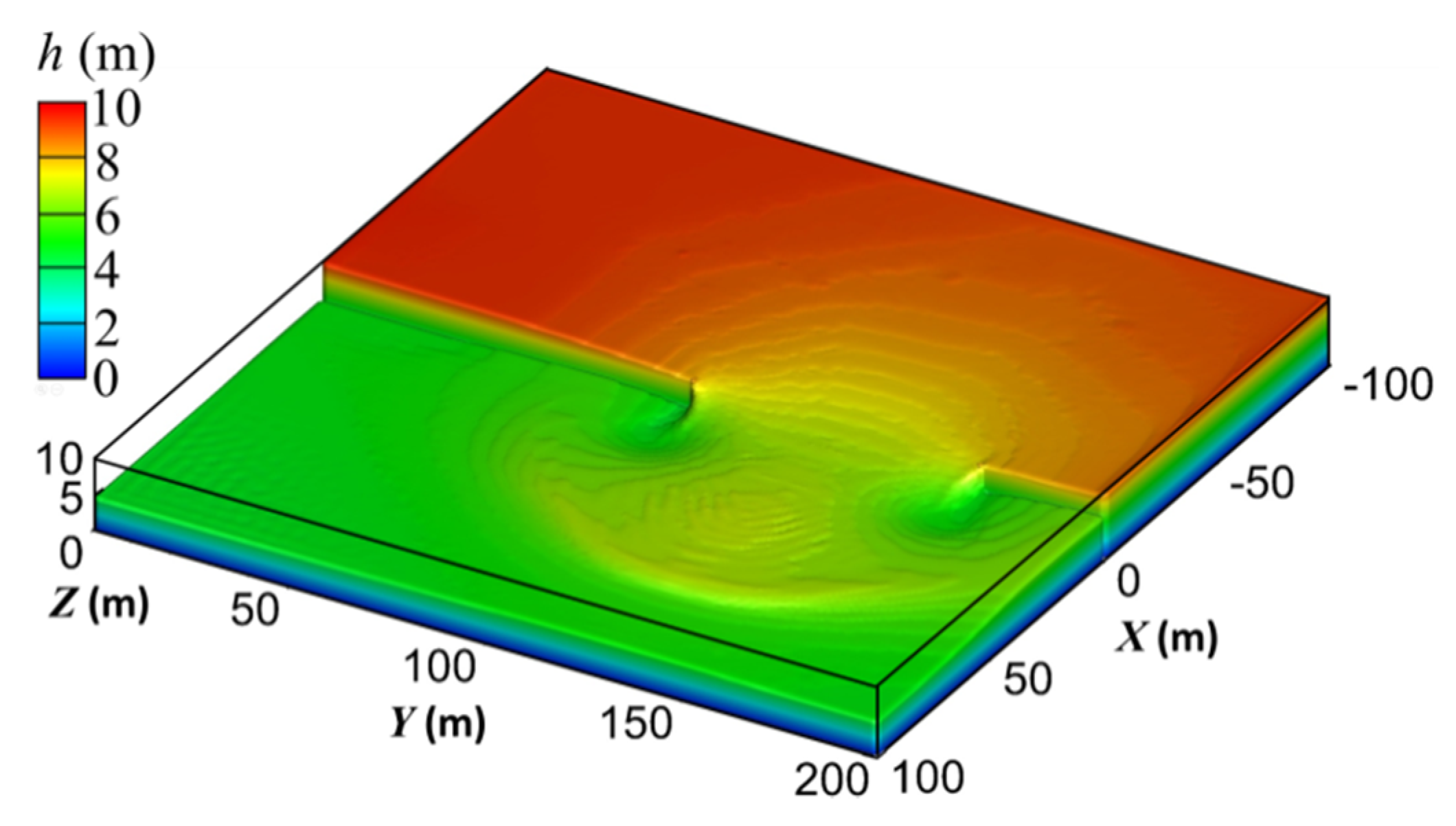
It is assumed that the upstream reservoir and downstream reservoir are both flat channels with a width of 200 m and a length of 100 m. The dam site is in the middle of the channel (
X = 0 m), and the gap is located 95–170 m from the dam body (
Y = 95–170 m, see
Figure 4). At the beginning of the simulation, the upstream water depth is
H = 10 m and downstream depth is
h = 5 m.
In this case, a 384 × 384 × 19 uniform lattice (Δ
x = 0.52 m) is conducted to the simulation. All the boundaries of the computational domain, including the dam body, are set as nonslip walls. The thickness of the dam body is double the lattice length (Δ
x). The water surface
t = 10.1 s after dam failure is shown in
Figure 3, and the velocity distribution and streamline are shown in
Figure 4 at time
t = 1.5 s, 6 s and 12 s.
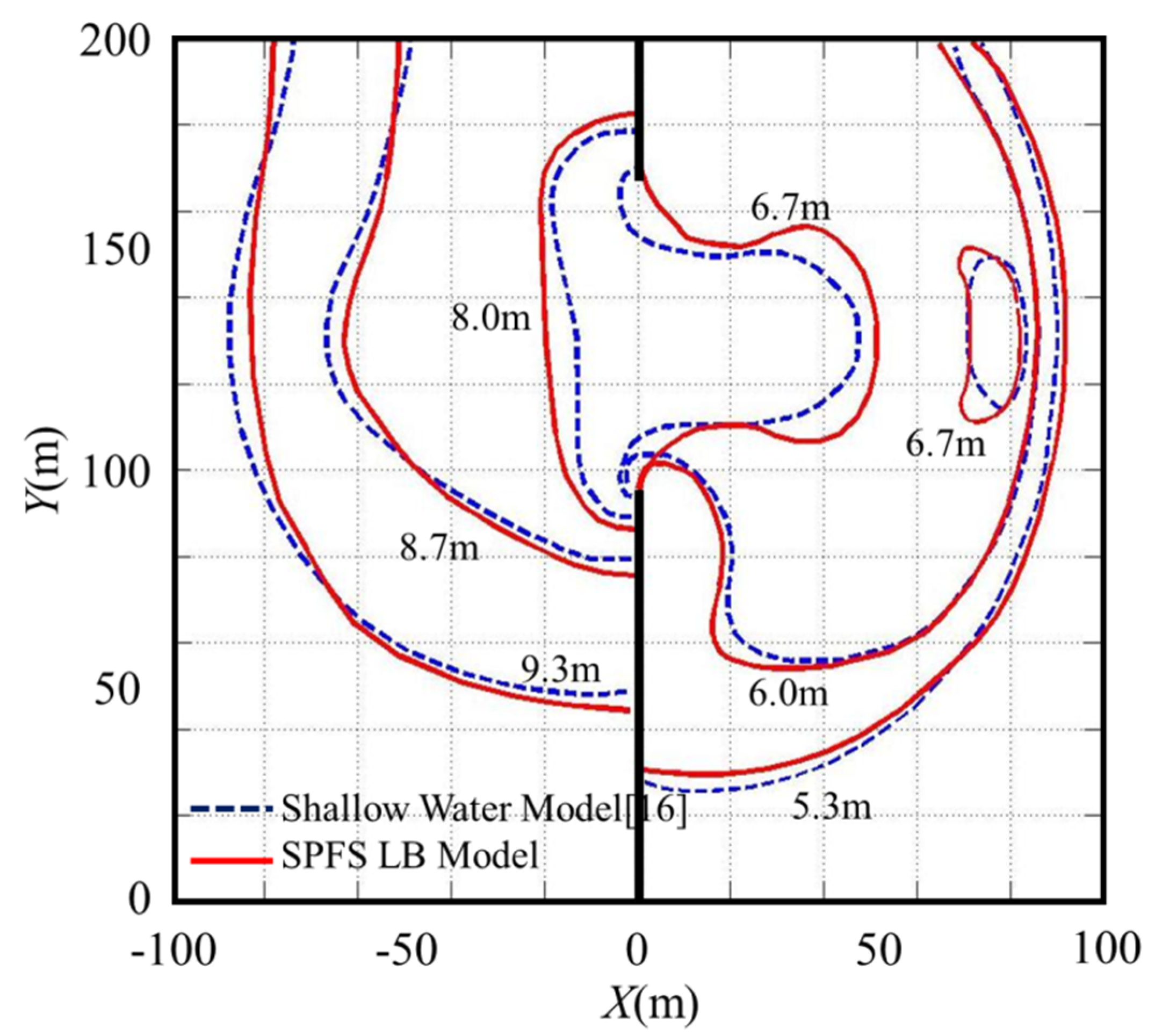
When the partial dam break appears, there is a negative wave propagating to the upstream channel and a positive wave propagating to the downstream channel, and the wave propels in an arc shape. Upstream of the dam, the water around the dam flows towards the gap, and the water surface forms a “funnel” shape. The “funnel” shape enlarges and moves upstream as time goes by. At the downstream of the dam, the positive wave generates backflows around the dam and forms vertical-axis vortices on both sides of the dam gap. The above simulated results are consistent with the existing knowledge on partial dam-break flows [
16,
20]. The computed results of the SPFS-LB model and shallow water model are compared in
Figure 5. It can be seen from
Figure 5 that the wavefront position and wave profile of SPFS-LB model are approximately the same as the reference [
16], which means that the model proposed in this paper can accurately capture the generation and development process of partial dam-break flow.
Besides of the horizontal wave profile, the SPFS-LB model can also be adopted to analyze the vertical flow structure of dam-break waves, as shown in
Figure 4. Under the shearing caused by the falling water from upstream, a horizontal-axis vortex parallel to the dam body forms at the bottom of channel at the initial stage of the dam-break flow (see
Figure 4a), and this vortex disappears until the stable and uniform flow state forms at the bottom of channel (see
Figure 4b). After a few seconds, as the propagation and reflection of the positive wave, two vertical-axis vortices successively form on both sides of the dam gap (see
Figure 4c).
3.3. Simulation of Dam-Break Flow over a Triangular Step
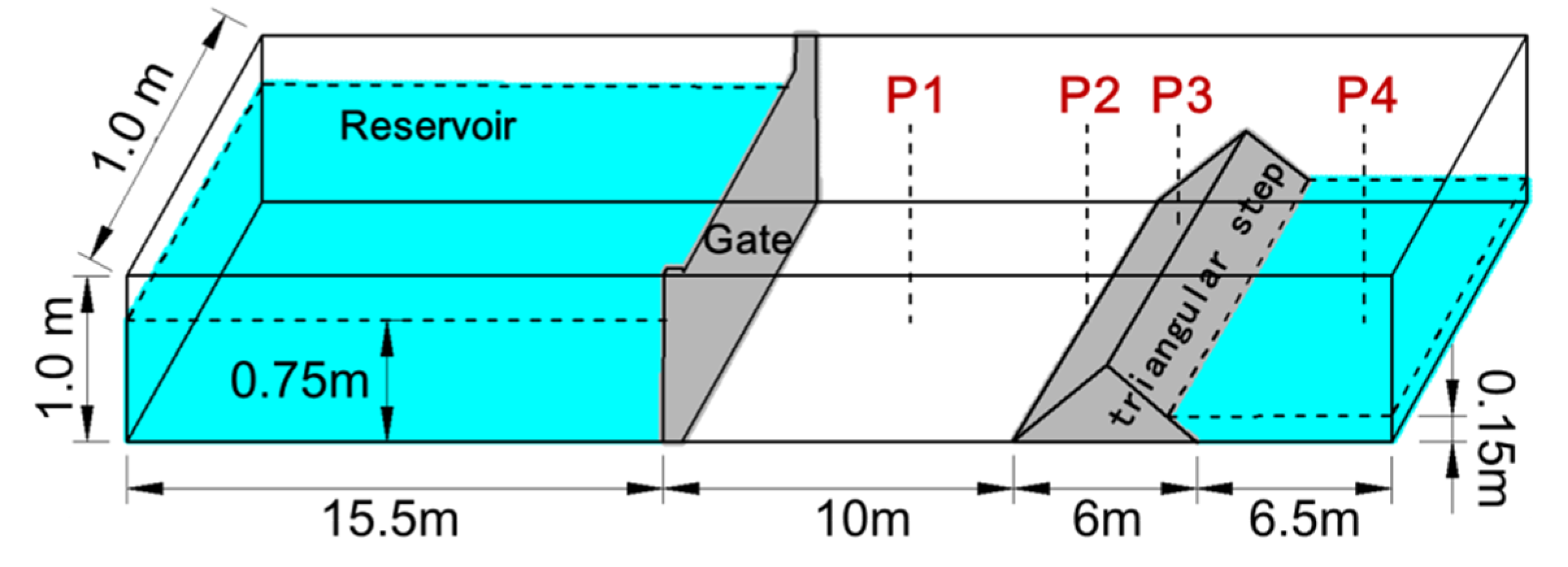
The experimental data of dam-break flow over a triangular step, tested by the European Union CADAM (the European Concerted Action on Dam-break Modeling) project [
21], were used to validate the SPFS-LB model. This case includes various free-surface flow phenomena including overtopping flows, partial reflections, hydraulic jumps, hydraulic drops, and multiple wave interactions. As shown in
Figure 6, the total length of the channel is 38 m, and the dam is 15.5 m away from the upstream boundary. A triangular step, with a length of 6.0 m and a height of 0.4 m, is placed 10 m downstream of the dam. The water depth at upstream of the dam is 0.75 m, and the water depth at downstream of the triangular step is 0.15 m. Four points to observe the evolutions of water depth are arranged along the central axis of the channel, and the distance away from the upstream dam is 4 m, 10 m, 13 m, and 20 m, respectively, which is the same as the experimental work in reference [
21]. The simulation is performed on a 2304 × 61 × 61 uniform lattice (Δ
x = 0.016 m, number of lattice nodes: 8.57 million), and all boundaries in the model are set as nonslip walls.
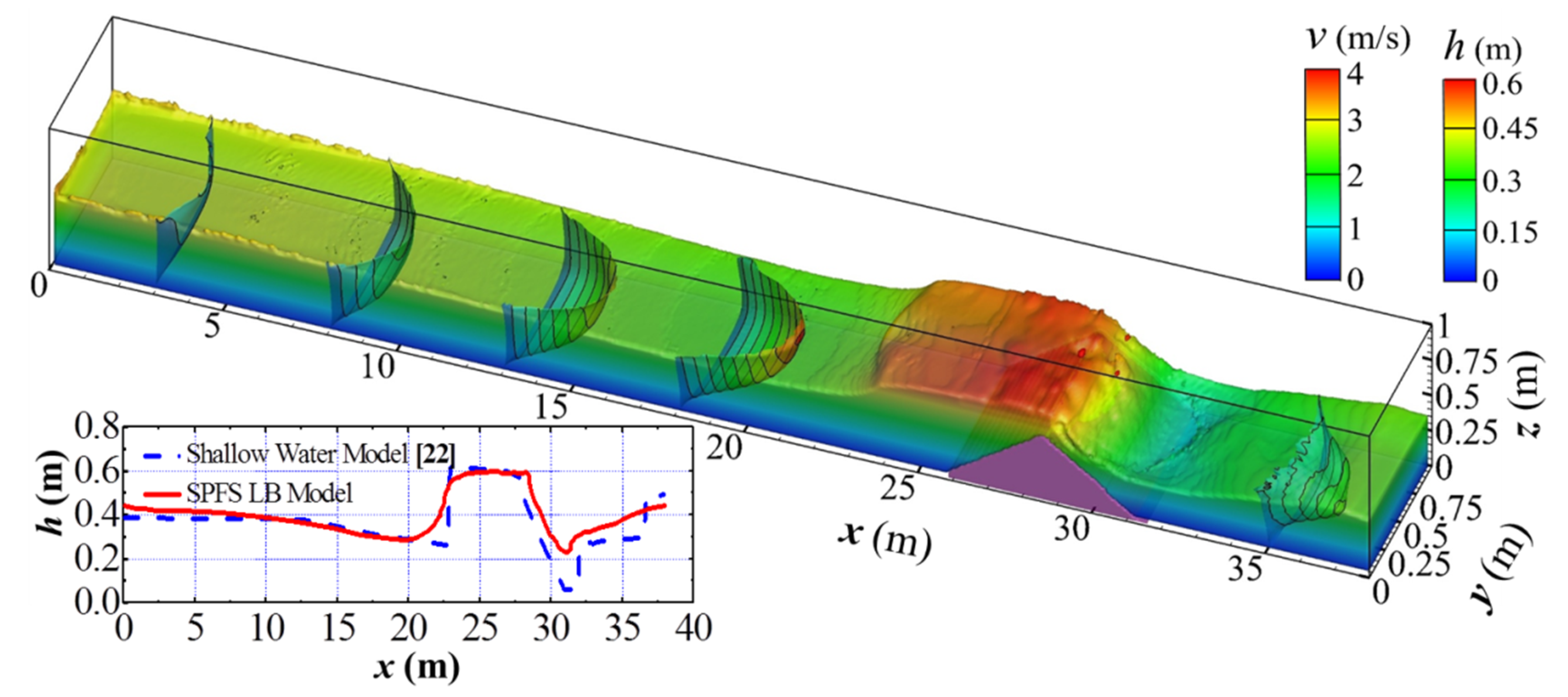
Figure 7 shows the water surface and flow field of the simulated dam break flow at
t = 9.7 s, and the water surface is compared with the results obtained by shallow water method. See
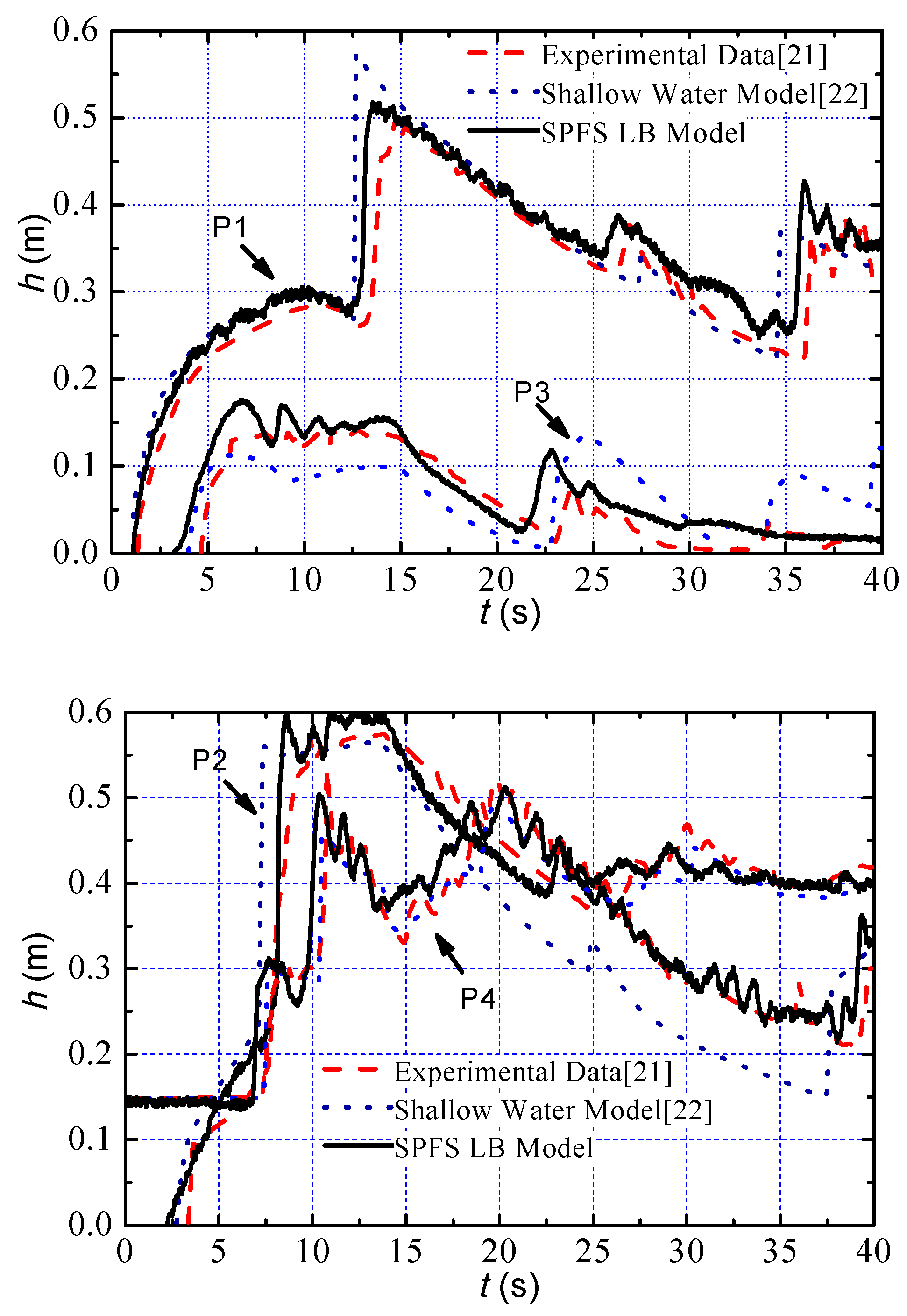
Figure 8 for comparison of the evolutions of water depth at four observation points between the present study and the references.
It can be seen from
Figure 8 that the waves reach observing point P1 at time
t = 1.2 s. During the evolution of dam-break waves, the velocity profile of flows forms a paraboloid shape. The dam-break waves reach P2 at
t = 2.4 s and begin to climb the slope, and partially reflected waves propagate back to P1, which causes a disturbance of water surface at P1 (
t = 4.8 s). After
t = 4.1 s, the water flow rushes down quickly over the triangular step and forms rapid flow. The hydraulic jump appears at downstream of the step (
X = 32–35 m) at this moment. Then, the waves caused by the hydraulic jump reach P4 at
t = 7.1 s. The waves reflected from the triangular step or the right wall reaches P2, P4, and P1 at 7.9 s, 9.8 s, and 13.1 s successively, which makes the water depth abruptly go up to 0.60 m, 0.48 m, and 0.52 m. After
t = 20.0 s, the water depths at the four observation points decrease with some fluctuations because the downstream boundary of the model is closed and oscillating flows appear in the channel.
In the present simulation, the fluctuated water depth at the observing points and the instantaneous water surface of dam-break wave at
t = 9.7 s agree well with the experimental data [
21] and the simulated result [
22] respectively, which means the SPFS-LB model can analyze the fluctuations of the water surface induced by the progressive and reflected dam-break waves well. As for the histories of the water depth at the observing points during the evolution of dam-break waves, the simulated result is obviously superior to that of reference [
22]. The reason is that the 2D shallow equation cannot simulate the vertical water flows effectively.
3.4. Simulation of Flood Discharge of an Arch Dam
3.4.1. Analysis of Flow Patterns
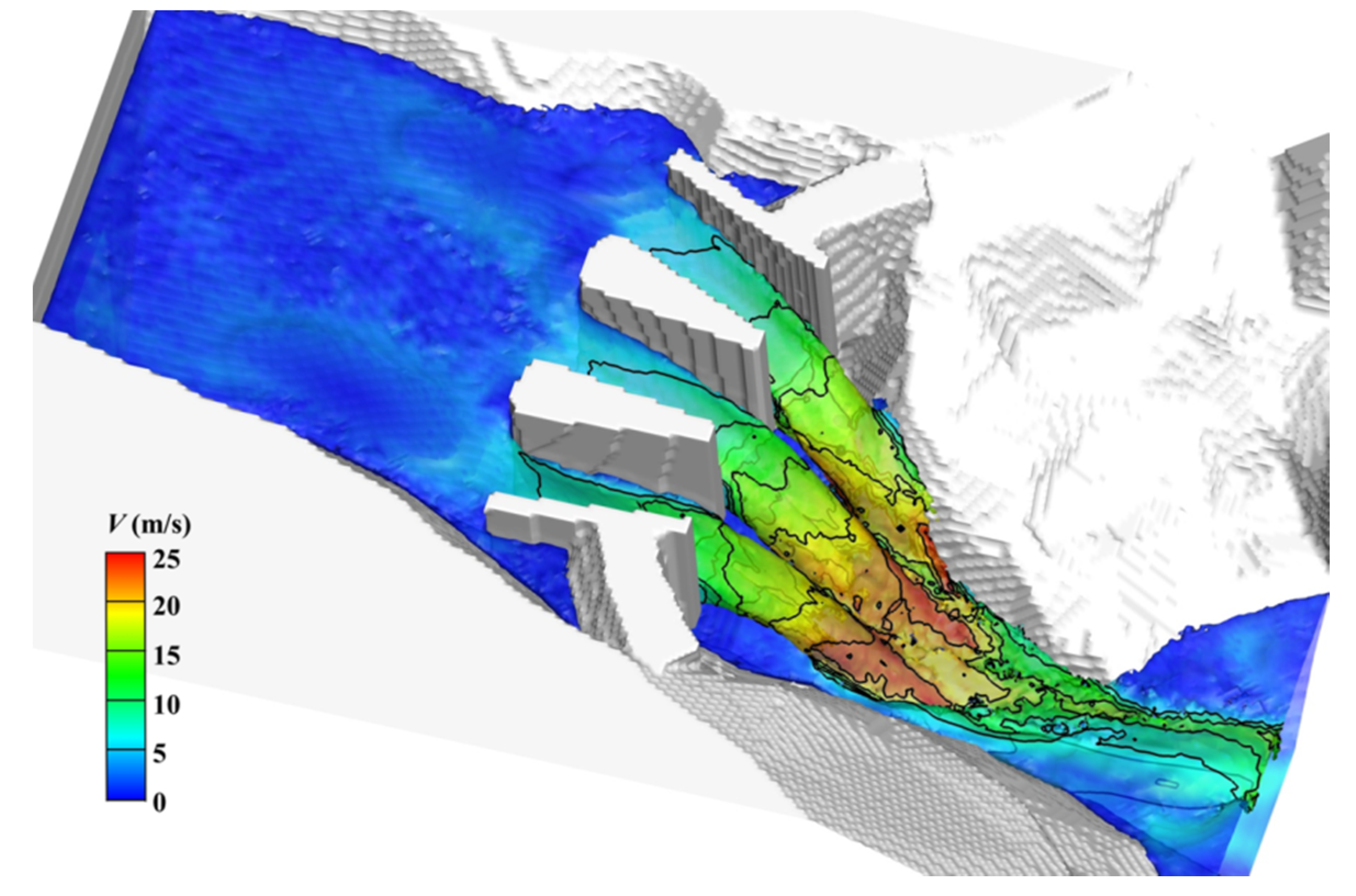
At last, the flood discharge of an arch dam is simulated. The outlet structures of the arc dam are three surface holes (10 m wide, 14.5 m high) on the dam crest. The bottom of the surface hole is made up of a practical weir (WES shape), of which the top and tail elevation are 442 m and 438 m, respectively. Among the surface holes, there are two central piers with variable width (upstream: 6.53 m, downstream: 2 m). A 384 × 512 × 192 uniform lattice is implemented for this computation. The present simulation analyzes flows within the spatial scale of 100 m × 133 m × 50 m (Δ
x = 0.2 6m, lattice node: 37.75 million), as seen in
Figure 9. In the computational domain, the upstream boundary is set as a fixed water level inflow boundary condition, while the downstream boundary is set as a zero-gradient outflow boundary condition (for details, see reference [
23]). Other boundaries, such as arc dam, riverbed, and mountains, are set as nonslip wall boundary conditions. See
Figure 10 for the simulated surface velocity distribution, and
Figure 11 for the liquid volume fraction of the vertical section.
According to the simulated results, after flowing through the surface holes of an arc dam, the water from the upstream reservoir freely falls into the downstream river channel and forms a tongue-shaped jet flow. The speed of the flow increases continuously during falling due to gravity. The discharge capacity of the two side holes is lower than that of the center hole under the influence of the reservoir banks, and the water trough formed from the center hole is thicker and larger. The water discharged from the surface holes collides with the water at the downstream of the arc dam, and the maximum local velocity of flow reaches approximately 25 m/s. The water in the downstream river channel rolls over strongly due to the impact of discharged water, and the water surface fluctuates randomly. The velocity of the plunging flow drastically decreases during the process of collision and rollover. As shown in
Figure 10, the flow velocity of the mainstream reduces to 10 m/s 50 m downstream of the arc dam, which significantly relieves the scouring effect of the plunging flow. The flow phenomena indicates the good energy dissipation by the trajectory jet flows, and it can meet the project’s requirements for flood energy dissipation. This work has successfully simulated the impact, breaking down, and merging of high-speed flows, which reflects the strong 3-D features of flow structure during the flood discharge of surface holes.
The present work has simulated the flood discharge of the arc dam with upstream reservoir water levels of 445 m, 450 m and 455 m. See
Table 1 for comparison of the discharge coefficients between the simulated results and those obtained by the empirical formula in reference [
24]. Factors such as side shrinkage and upstream weir surface form are taken into consideration when the discharge coefficients are calculated by the empirical formula. It can be seen that the simulated discharge coefficient agrees well with the value of the empirical formula, with maximal relative error of 4.10%, which is sufficient for simulating engineering applications. This simulation shows that the SPFS-LB model can be used to simulate the 3-D large-scale free-surface flow problems in the field of hydraulic projects, so as to provide technological basis for the relevant engineering design.
3.4.2. Analysis of Lattice Sensitivity
To study the lattice sensitivity of the present scheme, the normalized parameters are fixed and the lattice of the simulation is refined gradually (192 × 256 × 96, 288 × 384 × 144 and 384 × 512 × 192 uniform lattices, respectively). The relative deviations for the discharge coefficients are shown in
Table 2 with the reservoir water level fixed at
H = 450 m.
It can be seen in
Table 2 that the relative deviations for the discharge coefficients basically keep constant with the refinement of lattice, which means the simulated results would not significantly change with the increasing number of grid. This suggests that the results in
Section 3.4 are obtained on a convergent grid.
4. Conclusions
The SPFS-LB model is coupled with the large-eddy simulation method in this paper, and the model successfully simulates several large-scale free surface flow problems in the field of hydraulic projects. Then, the simulations are implemented on GPU chips to improve the computational efficiency. The results indicate that the proposed method is efficient and accurate enough to study practical engineering flow problems.
Firstly, the conventional dam-break waves and dam-break flows over a triangular step are simulated. Good agreements between the simulated results and the reference data validate the accuracy of the present model in studying large-scale free surface flows. Then, as a first attempt at analyzing practical engineering flows, the flood discharge of an arch dam is simulated, and the discharge coefficient also agrees well with the empirical results. Finally, parallel computations of the present model based on GPU codes can make full use of the algorithm advantage of the LB method with low coupling degree, which improves the computing efficiency of the simulations by dozens of times.
In the future, fluid–structure interaction, thermal model, mass transfer, and other mathematical models will be added to the present method. The new coupling model will be implemented on GPU chips, so as to achieve accurate and efficient analysis of other engineering problems, such as landslide surge waves, thermal stratification, and pollution diffusion in large reservoirs.