An Operational Forecasting System for Flash Floods in Mountainous Areas in Taiwan
Abstract
1. Introduction
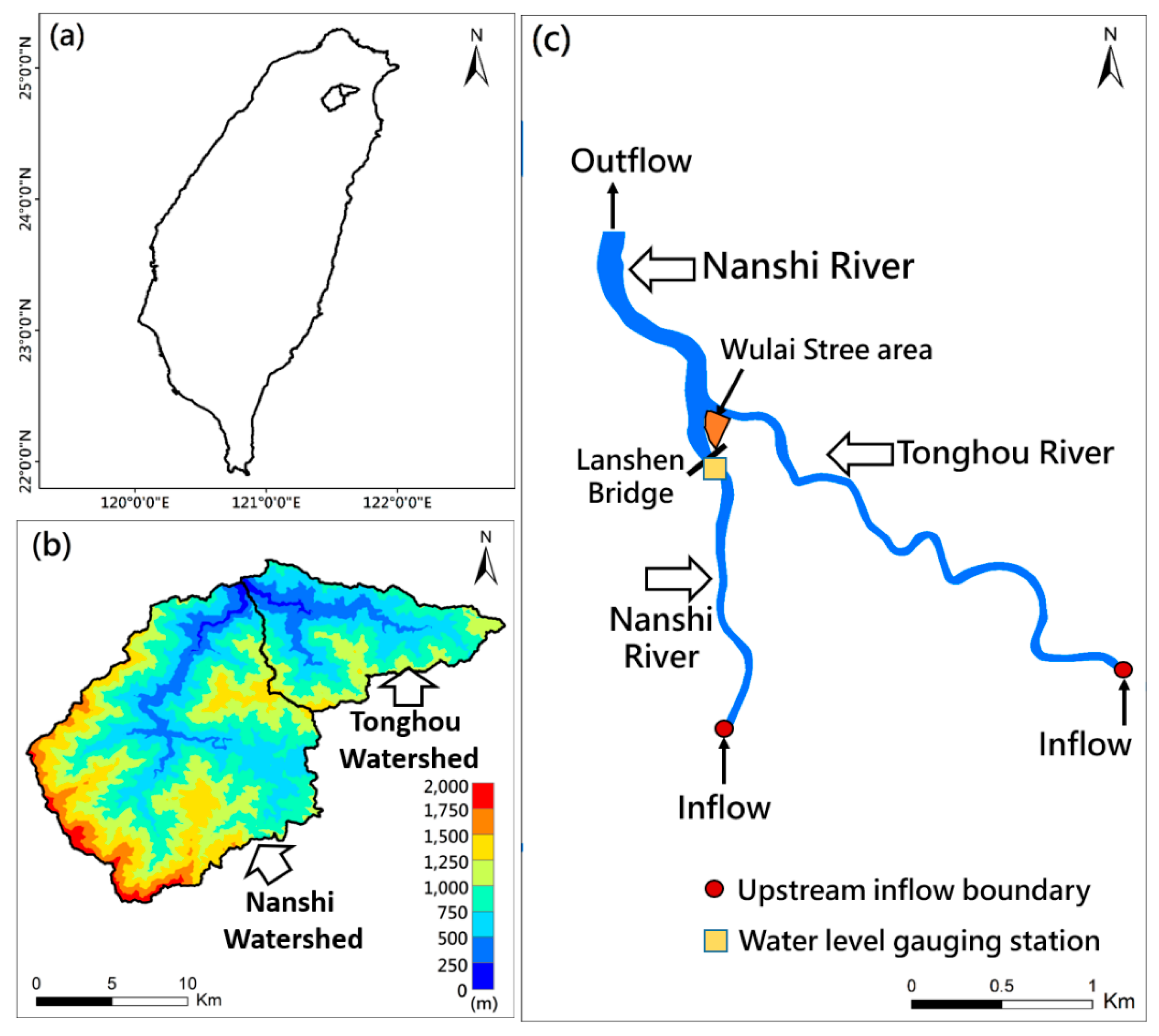
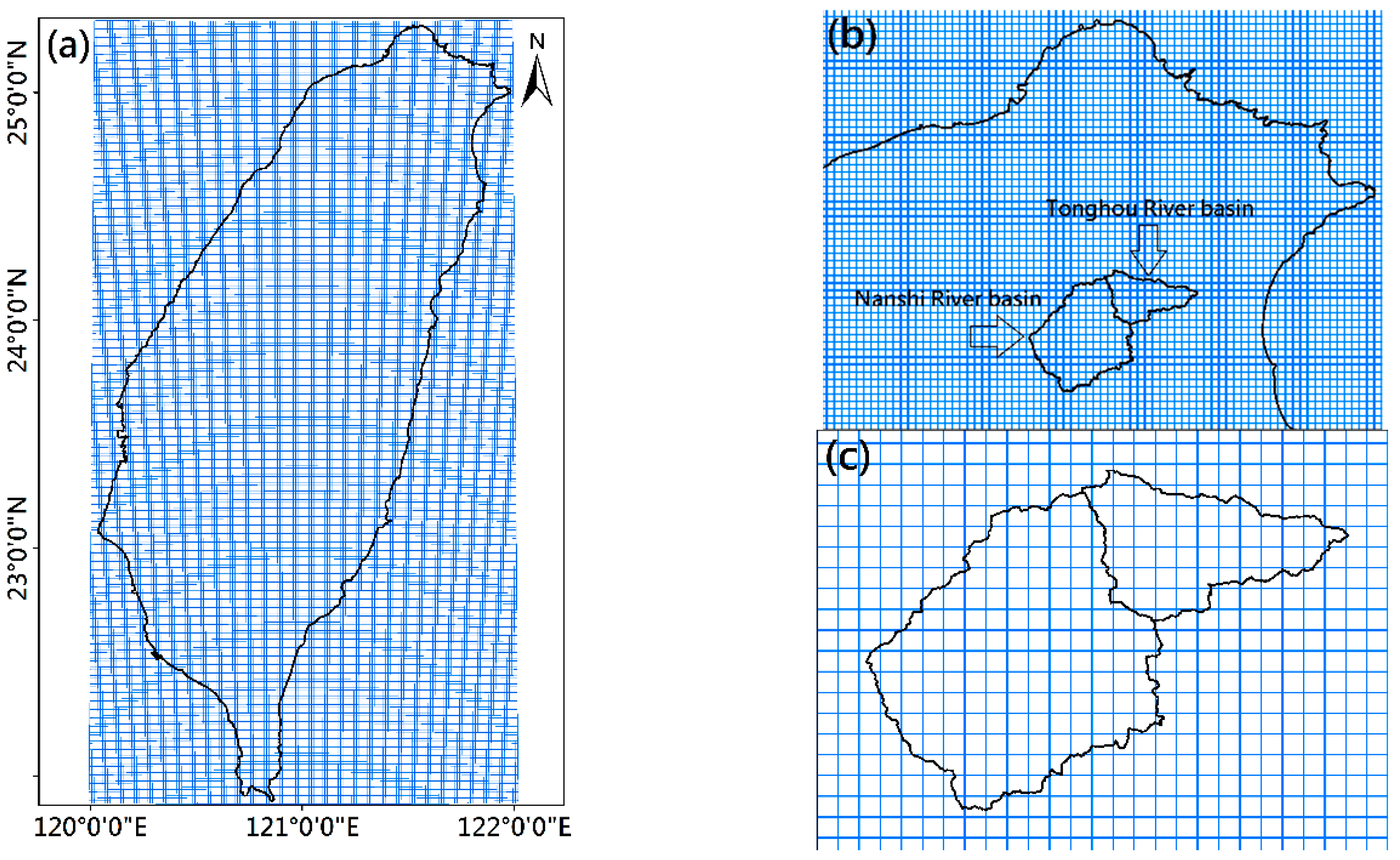
2. Materials and Methods
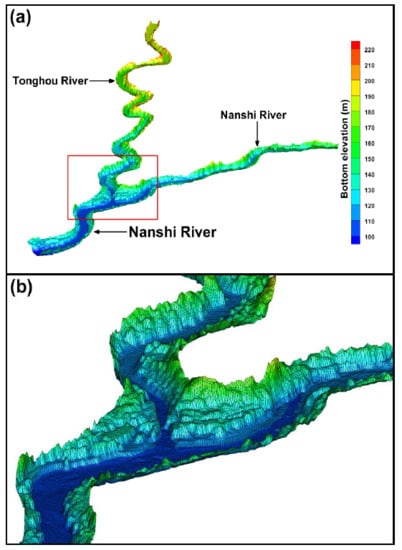
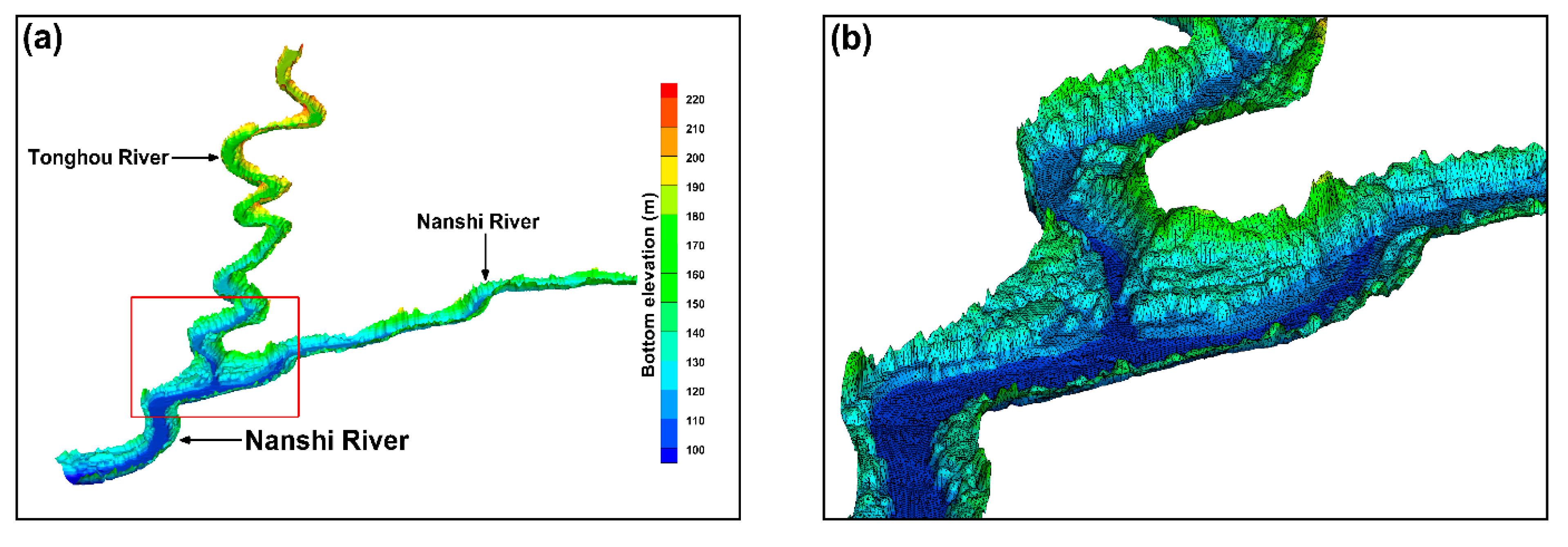
2.1. Airborne Light Detection and Ranging (LiDAR) Data
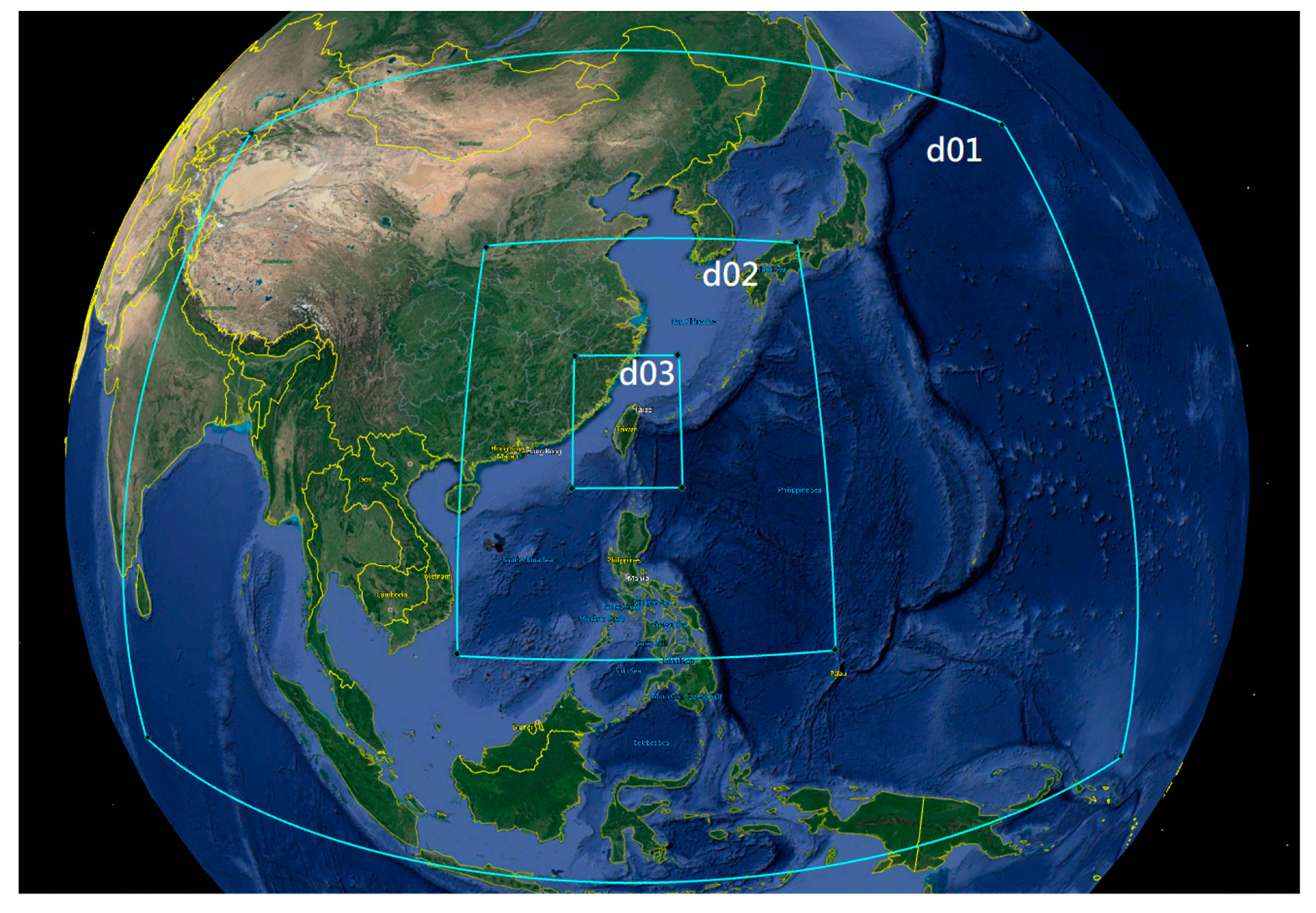
2.2. Atmospheric Model
2.3. Hydrological Model
2.4. Hydrodynamic Model
2.5. Configuration of the SCHISM (Semi-implicit Cross-scale Hydroscience Integrated System Model) Model
2.6. Gridded Rainfall Data
3. Results
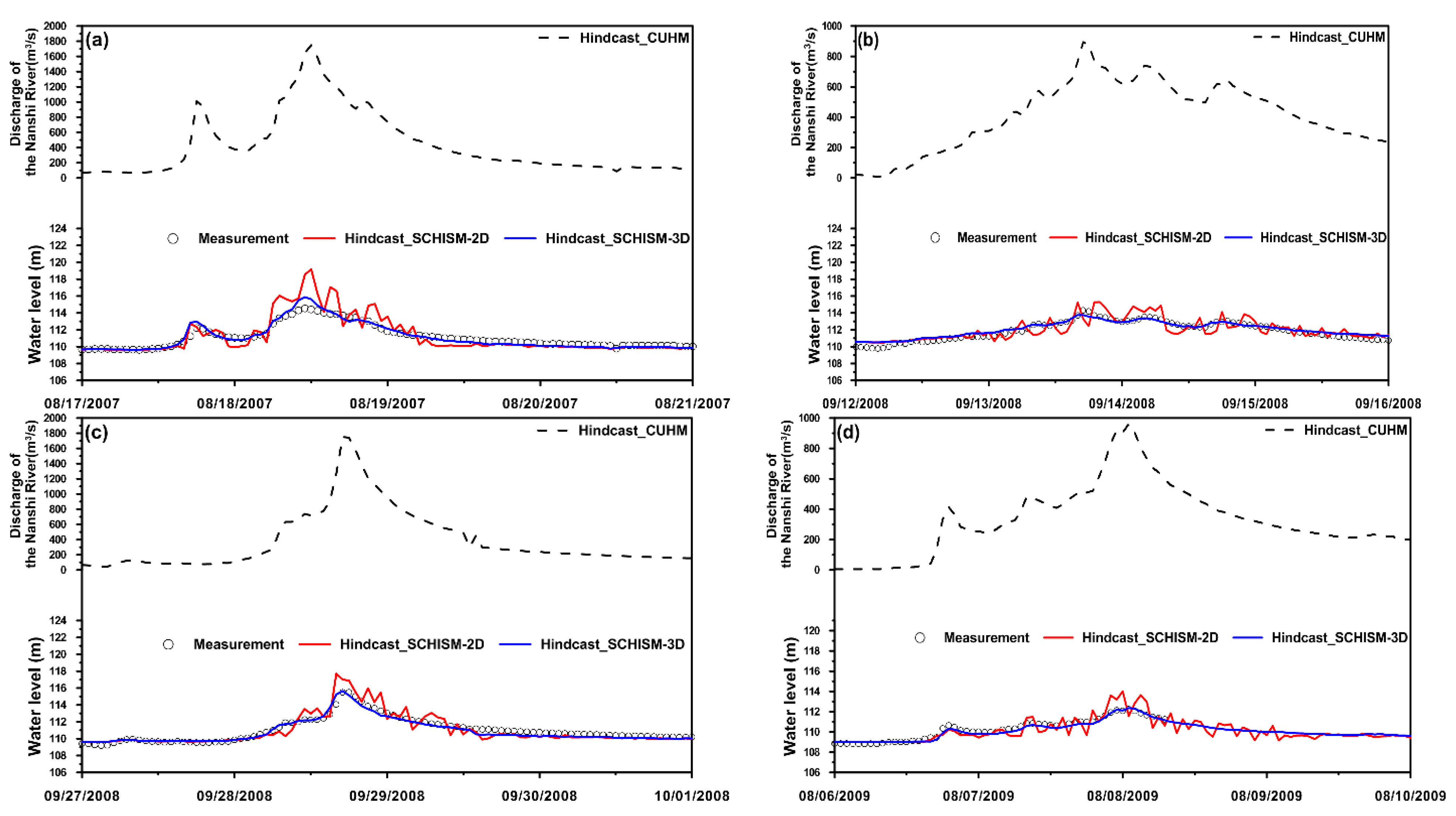
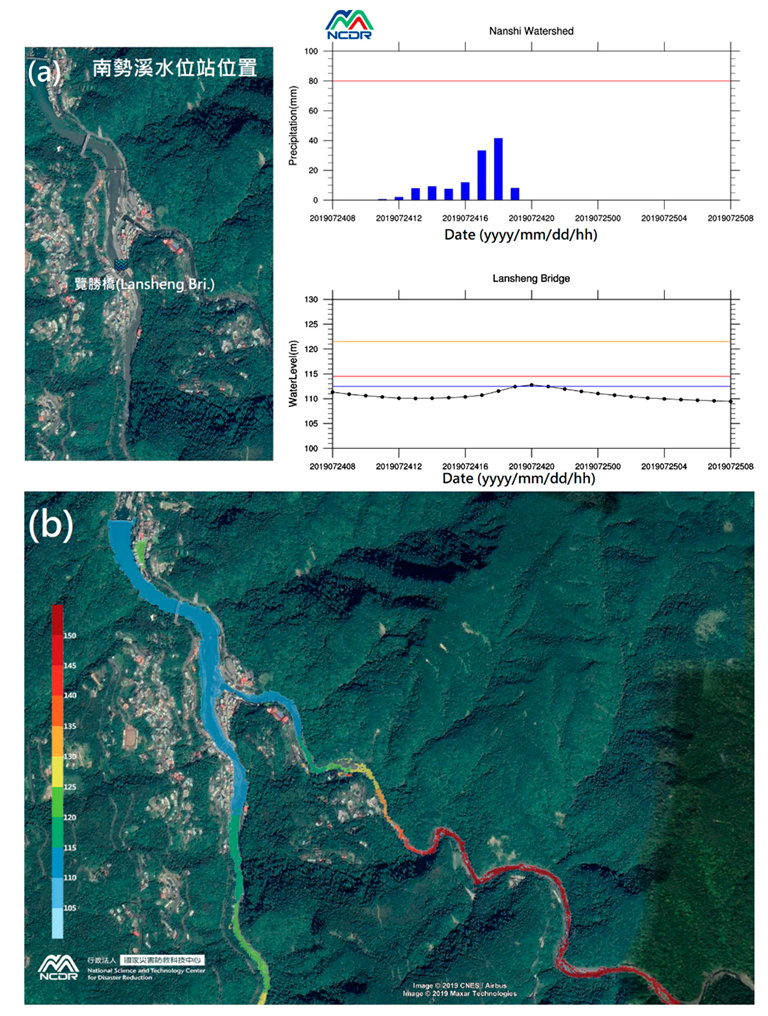
3.1. Model Validation
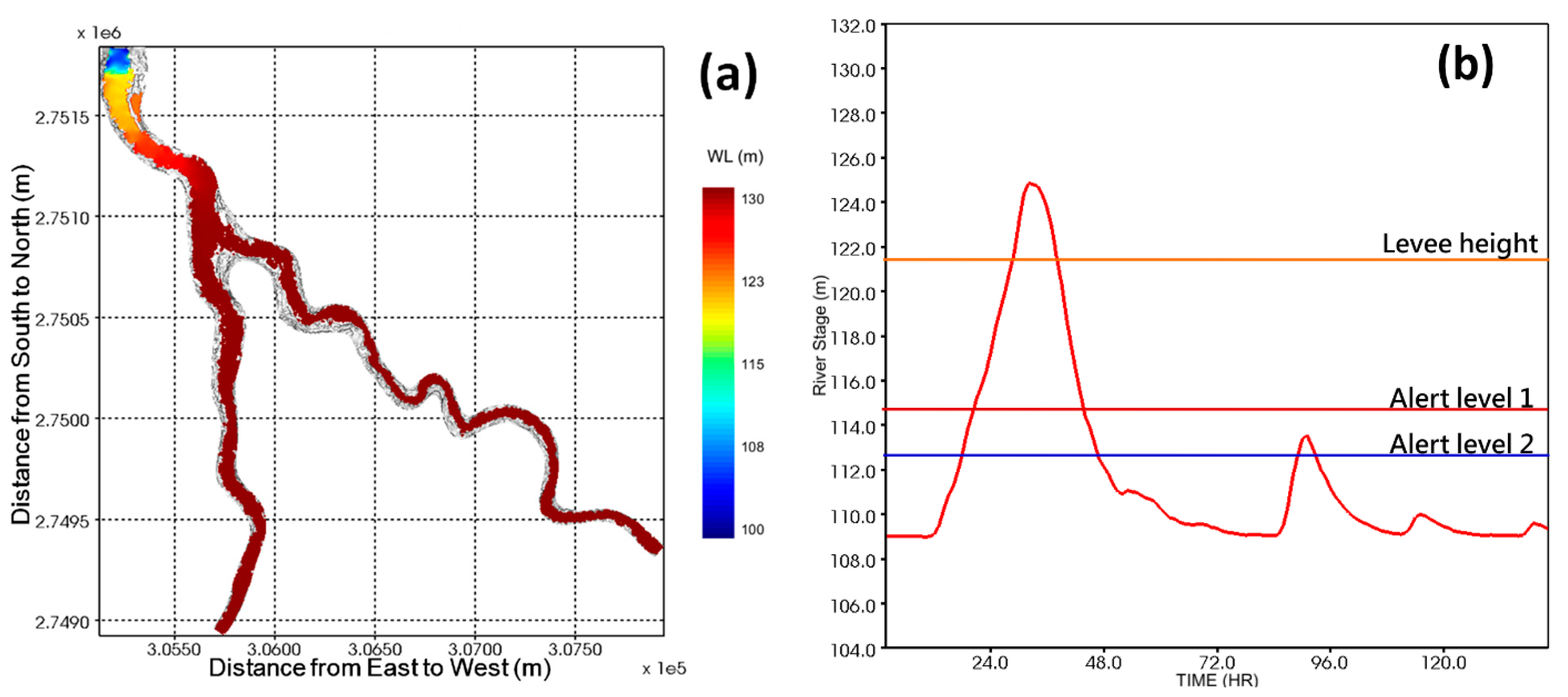
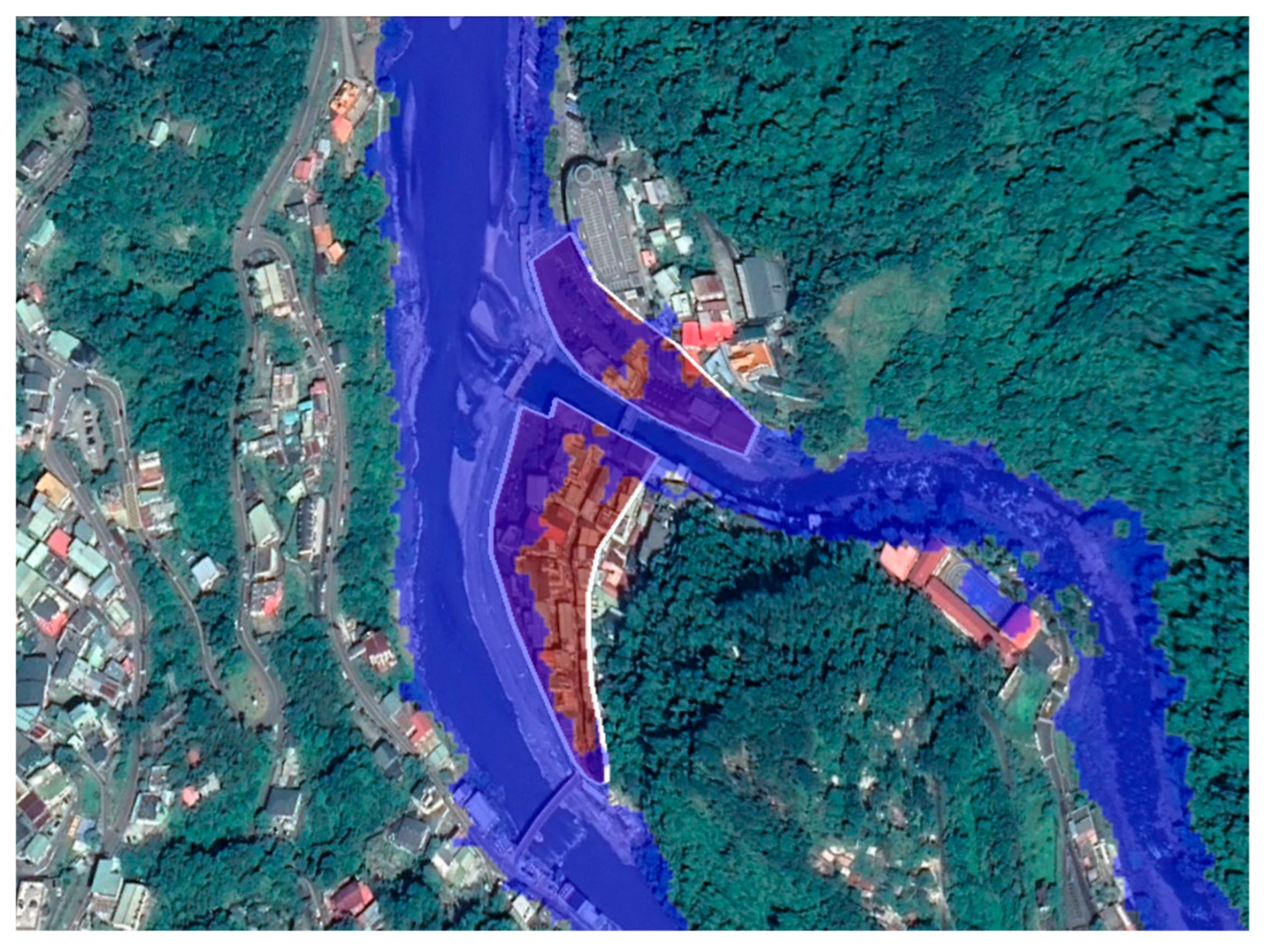
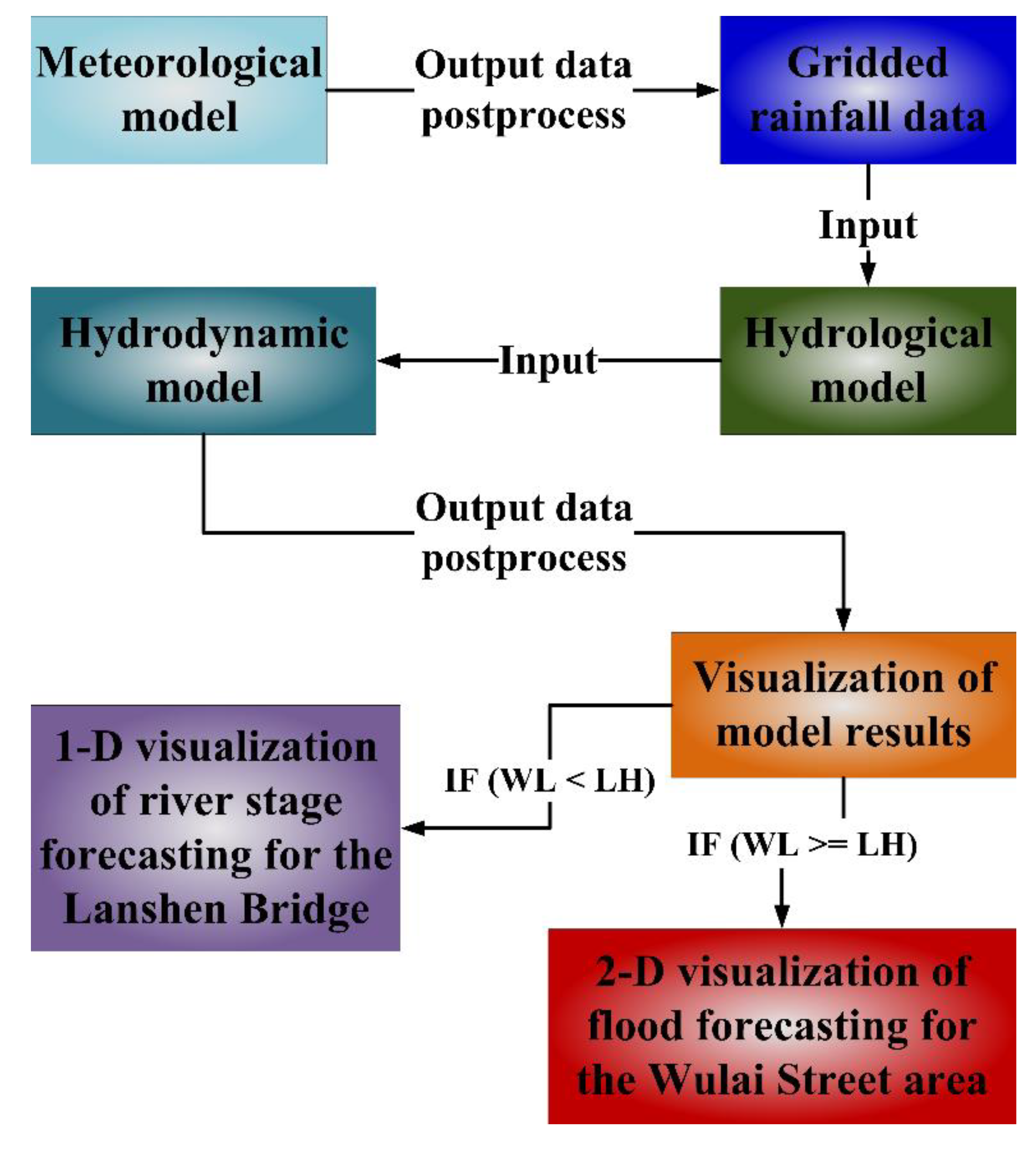
3.2. Implementation of an Operational Forecasting System (OFS) for Flash Floods in Mountainous Areas
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Borga, M.; Gaume, E.; Creutin, J.D.; Marchi, L. Surveying flash flood response: Gauging the ungauged extremes. Hydrol. Process. 2008, 22, 3883–3885. [Google Scholar] [CrossRef]
- Borga, M.; Stoffel, M.; Marchi, L.; Marra, F.; Jakob, M. Hydrogeomorphic response to extreme rainfall in headwater systems: Flash floods and debris flows. J. Hydrol. 2014, 518, 194–205. [Google Scholar] [CrossRef]
- Acosta-Coll, M.; Ballester-Merelo, F.; Martinez-Peiró, F.; De la Hoz-Franco, E. Real-Time Early Warning System Design for Pluvial Flash Floods—A Review. Sensor 2018, 18, 2255. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, J.; Yamakoshi, T.; Tamura, K. Studies on alleviation of death accidents by flash floods. J. Hydrosci. Hydraul. Eng. 2010, 53, 487–492. [Google Scholar]
- Ruiz-Villanueva, V.; Díez-Herrero, A.; Stoffel, M.; Bollschweiler, M.; Bodoque, J.M.; Ballesteros, J.A. Dendrogeomorphic analysis of flash floods in a small ungauged mountain catchment (Central Spain). Geomorphology 2010, 118, 383–392. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pradhan, B.; Hassan, A.M. Flash flood risk estimation along the St. Katherine road, southern Sinai, Egypt using GIS based morphometry and satellite imagery. Environ. Earth Sci. 2011, 62, 611–623. [Google Scholar] [CrossRef]
- Carpenter, T.M.; Sperfslage, J.A.; Georgakakos, K.P.; Sweeney, T.; Fread, D.L. National threshold runoff estimation utilizing GIS in support of operational flash flood warning systems. J. Hydrol. 1999, 224, 21–41. [Google Scholar] [CrossRef]
- Georgakakos, K.P. Real-Time Flash Flood Prediction. J. Geophys. Res. 1987, 92, 9615–9629. [Google Scholar] [CrossRef]
- Akbar, M.; Aliabadi, S.; Patel, R.; Watts, M. A fully automated and integrated multi-scale forecasting scheme for emergency preparedness. Environ. Model. Softw. 2013, 39, 24–38. [Google Scholar] [CrossRef]
- Georgakakos, K.P.; Graham, N.E.; Modrick, T.M.; Murphy, M.J., Jr.; Shamir, E.; Spencer, C.R.; Sperfslage, J.A. Evaluation of real-time hydrometeorological ensemble prediction on hydrologic scales in Northern California. J. Hydrol. 2014, 519, 2978–3000. [Google Scholar] [CrossRef]
- Modrick, M.T.; Georgakakos, K.P. The character and causes of flash flood occurrence changes in mountainous small basins of Southern California under projected climatic change. J. Hydrol. Reg. Stud. 2015, 3, 312–336. [Google Scholar] [CrossRef][Green Version]
- Leandro, J.; Martins, R. A methodology for linking 2D overland flow models with the sewer network model SWMM 5.1 based on dynamic link libraries. Water Sci. Technol. 2016, 73, 3017–3026. [Google Scholar] [CrossRef] [PubMed]
- Barthélémy, S.; Ricci, S.; Morel, T.; Goutal, N.; Le Pape, E.; Zaoui, F. On operational flood forecasting system involving 1D/2D coupled hydraulic model and data assimilation. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Shin, E.T.; Shin, J.; Rhee, D.S.; Kim, H.J.; Song, C.G. Integrated Inundation Modeling of Flooded Water in Coastal Cities. Appl. Sci. 2019, 9, 1313. [Google Scholar] [CrossRef]
- SET News Channel. Available online: https://www.setn.com/ (accessed on 15 September 2019).
- The News Lens. Available online: https://www.thenewslens.com/article/22437 (accessed on 15 September 2019).
- Horritt, M.S.; Bates, P.D. Effects of spatial resolution on a raster based model of flood flow. J. Hydrol. 2001, 253, 239–249. [Google Scholar] [CrossRef]
- Casas, A.; Benito, G.; Thorndycraft, V.; Rico, M. The topographic data source of digital terrain models as a key element in the accuracy of hydraulic flood modelling. Earth Surf. Process. Landf. 2006, 31, 444–456. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D.; Mattinson, M.J. Effects of mesh resolution and topographic representation in 2D finite volume models of shallow water fluvial flow. J. Hydrol. 2006, 329, 306–314. [Google Scholar] [CrossRef]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Caviedes-Voullieme, D.; Morales-Hernandez, M.; Lopez-Marijuan, I.; García-Navarro, P. Reconstruction of 2D river beds by appropriate interpolation of 1D cross-sectional information for flood simulation. Environ. Model. Softw. 2014, 61, 206–228. [Google Scholar] [CrossRef]
- Das, S.; Ashrit, R.; Iyengar, G.R.; Mohandas, S.; Gupta, M.D.; George, J.P.; Rajagopal, E.; Dutta, S.K. Skills of different mesoscale models over Indian region during monsoon season: Forecast errors. J. Earth Syst. Sci. 2008, 117, 603–620. [Google Scholar] [CrossRef]
- Li, L.; Gochis, D.J.; Sobolowski, S.; Mesquita, M.D. Evaluating the present annual water budget of a Himalayan headwater river basin using a high-resolution atmosphere-hydrology model. J. Geophys. Res. Atmos. 2017, 122, 4786–4807. [Google Scholar] [CrossRef]
- Chawla, I.; Osuri, K.K.; Mujumdar, P.P.; Niyogi, D. Assessment of the Weather Research and Forecasting (WRF) model for simulation of extreme rainfall events in the upper Ganga Basin. Hydrol. Earth Syst. Sci. 2018, 22, 1095–1117. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3. NCAR Technical Note, NCAR/TN-475+STR; Mesoscale and Microscale Meteorology Division, National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Routray, A.; Mohanty, U.; Niyogi, D.; Rizvi, S.; Osuri, K.K. Simulation of heavy rainfall events over Indian monsoon region using WRF-3DVAR data assimilation system. Meteorol. Atmos. Phys. 2010, 106, 107–125. [Google Scholar] [CrossRef]
- Mohanty, U.; Routray, A.; Osuri, K.K.; Prasad, S.K. A study on simulation of heavy rainfall events over Indian region with ARW-3DVAR modeling system. Pure Appl. Geophys. 2012, 169, 381–399. [Google Scholar] [CrossRef]
- Routray, A.; Mohanty, U.; Osuri, K.K.; Kar, S.; Niyogi, D. Impact of satellite radiance data on simulations of Bay of Bengal tropical cyclones using the WRF-3DVAR modeling system. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2285–2303. [Google Scholar] [CrossRef]
- Osuri, K.K.; Nadimpalli, R.; Mohanty, U.C.; Niyogi, D. Prediction of rapid intensification of tropical cyclone Phailin over the Bay of Bengal using the HWRF modelling system. Q. J. R. Meteorol. Soc. 2017, 143, 678–690. [Google Scholar] [CrossRef]
- Madala, S.; Satyanarayana, A.; Rao, T.N. Performance evaluation of PBL and cumulus parameterization schemes of WRF ARW model in simulating severe thunderstorm events over Gadanki MST radar facility–case study. Atmos. Res. 2014, 139, 1–17. [Google Scholar] [CrossRef]
- Osuri, K.; Nadimpalli, R.; Mohanty, U.; Chen, F.; Rajeevan, M.; Niyogi, D. Improved prediction of severe thunderstorms over the Indian Monsoon region using high-resolution soil moisture and temperature initialization. Sci. Rep. 2017, 7, 41377. [Google Scholar]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J. The Weather Research and Forecasting Model: Overview, system efforts, and future directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Chen, W.B.; Jang, J.H.; Chang, C.H. Predicting River Stages Using an Operational Forecasting System; National Science and Technology Center for Disaster Reduction: New Taipei City, Taiwan, 2017. (In Chinese) [Google Scholar]
- Wu, M.C.; Lin, G.F.; Lin, H.Y. Improving the forecasts of extreme streamflow by support vector regression with the data extracted by self organizing map. Hydrol. Process. 2014, 28, 386–397. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, G.R.; Huang, P.Y. Effective typhoon characteristics and their effects on hourly reservoir inflow forecasting. Adv. Water Resour. 2010, 33, 887–898. [Google Scholar] [CrossRef]
- Lin, G.F.; Wu, M.C. An RBF network with a two-step learning algorithm for developing a reservoir inflow forecasting model. J. Hydrol. 2011, 405, 439–450. [Google Scholar] [CrossRef]
- Lin, G.F.; Chou, Y.C.; Wu, M.C. Typhoon flood forecasting using integrated two stage support vector machine approach. J. Hydrol. 2014, 486, 334–342. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic. J. Hydrol. 2004, 292, 153–172. [Google Scholar] [CrossRef]
- Clark, C.O. Storage and the unit hydrograph. Trans. Am. Soc. Civ. Eng. 1945, 110, 1419–1488. [Google Scholar]
- Sabol, G.V. Clark unit hydrograph and R-parameter estimation. J. Hydraul. Eng. ASCE 1988, 114, 103–111. [Google Scholar] [CrossRef]
- Ahmad, M.M.; Ghumman, A.R.; Ahmad, S. Estimation of Clark’s Instantaneous Unit Hydrograph Parameters and Development of Direct Surface Runoff Hydrograph. Water Resour. Manag. 2009, 23, 2417–2435. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, F.; Stanev, E.V.; Grashorn, S. Seamless cross-scale modeling with SCHISM. Ocean Model. 2016, 102, 64–81. [Google Scholar] [CrossRef]
- Zhang, Y.; Baptisa, A.M. SELFE: A semi-implicit Eulerian-Lagrangian finite-element model for cross-scale ocean circulation. Ocean Model. 2008, 21, 71–96. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C. Modeling the Influence of River Cross-Section Data on a River Stage Using a Two-Dimensional/Three-Dimensional Hydrodynamic Model. Water 2017, 9, 203. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C. Modeling Flood Inundation Induced by River Flow and Storm. Water 2014, 6, 3182–3199. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C. Assessment of storm surge inundation and potential hazard maps for the southern coast of Taiwan. Nat. Hazards 2016, 82, 591–616. [Google Scholar] [CrossRef]
- Wang, H.V.; Loftis, J.D.; Liu, Z.; Forrest, D.; Zhang, J. The storm surge and sub-grid inundation modeling in New York City during hurricane Sandy. J. Mar. Sci. Eng. 2014, 2, 226–246. [Google Scholar] [CrossRef]
- Chen, W.B.; Chen, H.; Lin, L.Y.; Yu, Y.C. Tidal Current Power Resource and Influence of Sea-Level Rise in the Coastal Waters of Kinmen Island, Taiwan. Energies 2017, 10, 652. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Witter, R.C.; Priest, G.R. Tsunami-tide interaction in 1964 Prince William Sound tsunami. Ocean. Model. 2011, 40, 246–259. [Google Scholar] [CrossRef]
- Zhang, J.; Howard, K.; Chang, P.L.; Chiu, P.T.K.; Chen, C.R.; Langston, C.; Xia, W.W.; Kaney, B.; Lin, P.F. High-Resolution QPE System for Taiwan, Data Assimilation for Atmospheric, Oceanic, and Hydrologic Applications; Park, S.K., Xu, L., Eds.; Springer: Berlin, Germany, 2009; pp. 147–162. [Google Scholar]
- Kim, T.B.; Choi, S. Depth-averaged modeling of vegetated open-channel flows using finite element method. In Proceedings of the 16th IAHR-APD Congress and 3rd Symposium of IAHR-ISHS, Chapter in Advances in Water Resources and Hydraulic Engineering; Springer: Berlin/Heidelberg, Germany, 2008; pp. 411–416. [Google Scholar]
- Matsuda, I. River Morphology and Channel Processes. In Fresh Surface Water; Dooge, J.C.I., Ed.; In Encyclopedia of Life Support Systems (EOLSS), Developed under the Auspices of the UNESCO; Eolss Publishers: Oxford, UK, 2004. [Google Scholar]
- Hsiao, L.T.; Yang, M.J.; Lee, C.S.; Kuo, H.C.; Shih, D.S.; Tsai, C.C.; Wang, C.J.; Chang, L.Y.; Chen, Y.C.; Feng, L.; et al. Ensemble forecasting of typhoon rainfall and floods over a mountainous watershed in Taiwan. J. Hydrol. 2013, 506, 55–68. [Google Scholar] [CrossRef]
- Iacobellis, V.; Fiorentino, M.; Gioia, A.; Manfreda, S. Best fit and selection of theoretical flood frequency distributions based on different runoff generation mechanisms. Water 2010, 2, 239–256. [Google Scholar] [CrossRef]
- Hong, S.Y.; Lee, J.W. Assessment of the WRF model in reproducing a flash flood heavy rainfall event over Korea. Atmos. Res. 2009, 93, 818–831. [Google Scholar] [CrossRef]
- Weather Analysis and Taiwan Climate Hybrid monitor system (WATCH). Available online: https://watch.ncdr.nat.gov.tw/watch_wlfst (accessed on 15 September 2019).
- Brown, J.R.; Earnshaw, R.; Jern, M.; Vince, J. Visualization: Using Computer Graphics to Explore Data and Present Information; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-M.; Liu, C.-H.; Shih, H.-J.; Chang, C.-H.; Chen, W.-B.; Yu, Y.-C.; Su, W.-R.; Lin, L.-Y. An Operational Forecasting System for Flash Floods in Mountainous Areas in Taiwan. Water 2019, 11, 2100. https://doi.org/10.3390/w11102100
Chen Y-M, Liu C-H, Shih H-J, Chang C-H, Chen W-B, Yu Y-C, Su W-R, Lin L-Y. An Operational Forecasting System for Flash Floods in Mountainous Areas in Taiwan. Water. 2019; 11(10):2100. https://doi.org/10.3390/w11102100
Chicago/Turabian StyleChen, Yung-Ming, Che-Hsin Liu, Hung-Ju Shih, Chih-Hsin Chang, Wei-Bo Chen, Yi-Chiang Yu, Wen-Ray Su, and Lee-Yaw Lin. 2019. "An Operational Forecasting System for Flash Floods in Mountainous Areas in Taiwan" Water 11, no. 10: 2100. https://doi.org/10.3390/w11102100
APA StyleChen, Y.-M., Liu, C.-H., Shih, H.-J., Chang, C.-H., Chen, W.-B., Yu, Y.-C., Su, W.-R., & Lin, L.-Y. (2019). An Operational Forecasting System for Flash Floods in Mountainous Areas in Taiwan. Water, 11(10), 2100. https://doi.org/10.3390/w11102100