Abstract
In making short-term optimal operation schemes of cascade reservoirs, water flow hysteresis between the upper reservoir and the lower reservoir is often considered as constant, which cannot really reflect the hysteresis variation between different water flows and will lead to losses of the optimal operation scheme’s benefit. To depict the water flow hysteresis, a Dynamic Water Flow Hysteresis Method (DWFHM) is proposed, based on the space mapping principle. With the mapping operator in the DWFHM, the lower reservoir inflow can be directly obtained. Besides, the DWFHM is used to deal with the hydraulic relation constraint in the short-term optimal operation model of cascade reservoirs. Then, the improved model is applied to the Jinguan cascade reservoirs in the Yalong River basin and solved by an Improved Progressive Optimal Algorithm (IPOA). The results are as follows. (1) Compared with the traditional Fixed Water Flow Hysteresis Method (FWFHM), the inflow processes of the lower reservoir obtained by the DWFHM are more in line with the actual values, due to full consideration of the attenuation effect. (2) The optimal operation with the DWFHM can effectively increase the generated energy (2827 MW·h and 504 MW·h in the non-flood season and the flood season, respectively). Through the analysis of this case, the DWFHM developed in this study can effectively improve the practicability of the optimal operation scheme and reduce the risk in the operation of cascade reservoirs.
1. Introduction
In the process of the short-term optimal operation of cascade reservoirs, water balance between reservoirs is the most important constraint to be considered [1], and water flow hysteresis is a key factor related to the water balance constraint. If the problem of water flow hysteresis cannot be well addressed, the water flow between reservoirs will become unbalanced. Generally, water flow hysteresis refers to the water propagation time from the upper reservoir to the lower reservoir [2]. It results from complex hydraulic relation in cascade reservoirs and changes dynamically under the influence of various factors, such as the magnitude of upper reservoir discharge, the river channel storage, and the interval inflow [3,4]. The unreasonable disposal of water flow hysteresis makes it difficult to establish accurate schemes of the short-term optimization of cascade reservoirs [5,6], incurring benefit loss or risk in the operation of cascade reservoirs [7].
At present, the short-term optimal operation of cascade reservoirs considering water flow hysteresis is still under exploration. Traditionally, the water flow hysteresis was often ignored or fixed as a constant to simplify calculations [8,9,10]. For instance, in Yang’s study on the optimal operation of the Jinxi cascade reservoirs [11,12], the water propagation time was ignored and the upper reservoir outflow was directly taken as the lower reservoir inflow in the same calculation period of the operation cycle, which is obviously not in line with the reality. Xiao and Zong applied the Fixed Water Flow Hysteresis Method (FWFHM) to the short-term optimal operation study [13,14], in which the lower reservoir inflow in a calculation period was the same as the upper reservoir outflow in the previous calculation period. The FWFHM is suitable when the distance between the upper and lower reservoirs is short, because the water flow hysteresis variation is minor and can be ignored. Nevertheless, when the distance is relatively large, the water flow hysteresis variation will become large and considering the water flow hysteresis as a constant will result in operation risk. In the study of Ge et al. [15], the water flow hysteresis was regarded as dynamic via fitting the step function relation between the water flow hysteresis and the average upper reservoir outflow in various operation cycles, while the hysteresis variation of different periods in the same operation cycle was not considered. Although the above approach can improve the calculation accuracy to a certain extent, the actual change of water flow hysteresis caused by the dynamic flow process still cannot be reflected. Therefore, to fundamentally solve the dynamic change of water flow hysteresis in operation, especially with the attenuation effect in water flow propagation taken into account, some “real” dynamic mechanism is expected.
To further quantify the influence of water flow hysteresis on the optimal operation of cascade reservoirs, a Dynamic Water Flow Hysteresis Method (DWFHM) is proposed, based on the space mapping principle. The upper reservoir outflow and the lower reservoir inflow are taken as different linear spaces, and the mapping operator between the two linear spaces is solved by the data mining technology. With the solved mapping operator, the lower reservoir inflow can be directly obtained under the condition that the upper reservoir outflow is known in the previous periods of the calculation periods. In this way, the dynamic water flow hysteresis can be denoted as the mapping relationship between upper reservoir outflow and lower reservoir inflow. Then, a short-term optimal operation model of cascade reservoirs coupled with the Dynamic Water Flow Hysteresis Method is constructed. However, when the existence of water flow hysteresis is taken into account, the Dynamic Programming (DP) algorithm, traditionally used in solving the short-term optimal operation model, is not suitable, because the non-after-effect condition is not satisfied [16]. Moreover, the modern intelligent algorithms not only take a long time to iteratively solve the problem but also cannot avoid falling into the local optimal solution, and it is difficult to verify the accuracy of the solution [17]. In order to solve the after-effect problem that results from considering dynamic hysteresis [18], the Progressive Optimality Algorithm is improved by coupling with the space mapping principle.
In this study, the advantage of DWFHM on the short-term optimal operation of cascade reservoirs is demonstrated by comparing it with the FWFHM. The rest of the paper is organized as follows. First, the DWFHM based on the space mapping principle is proposed. Second, the short-term optimal operation model of cascade reservoirs considering water flow hysteresis is coupled with the DWFHM and the FWFHM separately, and the optimal operation schemes are obtained by solving the two different models. Finally, we discuss the generation benefits and the output processes of the two schemes. The Jinguan cascade reservoirs in Yalong River are taken as an example to verify the validity and rationality of the new method.
2. Influence of Water Flow Hysteresis
In the short-term optimal operation of cascade reservoirs, the hydraulic relationship between the upper and lower reservoirs is reflected by the water flow hysteresis. Water flow hysteresis has two main effects on the optimal operation of cascade reservoirs:
(1) Directly affecting the water balance of an operation cycle
In the traditional short-term optimal operation model of cascade reservoirs with fixed water flow hysteresis, there is a water flow balance constraint between the upper reservoir and the lower reservoir [19]:
where is the inflow of reservoir in period , unit: m3/s; is the water flow hysteresis between reservoir and reservoir , unit: h; is the number of tributaries between reservoir and reservoir ; is the water flow hysteresis between outflow of tributary and inflow of the reservoir , unit: h; is the outflow of reservoir in period , unit: m3/s. is the outflow of tributary in period , unit: m3/s.
Equation (1) indicates that, when water flow hysteresis is considered, the inflow of the lower reservoir is the sum of the outflow of the upper reservoir in the early periods and the outflow of the interval tributary in the early periods. Therefore, the inflow in one operation cycle is affected by the outflow in the previous operation cycle.
(2) Indirectly affecting the generation benefit during the operation cycle
When water flow hysteresis is considered, the generation benefit occurring in the current operation cycle consists of the benefit generated by the water from the end of the previous operation cycle () and the benefit generated by the water from the current operation cycle (). The benefit generated by the water from the current operation cycle consists of and the benefit generated in the next operation cycle (). Therefore, the current operation cycle benefit is not only affected by the previous operation cycle, but also affects the benefit of the next operation cycle.
where is the benefit generated by water from the previous operation cycle, unit: MW·h; is the benefit generated by the water from this operation cycle, unit: MW·h; is the benefit generated by the water from the current operation cycle while considered in the next operation cycle, unit: MW·h; is the total number of reservoirs; is the period during which the reservoir in this operation period is affected by the water flow in the previous operation period of the upper reservoir, unit: h; is the output of reservoir in period in the next operation period, unit: MW·h; is the period during which the reservoir in the next operation period is affected by the water flow of the upper reservoir in the current operation period.
In the short-term optimal operation of cascade reservoirs, the maximum of is taken as the operation objective. If the effect of water flow hysteresis on the operation is neglected, the operation objective is actually the maximum of . Such a difference will result in the aggregation of the output of lower reservoirs towards the early periods during the implementation of the scheme. Moreover, taking the water flow hysteresis as constant will also lead to deviation in the formulation of generation schemes, which will adversely affect the economic and safe operation of the cascade reservoirs. Therefore, we propose the DWFHM, which can consider the water flow hysteresis among cascade reservoirs as a dynamic mapping relation using the space mapping principle. The study is organized as in Figure 1.
Figure 1.
Structure of this study.
3. Dynamic Water Flow Hysteresis Method Based on the Space Mapping Principle
The DWFHM based on the space mapping principle is illustrated with a case study of mixed multi-reservoirs consisting of three reservoirs (Figure 2). It is assumed that in an operation cycle, are the inflow series of upper reservoir 1 and are the corresponding outflow series. Similarly, and are respectively the inflow and outflow of upper reservoir 2. The inflow of lower reservoir 3 is and the outflow is . Then, there is a mapping relation , where is a functional relation between and the outflow of the upper reservoir in period (), the outflow of upper reservoir 1 in the first periods (), and the outflow of upper reservoir 2 in the first periods ().
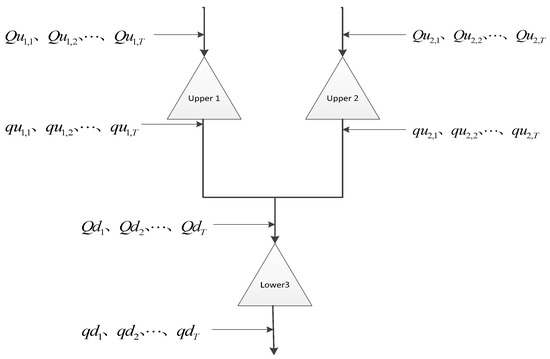
Figure 2.
Schematic diagram of the mixed multi-reservoirs.
Assume that the dimensional space formed by the outflow of the upper reservoir 1 and reservoir 2, and the dimensional space formed by the inflow of the lower reservoir, are linear spaces, among which , , and . If the inflow of the lower reservoir in the current period is only related to the outflow of the upper reservoir in the current period and the outflow process in the first and periods, then the dynamic water flow hysteresis from the upper reservoir to the lower reservoir can be regarded as a mapping relation (), which can be simplified as:
Given , Equation (3) is a system with variables, which can be determined uniquely with at least linearly independent equations. However, since there are only periods in an operation cycle, and , cannot be determined by solving the Equation (3). As the short-term optimal operation of cascade reservoirs is actually a cyclic process with periods, when there are long enough historical data, the series of inflow processes can be classified and the data mining technology can be adopted to mine the information of historical data. Then the mapping operator can be obtained:
where is the set of classification ; is the mapping operator in period .
Since in the mappings of period and period , the variable values of the upper reservoir outflow process are adjacent to each other, it is possible that the mapping operator is the same as the mapping operator . Through this method, the lower reservoir inflow can be attained by the mapping operator when the upper reservoir outflow is given. Besides, is closer to the real value than the upper reservoir outflow , thus reducing the error by directly using in scheme formulation. Due to the fact that water flow hysteresis is affected by multiple factors, each instance object of the mapping relationship between and may be different, and this research focuses on the difference in outflow magnitude and outflow processes. Multiple methods, such as multiple regression analysis, support vector machine, and artificial neural network, can be used to solve the mapping relation of multiple time periods, multiple indexes, or multiple variables. Here, we mainly analyze how the obtained mapping relation can improve the precision of scheme formulation, and do not consider the difference between multiple methods in solving the mapping operator. Therefore, only the artificial neural network, which can effectively deal with the nonlinear relation, is selected to solve the mapping relation [20,21].
4. Mathematical Model for Short-Term Optimal Operation of Cascade Reservoirs Considering Dynamic Water Flow Hysteresis
4.1. Objective Function
The short-term optimal operation target of cascade reservoirs can be divided into two modes: “electricity to water” and “water to electricity” [22]. This study mainly investigates the influence of different water flow hysteresis models on the generation benefit in the operation cycle. Therefore, the maximum generation benefit of the cascade system in the mode of “electricity to water” is adopted as the objective function:
where is the total generation benefit in the operation cycle, unit: MW·h.
4.2. Constraint Conditions
(1) Water balance constraint:
(2) Capacity constraint:
(3) The upper and lower bounds of flow rate:
(4) The upper and lower bounds of output:
(5) Water level constraint at the end of the operation cycle:
(6) Hydraulic relation constraint:
where and are the starting and ending storage capacities of reservoir in period , respectively, unit: 104m3; is the outflow of the reservoir in period , unit: m3/s; is the generation flow of reservoir in period , unit: m3/s; is the abandoned flow of reservoir in period , unit: m3/s; , are the lower and upper limits of storage capacity of reservoir , respectively, unit: 104 m3; and are the lower and upper limits of the outflow of reservoir , respectively, unit: m3/s; and are the lower and upper limits of the output of reservoir , respectively, unit: MW; and are the water level of reservoir in period and the controlled water level of reservoir , respectively, unit: m; is the space mapping operator.
Different from the short-term optimal operation model of cascade reservoirs that couples with the FWFHM, the cascade hydraulic relation constraint shown in Equation (12) is adopted in the dynamic scheme instead of the hydraulic relation constraint shown in Equation (1), in order to transform the dynamic water flow hysteresis into the dynamic mapping relationship between upper reservoir outflow, interval outflow, and lower reservoir inflow.
5. Model Solution
The existence of water flow hysteresis makes the solution of the short-term optimal operation model of cascade reservoirs a problem with an after-effect. Although the Progressive Optimal Algorithm (POA) can effectively deal with the after-effect problem [15], the traditional POA directly shifts the upper reservoir outflow in a single period and takes it as the lower reservoir inflow [23,24]. Here, the POA is coupled with the space mapping principle to develop an Improved Progressive Optimal Algorithm (IPOA) that can take into account the multi-period outflow of the upper reservoir. As shown in Figure 3, is the outflow of the upper reservoir in period and is the inflow of the lower reservoir in period . The outflow of the upper reservoir in period and the first periods are input into the mapping operator to obtain . The IPOA is conducted on Matlab.
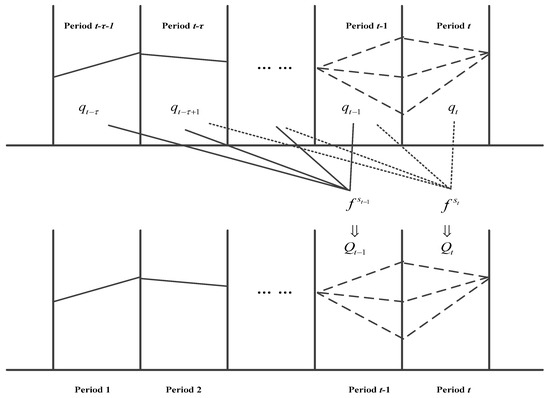
Figure 3.
Schematic diagram of Improved Progressive Optimal Algorithm
The calculation procedure of IPOA is detailed as follows:
Step 1: Select the input factors. Since the input factors between adjacent time periods contain redundant information, in order to ensure the validity of the input information and reduce the calculation amount, the joint mutual information method and the multiple stepwise regression method are adopted to select the input factors [25,26,27].
Step 2: Get the mapping operator. Use the Back Propagation (BP) neural network model to mine the historical data and obtain the mapping operator.
Step 3: Determine the initial solution. The determination of the initial solution has an important impact on the efficiency of the IPOA and the quality of the results. According to the constraints of cascade reservoirs, the actual daily operation process line of each reservoir in the previous day is taken as the initial solution of each operation cycle [28].
Step 4: ① Set the initial value of reservoir number and the initial value of period number ; ② The initial water level in period t is fixed and the final water level in period remains unchanged. The initial water level in period is adjusted to optimize the outflow under three conditions: initial water level + 1 step, initial water level, and initial water level - 1 step. The mapping operator is then used to calculate the inflow of reservoir in periods and . Let . Return to ② when , otherwise enter Step 5.
Step 5: Calculate the total cascade power generation benefit in period and period under various combinations of water levels, and select the water level combination with the maximum benefit as the alternative variable. When , return to Step 4-②, otherwise enter Step 6.
Step 6: Decide whether the value of the objective function after the iterative calculation meets the accuracy requirement. If so, the iterative result is taken as the final solution. Otherwise, the iterative result is taken as the new trajectory in Step 4-② for calculation until the accuracy requirement is satisfied.
6. Case Study
The Jinguan cascade reservoirs are located in the Yalong River basin in Sichuan province, which is composed of the Jinxi, Jindong, and Guandi reservoirs. The characteristic parameters of the Jindong and Guandi hydropower stations are listed in Table 1. The location of the Jinguan cascade reservoirs is displayed in Figure 4. The outflow of the Jinxi reservoir directly enters the Jindong reservoir, so the water flow hysteresis can be ignored. The water flow hysteresis in the Jinguan cascade reservoirs mainly happens in the process of the Jindong reservoir outflow reaching the Guandi reservoir. Therefore, for the convenience of research, only the Jindong and Guandi reservoirs were calculated and the interval inflow of Jiulong River was also considered.

Table 1.
Parameters of the Jindong–Guandi cascade hydropower stations.
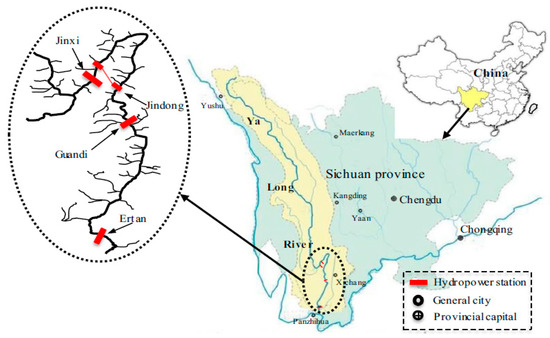
Figure 4.
The location of the Jinguan cascade reservoirs.
According to the climate characteristics of the basin, the non-flood season is from November to April of the next year, and the flood season is from May to October. The data include the inflow and outflow of the Jinxi and Guandi reservoirs and the outflow of Jiulong River. The BP neural network was used to acquire the mapping operators Net1 and Net2, and the data distribution ratio of training, testing, and examining was 7:2:1. The number of hidden layers was set to one, and the neuron of the hidden layer was determined by the cross-validation method. The number of neurons was set to seven in the flood season and three in the non-flood season. The weight and threshold were determined by the Levenberg-Maquardt method. At the same time, the model using the FWFHM during different periods was established as the comparison of the DWFHM. The outflow of the Jindong reservoir and Jiulong River in the 24 h before the calculated period was composed of 576 types of fixed water flow hysteresis, and the inflow of the Guandi reservoir at the calculated period with different fixed water flow hysteresis was calculated. The Nash-Sutcliffe efficiency coefficient (NSE), average relative error (ARE), and prediction qualification rate (QR) were used as evaluation indexes to select the optimal combination of fixed water flow hysteresis. In the flood season, the stagnation time of the Jindong reservoir is about 1 h, and the interval outflow stagnation is about 5 h. In the non-flood season, the stagnation time of the Jindong reservoir is about 2 h, and the interval outflow stagnation is about 1 h. The prediction results of the FWFHM were compared with those of the DWFHM. The results are shown in Figure 5, Figure 6 and Figure 7.
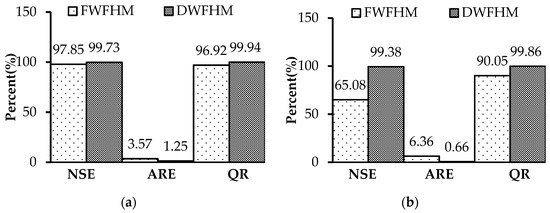
Figure 5.
Comparison of the calculated results of the FWFHM and the DWFHM; (a) Non-flood season; (b) Flood season.
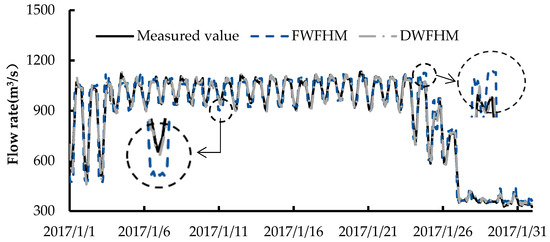
Figure 6.
Comparison of the calculated inflow of the Guandi reservoir during the non-flood season.
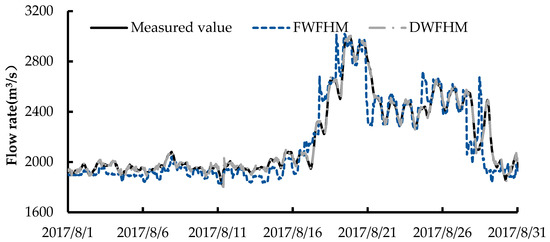
Figure 7.
Comparison of the calculated inflow of the Guandi reservoir during the flood season.
In Figure 5, it can be seen that, in different seasons, the calculated results of the DWFHM were better than those of the FWFHM. In the non-flood season, compared with the FWFHM, the NSE of the DWFHM increased by 1.88%, the ARE decreased by 2.32%, and the QR increased by 3.02%, indicating slight improvement by the DWFHM. In the flood season, compared with the FWFHM, the NSE of the DWFHM increased by 34.03%, the ARE decreased by 5.70%, and the QR increased by 9.80%, indicating significant improvment caused by the DWFHM.
January 2017 was taken as the typical month of the non-flood season for calculation, while August 2017 was taken as the typical month of the flood season for calculation. The calculation results are shown in Figure 6 and Figure 7.
From Figure 6 and Figure 7 we can see that, in the non-flood season, when using the FWFHM, the calculation results were similar to the measured values. But at certain periods where the measured value was at its valley or peak, the result of the FWFHM was relatively small or large, because the FWFHM directly uses the sum of the upper reservoir outflow and interval outflow as the lower reservoir inflow, without considering the attenuation effect. Actually, after the river channel storage, the peak flow value will decrease and the valley flow value will increase. In the flood season, the deviation between the calculated results was larger than that in the non-flood season. This was reflected in two aspects: (1) The calculated value of the FWFHM was larger than the measured flow; (2) The time deviation at peak and valley was also large.
At the same time, it can be seen that the time deviation of the peak inflow was small and the flow deviation was large, while for the valley inflow, the time deviation was large and the flow deviation was small. This is because, when the water flow hysteresis of the Jindong reservoir (1–2 h) is actually larger than that of the optimal combination (1 h) and the flow rate increases, the water flow hysteresis will decrease and the inflow will come earlier. Moreover, the flow rate at the flood peak is too large due to the lack of consideration of the attenuation effect. These results will be adverse to the flood operation of the Guandi reservoir. However, when using the DWFHM, the calculated results were better in both the flood season and the non-flood season, compared with using the FWFHM.
The typical days of the non-flood season and the flood season in 2017 were selected as examples for calculation. The short-term optimal operation models were established coupling with the FWFHM (Scheme 1) and the DWFHM (Scheme 3), and the models were solved by IPOA to obtain operation schemes. Meanwhile, the scheme coupling with the FWFHM was replaced by the DWFHM to form Scheme 2, which was implemented in accordance with the water level control mode to obtain the actual operation results [29].The accuracy of IPOA in different schemes was set as 0.0001. The opeartion results are shown in Table 2, Table 3, and Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

Table 2.
The generated energy of different schemes during the non-flood season.

Table 3.
The generated energy of different schemes during the flood season.
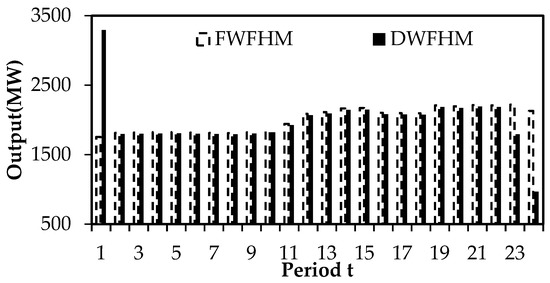
Figure 8.
The output of the Jindong reservoir during the non-flood season.
Figure 9.
The output of the Guandi reservoir during the non-flood season.
Figure 10.
The total output of cascade reservoirs during the non-flood season.
Figure 11.
The output of the Jindong reservoir during the flood season.
Figure 12.
The output of the Guandi reservoir during the flood season.
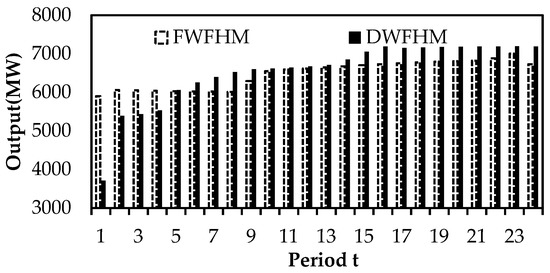
Figure 13.
Total output of cascade reservoirs during the flood season.
From Table 2 it can be seen that, in the typical day of the non-flood season, the total generated energy of Scheme 2, compared with Scheme 1, increased by 1640 MW·h. This is because the deviation between the inflow calculated by the FWFHM and the actual operation process was reduced in Scheme 2. Compared with Scheme 1, the total generated energy of Scheme 3 increased by 1187 MW·h. This is because the FWFHM only considers the influence of single-period flow while the DWFHM takes into account the influence of multi-period flow on the inflow of the Guandi reservoir in the current period. It can be seen from Figure 8, Figure 9 and Figure 10 that at the beginning of the cycle, by increasing the outflow of the Jindong reservoir, the output of the Jindong hydropower station was increased, the water level of the Guandi reservoir was raised, and the output of Guandi hydropower station was increased. Without considering the output constraint, the Jindong reservoir increased its output in period 1 to raise the water level of the Guandi reservoir. Although the overall generated energy decreased by 464 MW·h in the operation cycle of the Jindong reservoir, the generated energy of the Guandi reservoir in the later period was increased by 1650 MW·h, thus increasing the total generated energy in the operation period of the cascade reservoirs by 1186 MW·h. In addition, compared with the FWFHM, the actual operation results of the DWFHM increased by 2827 MW·h.
From Table 3, it can be seen that, in the typical days of the flood season, the total generated energy of Scheme 2, compared with Scheme 1, increased by 1600 MW·h, and the reason is the same as that in the non-flood season. Compared with Scheme 1, the total generated energy of Scheme 3 decreased by 1187 MW·h, but compared with Scheme 2, the total generated energy of Scheme 3 increased by 1564 MW·h, because the results calculated by the FWFHM were deviated from the actual inflow. Besides, it can be seen from Figure 11, Figure 12 and Figure 13 that the difference between Scheme 1 and Scheme 2 is reflected in the output of the Guandi hydropower station. Compared with Scheme 2, the increment of Scheme 3 included the generated energy of the Jindong hydropower station increasing by 1061 MW·h and the generated energy of the Guandi hydropower station increasing by 504 MW·h. This is because there is a large amount of incoming water in the flood season, so it is a priority to ensure that the output of the Jindong hydropower station, which has a huge installed capacity, is increased to reach full capacity, and then the output of the Guandi hydropower station is increased to increase the overall output of the cascade reservoirs.
7. Conclusions
Water flow hysteresis, which may cause the unbalance of water flow in the operation cycle and the deviation of the solution results of the optimization, is a potential factor influencing the accuracy of short-term optimal operation for cascade reservoirs. In the traditional way, the problem of water flow hysteresis is always solved through the FWFHM, but this method is not suitable when the upper and the lower reservoirs are far apart. In order to fundamentally address this problem in operation, we propose a dynamic water flow hysteresis method based on the space mapping principle, and put forth the short-term optimal operation model considering dynamic water flow hysteresis. The new method is applicable whether the distance between the upper and the lower reservoirs is small or large. Taking the Jinguan cascade reservoirs as an example, the rationality of the model is verified. The main conclusions are as follows:
- Compared with the FWFHM, the space mapping principle is adopted to establish a DWFHM that can fully consider the effect of multi-period outflow on the current period inflow. It can take into account both the change of water flow propagation time caused by the change of the magnitude of discharge and the impact of water flow attenuation caused by factors such as the river channel storage, thus leading to a more accurate calculation result.
- The short-term optimal operation model of cascade reservoirs with dynamic water flow hysteresis is put forward and solved by the IPOA. Compared with the traditional model using the FWFHM, the improved model can effectively increase the generated benefit. The new model can fully consider the impact of flow rate, water head, and the installed capacity of cascade reservoirs. In the non-flood season, when the inflow is small, the priority is given to raising the water head of the Guandi hydropower station, in order to increase the total generated energy. In the flood season, when the inflow is large, the improved model makes full use of the installed capacity of the Jindong hydropower station so as to increase the total generated energy.
Author Contributions
Y.Z. and C.J. conceived and designed the experiments; Y.L. performed the experiments; Y.L. and Q.M. analyzed the data; Y.L., Y.Z., and Q.M. wrote the paper. Y.W. edited the paper.
Funding
This study was financially supported by National Natural Science Foundation of China (51709105), the Fundamental Research Funds for the Central Universities (2014XS51).
Acknowledgments
The authors are grateful to the anonymous reviewers for their comments and valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, C.; Wu, X.; Shen, J.; Liao, S. Short-term optimal operation methods of large-scale hydropower plants I. General overview. J. Hydraul. Eng. 2011, 42, 1017–1024. [Google Scholar]
- Hou, C. Research on Water Dispatching System under Sanmenxia of Yellow River in Non-Flood Season. Master’s Thesis, Wuhan University, Wuhan, China, 2003. [Google Scholar]
- Deng, X. On the effect of time lag upon the economical operation of cascade hydroelectric power stations. J. Chongqin Univ. 1982, 2, 91–102. [Google Scholar]
- Wang, G.; Wei, J. Watershed Water Regulation Model and Application; Science Press: Beijing, China, 2006; pp. 224–267, 7030166019. [Google Scholar]
- Li, J. Study and Application of Short-Term Optimal Operation of Hydropower Station. Master’s Thesis, Wuhan University, Wuhan, China, 2005. [Google Scholar]
- Liu, X.; Zhang, S. Study of the Effect upon Flow through Delay Time for the Cascaded Hydroelectric Stations. J. Huazhong Univ. Sci. Technol. Med. Sci. 1999, 3, 47–49. [Google Scholar] [CrossRef]
- Zhang, P.; Ji, C.; Zhang, Y. Risk analysis model of short-term optimal operation for reservoir group considering flow time lag. Yangtze River 2017, 48, 107–111. [Google Scholar] [CrossRef]
- Zhang, M. Study on the Reservoir Operation Chart of Hydropower Station and Short-Term Optimal Operation. Master’s Thesis, Wuhan University, Wuhan, China, 2004. [Google Scholar]
- Li, A.; Wang, L.; Lin, W.; Ji, C. Application of immune particle swarm optimization algorithm to short-term optimal dispatch of cascade hydropower stations. J. Hydraul. Eng. 2008, 4, 426–432. [Google Scholar] [CrossRef]
- Huang, Q.; Chang, J. Theory and Method of Multidimensional Critical Regulation of Water Resources System; China Water & Power Press: Beijing, China, 2007; pp. 117–123, 9787508445571. [Google Scholar]
- Yang, B. Study on short-term optimal dispatching of cascade hydropower stations. Water Res Inf. 2018, 3, 32–35. [Google Scholar] [CrossRef]
- Shawwash, Z.K.; Siu, T.K. The BC hydro short term hydro scheduling optimization model. IEEE Trans. Power Syst. 2000, 15, 1125–1131. [Google Scholar] [CrossRef]
- Zong, H.; Yang, Y. Research and application for cascaded hydroelectric optimized scheduling based on modified adaptive POA. Comput. Eng. 2003, 17, 105–106. [Google Scholar]
- Xiao, G.; Chen, S.; Li, J.; Zou, Z.; Ma, G. Short-term optimal operation of cascade hydropower stations considering the delay of flow propagation. Water Power 2018, 44, 37–41. [Google Scholar] [CrossRef]
- Ge, X.; Zhang, L. Daily optimal scheduling model for cascade hydropower stations considering the flow delay time. East Chin. Electron. Power 2013, 41, 264–269. [Google Scholar]
- Zhong, P.; Zhang, J.; Xu, B.; Zhang, M. Daily optimal operation model of cascade reservoirs considering delay of flow propagation. J. Hydroelectr. Eng. 2012, 31, 34–38. [Google Scholar]
- Han, B.; Hu, X.; Ge, X.; Shu, J. An iterative method for short term cascade hydropower optimal scheduling. Power Syst. Prot. Control 2013, 41, 67–72. [Google Scholar]
- Ji, C.; Yu, H.; Wu, J.; Yan, X.; Li, R. Research on cascade reservoirs’ short-term optimal operation under the effect of reverse regulation. Water-Sui 2018, 10, 808. [Google Scholar] [CrossRef]
- Chen, S. Hydropower Station Reservoir Operation and Dispatch; China Electric Power Press: Beijng, China, 2008; pp. 151–153, 9787508372723. [Google Scholar]
- Wang, S. Hydrological Forecasting Method Research Based on Neural Work. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2009. [Google Scholar]
- Zhang, D. Matlab Neural Network Design and Application; China Machine Press: Beijing, China, 2009; pp. 115–190, 9787302313632. [Google Scholar]
- Zhao, T.; Yang, D. Mutual information-based input variable selection method for runoff-forecasting neural network model. J. Hydroelectr. Eng. 2011, 30, 24–30. [Google Scholar]
- Howson, H.R.; Sancho, N.G.F. A New algorithm for the solution of multi-state dynamic programming problems. Math. Program. 1974, 8, 104–116. [Google Scholar] [CrossRef]
- William, G.; Robert, E. Dynamic programming applications to water resource system operation and planning. J. Math. Anal. Appl. 1968, 24, 80–109. [Google Scholar]
- He, Y. The Analysis on Inflow Runoff Forecast Error and the Application in Reservoirs Short-Term Generation Scheduling. Master’s Thesis, North China Electric Power University, Beijing, China, 2016. [Google Scholar]
- Ji, C.; Yu, H.; Yan, X.; Li, R.; Wang, L. Selecting hydrological forecast factor sets based on joint mutual information. J. Hydraul. Eng. 2017, 36, 12–21. [Google Scholar] [CrossRef]
- Mai, Z.; Ceng, X.; Zhou, J.; Ye, L.; He, Q. Medium and long-term runoff forecasting based on input variables selected by partial mutual information. Yangtze River 2018, 49, 52–56. [Google Scholar] [CrossRef]
- Fang, H.; Wang, H.; Chen, J. Effect of original state locus on convergence of progressive optimization algorithm. J. Hydraul. Eng. 2002, 27–30. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Yu, H.; Ji, C. Formulation and implementation of short-Term optimal reservoir operation schemes integrated with operation rules. Water-Sui 2019, 11, 944. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).