Dune Contribution to Flow Resistance in Alluvial Rivers
Abstract
1. Introduction
2. Flow Resistance
3. Grain Contribution to Flow Resistance
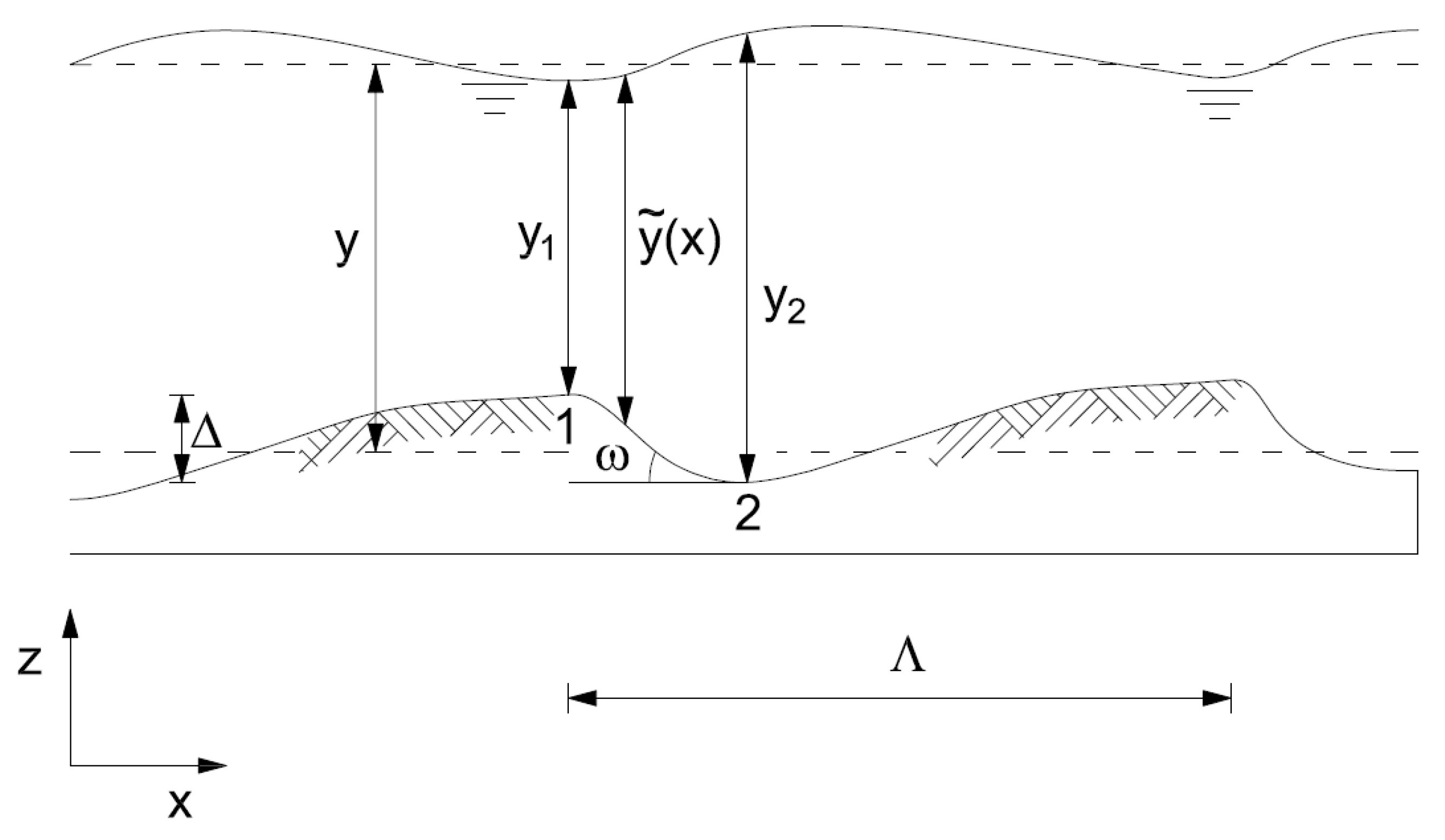
4. Sand Dune Contribution to Flow Resistance
Empirical Coefficient for Bed Form Drag
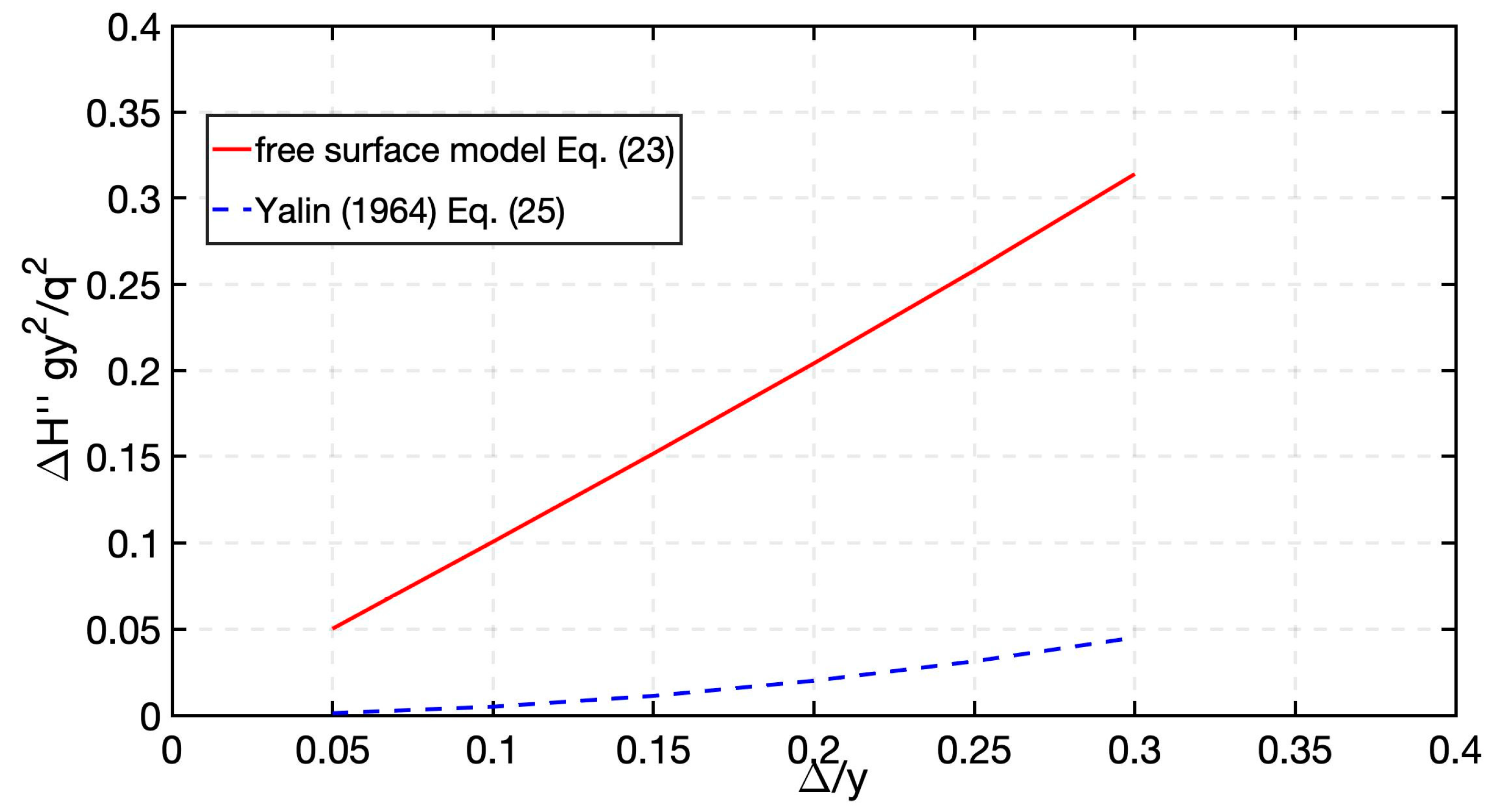
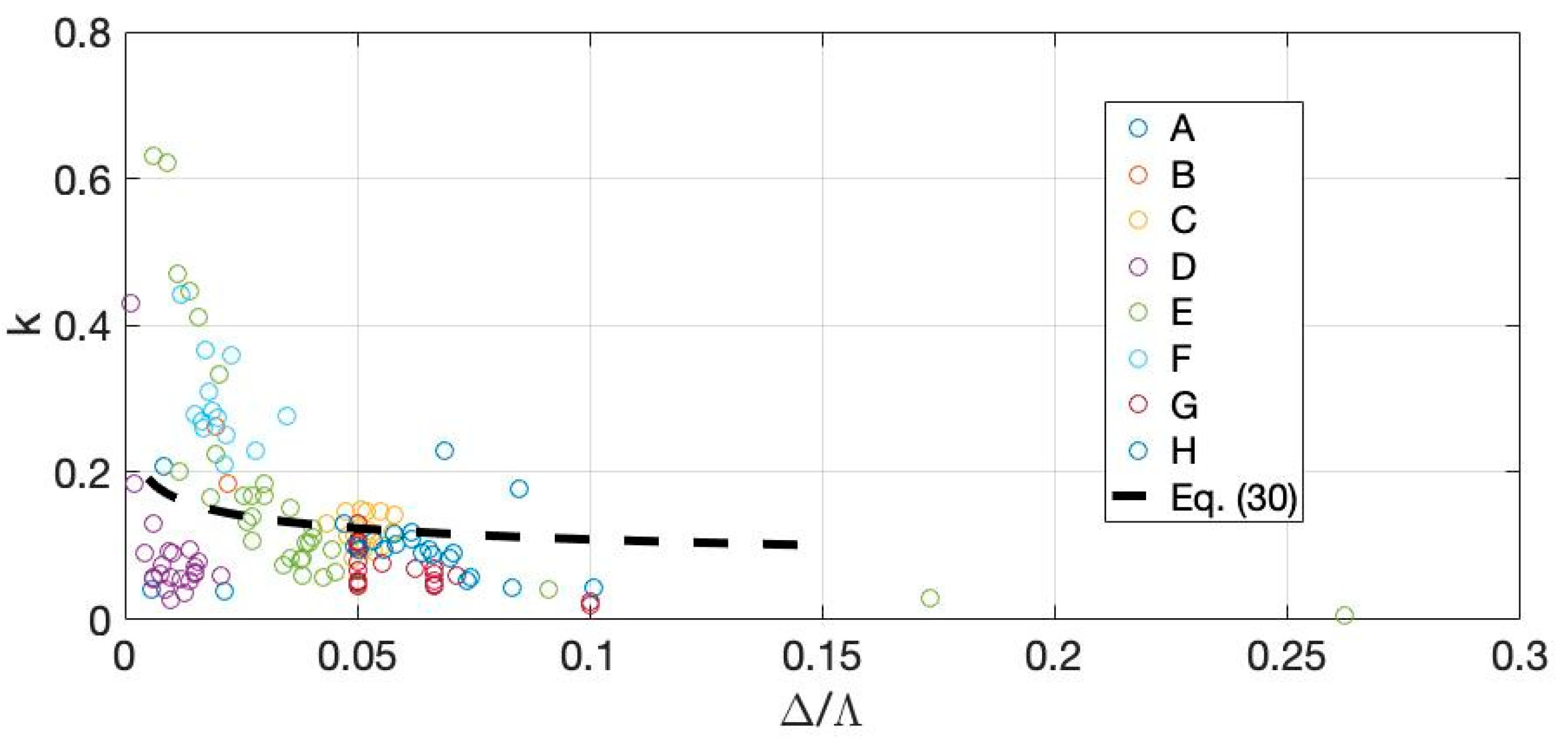
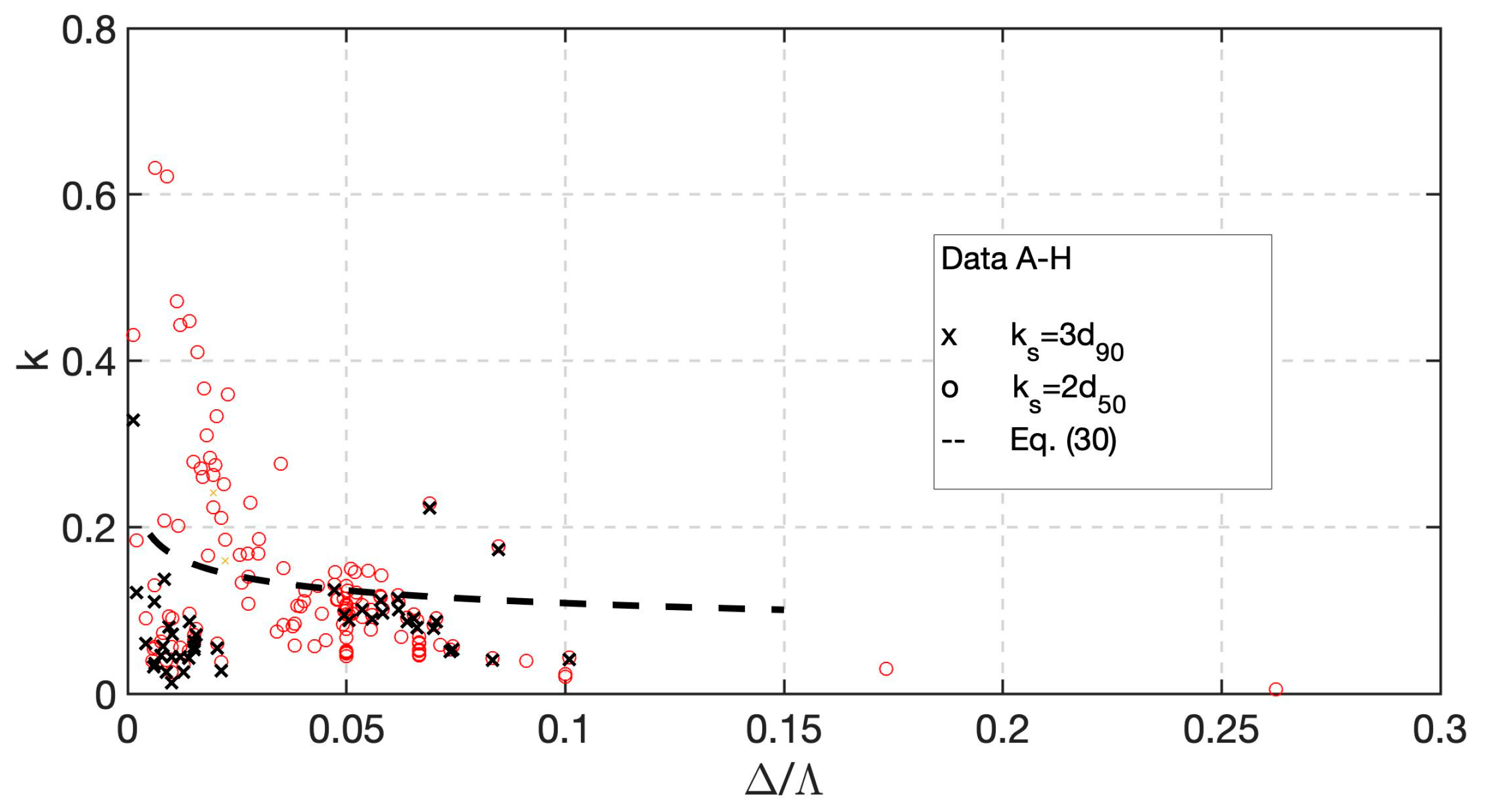
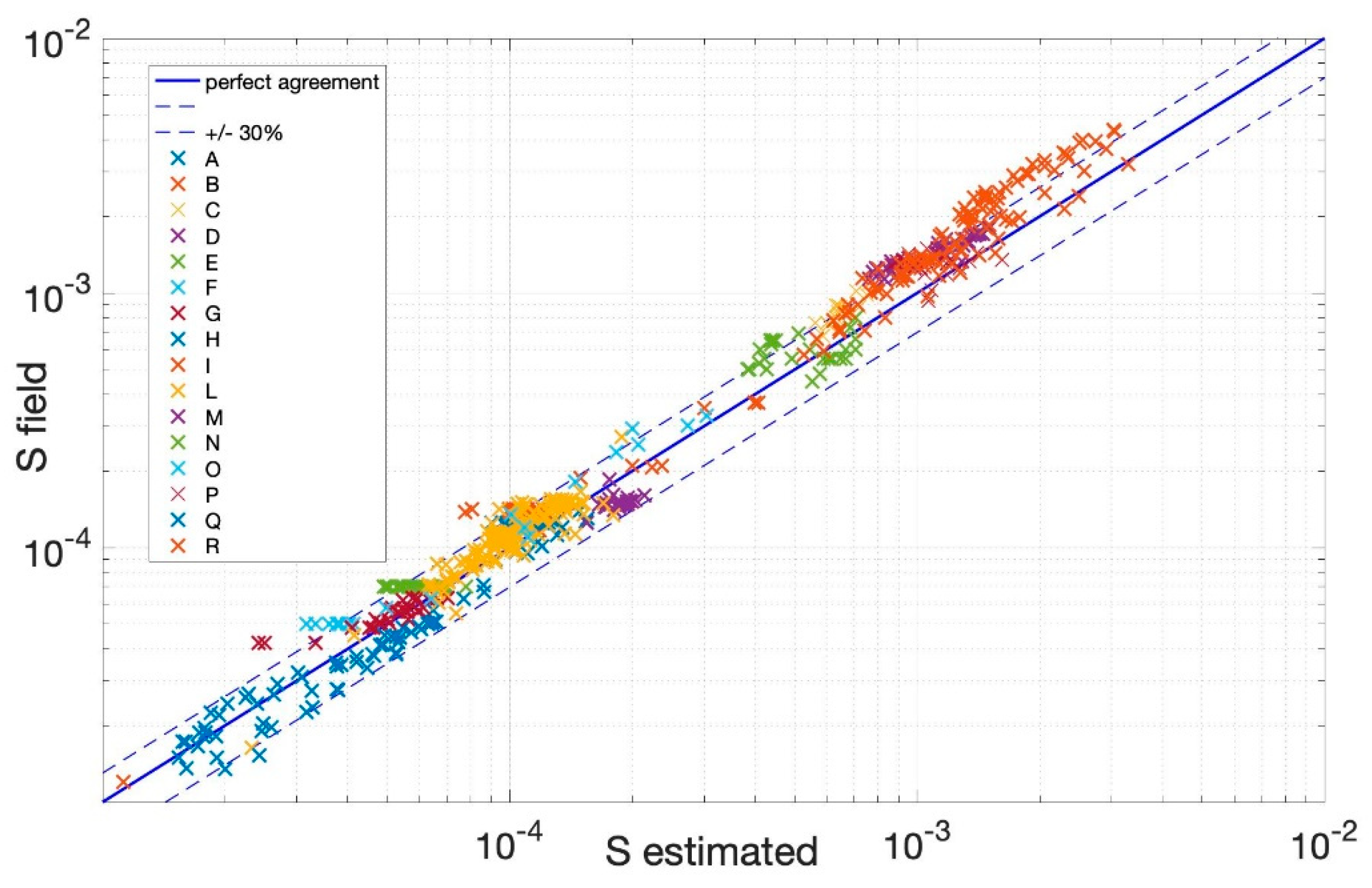
5. Model Validation and Sensitivity Analysis to the Bed Form Geometry and Skin Roughness
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| C′ | dimensionless conveyance Chezy coefficient related to the skin roughness |
| ds | representative sediment diameter |
| F | Froude number |
| g | gravity acceleration |
| G | mass force vector acting on the control volume of streamflow |
| k | Von Karman’s constant |
| ks’ | equivalent grain roughness |
| L | river reach length |
| m | fitting parameter of empirical correction function κ |
| M1, M2 | momentum flux in stream wise direction |
| M | momentum flux vector trough the surface of the control volume of the streamflow |
| n | fitting parameter of empirical correction function |
| n′ | Manning coefficient related to grain roughness |
| u | local flow velocity |
| shear velocity related to the skin roughness | |
| U | mean flow velocity |
| P1, P2,PL | pressure force acting on the upstream, downstream cross section, and on the lee side of the dune, with respect to the control volume of the streamflow |
| P | pressure vector acting on the boundary surface of the control volume of streamflow |
| q | water discharge per unit with of the channel |
| Re | Reynolds’ number |
| S | friction slope |
| S′ | friction slope due to the grain resistance |
| S″ | friction slope due to the dune drag |
| TL | shear stress on the lee side of the dune |
| y | mean flow depth |
| local water depth | |
| z | vertical elevation above the river bed |
| Z | relative submergence |
| αi | Coriolis coefficient |
| β | momentum coefficient |
| γs | specific weight of immersed sediment |
| ΓΔ/y and Γ PΔ/y | dune geometric correction function |
| δ | dune steepness |
| Δ | dune height |
| ΔH | total head loss |
| ΔH′ | head loss due to the grain resistance |
| ΔH″ | head loss due to the dune drag |
| ΔHP″ | head loss due to the dune drag according to pressure pipe flow approach |
| κ | empirical correction coefficient |
| Λ | dune length |
| ν | kinematic viscosity of water |
| ρ | density of water |
| σ | average river bedslope |
| τ | total bed shear stress |
| τ’ | grain shear stress contribution to the total bed shear stress |
| τ″ | bedform shear stress contribution to the total bed shear stress |
| ω | angle between the lee dune side and the horizontal |
References
- Cao, Z.; Carling, P.A. Mathematical modelling of alluvial rivers: Reality and myth. Part 1: General review. Proceedings of the Institution of Civil Engineers. Water Marit. Eng. 2002, 154, 207–219. [Google Scholar] [CrossRef]
- Wang, S.S.Y.; Wu, W. River sedimentation and morphology modeling—The state of the art and future development. In Proceedings of the 9th International Symposium on River Sedimentation, Yichang, China, 18–21 October 2004; pp. 71–94. [Google Scholar]
- Amoudry, L.O.; Souza, A.J. Deterministic coastal morphological and sediment transport modeling: A review and discussion. Rev. Geophys. 2011, 49. [Google Scholar] [CrossRef]
- Maldonado, S.; Borthwick, A.G.L. Quasi-two-layer morphodynamic model for bedload-dominated problems: Bed slope-induced morphological diffusion. R. Soc. Open Sci. 2018, 5, 172018. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Cao, Z.; Pender, G.; Liu, Q. A double layer-averaged model for dam-break flows over mobile bed. J. Hydraul. Res. 2013, 51, 518–534. [Google Scholar] [CrossRef]
- Iverson, R.M.; Ouyang, C. Entrainment of bed material by Earth-surface mass flows: Review and reformulation of depth-integrated theory. Rev. Geophys. 2015, 53, 27–58. [Google Scholar] [CrossRef]
- Abril, J.B.; Altinakar, M.S.; Wu, W. One-dimensional numerical modelling of river morphology processes with non-uniform sediment. In Proceedings of the River Flow 2012, San Jose, Costa Rica, 5–7 September 2012; pp. 529–535. [Google Scholar]
- Einstein, H.A.; Barbarossa, N.L. River channel roughness. Trans. Am. Soc. Civ. Eng. 1952, 117, 1121–1146. [Google Scholar]
- Engelund, F.; Hansen, E. A Monograph on Sediment Transport in Alluvial Streams; Teknisk Forlag: Copenhagen, Denmark, 1967; pp. 1–62. [Google Scholar]
- Van Rijn, L.C. Sediment Transport, Part III Bed Forms and Alluvial Roughness. J. Hydraul. Eng. ASCE 1984, 110, 1733–1755. [Google Scholar] [CrossRef]
- White, P.J.; Paris, E.; Bettess, R. The frictional characteristics of alluvial streams: A new approach. Proc. Inst. Civ. Eng. 1980, 69, 737–750. [Google Scholar] [CrossRef]
- Karim, M.F.; Kennedy, J.F. Menu of Coupled Velocity and Sediment Discharge Relations for Rivers. J. Hydraul. Eng. 1990, 116, 978–996. [Google Scholar] [CrossRef]
- Yang, S.; Tan, S. Flow resistance over mobile bed in an open channel flow. J. Hydraul. Eng. 2008, 134, 937–947. [Google Scholar] [CrossRef]
- Billi, P.; Salemi, E.; Preciso, E.; Ciavola, P.; Armaroli, C. Field measurement of bedload in a sand-bed river supplying a sediment starving beach. Z. Geomorphol. 2017, 61, 207–223. [Google Scholar] [CrossRef]
- Yalin, M.S. Mechanics of Sediment Transport, 2nd ed.; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Van Rjin, L.C. Equivalent roughness of alluvial bed. J. Hydraul. Eng. Div. ASCE 1982, 118, 1215–1218. [Google Scholar]
- Yu, G.L.; Lim, S.Y. Modified Manning Formula for Flow in Alluvial Channels with SandBeds. J. Hydraul. Res. 2003, 41, 597–608. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In Proceedings of the 3rd Meeting of IAHR, Stockholm, Sweden, 7 June 1948; pp. 39–64. [Google Scholar]
- Azareh, S.; Afzalimehr, H.; Poorhosein, M.; Singh, V.P. Contribution of Form Friction to Total Friction Factor. Int. J. Hydraul. Eng. 2014, 2, 77–84. [Google Scholar]
- Yalin, M.S.; Karahan, E. Steepness of sedimentary dunes. J. Hydraul. Div. 1979, 105, 381–392. [Google Scholar]
- Julien, P.Y.; Klaassen, G. Sand dune geometry of large rivers during floods. J. Hydraul. Eng. 1995, 121, 657–663. [Google Scholar] [CrossRef]
- Yalin, M.S. On the average velocity of flow over a mobile bed. La Houille Blanche 1964, 1, 45–53. [Google Scholar] [CrossRef]
- Agarwal, V.C.; Ranga Raju, K.G.; Garde, R.J. Bed-form geometry in sand-bed flows; Discussion. J. Hydraul. Eng. 2001, 127, 433–434. [Google Scholar] [CrossRef]
- Yalin, M.S. Geometrical properties of sand waves. J. Hydraul. Div. 1964, 90, 105–119. [Google Scholar]
- Aberle, J.; Nikora, V.; Henning, M.; Ettmer, B.; Hentschel, B. Statistical characterization of bed roughness due to bed forms: A field study in the Elbe River at Aken, Germany. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Yang, S.; Tan, S.; Lim, S. Flow resistance and bed form geometry in a wide alluvial channel. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Engelund, F. Hydraulic resistance of alluvial streams. J. Hydraul. Div. 1966, 922, 315–326. [Google Scholar]
- Ferreira Da Silva, A.M.; Yalin, M.S. Fluvial Processes, 2nd ed.; IAHR Monograph; Taylor & Francis Group: London, UK, 2017. [Google Scholar]
- Einstein, H.A. The Bed Load Function for Sediment Transportation in Open Channel Flows; Technical Bulletin 1026; U.S. Dept of Agriculture Soil Conservation Service: Washington, DC, USA, 1950.
- Ackers, P.; White, W. Sediment Transport: New Approach and Analysis. J. Hydraul. Div. 1973, 99, 2041–2060. [Google Scholar]
- Hey, R.D. Flow Resistance in Gravel-Bed Rivers. J. Hydraul. Div. 1979, 105, 365–379. [Google Scholar]
- Kamphuis, J.W. Determination of sand roughness for fixed beds. J. Hydraul. Res. 1974, 12, 193–203. [Google Scholar] [CrossRef]
- Whiting, P.J.; Dietrich, W.E. Boundary shear stress and roughness over mobile bed. J. Hydraul. Eng. 1990, 116, 1495–1511. [Google Scholar] [CrossRef]
- Millar, R.G. Grain and form resistance in gravel-bed rivers Résistances de grain et de forme dans les rivières à graviers. J. Hydraul. Res. 1999, 37, 303–312. [Google Scholar] [CrossRef]
- Tokyay, N.D.; Altan-Sakarya, A.B. Local energy losses at positive and negative steps in subcritical open channel flows. Water SA 2011, 37, 237–244. [Google Scholar] [CrossRef]
- van der Mark, C.F. A Semi-Analytical Model for Form Drag of River Bedforms. Ph.D. Thesis, University of Twente, Twente, The Nederlands, 1978. [Google Scholar]
- Engel, P. Length of flow separation over dunes. J. Hydraul. Div. 1981, 107, 1133–1143. [Google Scholar]
- Shen, H.W.; Fehlman, H.M.; Mendoza, C. Bed form resistances in open channel flows. J. Hydraul. Eng. 1990, 116, 799–815. [Google Scholar] [CrossRef]
- Cilli, S.; Ciavola, P.; Billi, P.; Schippa, L. Moving dunes constrain flow hydraulics in mobile sand-bed streams: The Fiumi Uniti and Savio River cases (Italy). Geomorphology 2019. submitted for publication. [Google Scholar]
- Gabel, S.L. Geometry and kinematics of dunes during steady and unsteady flows in the Calamus River, Nebraska, USA. Sedimentology 1993, 40, 237–269. [Google Scholar] [CrossRef]
- Brownlie, W.R. Compilation of Alluvial Channel Data: Laboratory and Field; Report No. KH-R-43B; California Institute of Technology, WM Keck Laboratory of Hydraulics and Water Resources Division of Engineering and Applied Science: Pasadena, CA, USA, 1981; pp. 1–209.
- Julien, P. Study of Bedform Geometry in Large Rivers; Report Q 1386 Delft Hydraulics; Delft Hydraulics: Delft, The Netherlands, 1992; pp. 1–79. [Google Scholar]
- Colby, B.R.; Hembxee, C.H. Computation of Total Sediment Discharge, Niobrara River Near Cody, Nebraska; Geological survey water-supply paper 1357; U.S. Government Printing Office: Washington, DC, USA, 1955; pp. 1–187. [CrossRef]
- Karim, F. Bed form geometry in sand dunes. J. Hydraul. Eng. 1999, 152, 1253–1261. [Google Scholar] [CrossRef]
- Yen, B.C. Open Channel Flow Resistance. J. Hydraul. Eng. 2002, 128, 20–39. [Google Scholar] [CrossRef]
- Keulegan, G.H. Laws of turbulent flow in open channels. J. Res. Nalt. Bur. Stand. 1938, 21, 707–741. [Google Scholar] [CrossRef]

| Code | River | N | Q (m3/s) | Y (m) | U (m/s) | S (m/km) | F (-) | d50 (mm) | d90 (mm) | Δ (m) | Λ (m) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | Fiumi Uniti | 22 | 358.40–21.17 | 4.72–1.31 | 1.66–0.20 | 0.139–0.002 | 0.24–0.04 | 0.655–0.390 | 2.100–0.630 | 0.28–0.10 | 17.53–13.1 |
| B | Savio | 9 | 132.06–7.04 | 3.58–1.77 | 1.50–0.21 | 0.354–0.012 | 0.28–0.05 | 0.548–0.412 | 1.702–0.694 | 0.16–0.12 | 7.16–6.14 |
| C | Calamus | 18 | 1.73–0.82 | 0.61–0.34 | 0.77–0.61 | 1.100–0.680 | 0.34–0.29 | 0.410–0.310 | - | 0.20–0.10 | 4.05–2.02 |
| D | Missouri | 25 | 1817.20–179.20 | 4.99–2.77 | 1.76–1.28 | 0.185–0.125 | 0.32–0.22 | 0.266–0.190 | 0.311–0.217 | 2.07–0.58 | 735.18–57.91 |
| E | Jamuna | 33 | 10000–5000 | 19.50–8.20 | 1.50–1.30 | 0.070 | 0.17–0.09 | 0.200 | - | 5.10–0.80 | 251.00–8.00 |
| F | Parana | 13 | 25000 | 26.00–22.00 | 1.50–1.00 | 0.050 | 0.10–0.07 | 0.370 | - | 7.50–3.00 | 450.00–100.00 |
| G | Zaire | 29 | 28490–284 | 17.60–6.80 | 1.69–0.32 | 0.345–0.042 | 0.16–0.03 | 0.545–0.430 | 1.900–0.430 | 1.90–1.20 | 450.00–90.00 |
| H | Bergsche Maas | 20 | 2160 | 10.50–5.80 | 1.70–1.30 | 0.125 | 0.20–0.13 | 0.520–0.210 | - | 2.50–0.40 | 50.00–6.00 |
| Code | River | N | Q (m3/s) | Y (m) | U (m/s) | S (m/km) | F (-) | d50 (mm) | d90 (mm) | Δ (m) | Λ (m) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | Meuse | 44 | 1743.0–1731.0 | 9.52–8.22 | 1.57–0.87 | 0.141–0.138 | 0.17–0.09 | 0.650–0.500 | 2.500–1.030 | 0.85–0.58 | 13.42–7.03 |
| L | ACP–ACOP | 151 | 528.68–27.50 | 4.30–0.76 | 1.29–0.35 | 0.271–0.016 | 0.23–0.12 | 0.364–0.083 | 0.466–0.105 | - | - |
| M | Niobrara | 40 | 16.06–5.86 | 0.59–0.40 | 1.27–0.65 | 1.799–1.136 | 0.54–0.30 | 0.359–0.212 | 0.849–0.326 | - | - |
| N | Rio Grande | 33 | 42.19–1.67 | 1.51–0.39 | 1–69–0.10 | 0.800–0.450 | 0.49–0.04 | 0.280–0.160 | 0.417–0.198 | - | - |
| O | AMC | 11 | 29.42–1.22 | 2.53–0.80 | 0.79–0.42 | 0.3300.058 | 0.25–0.10 | 7.000–0.096 | 1.440–0.331 | - | - |
| P | MID | 38 | 13.62–9.03 | 0.41–0.25 | 1.12–0.59 | 1.572–0.929 | 0.72–0.32 | 0.436–0.215 | 1.264–0.346 | - | - |
| Q | ATC | 55 | 14186.31–1449.78 | 14.75–6.92 | 2.03–0.64 | 0.051–0.014 | 0.17–0.06 | 0.303–0.085 | 0.708–0.169 | - | - |
| Dataset | Λ/y | S′ | Validated Data within Error Band | |
|---|---|---|---|---|
| 30% | 20% | |||
| model | 7.30 | Equation (11) ks’ = 2.0·d50 | 93.5% | 68.4% |
| test | 6.28 | 93.1% | 69.4% | |
| test | 5.00 | 91.3% | 68.6% | |
| test | 7.30 | Equation (11) ks’ = 1.0·d50 | 90.7% | 62.5% |
| test | Equation (38) | 88.2% | 63.9% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schippa, L.; Cilli, S.; Ciavola, P.; Billi, P. Dune Contribution to Flow Resistance in Alluvial Rivers. Water 2019, 11, 2094. https://doi.org/10.3390/w11102094
Schippa L, Cilli S, Ciavola P, Billi P. Dune Contribution to Flow Resistance in Alluvial Rivers. Water. 2019; 11(10):2094. https://doi.org/10.3390/w11102094
Chicago/Turabian StyleSchippa, Leonardo, Silvia Cilli, Paolo Ciavola, and Paolo Billi. 2019. "Dune Contribution to Flow Resistance in Alluvial Rivers" Water 11, no. 10: 2094. https://doi.org/10.3390/w11102094
APA StyleSchippa, L., Cilli, S., Ciavola, P., & Billi, P. (2019). Dune Contribution to Flow Resistance in Alluvial Rivers. Water, 11(10), 2094. https://doi.org/10.3390/w11102094






