Numerical Modeling of Multiple Inclined Dense Jets Discharged from Moderately Spaced Ports
Abstract
1. Introduction
2. Materials and Methods
2.1. Dimensional Analysis
2.2. Governing Equations
2.3. Turbulence Modeling
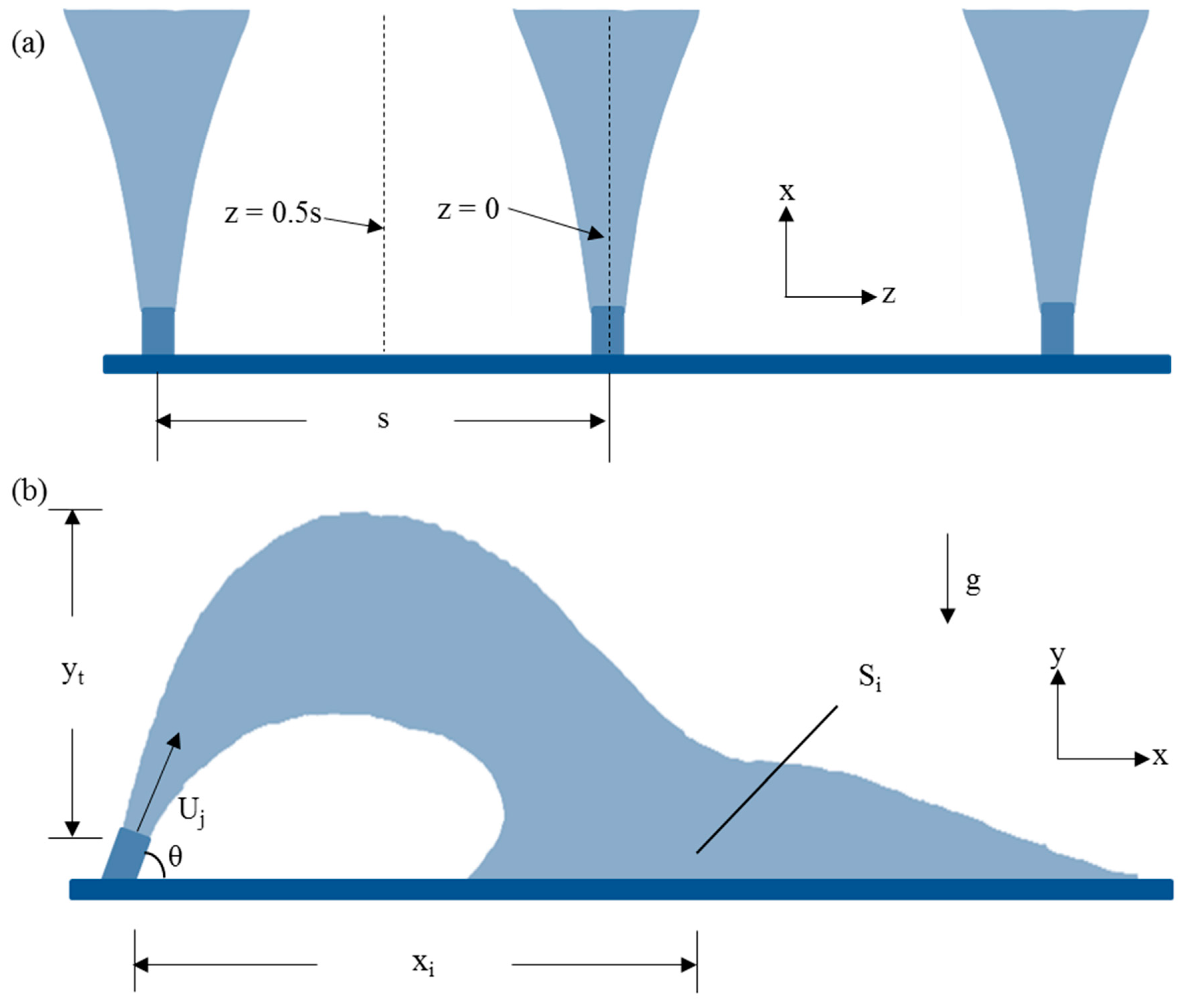
2.4. Model Setup
3. Results
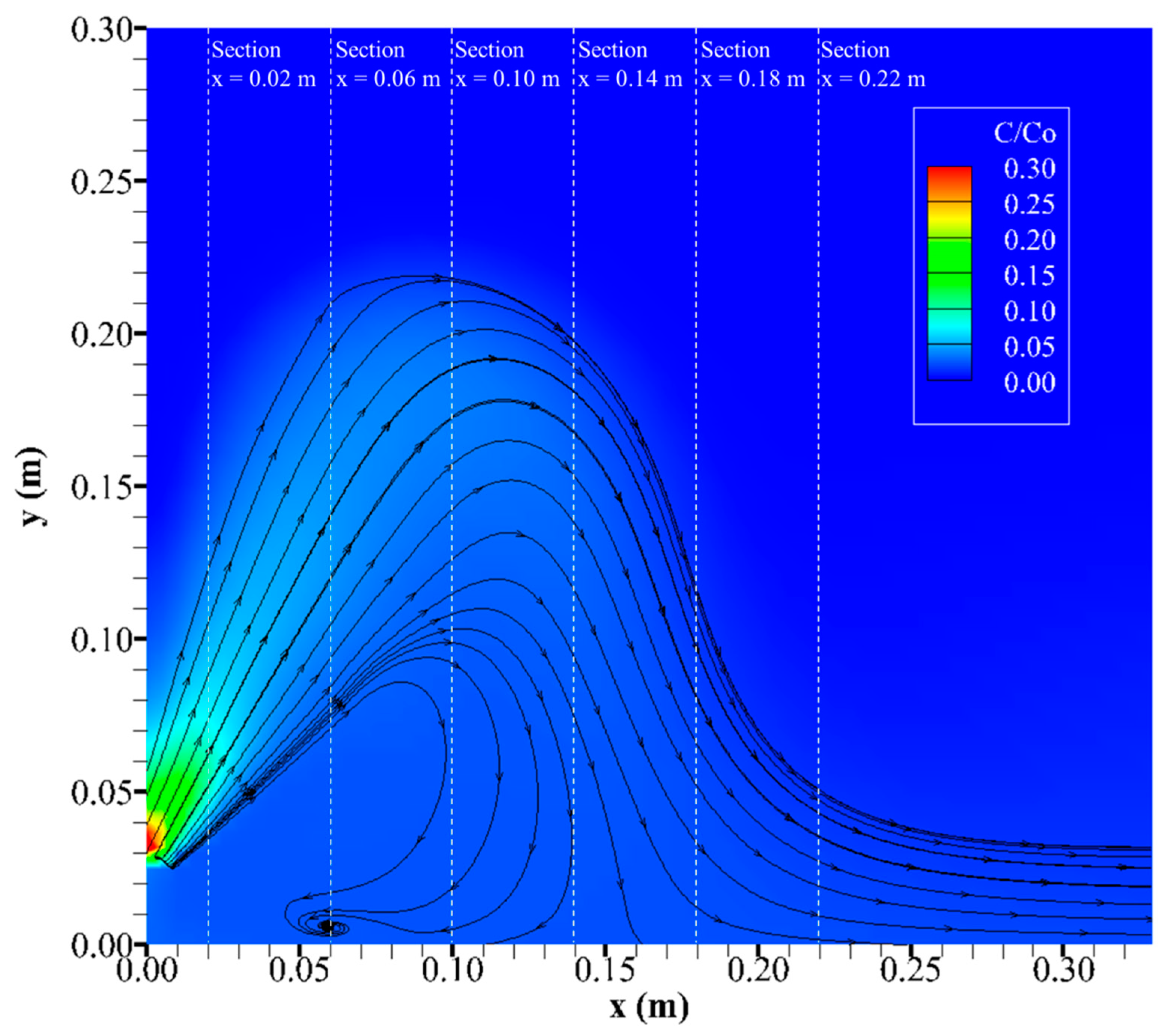
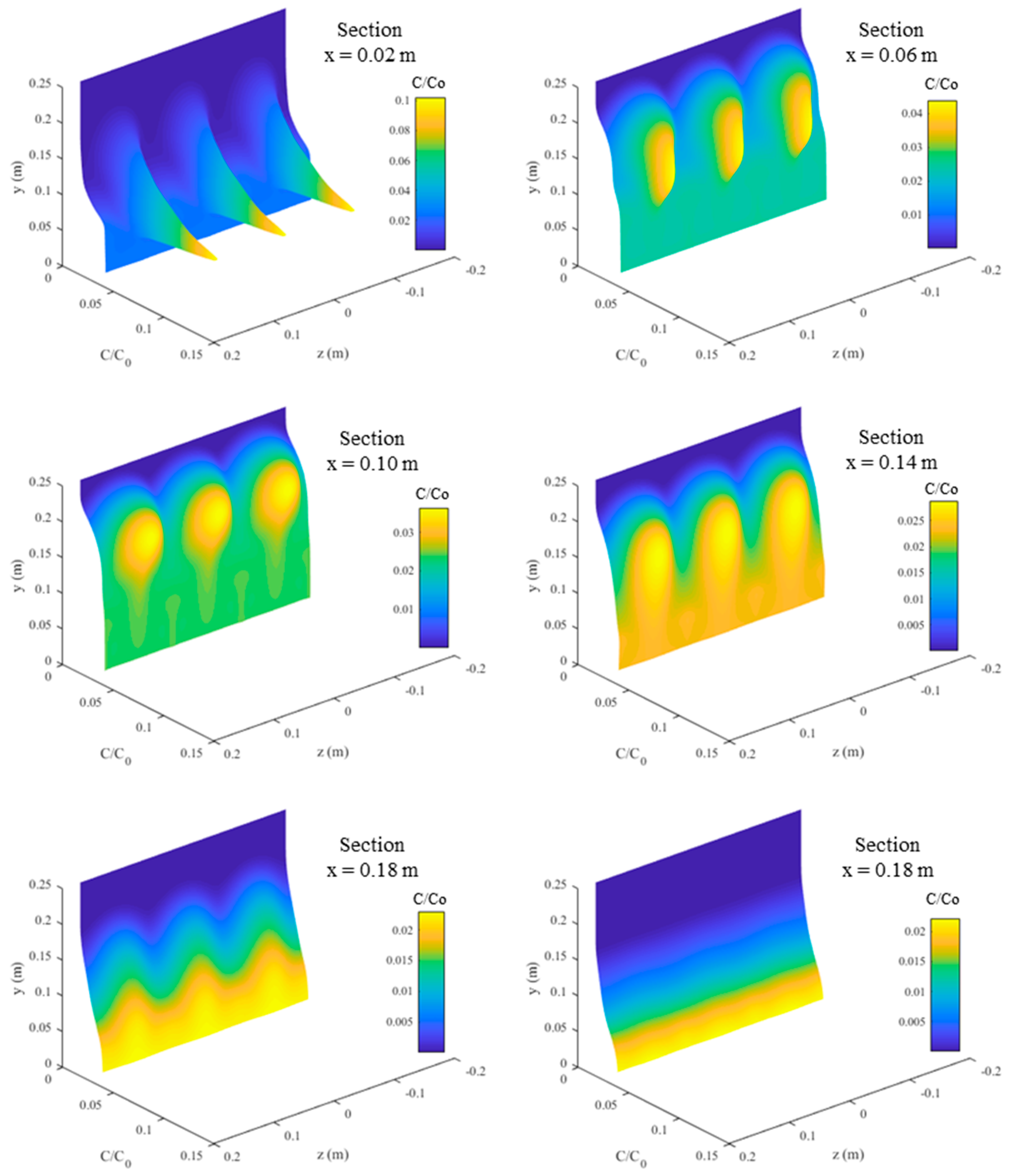
3.1. General Observations
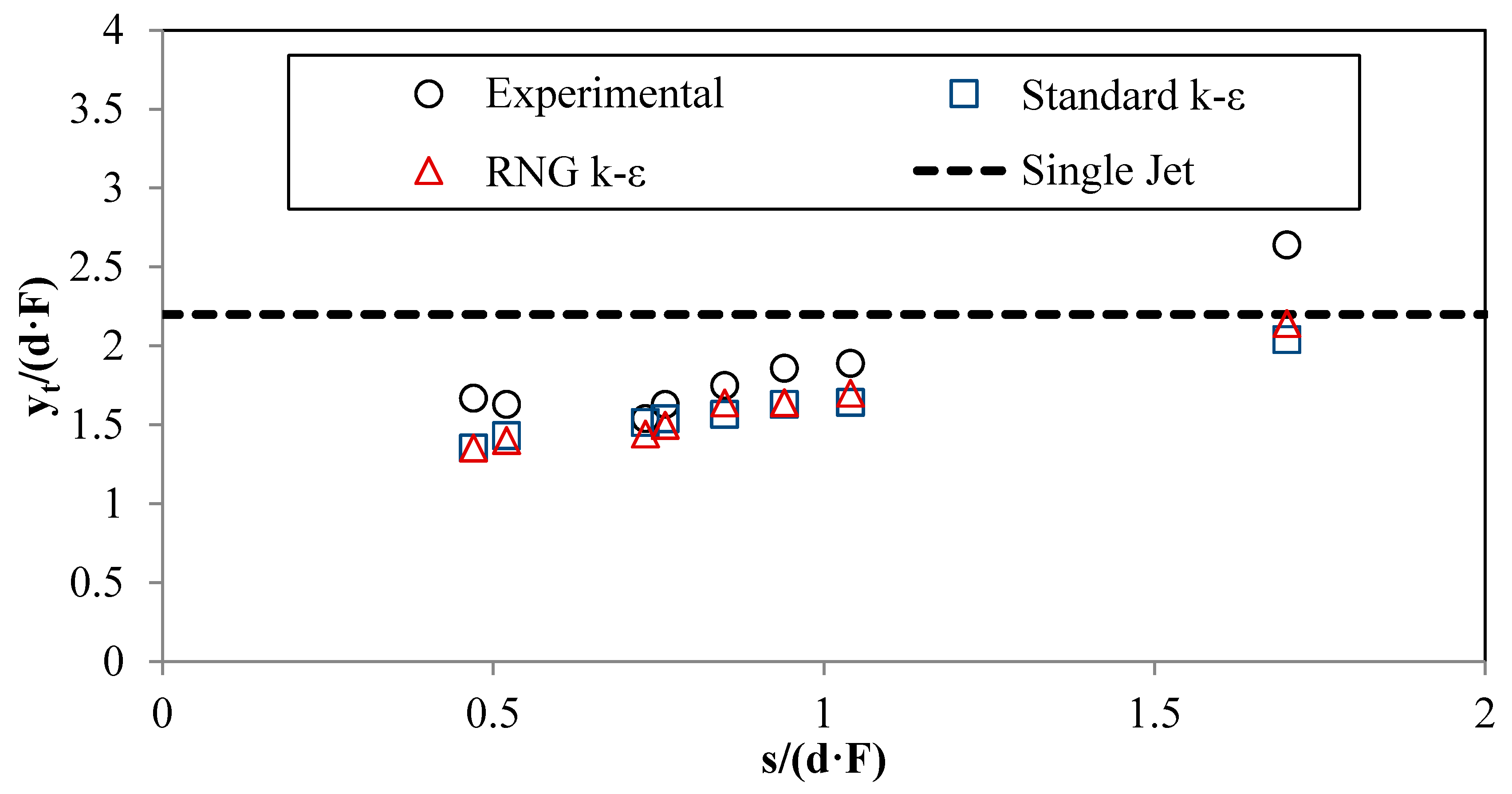
3.2. Terminal Rise Height
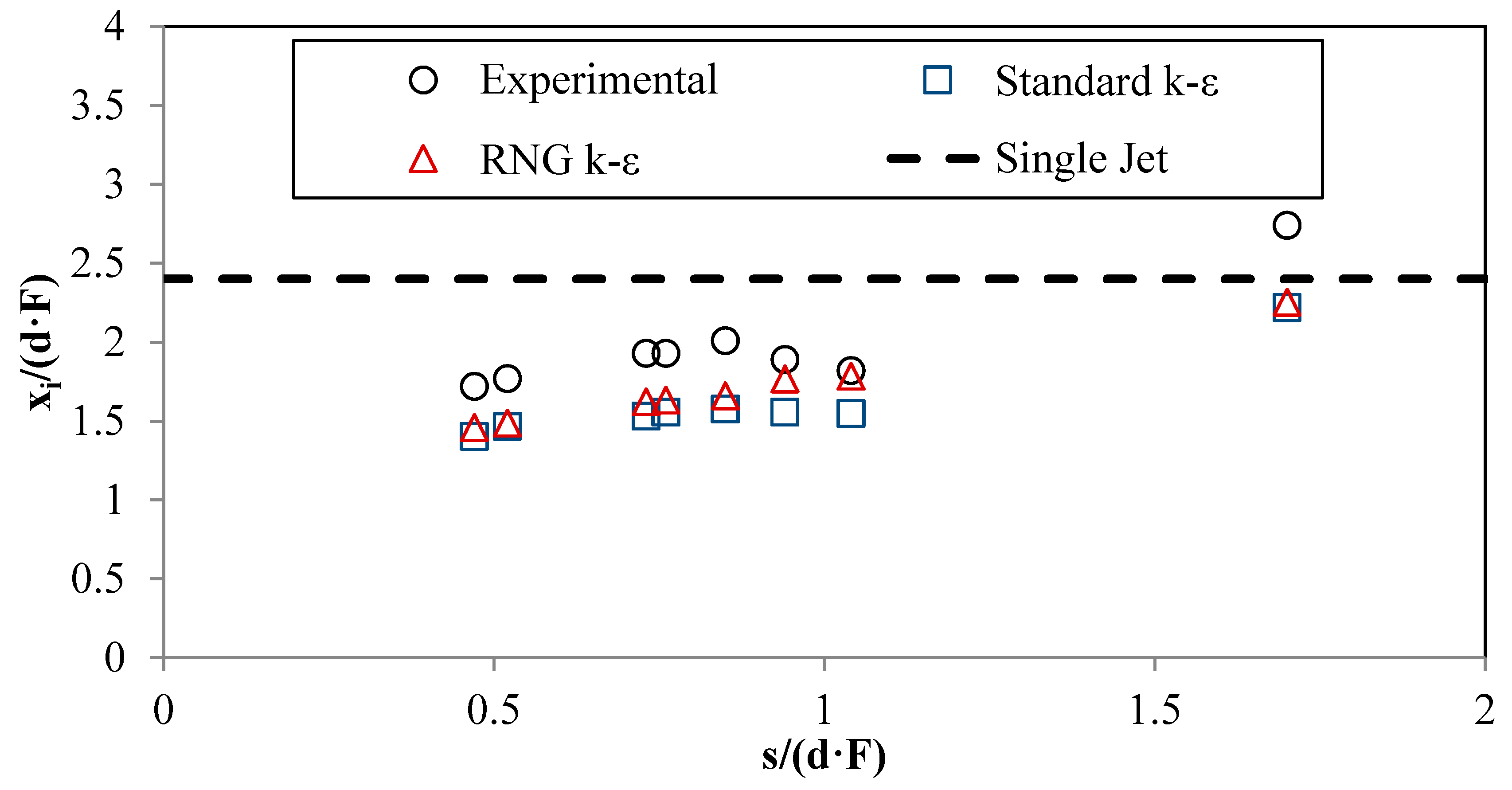
3.3. Impact Distance
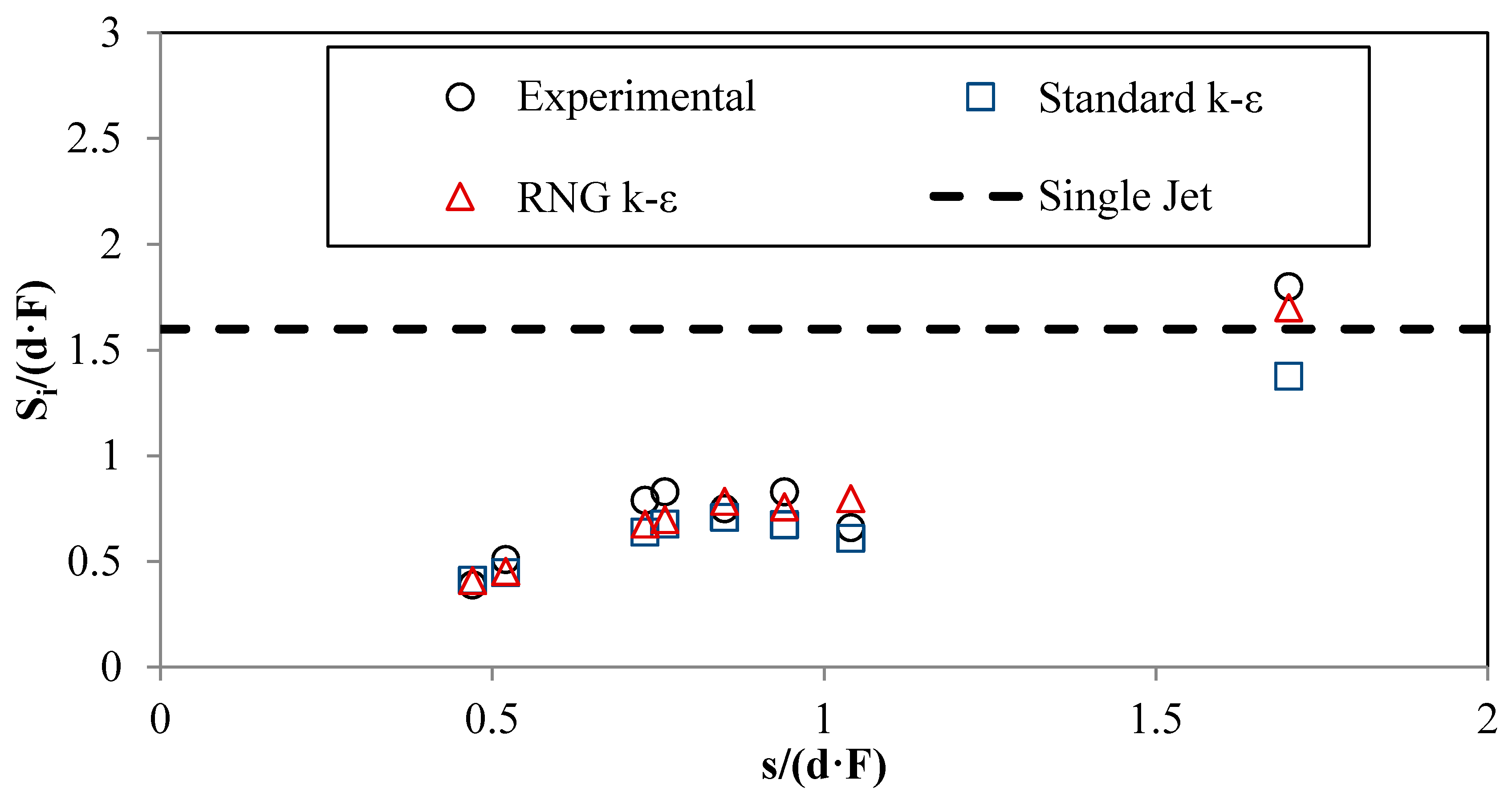
3.4. Impact Dilution
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shao, D.; Law, A.W.K. Boundary impingement and attachment of horizontal offset dense jets. J. Hydro-Environ. Res. 2011, 5, 15–24. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J. Multiport diffusers for dense discharges. J. Hydraul. Eng. 2014, 140, 04014032. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J. Multiport diffusers for dense discharge in flowing ambient water. J. Hydraul. Eng. 2017, 143, 04017003. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J. Rosette Diffusers for Dense Effluents in Flowing Currents. J. Hydraul. Eng. 2017, 144, 06017024. [Google Scholar] [CrossRef]
- Shrivastava, I.; Adams, E.E. Pre-dilution of desalination reject brine: Impact on outfall dilution in different water depths. J. Hydro-environ. Res. 2019, 24, 28–35. [Google Scholar] [CrossRef]
- Jiang, M.; Law, A.W.K.; Zhang, S. Mixing behavior of 45 inclined dense jets in currents. J. Hydro-Environ. Res. 2018, 18, 37–48. [Google Scholar] [CrossRef]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. Removing the boundary influence on negatively buoyant jets. Environ. Fluid Mech. 2013, 13, 625–648. [Google Scholar] [CrossRef]
- Lyu, S.; Seo, I.W.; Do Kim, Y. Experimental investigation on behavior of multiple vertical buoyant jets discharged into a stagnant ambient. KSCE J. Civil Eng. 2013, 17, 1820–1829. [Google Scholar] [CrossRef]
- Wang, H.J.; Davidson, M.J. Jet interaction in a still ambient fluid. J. Hydraul. Eng. 2003, 129, 349–357. [Google Scholar] [CrossRef]
- Knystautas, R. The turbulent jet from a series of holes in line. Aeronaut. Q. 1964, 15, 1–28. [Google Scholar] [CrossRef]
- Liseth, P. Mixing of merging buoyant jets from a manifold in stagnant receiving water of uniform density. In Advances in water pollution research. In Advances in Water Pollution Research Proceedings of the 6th International Conference, Jerusalem, Israel, 18–23 June 1972; Pergamon Press: Oxford, UK, 1973; pp. 921–936. [Google Scholar]
- Shinneeb, A.M.; Balachandar, R.; Bugg, J.D. Confinement effects in shallow-water jets. J. Hydraul. Eng. 2010, 137, 300–314. [Google Scholar] [CrossRef]
- Yannopoulos, P.C.; Noutsopoulos, G.C. Interaction of vertical round turbulent buoyant jets—Part I: Entrainment restriction approach. J. Hydraul. Res. 2006, 44, 218–232. [Google Scholar] [CrossRef]
- Adams, E.E. Submerged Multiport Diffusers in Shallow Water with Current. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1972. [Google Scholar]
- Shrivastava, I.; Adams, E.E. Mixing of Tee Diffusers in Shallow Water with Crossflow: A New Look. J. Hydraul. Eng. 2019, 145, 04019006. [Google Scholar] [CrossRef]
- Xu, Z.; Otoo, E.; Chen, Y.; Ding, H. 2D PIV Measurement of Twin Buoyant Jets in Wavy Cross-Flow Environment. Water 2019, 11, 399. [Google Scholar] [CrossRef]
- Hodgson, J.E.; Moawad, A.K.; Rajaratnam, N. Concentration field of multiple circular turbulent jets. J. Hydraul. Res. 1999, 37, 249–256. [Google Scholar] [CrossRef]
- Lai, A.C.; Lee, J.H. Dynamic interaction of multiple buoyant jets. J. Fluid Mech. 2012, 708, 539–575. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Multigene Genetic-Programming-Based Models for Initial Dilution of Laterally Confined Vertical Buoyant Jets. J. Mar. Sci. Eng. 2019, 7, 246. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Evolutionary modeling of inclined dense jets discharged from multiport diffusers. J. Coast. Res. 2019, in press. [Google Scholar] [CrossRef]
- Wang, R.Q.; Law, A.W.K.; Adams, E.E.; Fringer, O.B. Large-eddy simulation of starting buoyant jets. Environ. Fluid Mech. 2011, 11, 591–609. [Google Scholar] [CrossRef]
- Kheirkhah Gildeh, H.; Mohammadian, A.; Nistor, I.; Qiblawey, H.; Yan, X. CFD modeling and analysis of the behavior of 30° and 45° inclined dense jets—New numerical insights. J. Appl. Water Eng. Res. 2016, 4, 112–127. [Google Scholar] [CrossRef]
- Kheirkhah Gildeh, H.; Mohammadian, A.; Nistor, I.; Qiblawey, H. Numerical modeling of 30° and 45° inclined dense turbulent jets in stationary ambient. Environ. Fluid Mech. 2015, 15, 537–562. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, B.; Law, A.W.K.; Zhao, B. Large eddy simulations of 45 inclined dense jets. Environ. Fluid Mech. 2016, 16, 101–121. [Google Scholar] [CrossRef]
- Alfaifi, H.; Mohammadian, A.; Gildeh, H.K.; Gharavi, A. Experimental and numerical study of the characteristics of thermal and nonthermal offset buoyant jets discharged into stagnant water. Desalin. Water Treat. 2019, 141, 171–186. [Google Scholar] [CrossRef]
- Kheirkhah Gildeh, H.; Mohammadian, A.; Nistor, I.; Qiblawey, H. Numerical modeling of turbulent buoyant wall jets in stationary ambient water. J. Hydraul. Eng. 2014, 140, 04014012. [Google Scholar] [CrossRef]
- Zhang, S.; Law, A.W.K.; Zhao, B. Large eddy simulations of turbulent circular wall jets. Int. J. Heat Mass Transf. 2014, 80, 72–84. [Google Scholar] [CrossRef]
- Zhang, S.; Law, A.W.K.; Jiang, M. Large eddy simulations of 45° and 60° inclined dense jets with bottom impact. J. Hydro-environ. Res. 2017, 15, 54–66. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Numerical Modeling of Vertical Buoyant Jets Subjected to Lateral Confinement. J. Hydraul. Eng. 2017, 143, 04017016. [Google Scholar] [CrossRef]
- Lou, Y.; He, Z.; Jiang, H.; Han, X. Numerical simulation of two coalescing turbulent forced plumes in linearly stratified fluids. Phys. Fluids 2019, 31, 037111. [Google Scholar]
- Fischer, H.B.; List, E.J.; Koh, R.C.H.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM®; Holzmann CFD: Loeben, Germany, 2016. [Google Scholar]
- OpenFOAM User Guide; Version 4.0; The OpenCFD Foundation: London, UK, 2016.
- Lai, A.C.; Zhao, B.; Law, A.W.K.; Adams, E.E. A numerical and analytical study of the effect of aspect ratio on the behavior of a round thermal. Environ. Fluid Mech. 2015, 15, 85–108. [Google Scholar] [CrossRef]
- Roberts, P.J.; Ferrier, A.; Daviero, G. Mixing in inclined dense jets. J. Hydraul. Eng. 1997, 123, 693–699. [Google Scholar] [CrossRef]
- Fang, S.; Chen, Y.; Xu, Z.; Otoo, E.; Lu, S. An Improved Integral Model for a Non-Buoyant Turbulent Jet in Wave Environment. Water 2019, 11, 765. [Google Scholar] [CrossRef]
| Cases | d (mm) | s (mm) | F (—) | s/(d·F) (—) |
|---|---|---|---|---|
| C1 | 1.93 | 114 | 62.9 | 0.94 |
| C2 | 1.93 | 114 | 56.8 | 1.04 |
| C3 | 1.93 | 114 | 77.3 | 0.76 |
| C4 | 1.93 | 114 | 81.1 | 0.73 |
| C5 | 1.93 | 57 | 17.3 | 1.71 |
| C6 | 1.93 | 57 | 34.7 | 0.85 |
| C7 | 1.93 | 57 | 63.1 | 0.47 |
| C8 | 1.93 | 57 | 56.8 | 0.52 |
| Model | MBE | MAE | MAPE (%) | RMSE | NRMSE (%) | R2 |
|---|---|---|---|---|---|---|
| Standard k-ε | −0.24 | 0.24 | 12.10 | 0.29 | 0.16 | 0.88 |
| RNG k-ε | −0.22 | 0.22 | 11.81 | 0.26 | 0.14 | 0.91 |
| Model | MBE | MAE | MAPE (%) | RMSE | NRMSE (%) | R2 |
|---|---|---|---|---|---|---|
| Standard k-ε | −0.37 | 0.37 | 18.56 | 0.38 | 0.19 | 0.98 |
| RNG k-ε | −0.27 | 0.27 | 13.26 | 0.30 | 0.15 | 0.84 |
| Model | MBE | MAE | MAPE (%) | RMSE | NRMSE (%) | R2 |
|---|---|---|---|---|---|---|
| Standard k-ε | −0.13 | 0.13 | 13.82 | 0.18 | 0.22 | 0.99 |
| RNG k-ε | −0.04 | 0.08 | 10.76 | 0.09 | 0.11 | 0.96 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Mohammadian, A. Numerical Modeling of Multiple Inclined Dense Jets Discharged from Moderately Spaced Ports. Water 2019, 11, 2077. https://doi.org/10.3390/w11102077
Yan X, Mohammadian A. Numerical Modeling of Multiple Inclined Dense Jets Discharged from Moderately Spaced Ports. Water. 2019; 11(10):2077. https://doi.org/10.3390/w11102077
Chicago/Turabian StyleYan, Xiaohui, and Abdolmajid Mohammadian. 2019. "Numerical Modeling of Multiple Inclined Dense Jets Discharged from Moderately Spaced Ports" Water 11, no. 10: 2077. https://doi.org/10.3390/w11102077
APA StyleYan, X., & Mohammadian, A. (2019). Numerical Modeling of Multiple Inclined Dense Jets Discharged from Moderately Spaced Ports. Water, 11(10), 2077. https://doi.org/10.3390/w11102077





