Impacts of Hydro-Climatically Varying Years on Ice Growth and Decay in a Subarctic River
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
3.1. Field Measurements
3.2. Applied Ice Growth and Decay Equations
4. Results
4.1. The Annual Variation of the Ice Cover Development
4.2. The Performance of the Ice Growth and Decay Equations
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Clark, S. Border and skim ice. In River Ice Formation; Beltaos, S., Ed.; CGU-HS CRIPE: Edmonton, AB, Canada, 2013; pp. 77–106. [Google Scholar]
- Ansari, S.; Rennie, C.; Seidou, O.; Malenchak, J.; Zare, S. Automated monitoring of river ice processes using shore-based imagery. Cold Reg. Sci. Technol. 2017, 142, 1–16. [Google Scholar] [CrossRef]
- Stefan, J. Über die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere; Sitzungsberichte der Österreichischen Akademie der Wissenschaften Mathematisch-Naturwissenschaftliche Klasse; Abteilung 2. Mathematik, Astronomie, Physik, Meteorologie und Technik, Österreichischen Akademie: Austria, 1889; Volume 98, pp. 965–983. [Google Scholar]
- U.S. Army Corps of Engineers (USACE). Engineering and Design, Ice Engineering; Manual No. 1110-2-1612; Department of the army, U.S. Army Corps of Engineers: Washington, DC, USA, 2002; p. 479.
- Ashton, G.D. Thin ice growth. Water Resour. Res. 1989, 25, 564–566. [Google Scholar] [CrossRef]
- Michel, B. Winter Regime of River and Lakes; Cold Regions Science and Engineering Monograph III-B1a; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1971; p. 131. [Google Scholar]
- Ashton, G.D. River and lake ice thickening, thinning, and snow ice formation. Cold Reg. Sci. Technol. 2011, 68, 3–19. [Google Scholar] [CrossRef]
- Sagin, J.; Van Der Sanden, J.J.; Evans, E.; McKay, H.; Das, A.; Lindenschmidt, K.-E. Monitoring the freeze-up and ice cover progression of the Slave River. Can. J. Civ. Eng. 2015, 42, 609–621. [Google Scholar]
- Dornan, L. Development of site specific ice growth models for hydrometric purposes. In Proceedings of the 13th Workshop on the Hydraulics of Ice Covered Rivers, CGU HS Committee on River Ice Processes and the Environment (CRIPE), Hanover, NH, USA, 15–16 September 2005; pp. 101–131. [Google Scholar]
- Brooks, R.N.; Prowse, T.D.; O’Connell, I.J. Quantifying Northern Hemisphere freshwater ice. Geophys. Res. Lett. 2013, 40, 1128–1131. [Google Scholar] [CrossRef]
- Kämäri, M.; Alho, P.; Colpaert, A.; Lotsari, E. Spatial variation of river-ice thickness in a meandering river. Cold Reg. Sci. Technol. 2017, 137, 17–29. [Google Scholar] [CrossRef]
- Lind, L.; Alfredsen, K.; Kuglerová, L.; Nilsson, C. Hydrological and thermal controls of ice formation in 25 boreal stream reaches. J. Hydrol. 2016, 540, 797–811. [Google Scholar] [CrossRef]
- Zhang, F.; Li, Z.; Lindenschmidt, K.-E. Potential of RADARSAT-2 to Improve Ice Thickness Calculations in Remote, Poorly Accessible Areas: A Case Study on the Slave River, Canada. Can. J. Remote Sens. 2019, 45, 234–245. [Google Scholar] [CrossRef]
- Ashton, G.D. River and Lake Ice Engineering; Water Resources Publications: Littleton, CO, USA, 1986; p. 504. [Google Scholar]
- Hicks, F. An Introduction to River Ice Engineering for Civil Engineers and Geoscientists; CreateSpace Independent Publishing Platform: Charleston, SC, USA, 2016; p. 159. [Google Scholar]
- Guo, Q. Applicability of Criterion for Onset of River Ice Breakup. J. Hydraul. Eng. 2002, 128, 1023–1026. [Google Scholar] [CrossRef]
- Bilello, M.A. Maximum Thickness and Subsequent Decay of Lake, River and Fast Sea Ice in Canada and Alaska; CRREL, REPORT 80-6; United States Army Corps of Engineers, Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1980; p. 160. [Google Scholar]
- Shen, H.T.; Yapa, P.D. A unified degree-day method for river ice cover thickness simulation. Can. J. Civ. Eng. 1985, 12, 54–62. [Google Scholar] [CrossRef]
- Ma, X.; Fukushima, Y. A numerical model of the river freezing process and its application to the Lena River. Hydrol. Process. 2002, 16, 2131–2140. [Google Scholar] [CrossRef]
- Ma, X.; Yasunari, T.; Fukushima, Y. Modeling of river ice breakup date and thickness in the lena river. In Ice in the Environment, Proceedings of the 16th IAHR International Symposium on Ice; International Association of Hydraulic Engineering and Research: Dunedin, New Zealand, 2–6 December 2002; p. 15. [Google Scholar]
- Autio, J.; Heikkinen, O. The Climate of Northern Finland. Fennia 2002, 180, 61–66. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Summary for policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the IPCC; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2014; pp. 3–29. [Google Scholar]
- AMAP. Snow, Water, Ice and Permafrost in the Arctic (SWIPA): Climate Change and the Cryosphere; Arctic Monitoring and Assessment Programme (AMAP): Oslo, Norway, 2011. [Google Scholar]
- Klavins, M.; Briede, A.; Rodinov, V. Long term changes in ice and discharge regime of rivers in the Baltic region in relation to climatic variability. Clim. Chang. 2009, 95, 485–498. [Google Scholar] [CrossRef]
- Stonevicius, E.; Stankunavicius, G.; Kilkus, K. Ice regime dynamics in the Nemunas River, Lithuania. Clim. Res. 2008, 36, 17–28. [Google Scholar] [CrossRef]
- Šarauskienė, D.; Jurgelėnaitė, A. Impact of Climate Change on River Ice Phenology in Lithuania. Environmental Research. Eng. Manag. 2008, 4, 13–22. [Google Scholar]
- Gordeev, V. Fluvial sediment flux to the Arctic Ocean. Geomorphology 2006, 80, 94–104. [Google Scholar] [CrossRef]
- Kämäri, M.; Alho, P.; Aaltonen, J.; Veijalainen, N.; Huokuna, M.; Lotsari, E. River ice cover influence on sediment transportation at present and under projected hydro-climatic conditions. Hydrol. Process. 2015, 29, 4738–4755. [Google Scholar] [CrossRef]
- Syvitski, J.P.M. Sediment discharge variability in Arctic rivers: Implications for a warmer future. Polar Res. 2002, 21, 323–330. [Google Scholar] [CrossRef]
- Veijalainen, N.; Lotsari, E.; Alho, P.; Vehviläinen, B.; Käyhkö, J. National scale assessment of climate change impacts on flooding in Finland. J. Hydrol. 2010, 391, 333–350. [Google Scholar] [CrossRef]
- Prowse, T.; Alfredsen, K.; Beltaos, S.; Bonsal, B.R.; Bowden, W.B.; Duguay, C.R.; Korhola, A.; McNamara, J.; Vincent, W.-F.; Vuglinsky, V.; et al. Effects of Changes in Arctic Lake and River Ice. Ambio 2011, 40, 63–74. [Google Scholar] [CrossRef]
- Turcotte, B.; Morse, B.; Bergeron, N.E.; Roy, A.G. Sediment transport in ice-affected rivers. J. Hydrol. 2011, 409, 561–577. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Demers, S.; Buffin-Bélanger, T.; Roy, A.G. Macroturbulent coherent structures in an ice-covered river flow using a pulse-coherent acoustic Doppler profiler. Earth Surf. Process. Landf. 2013, 38, 937–946. [Google Scholar] [CrossRef]
- Kasvi, E.; Vaaja, M.; Alho, P.; Hyyppä, H.; Hyyppä, J.; Kaartinen, H.; Kukko, A. Morphological changes on meander point bars associated with flow structure at different discharges. Earth Surf. Process. Landf. 2013, 38, 577–590. [Google Scholar] [CrossRef]
- Lotsari, E.; Kasvi, E.; Kämäri, M.; Alho, P. The effects of ice cover on flow characteristics in a subarctic meandering river. Earth Surf. Process. Landf. 2017, 42, 1195–1212. [Google Scholar] [CrossRef]
- Walsh, S.E.; Fisher, V.A.; Wynne, R.H.; Lenters, J.D.; Vavrus, S.J.; Foley, J.A. Global patterns of lake ice phenology and climate: Model simulations and observations. J. Geophys. Res. Space Phys. 1998, 103, 28825–28837. [Google Scholar] [CrossRef]
- Brooks, R.N. Quantifying Peak Freshwater Ice across the Northern Hemisphere Using a Regionally Defined Degree-Day Ice-Growth Model; Department of Geography, University of Victoria: Victoria, BC, Canada, 2012. [Google Scholar]
- Bonsal, B.R.; Prowse, T.D. Trends and Variability in Spring and Autumn 0 °C-Isotherm Dates over Canada. Clim. Chang. 2013, 57, 341–358. [Google Scholar] [CrossRef]
- White, K.D. Method to Estimate River Ice Thickness Based on Meteorological Data; U.S. Army Corps of Engineers Cold Regions Research and Engineering Laboratory, ERDC/CRREL Technical Note 04–3; Research and Development Center: Hanover, NH, USA, 2004; pp. 1–6. [Google Scholar]
- Washanta Lal, A.; Shen, H.T. A mathematical model for river ice processes. J. Hydrol. Eng. 1993, 7, 851–867. [Google Scholar]
- Ashton, G.D.; Beltaos, S. Thermal growth of ice cover. In River Ice Formation; Beltaos, S., Ed.; Committee on River Ice Processes and the environment, CHU-HS: Edmonton, AB, Canada, 2013; p. 552. [Google Scholar]
- Persson, G.; Bärring, L.; Kjellström, E.; strandberg, G.; Rummukainen, M. Climate Indices for Vulnerability Assessments; Swedish Meteorological and hydrological Institute: Norrköping, Sweden, 2007; p. 64. [Google Scholar]
- Beltaos, S. Threshold between mechanical and thermal breakup of river ice cover. Cold Reg. Sci. Technol. 2003, 37, 1–13. [Google Scholar] [CrossRef]
- Leppäranta, M. A review of analytical models of sea-ice growth. Atmos. Ocean 1993, 31, 123–138. [Google Scholar] [CrossRef]
- Beltaos, S.; Prowse, T.D.; Carter, T. Ice regime of the lower Peace River and ice-jam flooding of the Peace-Athabasca Delta. Hydrol. Process. 2006, 20, 4009–4029. [Google Scholar] [CrossRef]
- Huokuna, M.; Aaltonen, J.; Veijalainen, N. Frazil ice problems in changing climate conditions. CGU HS Committee on River Ice Processes and the Environment. In Proceedings of the 15th Workshop on River Ice, St. John’s, NL, Cannada, 15–17 June 2009; pp. 118–126. [Google Scholar]
- Turcotte, B.; Burrell, B.; Beltaos, S. The Impact of Climate Change on Breakup Ice Jams in Canada: State of knowledge and research approaches. CGU HS Committee on River Ice Processes and the Environment. In Proceedings of the 20th Workshop on the Hydraulics of Ice Covered Rivers, Ottawa, ON, Canada, 14–16 May 2019; p. 30. [Google Scholar]
- Helama, S.; Jiang, J.; Korhonen, J.; Holopainen, J.; Timonen, M. Quantifying temporal changes in Tornionjoki river ice breakup dates and spring temperatures in Lapland since 1802. J. Geogr. Sci. 2013, 23, 1069–1079. [Google Scholar] [CrossRef]
- Norrgård, S.; Helama, S. Historical trends in spring ice breakup for the Aura River in Southwest Finland, AD 1749–2018. Holocene 2019, 29, 953–963. [Google Scholar] [CrossRef]
- Sharma, S.; Magnuson, J.J.; Batt, R.D.; Winslow, L.A.; Korhonen, J.; Aono, Y. Direct observations of ice seasonality reveal changes in climate over the past 320–570 years. Sci. Rep. 2016, 6, 25061. [Google Scholar] [CrossRef] [PubMed]
- Beltaos, S. Hydro-climatic impacts on the ice cover of the lower Peace River. Hydrol. Process. 2008, 22, 3252–3263. [Google Scholar] [CrossRef]
- Turcotte, B.; Morse, B. A global river ice classification model. J. Hydrol. 2013, 507, 134–148. [Google Scholar] [CrossRef]
- Park, H.; Yoshikawa, Y.; Oshima, K.; Kim, Y.; Ngo-Duc, T.; Kimball, J.S.; Yang, D. Quantification of Warming Climate-Induced Changes in Terrestrial Arctic River Ice Thickness and Phenology. J. Clim. 2016, 29, 1733–1754. [Google Scholar] [CrossRef]
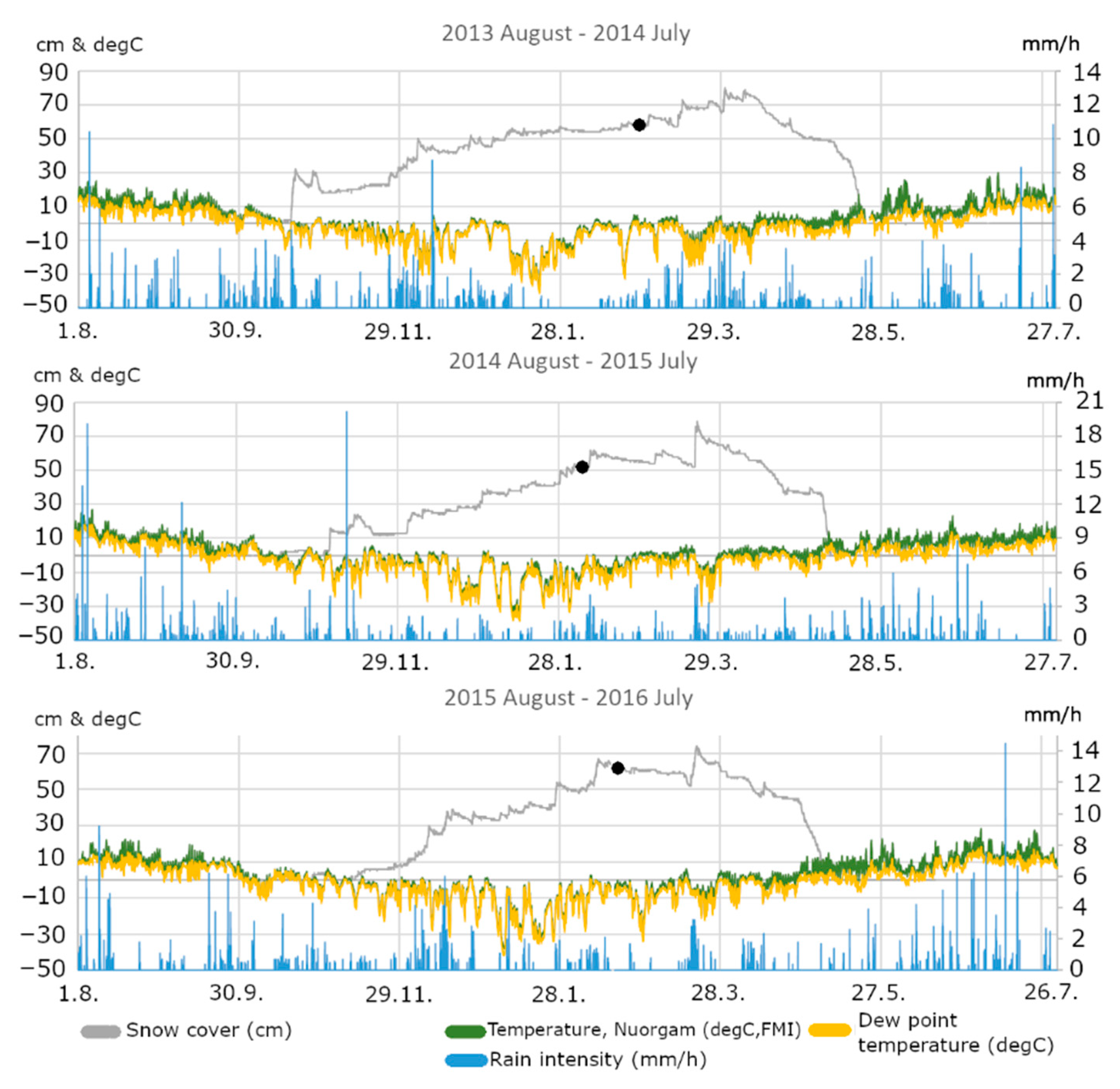
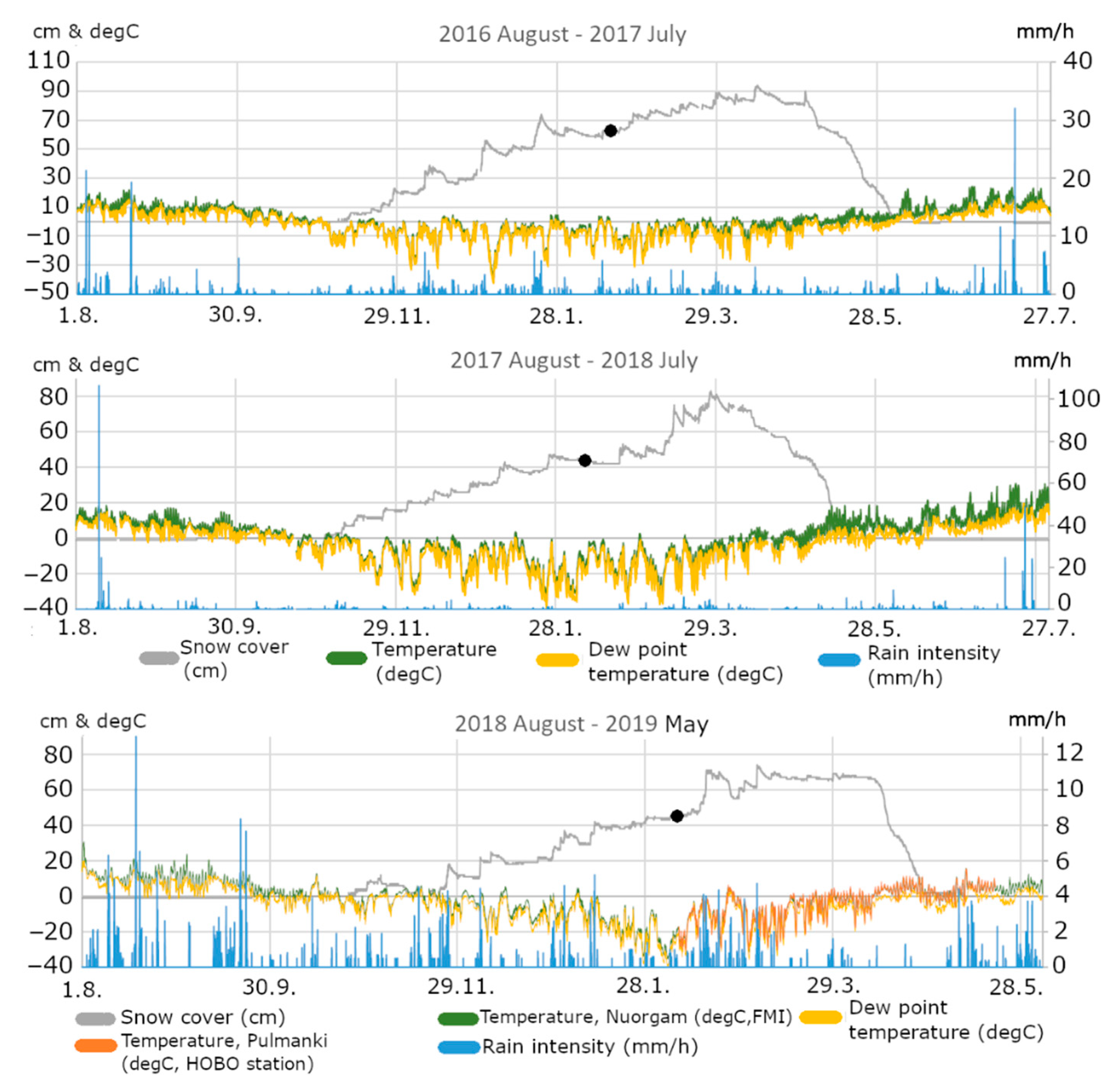
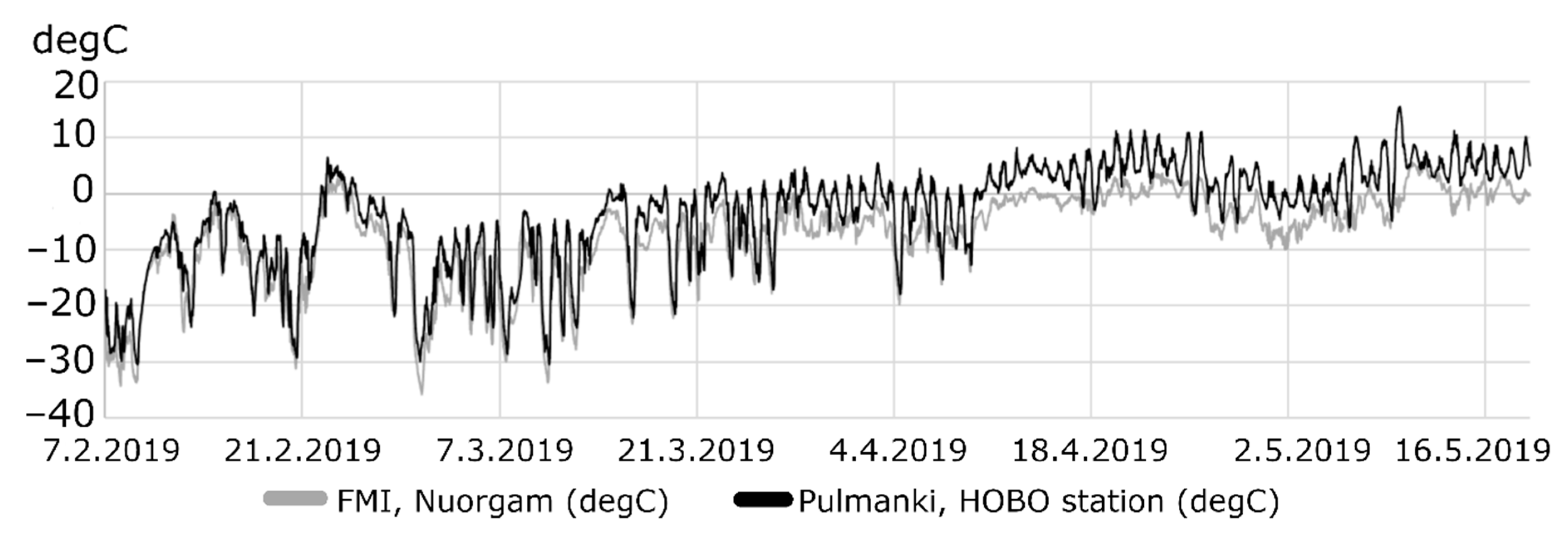






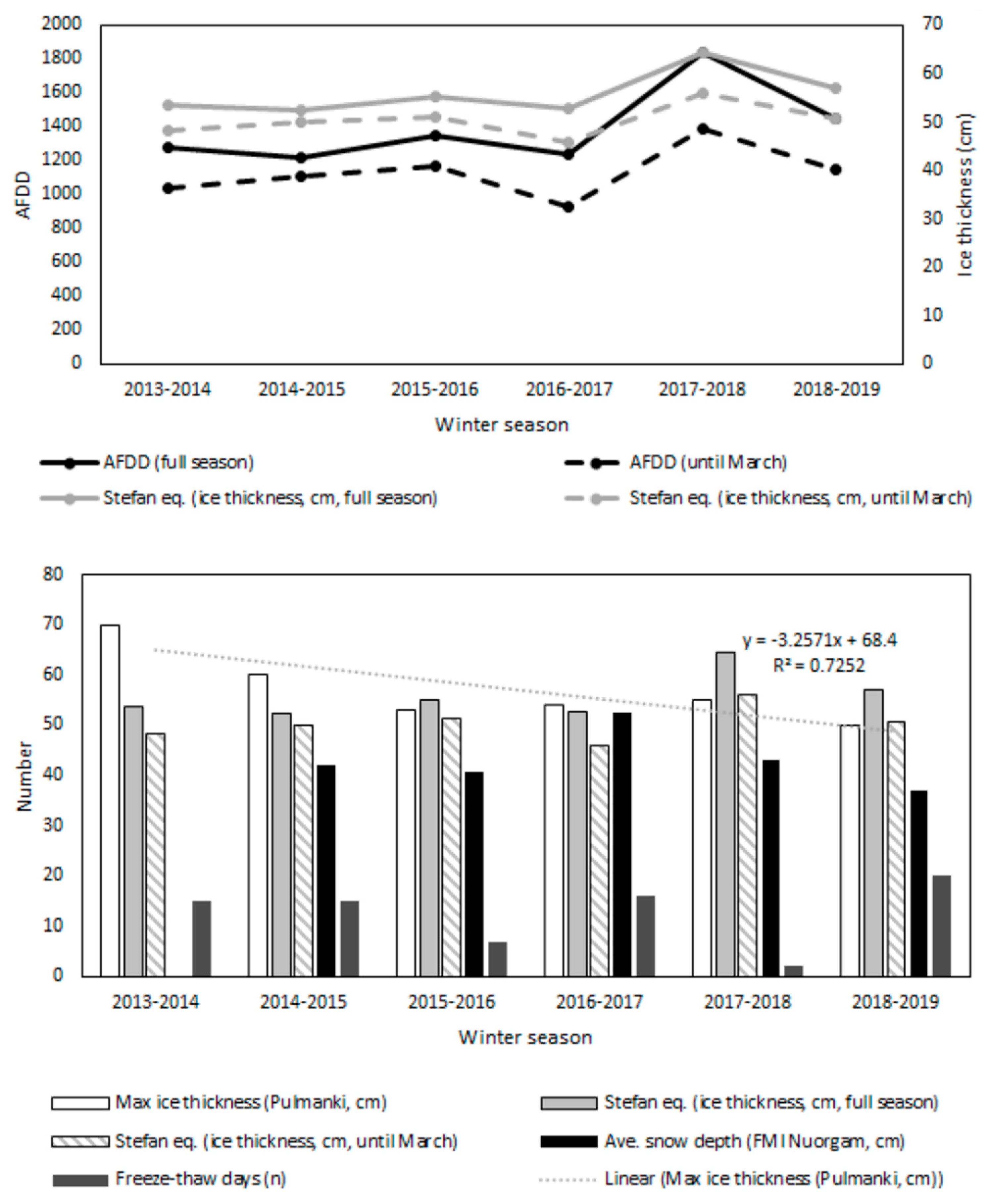
| Winter | Frazil Ice Occurrence Days in Autumn (n) | Average Snow Depth (FMI, cm) | Freeze-Thaw Days (n) | Max Ice (Pulmanki, cm) | AFDD (Degree Celsius, Whole Winter) | Stefan Equation (cm, Whole Winter) | Difference (cm, Whole Winter Calculation versus Measured Max Thickness) | Average Ice (Pulmanki cm) | AFDD (until March) | Stefan Equation (until March) | Difference (cm, March Calculation Versus Measured Max Ice Thickness) | Difference (cm March Calculation Versus Measured Average Thickness) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2013–2014 | no data | no data | 15 | 70 | 1274 | 53.6 | −16.4 | 57.4 | 1041 | 48.4 | −21.6 | −9 |
| 2014–2015 | no data | 42.0 | 15 | 60 | 1221 | 52.4 | −7.6 | 46.6 | 1109 | 49.9 | −10.1 | 3.3 |
| 2015–2016 | 3 | 40.5 | 7 | 53 | 1350 | 55.1 | 2.1 | 43.5 | 1166 | 51.2 | −1.8 | 7.7 |
| 2016–2017 | 2 | 52.4 | 16 | 54 | 1237 | 52.8 | −1.2 | 44 | 931 | 45.8 | −8.2 | 1.8 |
| 2017–2018 | 2 | 43.2 | 2 | 55 | 1840 | 64.3 | 9.3 | 38 | 1390 | 55.9 | 0.9 | 17.9 |
| 2018–2019 | 5 | 37.0 | 20 | 50 | 1450 | 57.1 | 7.1 | 33.9 | 1144 | 50.7 | 0.7 | 16.8 |
| Winter | Minimum Snow Depth (cm) | Average Snow Depth (cm) | Maximum Snow Depth (cm) | Minimum Air Temperature (°C) | Average Air Temperature (°C) | Maximum Air Temperature (°C) |
|---|---|---|---|---|---|---|
| 2013–2014 | 0 | 3 | 5 | −30.3 | −4.3 | 4.8 |
| 2014–2015 | 10 | 21 | 26 | −30.1 | −6.8 | 2.1 |
| 2015–2016 | 22 | 33 | 62 | −31 | −8.1 | 2.7 |
| 2016–2017 | 10 | 26 | 54 | −28.5 | −8.4 | 3.9 |
| 2017–2018 | 4 | 17 | 30 | −32.6 | −14.4 | 2.7 |
| 2018–2019 | 15 | 27 | 43 | −35.6 | −14 | 5.1 |
| Calculated Ice Clearance Date (Decay Calculations with Max Ice Thickness) | Observed Ice Clearance Date (Cameras) | Difference (Days) | Beginning of Ice Melt/Cracking (Decay Calculations with Average Ice Thickness) | Observed Date of Beginning of Ice Melt/Cracking (Cameras) | Difference (Days) |
|---|---|---|---|---|---|
| 23 May 2014 | no data | 20 May 2014 | no data | ||
| 8 May 2015 | no data | 2 May 2015 | no data | ||
| 3 May 2016 | 27 April 2016 | 6 days overestimation | 28 April 2016 | 9 April 2016 | 19 days overestimation |
| 8 May 2017 | 8 May 2017 | exact | 2 May 2017 | 1 May 2017 | 1 day overestimation |
| 11 May 2018 | 6 May 2018 | 5 days overestimation | 9 May 2018 | 24 April 2018 | 15 days overestimation |
| 25 April 2019 (24 April 2019) | 17 April 2019 at the bank location; 22 April 2019 at the HOBO location | 8 days overestimation; 3 days overestimation | 21 April 2019 (20 April 2019) | 14 April 2019 at the bank location; 16 April 2019 at the HOBO location | 7 days overestimation; 5 days overestimation |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lotsari, E.; Lind, L.; Kämäri, M. Impacts of Hydro-Climatically Varying Years on Ice Growth and Decay in a Subarctic River. Water 2019, 11, 2058. https://doi.org/10.3390/w11102058
Lotsari E, Lind L, Kämäri M. Impacts of Hydro-Climatically Varying Years on Ice Growth and Decay in a Subarctic River. Water. 2019; 11(10):2058. https://doi.org/10.3390/w11102058
Chicago/Turabian StyleLotsari, Eliisa, Lovisa Lind, and Maria Kämäri. 2019. "Impacts of Hydro-Climatically Varying Years on Ice Growth and Decay in a Subarctic River" Water 11, no. 10: 2058. https://doi.org/10.3390/w11102058
APA StyleLotsari, E., Lind, L., & Kämäri, M. (2019). Impacts of Hydro-Climatically Varying Years on Ice Growth and Decay in a Subarctic River. Water, 11(10), 2058. https://doi.org/10.3390/w11102058




