Predicting Habitat Suitability and Conserving Juniperus spp. Habitat Using SVM and Maximum Entropy Machine Learning Techniques
Abstract
1. Introduction
2. Materials and Methods
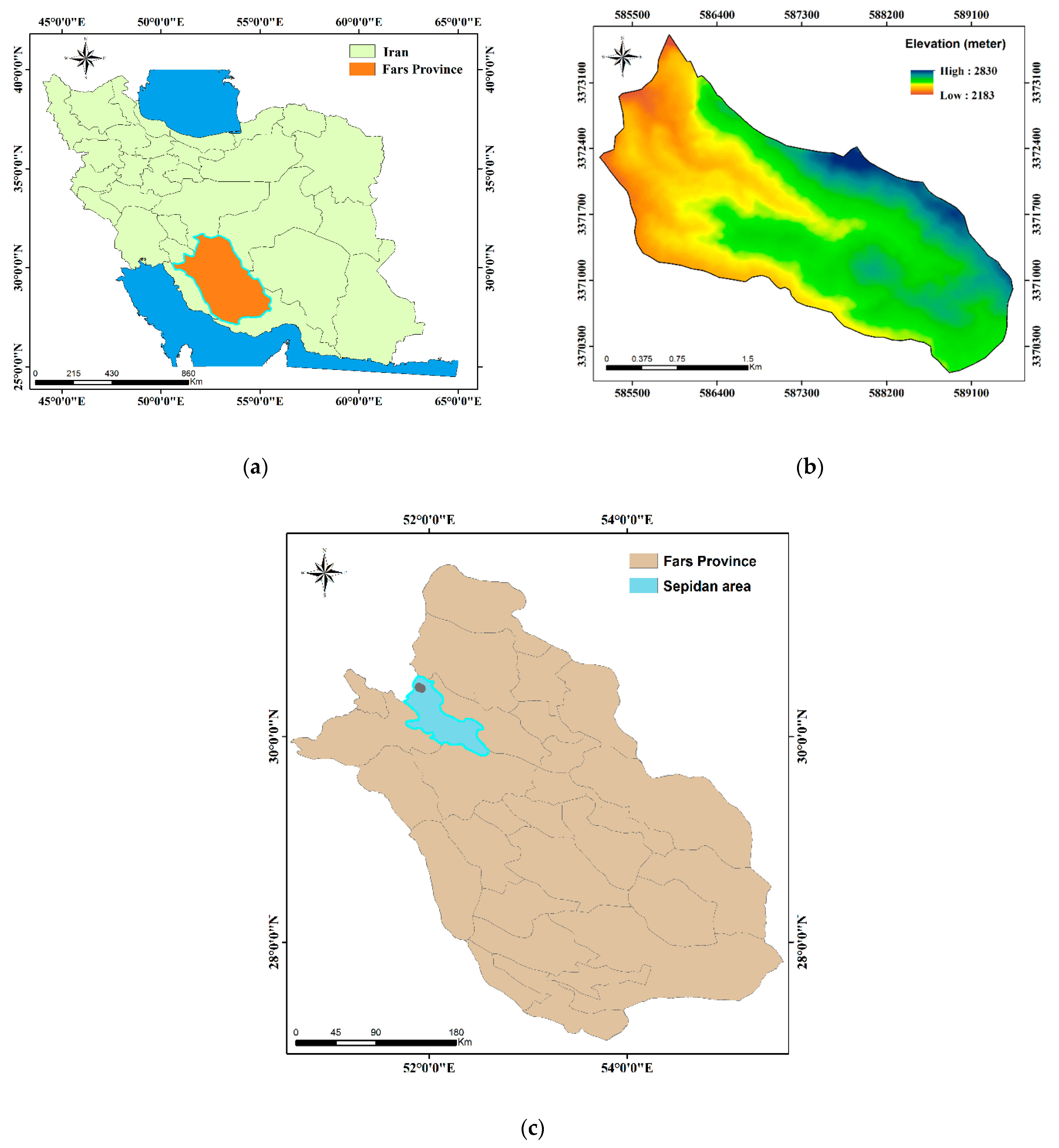
2.1. Study Area
2.2. Ecology of Juniperus Habitat in Southern Iran
2.3. Methodology
2.3.1. Creating a Species Distribution Inventory Map of Juniperus spp. in its Natural Habitats
2.3.2. Multicollinearity Analysis among Independent Variables
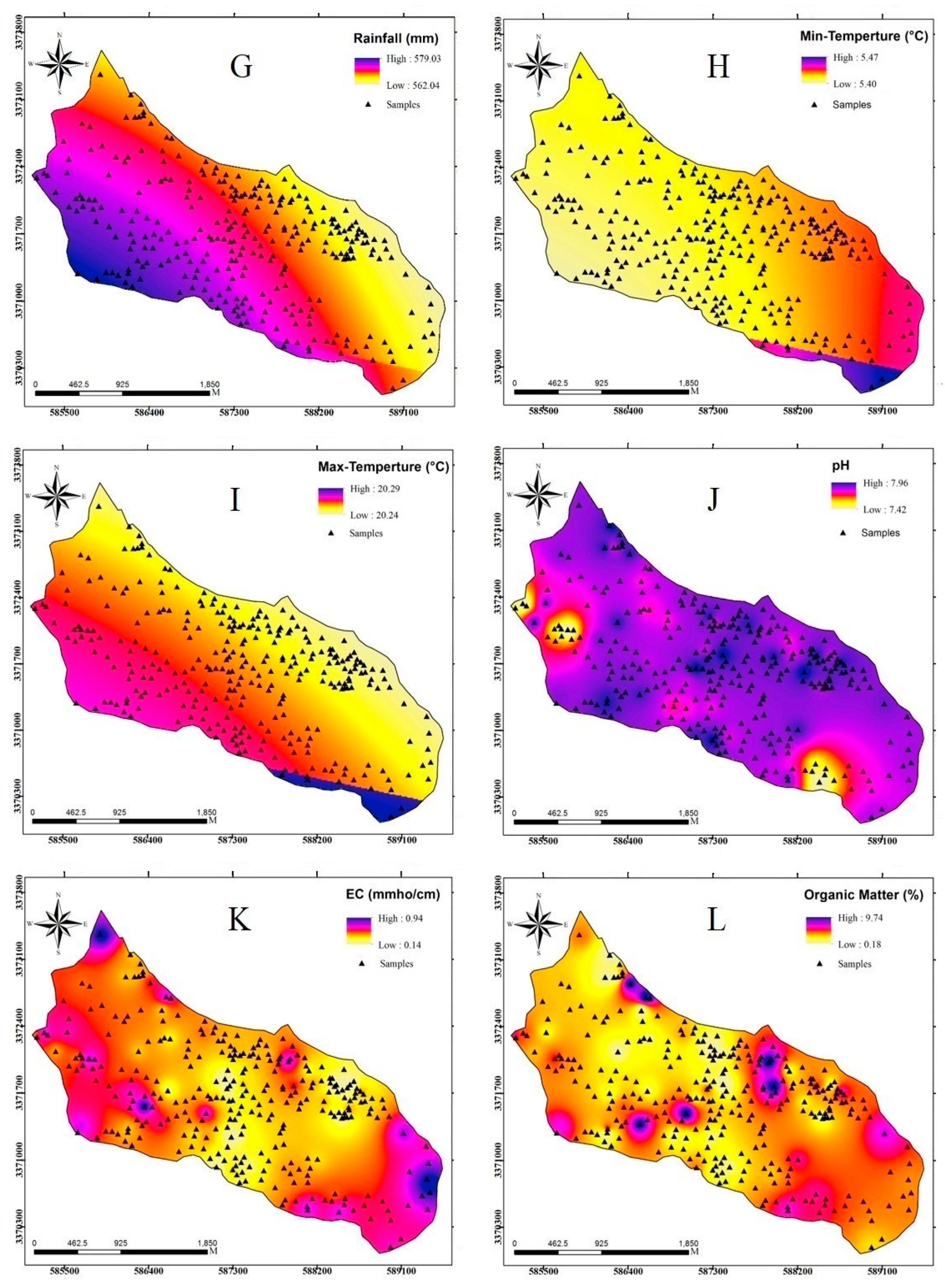
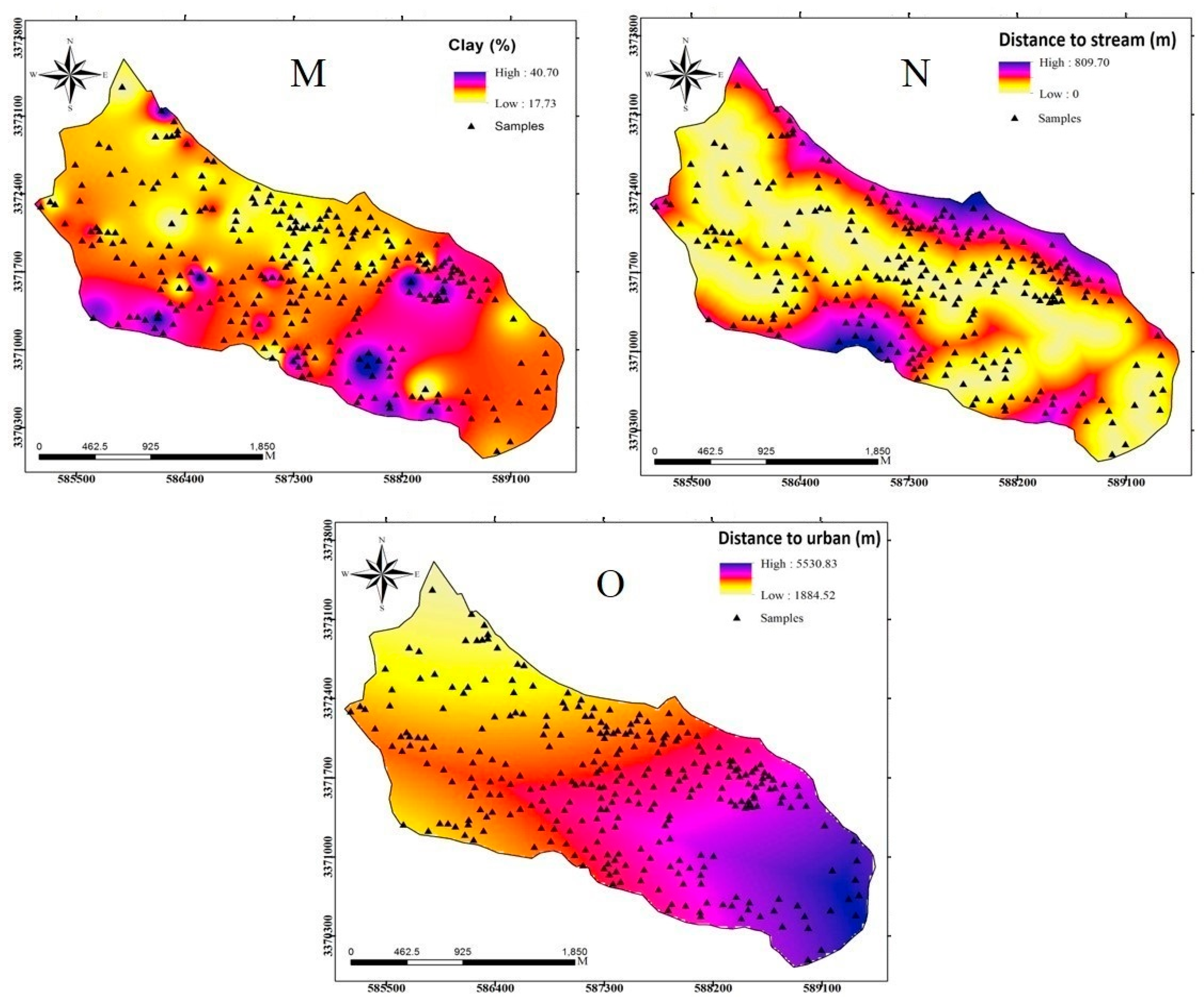
2.3.3. Dataset Preparation
2.4. Habitat Suitability Spatial Modeling
2.4.1. Maximum Entropy (MaxEnt) Model
2.4.2. Support Vector Machine (SVM) Model
2.5. Validation of Habitat Suitability Maps (HSMs)
3. Results
3.1. Collinearity of Conditioning Factors
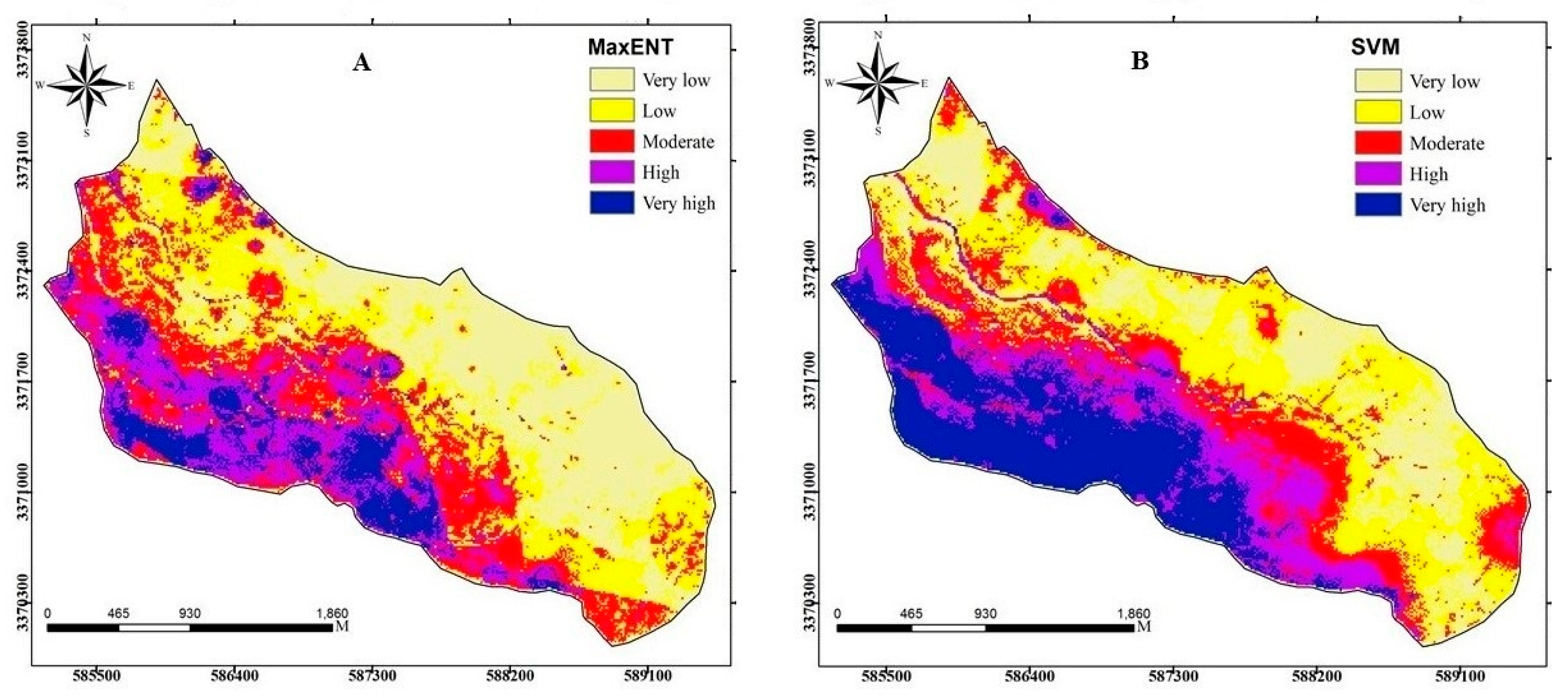
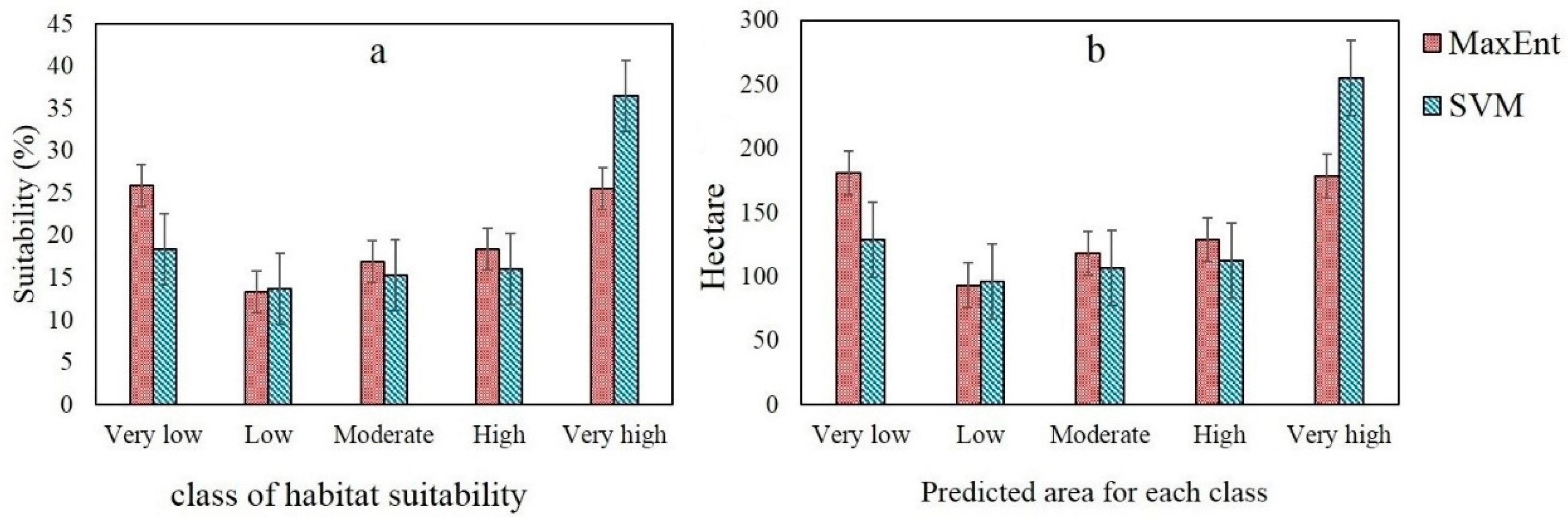
3.2. Implementation of MaxEnt and SVM Models
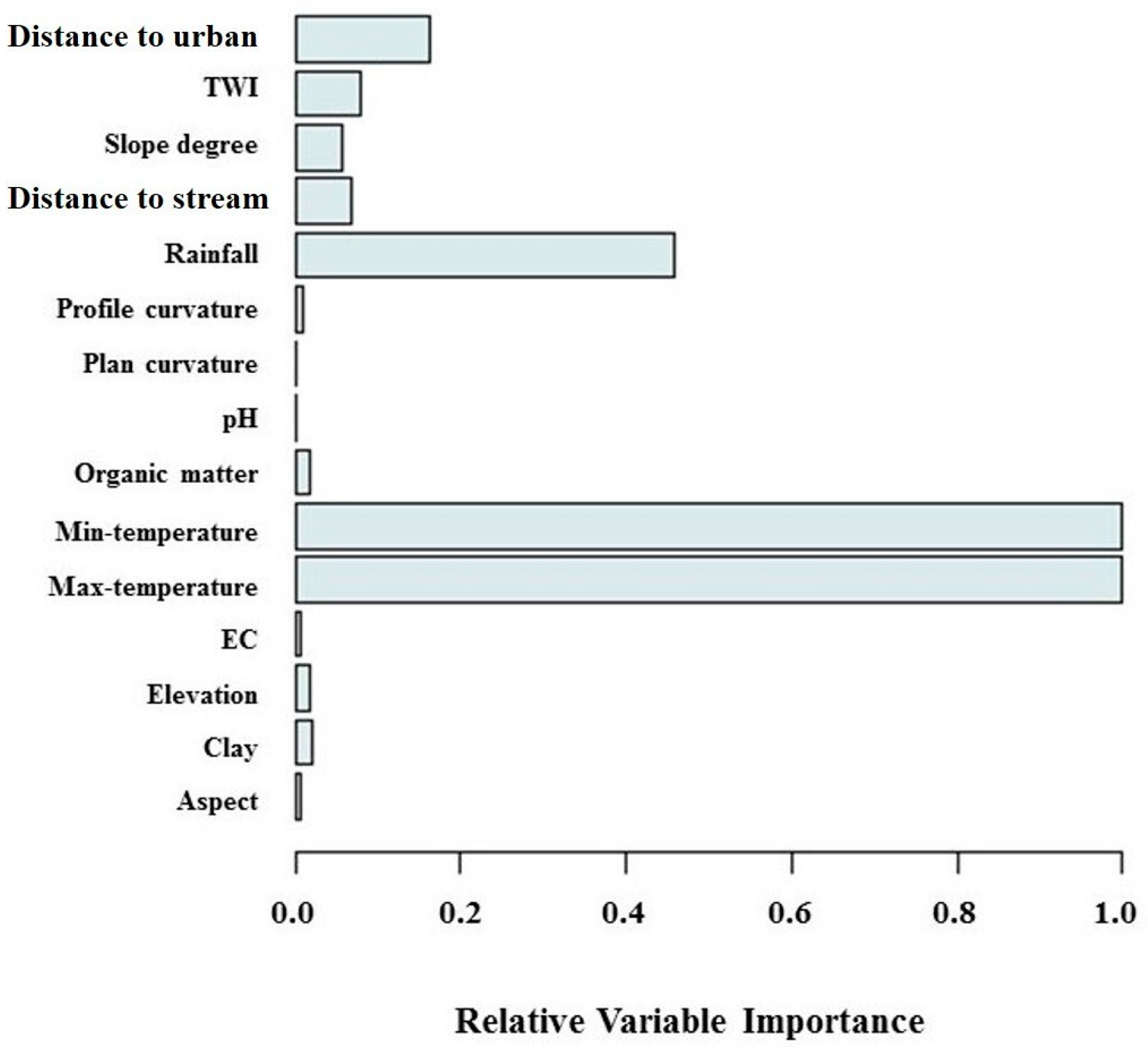
3.3. Importance of Effective Factors
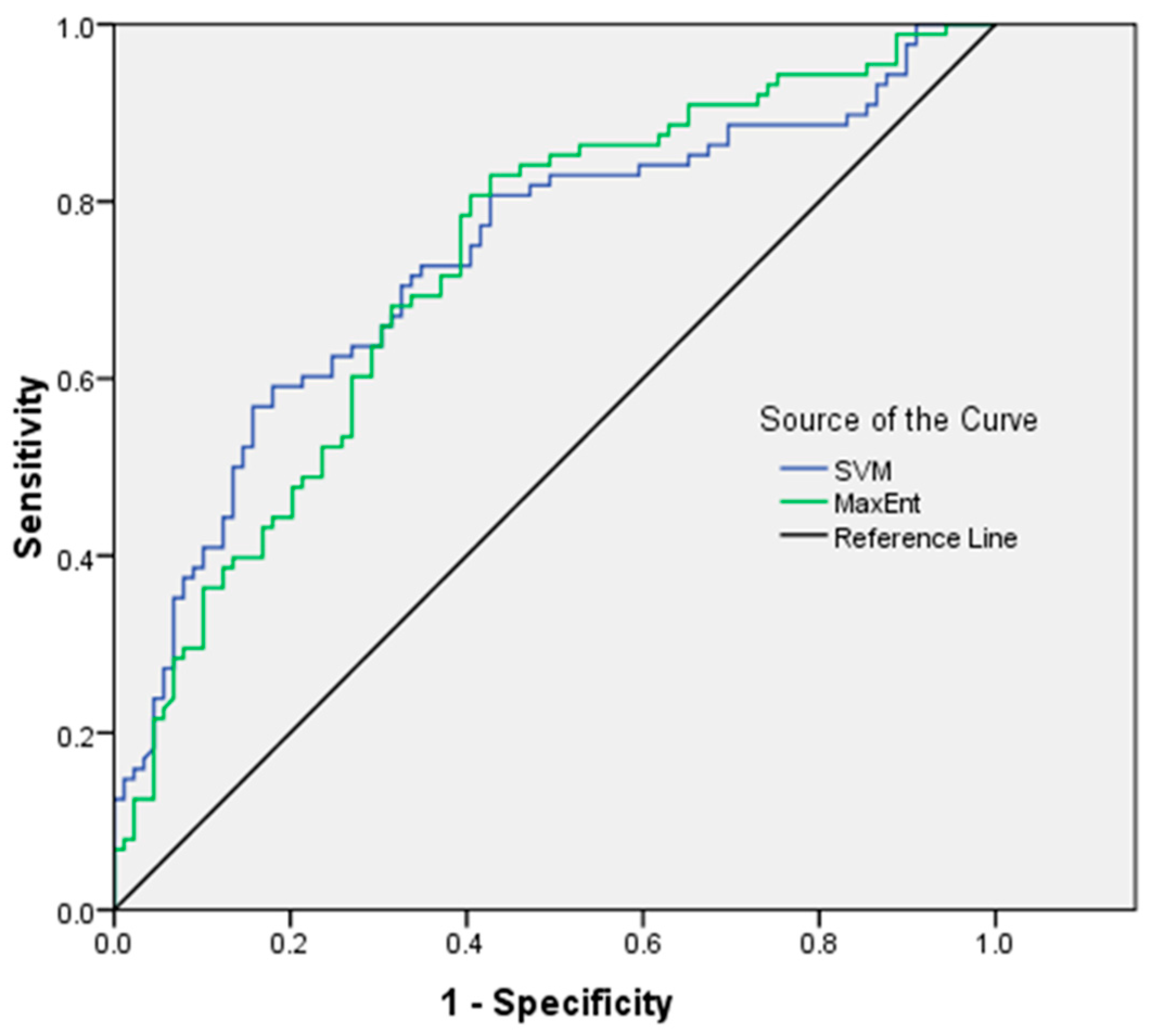
3.4. Validation of MaxEnt and SVM Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cahill, A.E.; Aiello-Lammens, M.E.; Fisher-Reid, M.C.; Hua, X.; Karanewsky, C.J.; Yeong Ryu, H.; Sbeglia, G.C.; Spagnolo, F.; Waldron, J.B.; Warsi, O.; et al. How does climate change cause extinction? Proc. R. Soc. B Biol. Sci. 2013, 280, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Skogen, K.; Helland, H.; Kaltenborn, B. Concern about climate change, biodiversity loss, habitat degradation and landscape change: Embedded in different packages of environmental concern? J. Nat. Conserv. 2018, 44, 12–20. [Google Scholar] [CrossRef]
- Sosa, V.; Loera, I.; Angulo, D.F.; Vásquez-Cruz, M.; Gándara, E. Climate change and conservation in a warm North American desert: Effect in shrubby plants. PeerJ 2019, 7, e6572. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.W.; Jackson, S.T.; Kutzbach, J.E. Projected distributions of novel and disappearing climates by 2100 AD. Proc. Natl. Acad. Sci. USA 2007, 104, 5738–5742. [Google Scholar] [CrossRef] [PubMed]
- Füssel, H.M. Review and Quantitative Analysis of Indices of Climate Change Exposure, Adaptive Capacity, Sensitivity, and Impacts; World Development Report; Potsdam Institute for Climate Impact Research (PIK): Potsdam, Germany, 2010; pp. 1–35. [Google Scholar]
- Duflot, R.; Avon, C.; Roche, P.; Bergès, L. Combining habitat suitability models and spatial graphs for more effective landscape conservation planning: An applied methodological framework and a species case study. J. Nat. Conserv. 2018, 46, 38–47. [Google Scholar] [CrossRef]
- Sharma, S.; Arunachalam, K.; Bhavsa, D.; Kala, R. Modeling habitat suitability of Perilla frutescens with MaxEnt in Uttarakhand—A conservation approach. J. Appl. Res. Med. Aromat. Plants 2018, 10, 99–105. [Google Scholar] [CrossRef]
- Wei, B.; Wang, R.; Hou, K.; Wang, X.; Wu, W. Predicting the current and future cultivation regions of Carthamus tinctorius L. using MaxEnt model under climate change in China. Glob. Ecol. Conserv. 2018, 16, e00477. [Google Scholar] [CrossRef]
- Graham, C.H.; Hijmans, R.J. A comparison of methods for mapping species ranges and species richness. Glob. Ecol. Biogeogr. 2006, 15, 578–587. [Google Scholar] [CrossRef]
- Sadeghi, R.; Zarkami, R.; Sabetraftar, K.; Damme, P.V. Use of support vector machines (SVMs) to predict distribution of an invasive water fern Azolla filiculoides (Lam.) in Anzali wetland, southern Caspian Sea, Iran. Ecol. Model. 2012, 244, 117–126. [Google Scholar] [CrossRef]
- Abolmaali, S.M.R.; Tarkesh, M.; Bashari, H. MaxEnt modeling for predicting suitable habitats and identifying the effects of climate change on a threatened species, Daphne mucronata, in central Iran. Ecol. Inform. 2018, 43, 116–123. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Zhou, C.; Meng, J.; Sun, J.; Zhou, T.; Tao, J. Impact of climate factors on future distributions of Paeonia ostii across China estimated by MaxEnt. Ecol. Inform. 2019, 50, 62–67. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Hoang, T.H.; Lock, K.; Mouton, A.; Goethals, P.L.M. Application of classification trees and support vector machines to model the presence of macroinvertebrates in rivers in Vietnam. Ecol. Inform. 2010, 5, 140–146. [Google Scholar] [CrossRef]
- Muñoz-Mas, R.; Fukuda, S.; Pórtoles, J.; Martínez-Capel, F. Revisiting probabilistic neural networks: A comparative study with support vector machines and the microhabitat suitability for the Eastern Iberian chub (Squalius valentinus). Ecol. Inform. 2018, 43, 24–37. [Google Scholar] [CrossRef]
- Hallgren, W.; Santana, F.; Low-Choy, S.; Zhao, Y.; Mackey, B. Species distribution models can be highly sensitive to algorithm configuration. Ecol. Model. 2019, 408, 108719. [Google Scholar] [CrossRef]
- Jayasinghe, S.L.; Kumar, L. Modeling the climate suitability of tea [Camellia sinensis (L.) O. Kuntze] in SriLanka in response to current and future climate change scenarios. Agric. For. Meteorol. 2019, 272, 102–117. [Google Scholar] [CrossRef]
- Zhen, J.; Wang, X.; Meng, Q.; Song, J.; Liao, Y.; Xiang, B.; Guo, H.; Liu, C.; Yang, R.; Luo, L. Fine-Scale Evaluation of Giant Panda Habitats and Countermeasures against the Future Impacts of Climate Change and Human Disturbance (2015–2050): A Case Study in Ya’an, China. Sustainability 2018, 10, 1081. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Chao, L.; Zhipeng, J.; Yuanjie, Z. A novel reconstructed training-set SVM with roulette cooperative coevolution for financial time series classification. Expert Syst. Appl. 2019, 123, 283–298. [Google Scholar] [CrossRef]
- Mollalo, A.; Sadeghian, A.; Israel, G.D.; Rashidi, P.; Sofizadeh, A.; Glass, G.E. Machine learning approaches in GIS-based ecological modeling of the sand fly Phlebotomus papatasi, a vector of zoonotic cutaneous leishmaniasis in Golestan province, Iran. Acta Trop. 2018, 188, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Poursanidis, D.; Traganos, D.; Reinartz, P.; Chrysoulakis, N. On the use of Sentinel-2 for coastal habitat mapping and satellite-derived bathymetry estimation using downscaled coastal aerosol band. Int. J. Appl. Earth. Obs. Geoinf. 2019, 80, 58–70. [Google Scholar] [CrossRef]
- Buck, O.; Garcia Millán, V.E.; Klink, A.; Pakzad, K. Using information layers for mapping grassland habitat distribution atlocal to regional scales. Int. J. Appl. Earth Obs. Geoinf. 2015, 37, 83–89. [Google Scholar] [CrossRef]
- Fukuda, S.; De Baets, B. Data prevalence matters when assessing species’ responses using data-driven species distribution models. Ecol. Inform. 2016, 32, 69–78. [Google Scholar] [CrossRef]
- Edalat, M.; Jahangiri, E.; Dastras, E.; Pourghasemi, H.R. Prioritization of Effective Factors on Zataria multiflora Habitat Suitability and its Spatial Modeling. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Pourghasemi, H.R., Gokceoglu, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 411–427. [Google Scholar]
- Zhang, J.; Huang, Y.; Pu, R.; Gonzalez-Moreno, P.; Yuan, L.; Wu, K.; Huang, W. Monitoring plant diseases and pests through remote sensing technology: A review. Comput. Electron. Agric. 2019, 165, 104943. [Google Scholar] [CrossRef]
- Farrell, A.; Wang, G.; Rush, S.A.; Martin, J.A.; Belant, J.L.; Butler, A.B.; Godwin, D. Machine learning of large-scale spatial Distributions of wild turkeys with high-dimensional environmental data. Ecol. Evol. 2019, 9, 5938–5949. [Google Scholar] [CrossRef] [PubMed]
- Byeon, D.H.; Jung, S.; Lee, W.H. Review of CLIMEX and MaxEnt for studying species distribution in South Korea. J. Asia Pac. Biodivers. 2018, 11, 325–333. [Google Scholar] [CrossRef]
- Pratumchart, K.; Suwannatrai, K.; Sereewong, C.; Thinkhamrop, K.; Chaiyos, J.; Boonmars, T.; Suwannatrai, A.T. Ecological Niche Model based on Maximum Entropy for mapping distribution of Bithynia siamensis goniomphalos, first intermediate host snail of Opisthorchis viverrini in Thailand. Acta Trop. 2019, 193, 183–191. [Google Scholar] [CrossRef]
- Redon, M.; Luque, S. Presence-only modelling for indicator species distribution: Biodiversity monitoring in the French Alps. In Proceedings of the 6th Spatial Analysis and Geomatics International Conference (SAGEO), Toulouse, France, 17–19 November 2010; pp. 42–55, hal-00558859. [Google Scholar]
- Dunn, J.C.; Buchanan, G.M.; Stein, R.W.; Whittingham, M.J.; McGowan, P.J.K. Optimising different types of biodiversity coverage of protected areas with a case study using Himalayan Galliformes. Biol. Conserv. 2016, 196, 22–30. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, S.; An, K. Distribution pattern prediction of an invasive alien species largemouth bass using a maximum entropy model (MaxEnt) in the Korean peninsula. J. Asia Pac. Biodivers. 2018, 11, 516–524. [Google Scholar] [CrossRef]
- Afify, H.M.; Al-Masni, M.A. Taxonomy metagenomic analysis for microbial sequences in three domains system via machine learning approaches. Inform. Med. Unlocked 2018, 13, 151–157. [Google Scholar] [CrossRef]
- García, D.; Zamora, R.; Hódar, J.A.; Gómez, J.M. Age structure of Juniperus communis L. in the Iberian peninsula: Conservation of remnant populations in Mediterranean mountains. Biol. Conserv. 1999, 87, 215–220. [Google Scholar]
- Milios, E.; Pipinis, E.; Petrou, P.; Akritidou, S.; Smiris, P.; Aslanidou, M. Structure and regeneration patterns of the Juniperus excelsa Bieb. stands in the central part of the Nestos valley in the northeast of Greece. Ecol. Res. 2007, 22, 713–723. [Google Scholar] [CrossRef]
- El-Juhany, L. Forestland degradation and potential rehabilitation in southwest Saudi Arabia. Aust. J. Basic Appl. Sci. 2009, 3, 2677–2696. [Google Scholar]
- Mao, K.; Milne, R.I.; Zhang, L.; Peng, Y.; Liu, J.; Thomas, P.; Mill, R.R.; Susanne SRenner, S.S. Distribution of living Cupressaceae reflects the breakup of Pangea. Proc. Natl. Acad. Sci. USA 2012, 109, 7793–7798. [Google Scholar] [CrossRef]
- Wazen, N.; Fady, B. Technical Report, Geographic Distribution of 24 Major Tree Species in the Mediterranean; FAO Forest and Landscape Restoration Mechanism, Forestry Department, Forestry Policy and Resources Division: Rome, Italy, 2016; pp. 1–59. [Google Scholar]
- MacLaren, C.A. Climate change drives decline of Juniperus seravschanica in Oman. J. Arid Environ. 2016, 128, 91–100. [Google Scholar] [CrossRef]
- Pirani, A.; Moazzeni, H.; Mirinejad, S.; Naghibi, F.; Mosaddegh, M. Ethnobotany of Juniperus excelsa M. Bieb. (Cupressaceae) in Iran. Ethnobot. Res. Appl. 2011, 9, 335–341. [Google Scholar] [CrossRef]
- Adams, R.P.; Hojjati, F. Taxonomy of Juniperus in Iran: Insight from DNA sequencing. Phytologia 2012, 94, 219–227. [Google Scholar]
- Ahani, H.; Jalilvand, H.; Hosseini Nasr, S.M.; Soltani Kouhbanani, H.; Mohammadzadeh, H. Reproduction of juniper (Juniperus polycarpos) in Khorasan Razavi, Iran. For. Sci. Pract. 2013, 15, 231–237. [Google Scholar] [CrossRef]
- Heshmati, G.A. Vegetation characteristics of four ecological zones of Iran. Int. J. Plant Prod. 2007, 1, 215–224. [Google Scholar]
- Jafari, M. Forests Genetic Resources in Iran. The Report on the State of the World’s Forest Genetic Resources. 2012. Available online: www.fao.org/documents (accessed on 13 June 2012).
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- O’Brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Heubes, J.; Schmidt, M.; Stuch, B.; García Márquez, J.R.; Wittig, R.; Zizka, G.; Thiombiano, A.; Sinsin, B.; Schaldach, R.; Hahn, K. The projected impact of climate and land use change on plant diversity: An example from West Africa. J. Arid Environ. 2013, 96, 48–54. [Google Scholar] [CrossRef]
- Yi, Y.J.; Cheng, X.; Yang, Z.F.; Zhang, S.H. Maxent modeling for predicting the potential distribution of endangered medicinal plant (H. riparia Lour) in Yunnan, China. Ecol. Eng. 2016, 92, 260–269. [Google Scholar] [CrossRef]
- Aguilar, G.D.; Blanchon, D.J.; Foote, H.; Pollonais, C.W.; Mosee, A.N. A performance based consensus approach for predicting spatial extent of the Chinese windmill palm (Trachycarpus fortunei) in New Zealand under climate change. Ecol. Inform. 2017, 39, 130–139. [Google Scholar] [CrossRef]
- Abdelaal, M.; Fois, M.; Fenu, G.; Bacchetta, G. Using MaxEnt modeling to predict the potential distribution of the endemic plant Rosa arabica Crép. in Egypt. Ecol. Inform. 2019, 50, 68–75. [Google Scholar] [CrossRef]
- Mousazade, M.; Ghanbarian, G.; Pourghasemi, H.R.; Safaeian, R.; Cerdà, A. Maxent Data Mining Technique and Its Comparison with a Bivariate Statistical Model for Predicting the Potential Distribution of Astragalus Fasciculifolius Boiss. in Fars, Iran. Sustainability 2019, 11, 3452. [Google Scholar] [CrossRef]
- Fois, M.; Cuena-Lombraña, A.; Fenu, G.; Bacchetta, G. Using species distribution models at local scale to guide the search of poorly known species: Review, methodological issues and future directions. Ecol. Model. 2018, 385, 124–132. [Google Scholar] [CrossRef]
- Bosso, L.; Rebelo, H.; Garonna, A.P.; Russo, D. Modelling geographic distribution and detecting conservation gaps in Italy for the threatened beetle Rosalia alpina. J. Nat. Conserv. 2013, 21, 72–80. [Google Scholar] [CrossRef]
- Sanchez-Hernandez, C.; Boyd, D.S.; Foody, G.M. Mapping specific habitats from remotely sensed imagery: Support vector machine and support vector data description based classification of coastal saltmarsh habitats. Ecol. Inform. 2007, 2, 83–88. [Google Scholar] [CrossRef]
- Sousa, R.; Yevseyeva, I.; da Costa, J.F.P.; Cardoso, J.S. Multicriteria models for learning ordinal data: A literature review. In Artificial Intelligence, Evolutionary Computing and Metaheuristics; Yang, X.-S., Ed.; Springer: Berlin, Germany, 2013; pp. 109–138. [Google Scholar]
- Blahut, J.; Westen, C.J.V.; Sterlacchini, S. Analysis of landslide inventories for accurate prediction of debris-flow source areas. Geomorphology 2010, 119, 36–51. [Google Scholar] [CrossRef]
- Xu, W.; Dai, J.; Hung, Y.S.; Wang, Q. Estimating the area under a receiver operating characteristic (ROC) curve: Parametric and non-parametric. Signal Process. 2013, 93, 3111–3123. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Feng, Y.; Liu, Z. The use of ROC and AUC in the validation of objective image fusion evaluation metrics. Signal Process. 2013, 115, 38–48. [Google Scholar] [CrossRef]
- Khanum, R.; Mumtaz, A.S.; Kumar, S. Predicting impacts of climate change on medicinal asclepiads of Pakistan using Maxent modeling. Acta Oecol. 2013, 49, 23–31. [Google Scholar] [CrossRef]
- Całka, B. Comparing continuity and compactness of choropleth map classes. Geod. Cartogr. 2018, 67, 21–34. [Google Scholar]
- Chun, Y.; Koo, H.; Griffith, D.A. A comparison of optimal map classification methods incorporating uncertainty information. In Proceedings of the Spatial Accuracy, Avignon, France, 20–22 April 2016; pp. 177–181. [Google Scholar]
- Jenks, G.; Coulson, M. Class Intervals for Statistical Maps. Ann. Assoc. Am. Geogr. 1963, 3, 119–134. [Google Scholar]
- Hirzel, A.H.; Hausser, J.; Perrin, N. Biomapper 4.0. Lab. of Conservation Biology; Department of Ecology and Evolution, University of Lausanne: Lausanne, Switzerland, 2007. [Google Scholar]
- Tuv, E.; Borisov, A.; Runger, G.; Torkkola, K. Feature selection with ensembles, artificial variables, and redundancy elimination. J. Mach. Learn. Res. 2009, 10, 1341–1366. [Google Scholar]
- Wang, R.; Li, Q.; He, S.; Liu, Y.; Wang, M.; Jiang, G. Modeling and mapping the current and future distribution of Pseudomonas syringae pv. actinidiae under climate change in China. PLoS ONE 2018, 13, e0192153. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Li, G.Q.; Du, S. Simulating the potential distribution of Elaeagnus angustifolia L. based on climatic constraints in China. Ecol. Eng. 2018, 113, 27–34. [Google Scholar] [CrossRef]
- Fourcade, Y.; Engler, J.O.; Rodder, D.; Secondi, J. Mapping species distributions with MAXENT using a geographically biased sample of presence data: A performance assessment of methods for correcting sampling bias. PLoS ONE 2014, 9, e97122. [Google Scholar] [CrossRef]
- Muñoz-Mas, R.; Lopez-Nicolas, A.; Martínez-Capel, F.; Pulido-Velazquez, M. Shifts in the suitable habitat available for brown trout (Salmo trutta L.) under short-term climate change scenarios. Sci. Total Environ. 2016, 544, 686–700. [Google Scholar]
- Sofizadeh, A.; Rassi, Y.; Vatandoost, H.; Hanafi-Bojd, A.A.; Mollalo, A.; Rafizadeh, S.; Akhavan, A.A. Predicting the distribution of Phlebotomus papatasi (Diptera: Psychodidae), the primary vector of zoonotic cutaneous leishmaniasis, in Golestan Province of Iran using ecological niche modeling: Comparison of MaxEnt and GARP models. J. Med. Entomol. 2016, 54, 312–320. [Google Scholar]
- Yuan, H.; Wei, Y.; Wang, X. Maxent modeling for predicting the potential distribution of Sanghuang, an important group of medicinal fungi in China. Fungal Ecol. 2015, 17, 140–145. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jimenez-Valverde, A.; Real, R. AUC: Amisleading measure of the performance of predictive distribution models. Glob. Ecol. Biogeogr. 2007, 17, 145–151. [Google Scholar] [CrossRef]
- Václavík, T.; Meentemeyer, R.K. Invasive species distribution modeling (iSDM): Are absence data and dispersal constraints needed to predict actual distributions? Ecol. Model. 2009, 220, 3248–3258. [Google Scholar] [CrossRef]
- Fortunel, C.; Paine, C.; Fine, P.; Kraft, N.; Baraloto, C. Environmental factors predict community functional composition in Amazonian forests. J. Ecol. 2014, 102, 145–155. [Google Scholar] [CrossRef]
- Silva, L.D.; Costa, H.; de Azevedo, E.B.; Medeiros, V.; Alves, M.; Elias, R.B.; Silva, L. Modelling Native and Invasive Woody Species: A Comparison of ENFA and MaxEnt Applied to the Azorean Forest. In Modeling, Dynamics, Optimization and Bioeconomics II, Proceedings in Mathematics & Statistics; Pinto, A.A., Zilberman, D., Eds.; Springer: Berlin, Germany, 2017; Volume 195, pp. 415–444. [Google Scholar]
- Chiogna, G.; Marcolini, G.; Liu, W.; Ciria, T.P.; Tuo, Y. Coupling hydrological modeling and support vector regression to model hydropeaking in alpine catchments. Sci. Total Environ. 2018, 633, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Bradie, L.; Leung, B. A quantitative synthesis of the importance of variables used in MaxEnt species distribution models. J. Biogeogr. 2017, 44, 1344–1361. [Google Scholar] [CrossRef]
- Douaihy, B.; Restoux, G.; Machon, N.; Dagher-Kharrat, M.B. Ecological characterization of the Juniperus excelsa stands in Lebanon. Ecol. Mediterr. 2013, 39, 169–180. [Google Scholar]
- Walas, Ł.; Sobierajska, K.; Ok, T.; Dönmez, A.A.; Kanoğlu, S.S.; Dagher-Kharrat, M.B.; Douaihy, B.; Romo, A.; Stephan, J.; Jasińska, A.K.; et al. Past, present, and future geographic range of an oro-Mediterranean Tertiary relict: The Juniperus drupacea case study. Reg. Environ. Chang. 2019, 19, 1507–1520. [Google Scholar] [CrossRef]
- Miller, R.F.; Bates, J.D.; Svejcar, T.J.; Pierson, F.B.; Eddleman, L.E. Biology, Ecology, and Management of Western Juniper (Juniperus occidentalis). Oregon State University. Tech. Bull. 2005, 152, 1–77. [Google Scholar]
| Category | Conditioning Factors | Data Scale |
|---|---|---|
| Topographic factors | Slope degree | Continuous |
| Aspect | Categorical (5 classes) | |
| Plan curvature | Continuous | |
| Profile curvature | Continuous | |
| Elevation | Continuous | |
| TWI | Continuous | |
| Climatic factors | Rainfall | Continuous |
| Min temperature | Continuous | |
| Max temperature | Continuous | |
| Soil factors | pH | Continuous |
| EC | Continuous | |
| Clay | Continuous | |
| Organic matter | Continuous | |
| Environmental factors | Distance to stream | Continuous |
| Distance to urban | Continuous |
| Model | Unstandardized Coefficients | Standardized Coefficients | t-statistics | Sig. | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| B | Std. Error | Beta | Tolerance (T) | VIF | |||
| (Constant) | −149.246 | 69.238 | −2.156 | 0.032 | |||
| Distance to urban | 6.382 × 10−5 | 0.000 | 0.092 | 0.988 | 0.324 | 0.235 | 4.253 |
| TWI | 0.029 | 0.016 | 0.119 | 1.799 | 0.073 | 0.469 | 2.133 |
| Slope degree | 0.007 | 0.003 | 0.110 | 1.892 | 0.059 | 0.612 | 1.634 |
| Rainfall | 0.039 | 0.018 | 0.119 | 2.174 | 0.030 | 0.685 | 1.460 |
| Distance to Stream | 0.000 | 0.000 | 0.084 | 1.401 | 0.162 | 0.574 | 1.743 |
| Profile curvature | −0.029 | 0.034 | −0.046 | −0.869 | 0.385 | 0.728 | 1.374 |
| Plan curvature | −0.006 | 0.041 | −0.009 | −0.148 | 0.882 | 0.623 | 1.604 |
| pH | −0.453 | 0.379 | −0.069 | −1.194 | 0.233 | 0.626 | 1.598 |
| Organic matter | 0.039 | 0.027 | 0.089 | 1.451 | 0.148 | 0.543 | 1.842 |
| Min temperature | −11.712 | 3.311 | −0.252 | −3.537 | 0.000 | 0.407 | 2.459 |
| Max temperature | 10.670 | 3.435 | 0.205 | 3.107 | 0.002 | 0.473 | 2.115 |
| EC | −0.170 | 0.273 | −0.038 | −0.623 | 0.533 | 0.541 | 1.848 |
| Elevation | 0.000 | 0.001 | −0.063 | −0.580 | 0.562 | 0.172 | 5.803 |
| Clay | 0.013 | 0.009 | 0.082 | 1.444 | 0.150 | 0.646 | 1.549 |
| Aspect | 0.009 | 0.023 | 0.019 | 0.389 | 0.697 | 0.862 | 1.160 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahimian Boogar, A.; Salehi, H.; Pourghasemi, H.R.; Blaschke, T. Predicting Habitat Suitability and Conserving Juniperus spp. Habitat Using SVM and Maximum Entropy Machine Learning Techniques. Water 2019, 11, 2049. https://doi.org/10.3390/w11102049
Rahimian Boogar A, Salehi H, Pourghasemi HR, Blaschke T. Predicting Habitat Suitability and Conserving Juniperus spp. Habitat Using SVM and Maximum Entropy Machine Learning Techniques. Water. 2019; 11(10):2049. https://doi.org/10.3390/w11102049
Chicago/Turabian StyleRahimian Boogar, Abdolrahman, Hassan Salehi, Hamid Reza Pourghasemi, and Thomas Blaschke. 2019. "Predicting Habitat Suitability and Conserving Juniperus spp. Habitat Using SVM and Maximum Entropy Machine Learning Techniques" Water 11, no. 10: 2049. https://doi.org/10.3390/w11102049
APA StyleRahimian Boogar, A., Salehi, H., Pourghasemi, H. R., & Blaschke, T. (2019). Predicting Habitat Suitability and Conserving Juniperus spp. Habitat Using SVM and Maximum Entropy Machine Learning Techniques. Water, 11(10), 2049. https://doi.org/10.3390/w11102049








