Abstract
Support vector machine (SVM) and maximum entropy (MaxEnt) machine learning techniques are well suited to model the habitat suitability of species. In this study, SVM and MaxEnt models were developed to predict the habitat suitability of Juniperus spp. in the Southern Zagros Mountains of Iran. In recent decades, drought extension and climate alteration have led to extensive changes in the geographical occurrence of this species and its growth and regeneration are extremely limited in this area. This study evaluated the habitat suitability of Juniperus through spatial modeling and predicts appropriate regions for future cultivation and resource conservation. We modeled the natural habitat of Juniperus for an area of 700 ha in Sepidan Area in the Fars province using (1) data regarding the presence of the species (295 samples) collected through field surveys and GPS, (2) habitat soil information and indices derived from 60 soil samples collected in the study area, and (3) climatic and topographic datasets collected from various sources. In total, 15 conditioning factors were used for this spatial modeling approach. Receiver operator characteristic (ROC) curves were applied to estimate the accuracy of the habitat suitability models produced by the SVM and MaxEnt techniques. Results indicated logical and similar area under the curve (AUC)-ROC values for the SVM (0.735) and MaxEnt (0.728) models. Both the SVM and MaxEnt methods revealed a significant relationship between the Juniperus spp. distribution and conditioning factors. Environmental factors played a vital role in evaluating the presence of Juniperus sp. as Max and Min temperatures and annual mean rainfall were the three most important factors for habitat suitability in the study area. Finally, an area with high and very high suitability for the future cultivation of Juniperus sp. and for landscape conservation was suggested based on the SVM model.
1. Introduction
Habitat and biodiversity loss are global concerns related to climate change—especially drought—and serve as an enormous warnings for the future [1,2,3]. Based on a continuous rate of global warming, a temperature increase of ~4 °C is anticipated in tropical zones and a mean global temperature increase of ~2.5 °C is anticipated by 2100 AD [4,5], which, in turn, changes the habitat of species. Conservation of natural resources and ecological landscapes is a very important measure to combat the deleterious impact of climate change on ecosystems. Habitat suitability assessment is a valuable modeling approach that can be used to predict the appropriate conditions for cultivating plants to help prevent habitat demolition and biodiversity degradation [6,7,8]. Furthermore, modeling and habitat mapping are effective and applicable techniques for assessing the relationship between environmental factors and the environment, creating an ecological landscape with high biological diversity, and protecting the natural ecosystem [6,9,10]. Statistical modeling and geographic information systems (GIS) have been widely used in recent years to evaluate the ecological theories in the field of ecosystem and resource conservation and to predict suitable regions for future cultivation in accordance with climate change [8,11,12]. Maximum entropy (MaxEnt) [13] and support vector machines (SVMs) [14,15] are flexible and very powerful techniques. MaxEnt is a machine learning algorithm with a high capability in artificial fitting rules or functional connections (e.g., nonlinear relation) according to appearance information, usage of species’ presence, and background data for the prediction of species distribution and habitat suitability [8,16,17,18]. The MaxEnt algorithm is applied to detect the maximum entropy distribution likelihood and is used to forecast the possible distribution of a target species according to its maximum entropy under different conditions. In addition, MaxEnt can be used with limited distribution data and its classifications are created using only highly accurate presence information [13,16]. SVMs are generally controlled classifiers, which require training samples, and they are not relatively susceptible to training sample size [19,20]. Generally, the self-adaptability, rapid learning speed, and insensitivity to training size make the SVM a reliable method for the intelligent processing of remote sensing data [19,20,21]. Therefore, the SVM algorithm has the deterministic learning features of nonparametric data, and its high accuracy makes it an important and pleasant tool for habitat suitability mapping with an impressive predictive accuracy [22,23,24,25,26]. MaxEnt and SVMs yielded a good performance with the original data, indicating their sufficient regulation of multicollinearity in spatial distributions studies [25,27]. Their suitability for the assessment of species distribution and habitat suitability models has led them to become popular methods for evaluating habitat requirements in recent years. Both methods are applicable for predicting distribution patterns of plants and assessing their habitat suitability [6,7,15,28,29], biodiversity in the natural landscape [30,31], and the distribution pattern of living creatures [18,32,33]. Genus Juniperus is a coniferous plant with a variety of species occurring in the cool and temperate zones of the Northern Hemisphere’s mountainous regions. In recent years, drought extension and climate change have impacted the native habitat of juniper in all regions, and many habitats of the Juniperus species are threatened around the world [34,35,36,37,38,39]. Some species of juniper trees are distributed in Iran, with a geographical distribution throughout different regions. In Iran, the north of the Alborz Mountain, the northeast of Kopet Dāg Mountain, the west and southwest of Zagros Mountain, and the south of Jebale-e-Barez Mountains are recognized as natural habitats of Juniperus [40,41,42]. The main objective of the current study was mapping the habitat suitability of Juniperus spp. based on presence data of the species in its natural habitat using two machine learning techniques, namely SVM and MaxEnt. The second objective was to compare the performance of two prediction approaches to identify patterns and determine the models’ capacity for recognizing and analyzing the habitat suitability of Juniperus spp. The graphical outputs of quantitative data depicting the natural habitat of Juniperus in Sepidan Area may be used in the decision-making process for landscape planning, i.e., to detect suitable habitats for future cultivation, and for resource conservation through habitat optimization, in particular, considering the importance of environmental factors for species conservation.
2. Materials and Methods
2.1. Study Area
The study area is located in the Sepidan Area of the Fars province. This area contains approximately 700 ha of the natural habitat of juniper and is located in Southern Iran (Figure 1). As part of the Zagros mountain range, the studied area has a moderate climate, distinctive seasons, and abundant rainfall (http://www.irimo.ir). Long-term annual average temperature and rainfall are 12–13 °C and 500–550 mm, respectively. Topographically, the elevation of Sepidan Area ranges from 2183 to 2830 m a.s.l. according to the digital elevation model (DEM) of the study area, while slope degrees range from 0 to 73°.

Figure 1.
Location map of the study area. Fars province in Iran (a), Sepidan Area in Fars province (b), habitat basin and DEM (c).
2.2. Ecology of Juniperus Habitat in Southern Iran
Juniperus species is an evergreen tree with habitats distributed in dry and semi-dry, cold climates with moderate summer temperatures and an annual rainfall of about 400 mm in the high-mountain environments of the Irano—Turanian region [43,44]. Drought extension, climate change, human activity (fuelwood), and overgrazing in the past decades have led to a recession of Juniperus habitats. Today, the remaining habitats of juniperus—an endangered species—are in scattered spots [44].
2.3. Methodology
To generate habitat suitability maps, the current study was conducted in five main phases, (i) creating a species distribution inventory map of Juniperus spp. in their natural habitats, (ii) dataset preparation, (iii) multicollinearity analysis of different independent variables, (iv) habitat suitability modeling using MaxEnt and SVM models, and (v) validation and selection of the best model.
2.3.1. Creating a Species Distribution Inventory Map of Juniperus spp. in its Natural Habitats
To create a species distribution inventory map, we first identified the natural habitats of the Juniperus spp. in the Sepidan Area. Next, we registered the location of 295 samples of this species in 700 ha of the studied site using extensive field surveys and a Handy GPS app Android (version 32.6, https://www.binaryearth.net/HandyGPS/index.php). We then selected 70% (206 trees) of the identified samples for modeling and used the remaining 30% (89 trees) to validate two machine learning models using a random selection method [45]. This selection was conducted using geospatial modeling environment (GME) tools in ArcGIS 10.6.1 (ESRI, Redlands, CA, USA).
2.3.2. Multicollinearity Analysis among Independent Variables
Next, we conducted a collinearity test among 15 conditioning factors, including topographical, climatic, and soil data, using two indices. These indices were VIF (variance inflation factor) and tolerance (T). According to O’Brian [46], when VIF is greater than or equal to five and T is lower than 0.1, then collinearity exists among independent variables. This status can decrease the accuracy of models.
2.3.3. Dataset Preparation
Our literature review revealed that different topographical, climatic, and soil data are required to evaluate a species habitat model [12,47,48,49,50,51]. Therefore, we selected fifteen factors that affect habitat suitability to model the juniper species habitat, including elevation, slope degree, aspect, profile and plan curvatures, topographic wetness index (TWI), annual mean rainfall, distance to streams, distance to urban areas, annual mean Min/Max temperatures, and soil indices such as pH, electrical conductivity (EC), presence of clay, and organic matter (OM). We extracted topographical features, such as slope, aspect, plan and profile curvatures, elevation, and TWI, from ALOS-DEM with 12.5 m × 12.5 m resolution (Figure 2A–F). This DEM was downloaded from the ALOS PALSAR (The Phased Array type L-band Synthetic Aperture Radar) satellite website (https://vertex.daac.asf.alaska.edu/). Furthermore, we obtained climate data, including annual mean rainfall and Min and Max annual mean temperatures (Figure 2G–I), from Fars Meteorological Bureau (http://www.farsmet.ir). In terms of soil data, we collected 60 soil samples from the study area in a depth of 0–30 cm to prepare the soil feature maps. These samples were then sent to the Shiraz University Laboratory, where the values of pH, EC, organic matter, and percentage of clay were measured for each sample. We then applied the inverse distance weight (IDW) interpolation method to create soil feature maps (Figure 2J–M). In addition, distance to streams and distance to urban areas were constructed from the topographical map at a scale of 1:25,000 (Figure 2N–O). A description of these habitat suitability conditioning factors is shown in Table 1.
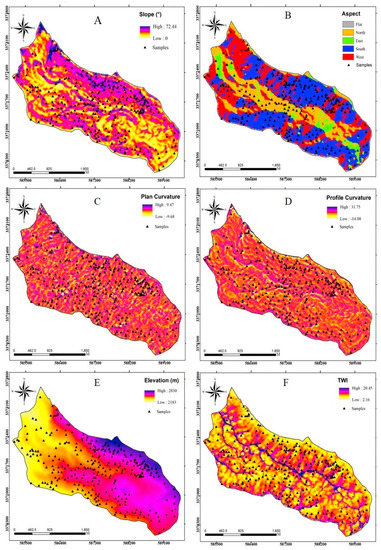

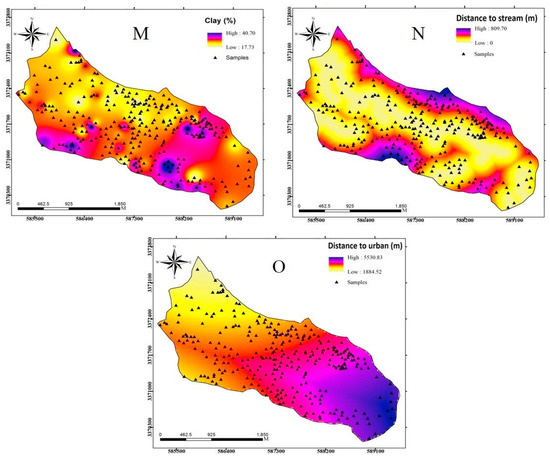
Figure 2.
Conditioning factor maps of the study area: slope (A), aspect (B), plan curvature (C), profile curvatures (D), elevation (E), topographic wetness index (TWI) (F), rainfall (G), Min temperature (H), Max temperature (I), pH (J), electrical conductivity (EC) (K), organic matter (L), percentage of clay (M), distance to stream (N), and distance to urban (O).

Table 1.
Habitat suitability conditioning factors in the present study.
2.4. Habitat Suitability Spatial Modeling
2.4.1. Maximum Entropy (MaxEnt) Model
To model the species habitat using the MaxEnt model, we first downloaded MaxEnt software version 3.4.0 from a portal (https://biodiversityinformatics.amnh.org/open_source/maxent/), and used it to predict the Juniperus habitat suitability. The MaxEnt model has been used to estimate the likelihood of species livability based on presence data and randomly generated background points to detect the maximum entropy distribution [7,8,11,12]. Entropy is the property that is well-known as a link between data and information. The maximum entropy model led to greater utilization of data entropy, allowing us to explore and extract information and develop unexpected outcomes [45,50]. The MaxEnt model is an advantageous approach to simulating habitat suitability because it can be used for presence-only data with a small sample size and works very well for inadequate or incomplete data [48,52]. Moreover, environmental layers in both categorical and continuous format can be used by MaxEnt, and its likelihood is correct, constant, and reliable even if the sample size is small. Also, its capability of creating a habitat suitability map with simple commentary and high explicit result is useful for future species cultivation and conservation programs [49,52,53]. We assessed the relative importance of conditioning factors using the Jackknife test [12,13].
2.4.2. Support Vector Machine (SVM) Model
The support vector machine (SVM) model is a controlled machine learning system, which is used to predict habitat suitability with remote sensing information, and is applicable for handling small data samples [19]. The SVM model, as a binary classifier, is used to optimize algorithms to determine the optimal hyperplane of two separate classes [54]. Generalization of limited training samples is a general restriction in remote sensing, and SVMs are a well-suited model for generalizing the limited samples in remote sensing applications [15,19,24]. The SVM was used to enhance the accuracy of predictions while avoiding the drawbacks of overfitting associated with learning algorithms based on statistical and optimization theories [15,19,55]. The SVM is a desirable model due to its superior experimental function in comparison to artificial neural network functions. The training process of the SVM is easy and avoids overfitting bugs, and the model can be applied as a proper algorithmic approach for big data and to detect the preeminent trade-off between overfitting and over generalization [19].
2.5. Validation of Habitat Suitability Maps (HSMs)
We used the receiver operator characteristic (ROC) curve to validate the HSMs that were created using two machine learning methods, as mentioned before. In the ROC method, the cumulative percentage of the suitability classes is located on the X-axis, versus the cumulative percentage of the training set within those classes on the Y-axis [45,56]. ROC curve analyses have been extensively used in modeling studies to assess binary classifications and evaluate the diagnostic accuracy of an event occurrence [57,58]. Moreover, the ROC method has a graphical display with a high discrimination capability that depicts sensitivity estimates (probability of a true positive) versus one minus specificity (probability of a false positive) of an occurrence for all possible threshold values, and it is an effective method for modeling the anticipated distribution of a plant species [58,59].
3. Results
3.1. Collinearity of Conditioning Factors
Results of the multicollinearity test of independent variables are shown in Table 2. These results indicate that the lowest T and highest VIF for elevation are 0.172 and 5.803, respectively. Therefore, in this research, there is no multicollinearity among the effective independent factors.

Table 2.
Multicollinearity of the effective factors in the study area.
3.2. Implementation of MaxEnt and SVM Models
Subsequent to the models’ implementation, we prepared the HSMs using two machine learning methods and categorized them into five suitability classes, namely, very low, low, moderate, high, and very high according to the natural breaks (jenks) classification technique [45,60,61,62]. According to the created habitat suitability maps, the examined models showed different patterns in regard to habitat suitability area (Figure 3). The SVM model achieved the highest areal percentage of the very high suitability class (36%), whereas the MaxEnt model achieved the highest areal percentage of the very low suitability class (25%) (Figure 4). The predicted percentage and area for each habitat suitability class within each model are presented in Figure 4a,b. Therefore, the results of the MaxEnt and SVM comparison showed a significant difference between the models regarding the anticipated suitability classes and the percentage of predicted area in two very low and very high classes (Figure 4a). The area of each suitability class was determined, and the results indicate that the very high class of the SVM model covers the largest area; furthermore, the predicted area for the very low and very high classes significantly differs among the models (Figure 4b). However, there is no significant variation between the models regarding the percentage and area in the low, moderate, and high suitability classes (Figure 4a,b).
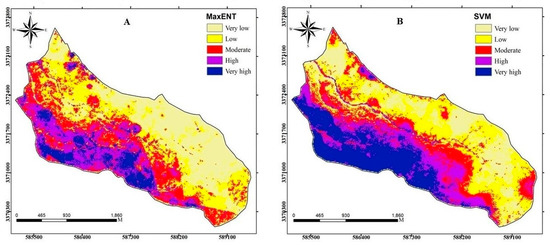
Figure 3.
Habitat suitability maps using: (A) maximum Entropy (MaxEnt), and (B) support vector machines (SVM) models.
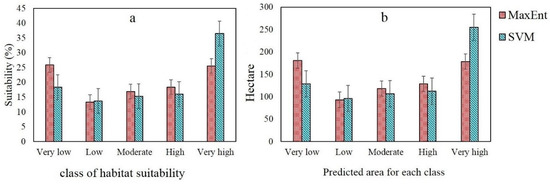
Figure 4.
Percentages of different habitat suitability classes (a), and (b) predicated area for each class of habitat suitability.
3.3. Importance of Effective Factors
We assessed the relative importance of the effective factors with the Jackknife variance estimation method for the area under the curve (AUC), and the analysis results are shown in Figure 5. According to the results of the relative importance test, the Max and Min temperature factors are deemed most important for HSM, followed by annual mean rainfall, distance from urban area, TWI, distance to streams, slope degree, clay percentage, organic matter, elevation, profile curvature, EC, aspect, plan curvature, and pH (Figure 5).
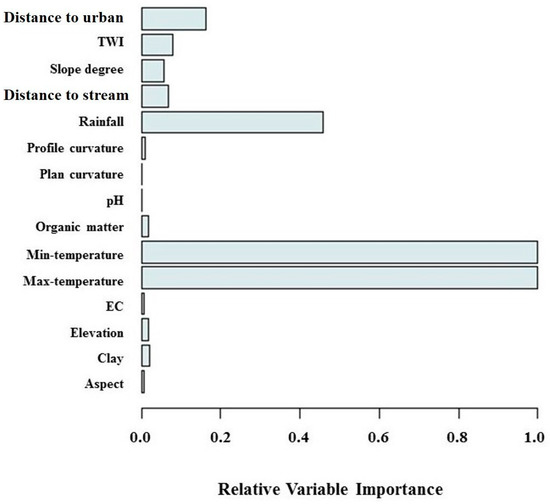
Figure 5.
Analysis of the relative importance of effective factors.
3.4. Validation of MaxEnt and SVM Models
We validated the Juniperus habitat suitability maps using the ROC curve for both the SVM and MaxEnt models. Figure 6 depicts the validation results of both models. The area under the curve (AUC) value was used to assess the SVM and MaxEnt models separately and in comparison. According to the AUC values of SVM (0.735) and MaxEnt (0.728), both models suggested a logical and satisfactory output for the prediction of Juniperus habitat suitability (Figure 6). Furthermore, there are no significant differences between the two approaches for evaluating the species’ habitat suitability.
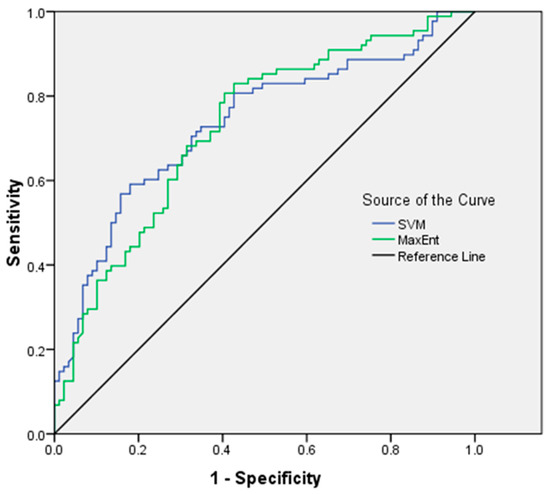
Figure 6.
Receiver operator characteristic (ROC) curve of sensitivity vs specificity of Juniperus habitat for SVM and MaxEnt models.
4. Discussion
Habitat fragmentation has negative effects on biodiversity. Therefore, the conservation and restoration of the habitat system is the main objective in future conservation scheduling [63]. Assessing the effective factors of natural habitat and habitat mapping are crucial for enforcing useful acts. Generally, in the evaluation of habitat suitability, multicollinearity of effective factors as a negative parameter increases the extra noise in all the models [8,64,65]. In this study, however, no multicollinearity was detected among any of the climatic, environmental, and soil condition variables used as conditioning factors for the Juniperus habitat suitability model.
MaxEnt and SVM have been widely used for modeling the habitat suitability of species [8,10,15,48,66]. Therefore, recent and future occurrences of species can be quickly and easily evaluated using MaxEnt [67]. Moreover, Mollalo et al. [21] suggested that the SVM classifier—when joined with GIS and remote sensing data—is a beneficial and inexpensive method for identifying the habitat suitability of species. Previous studies indicated a higher accuracy of the SVM [21,68] model compared to the MaxEnt [69] model for evaluating Papatasi habitat suitability. The findings of our study suggest the habitat suitability map generated by the SVM model has the largest suitable area for future cultivation of Juniperus. SVM is an efficient classifier with a strong capability of recognizing and detecting the habitat suitability of Juniperus. In this regard, previous studies comparing the SVM and random forests (RF) methods determined the highest overall accuracy of the SVM classifier for modeling coastal habitats, with a minor misclassification occurring in the SVM model [22]. Also, SVM and MaxEnt were comparatively used to spatially model landslide occurrence, and the results show that the highest areal percentage was allocated to the high susceptibility class by the SVM model, whereas the MaxEnt model allocated the lowest areal percentage to the high susceptibility class [45]. Therefore, this result highlights the superior performance of SVM in detecting the habitat suitability of Zataria multiflora Boiss [25]. Hence, the SVM is a useful tool for future planning regarding the conservation and management of plant species habitats.
Moreover, SVM optimization will be carried out in the shortest time and the SVM method requires a training sample, hence it needs to segregate the optimization of training patterns for each proximity, density, and inhomogeneity variable. Preparing the training data can lead to improving the results of the SVMs [15,68]. In presence and absence classification models (MaxEnt and SVM), the AUC-ROC is an important threshold for related indices to assess a model’s capability of distinguishing presence from absence [21,48,70]. Hence, the AUC statistically prepares a single differentiation measure for all ranges of thresholds that is equal to the nonparametric Wilcoxon test [71]. Models with AUC < 0.5 showed the worst performance (which rarely occurred in reality), while models with AUC > 0.5 performed better than random [8]. Our results showed a nonsignificant difference between the AUC value of the SVM (0.735) and MaxEnt (0.728) models, and both models had logical and acceptable AUC values. Previous studies confirmed a slight difference in outcomes of AUC for the SVM, Logistic regression (LR), and RF classifiers [21], but other studies suggested a better performance of the MaxEnt model when dealing with a small sample, and it tends to create restricted predictions [72].
Environmental factors have important effects on the distribution of species within their habitat [73,74]. Previous studies indicated the strong dependence between the ecogeographical variables (EGV) and the size of the training dataset on habitat suitability predictions using MaxEnt and SVM models [8,10,74,75]. In general, temperature and precipitation factors were found to have a more damaging impact on environmental factors related to species distribution [76]. The distribution pattern of Juniperus species in natural habitats depends on climatic and ecological conditioning factors [77,78]. Miller et al. [79] reported that temperature changes in the long-term, rainfall amount and distribution, and the expanse and duration of fire events are the main effective factors determining abundance and distribution of forests of Juniperus occidentalis Hook. Furthermore, temperature, rainfall, and altitude are the most effective factors determining the distribution of J. drupacea Labill. [76,78]. Moreover, the distribution patterns of J. excelsa Bieb. in Lebanon were affected by humidity and slope degrees [77]. The results of our importance analysis of efficient factors indicated that Max and Min temperatures are the most important variables in habitat suitability modeling of Juniperus. In this regard, Wei et al. [8] used the MaxEnt model to predict suitable regions for current and future cultivation of safflower (Carthamus tinctorius L.), and their results showed that Max temperature and rainfall played an important role in forecasting the possible distribution of safflower. Also, effects of environmental variables on modeling the distribution pattern of native (Morella Faya L.) and invasive (Pittosporum undulatum Vent., and Acacia melanoxylonin R. Br.) woody species in the Azorean forests showed that annual mean temperature (TM) and annual mean relative humidity (RHM) played the most important role in the distribution pattern of species in the final model [74].
Furthermore, other conditioning factors, including the amount of rainfall, distance to urban areas, TWI, distance to streams, and slope degree, were recognized as important variables influencing juniper habitat suitability. This result is in line with the previous results of studies assessing the importance of various environmental factors on distribution patterns and habitat suitability modeling [76,77,78]. Consequently, although the models correctly analyzed the effects of different possible conditioning factors on habitat suitability, the areas predicted by the models are not definite. On the other hand, regarding species conservation and future cultivation, landscape planners should make correct and farsighted decisions about target species and their relationships with the conditioning factors, suitability of the cultivation area, and climate change.
5. Conclusions
In this study, two different machine learning models, namely, SVM and MaxEnt, were used to assess the habitat suitability of Juniperus sp. using 295 occurrence records and 15 effective habitat factors. Results suggested that the abilities of SVM and MaxEnt are similar for assessing the habitat suitability of this species based on its presence data and the effective factors used in this study. The SVM is a sensible model for assessing habitat ecosystems, even with a comparatively limited dataset. The results indicated that the most important input factors for modeling the habitat suitability of Juniperus sp. are climatic variables. The study area of Juniperus sp. in this research ranged in elevation between 2180–2830 m a.s.l. Therefore, in these conditions, results indicated that Max and Min temperatures and rainfall are the three most important climatic factors, and TWI and slope degree are the two most important topographical factors, as they had the strongest effect on habitat suitability. Accordingly, landscape and conservation managers should pay more attention to Max and Min air temperature and rainfall. Otherwise, these habitats will become unmanageable within a relatively short period of time. Moreover, future cultivations should pay particular attention to the parameters TWI index, slope degree, and distance to streams.
Author Contributions
Conceptualization, A.R.B., H.S., and H.R.P.; Methodology, A.R.B., H.S., and H.R.P.; Software, A.R.B., and H.R.P.; Validation, A.R.B., H.S. and H.R.P.; Formal analysis, A.R.B., H.R.P., H.S., T.B.; investigation, A.R.B., H.S., and H.R.P.; Writing—original draft preparation, A.R.B., H.S., and H.R.P., T.B.; Writing—review and editing, A.R.B., H.R.P., T.B.; Project administration, A.R.B., H.R.P., and T.B.; Funding acquisition, T.B.
Funding
This research was partly funded by the Austrian Science Fund (FWF) through the Doctoral College GIScience (DK W 1237-N23) at the University of Salzburg.
Acknowledgments
The authors are thankful to Farhad Nikbakht and Kihan Mafakheri for their fieldwork support and laboratory works.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cahill, A.E.; Aiello-Lammens, M.E.; Fisher-Reid, M.C.; Hua, X.; Karanewsky, C.J.; Yeong Ryu, H.; Sbeglia, G.C.; Spagnolo, F.; Waldron, J.B.; Warsi, O.; et al. How does climate change cause extinction? Proc. R. Soc. B Biol. Sci. 2013, 280, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Skogen, K.; Helland, H.; Kaltenborn, B. Concern about climate change, biodiversity loss, habitat degradation and landscape change: Embedded in different packages of environmental concern? J. Nat. Conserv. 2018, 44, 12–20. [Google Scholar] [CrossRef]
- Sosa, V.; Loera, I.; Angulo, D.F.; Vásquez-Cruz, M.; Gándara, E. Climate change and conservation in a warm North American desert: Effect in shrubby plants. PeerJ 2019, 7, e6572. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.W.; Jackson, S.T.; Kutzbach, J.E. Projected distributions of novel and disappearing climates by 2100 AD. Proc. Natl. Acad. Sci. USA 2007, 104, 5738–5742. [Google Scholar] [CrossRef] [PubMed]
- Füssel, H.M. Review and Quantitative Analysis of Indices of Climate Change Exposure, Adaptive Capacity, Sensitivity, and Impacts; World Development Report; Potsdam Institute for Climate Impact Research (PIK): Potsdam, Germany, 2010; pp. 1–35. [Google Scholar]
- Duflot, R.; Avon, C.; Roche, P.; Bergès, L. Combining habitat suitability models and spatial graphs for more effective landscape conservation planning: An applied methodological framework and a species case study. J. Nat. Conserv. 2018, 46, 38–47. [Google Scholar] [CrossRef]
- Sharma, S.; Arunachalam, K.; Bhavsa, D.; Kala, R. Modeling habitat suitability of Perilla frutescens with MaxEnt in Uttarakhand—A conservation approach. J. Appl. Res. Med. Aromat. Plants 2018, 10, 99–105. [Google Scholar] [CrossRef]
- Wei, B.; Wang, R.; Hou, K.; Wang, X.; Wu, W. Predicting the current and future cultivation regions of Carthamus tinctorius L. using MaxEnt model under climate change in China. Glob. Ecol. Conserv. 2018, 16, e00477. [Google Scholar] [CrossRef]
- Graham, C.H.; Hijmans, R.J. A comparison of methods for mapping species ranges and species richness. Glob. Ecol. Biogeogr. 2006, 15, 578–587. [Google Scholar] [CrossRef]
- Sadeghi, R.; Zarkami, R.; Sabetraftar, K.; Damme, P.V. Use of support vector machines (SVMs) to predict distribution of an invasive water fern Azolla filiculoides (Lam.) in Anzali wetland, southern Caspian Sea, Iran. Ecol. Model. 2012, 244, 117–126. [Google Scholar] [CrossRef]
- Abolmaali, S.M.R.; Tarkesh, M.; Bashari, H. MaxEnt modeling for predicting suitable habitats and identifying the effects of climate change on a threatened species, Daphne mucronata, in central Iran. Ecol. Inform. 2018, 43, 116–123. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Zhou, C.; Meng, J.; Sun, J.; Zhou, T.; Tao, J. Impact of climate factors on future distributions of Paeonia ostii across China estimated by MaxEnt. Ecol. Inform. 2019, 50, 62–67. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Hoang, T.H.; Lock, K.; Mouton, A.; Goethals, P.L.M. Application of classification trees and support vector machines to model the presence of macroinvertebrates in rivers in Vietnam. Ecol. Inform. 2010, 5, 140–146. [Google Scholar] [CrossRef]
- Muñoz-Mas, R.; Fukuda, S.; Pórtoles, J.; Martínez-Capel, F. Revisiting probabilistic neural networks: A comparative study with support vector machines and the microhabitat suitability for the Eastern Iberian chub (Squalius valentinus). Ecol. Inform. 2018, 43, 24–37. [Google Scholar] [CrossRef]
- Hallgren, W.; Santana, F.; Low-Choy, S.; Zhao, Y.; Mackey, B. Species distribution models can be highly sensitive to algorithm configuration. Ecol. Model. 2019, 408, 108719. [Google Scholar] [CrossRef]
- Jayasinghe, S.L.; Kumar, L. Modeling the climate suitability of tea [Camellia sinensis (L.) O. Kuntze] in SriLanka in response to current and future climate change scenarios. Agric. For. Meteorol. 2019, 272, 102–117. [Google Scholar] [CrossRef]
- Zhen, J.; Wang, X.; Meng, Q.; Song, J.; Liao, Y.; Xiang, B.; Guo, H.; Liu, C.; Yang, R.; Luo, L. Fine-Scale Evaluation of Giant Panda Habitats and Countermeasures against the Future Impacts of Climate Change and Human Disturbance (2015–2050): A Case Study in Ya’an, China. Sustainability 2018, 10, 1081. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Chao, L.; Zhipeng, J.; Yuanjie, Z. A novel reconstructed training-set SVM with roulette cooperative coevolution for financial time series classification. Expert Syst. Appl. 2019, 123, 283–298. [Google Scholar] [CrossRef]
- Mollalo, A.; Sadeghian, A.; Israel, G.D.; Rashidi, P.; Sofizadeh, A.; Glass, G.E. Machine learning approaches in GIS-based ecological modeling of the sand fly Phlebotomus papatasi, a vector of zoonotic cutaneous leishmaniasis in Golestan province, Iran. Acta Trop. 2018, 188, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Poursanidis, D.; Traganos, D.; Reinartz, P.; Chrysoulakis, N. On the use of Sentinel-2 for coastal habitat mapping and satellite-derived bathymetry estimation using downscaled coastal aerosol band. Int. J. Appl. Earth. Obs. Geoinf. 2019, 80, 58–70. [Google Scholar] [CrossRef]
- Buck, O.; Garcia Millán, V.E.; Klink, A.; Pakzad, K. Using information layers for mapping grassland habitat distribution atlocal to regional scales. Int. J. Appl. Earth Obs. Geoinf. 2015, 37, 83–89. [Google Scholar] [CrossRef]
- Fukuda, S.; De Baets, B. Data prevalence matters when assessing species’ responses using data-driven species distribution models. Ecol. Inform. 2016, 32, 69–78. [Google Scholar] [CrossRef]
- Edalat, M.; Jahangiri, E.; Dastras, E.; Pourghasemi, H.R. Prioritization of Effective Factors on Zataria multiflora Habitat Suitability and its Spatial Modeling. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Pourghasemi, H.R., Gokceoglu, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 411–427. [Google Scholar]
- Zhang, J.; Huang, Y.; Pu, R.; Gonzalez-Moreno, P.; Yuan, L.; Wu, K.; Huang, W. Monitoring plant diseases and pests through remote sensing technology: A review. Comput. Electron. Agric. 2019, 165, 104943. [Google Scholar] [CrossRef]
- Farrell, A.; Wang, G.; Rush, S.A.; Martin, J.A.; Belant, J.L.; Butler, A.B.; Godwin, D. Machine learning of large-scale spatial Distributions of wild turkeys with high-dimensional environmental data. Ecol. Evol. 2019, 9, 5938–5949. [Google Scholar] [CrossRef] [PubMed]
- Byeon, D.H.; Jung, S.; Lee, W.H. Review of CLIMEX and MaxEnt for studying species distribution in South Korea. J. Asia Pac. Biodivers. 2018, 11, 325–333. [Google Scholar] [CrossRef]
- Pratumchart, K.; Suwannatrai, K.; Sereewong, C.; Thinkhamrop, K.; Chaiyos, J.; Boonmars, T.; Suwannatrai, A.T. Ecological Niche Model based on Maximum Entropy for mapping distribution of Bithynia siamensis goniomphalos, first intermediate host snail of Opisthorchis viverrini in Thailand. Acta Trop. 2019, 193, 183–191. [Google Scholar] [CrossRef]
- Redon, M.; Luque, S. Presence-only modelling for indicator species distribution: Biodiversity monitoring in the French Alps. In Proceedings of the 6th Spatial Analysis and Geomatics International Conference (SAGEO), Toulouse, France, 17–19 November 2010; pp. 42–55, hal-00558859. [Google Scholar]
- Dunn, J.C.; Buchanan, G.M.; Stein, R.W.; Whittingham, M.J.; McGowan, P.J.K. Optimising different types of biodiversity coverage of protected areas with a case study using Himalayan Galliformes. Biol. Conserv. 2016, 196, 22–30. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, S.; An, K. Distribution pattern prediction of an invasive alien species largemouth bass using a maximum entropy model (MaxEnt) in the Korean peninsula. J. Asia Pac. Biodivers. 2018, 11, 516–524. [Google Scholar] [CrossRef]
- Afify, H.M.; Al-Masni, M.A. Taxonomy metagenomic analysis for microbial sequences in three domains system via machine learning approaches. Inform. Med. Unlocked 2018, 13, 151–157. [Google Scholar] [CrossRef]
- García, D.; Zamora, R.; Hódar, J.A.; Gómez, J.M. Age structure of Juniperus communis L. in the Iberian peninsula: Conservation of remnant populations in Mediterranean mountains. Biol. Conserv. 1999, 87, 215–220. [Google Scholar]
- Milios, E.; Pipinis, E.; Petrou, P.; Akritidou, S.; Smiris, P.; Aslanidou, M. Structure and regeneration patterns of the Juniperus excelsa Bieb. stands in the central part of the Nestos valley in the northeast of Greece. Ecol. Res. 2007, 22, 713–723. [Google Scholar] [CrossRef]
- El-Juhany, L. Forestland degradation and potential rehabilitation in southwest Saudi Arabia. Aust. J. Basic Appl. Sci. 2009, 3, 2677–2696. [Google Scholar]
- Mao, K.; Milne, R.I.; Zhang, L.; Peng, Y.; Liu, J.; Thomas, P.; Mill, R.R.; Susanne SRenner, S.S. Distribution of living Cupressaceae reflects the breakup of Pangea. Proc. Natl. Acad. Sci. USA 2012, 109, 7793–7798. [Google Scholar] [CrossRef]
- Wazen, N.; Fady, B. Technical Report, Geographic Distribution of 24 Major Tree Species in the Mediterranean; FAO Forest and Landscape Restoration Mechanism, Forestry Department, Forestry Policy and Resources Division: Rome, Italy, 2016; pp. 1–59. [Google Scholar]
- MacLaren, C.A. Climate change drives decline of Juniperus seravschanica in Oman. J. Arid Environ. 2016, 128, 91–100. [Google Scholar] [CrossRef]
- Pirani, A.; Moazzeni, H.; Mirinejad, S.; Naghibi, F.; Mosaddegh, M. Ethnobotany of Juniperus excelsa M. Bieb. (Cupressaceae) in Iran. Ethnobot. Res. Appl. 2011, 9, 335–341. [Google Scholar] [CrossRef]
- Adams, R.P.; Hojjati, F. Taxonomy of Juniperus in Iran: Insight from DNA sequencing. Phytologia 2012, 94, 219–227. [Google Scholar]
- Ahani, H.; Jalilvand, H.; Hosseini Nasr, S.M.; Soltani Kouhbanani, H.; Mohammadzadeh, H. Reproduction of juniper (Juniperus polycarpos) in Khorasan Razavi, Iran. For. Sci. Pract. 2013, 15, 231–237. [Google Scholar] [CrossRef]
- Heshmati, G.A. Vegetation characteristics of four ecological zones of Iran. Int. J. Plant Prod. 2007, 1, 215–224. [Google Scholar]
- Jafari, M. Forests Genetic Resources in Iran. The Report on the State of the World’s Forest Genetic Resources. 2012. Available online: www.fao.org/documents (accessed on 13 June 2012).
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- O’Brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Heubes, J.; Schmidt, M.; Stuch, B.; García Márquez, J.R.; Wittig, R.; Zizka, G.; Thiombiano, A.; Sinsin, B.; Schaldach, R.; Hahn, K. The projected impact of climate and land use change on plant diversity: An example from West Africa. J. Arid Environ. 2013, 96, 48–54. [Google Scholar] [CrossRef]
- Yi, Y.J.; Cheng, X.; Yang, Z.F.; Zhang, S.H. Maxent modeling for predicting the potential distribution of endangered medicinal plant (H. riparia Lour) in Yunnan, China. Ecol. Eng. 2016, 92, 260–269. [Google Scholar] [CrossRef]
- Aguilar, G.D.; Blanchon, D.J.; Foote, H.; Pollonais, C.W.; Mosee, A.N. A performance based consensus approach for predicting spatial extent of the Chinese windmill palm (Trachycarpus fortunei) in New Zealand under climate change. Ecol. Inform. 2017, 39, 130–139. [Google Scholar] [CrossRef]
- Abdelaal, M.; Fois, M.; Fenu, G.; Bacchetta, G. Using MaxEnt modeling to predict the potential distribution of the endemic plant Rosa arabica Crép. in Egypt. Ecol. Inform. 2019, 50, 68–75. [Google Scholar] [CrossRef]
- Mousazade, M.; Ghanbarian, G.; Pourghasemi, H.R.; Safaeian, R.; Cerdà, A. Maxent Data Mining Technique and Its Comparison with a Bivariate Statistical Model for Predicting the Potential Distribution of Astragalus Fasciculifolius Boiss. in Fars, Iran. Sustainability 2019, 11, 3452. [Google Scholar] [CrossRef]
- Fois, M.; Cuena-Lombraña, A.; Fenu, G.; Bacchetta, G. Using species distribution models at local scale to guide the search of poorly known species: Review, methodological issues and future directions. Ecol. Model. 2018, 385, 124–132. [Google Scholar] [CrossRef]
- Bosso, L.; Rebelo, H.; Garonna, A.P.; Russo, D. Modelling geographic distribution and detecting conservation gaps in Italy for the threatened beetle Rosalia alpina. J. Nat. Conserv. 2013, 21, 72–80. [Google Scholar] [CrossRef]
- Sanchez-Hernandez, C.; Boyd, D.S.; Foody, G.M. Mapping specific habitats from remotely sensed imagery: Support vector machine and support vector data description based classification of coastal saltmarsh habitats. Ecol. Inform. 2007, 2, 83–88. [Google Scholar] [CrossRef]
- Sousa, R.; Yevseyeva, I.; da Costa, J.F.P.; Cardoso, J.S. Multicriteria models for learning ordinal data: A literature review. In Artificial Intelligence, Evolutionary Computing and Metaheuristics; Yang, X.-S., Ed.; Springer: Berlin, Germany, 2013; pp. 109–138. [Google Scholar]
- Blahut, J.; Westen, C.J.V.; Sterlacchini, S. Analysis of landslide inventories for accurate prediction of debris-flow source areas. Geomorphology 2010, 119, 36–51. [Google Scholar] [CrossRef]
- Xu, W.; Dai, J.; Hung, Y.S.; Wang, Q. Estimating the area under a receiver operating characteristic (ROC) curve: Parametric and non-parametric. Signal Process. 2013, 93, 3111–3123. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Feng, Y.; Liu, Z. The use of ROC and AUC in the validation of objective image fusion evaluation metrics. Signal Process. 2013, 115, 38–48. [Google Scholar] [CrossRef]
- Khanum, R.; Mumtaz, A.S.; Kumar, S. Predicting impacts of climate change on medicinal asclepiads of Pakistan using Maxent modeling. Acta Oecol. 2013, 49, 23–31. [Google Scholar] [CrossRef]
- Całka, B. Comparing continuity and compactness of choropleth map classes. Geod. Cartogr. 2018, 67, 21–34. [Google Scholar]
- Chun, Y.; Koo, H.; Griffith, D.A. A comparison of optimal map classification methods incorporating uncertainty information. In Proceedings of the Spatial Accuracy, Avignon, France, 20–22 April 2016; pp. 177–181. [Google Scholar]
- Jenks, G.; Coulson, M. Class Intervals for Statistical Maps. Ann. Assoc. Am. Geogr. 1963, 3, 119–134. [Google Scholar]
- Hirzel, A.H.; Hausser, J.; Perrin, N. Biomapper 4.0. Lab. of Conservation Biology; Department of Ecology and Evolution, University of Lausanne: Lausanne, Switzerland, 2007. [Google Scholar]
- Tuv, E.; Borisov, A.; Runger, G.; Torkkola, K. Feature selection with ensembles, artificial variables, and redundancy elimination. J. Mach. Learn. Res. 2009, 10, 1341–1366. [Google Scholar]
- Wang, R.; Li, Q.; He, S.; Liu, Y.; Wang, M.; Jiang, G. Modeling and mapping the current and future distribution of Pseudomonas syringae pv. actinidiae under climate change in China. PLoS ONE 2018, 13, e0192153. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Li, G.Q.; Du, S. Simulating the potential distribution of Elaeagnus angustifolia L. based on climatic constraints in China. Ecol. Eng. 2018, 113, 27–34. [Google Scholar] [CrossRef]
- Fourcade, Y.; Engler, J.O.; Rodder, D.; Secondi, J. Mapping species distributions with MAXENT using a geographically biased sample of presence data: A performance assessment of methods for correcting sampling bias. PLoS ONE 2014, 9, e97122. [Google Scholar] [CrossRef]
- Muñoz-Mas, R.; Lopez-Nicolas, A.; Martínez-Capel, F.; Pulido-Velazquez, M. Shifts in the suitable habitat available for brown trout (Salmo trutta L.) under short-term climate change scenarios. Sci. Total Environ. 2016, 544, 686–700. [Google Scholar]
- Sofizadeh, A.; Rassi, Y.; Vatandoost, H.; Hanafi-Bojd, A.A.; Mollalo, A.; Rafizadeh, S.; Akhavan, A.A. Predicting the distribution of Phlebotomus papatasi (Diptera: Psychodidae), the primary vector of zoonotic cutaneous leishmaniasis, in Golestan Province of Iran using ecological niche modeling: Comparison of MaxEnt and GARP models. J. Med. Entomol. 2016, 54, 312–320. [Google Scholar]
- Yuan, H.; Wei, Y.; Wang, X. Maxent modeling for predicting the potential distribution of Sanghuang, an important group of medicinal fungi in China. Fungal Ecol. 2015, 17, 140–145. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jimenez-Valverde, A.; Real, R. AUC: Amisleading measure of the performance of predictive distribution models. Glob. Ecol. Biogeogr. 2007, 17, 145–151. [Google Scholar] [CrossRef]
- Václavík, T.; Meentemeyer, R.K. Invasive species distribution modeling (iSDM): Are absence data and dispersal constraints needed to predict actual distributions? Ecol. Model. 2009, 220, 3248–3258. [Google Scholar] [CrossRef]
- Fortunel, C.; Paine, C.; Fine, P.; Kraft, N.; Baraloto, C. Environmental factors predict community functional composition in Amazonian forests. J. Ecol. 2014, 102, 145–155. [Google Scholar] [CrossRef]
- Silva, L.D.; Costa, H.; de Azevedo, E.B.; Medeiros, V.; Alves, M.; Elias, R.B.; Silva, L. Modelling Native and Invasive Woody Species: A Comparison of ENFA and MaxEnt Applied to the Azorean Forest. In Modeling, Dynamics, Optimization and Bioeconomics II, Proceedings in Mathematics & Statistics; Pinto, A.A., Zilberman, D., Eds.; Springer: Berlin, Germany, 2017; Volume 195, pp. 415–444. [Google Scholar]
- Chiogna, G.; Marcolini, G.; Liu, W.; Ciria, T.P.; Tuo, Y. Coupling hydrological modeling and support vector regression to model hydropeaking in alpine catchments. Sci. Total Environ. 2018, 633, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Bradie, L.; Leung, B. A quantitative synthesis of the importance of variables used in MaxEnt species distribution models. J. Biogeogr. 2017, 44, 1344–1361. [Google Scholar] [CrossRef]
- Douaihy, B.; Restoux, G.; Machon, N.; Dagher-Kharrat, M.B. Ecological characterization of the Juniperus excelsa stands in Lebanon. Ecol. Mediterr. 2013, 39, 169–180. [Google Scholar]
- Walas, Ł.; Sobierajska, K.; Ok, T.; Dönmez, A.A.; Kanoğlu, S.S.; Dagher-Kharrat, M.B.; Douaihy, B.; Romo, A.; Stephan, J.; Jasińska, A.K.; et al. Past, present, and future geographic range of an oro-Mediterranean Tertiary relict: The Juniperus drupacea case study. Reg. Environ. Chang. 2019, 19, 1507–1520. [Google Scholar] [CrossRef]
- Miller, R.F.; Bates, J.D.; Svejcar, T.J.; Pierson, F.B.; Eddleman, L.E. Biology, Ecology, and Management of Western Juniper (Juniperus occidentalis). Oregon State University. Tech. Bull. 2005, 152, 1–77. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).