1. Introduction
For reservoirs worldwide, storage preservation through sustainable sediment management operations is a critical issue due to the severe problem of reservoir sedimentation. The available total storage capacity of global reservoirs has been decreasing in recent years because of the lack of effective sediment management practices [
1]. Sediment trapping in a reservoir or dam interferes with the course of sediment transport through a river system; such interference exerts a considerable influence on the sustainability of future water supplies from the reservoir, engenders channel erosion, and negatively affects the downstream ecosystem. Morphological effects on downstream river channels include riverbed incision, riverbank instability, damage to embankments and levees, and channel width variation [
2,
3,
4,
5].
Studies have investigated many management strategies and efficient countermeasures for reducing the influence of sedimentation [
3,
6,
7,
8]. Dredging is a commonly used measure to remove mechanically deposited sediment from reservoirs. The disposal of dredged sediment is costly due to the involved engineering, permission, and placement site requirements. However, dredged sediment can be considered as a resource that provides effective environmental benefits and may be added to the downstream river of a dam to compensate for the lack of sediment supply. Accordingly, an approach called sediment replenishment (sediment augmentation) can be adopted for the effective replenishment due to dam interruption. [
3,
9,
10]. Since the 1980s, sediment has been added into rivers to replenish the downstream river reaches of dams. The sediment replenishment method has been implemented to prevent downstream riverbed degradation and to improve the suitable living habitat of aquatic animals. Field investigations and laboratory experiments have been conducted for rivers in America, Europe, Japan, and Taiwan to improve knowledge about the transport processes during sediment replenishment [
11,
12,
13].
In field practice, the sediment replenishment method can be planned and practiced in specific hydrological and geographic areas. Okano et al. (2004) [
14] investigated reservoir sedimentation management by depositing coarse sediment (mainly sand and gravel sizes) with a volume of 0.3–25 × 10
3 m
3 for replenishing downstream areas. They summarized sediment replenishment projects conducted at eight dams in Japan from 1999 to 2003. Moreover, researchers have investigated the influences of sediment replenishment conducted using appropriate grain sizes on the downstream river of Yahagi dam and the upper basin of Kizu river [
15,
16]. Researchers also analyzed the interaction between the relative flow field and morphological evolution during field experiments of sediment replenishment [
13]. The conceptual idea of the replenishment method is to place sediment in the downstream floodplain before the arrival of floods. If the replenishment areas experience floods, the replenished sediment can be scoured and transported further downstream. As mentioned, field tests in Japan have focused on the deposition of coarse materials in reservoirs to subsequently replenish downstream rivers of the dams in order to create a suitable environment for aquatic organisms. The applied replenishment method requires a sufficient amount of discharge in order to scour replenished sediment; replenished sediment is thus always placed on floodplains before the discharge of water from a reservoir during the wet season. Sediment deposited in a reservoir can be periodically dredged or excavated and then temporarily deposited on the floodplain for transportation to the downstream river of a dam. Moreover, the replenished volume is based on the sediment transport capacity of the channel and environmental conditions. According to reports in Japan regarding the replenished volume, up to 10% of the annual deposition volume in a reservoir could be successfully executed [
6,
7]. Ock et al. (2013) [
17] reviewed methods in the context of sediment replenishment and compared implementation activities undertaken in the Nunome river of Japan and Trinity river of California, USA. According to sediment placement or injection types, sediment replenishment methods were implemented with mechanical rehabilitation for re-creating gravel or sand bar features through fluvial processes. This comparative study provided useful information to adopt proper methods corresponding to river specific high-flow and sediment regimes. In 2009, a field test for coarse sediment replenishment was conducted at the downstream floodplain of Shihkang dam across the Dachia river in Central Taiwan [
12]. The total replenished volume of the coarse sediment excavated (median grain size: 80 mm) from the Shigang Reservoir was approximately 50 × 10
3 m
3. The field experiment revealed that the replenished sediment was entirely scoured further downstream in a typhoon flood event with a peak discharge of 5400 m
3/s in 2009.
On the basis of the aforementioned studies, field and laboratory experiments for sediment replenishment have mainly focused on coarse materials, with few fine sediment examples being provided. In fact, fine replenished sediment dredged from reservoirs is valuable for coastline or estuary restoration and for the respiration of aquatic organisms. However, if a high concentration of fine replenished sediment is scoured by a reservoir flood discharge, the water quality of water treatment plants connected to the relevant reservoir may deteriorate.
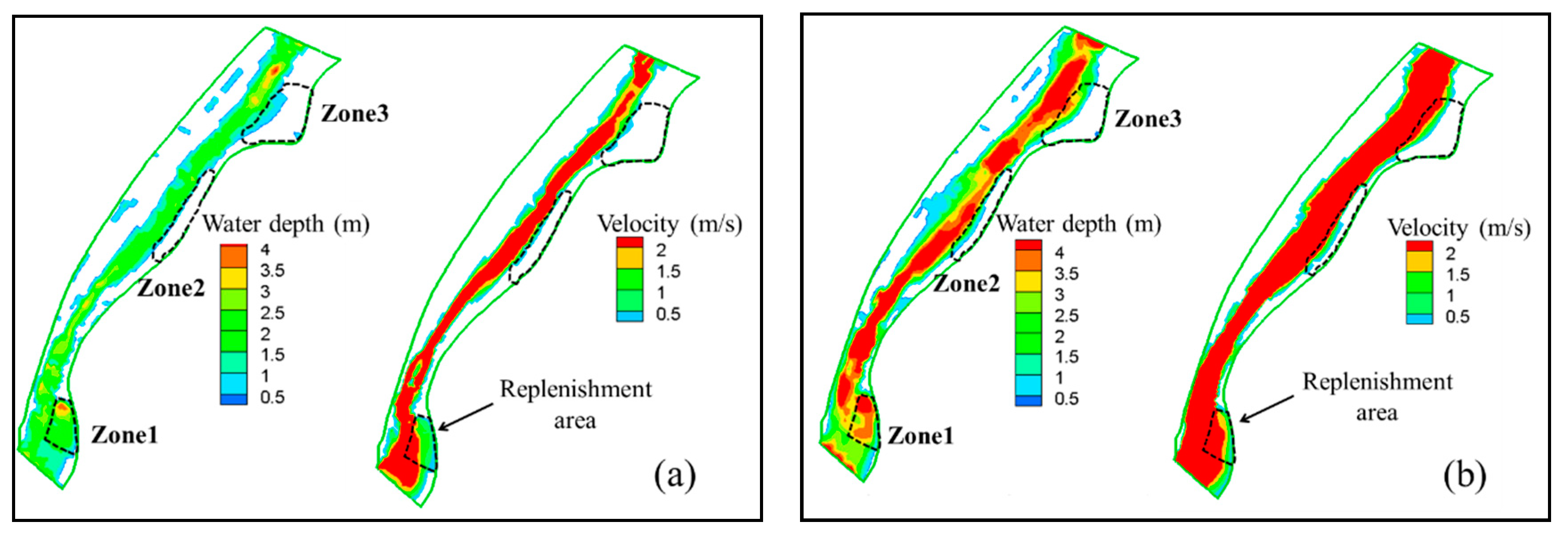
In the present study, the Shihmen Reservoir was used as the study site to investigate the feasibility of fine-sediment replenishment. First, possible areas for replenishment were analyzed through a numerical simulation conducted using a two-dimensional (2D) numerical model [
18]. On the basis of the framework of the finite volume method, the 2D numerical model was used to solve the shallow water equations coupled with the advection–diffusion equation in order to simulate the suspended sediment transport phenomenon in the river. A physical model was built to mimic the scouring process of replenished sediment in the downstream river reach of Shihmen dam. Experiments involving different water content levels of dredged fine sediment were conducted in the physical model to investigate the incipient motion of the replenished sediment with cohesiveness. Through the experiments, the scour ratio was analyzed using relevant factors such as flood discharge, flood duration, and water content of the replenished sediment. The effect of the scouring of fine sediment from the replenishment area on the downstream water intake was also investigated.
2. Description of Study Site
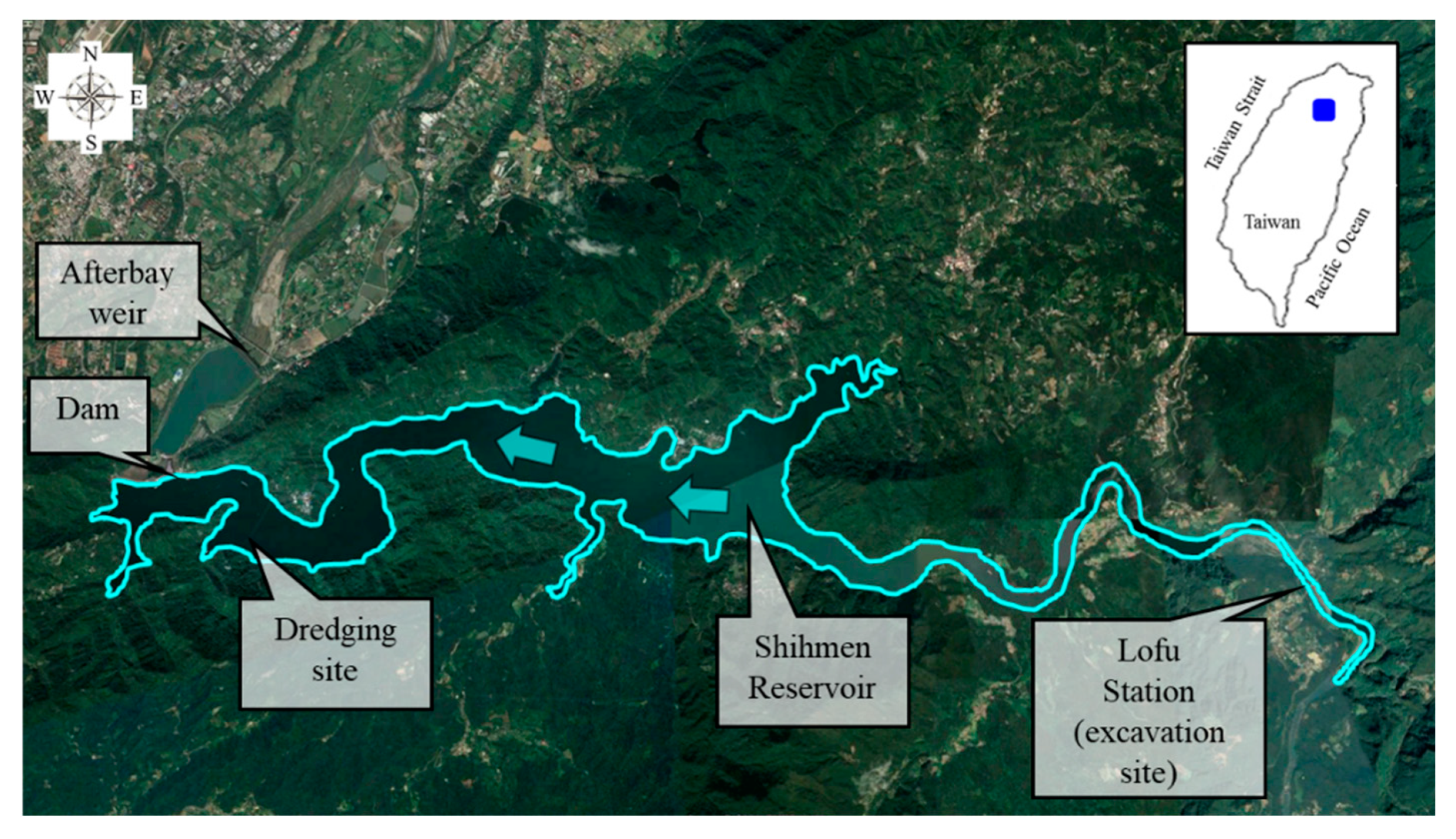
The Shihmen Reservoir was built in 1964 in northern Taiwan (
Figure 1). Shihmen dam is a 133.1-m-high embankment dam and is equipped with spillways, flood diversion tunnels, a bottom outlet, a power plant inlet, a sediment-sluicing tunnel, and an irrigation inlet. The design capacity of the three spillways is 11,400 m
3/s, that of the flood diversion tunnels is 2400 m
3/s, that of the bottom outlet is 34 m
3/s, that of the power plant inlet is 56 m
3/s, that of the sediment-sluicing tunnel is 300 m
3/s, and that of the irrigation inlet is 18.4 m
3/s. At a normal water level of EL. 245 m, the reservoir pool is approximately 16.5 km in length and forms a water surface area of 8 km
2. The initial storage capacity is 30.9 × 10
6 m
3. The reservoir is multifunctional and is used for water supply, irrigation, electric power generation, and flood mitigation; it is also a tourist attraction. In particular, the reservoir supplies water to 2.1 million people in Taoyuan City and New Taipei City for daily use.
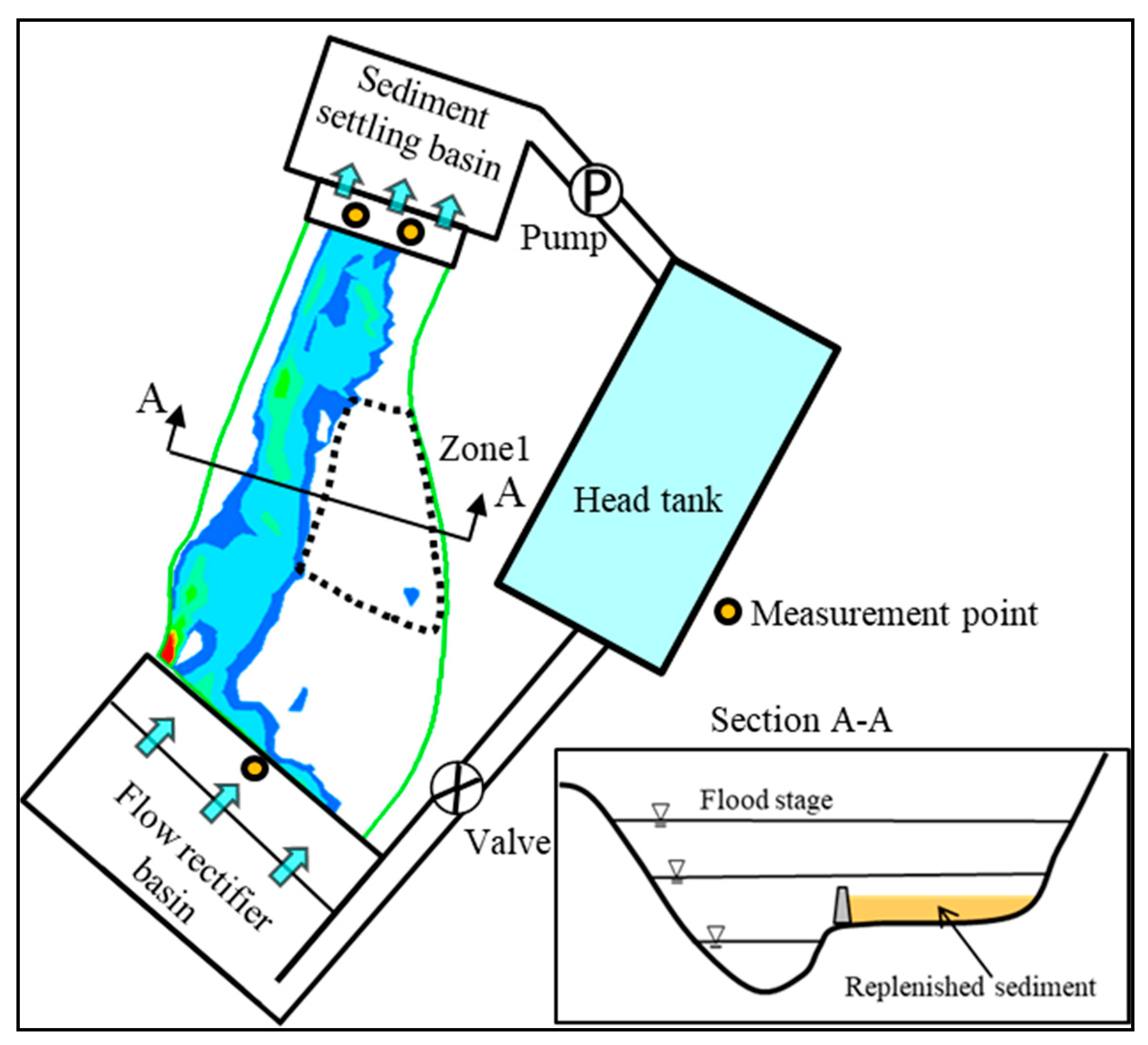
According to the data of a survey conducted in 2018, the reservoir’s storage capacity was estimated to be 65.72% of its initial capacity. The average annual deposited sediment volume from 1963 to 2018 was approximately 1.93 × 106 m3/year. Except for hydraulic desilting measures, mechanical excavation constitutes the strategies adopted for maintaining the Shihmen Reservoir. The mechanical excavation includes the dredging and dry excavation. The dredging is mainly performed under the water surface, and the main purpose of dry excavation is to remove exposed sediment. The dry excavation site in this study is located at the Lofu gauge station, and the averaged exaction volume between 2009 and 2018 was approximately 0.47 × 106 m3/year. The dredging site is near the dam, and the dredged sediment volume between 2009 and 2018 was nearly 0.36 × 106 m3/year. Fine sediment deposited in front of Shihmen Dam is typically removed through a pipeline by a hydraulic dredging system that applies siphon dredging; before executing the dredging process, the system calculates the head difference between the reservoir water surface and the pipeline outlet. However, finding a disposal location for the dredged sediment is a problem. Therefore, one of the implemented reservoir-desilting strategies entails conducting sediment replenishment by placing the reservoir deposits on the downstream floodplain, which may be used in the Shihmen Reservoir.
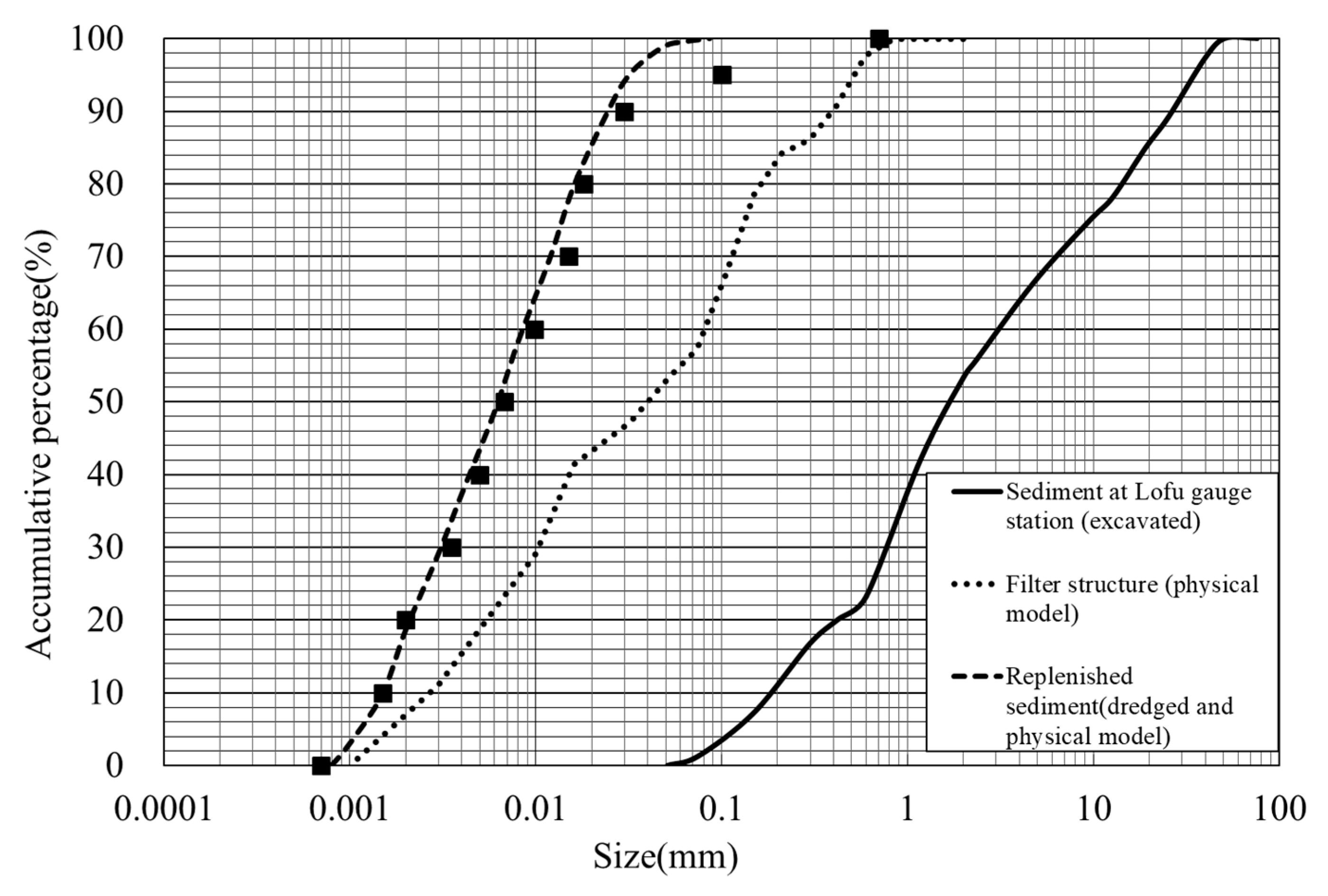
Referring to the particle size distribution presented in
Figure 2, the dredged sediment near the dam site is almost entirely composed of silt and clay; thus, it is classified as a cohesive material. The sediment excavated at the Lofu gauge station is coarse sand. In this study, sediment obtained from both dredging and dry excavation was used for sediment replenishment investigation on the downstream floodplain. According to the regulation of the water pollution control action [
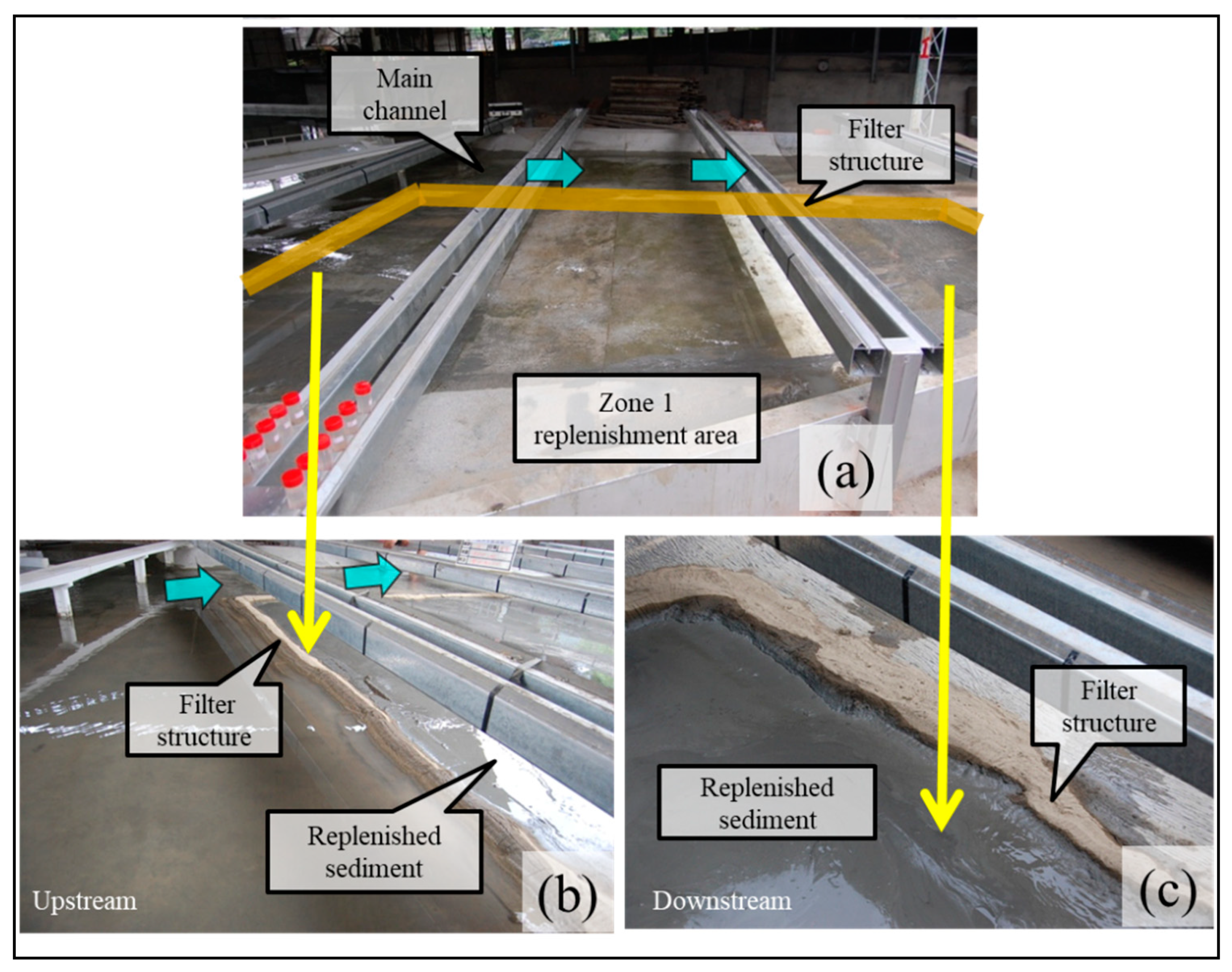
19], the replenished material should be placed at the floorplan and confined by a filter structure that serves as a permeable barrier to avoid the replenished fine sediment from polluting the water in nearby main channels during low-flow periods.
The available flood discharges from the reservoir and the flood duration are key factors for implementing sediment replenishment. Based on historical records from 1911 to 2017, three typhoons hit Taiwan each year on average. According to a frequency analysis, the 2-, 10-, and 20-year return period floods have peak discharges of 1700, 3500, and 6100 m
3/s, respectively [
20].
5. Experimental Results and Analysis
Flood discharges from a reservoir and flood duration are key factors for investigating scouring processes in the sediment replenishment area. On the basis of data regarding flood discharges from the Shihmen Reservoir in the past 10 years, we observed that the flood discharges were higher than 500 and 1000 m3/s for 38 and 22 h, respectively, in all flood events. Apart from 2-, 10-, and 20-year return period flood discharges, we considered lower discharges of 500 and 1000 m3/s as the inflow discharges for practical purposes in the physical model tests. These discharges generated overbank flow to flood over the replenishment area on the floodplain.
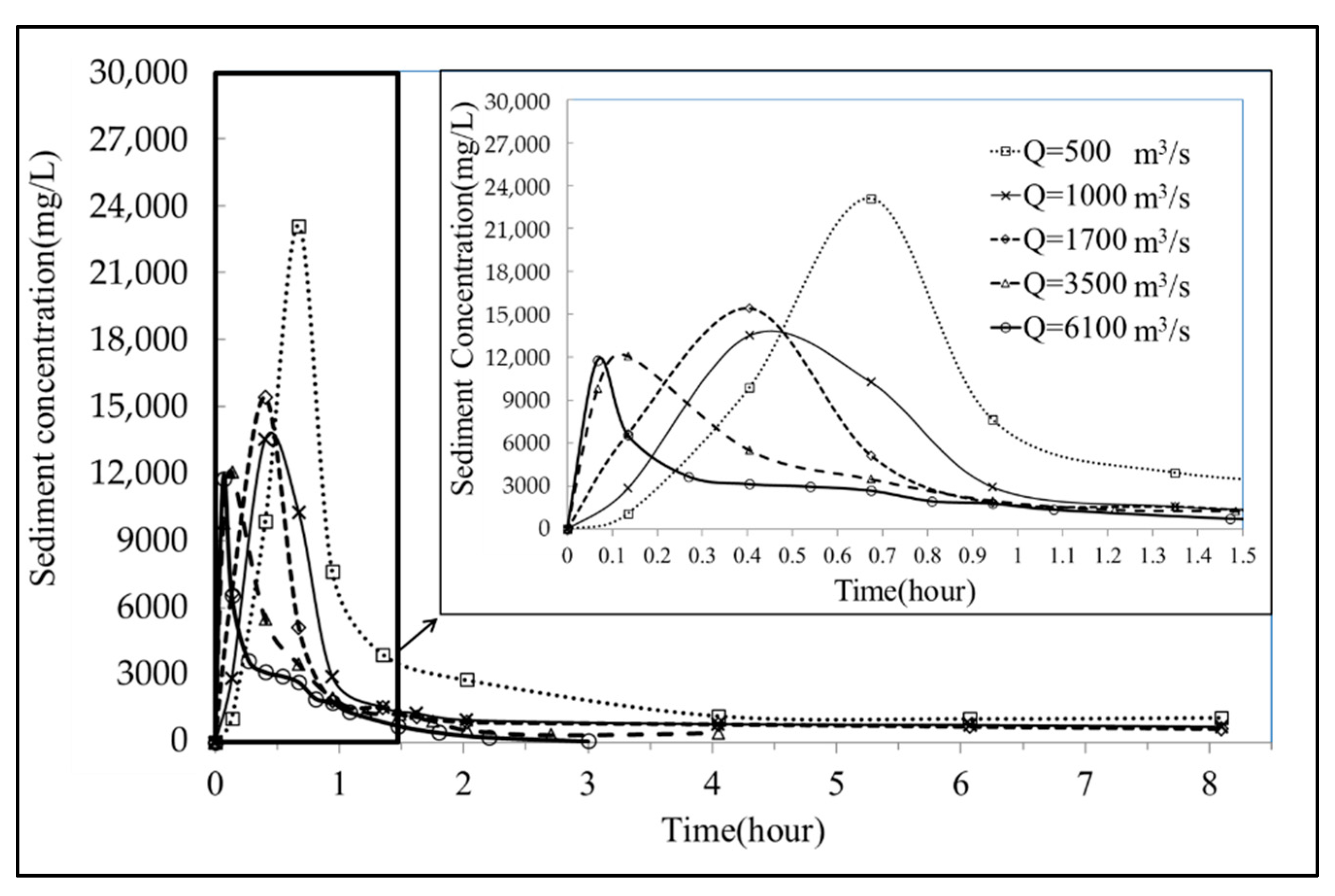
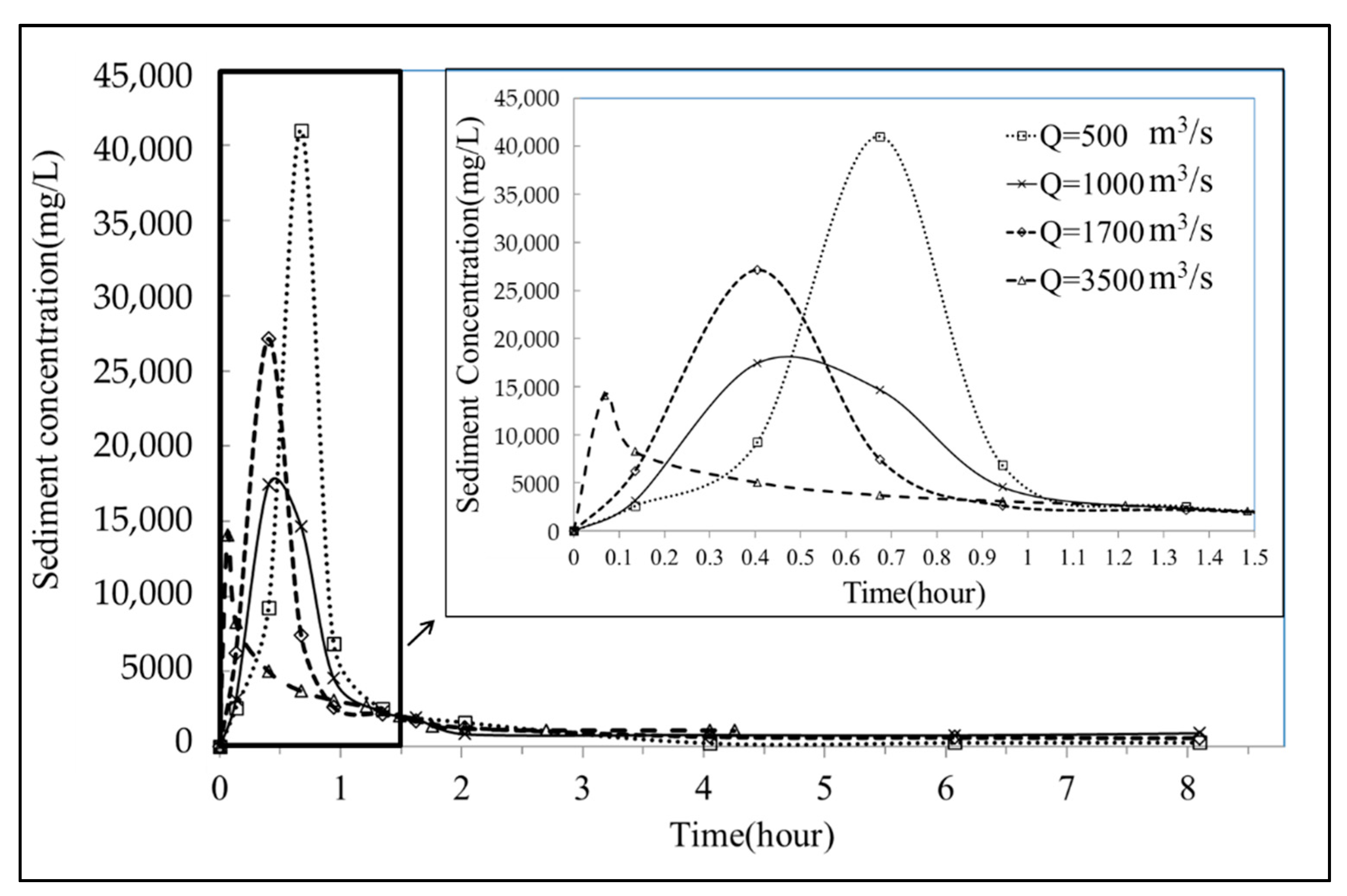
Figure 10 illustrates the outflow sediment concentration measured against time in test cases involving various inflow discharges (from 500 to 6100 m
3/s) at the downstream end (Section 85) of the physical model. In this figure, the hydrographs in the first 1.5-h period are enlarged to enhance the visualization of changes in the measured sediment concentration. In the test case that involved a
Q value of 6100 m
3/s, the peak sediment concentration (12,000 mg/L) was observed at 0.07 h because a higher discharge could generate a higher flow velocity to scour most of the replenished sediment. For comparison, in the test case that involved a
Q value of 500 m
3/s, the peak sediment concentration (24,000 mg/L) occurred at 0.7 h. Although a higher discharge could generate a higher flow velocity to scour the replenished sediment, the concentration of suspended sediments may not have increased further due to the larger water volume. The peak sediment concentration for the test case that involved the
Q value of 6100 m
3/s was lower than that for the test case that involved the
Q value of 500 m
3/s. However, the peak sediment discharge (product of flow discharge and sediment concentration) should be considerably increased due to higher flow discharge. Moreover, the hydrographs revealed that major variations obviously occurred in the first 1.5 h. After 1.5 h, the measured sediment concentrations of all the test cases were lower than 6000 mg/L. This concentration can be managed by the Bansin water treatment plant. Consequently, only the first 1.5 h would be required for complete scouring in the replenishment area.
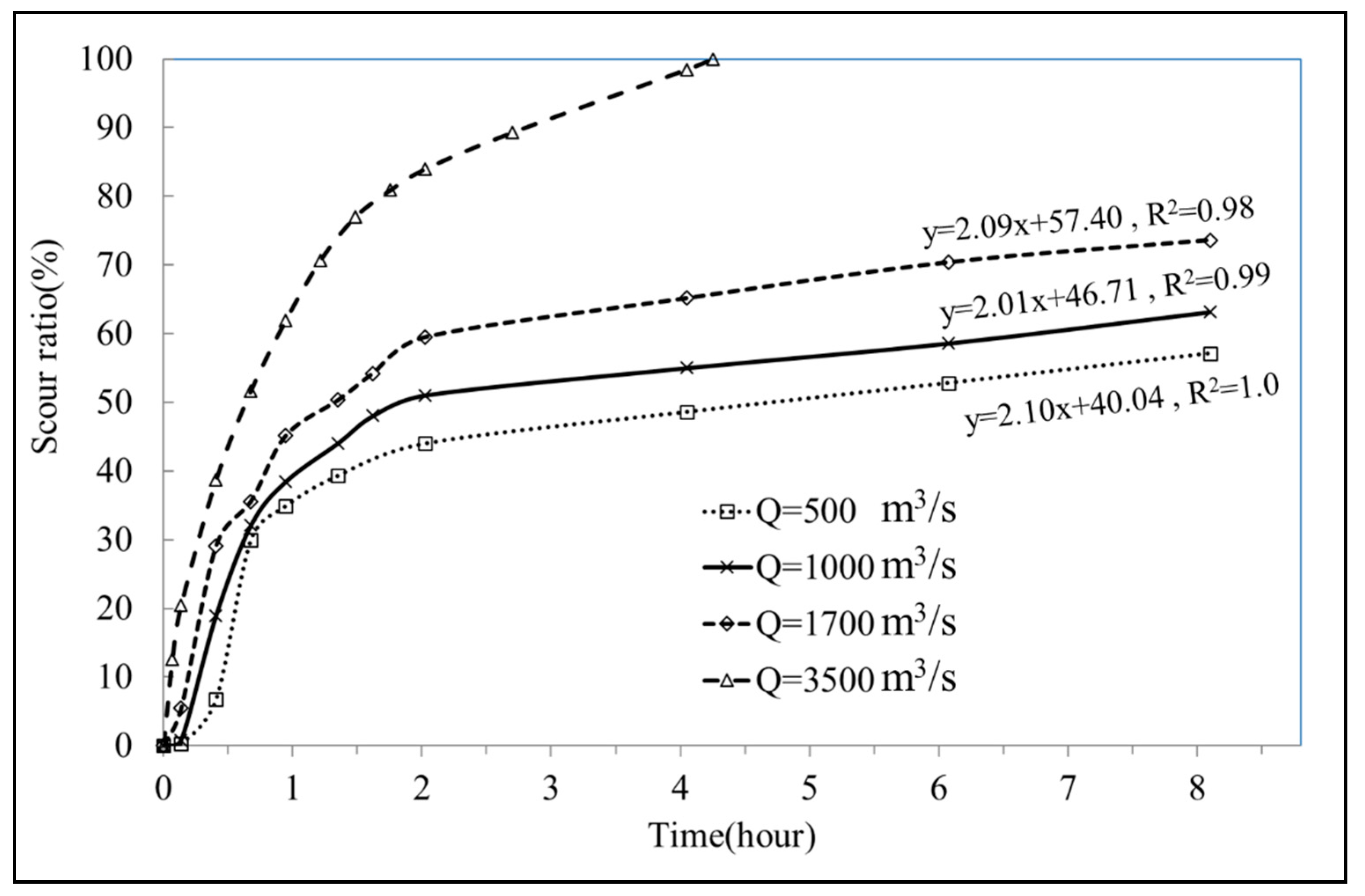
The volume of scoured sediment could be obtained from the sediment concentration measured at the downstream boundary in the physical model. The scour ratio could be defined as the ratio of the cumulative volume of the scoured sediment to the total amount of replenished sediment. As plotted in
Figure 11 for each given discharge, except for 6100 m
3/s, the variations in the scour ratio exhibited a linear trend approximately after 3 h. This indicates that the replenished sediment was scoured at a constant rate with time. According to the observed linear trend, the regression equation could be derived (
Figure 11), and the corresponding R-squared value revealed good agreement. By using the regression equation for each given discharge, we estimated the time required for complete scouring (i.e., 100% scour ratio) of replenished sediment (with water content of 40%); the estimation results are listed in
Table 2. The results indicated that the scour ratio increased with the discharge; complete scouring was achieved within 8 h. Moreover, when the
Q value was 6100 m
3/s, the entire amount of the replenished sediment was scoured (i.e., scour ratio = 100%) within 3 h. These results demonstrate that the scour ratio depends on the flood discharge and scour duration.
Figure 12 illustrates hydrographs of the measured sediment concentration against time for the test cases that involved replenished sediment with a water content level of 80%. Because of the lower erodibility of the replenished sediment, the experimental duration was too short to execute the physical model for a
Q value of 6100 m
3/s. Therefore, the test cases were conducted under only discharge values ranging from 500 to 3500 m
3/s. In the test case that involved a
Q value of 3500 m
3/s, the peak sediment concentration (14,500 mg/L) was observed at 0.07 h. For comparison, in the test case that involved a
Q value of 500 m
3/s, the peak sediment concentration (42,000 mg/L) was observed at 0.7 h. Similarly, the peak sediment concentration observed in the test case that involved the
Q value of 3500 m
3/s was lower than that observed in the test case that involved the
Q value of 500 m
3/s; however, the peak sediment discharge in the test case of 3500 m
3/s was higher. Furthermore, as revealed in the hydrographs, major variations obviously occurred in the first 1.5 h. After 1.5 h, the measured sediment concentrations for all test cases were lower than 3000 mg/L.
As plotted in
Figure 13, the variations in the scour ratio after approximately 2 h presented a linear trend, indicating the steady rate of the scour ratio at each given discharge with time. Accordingly, the regression equation at each given discharge could be obtained, and the corresponding R-squared values demonstrated good agreement with the measured data. By applying the regression equation to each given discharge value, we estimated the time required for complete scouring of the replenished sediment (with water content of 80%); the estimation results are presented in
Table 2. Except for the test case that involved the
Q value of 3500 m
3/s, the experiments were conducted within 8 h, and the scour ratio increased with the discharge. When
Q was 3500 m
3/s, 4.25 h was required to scour the entire amount of the replenished sediment (i.e., scour ratio = 100%). The experimental results reveal that a higher water content was associated with a higher scour ratio. The estimated time required to achieve a scour ratio of 100% was also longer when the water content was lower. On the basis of these experimental results, we can conclude that the scour ratio depends on the flood discharge, flood duration, and water content of replenished sediment.
6. Influence of Scouring on Downstream Water Intake
Scouring replenished sediment may influence the water quality at the downstream water intake section. Using the derived experimental data regarding outflow sediment concentrations, we investigated the influence of scouring on downstream water intake by conducting a 2D numerical simulation of suspended sediment transport in the downstream river. The Yuanshan weir is located downstream the Shihmen Reservoir, which is approximately 16.5 km away from the replenishment area. Water is typically withdrawn from the water intake section at the Yuanshan weir to the Bansin water treatment plant, which has a concentration limit of 6000 mg/L. According to the experimental results, the outflow sediment concentrations measured in all the test cases when the water content was 40% were rather high during the first 1.5 h. This may affect the suspended sediment concentration at the water intake and exceed the concentration limit stipulated by the Bansin water treatment plant. Considering the facilities of the treatment plant, the water turbidity can be treated if the sediment concentration decreases to 6000 mg/L or lower [
34].
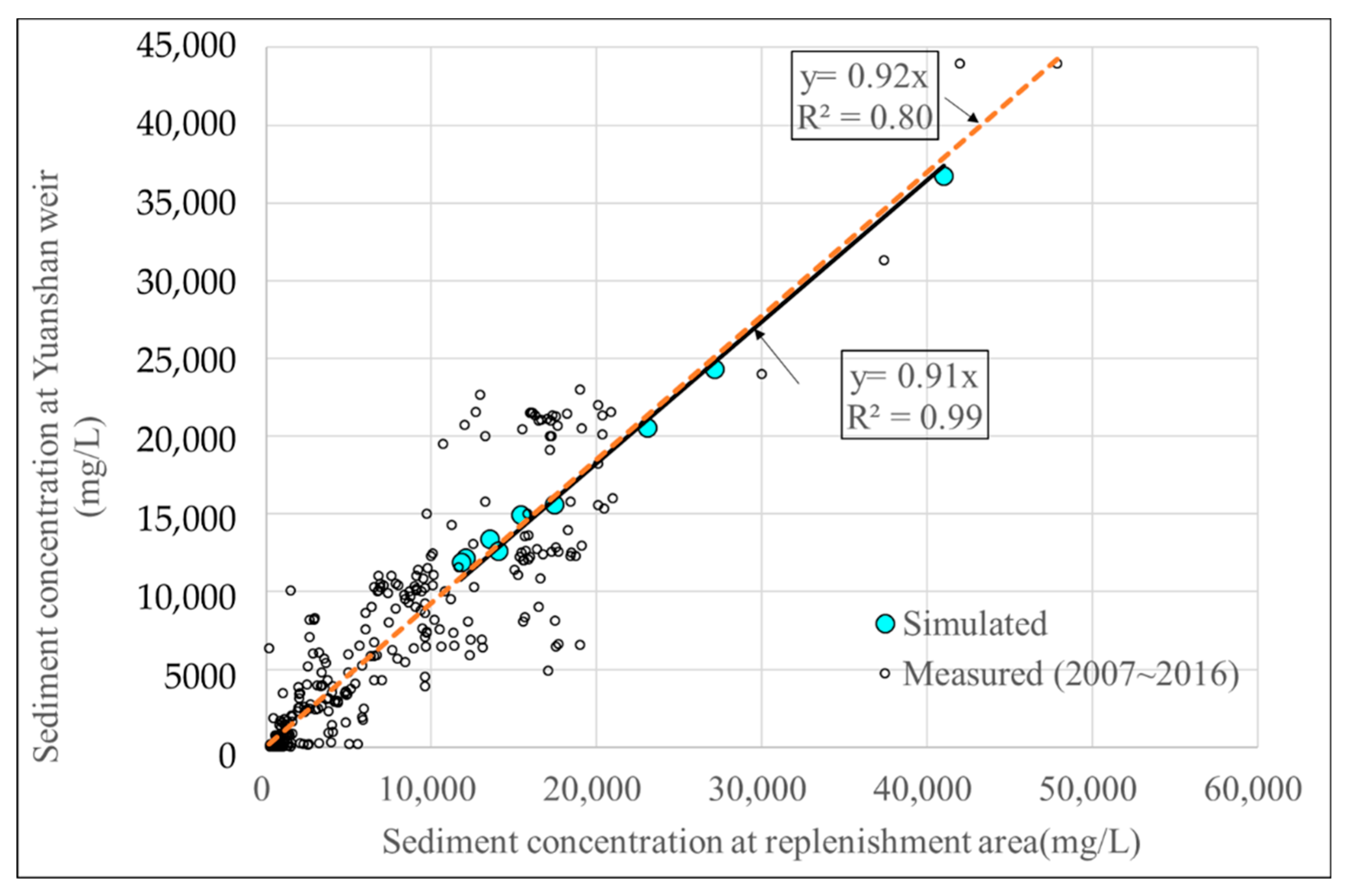
To understand the effect of the scouring of replenished sediment on the downstream water intake, the reduction ratio of sediment concentration should be investigated. By using field measurement data obtained from 2007 to 2016, we derived the relationship between the suspended sediment concentrations at the Yuanshan weir and afterbay weir (nearby replenishment area), and the results are plotted in
Figure 14. For modelling suspended sediment transport along the downstream river reach, we applied the 2D numerical model to solve the shallow water equations coupled with the advection–diffusion equation. According to the peak sediment concentration observed for each test case, we simulated the transport of suspended sediment and dissipation of replenished sediment under steady-flow conditions within the river reach, as described in
Section 3.2.
Figure 14 shows a plot of the simulated sediment concentration in the water intake section of the Yuanshan weir against the concentration in the replenishment area; the figure also shows a plot of the regressed relationship between the field data measured during flood discharge at the Yuanshan weir and the afterbay weir (around the replenishment area). By comparing the regression equations, we observed the simulated results to be close to the measured results. Clearly, the sediment concentration reduction ratio ranged from 91% to 92%. Thus, the reduction ratio of the concentration of suspended sediment scoured from the replenishment area to the concentration of suspended sediment at the Yuanshan weir was approximately 90%. According to the suspended sediment concentration limit (6000 mg/L) imposed at the Bansin water treatment plant, the outflow sediment concentration from the replenishment area was limited to 6667 mg/L.
7. Summary and Conclusions
Many reservoir management strategies and countermeasures have been implemented for reducing sedimentation effects. Dredging is a commonly used measure to remove mechanically deposited sediment. However, the disposal of dredged sediment can be costly because of engineering, permission, or placement site problems. Nevertheless, dredged sediment can be considered a beneficial resource that can be added to downstream rivers to compensate for dam-induced interruptions of sediment supply. The sediment replenishment method is an experimentally determined strategy in which sediment dredged or excavated from a reservoir can be used for riverbed replenishment to prevent downstream riverbed degradation, reduce coastline erosion, and execute estuary restoration for aquatic habitats. Nevertheless, high concentrations of fine replenished sediment may be scoured during reservoir flood discharges, which may deteriorate the water quality at the water intake in downstream river reaches.
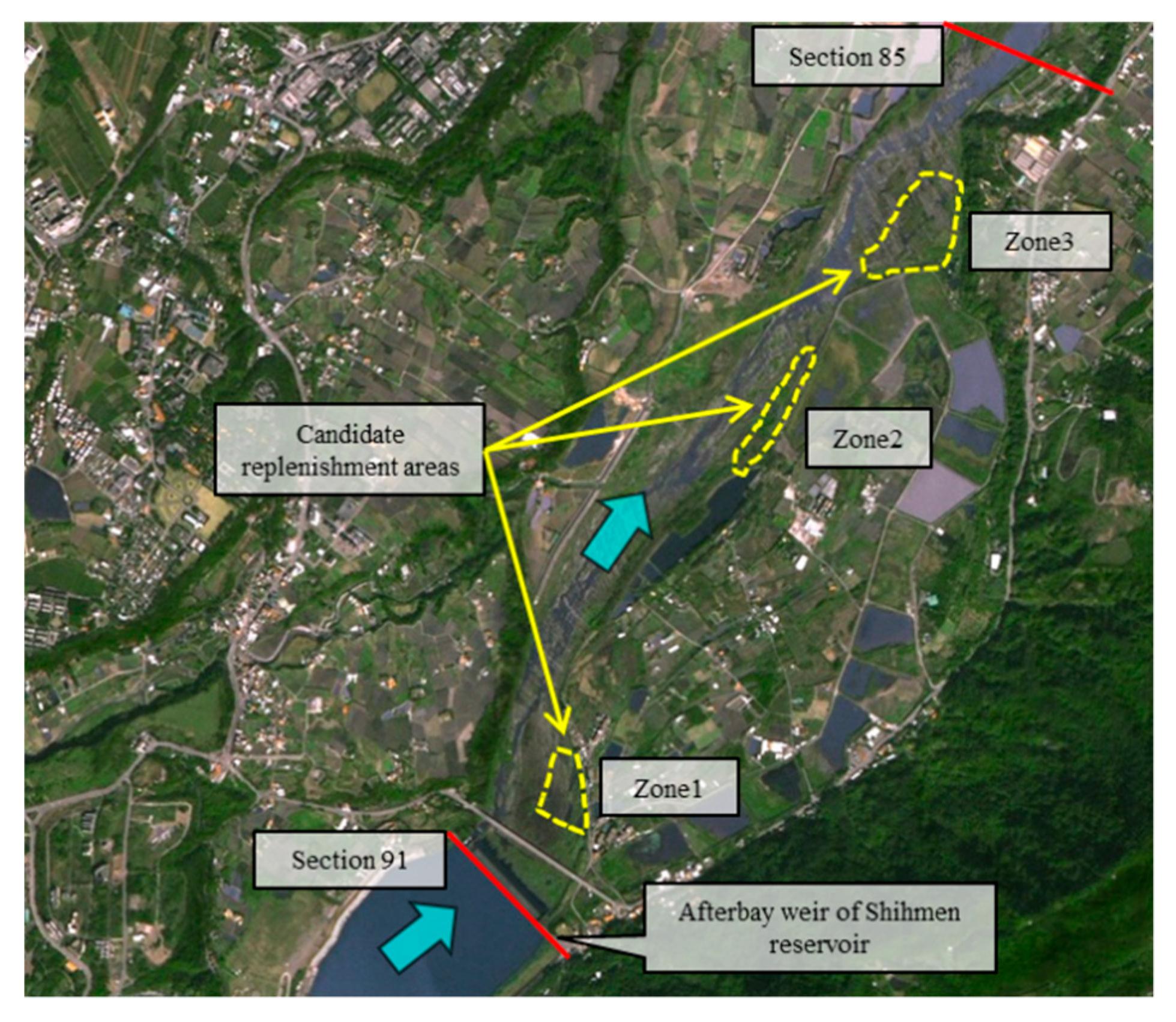
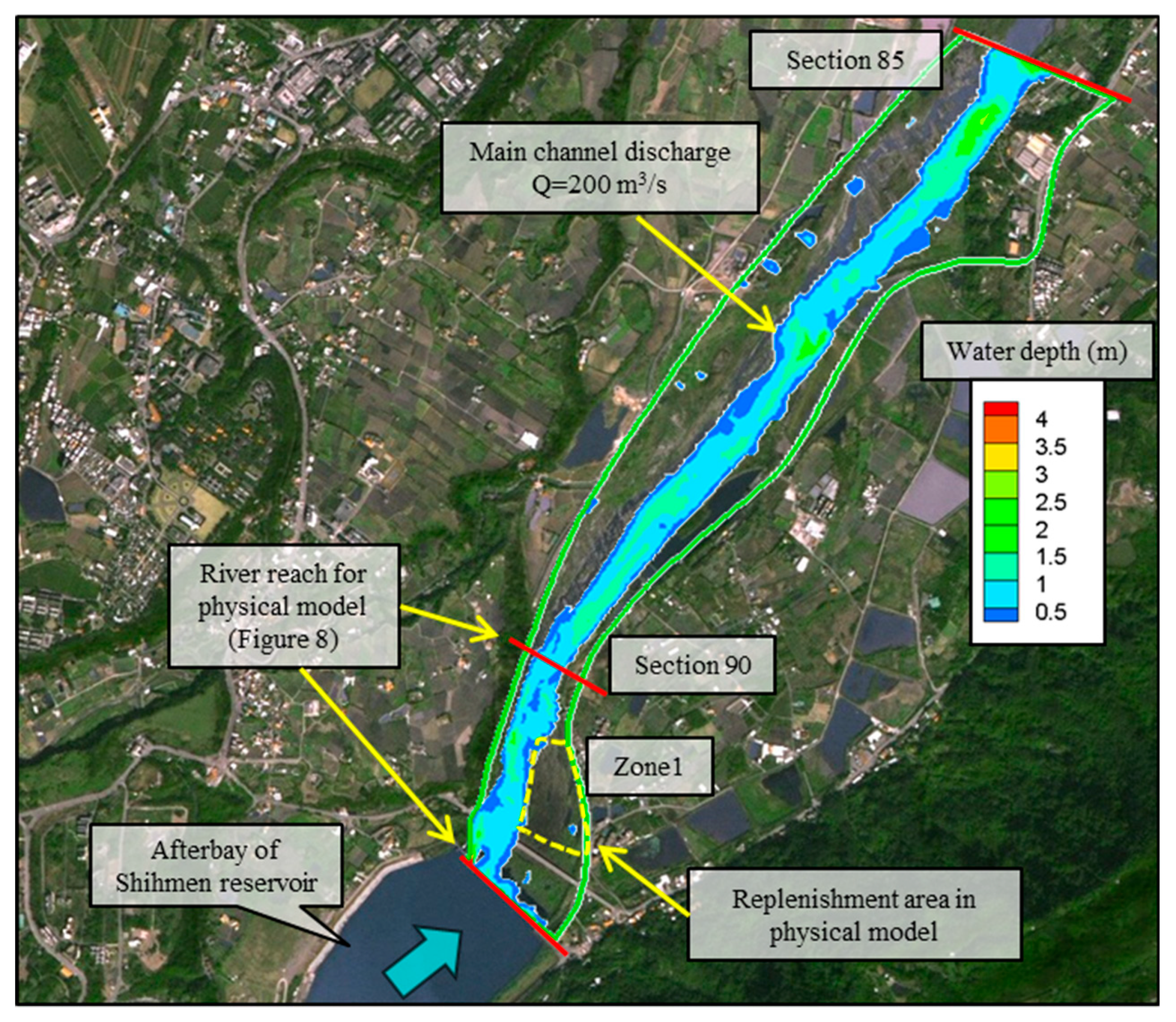
This study selected the Shihmen Reservoir located in Northern Taiwan to investigate the feasibility of reservoir replenishment using fine sediment. Previous studies on sediment replenishment in field or laboratory experiments have mainly focused on coarse materials, with few studies providing examples for fine sediment. In this study, candidate replenishment areas were first analyzed using a validated 2D numerical model to simulate flow velocity fields and water depths. To simulate suspended sediment transport in the model, the 2D shallow water equations along with the advection–diffusion equation was solved numerically in the framework of the finite volume method. On the basis of the analysis of the critical scour velocity, we adopted a flow velocity of 1.5 m/s along with a sufficient water depth to evaluate the incipient motion of both very fine and coarse replenished sediment. Although the concept of critical scour velocity is used herein for illustrative purposes, it indeed provided the preliminary criterion to assess the most feasible replenishment area. By comparing the simulated velocity fields and water depths in the candidate replenishment areas through hydraulic assessment, we identified the most feasible replenishment area, namely Zone 1, as the experimental domain (
Figure 6) for the physical model.
For satisfying the similitude of model scaling, the physical model was developed to mimic the scouring process of replenished sediment in the downstream river reach of Shihmen dam. As mentioned, similarities in sediment transport mechanisms engender difficulties in combining coarse and fine materials because of the difference in sediment particle sizes. The dimensionless shear parameter in the Shields diagram was employed for scaling the incipient particle motion by using Equation (8) for coarse sediment in the filter structure. For determining the scouring similarity of the fine replenished sediment, the relationship between flow-critical velocity and sediment dry density was regressed through flume experiments by using Equation (10). Using different water content levels (40% and 80% corresponding to dry densities of 1.2 and 0.84 t/m3, respectively) of the dredged fine sediment, we performed experiments in the physical model to investigate the incipient motion of replenished sediment with cohesiveness. On the basis of dynamic similarity during scouring, the sediment concentration scale ratio was equal to the dry density scale ratio presented in Equation (11). The time scale ratio of the scouring process was the same as that of the flow similarity derived from the Froude number. This indicates that the scouring time scale of flood flow is equal to that of sediment transport.
According to flood discharge data and frequency analysis data available for the Shihmen Reservoir, five inflow discharge values ranging from 500 to 6100 m
3/s were used in the physical model tests as the upstream boundary conditions, which generated overbank flow during a flood in the replenishment area on the floodplain. The hydrographs obtained from the test cases that involved the water content of 40% (
Figure 10) revealed that the variations in the sediment concentration apparently occurred in the first 1.5 h. After 1.5 h, the measured sediment concentrations for all test cases were lower than 6000 mg/L. This concentration value was determined to be suitable for the downstream water intake stipulated by the Bansin water treatment plant. For the test cases that involved the water content of 80% (
Figure 12), the measured sediment concentrations after 1.5 h were lower than 3000 mg/L for all test cases. Thus, for all test cases, the entire scouring operation took less than 1.5 h in the replenishment area to affect the downstream water treatment plant.
In the scouring process, the scour ratio was defined as the cumulative amount of scoured volume to the total amount of replenished sediment. Through experiments, the scour ratio was analyzed using relevant factors, including flood discharge and duration and water content of the replenished sediment. The scour ratio presented a linear trend, which provided the basis for obtaining the regression equation for each given discharge value (
Figure 11 and
Figure 13). Using the regression equation, we estimated the time required to scour the entire amount of the replenished sediment (i.e., scour ratio = 100%), as presented in
Table 2. As the scour ratio increased, the inflow discharge increased, and the time required to scour the entire amount of the replenished sediment decreased.
According to the experimental results obtained for the study site, high concentrations of replenished sediment in the outflow could affect the suspended sediment concentrations at the water intake and exceed the concentration limit stipulated by the Bansin water treatment plant. The reduction ratio of sediment concentration was investigated by establishing the relationship between the suspended sediment concentration data obtained at the Yuanshan weir and those obtained at the afterbay weir near the replenishment area (
Figure 14). Through the use of the 2D numerical model, the peak sediment concentration in each test case was provided as the input to obtain the simulated sediment concentration at the water intake of the Yuanshan weir. By comparing the regression equations, it was found that the sediment concentration reduction ratio ranged from 91% to 92%. The reduction ratio of the concentration of the suspended sediment scoured from the replenishment area to the concentration of the sediment at the Yuanshan weir was approximately 90%. Thus, the concentration of the outflow sediment produced at the replenishment area was limited to 6667 mg/L, thus matching the concentration limit of 6000 mg/L stipulated by the Bansin water treatment plant.