The Multi-Scale Temporal Variability of Extreme Precipitation in the Source Region of the Yellow River
Abstract
1. Introduction
2. Study Area and Method
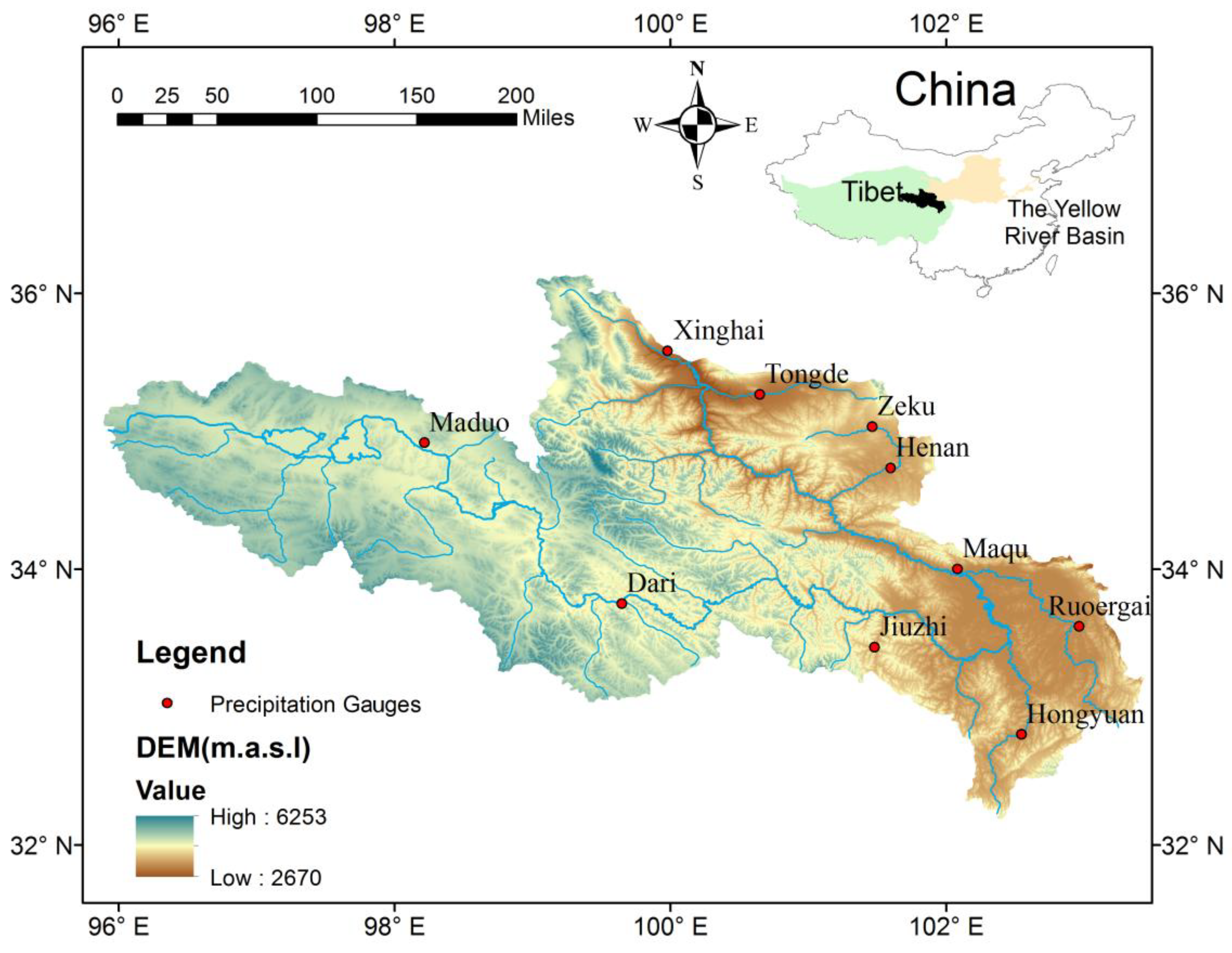
2.1. Study Area
2.2. Data and Method
3. Results and Discussion
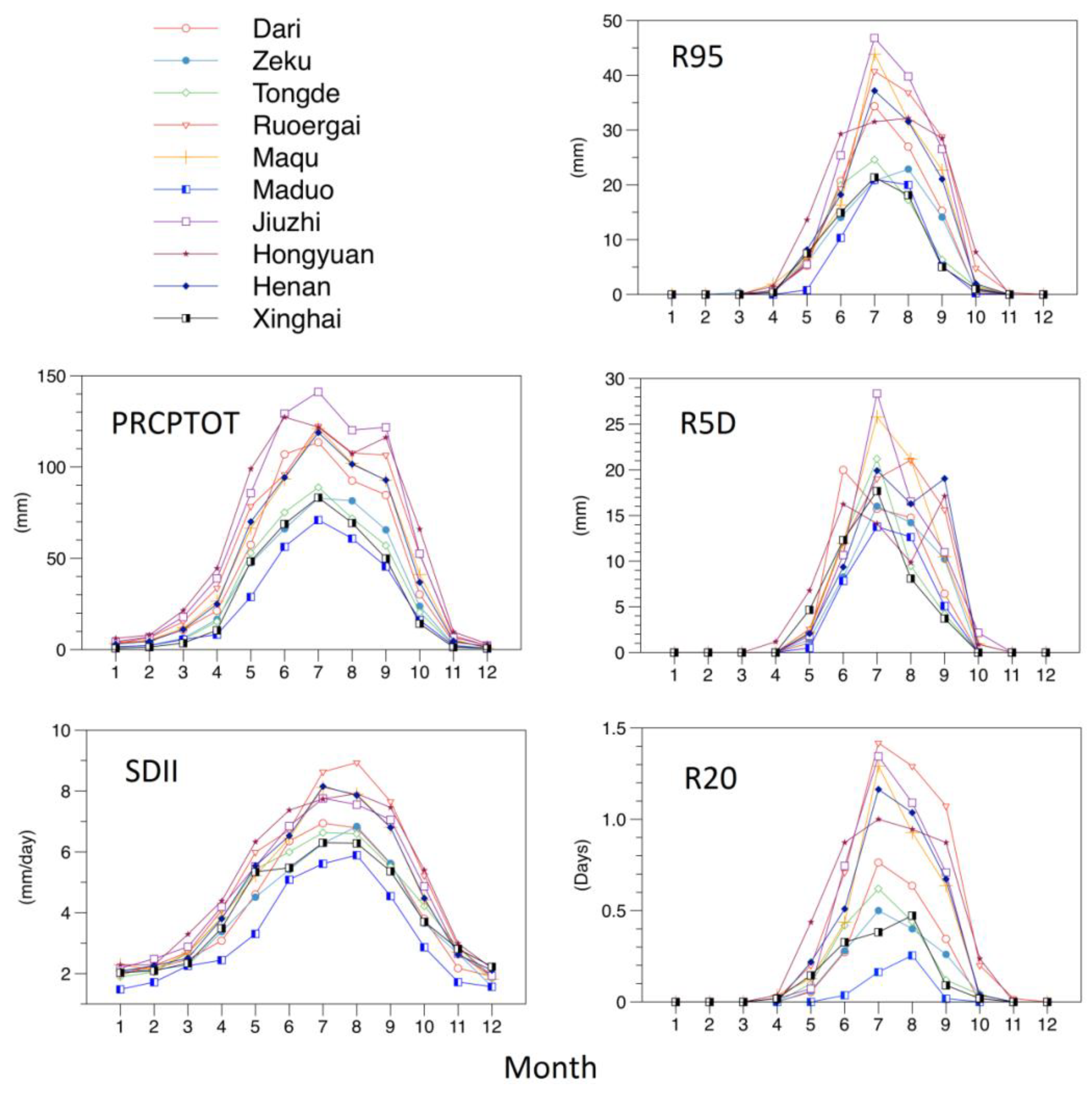
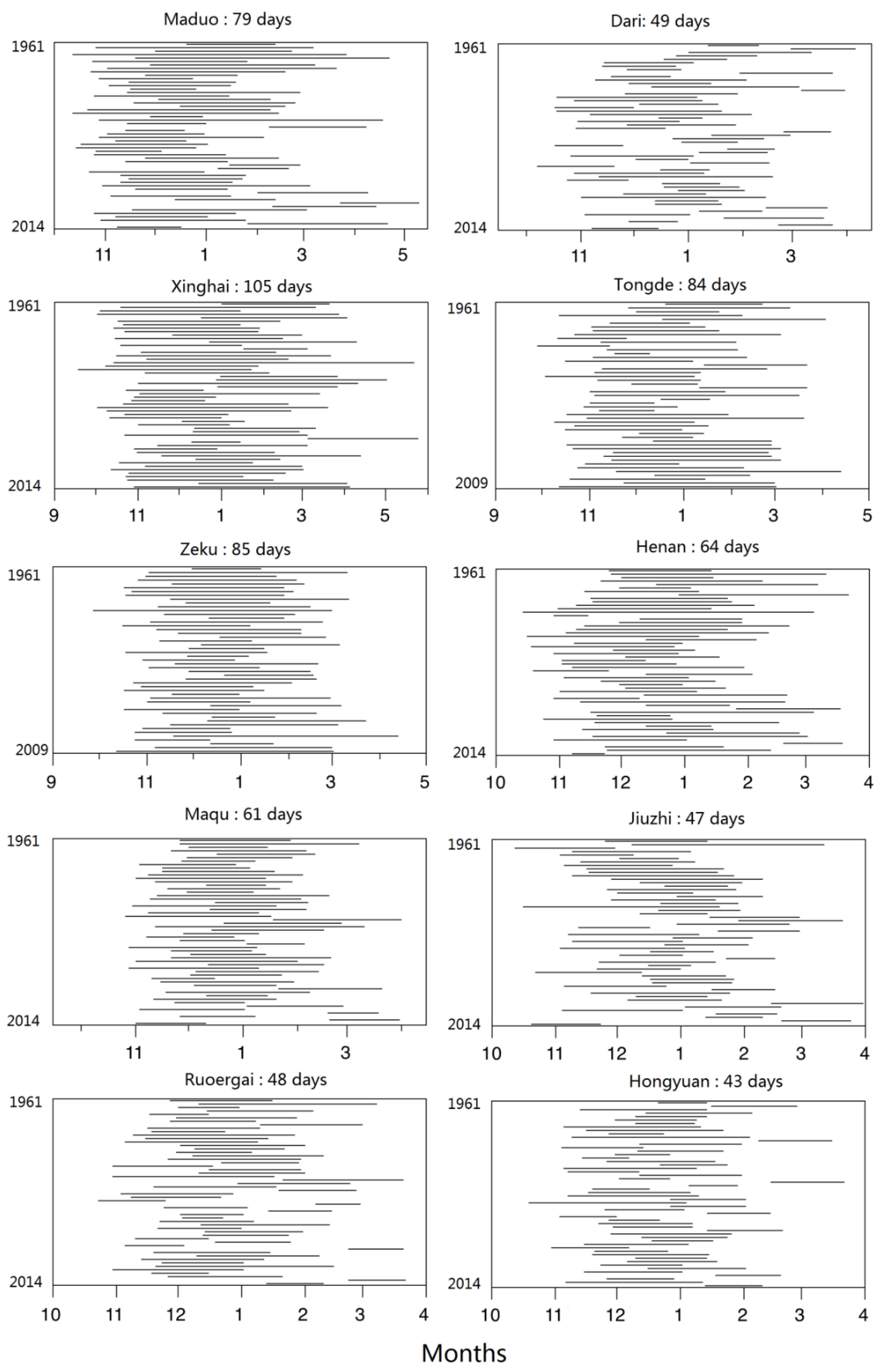
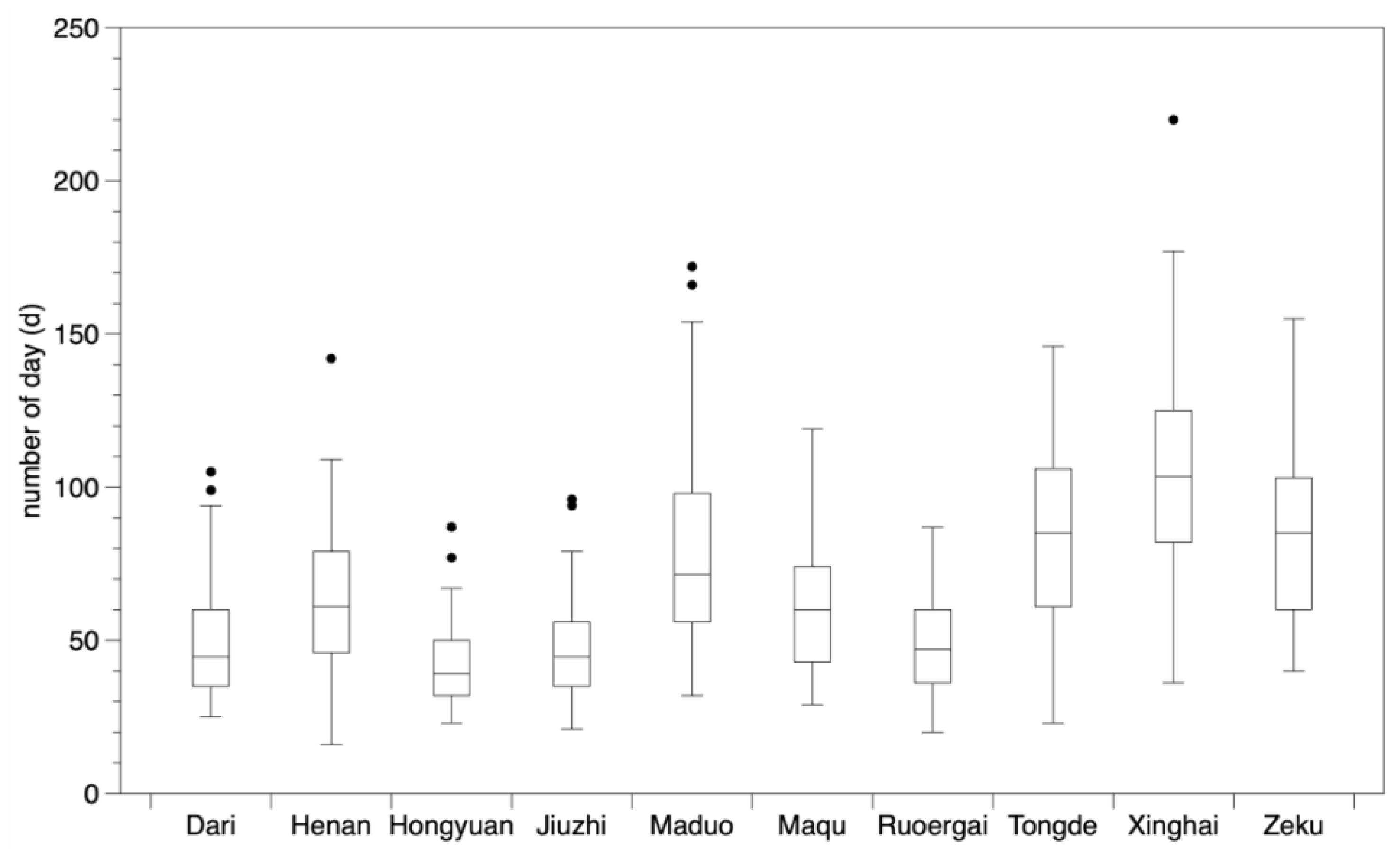
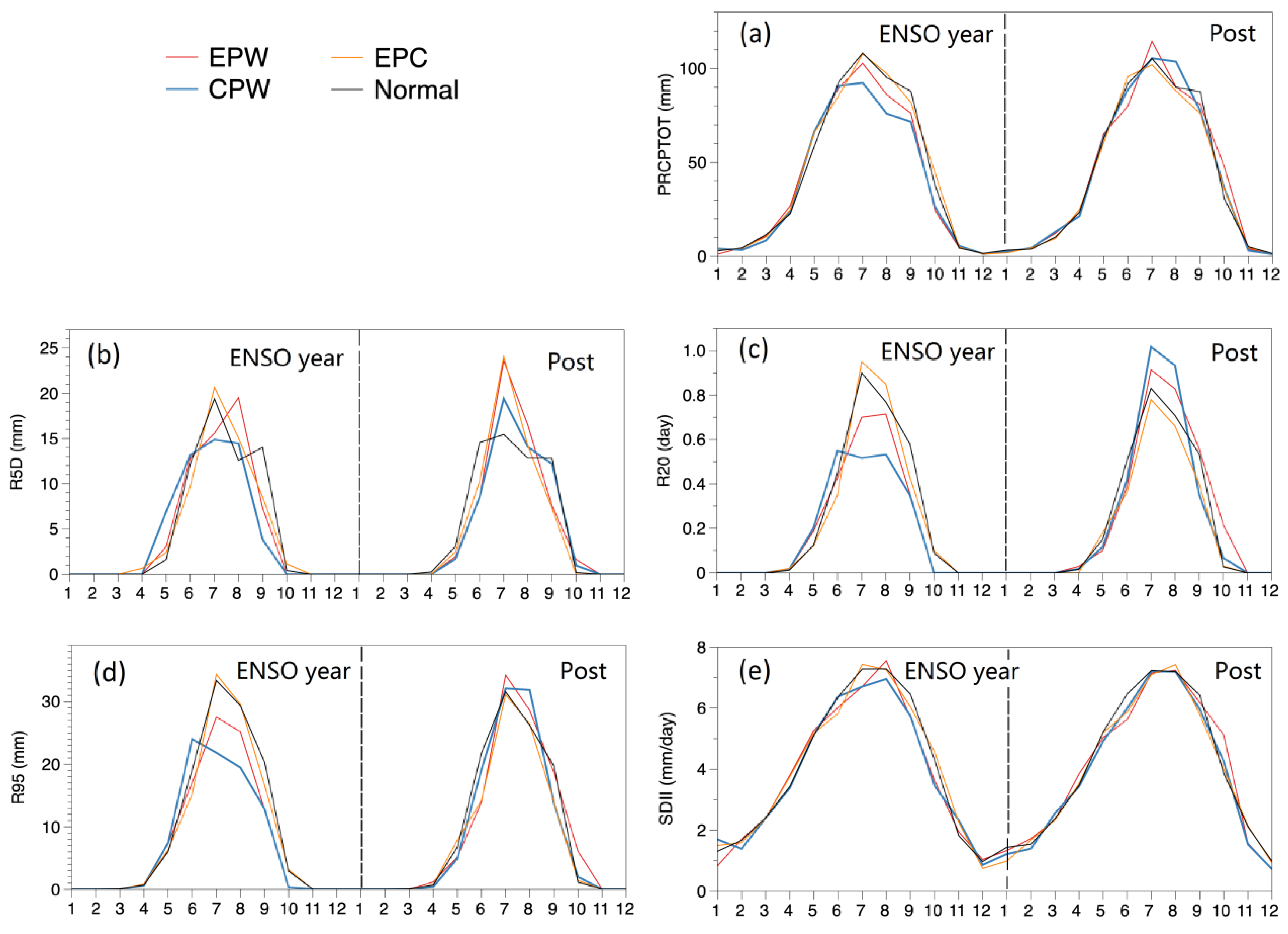
3.1. Seasonal Variability of Extreme Precipitation
3.2. Annual Trend of the Extreme Precipitation
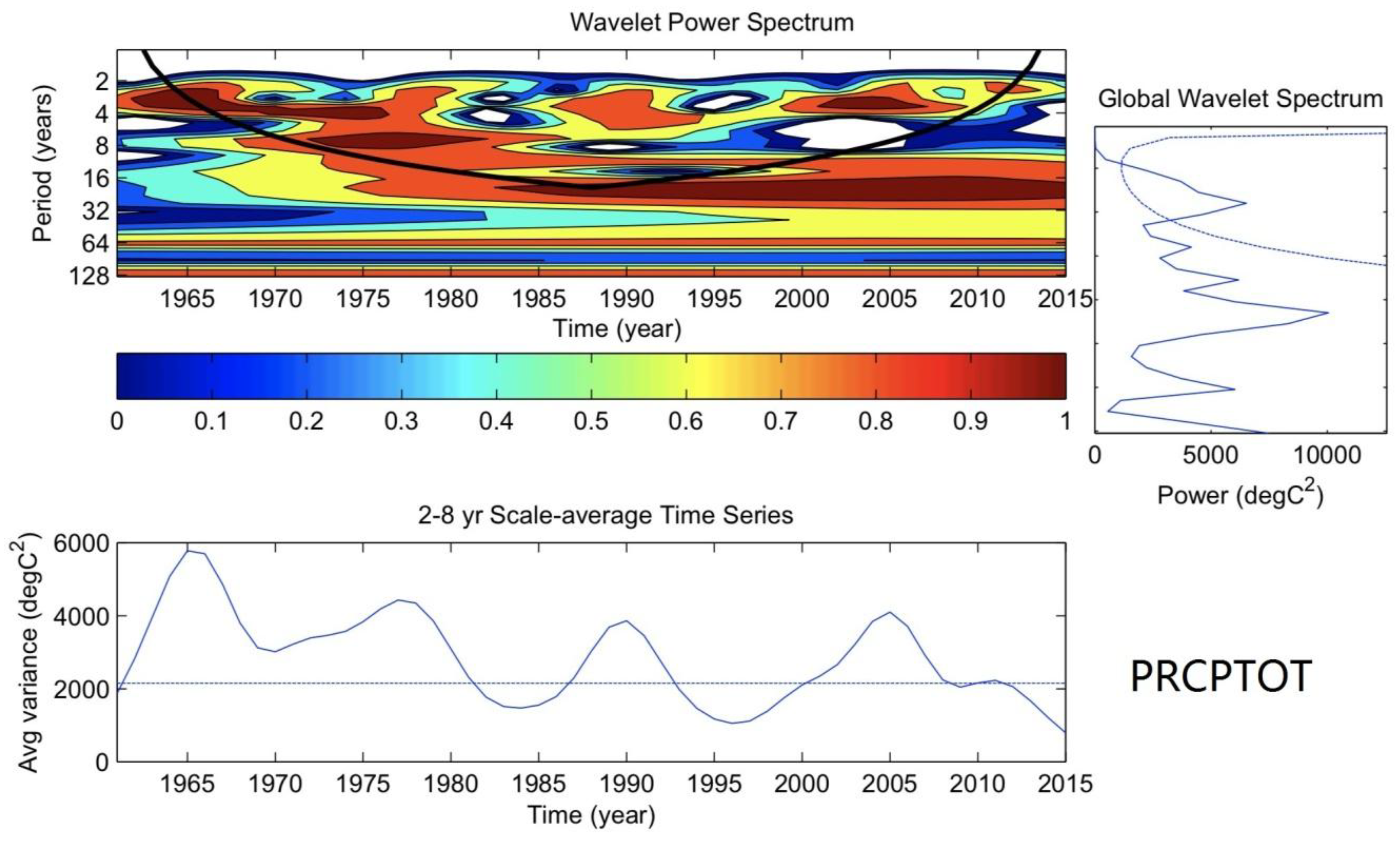
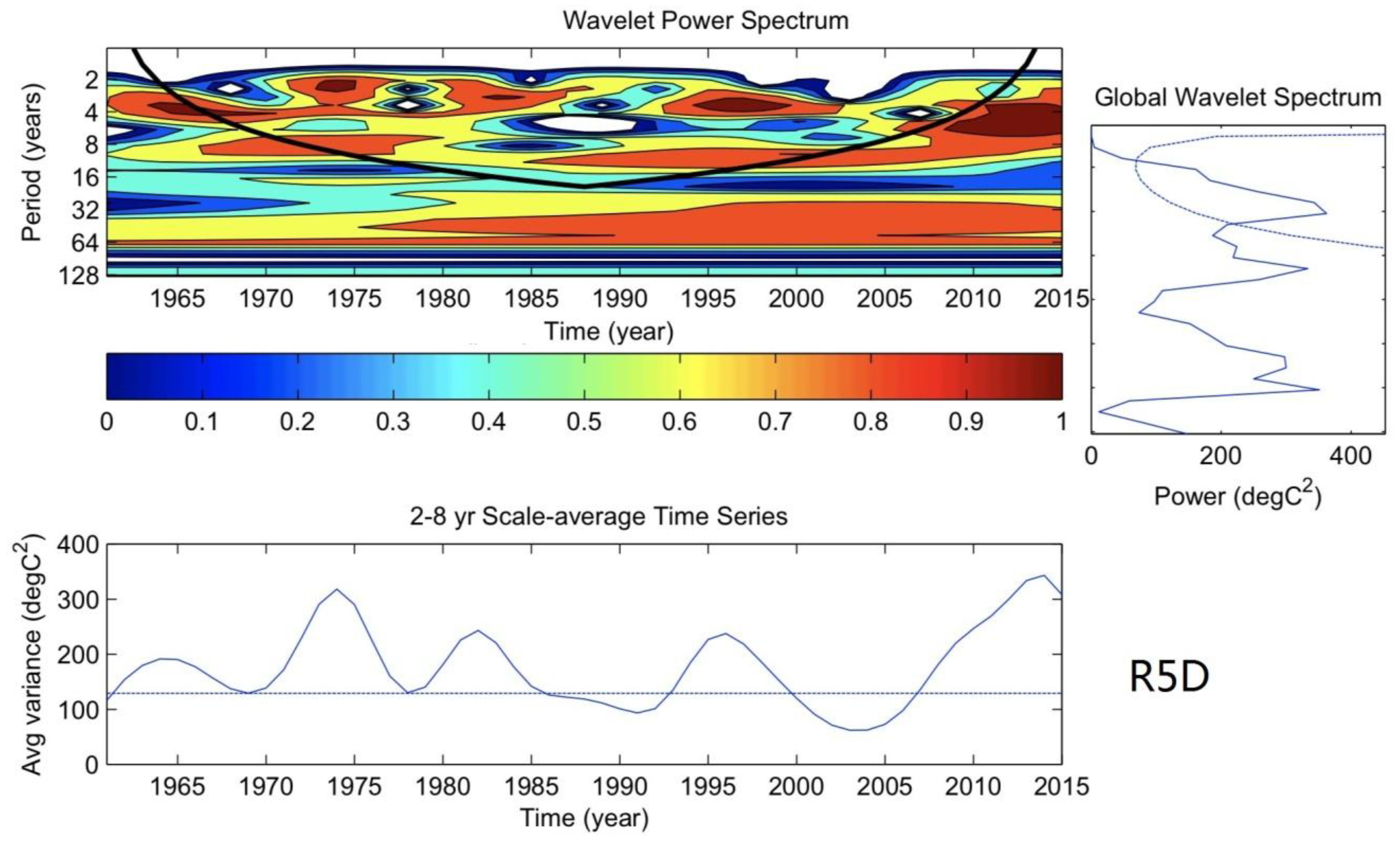
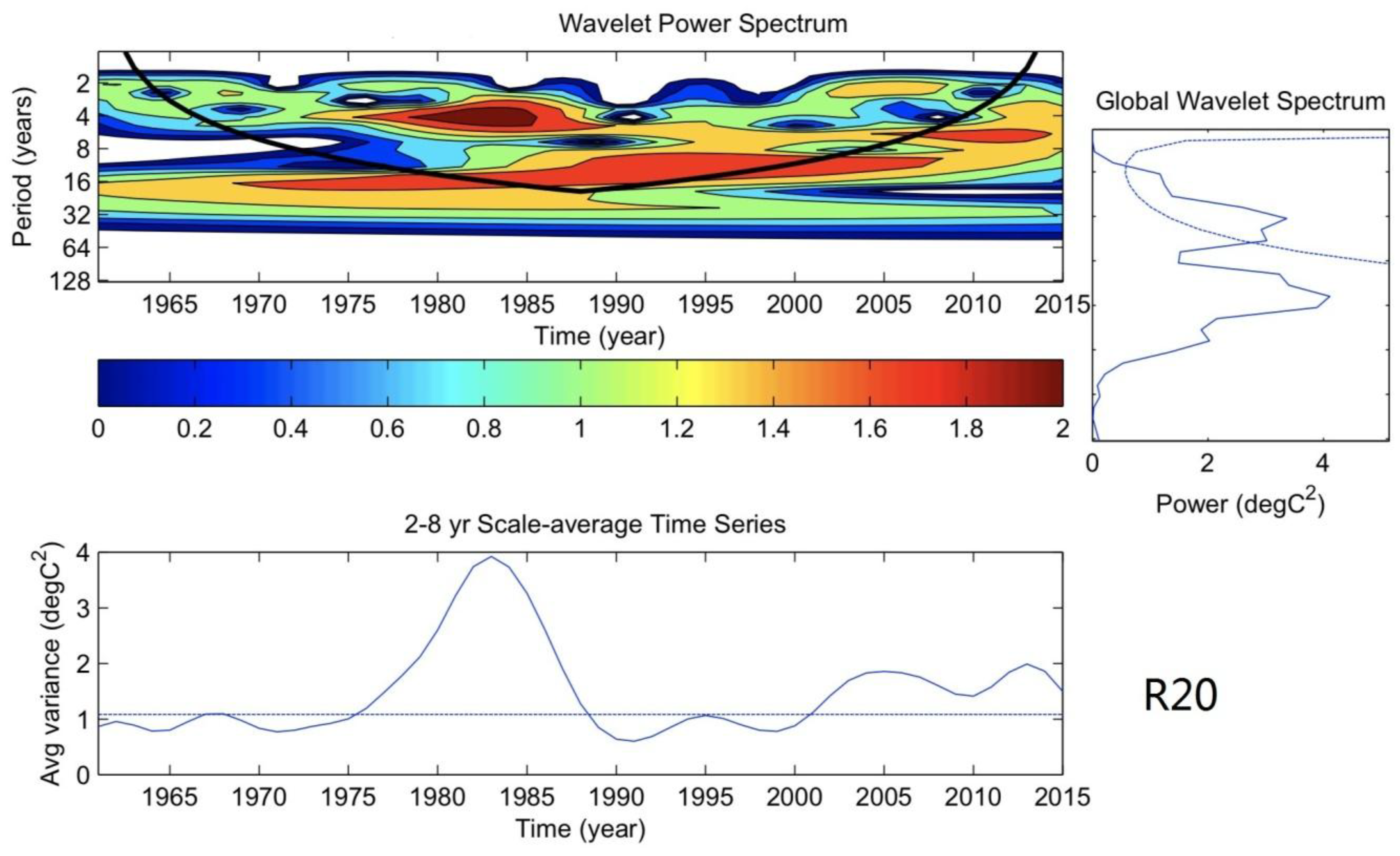
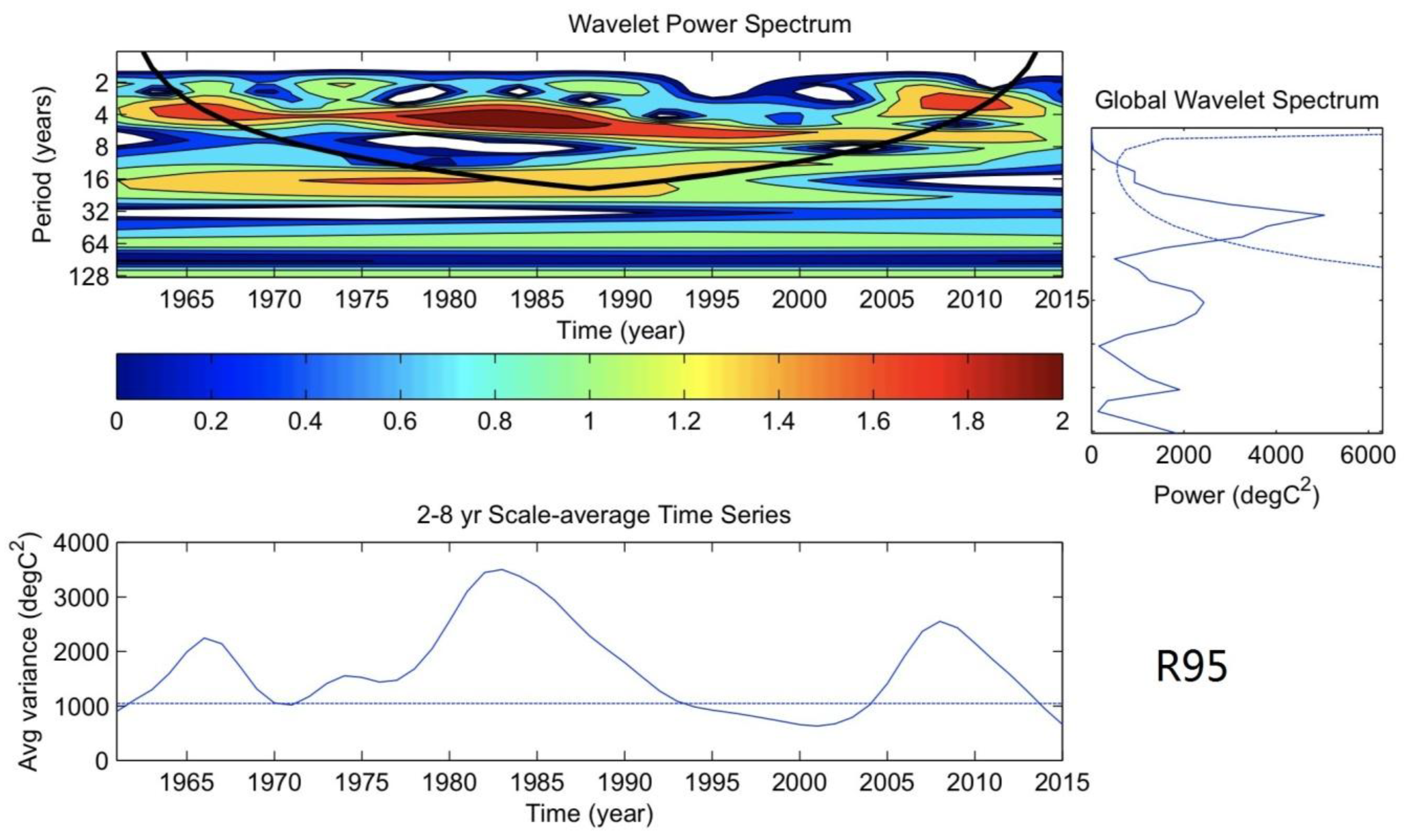
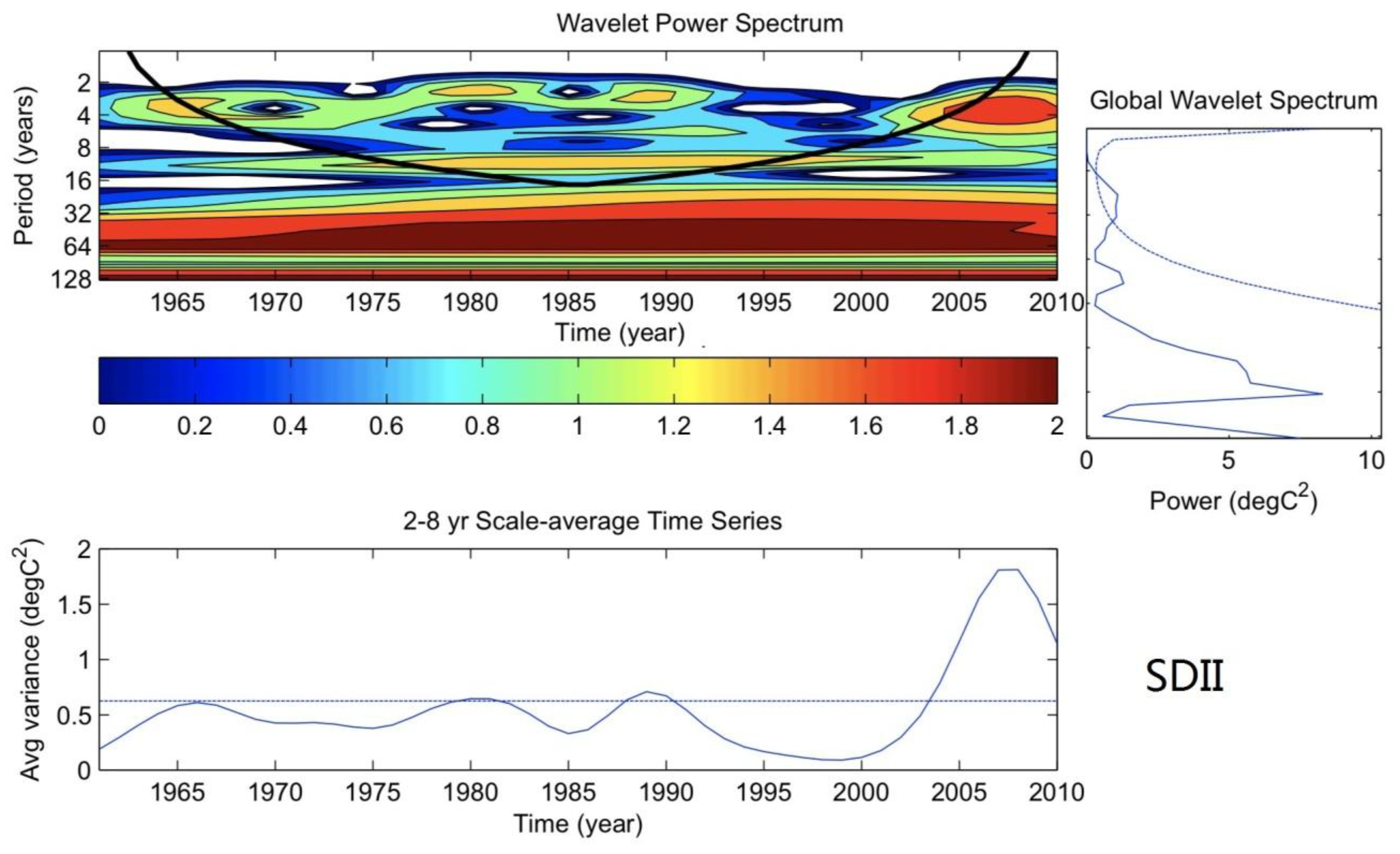
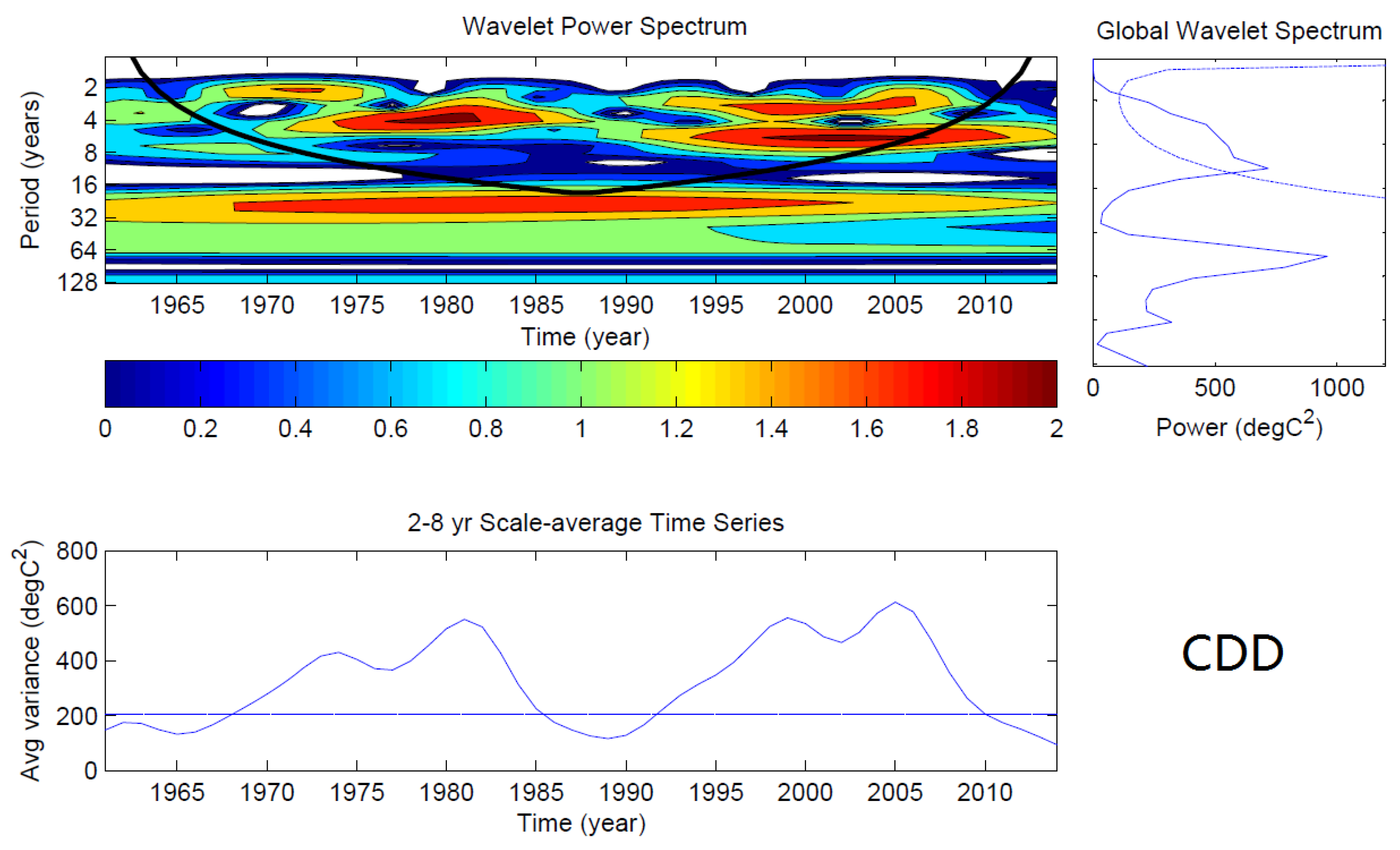
3.3. Inter-Annual and Decadal Variation of the Extreme Precipitation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Fu, G.; Yu, J.; Yu, X.; Ouyang, R.; Zhang, Y.; Wang, P.; Liu, W.; Min, L. Temporal variation of extreme rainfall events in China, 1961–2009. J. Hydrol. 2013, 487, 48–59. [Google Scholar] [CrossRef]
- Penalba, O.C.; Robledo, F.A. Spatial and temporal variability of the frequency of extreme daily rainfall regime in the La Plata Basin during the 20th century. Clim. Chang. 2010, 98, 531–550. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Aguilar, E.; Yan, Y. Changes in daily climate extremes in the eastern and central Tibetan Plateau during 1961–2005. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, X.; Wu, D.; Tang, B.; Xu, P.; Du, X.; Wang, H. Spatiotemporal variability in extreme precipitation in China from observations and projections. Water 2018, 10, 1089. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Meehl, G.A.; Zwiers, F.; Evans, J.; Knutson, T.; Mearns, L.; Whetton, P. Trends in extreme weather and climate events: Issues related to modeling extremes in projections of future climate change. Bull. Am. Meteorol. Soc. 2000, 81, 427–436. [Google Scholar] [CrossRef]
- Semenov, V.; Bengtsson, L. Secular trends in daily precipitation characteristics: Greenhouse gas simulation with a coupled AOGCM. Clim. Dyn. 2002, 19, 123–140. [Google Scholar]
- Groisman, P.Y.; Knight, R.W.; Easterling, D.R.; Karl, T.R.; Hegerl, G.C.; Razuvaev, V.N. Trends in intense precipitation in the climate record. J. Clim. 2005, 18, 1326–1350. [Google Scholar] [CrossRef]
- Hu, Y.; Maskey, S.; Uhlenbrook, S. Trends in temperature and rainfall extremes in the Yellow River source region, China. Clim. Chang. 2012, 110, 403–429. [Google Scholar] [CrossRef]
- Klein Tank, A.; Peterson, T.; Quadir, D.; Dorji, S.; Zou, X.; Tang, H.; Santhosh, K.; Joshi, U.; Jaswal, A.; Kolli, R. Changes in daily temperature and precipitation extremes in central and South Asia. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Song, X.; Song, S.; Sun, W.; Mu, X.; Wang, S.; Li, J.; Li, Y. Recent changes in extreme precipitation and drought over the Songhua River basin, China, during 1960–2013. Atmos. Res. 2015, 157, 137–152. [Google Scholar] [CrossRef]
- Min, S.-K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human contribution to more-intense precipitation extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Kunkel, K.E.; Easterling, D.R.; Redmond, K.; Hubbard, K. Temporal variations of extreme precipitation events in the United States: 1895–2000. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Jiang, P.; Yu, Z.; Gautam, M.R. Pacific and Atlantic Ocean influence on the spatiotemporal variability of heavy precipitation in the western United States. Glob. Planet. Chang. 2013, 109, 38–45. [Google Scholar]
- Jiang, P.; Yu, Z.; Gautam, M.R.; Acharya, K. The spatiotemporal characteristics of extreme precipitation events in the western United States. Water Resour. Manag. 2016, 30, 4807–4821. [Google Scholar] [CrossRef]
- Zhang, X.; Zwiers, F.W.; Hegerl, G.C.; Lambert, F.H.; Gillett, N.P.; Solomon, S.; Stott, P.A.; Nozawa, T. Detection of human influence on twentieth-century precipitation trends. Nature 2007, 448, 461–465. [Google Scholar] [CrossRef] [PubMed]
- Cayan, D.R.; Redmond, K.T.; Riddle, L.G. Enso and hydrologic extremes in the western United States. J. Clim. 1999, 12, 2881–2893. [Google Scholar] [CrossRef]
- Meehl, G.A.; Tebaldi, C.; Teng, H.; Peterson, T.C. Current and future us weather extremes and El Niño. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Yuan, F.; Berndtsson, R.; Uvo, C.B.; Zhang, L.; Jiang, P. Summer precipitation prediction in the source region of the Yellow River using climate indices. Hydrol. Res. 2016, 47, 847–856. [Google Scholar] [CrossRef]
- Hu, Y.; Maskey, S.; Uhlenbrook, S.; Zhao, H. Streamflow trends and climate linkages in the source region of the Yellow River, China. Hydrol. Process. 2011, 25, 3399–3411. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Liu, C.; Shao, Q.; Fukushima, Y. Changes in stream flow regime in headwater catchments of the Yellow River basin since the 1950s. Hydrol. Process. 2007, 21, 886–893. [Google Scholar] [CrossRef]
- Katz, R.W.; Brown, B.G. Extreme events in a changing climate: Variability is more important than averages. Clim. Chang. 1992, 21, 289–302. [Google Scholar] [CrossRef]
- Taniguchi, K. Future changes in precipitation and water resources for Kanto region in Japan after application of pseudo global warming method and dynamical downscaling. J. Hydrol. 2016, 8, 287–303. [Google Scholar] [CrossRef]
- Afzal, M.; Gagnon, A.S.; Mansell, M.G. The impact of the variability and periodicity of rainfall on surface water supply systems in Scotland. J. Water Clim. Chang. 2016, 7, 321–339. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, J.-K.; Miao, Q.-S.; Gao, X.-M. The interannual trend and preliminary quantitative estimation of the oceans condition in the Bohai Sea area. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2017; p. 012061. [Google Scholar]
- Yue, S.; Wang, C. The mann-kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Xiao, Z.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Wang, J. The spatiotemporal variations of runoff in the Yangtze River basin under climate change. Adv. Meteorol. 2018, 2018, 5903451. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Goyal, M.K. Monthly rainfall prediction using wavelet regression and neural network: An analysis of 1901–2002 data, Assam, India. Theor. Appl. Climatol. 2014, 118, 25–34. [Google Scholar] [CrossRef]
- He, X.; Guan, H. Multiresolution analysis of precipitation teleconnections with large-scale climate signals: A case study in South Australia. Water Resour. Res. 2013, 49, 6995–7008. [Google Scholar] [CrossRef]
- Liu, S.; Huang, S.; Huang, Q.; Xie, Y.; Leng, G.; Luan, J.; Song, X.; Wei, X.; Li, X. Identification of the non-stationarity of extreme precipitation events and correlations with large-scale ocean-atmospheric circulation patterns: A case study in the Wei River basin, China. J. Hydrol. 2017, 548, 184–195. [Google Scholar] [CrossRef]
- Rashid, M.M.; Johnson, F.; Sharma, A. Identifying sustained drought anomalies in hydrological records: A wavelet approach. J. Geophys. Res. 2018, 123, 7416–7432. [Google Scholar] [CrossRef]
- Asong, Z.E.; Wheater, H.S.; Bonsal, B.; Razavi, S.; Kurkute, S. Historical drought patterns over Canada and their teleconnections with large-scale climate signals. Hydrol. Earth Syst. Sci. 2018, 22, 3105–3124. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Mehr, A.D.; Kahya, E.; Olyaie, E. Streamflow prediction using linear genetic programming in comparison with a neuro-wavelet technique. J. Hydrol. 2013, 505, 240–249. [Google Scholar] [CrossRef]
- Hu, Y.; Maskey, S.; Uhlenbrook, S. Downscaling daily precipitation over the Yellow River source region in china: A comparison of three statistical downscaling methods. Theor. Appl. Climatol. 2013, 112, 447–460. [Google Scholar] [CrossRef]
- Alexander, L.; Zhang, X.; Peterson, T.; Caesar, J.; Gleason, B.; Tank, A.K.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Frich, P.; Alexander, L.V.; Della-Marta, P.; Gleason, B.; Haylock, M.; Tank, A.K.; Peterson, T. Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Kim, H.-M.; Webster, P.J.; Curry, J.A. Impact of shifting patterns of Pacific Ocean warming on North Atlantic tropical cyclones. Science 2009, 325, 77–80. [Google Scholar] [CrossRef]
- Smith, T.M.; Reynolds, R.W. Improved extended reconstruction of SST (1854–1997). J. Clim. 2004, 17, 2466–2477. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Singh, V.P.; Xu, C.Y.; Deng, J. Influence of ENSO on precipitation in the East River basin, South China. J. Geophys. Res. 2013, 118, 2207–2219. [Google Scholar] [CrossRef]
- Xue, X.; Chen, W.; Chen, S.; Feng, J. PDO modulation of the ENSO impact on the summer South Asian high. Clim. Dyn. 2018, 50, 1393–1411. [Google Scholar] [CrossRef]
- Jiang, P.; Gautam, M.R.; Zhu, J.; Yu, Z. How well do the GCMS/RCMS capture the multi-scale temporal variability of precipitation in the southwestern United States? J. Hydrol. 2013, 479, 75–85. [Google Scholar] [CrossRef]
- Chan, J.C.; Zhou, W. PDO, ENSO and the early summer monsoon rainfall over south China. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Cao, Q.; Hao, Z.; Yuan, F.; Su, Z.; Berndtsson, R.; Hao, J.; Nyima, T. Impact of enso regimes on developing-and decaying-phase precipitation during rainy season in China. Hydrol. Earth Syst. Sci. 2017, 21, 5415–5426. [Google Scholar] [CrossRef]
- Xiang, B.; Wang, B.; Li, T. A new paradigm for the predominance of standing central Pacific warming after the late 1990s. Clim. Dyn. 2013, 41, 327–340. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, T.; Lu, C.; Guo, Y.; Chen, B.; Liu, R.; Li, Y.; Shi, X. An important mechanism sustaining the atmospheric “water tower” over the Tibetan Plateau. Atmos. Chem. Phys. 2014, 14, 11287–11295. [Google Scholar] [CrossRef]
- Li, Q.; Yang, M.; Wan, G.; Wang, X. Spatial and temporal precipitation variability in the source region of the Yellow River. Environ. Earth Sci. 2016, 75, 594. [Google Scholar] [CrossRef]
- Feng, J.; Chen, W.; Tam, C.Y.; Zhou, W. Different impacts of El Niño and El Niño modoki on China rainfall in the decaying phases. Int. J. Climatol. 2011, 31, 2091–2101. [Google Scholar] [CrossRef]
- Jin, F.F.; An, S.I.; Timmermann, A.; Zhao, J. Strong El Niño events and nonlinear dynamical heating. Geophys. Res. Lett. 2003, 30, 20–21. [Google Scholar] [CrossRef]
- Timmermann, A.; Oberhuber, J.; Bacher, A.; Esch, M.; Latif, M.; Roeckner, E. Increased El Niño frequency in a climate model forced by future greenhouse warming. Nature 1999, 398, 694–697. [Google Scholar] [CrossRef]
- Yeh, S.-W.; Kug, J.-S.; Dewitte, B.; Kwon, M.-H.; Kirtman, B.P.; Jin, F.-F. El Niño in a changing climate. Nature 2009, 461, 511–514. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.-Y.; Kao, H.-Y.; Lee, T. Subtropics-related interannual sea surface temperature variability in the central equatorial Pacific. J. Clim. 2010, 23, 2869–2884. [Google Scholar] [CrossRef]
| Index | Definitions | Units |
|---|---|---|
| R20 | Total count of days when RR ≥ 20 mm | days |
| CDD | Maximum number of consecutive dry days with RR < 1 mm | days |
| R5D | Maximum 5-day precipitation total | mm |
| SDII | Total precipitation divided by the number of wet days | mm/day |
| R95 | Total precipitation when RR > 95th percentile | mm |
| PRCPTOT | Total precipitation of wet days | mm |
| ENSO Event | Years |
|---|---|
| EPW | 1963, 1965, 1972, 1976, 1982, 1987, 1997 |
| CPW | 1969, 1991, 1994, 2002, 2004, 2009 |
| EPC | 1964, 1970, 1971, 1973, 1975, 1985, 1988, 1995, 1998, 1999, 2007, 2010, 2011 |
| Location | Extreme Precipitation Indices | |||||
|---|---|---|---|---|---|---|
| SDII (mm/d/y) | R20 (d/y) | R95 (mm/y) | R5D (mm/y) | CDD (d/y) | PRCPTOT (mm/y) | |
| Dari | 0.004 | 0.002 | 0.57 | 0.05 | −0.09 | 0.34 |
| Zeku | −0.037 | −0.034 | −1 | −0.3 | −0.18 | −3.32 |
| Tongde | −0.01 | −0.01 | −0.9 | −0.23 | 0.55 | −1.77 |
| Ruoergai | −0.001 | −0.007 | −0.14 | 0.01 | −0.2 | −1.13 |
| Maqu | 0.009 | 0.015 | 0.58 | 0.13 | −0.18 | 0.67 |
| Maduo | 0.003 | 0.007 | 0.17 | 0.03 | −0.84 | 1.17 |
| Jiuzhi | −0.017 | −0.028 | −1.33 | −0.5 | −0.37 | −1.34 |
| Hongyuan | 0.001 | −0.025 | −0.71 | −0.02 | −0.08 | −1.01 |
| Henan | 0.002 | 0.005 | 0.05 | −0.1 | −0.17 | −1.48 |
| Xinghai | 0.018 | 0.016 | 0.65 | 0.17 | −0.49 | 1.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, P.; Yu, Z.; Yuan, F.; Acharya, K. The Multi-Scale Temporal Variability of Extreme Precipitation in the Source Region of the Yellow River. Water 2019, 11, 92. https://doi.org/10.3390/w11010092
Jiang P, Yu Z, Yuan F, Acharya K. The Multi-Scale Temporal Variability of Extreme Precipitation in the Source Region of the Yellow River. Water. 2019; 11(1):92. https://doi.org/10.3390/w11010092
Chicago/Turabian StyleJiang, Peng, Zhongbo Yu, Feifei Yuan, and Kumud Acharya. 2019. "The Multi-Scale Temporal Variability of Extreme Precipitation in the Source Region of the Yellow River" Water 11, no. 1: 92. https://doi.org/10.3390/w11010092
APA StyleJiang, P., Yu, Z., Yuan, F., & Acharya, K. (2019). The Multi-Scale Temporal Variability of Extreme Precipitation in the Source Region of the Yellow River. Water, 11(1), 92. https://doi.org/10.3390/w11010092





