Generation of Monthly Precipitation Climatologies for Costa Rica Using Irregular Rain-Gauge Observational Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets and Data Transformation
2.3. Kriging Variance Reduction Efficiency
2.4. Interpolation Methods and Experimental Setup
2.5. Performance Assessment of the Interpolation Methods
2.6. Validation Datasets
3. Results and Discussion
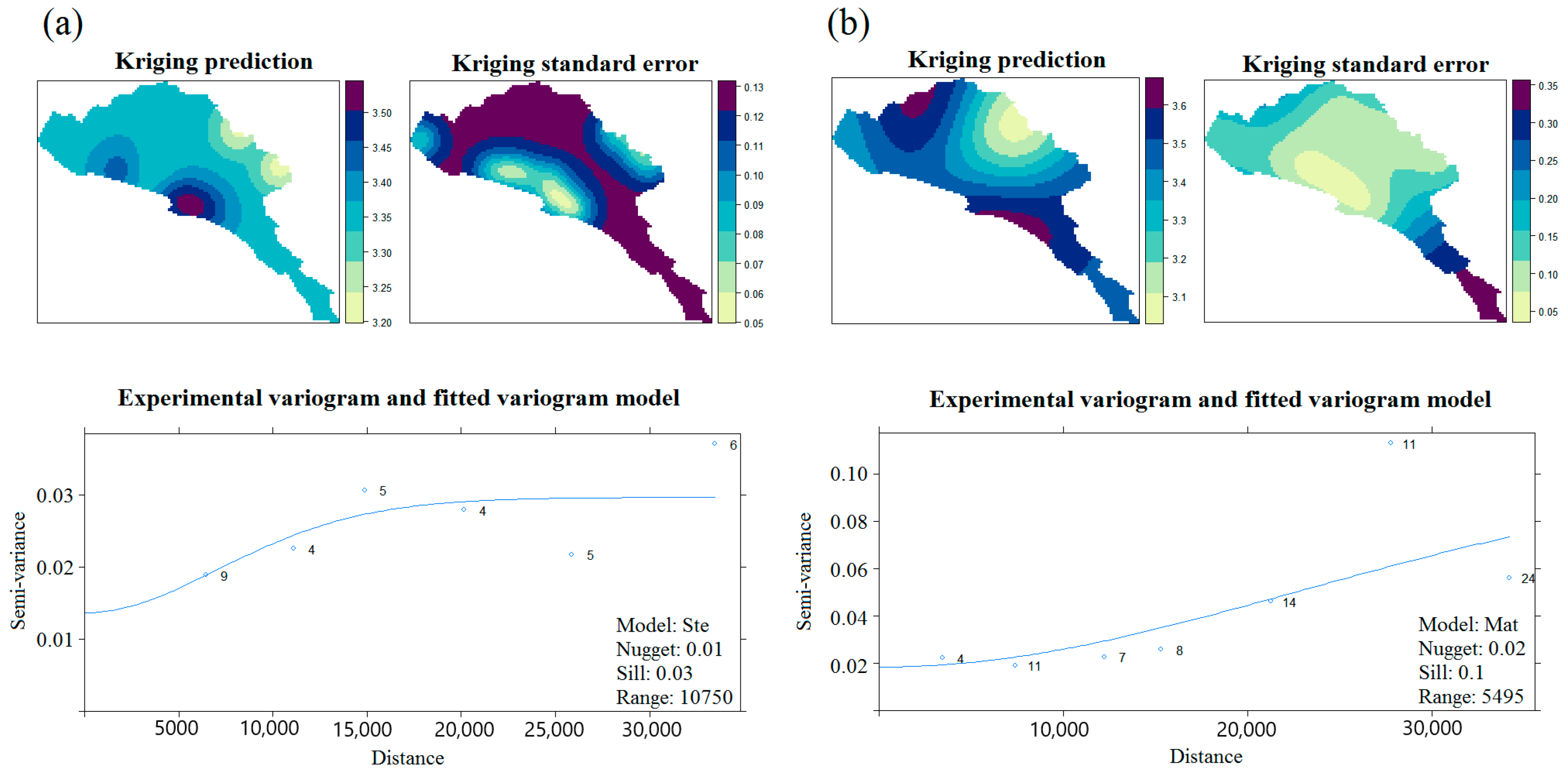
3.1. Kriging Reduction Efficiency
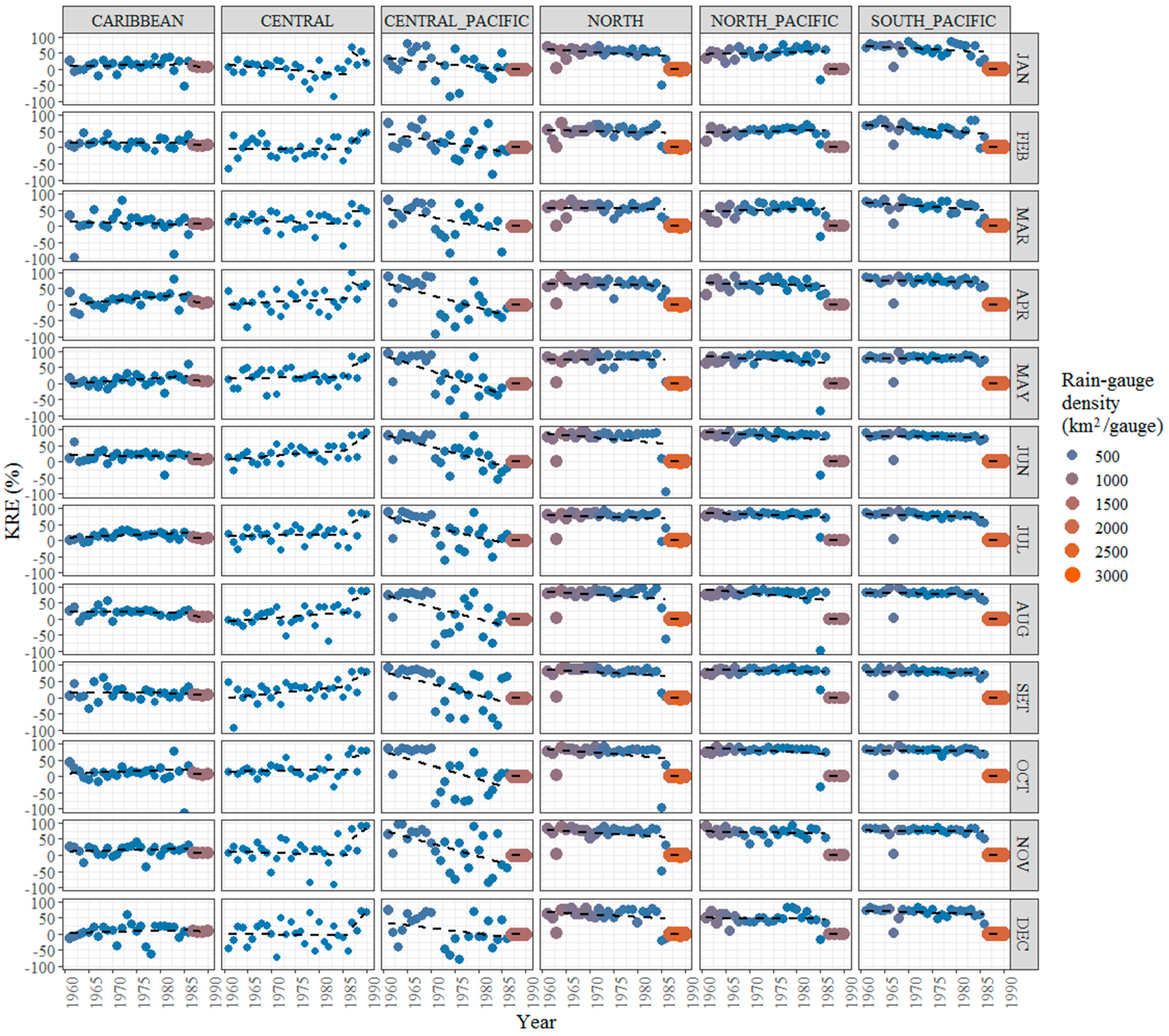
3.2. Temporal Evolution of the Observational Network
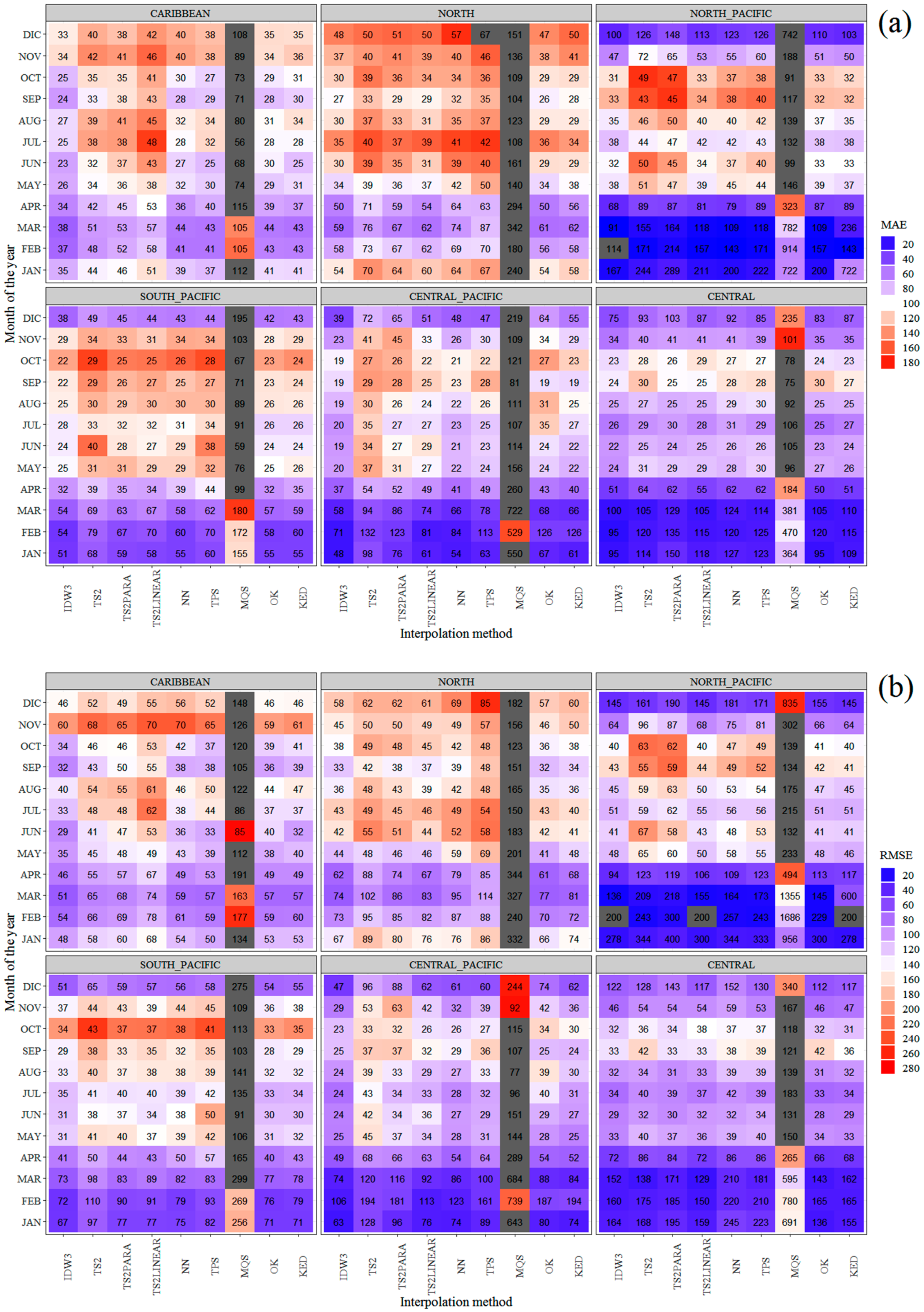
3.3. Performance of the Interpolation Methods
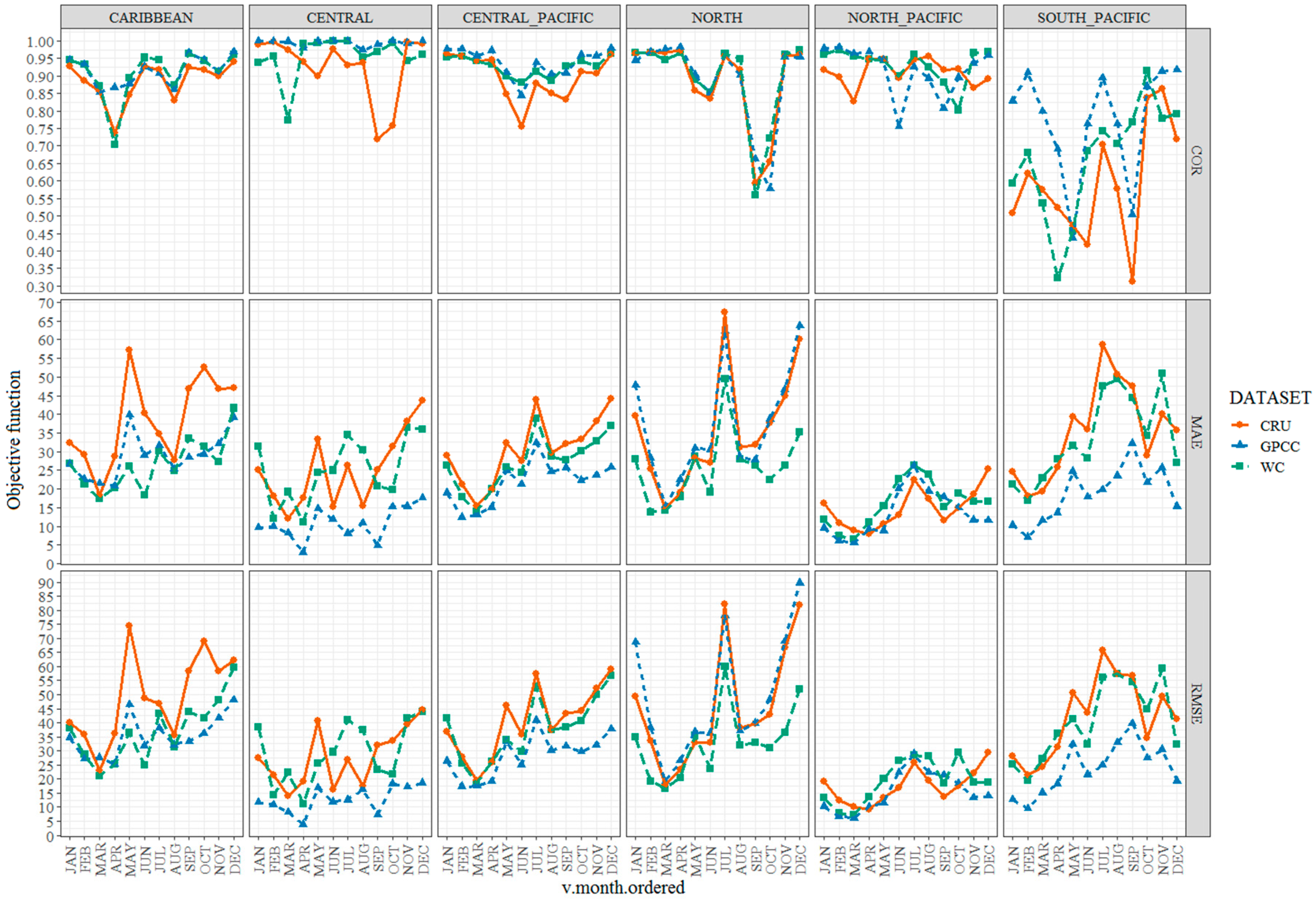
3.4. Comparison with Global Validation Datasets
4. Conclusions
- Based on the analysis of the Kriging Reduction efficiency objective function (KRE), the HSR sub-network captures a more detailed spatio-temporal distribution of the precipitation patterns over most climatic regions of Costa Rica even when the network is temporally discontinuous and irregularly distributed. Consequently, in the case of Costa Rica, it is better to increase the density of the rain-gauge network at the expense of temporal fidelity by including more stations even though their records may not exactly represent the same time step.
- The accuracy of the spatial interpolation methods and the subsequent estimation of the KRE increases as rain-gauge sample densities also increase. Conversely, rain-gauge densities above 250 km2/gauge severely impact KRE regardless of the climatic region.
- IDW interpolation is marginally superior to OK and KED concerning error metrics and computational efficiency. The remaining deterministic interpolation methods considerably deviate from IDW, OK or KED, which suggests that these methods are incapable of properly capturing the true-nature of spatial precipitation patterns over the considered climatic regions.
- Box–Cox data transformation is more effective in regions with lower network densities. In regions with higher network densities however, data transformation is more effecting during the wettest months. Data stationarity and normality required by OK and KED cannot always be satisfied by Box–Cox transformation, which might not be the most appropriate technique for all time steps.
- The mechanical models selected for variogram auto-fitting may not be sufficient to capture specific spatial structures of particular time lapses and therefore could represent a disadvantage of the adopted automation process. In spite of the fact that elevation and the orientation of the major cordilleras in Costa Rica are important modifiers of local precipitation patterns, their exact role in enhancing or reducing precipitation in the various climatic regions is a question open to debate.
- The overall spatial and temporal coherence of the generated IDW climatology with GPCC, CRU and WorldClim global datasets is considered satisfactory for all climatic regions except for the South-Pacific region. Nonetheless, GPCC performed generally better in capturing the spatial and temporal patterns of observed precipitation in most climatic regions. Such agreement gives assurance about the use this new climatology in the development of local climate impact studies, which are needed to provide fine-scale climate information for impact assessment and adaptation purposes.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, X.; Xie, X.; Liu, D.L.; Ji, F.; Wang, L. Spatial interpolation of daily rainfall data for local climate impact assessment over Greater Sydney Region. Adv. Meteorol. 2015, 1, 1–12. [Google Scholar] [CrossRef]
- Luo, L.; Mu, P.; Xue, H.; Ngo-Duc, T.; Dang-Dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. 2018, 8, 12623. [Google Scholar] [CrossRef] [PubMed]
- Luo, P.; Apip; He, B.; Duan, W.; Takara, K.; Nover, D. Impact assessment of rainfall scenarios and land-use change on hydrologic response using synthetic Area IDF curves. J. Flood. Risk Manag. 2018, 11, S84–S97. [Google Scholar] [CrossRef]
- Legates, D.R. Global and terrestrial precipitation: A comparative assessment of existing climatologies. Int. J. Climatol. 1995, 15, 237–258. [Google Scholar] [CrossRef]
- Addor, N.; Fischer, E.M. The influence of natural variability and interpolation errors on bias characterization in RCM simulations. J. Geophys. Res. Atm. 2015, 120, 180–195. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Feddema, J.J. Estimating continental and terrestrial precipitation averages from rain-gauge networks. Int. J. Climatol. 1994, 14, 403–414. [Google Scholar] [CrossRef]
- Chen, M.; Xie, P.; Janowiak, J.E.; Arkin, P.A. Global land precipitation: A 50-yr monthly analysis based on gauge observations. J. Hydrometeorol. 2002, 3, 249–266. [Google Scholar] [CrossRef]
- Jeniffer, K.; Su, Z.; Woldai, T.; Maathuis, B.H.P. Estimation of spatial–temporal rainfall distribution using remote sensing techniques: A case study of Makanya catchment, Tanzania. Int. J. Appl. Earth. Obs. Geoinf. 2010, 12, S90–S99. [Google Scholar] [CrossRef]
- Tsidu, G.M. High-resolution monthly rainfall database for Ethiopia: Homogenization, reconstruction, and gridding. J. Clim. 2012, 25, 8422–8443. [Google Scholar] [CrossRef]
- Karl, T.; Williams, C.N. An approach to adjusting climatological time series for discontinuous inhomogeneities. J. Clim. Appl. Meteor. 1987, 26, 1744–1763. [Google Scholar] [CrossRef]
- Peterson, T.C.; Easterling, D.R.; Karl, T.R.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Keller, V.D.J.; Tanguy, M.; Prosdocimi, I.; Terry, J.A.; Hitt, O.; Cole, S.J.; Dixon, H. CEH-GEAR: 1 km resolution daily and monthly areal rainfall estimates for the UK for hydrological and other applications. Hydrol. Earth Syst. Sci. 2015, 7, 143–155. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Janis, M.J. Comparison of approaches for estimating time-averaged precipitation using data from the USA. Int. J. Climatol. 1996, 16, 1103–1115. [Google Scholar] [CrossRef]
- Cheng, K.; Lin, Y.; Liou, J. Rain-gauge network evaluation and augmentation using geostatistics. Hydrol. Proc. 2008, 22, 2554–2564. [Google Scholar] [CrossRef]
- Nerini, D.; Zulkafli, Z.; Wang, L.P.; Onof, C.; Buytaert, W.; Lavado-Casimiro, W.; Guyot, J.L. A comparative analysis of TRMM rain-gauge data merging techniques at the daily time scale for distributed rainfall-runoff modelling applications. J. Hydrometeorol. 2015, 16, 2153–2168. [Google Scholar] [CrossRef]
- Legates, D.R.; Willmott, C.J. Meanseasonal and spatial variability in gauge-corrected, global precipitation. Int. J. Climatol. 1990, 10, 111–127. [Google Scholar] [CrossRef]
- Hulme, M. A 1951–80 global land precipitation climatology for the evaluation of general circulation models. Clim. Dyn. 1992, 7, 57–72. [Google Scholar] [CrossRef]
- Hulme, M. An intercomparison of model and observed global precipitation climatologies. Geophys. Res. Lett. 1991, 18, 1715–1718. [Google Scholar] [CrossRef]
- New, M.; Lister, D.; Hulme, M.; Makin, I. A high-resolution data set of surface climate over global land areas. Clim. Res. 2002, 21, 1–25. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M. GPCC Full Data Monthly Product Version 2018 at 0.25°: Monthly Land-Surface Precipitation from Rain-Gauges Built on GTS-Based and Historical Data; GPCC: Offenbach, Germany, 2018. [Google Scholar] [CrossRef]
- Kilibarda, M.; Hengl, T.; Heuvelink, G.B.M.; Gräler, B.; Pebesma, E.; Perčec Tadić, M.; Bajat, B. Spatio-temporal interpolation of daily temperatures for global land areas at 1 km resolution. J. Geophys. Res. Atmos. 2014, 119, 2294–2313. [Google Scholar] [CrossRef]
- Moral, F.J. Comparison of different geostatistical approaches to map climate variables: Application to precipitation. Int. J. Climatol. 2010, 30, 620–631. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Hu, D.; Shu, H.; Hu, H.; Xu, J. Spatiotemporal regression kriging to predict precipitation using time-series MODIS data. Clust. Comput. 2017, 20, 347–357. [Google Scholar] [CrossRef]
- Daly, C.; Neilson, R.P.; Phillips, D.L. A statistical-topographic model for mapping climatological precipitation over mountainous terrain. J. Appl. Meteorol. 1994, 33, 140–158. [Google Scholar] [CrossRef]
- Sanchez-Moreno, J.F.; Mannaerts, C.M.; Jetten, V. Influence of topography on rainfall variability in Santiago Island, Cape Verde. Int. J. Climatol. 2014, 34, 1081–1097. [Google Scholar] [CrossRef]
- Otieno, H.; Yang, J.; Liu, W.; Han, D. Influence of rain gauge density on interpolation method selection. J. Hydrol. Eng. 2014, 19. [Google Scholar] [CrossRef]
- Sunyer, M.A.; Sørup, H.J.D.; Christensen, O.B.; Madsen, H.; Rosbjerg, D.; Mikkelsen, P.S.; Arnbjerg-Nielsen, K. On the importance of observational data properties when assessing regional climate model performance of extreme precipitation. Hydrol. Earth. Syst. Sci. 2013, 17, 4323–4337. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Huang, Z.; Daniell, J.J. Can we improve the spatial predictions of seabed sediments? A case study of spatial interpolation of mud content across the southwest Australian margin. Cont. Shelf. Res. 2011, 31, 1365–1376. [Google Scholar] [CrossRef]
- Cecinati, F.; Wani, O.; Rico-Ramirez, M.A. Comparing approaches to deal with non-gaussianity of rainfall data in kriging-based radar-gauge rainfall merging: Gaussianity in KED rainfall merging. Water. Resour. Res. 2017, 53, 8999–9018. [Google Scholar] [CrossRef]
- Yeh, H.C.; Chen, Y.C.; Chang, C.H.; Ho, C.H.; Wei, C. Rainfall Network Optimization Using Radar and Entropy. Entropy 2017, 19, 553. [Google Scholar] [CrossRef]
- Bastin, G.; Lorent, B.; Duque, C.; Gevers, M. Optimal estimation of the average rainfall and optimal selection of rain gauge locations. Water. Resour. Res. 1984, 20, 463–470. [Google Scholar] [CrossRef]
- Kassim, A.H.M.; Kottegoda, N.T. Rainfall network design through comparative kriging methods. Hydrol. Sci. J. 1991, 36, 223–240. [Google Scholar] [CrossRef]
- Chebbi, A.; Bargaoui, Z.K.; da Conceição-Cunha, M. Development of a method of robust rain gauge network optimization based on intensity-duration-frequency results. Hydrol. Earth. Syst. Sci. 2013, 17, 4259–4268. [Google Scholar] [CrossRef]
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Karmalkar, A.V.; Bradley, R.S.; Diaz, H.F. Climate change in Central America and Mexico: Regional climate model validation and climate change projections. Clim. Dyn. 2011, 37, 605–629. [Google Scholar] [CrossRef]
- Karmalkar, A.V.; Taylor, M.A.; Campbell, J.; Stephenson, T.; New, M.; Centella, A.; Charlery, J. A review of observed and projected changes in climate for the islands in the Caribbean. Atmosfera 2013, 26, 283–309. [Google Scholar] [CrossRef]
- Vargas, A.B.; Trejos, V.F.S. Changes in the general circulation and its influences on precipitation trends in Central America: Costa Rica. Ambio 1994, 23, 87–90. [Google Scholar]
- Aguilar, E.; Peterson, T.C.; Obando, P.R.; Frutos, R.; Retana, J.A.; Solera, M.; Soley, J.; García, I.G.; Araujo, R.M.; Santos, A.R.; et al. Changes in precipitation and temperature extremes in Central America and northern South America, 1961–2003. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Waylen, P.R.; Quesada, M.E.; Caviedes, C.N. Temporal and spatial variability of annual precipitation in Costa Rica and the southern oscillation. Int. J. Climatol. 1996, 16, 173–193. [Google Scholar] [CrossRef]
- Rapp, A.D.; Peterson, A.G.; Frauenfeld, O.W.; Quiring, S.M.; Roark, E.B. Climatology of Storm Characteristics in Costa Rica using the TRMM Precipitation Radar. J. Hydrometeorol. 2014, 15, 2615–2633. [Google Scholar] [CrossRef]
- Waylen, P.R.; Harrison, M. The coincidence of daily rainfall events in Liberia, Costa Rica and tropical cyclones in the Caribbean basin. Int. J. Climatol. 2005, 25, 1665–1674. [Google Scholar] [CrossRef]
- Ministerio de Recursos Naturales, Energia y Minas (MINAE). Catatro de las Series de Precipitaciones Medidas en Costa Rica 1888–1988; Instituto Meteorologico Nacional: San Jose, Costa Rica, 1988. [Google Scholar]
- Grandoso, H.; de Montero, V.; Castro, V. Caracteristicas de la atmósfera libre sobre Costa Rica y sus relaciones con la Precipitación; Technical Report; Instituto Geográfico Nacional, Ministerio de Obras Públicas y Transportes: Madrid, Spain, 1982.
- World Meteorological Organization. Guide to Hydrological Practices, WMO-168; WHO: Geneva, Switzerland, 2008. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Erdin, R.; Frei, C.; Kunsch, H.R. Data transformation and uncertainty in geostatistical combination of radar and rain gauges. J. Hydrometeorol. 2012, 13, 1332–1346. [Google Scholar] [CrossRef]
- Woldemeskel, F.; McInerney, D.; Lerat, J.; Thyer, M.; Kavetski, D.; Shin, D.; Tuteja, N. Kuczera, G. Evaluating post-processing approaches for monthly and seasonal streamflow forecasts. Hydrol. Earth Syst. Sci. 2018, 22, 6257–6278. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Price, D.T.; McKenney, D.W.; Nalder, I.A.; Hutchinson, M.F.; Kesteven, J.L. A comparison of two statistical methods for spatial interpolation of Canadian monthly mean climate data. Agric. For. Meteorol. 2000, 101, 81–94. [Google Scholar] [CrossRef]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.; Frei, C. Comparison of six methods for the interpolation of daily, European climate data. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Mendez, M.; Calvo-Valverde, L. Assessing the Performance of Several Rainfall Interpolation Methods as Evaluated by a Conceptual Hydrological Model. Procedia Eng. 2016, 154, 1050–1057. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, 71. [Google Scholar] [CrossRef]
- Berndt, C.; Rabiei, E.; Haberlandt, U. Geostatistical merging of rain gauge and radar data for high temporal resolutions and various station density scenarios. J. Hydrol. 2014, 508, 88–101. [Google Scholar] [CrossRef]
- Dirks, K.N.; Hay, J.E.; Stow, C.D.; Harris, D. High-resolution studies of rainfall on Norfolk Island: Part II: Interpolation of rainfall data. J. Hydrol. 1998, 208, 187–193. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degre, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Cheng, M.; Wang, Y.; Engel, B.; Zhang, W.; Peng, H.; Chen, X.; Xia, H. Performance Assessment of Spatial Interpolation of Precipitation for Hydrological Process Simulation in the Three Gorges Basin. Water 2017, 9, 838. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Maathuis, B.H.P.; Adem, A.A.; Demissie, S.S.; Langan, S.; Steenhuis, T.S. Comparison of rainfall estimations by TRMM 3B42, MPEG and CFSR with ground-observed data for the Lake Tana basin in Ethiopia. Hydrol. Earth Syst. Sci. 2014, 18, 4871–4881. [Google Scholar] [CrossRef]
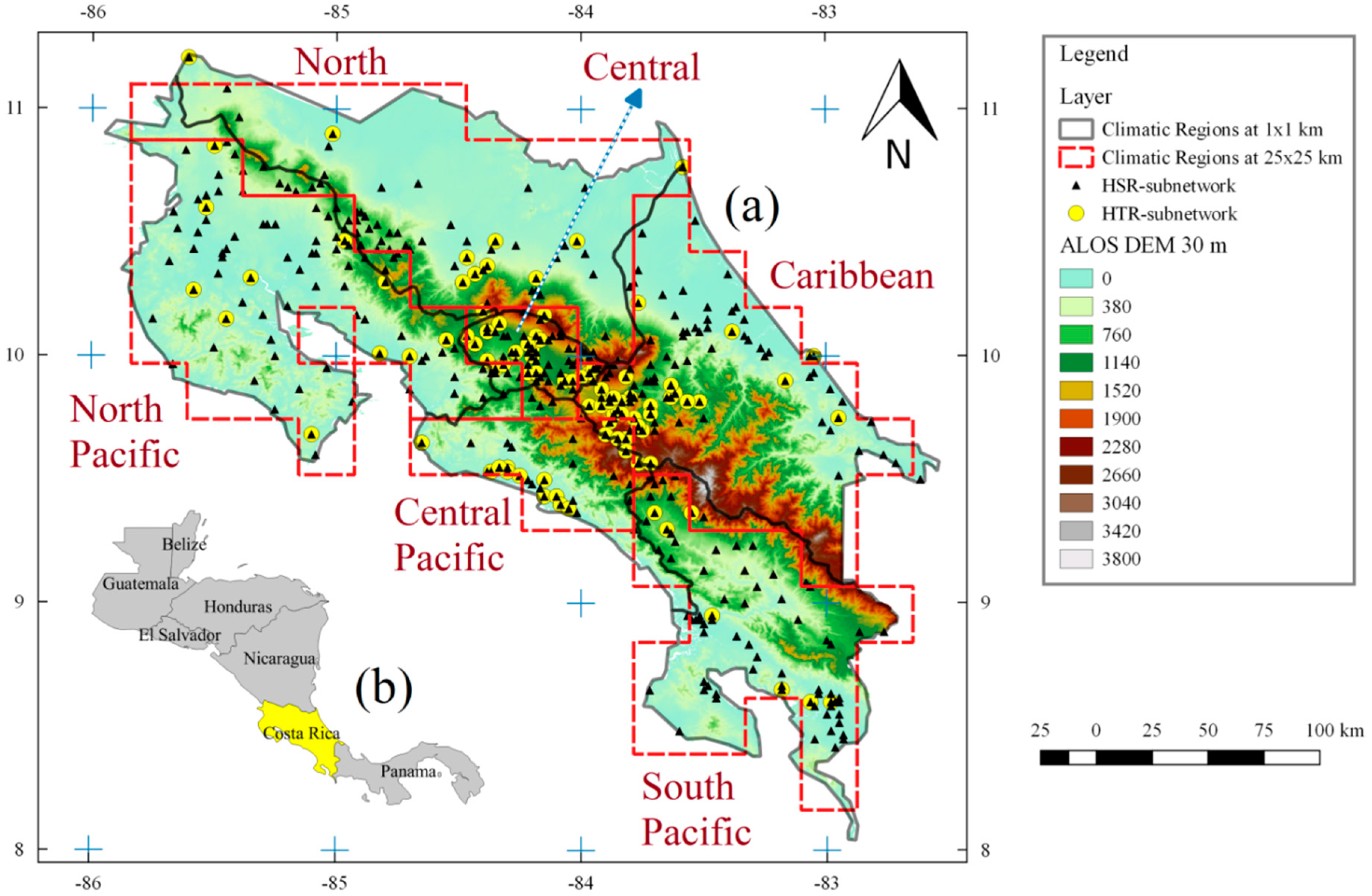
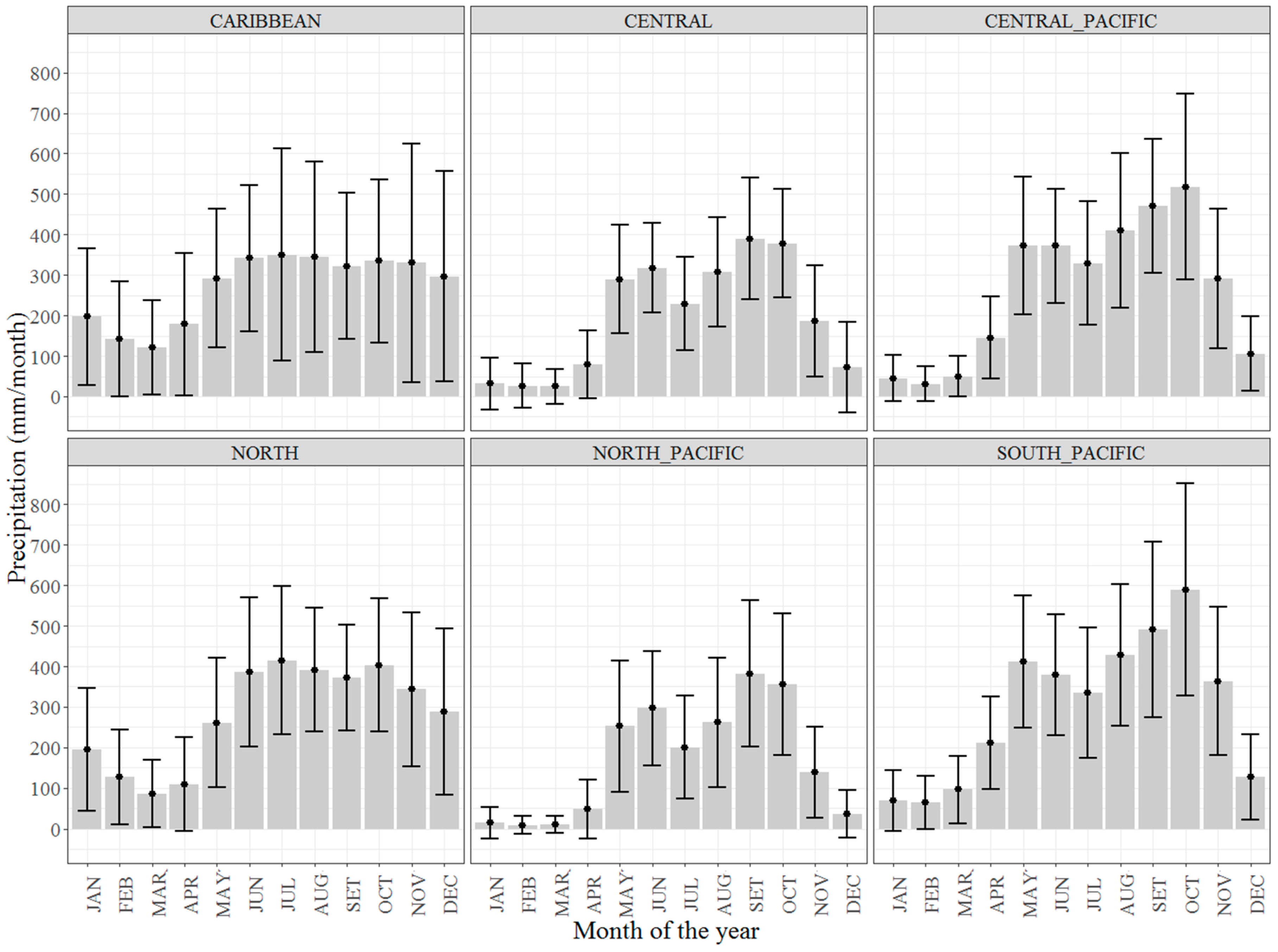
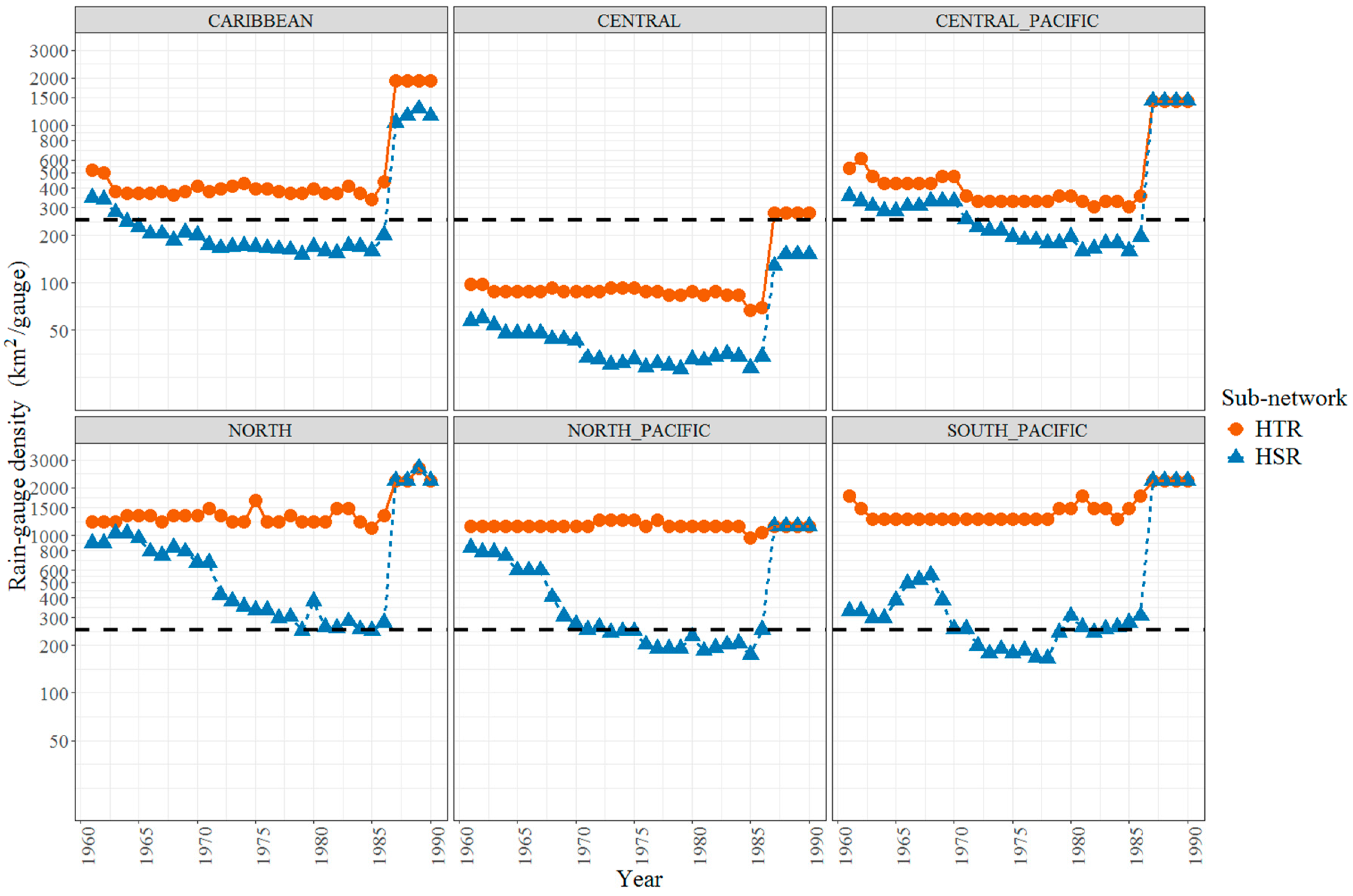
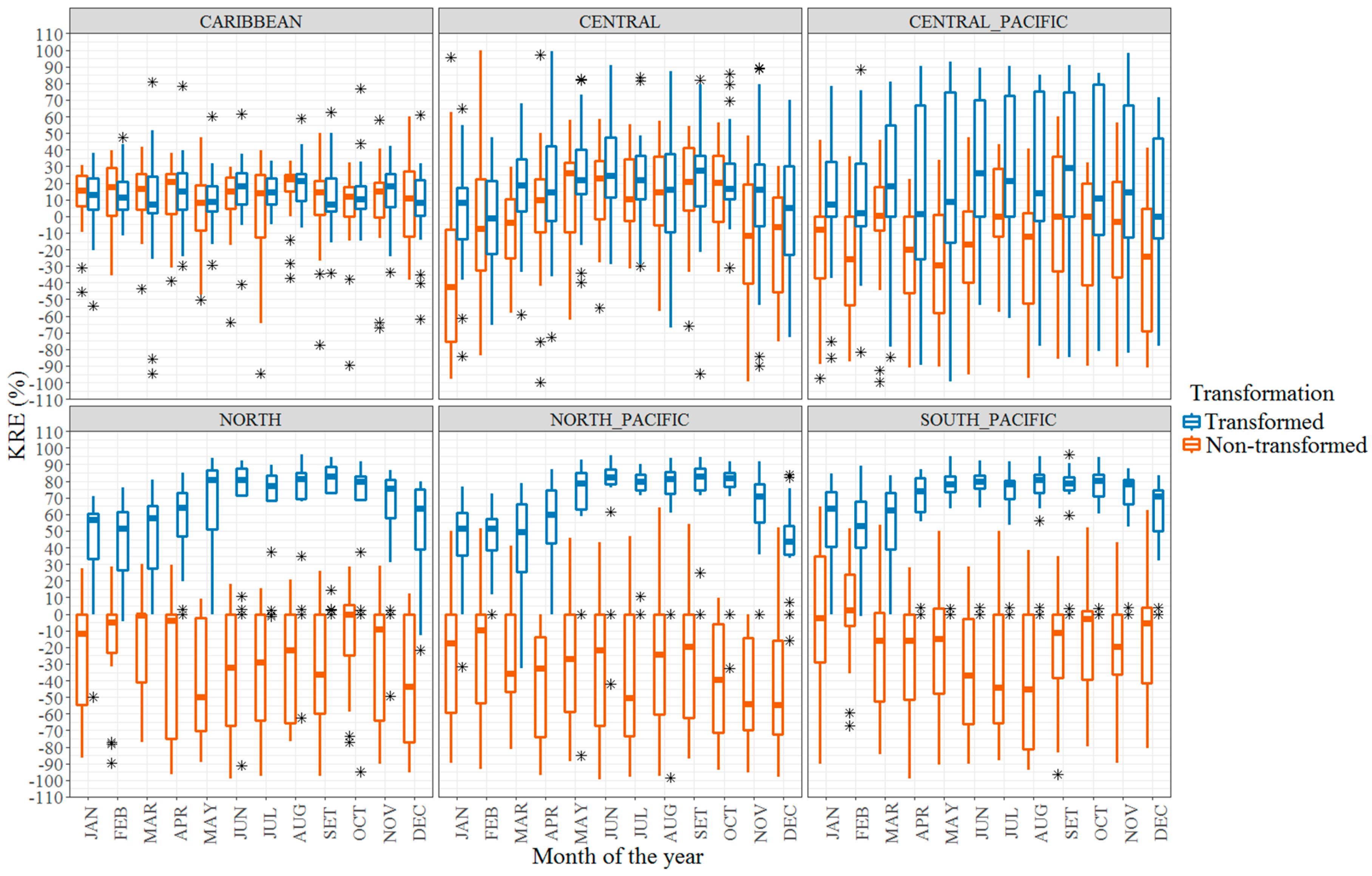
| Abbreviation | Method | R_package | Class |
|---|---|---|---|
| IDW | Inverse Distance Weighting | gstat, sp, raster | Deterministic |
| TS2 | Trend surface, 2nd. polyn. surface | gstat, sp, raster | Deterministic |
| TS2PARA | Trend surface, 2nd. parab. surface | gstat, sp, raster | Deterministic |
| TS2LINEAR | Trend surface 2nd planar surface | gstat, sp, raster | Deterministic |
| TPS | Thin Plate Spline | gstat, sp, raster, rsaga | Deterministic |
| MQS | Modified Quadratic Shepard | gstat, sp, raster, rsaga | Deterministic |
| NN | Nearest Neighbour | gstat, sp, raster, rsaga | Deterministic |
| OK | Ordinary Kriging | gstat, raster, automap | Geostatistical |
| KED | Kriging with External Drift | gstat, raster, automap | Geostatistical |
| METHOD | CARIBBEAN | NORTH | NORTH_PACIFIC | SOUTH_PACIFIC | CENTRAL_PACIFIC | CENTRAL | OF |
|---|---|---|---|---|---|---|---|
| IDW3 | 1 | 2 | 1 | 1 | 1 | 1 | MAE |
| TS2 | 7 | 7 | 7 | 7 | 8 | 4 | MAE |
| TS2PARA | 6 | 6 | 8 | 6 | 7 | 6 | MAE |
| TS2LINEAR | 8 | 4 | 4 | 4 | 5 | 5 | MAE |
| NN | 4 | 5 | 5 | 5 | 4 | 8 | MAE |
| TPS | 5 | 8 | 6 | 8 | 2 | 7 | MAE |
| MQS | 9 | 9 | 9 | 9 | 9 | 9 | MAE |
| OK | 3 | 1 | 3 | 2 | 6 | 2 | MAE |
| KED | 2 | 3 | 2 | 3 | 3 | 3 | MAE |
| IDW3 | 1 | 2 | 1 | 1 | 1 | 1 | RMSE |
| TS2 | 7 | 7 | 7 | 7 | 8 | 4 | RMSE |
| TS2PARA | 6 | 6 | 8 | 6 | 7 | 6 | RMSE |
| TS2LINEAR | 8 | 4 | 4 | 4 | 5 | 5 | RMSE |
| NN | 4 | 5 | 6 | 5 | 2 | 8 | RMSE |
| TPS | 5 | 8 | 5 | 8 | 4 | 7 | RMSE |
| MQS | 9 | 9 | 9 | 9 | 9 | 9 | RMSE |
| OK | 3 | 1 | 3 | 2 | 6 | 2 | RMSE |
| KED | 2 | 3 | 2 | 3 | 3 | 3 | RMSE |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendez, M.; Calvo-Valverde, L.-A.; Maathuis, B.; Alvarado-Gamboa, L.-F. Generation of Monthly Precipitation Climatologies for Costa Rica Using Irregular Rain-Gauge Observational Networks. Water 2019, 11, 70. https://doi.org/10.3390/w11010070
Mendez M, Calvo-Valverde L-A, Maathuis B, Alvarado-Gamboa L-F. Generation of Monthly Precipitation Climatologies for Costa Rica Using Irregular Rain-Gauge Observational Networks. Water. 2019; 11(1):70. https://doi.org/10.3390/w11010070
Chicago/Turabian StyleMendez, Maikel, Luis-Alexander Calvo-Valverde, Ben Maathuis, and Luis-Fernando Alvarado-Gamboa. 2019. "Generation of Monthly Precipitation Climatologies for Costa Rica Using Irregular Rain-Gauge Observational Networks" Water 11, no. 1: 70. https://doi.org/10.3390/w11010070
APA StyleMendez, M., Calvo-Valverde, L.-A., Maathuis, B., & Alvarado-Gamboa, L.-F. (2019). Generation of Monthly Precipitation Climatologies for Costa Rica Using Irregular Rain-Gauge Observational Networks. Water, 11(1), 70. https://doi.org/10.3390/w11010070





