Abstract
This paper presents an application of the Bayesian belief network for coastal erosion management at the regional scale. A “Bayesian ERosion Management Network” (BERM-N) is developed and trained based on yearly cross-shore profile data available along the Holland coast. Profiles collected for over 50 years and at 604 locations were combined with information on different sand nourishment types (i.e., beach, dune, and shoreface) and volumes implemented during the analyzed time period. The network was used to assess the effectiveness of nourishments in mitigating coastal erosion. The effectiveness of nourishments was verified using two coastal state indicators, namely the momentary coastline position and the dune foot position. The network shows how the current nourishment policy is effective in mitigating the past erosive trends. While the effect of beach nourishment was immediately visible after implementation, the effect of shoreface nourishment reached its maximum only 5–10 years after implementation of the nourishments. The network can also be used as a predictive tool to estimate the required nourishment volume in order to achieve a predefined coastal erosion management objective. The network is interactive and flexible and can be trained with any data type derived from measurements as well as numerical models.
1. Introduction
Coastline retreat is a worldwide phenomenon caused by an imbalance between sediment supply and demand. The authors of [1] showed that 24% of the world’s sandy beaches are eroding, with erosion rates exceeding 0.5 m/year, while 28% are accreting and 48% are stable. Causes of erosion may be either anthropogenic (e.g., construction of river dams, ports or coastal protection works, sediment mining) or natural (e.g., natural gradients in alongshore sediment transport, storms, presence of submarine canyons near the coastline) [2]. Additionally, coastal retreat can be exacerbated by the effects of sea level rise and soil subsidence. The Holland coast is a typical example of an erosive coastline, along which coastal erosion is managed by applying sand nourishments.
The management of coastal erosion relies on the continuous development of new and flexible solutions and tools, which can account for changes in natural hazard conditions and anthropogenic interventions and which are based on long-term observations [3,4]. Coastal erosion is, however, a process characterized by high temporal and spatial variability. Several examples are available of small-scale data or numerical modeling studies with long-term datasets (e.g., [5,6,7]). However, the use of data analysis or numerical modeling at the local scale often provides information which is site-dependent and only reliable for a short time period for which they are validated. This may not be sufficient for decision makers and coastal managers to assess the effectiveness of coastal erosion strategies at larger spatial and temporal scales.
The use of a Bayesian belief network (BBN) can provide a very powerful tool to bridge the existing gap between the needs of coastal managers and the currently available data and numerical models [8]. BBN is a method of reasoning using probabilistic relationships between causes and effects. Bayesian statistics have been applied to very diverse fields. In the field of coastal engineering, they have been used for predicting coastal dune and beach erosion and overwash [9,10,11,12,13], assessing wave height evolution in the surf zone [14], and estimating offshore wave heights and depth given limited offshore information [15]. Recent studied have used BBN to evaluate the coastal vulnerability due to sea level rise [16], the relationships between observed damages and multiple hazard indicators due to hurricanes [17], and the estimation of flooding hazards at coral reef islands [18]. They have also been used to assess the applicability of parametric morphodynamic classification of beach states [19]. BBN can also be an effective tool for data mining where large datasets are available [20,21].
The studies in which BBN was applied to evaluate the effectiveness of disaster risk reduction (DRR) measures are still rather limited in number and are restricted to local study cases. The authors of [22] applied BBN to assess the effectiveness of coastal protection measures (i.e., a seawall) and vulnerability reduction strategies at a small town in North Norfolk (UK). The effectiveness of exposure reduction strategies (i.e., partial house removal) and beach replenishment, at one coastal sector in South Portugal was also assessed using BBN [23]. The authors of [24] applied BBN to assess the effectiveness of measures against sea-level rise (i.e., salt marsh restoration and beach nourishments) in a lagoon in northeast Italy.
This paper describes the implementation and application of a “Bayesian ERosion Management Network” (BERM-N) to be used for coastal erosion management at a larger (regional) scale. The network is based on data collected over more than 50 years along the entire Holland coast, one of the most data-rich environments in the world. The large data availability allows to capture the spatial and temporal variability related to coastal erosion processes and human interventions. BERM-N is used in this manuscript to assess the effectiveness of different adaptation solutions in the form of beach and shoreface nourishments, and also as a predictive tool to achieve a predefined coastal erosion management objective.
2. Bayesian Modeling for Coastal Erosion Management
A Bayesian network is a method of reasoning using probabilities, where the nodes of the network represent variables and the arrows indicate the cause–effect relationships between the nodes. The advantage of using this approach is that by combining the information from multiple variables, it makes it possible to make robust data-driven or model-driven forecasts.
At the heart of Bayesian networks lies the Bayes rule, generally expressed as:
where the left-hand term is the updated conditional probability (or ‘posterior probability’) of a forecast Fi, given a particular set of observations, Oj (Pearl, 1988). The first term on the right-hand side is the likelihood of observations Oj given that the forecast Fi is true. The second term on the right is the prior probability distribution of Fi (e.g., the probability of a given forecast based on the entire training dataset, in the absence of any additional observations). The denominator on the right side is the prior probability distribution of Oj.
In this specific case, the posterior probability is described by the distribution of a chosen coastal state indicator (e.g., changes in shoreline or dune foot position), in response to a nourishment strategy (e.g., nourishment type or nourishment volume), representing the observations. Constructing a network first involves defining the variables which best describe the process to be studied. In this study, the main variables are selected through the identification of measurable indicators describing the coastal erosion process and the relation between adaptation measures and coastal response. The selected variables are represented by nodes in the BBN. The states of these nodes must be mutually exclusive and collectively exhaustive. A BBN is a directed acyclic graph, where the direct cause–effect relationship between two variables in a BBN is illustrated by an arrow. The feeding of information into the Bayesian network in order to construct the conditional probability tables is called “training”.
An advantage of BBN is that it is interactive and fast to operate. Once the network is trained, it can be used to carry out quick simulations based on the data included in the network. Moreover, being a probabilistic method, it can account for uncertainties by specifying probability distributions for input variables and generating such distributions as output.
3. Study Area
The Holland coast is a sandy, microtidal, wave-dominated coast located in the central part of the Netherlands (Figure 1). The region is divided in three subregions: Noord-Holland, Rijnland, and Delfland. The coastline is bounded in the north by a tidal inlet named the Marsdiep, connecting the Wadden Sea to the North Sea, and in the south by the long jetty near Hook of Holland, which allows ships to access the Port of Rotterdam. The coastal defense mainly consists of a sandy dune system 117 km long.
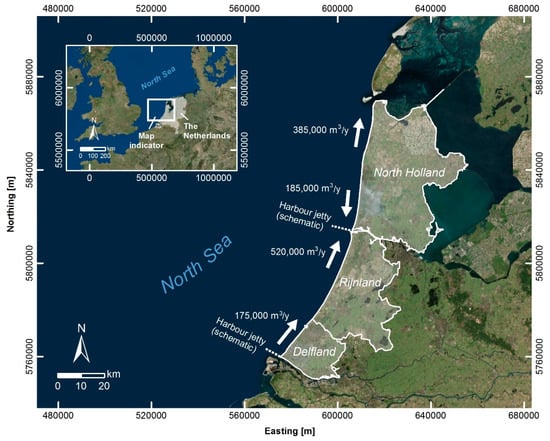
Figure 1.
Map of Holland, the Netherlands, including the three subregions considered in this study: Delfland, Rijnland, and North Holland. Net yearly alongshore sediment transport rates are also shown [25].
A detailed sediment budget analysis for the entire country has been presented by several authors (see for example: [25,26]). Net alongshore sediment transport is mostly northward directed, with yearly rates ranging approximately between 200,000 and 500,000 m3/year (Figure 1). In general, the natural supply of sediment to the coast is very limited and, consequently, the coastline is retreating [4,27].
Protection against flooding is traditionally the primary objective of coastal policy in the Netherlands. However, since 1990, additional objectives have been included: the sustainable preservation of safety against flooding and of values and functions in the dune area [28]. To fulfill these objectives, the yearly volume of sand for nourishments along the entire Dutch coast was first increased from about 3 million m3 to 6 million m3 of sand in 1990, and then to 12 million m3 in 2001 [29]. Even higher volumes might be necessary in the future to cope with the more severe predicted sea level rise scenarios. The total nourishment volumes implemented along the Holland Coast between 1965–1990, 1991–2000, and 2001–2016, and divided for different nourishment types (beach nourishments, shoreface nourishments, dune nourishments, and others), are shown in Figure 2. Beach and dune nourishments are generally implemented directly on the beach or dunes. Shoreface nourishments are implemented in proximity of the breaker bars (≈3 to 5 m water depth). As shown in Figure 2, the total volume of shoreface nourishments has been increasing since 1990, due to their lower cost (relative to beach nourishments) and lower interference with the coastal environment.
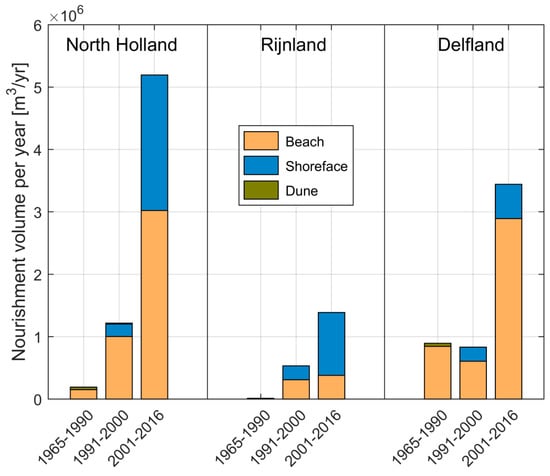
Figure 2.
Nourishment volumes (millions m3/year) at the Holland coast for the three periods: 1965–1990, 1991–2000, and 2001–2016. Note that the North Holland coast is ≈55 km long, Rijnland ≈41 km, and Delfland ≈21 km.
As a result of these large nourishment works, the generally erosive trends which characterized the shoreline before 1990 have changed into generally accretive trends. This was confirmed for example by analyzing volume changes within different water depths (−8 ÷ −3 m NAP and −3 ÷ +3 m NAP) for different time periods [30].
4. Material and Methods
4.1. Data Availability
Two main data types were used to build BERM-N: (a) Information on nourishment types and volumes and (b) changes in coastal state indicators to quantify the coastal erosion processes and the effects of different nourishment schemes.
The nourishment database supplied by Rijkswaterstaat (Ministry of Transport, Public Works, and Water Management) was used, which includes information on nourishment type, year and month when construction started/ended, location, and volume. For simplicity, the nourishment volumes were converted to m3 of sand nourishment per linear meter of coastal length where the nourishment was built.
The coastal state indicators were derived based on the JarKus profiles. The JarKus (“Jaarlijkse Kustmeting”, Annual Coastal Measurement) program was started in 1963 by Rijkswaterstaat. Coastal elevation profiles are measured yearly, during spring, with a longshore spacing of 250 m. Measurements above land were carried out until the 1990s using a differential GPS (dGPS), while measurements are currently carried out using LIDAR. Measurements below water are carried out using multibeam surveying techniques.
Thus, in total, coastal indicators were derived from 31,408 cross-shore profile measurements (604 transects × 52 years). In the cross-shore direction, measurements begin at approximately the first dune row and continue until the −8 m ≈ −12 m contour with respect to MSL (mean sea level), depending on the transect and the year. The cross-shore resolution of the measurements increases from 20 m offshore up to 5 m at the coast. An example of a series of JarKus profile measurements at a single location is given in Figure 3.
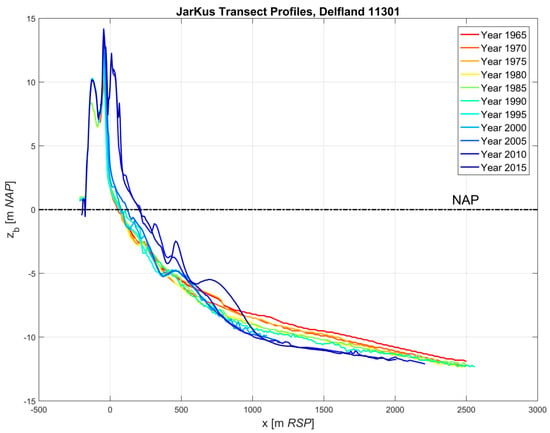
Figure 3.
Example of the morphological development of a single cross-shore JarKus profile (transect 11,301) located at Delfland, between 1965 and 2015.
The authors of [31] defined suitable coastal indicators to assess the morphological development of the Holland coastline due to natural and anthropogenic pressure factors. In particular, the following indicators were used for setting up BERM-N:
- -
- Changes in MCL (momentary coastline) position, defining the position of the coastline as a function of the volumes of sand in the near shore zone, approximately between the dune foot (+3 m NAP, where NAP ≈ mean sea level) and −5 m NAP (Figure 4) [32]. Positions are given with respect to predefined reference points at each transect (i.e., the RSP points “RijkStrandPalen” = “Beach Poles”).
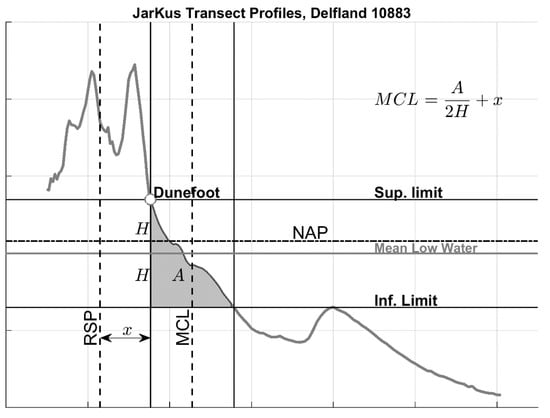 Figure 4. Computation of the momentary coastline (MCL) volume for a given JarKus transect. A is the area used to compute the Momentary Coastline position. A is delimited by an upper boundary, corresponding to the dune foot position, and a lower boundary, at a distance equal to 2 x H from the dune foot position. H is defined as the distance between the dune foot position and the mean low water line. RSP is the reference point from which distances are computed (“rijksstrandpalen”). Therefore, the MCL position can be estimated as MCL = (A/2H) + x, with x being the distance between the RSP line and the dune foot position.
Figure 4. Computation of the momentary coastline (MCL) volume for a given JarKus transect. A is the area used to compute the Momentary Coastline position. A is delimited by an upper boundary, corresponding to the dune foot position, and a lower boundary, at a distance equal to 2 x H from the dune foot position. H is defined as the distance between the dune foot position and the mean low water line. RSP is the reference point from which distances are computed (“rijksstrandpalen”). Therefore, the MCL position can be estimated as MCL = (A/2H) + x, with x being the distance between the RSP line and the dune foot position. - -
- Changes in DF (dune foot) position, defining the position of the dune foot, and estimated as the most seaward intersection of the +3 m NAP line and the cross-shore profile.
4.2. Bayesian Network
To construct the Bayesian belief network, the Netica software package [33] was chosen. Netica uses the probabilistic inference algorithms of Reference [34], and it is widely used for coastal applications (e.g., [12,14,18,20]). The standard network construction and updating procedures outlined in [33] were followed to create BERM-N.
BERM-N, after construction and training in Netica, is shown in Figure 5. In the network, nodes have been grouped in three categories, namely:
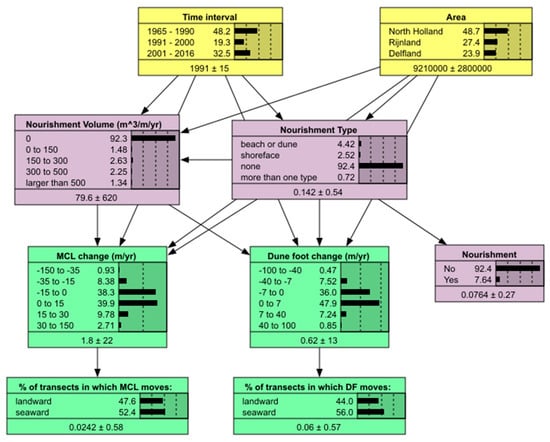
Figure 5.
Visualization of BERM-N. Nodes have been grouped in three categories according to the color. Yellow is used for the nodes describing the spatial characterization of the study area and the time interval; purple for the nodes describing the nourishment types and volumes; and green for the nodes describing the effects on the morphological indicators. At each node, the first column indicates the chosen discretization intervals, while the second column (adjacent to the histogram) is the percentage of the prior distribution in each bin. The last line indicates the mean of the prior distribution ± one standard deviation.
- ▪
- Time interval and spatial characterization of the study area (in yellow);
- ▪
- nourishment type and volume (in purple);
- ▪
- effects on the morphological indicators (in green).
These are discussed in greater detail below.
4.2.1. Time Interval and Spatial Characterization of the Study Area
It includes the following nodes:
- ▪
- Time interval: 1965–1990; 1991–2000; 2001–2016. Time intervals have been chosen in order to discriminate different periods in which the nourishment policy has been adapted (i.e., in 1990 and 2000).
- ▪
- Area: North Holland, Rijland, and Delfland. These are the three coastal sections in which the Holland coast is divided.
4.2.2. Nourishment Type and Volume
It includes the following nodes:
- ▪
- Nourishment volume (in m3/m/year): Yearly nourishment volume divided by the length of the nourishment.
- ▪
- Nourishment type: Beach or dune nourishment; shoreface nourishment; no nourishment; more than one type of nourishment at the same transect. It describes the nourishment type.
- ▪
- Nourishment: Yes; no. To discriminate transects which have been nourished at least once during the entire period (1965–2016) from the ones which have never been nourished.
4.2.3. Effects on the Morphological Indicators
- ▪
- MCL change (m/year): To quantify changes in coastline (MCL) position.
- ▪
- Dune foot (DF) change (m/year): To quantify changes in dune foot position.
- ▪
- Percentage of transects in which the momentary coastline (MCL) moves: Landward; seaward. To quantify the percentage of transects in which MCL has a positive (seaward), negative (landward) shift as a result of the effects of natural morphological changes and nourishments.
- ▪
- Percentage of transects in which the dune foot (DF) moves: Landward; seaward. To quantify the percentage of transects in which the dune foot has a positive (seaward), negative (landward) shift as a result of the effects of natural morphological changes and nourishments.
5. Results
In this section, a number of possible applications of BERM-N and results are described. The predictive skill of the network was evaluated by means of confusion matrixes (similarly to References [12,18]). This resulted in predictive skills of 77% and 87%, respectively, for MCL and DF changes.
5.1. Prior Probability Distributions
The prior probability distribution describes the baseline situation, in which no node is constrained, and the network is trained based on all data from all the available 604 transects at the 52 years in which measurements were available (Figure 5). Some relevant information can be depicted from this baseline situation.
First of all, the node “Area” shows that most of the observations are available for the North Holland coastal section, in view of its wider extension, considering that JarKus transects are almost equally spaced.
Of all data, 92.4% fall in the category no nourishment, meaning that when considering all the transects for all the years, 92.4% of them do not contain a nourishment at a given year (see node “Nourishment Type”). Of all data, 4.42% include a beach or a dune nourishment, 2.52% a shoreface nourishment and only 0.72% more than one nourishment type per year. As a consequence, most of the data indicate a nourishment volume equal to 0 (see node “Nourishment Volume”).
The nodes “MCL change” and “dune foot change” show that the indicators MCL and dune foot, based on all data, tend to move, in average, seaward 1.8 m/year and 0.6 m/year, respectively. This also suggests that beaches are becoming wider since the MCL position is moving seaward at a faster rate than the dune foot position, as a result of the volume of sediments in the nearshore zone.
The fact that most of the data show a seaward migration is confirmed by the nodes “percentage of transects in which MCL moves” and “percentage of transects in which DF moves”. In particular, 52.4% of data show a seaward migration of MCL and 56.0% of the data a seaward migration of DF. Nevertheless, there is also a consistent percentage of transects which are characterized by a landward trend (i.e., erosion).
5.2. Assessment of the Effectiveness of Sand Nourishments Against Erosion
This section illustrates the effectiveness of past nourishments in addressing the coastal erosion along the Holland coast. In order to do so, the node “Nourishment” was constrained to a “No” then to a “Yes” value, to consider, respectively, transects which have not been nourished and transects which have been nourished (see Figure 6). The nodes: “Percentage of transects in which MCL moves” and “percentage of transects in which DF moves” show, respectively, the percentages of transects in which an erosive and accretive trend has to be expected. In particular, in case of no nourishment, about half of the cases are characterized by an erosive trend (i.e., 49.3% if considering MCL and 45.2% if considering the dune foot position as coastal indicator). The effect of nourishment is to decrease the number of erosive transects to 26.6%, when considering MCL as indicator, and 29.5% when considering dune foot as indicator.
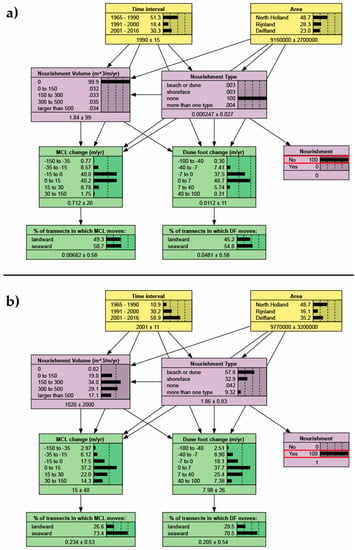
Figure 6.
BERM-N application to assess the effectiveness of sand nourishments. Panel above (a): BERM-N constrained in order to consider only transects which have not been nourished (see red box). Panel below (b): BERM-N constrained in order to consider only transects which have been nourished (see red box).
5.3. Assessment of the Effectiveness of Different Nourishment Designs
In this section, the effectiveness of the two most common nourishment designs in the Netherlands (i.e., beach and shoreface nourishments) has been assessed using BERM-N. In order to do so, the node “nourishment type” was constrained first to “beach or dune” and then to “shoreface”. To facilitate the visualization, the resulting changes in MCL and DF position (i.e., landward or seaward) are shown using a pie chart in Figure 7.
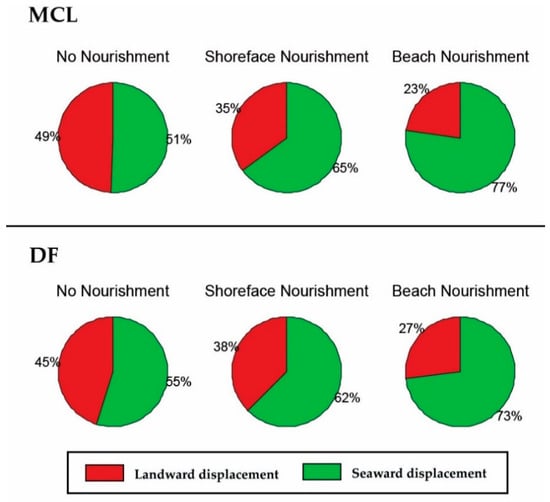
Figure 7.
Effects of no nourishments, shoreface, and beach nourishments on MCL (upper panel) and dune foot (DF) (lower panel) indicators. The red color represents the probability of a landward displacement of the indicator, whereas a green color represents the probability of a seaward displacement. Values indicate the mean values of the distributions.
The figure confirms the positive effect of nourishments on counteracting coastal erosion on both indicators of MCL and DF position, as indicated by the green color (i.e., seaward displacement). Among the two types of nourishments, the effect of beach nourishments appears more pronounced than the effect of shoreface nourishments.
To shed light on the effect of different nourishment type in time, after implementation of a nourishment, the same network was trained with three different datasets. These three datasets were derived considering the effects on the indicators, respectively, one year, five years, and ten years after implementation of a nourishment. In case of multiple nourishments taking place within the considered time window, only the first nourishment was taken into account.
The results are shown in Figure 8, respectively, for the MCL indicator (upper panel) and DF indicator (lower panel). A first, important observation which can be derived from the figure is that even in the case of no nourishment, the percentage of transects characterized by indicators experiencing a landward trend (erosion) decreases when moving from a one-year time window to a five- or ten-year time window. This is the result of the large nourishment volumes implemented along the entire Holland coast. As nourished sand tends to move in an alongshore direction (Figure 1), even transects which have not been nourished tend to benefit from the sand nourished at neighboring transects.
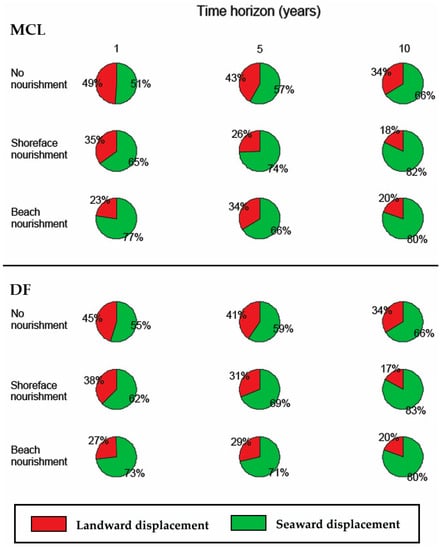
Figure 8.
Effects of no nourishments, shoreface, and beach nourishments on MCL (upper panel) and DF (lower panel) indicators. The effects are shown in three different columns, to indicate the effects one year, five years and ten years after implementation of a nourishment.
The effect of nourishments is to further decrease the number of transects experiencing erosion with a similar qualitative effect on both indicators. When comparing the effect of shoreface and beach nourishments on the two indicators, one can see that the effect of shoreface nourishments is less evident than that of beach nourishments one year after construction. In the case of shoreface nourishments, 35% of the transects at which MCL was computed still experience a landward trend one year after implementation of the nourishment, compared with 23% in the case of beach nourishments. Similarly, for the DF position, 38% of the cases show a landward trend one year after implementation of a shoreface nourishment, against just 27% in case of a beach nourishment. However, the positive effect of shoreface nourishments on the indicators continues in time and becomes more noticeable 5 years after implementation of the nourishment, with a similar (i.e., for DF indicator) or even higher (i.e., for MCL indicator) impact than for beach nourishments.
The comparison of the effect of beach and shoreface nourishment after 10 years requires careful interpretation. In particular, the figure seems to suggest that the effectiveness of beach nourishments starts increasing again 10 years after implementation of the nourishments, after a drop at 5 years. In particular, the number of cases receiving a positive effect from beach nourishments after 10 years is 80% for both MCL and DF indicators, and only 66% for MCL and 71% for DF after 5 years. This is, however, rather due to the effect of sand coming from neighboring transects than the result of sand from the nourished transects. Beach nourishments have lifetimes in the order of 1–5 years, depending on the size of the nourishment and the local wave climate [30]. The effect of shoreface nourishments 10 years after implementation is consistent with the observation at 5 years, with a larger effect of shoreface nourishments on the indicators compared to that of beach nourishments.
5.4. Application of BERM-N as Predictive Tool to Achieve a Predefined Coastal Management Objective
In this last application, BERM-N was used as predictive tool to quantify the sand volumes required in order to reach a specific objective. The objective which is tested in this example is a coastline at which any erosion trend (i.e., described by the MCL and DF indicators) is stopped and replaced by accretive trends over the entire region. In order to do so, the two nodes (“% of transects in which MCL/DF moves”) are constrained to a value equal to “seaward”.
Figure 9 shows that in order to achieve this objective, an average nourishment volume of 161 m3/m/year would be required, distributed over 13.7% of the transects. Considering a total length of the coastline equal to 117 km, this would correspond to a yearly volume of about 2.5 million m3 of sand/year (i.e., 161 m3/m/year × 117,000 m × 0.137). This is less than the current nourishment volume applied along the Holland coast, which currently results in an average accreting coastline as a result of the large nourishment volumes applied yearly. These nourishments are applied not just to preserve the current position of the coastline, but to maintain the entire coastal foundation in future sea level rise scenarios, as well as to provide the boundary conditions for the developments of additional functions, such as wide beach and dunes for nature and recreation (Section 3).
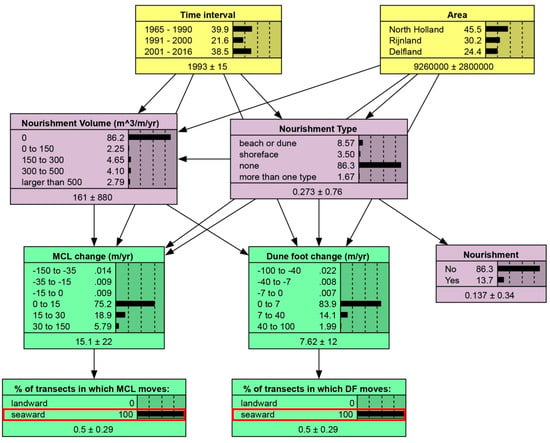
Figure 9.
BERM-N application as predictive tool to assess the required nourishment volume in order to reach a predefined coastal erosion management objective: Reduce to zero the erosion over the entire coastline, only allowing for accretion. The red boxes show the two nodes constrained to a condition of “seaward” movement at the two coastline indicators.
6. Discussions
For clarity, discussion points have been grouped under three main topics.
6.1. General Assumptions Related to the Construction of the BERM-N
In order to develop BERM-N, a number of general assumptions have been adopted. First of all, the indicators chosen to describe the morphological development of the region (i.e., MCL and DF positions) are arbitrary. In principle, other indicators could also be selected, such as beach width (i.e., useful for recreational purposes) or the probability of dune breaching (i.e., important for safety). However, we have given preference to these indicators, as they are widely used for similar studies in the region [31,32] as well as by the local government.
The choice of processes to be included in the network is also arbitrary. In this paper, we have chosen to focus on the effects of anthropogenic forcing (i.e., nourishments) as the major driver for coastal development along the Holland coast. On the other hand, natural forcing has been omitted from the network. This choice is due to the fact that the large-scale and multi-year development of this coastline in the recent years are mainly the result of the large nourishment volumes which have been applied to manage coastal erosion. However, this is not the case at most coastlines around the world, where the effect of natural forcing is dominant. Another assumption relates to the discretization (i.e., number of bins and size of each bin) [35] of the continuous variables such as MCL change. We followed the guidance of the authors of [15], who suggest that each bin should be as wide as possible to limit the computational expense and capture multiple data points, but narrow enough to give meaningful forecasts and resolve uncertainty. Hence, node discretization presents a tradeoff between the precision and accuracy of predictions. In this study, the bin width was chosen in such a way that each bin would contain a sufficient number of data points, so we have avoided using bins with a very small size. Similarly, there should be a sufficient number of bins in order to properly describe the statistical distribution of the variable under consideration. BBN cannot extrapolate, only interpolate within the bounds of the data with which they have been trained, so the extremes of the training dataset determine the upper and lower limits of each node.
A final assumption relates to how to account for the effects of multiple nourishments in subsequent years, when considering time windows of several years (i.e., 5 or 10), and specifically at the transects where multiple nourishments occurred. This effect is currently included in BERM-N by only looking at the first nourishment within the considered time window. Although other options may be possible and were explored while setting up the network (i.e., adding the total volumes or correcting volumes with functions which would account for the exact timing when a nourishment occurred), it should be recognized that each of these approaches contains a bias. It was finally decided to adopt the approach used in the paper, because of its simplicity and because it provided the highest predictive skill.
6.2. Alongshore Effects of Sand Nourishments
The analysis as presented in this study fully relies on data measured at cross-shore transects along the entire region (i.e., nourishment volumes, types and spatial displacement of the indicators resulting from the nourishments). The basic assumption is that the effect of nourishments can be described by cross-shore processes and that a nourishment will only affect the coastal indicators at the transect in which it has been applied. In reality, sand nourishments, and in particular shoreface nourishments, also have an alongshore effect, as discussed in Section 5.3. This is a simplification, as it is not straightforward to link the displacement of a coastal indicator resulting from a sand nourishment applied at a different location.
This alongshore effect is also visible as a background signal in the displacements of the coastal indicators. For example, Figure 7 and Figure 8 show that, even without nourishments, the coastal indicators are characterized by accretive trends, which is most likely related to the positive effect of sand nourishments applied at neighboring transects.
6.3. BERM-N Tool for Coastal Erosion Management of Past and Future Conditions
BERM-N, as presented in this study, is fully trained based on data from past observations, collected over more than 50 years. This means that the response and outcome of the network is derived based on these past observations. This further implies that in case of future changes to the physical system (e.g., accelerated sea level rise) or development of new anthropogenic interventions which may interfere with the coastal systems, the model may have insufficient data on which to base its predictions. Bayesian networks can interpolate but not extrapolate beyond the data with which they have been trained. A possibility to overcome this is by complementing and retraining the BERM-N with data derived from numerical modeling simulations (e.g., [36]), which may also include information on possible future scenarios.
Similarly, the network has been trained with data from all past nourishment projects carried out in the region, i.e., one of the most nourished region in the world, per kilometer length of coastline (see, e.g., [37]). This is a very extensive database, including nourishments with different sizes and volumes. Nevertheless, this also means that the network can only be used as a predictive tool to simulate cases which are included within the statistical distribution of these past nourishment projects. In case, for example, the effects of a very different type of nourishment should be simulated (e.g., much larger in size than the ones included in the database), it may be required to extend the database with data derived from numerical modeling simulations, which include these new nourishments as synthetic cases.
7. Conclusions
In this study, an application of Bayesian statistics for coastal erosion management at the regional scale has been presented. A tool based on the use of a Bayesian network (BERM-N) was constructed using measured data collected along the entire Holland coast for a period of over 50 years at 604 cross-shore transects. The effects of different sand nourishment designs on two pre-identified coastal indicators (i.e., dune foot and momentary coastline position) were assessed at these transects.
Different applications of BERM-N have been described. A first application was used to quantify the issue of coastal erosion along the Holland coast region. Additionally, the tool has shown how sand nourishments have been effective in counteracting this issue. In a second application, the tool was used to assess the effectiveness of different nourishment designs (i.e., shoreface vs. beach nourishments) in counteracting coastal erosion. The results have shown how beach nourishments have an immediate effect on the chosen indicators. On the other hand, shoreface nourishments become more effective with time, reaching a similar effect to the one of beach nourishments after about five years. For coastal managers, this is important, as beach nourishments may be more suitable for achieving short-term safety objectives (≈months/years), whereas shoreface nourishment may be more appropriate to counteract erosion at medium- and long-term (≈decades) temporal scale. In a last application, the tool was used as a predictive tool to assess the nourishment volumes required in order to achieve a specific coastal management objective (e.g., extending the coastline in seaward direction of a given value).
The advantage of the tool is that it is flexible, fast, and interactive and can accommodate the use of measured data (i.e., as shown in this study) as well as synthetic data derived from numerical modeling simulations. This makes it suitable for discussions with policy makers and other stakeholders, following a collaborative modeling approach [38].
Author Contributions
A.G. and E.D. conceptualized the research; E.D. implemented the methodology; E.D. and G.S. contributed to data analyses and figures; A.G. prepared the original draft of the manuscript and contributed to further revisions; S.P. and K.d.H. supervised the research; S.P. reviewed and edited the original manuscript and further revisions.
Funding
This research received no external funding.
Acknowledgments
We would like to thank Dirk Knipping, who has helped developing the first setup of the Bayesian network. We are also thankful to Matthijs Kok, Saskia van Vuren, and Sierd de Vries for their suggestions in developing this research. Finally, we would like to thank Björn Röbke for his help in preparing Figure 1.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef] [PubMed]
- Giardino, A.; Schrijvershof, R.; Nederhoff, C.M.; de Vroeg, H.; Brière, C.; Tonnon, P.K.; Caires, S.; Walstra, D.J.; Sosa, J.; van Verseveld, W.; et al. A quantitative assessment of human interventions and climate change on the West African sediment budget. Ocean Coast. Manag. 2018, 156, 249–265. [Google Scholar] [CrossRef]
- Giardino, A.; De Boer, W.; Den Heijer, K.; Huisman, B.; Mulder, J.; Walstra, D.-J. Innovative approaches and tools for erosion control and coastline management. In Proceedings of the 10th Global Congress on ICM: Lessons Learned to Address New Challenges, EMECS 2013—MEDCOAST 2013 Joint Conference, Marmaris, Turkey, 30 October–3 November 2013; Volume 2. [Google Scholar]
- Stronkhorst, J.; Huisman, B.; Giardino, A.; Santinelli, G.; Santos, F.D. Sand nourishment strategies to mitigate coastal erosion and sea level rise at the coasts of Holland (The Netherlands) and Aveiro (Portugal) in the 21st century. Ocean Coast. Manag. 2018, 156, 266–276. [Google Scholar] [CrossRef]
- Robinet, A.; Idier, D.; Castelle, B.; Marieu, V. Environmental Modelling Software A reduced-complexity shoreline change model combining longshore and cross-shore processes: The LX-Shore model. Environ. Model. Softw. 2018, 109, 1–16. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Callaghan, D.; Stive, M.J.F. Estimating coastal recession due to sea level rise: Beyond the Bruun rule. Clim. Chang. 2012, 110, 561–574. [Google Scholar] [CrossRef]
- Callaghan, D.P.; Nielsen, P.; Short, A.; Ranasinghe, R. Statistical simulation of wave climate and extreme beach erosion. Coast. Eng. 2008, 55, 375–390. [Google Scholar] [CrossRef]
- Callaghan, D.P.; Baldock, T.E.; Shabani, B.; Mumby, P.J. Communicating physics-based wave model predictions of coral reefs using Bayesian belief networks. Environ. Model. Softw. 2018, 108, 123–132. [Google Scholar] [CrossRef]
- Hapke, C.; Plant, N. Predicting coastal cliff erosion using a Bayesian probabilistic model. Mar. Geol. 2010, 278, 140–149. [Google Scholar] [CrossRef]
- Den Heijer, C.K.; Baart, F.; van Koningsveld, M. Assessment of dune failure along the Dutch coast using a fully probabilistic approach. Geomorphology 2012, 143–144, 95–103. [Google Scholar] [CrossRef]
- Wilson, K.E.; Adams, P.N.; Hapke, C.J.; Lentz, E.E.; Brenner, O. Application of Bayesian Networks to hindcast barrier island morphodynamics. Coast. Eng. 2015, 102, 30–43. [Google Scholar] [CrossRef]
- Poelhekke, L.; Jäger, W.S.; van Dongeren, A.; Plomaritis, T.A.; McCall, R.; Ferreira, Ó. Predicting coastal hazards for sandy coasts with a Bayesian Network. Coast. Eng. 2016, 118, 21–34. [Google Scholar] [CrossRef]
- Plant, N.G.; Stockdon, H.F. Probabilistic prediction of barrier-island response to hurricanes. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Plant, N.G.; Holland, K.T. Prediction and assimilation of surf-zone processes using a Bayesian network. Part I: Forward models. Coast. Eng. 2011, 58, 119–130. [Google Scholar] [CrossRef]
- Plant, N.G.; Holland, K.T. Prediction and assimilation of surf-zone processes using a Bayesian network. Part II: Inverse models. Coast. Eng. 2011, 58, 256–266. [Google Scholar] [CrossRef]
- Gutierrez, B.T.; Plant, N.G.; Thieler, E.R. A Bayesian network to predict coastal vulnerability to sea level rise. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- van Verseveld, H.C.W.; van Dongeren, A.R.; Plant, N.G.; Jäger, W.S.; den Heijer, C. Modelling multi-hazard hurricane damages on an urbanized coast with a Bayesian Network approach. Coast. Eng. 2015, 103, 1–14. [Google Scholar] [CrossRef]
- Pearson, S.G.; Storlazzi, C.D.; van Dongeren, A.R.; Tissier, M.F.S.; Reniers, A.J.H.M. A Bayesian-Based System to Assess Wave-Driven Flooding Hazards on Coral Reef-Lined Coasts. J. Geophys. Res. Oceans 2017, 122, 10099–10117. [Google Scholar] [CrossRef]
- Loureiro, C.; Ferreira, Ó.; Cooper, J.A.G. Applicability of parametric beach morphodynamic state classification on embayed beaches. J. Mar. Geol. 2013, 346, 153–164. [Google Scholar] [CrossRef]
- Yates, M.L.; Le Cozannet, G. Brief communication “evaluating European Coastal Evolution using Bayesian Networks”. Nat. Hazards Earth Syst. Sci. 2012, 12, 1173–1177. [Google Scholar] [CrossRef]
- Bulteau, T.; Baills, A.; Petitjean, L.; Garcin, M.; Palanisamy, H.; Le Cozannet, G. Gaining insight into regional coastal changes on La Réunion island through a Bayesian data mining approach. Geomorphology 2015, 228, 134–146. [Google Scholar] [CrossRef]
- Jäger, W.S.; Christie, E.K.; Hanea, A.M.; den Heijer, C.; Spencer, T. A Bayesian network approach for coastal risk analysis and decision making. Coast. Eng. 2018, 134, 48–61. [Google Scholar] [CrossRef]
- Plomaritis, T.A.; Costas, S.; Ferreira, Ó. Use of a Bayesian Network for coastal hazards, impact and disaster risk reduction assessment at a coastal barrier (Ria Formosa, Portugal). Coast. Eng. 2018, 134, 134–147. [Google Scholar] [CrossRef]
- Catenacci, M.; Giupponi, C. Integrated assessment of sea-level rise adaptation strategies using a Bayesian decision network approach. Environ. Model. Softw. 2013, 44, 87–100. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport and budget of the central coastal zone of Holland. Coast. Eng. 1997, 32, 61–90. [Google Scholar] [CrossRef]
- Van Der Spek, A.J.F.; Lodder, Q. A new sediment budget for The Netherlands; the effects of 15 years of nourishing (1991–2005). In The Proceedings of the Coastal Sediments 2015; Word Scientific Publishing: Singapore, 2015. [Google Scholar]
- Beets, D.J.; Van Der Spek, A.J.F. The Holocene evolution of the barrier and the back-barrier basins of Belgium and the Netherlands as a function of late Weichselian morphology, relative sea-level rise and sediment supply. Neth. J. Geosci. 2000, 79, 3–16. [Google Scholar] [CrossRef]
- Mulder, J.P.M.; Hommes, S.; Horstman, E.M. Implementation of coastal erosion management in the Netherlands. Ocean Coast. Manag. 2011, 54, 888–897. [Google Scholar] [CrossRef]
- Giardino, A.; Mulder, J.; De Ronde, J.; Stronkhorst, J.; Giardino, A. Sustainable Development of the Dutch Coast: Present and Future. J. Coast. Res. 2011, 61, 166–172. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Coastal erosion and control. Ocean Coast. Manag. 2011, 54, 867–887. [Google Scholar] [CrossRef]
- Giardino, A.; Santinelli, G.; Vuik, V. Coastal state indicators to assess the morphological development of the Holland coast due to natural and anthropogenic pressure factors. Ocean Coast. Manag. 2014, 87, 93–101. [Google Scholar] [CrossRef]
- van Koningsveld, M.; Mulder, J.P.M. Sustainable Coastal Policy Developments in The Netherlands. A Systematic Approach Revealed. J. Coast. Res. 2004, 202, 375–385. [Google Scholar] [CrossRef]
- Norsys Software Corp. Netica TM, Application for Belief Networks and Influence Diagrams: User’s Guide; Norsys Software Corp: Vancouver, BC, Canada, 2003; pp. 1–91. [Google Scholar]
- Spiegelhalter, D.J.; Dawid, A.P.; Lauritzen, S.L.; Robert, G.; Spiegelhalter, D.J.; Dawid, A.P.; Lauritzen, S.L.; Cowell, R.G. Bayesian Analysis in Expert Systems Linked references are available on JSTOR for this article. Bayesian Anal. Expert Syst. 1993, 8, 219–247. [Google Scholar]
- Beuzen, T.; Splinter, K.D.; Marshall, L.A.; Turner, I.L.; Harley, M.D.; Palmsten, M.L. Bayesian Networks in coastal engineering: Distinguishing descriptive and predictive applications. Coast. Eng. 2018, 135, 16–30. [Google Scholar] [CrossRef]
- Giardino, A.; den Heijer, K.; Santinelli, G.; van der Werf, J. Tools for Medium- and Long-Term Prediction of Nourishments; Deltares: Delft, The Netherlands, 2013. [Google Scholar]
- Hamm, L.; Capobianco, M.; Dette, H.H.; Lechuga, A.; Spanhoff, R.; Stive, M.J. A summary of European experience with shore nourishment. J. Coast. Eng. 2002, 47, 237–264. [Google Scholar] [CrossRef]
- Basco-Carrera, L.; Warren, A.; van Beek, E.; Jonoski, A.; Giardino, A. Collaborative modelling or participatory modelling? A framework for water resources management. Environ. Model. Softw. 2017, 91, 95–110. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).