Mass and Energy Balance Estimation of Yala Glacier (2011–2017), Langtang Valley, Nepal
Abstract
1. Introduction
Previous Studies
2. Materials and Methods
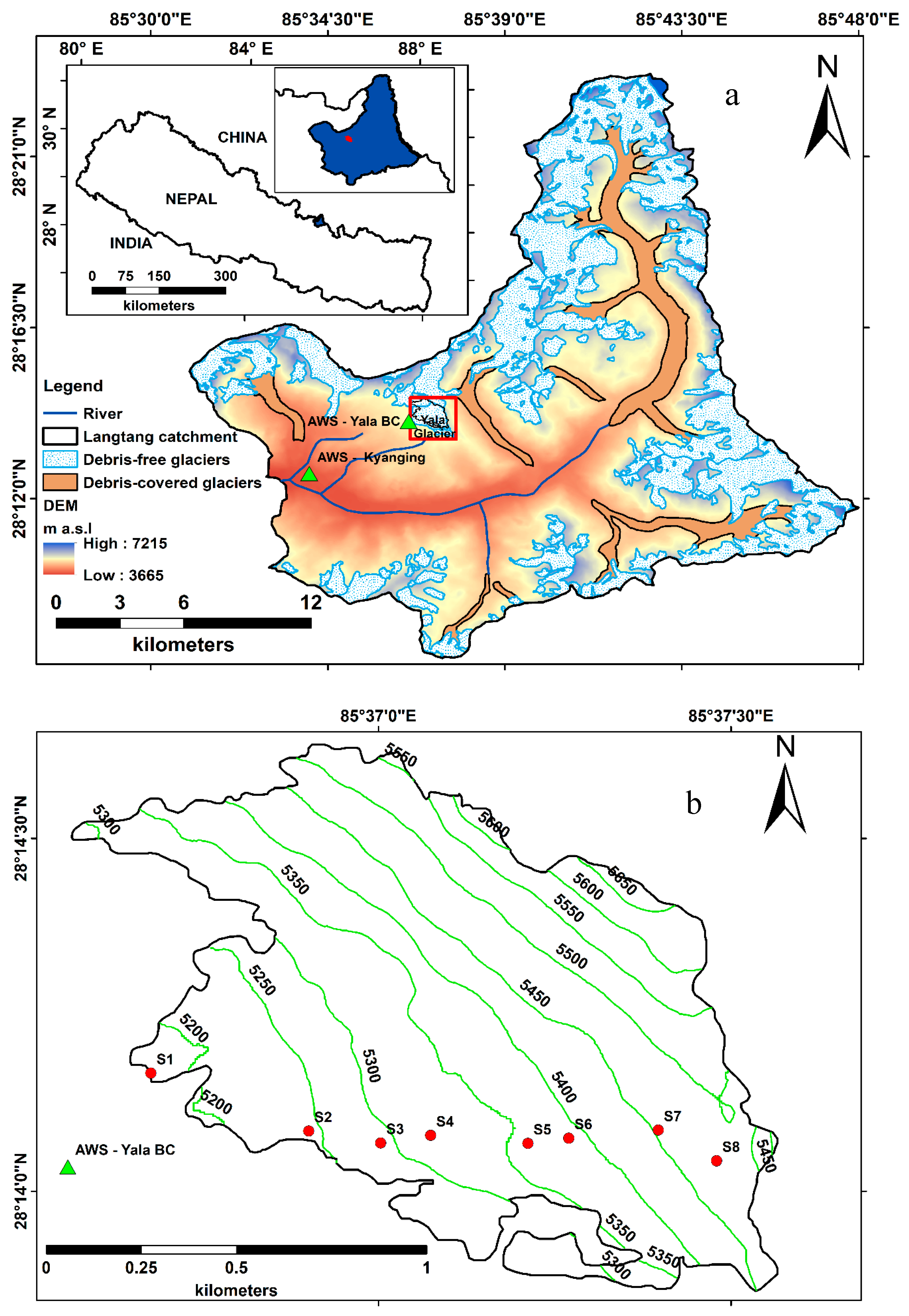
2.1. Description of Study Area
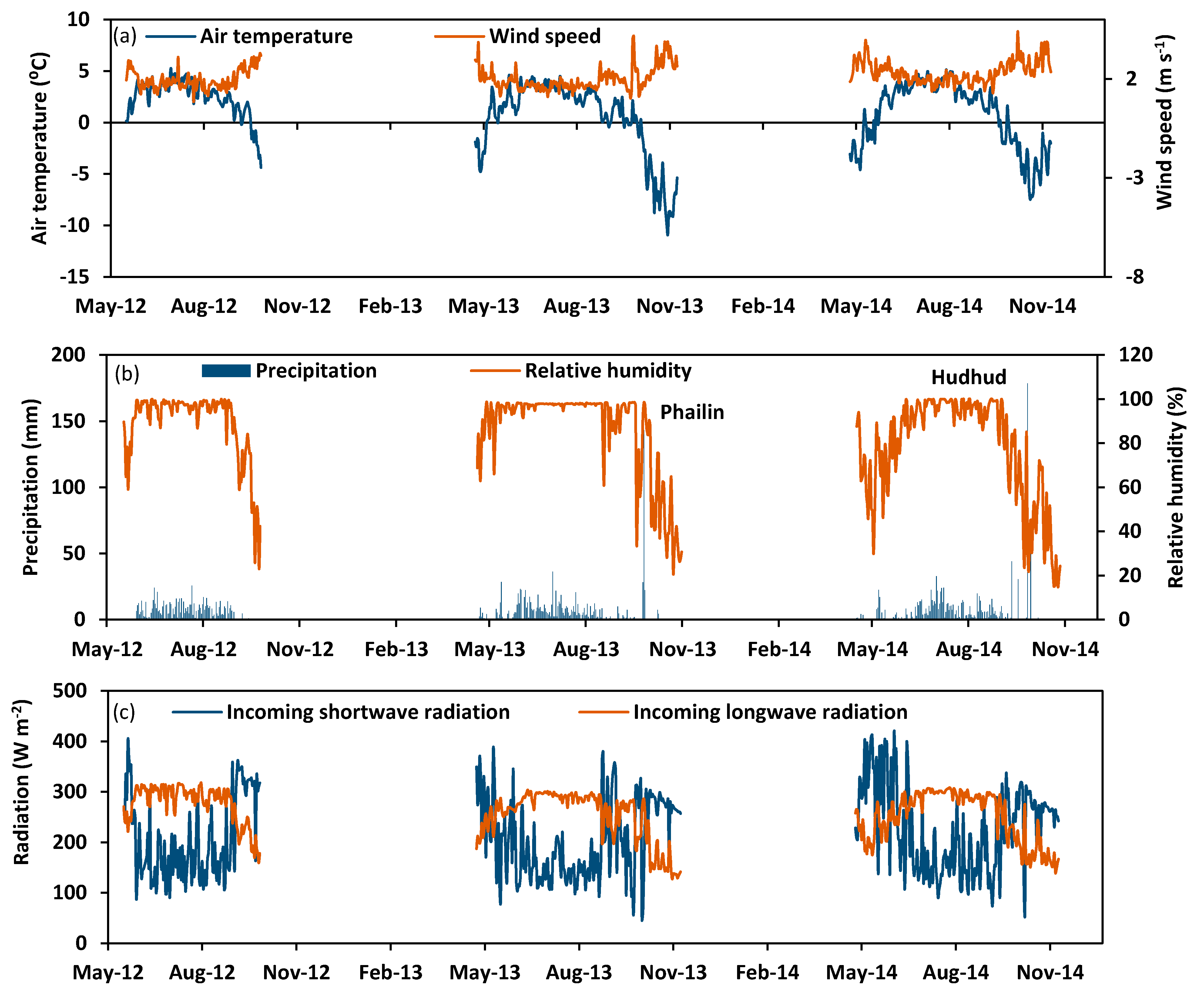
2.2. Meteorological Datasets
2.3. Glacier-Wide Mass Balance Using Glaciological Method
2.4. Mass Balance Calculation using Surface Energy Balance Model
2.4.1. Net Radiation
2.4.2. Turbulent Sensible Heat Flux
2.4.3. Turbulent Latent Heat Flux
2.4.4. Heat Conduction Flux
2.4.5. Point Mass Balance
3. Results
3.1. Meteorological Conditions at the Study Site
3.2. Observed Mass Balance
3.2.1. Annual and Cumulative Glacier-Wide Mass Balance of Yala Glacier
3.2.2. Seasonal Glacier-wide Mass Balance
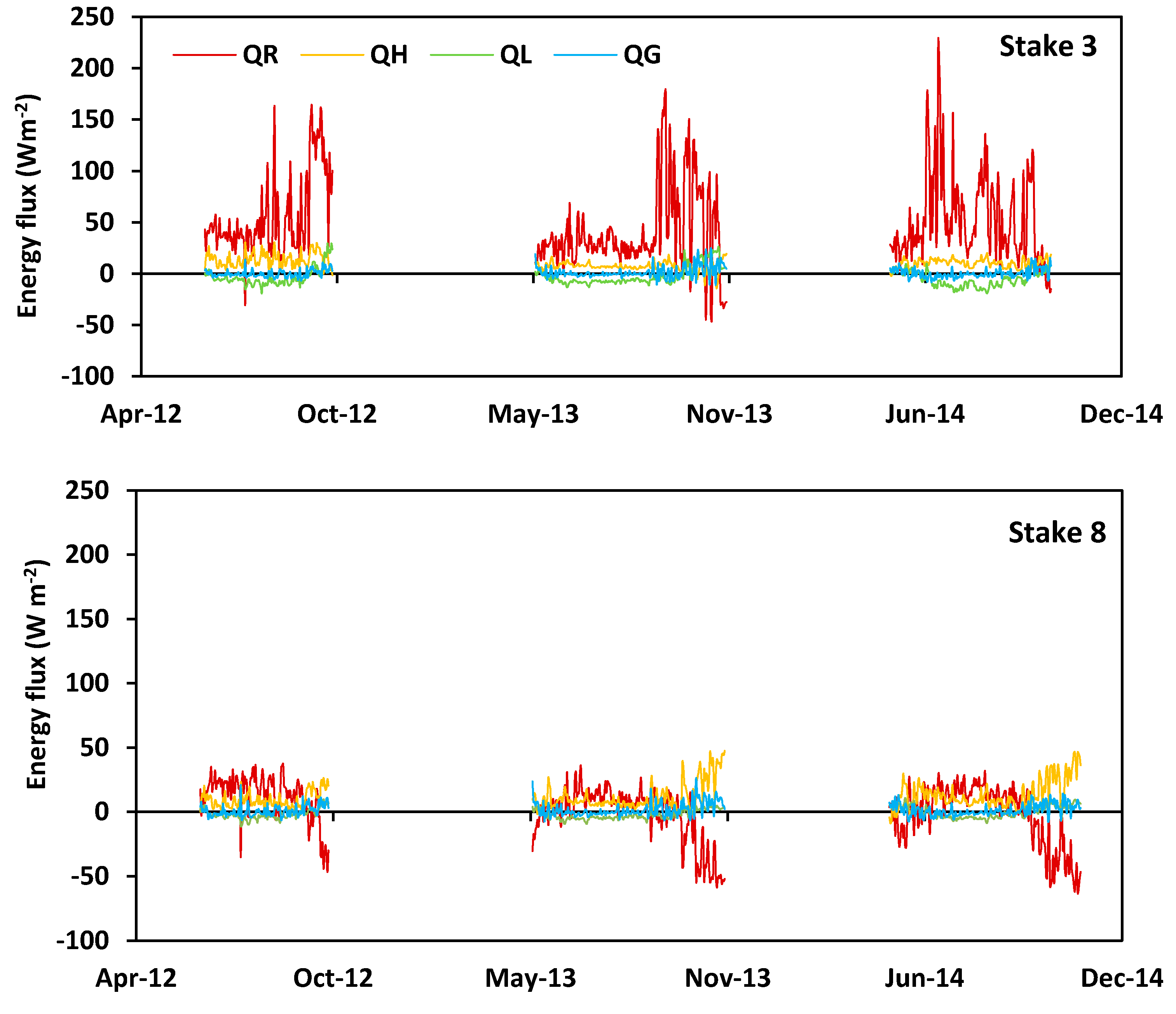
3.3. Calculated (Modelled) Energy and Mass Balance
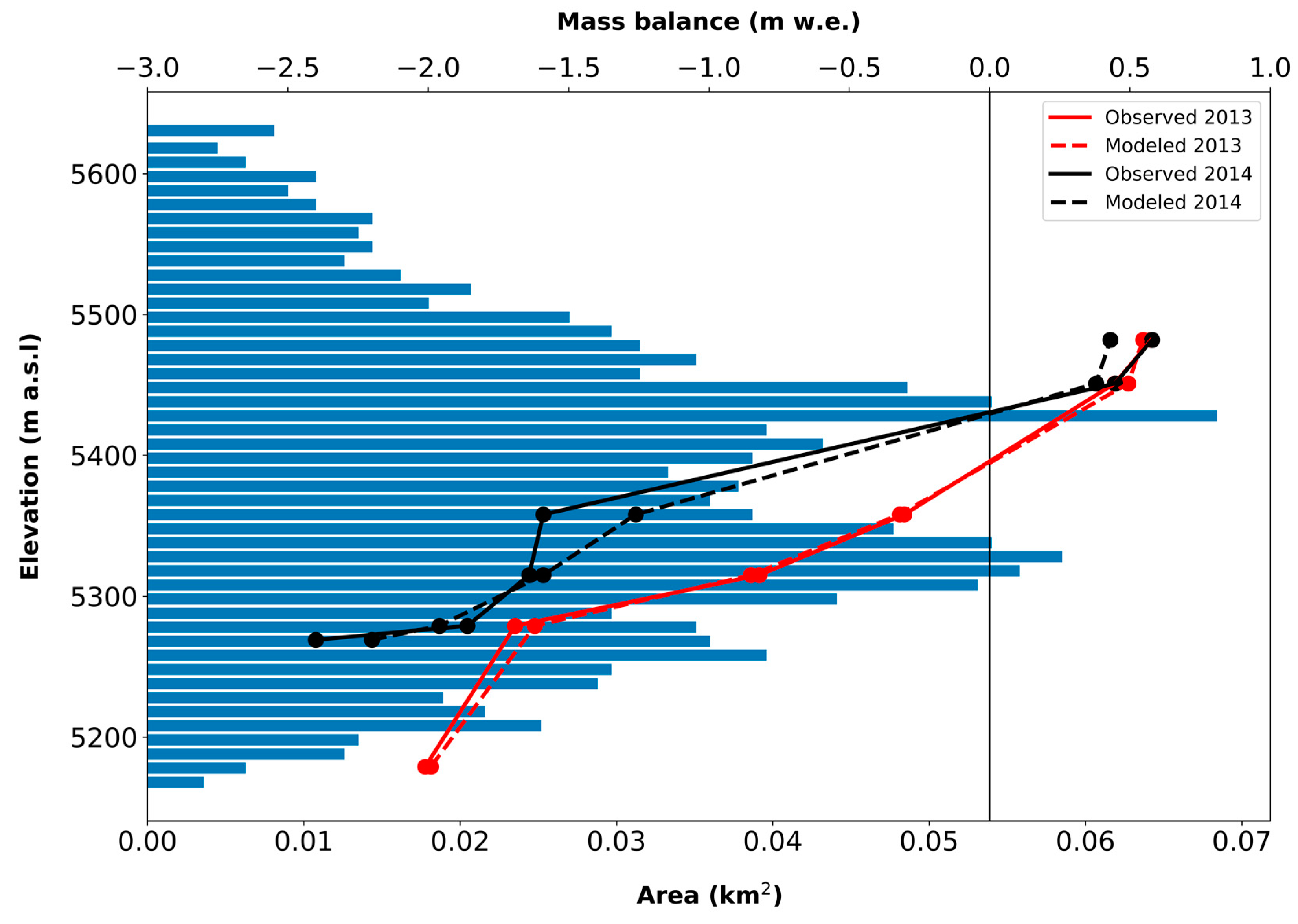
3.4. Glacier-Wide Mass Balance
3.5. Validation of Energy-Mass Balance Model
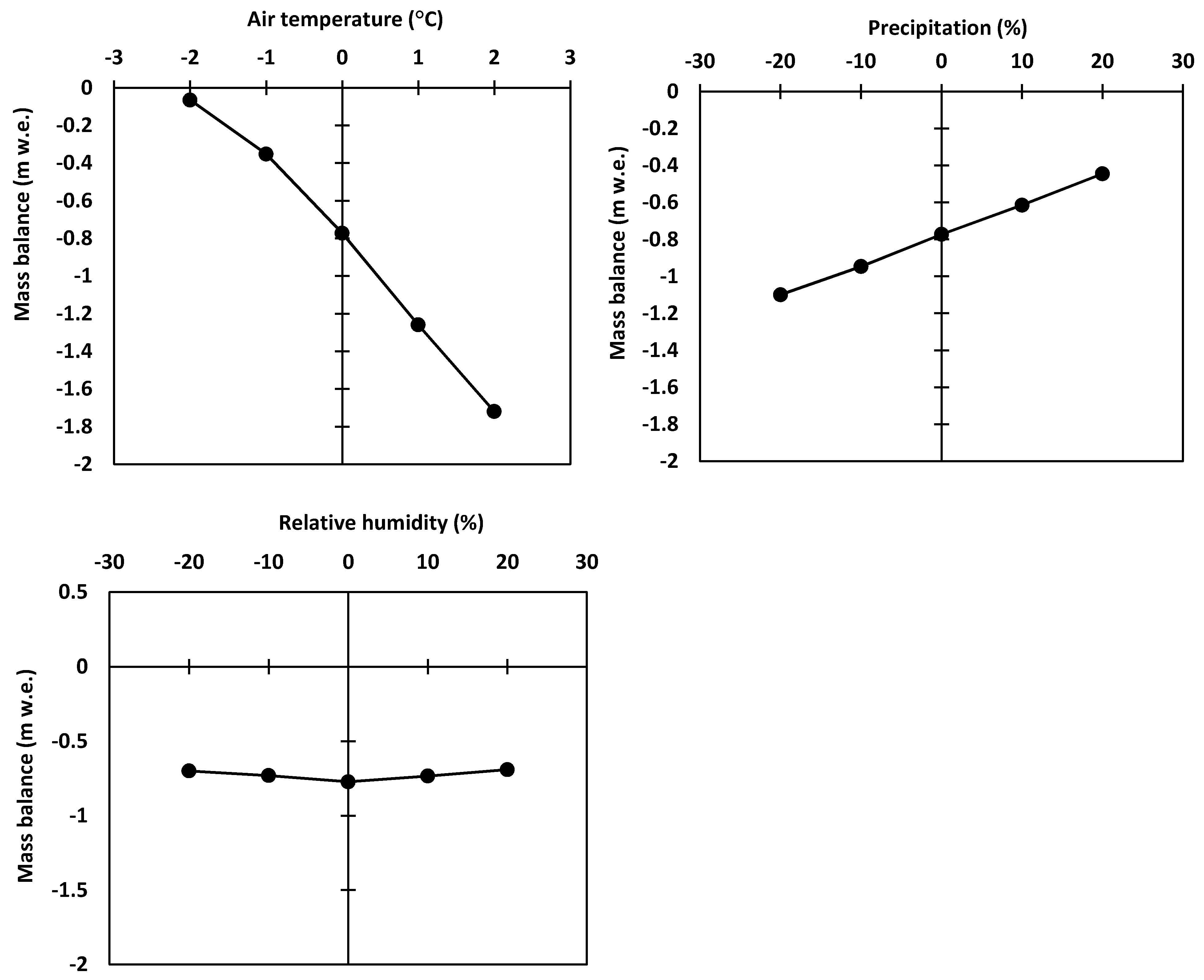
3.6. Sensitivity Analysis
4. Discussion
4.1. Annual and Seasonal Glacier-Wide Mass Balance
4.2. Comparison of Present Mass Balance and Energy Balance Studies with Other Studies in the High Mountain Asia
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Immerzeel, W.W.; Petersen, L.; Ragettli, S.; Pellicciotti, F. The Importance of Observed Gradients of Air Temperature and Precipitation for Modeling Runoff from a Glacierized Watershed in the Nepalese Himalayas. Water Resour. Res. 2014, 50, 2212–2226. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Pellicciotti, F.; Bierkens, M.F.P. Rising River Flows throughout the Twenty-First Century in Two Himalayan Glacierized Watersheds. Nat. Geosci. 2013, 6, 742–745. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Van Beek, L.P.; Bierkens, M.F. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Kaser, G.; Cogley, J.G.; Dyurgerov, M.B.; Meier, M.F.; Ohmura, A. Mass Balance of Glaciers and Ice Caps: Consensus Estimates for 1961–2004. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M. The State and Fate of Himalayan Glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [PubMed]
- Bahadur, J. The Himalayas: A Third Polar Region. In Snow and Glacier Hydrology, Proceedings of the International Symposium, Kathmandu, Nepal, 16–21 November 1992; IAHS Publication: Wallingford, UK, 1993; Volume 218, pp. 181–190. [Google Scholar]
- Wang, X.; Tseng, Z.J.; Li, Q.; Takeuchi, G.T.; Xie, G. From “third Pole”to North Pole: A Himalayan Origin for the Arctic Fox. Proc. R. Soc. B 2014, 281, 20140893. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B. Different Glacier Status with Atmospheric Circulations in Tibetan Plateau and Surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- De Smedt, B.; Pattyn, F. Numerical Modelling of Historical Front Variations and Dynamic Response of Sofiyskiy Glacier, Altai Mountains, Russia. Ann. Glaciol. 2003, 37, 143–149. [Google Scholar] [CrossRef]
- Oerlemans, J. Quantifying Global Warming from the Retreat of Glaciers. Science 1994, 264, 243–245. [Google Scholar] [CrossRef]
- Oerlemans, J. Glaciers as Indicators of a Carbon Dioxide Warming. Nature 1986, 320, 607–609. [Google Scholar] [CrossRef]
- Vincent, C.; Ribstein, P.; Favier, V.; Wagnon, P.; Francou, B.; Le Meur, E.; Six, D. Glacier Fluctuations in the Alps and in the Tropical Andes. C. R. Geosci. 2005, 337, 97–106. [Google Scholar] [CrossRef]
- Bolch, T.; Pieczonka, T.; Benn, D.I. Multi-Decadal Mass Loss of Glaciers in the Everest Area (Nepal Himalaya) Derived from Stereo Imagery. Cryosphere 2011, 5, 349–358. [Google Scholar] [CrossRef]
- Mayewski, P.A.; Jeschke, P.A. Himalayan and Trans-Himalayan Glacier Fluctuations since AD 1812. Arct. Alp. Res. 1979, 11, 267–287. [Google Scholar] [CrossRef]
- Bajracharya, S.R.; Maharjan, S.B.; Shrestha, F.; Guo, W.; Liu, S.; Immerzeel, W.; Shrestha, B. The Glaciers of the Hindu Kush Himalayas: Current Status and Observed Changes from the 1980s to 2010. Int. J. Water Resour. Dev. 2015, 31, 161–173. [Google Scholar] [CrossRef]
- Sherpa, S.F.; Wagnon, P.; Brun, F.; Berthier, E.; Vincent, C.; Lejeune, Y.; Arnaud, Y.; Kayastha, R.B.; Sinisalo, A. Contrasted Surface Mass Balances of Debris-Free Glaciers Observed between the Southern and the Inner Parts of the Everest Region (2007–2015). J. Glaciol. 2017, 63, 637–651. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Slight Mass Gain of Karakoram Glaciers in the Early Twenty-First Century. Nat. Geosci. 2012, 5, 322–325. [Google Scholar] [CrossRef]
- Hewitt, K. The Karakoram Anomaly? Glacier Expansion and the “elevation effect,” Karakoram Himalaya. Mt. Res. Dev. 2005, 25, 332–340. [Google Scholar] [CrossRef]
- Ageta, Y.; Higuchi, K. Estimation of Mass Balance Components of a Summer-Accumulation Type Glacier in the Nepal Himalaya. Geogr. Ann. Ser. Phys. Geogr. 1984, 66, 249–255. [Google Scholar] [CrossRef]
- Quincey, D.J.; Braun, M.; Glasser, N.F.; Bishop, M.P.; Hewitt, K.; Luckman, A. Karakoram Glacier Surge Dynamics. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Fujita, K.; Ageta, Y. Effect of Summer Accumulation on Glacier Mass Balance on the Tibetan Plateau Revealed by Mass-Balance Model. J. Glaciol. 2000, 46, 244–252. [Google Scholar] [CrossRef]
- Kayastha, R.B.; Ohata, T.; Ageta, Y. Application of a Mass-Balance Model to a Himalayan Glacier. J. Glaciol. 1999, 45, 559–567. [Google Scholar] [CrossRef]
- Hock, R. Glacier Melt: A Review of Processes and Their Modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Hock, R. Temperature Index Melt Modelling in Mountain Areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Hock, R. A Distributed Temperature-Index Ice-and Snowmelt Model Including Potential Direct Solar Radiation. J. Glaciol. 1999, 45, 101–111. [Google Scholar] [CrossRef]
- Laumann, T.; Reeh, N. Sensitivity to Climate Change of the Mass Balance of Glaciers in Southern Norway. J. Glaciol. 1993, 39, 656–665. [Google Scholar] [CrossRef]
- Oerlemans, J.; Anderson, B.; Hubbard, A.; Huybrechts, P.; Johannesson, T.; Knap, W.H.; Schmeits, M.; Stroeven, A.P.; Van de Wal, R.S.W.; Wallinga, J. Modelling the Response of Glaciers to Climate Warming. Clim. Dyn. 1998, 14, 267–274. [Google Scholar] [CrossRef]
- Nemec, J.; Huybrechts, P.; Rybak, O.; Oerlemans, J. Reconstruction of the Annual Balance of Vadret Da Morteratsch, Switzerland, since 1865. Ann. Glaciol. 2009, 50, 126–134. [Google Scholar] [CrossRef]
- Zhang, G.; Kang, S.; Fujita, K.; Huintjes, E.; Xu, J.; Yamazaki, T.; Haginoya, S.; Wei, Y.; Scherer, D.; Schneider, C. Energy and Mass Balance of Zhadang Glacier Surface, Central Tibetan Plateau. J. Glaciol. 2013, 59, 137–148. [Google Scholar] [CrossRef]
- Fijita, K.; Takeuchi, N.; Seko, K. Glaciological observations of Yala Glacier in Langtang Valley, Nepal Himalayas, 1994 and 1996. Bull. Glacier Res. 1998, 16, 75–78. [Google Scholar]
- Nuimura, T.; Fujita, K.; Yamaguchi, S.; Sharma, R.R. Elevation Changes of Glaciers Revealed by Multitemporal Digital Elevation Models Calibrated by GPS Survey in the Khumbu Region, Nepal Himalaya, 1992–2008. J. Glaciol. 2012, 58, 648–656. [Google Scholar] [CrossRef]
- Fujii, Y. Field Experiment on Glacier Ablation under a Layer of Debris Cover. J. Jpn. Soc. Snow Ice 1977, 39, 20–21. [Google Scholar] [CrossRef]
- Fujita, K.; Nakawo, M.; Fujii, Y.; Paudyal, P. Changes in Glaciers in Hidden Valley, Mukut Himal, Nepal Himalayas, from 1974 to 1994. J. Glaciol. 1997, 43, 583–588. [Google Scholar] [CrossRef]
- Ageta, Y.; Naito, N.; Nakawo, M.; Fujita, K.; Shankar, K.; Pokhrel, A.P.; Wangda, D. Study Project on the Recent Rapid Shrinkage of Summer-Accumulation Type Glaciers in the Himalayas. Bull. Glaciol. Res. 2001, 18, 45–49. [Google Scholar]
- Fujita, K.; Kadota, T.; Rana, B.; Kayastha, R.B.; Ageta, Y. Shrinkage of Glacier AX010 in Shorong Region, Nepal Himalayas in the 1990s. Bull. Glaciol. Res. 2001, 18, 51–54. [Google Scholar]
- Ageta, Y.; Ohata, T.; Tanaka, Y.; Ikegami, K.; Higuchi, K. Mass Balance of Glacier AX010 in Shorong Himal, East Nepal during the Summer Monsoon Season. J. Jpn. Soc. Snow Ice 1980, 41, 34–41. [Google Scholar] [CrossRef]
- Baral, P.; Kayastha, R.B.; Immerzeel, W.W.; Pradhananga, N.S.; Bhattarai, B.C.; Shahi, S.; Galos, S.; Springer, C.; Joshi, S.P.; Mool, P.K. Preliminary Results of Mass-Balance Observations of Yala Glacier and Analysis of Temperature and Precipitation Gradients in Langtang Valley, Nepal. Ann. Glaciol. 2014, 55, 9–14. [Google Scholar] [CrossRef]
- Wagnon, P.; Vincent, C.; Arnaud, Y.; Berthier, E.; Vuillermoz, E.; Gruber, S.; Ménégoz, M.; Gilbert, A.; Dumont, M.; Shea, J.M. Seasonal and Annual Mass Balances of Mera and Pokalde Glaciers (Nepal Himalaya) since 2007. Cryosphere 2013, 7, 1769–1786. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Stephan, C.; Miles, E.; Herreid, S.; Immerzeel, W.W.; Bolch, T. Mass-Balance Changes of the Debris-Covered Glaciers in the Langtang Himal, Nepal, from 1974 to 1999. J. Glaciol. 2015, 61, 373–386. [Google Scholar] [CrossRef]
- Naito, N.; Kadota, T.; Fujita, K.; Sakai, A.; Nakawo, M. Surface Lowering over the Ablation Area of Lirung Glacier, Nepal Himalayas. Bull. Glaciol. Res. 2002, 19, 41–46. [Google Scholar]
- Chand, M.B.; Kayastha, R.B.; Parajuli, A.; Mool, P.K. Seasonal Variation of Ice Melting on Varying Layers of Debris of Lirung Glacier, Langtang Valley, Nepal. Proc. Int. Assoc. Hydrol. Sci. 2015, 368, 21–26. [Google Scholar] [CrossRef]
- Cogley, J.G. Geodetic and Direct Mass-Balance Measurements: Comparison and Joint Analysis. Ann. Glaciol. 2009, 50, 96–100. [Google Scholar] [CrossRef]
- Wagnon, P.; Linda, A.; Arnaud, Y.; Kumar, R.; Sharma, P.; Vincent, C.; Pottakkal, J.G.; Berthier, E.; Ramanathan, A.; Hasnain, S.I.; et al. Four Years of Mass Balance on Chhota Shigri Glacier, Himachal Pradesh, India, a New Benchmark Glacier in the Western Himalaya. J. Glaciol. 2007, 53, 603–611. [Google Scholar] [CrossRef]
- Fountain, A.G.; Vecchia, A. How Many Stakes Are Required to Measure the Mass Balance of a Glacier? Geogr. Ann. Ser. Phys. Geogr. 1999, 81, 563–573. [Google Scholar] [CrossRef]
- Fujita, K. Effect of Dust Event Timing on Glacier Runoff: Sensitivity Analysis for a Tibetan Glacier. Hydrol. Process. 2007, 21, 2892–2896. [Google Scholar] [CrossRef]
- Van de Wal, R.S.W.; Oerlemans, J.; Van der Hage, J.C. A Study of Ablation Variations on the Tongue of Hintereisferner, Austrian Alps. J. Glaciol. 1992, 38, 319–324. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. Mass Balance Processes: 2. Surface Ablation and Energy Budget. In The Physics of Glaciers, 4th ed.; Butterworth-Heinemann of Elsevier: Oxford, UK, 2010; pp. 137–173. ISBN 978-0-12-369461-4. [Google Scholar]
- Ohata, T.; Ikegami, K.; Higuchi, K. Albedo of Glacier AX 010 during the Summer Season in Shorong Himal, East Nepal. J. Jpn. Soc. Snow Ice 1980, 41, 48–54. [Google Scholar] [CrossRef]
- Van Dusen, M.S. Thermal Conductivity of Non-Metallic Solids. Int. Crit. Tables Numer. Data Phys. Chem. Technol. 1929, 5, 216–217. [Google Scholar]
- Thibert, E.; Blanc, R.; Vincent, C.; Eckert, N. Glaciological and Volumetric Mass-Balance Measurements: Error Analysis over 51 Years for Glacier de Sarennes, French Alps. J. Glaciol. 2008, 54, 522–532. [Google Scholar] [CrossRef]
- Zemp, M.; Hoelzle, M.; Haeberli, W. Six Decades of Glacier Mass-Balance Observations: A Review of the Worldwide Monitoring Network. Ann. Glaciol. 2009, 50, 101–111. [Google Scholar] [CrossRef]
- Racoviteanu, A.E.; Armstrong, R.; Williams, M.W. Evaluation of an Ice Ablation Model to Estimate the Contribution of Melting Glacier Ice to Annual Discharge in the Nepal Himalaya. Water Resour. Res. 2013, 49, 5117–5133. [Google Scholar] [CrossRef]
- Azam, M.F.; Wagnon, P.; Vincent, C.; Ramanathan, A.L.; Favier, V.; Mandal, A.; Pottakkal, J.G. Processes Governing the Mass Balance of Chhota Shigri Glacier (Western Himalaya, India) Assessed by Point-Scale Surface Energy Balance Measurements. Cryosphere 2014, 8, 2195–2217. [Google Scholar] [CrossRef]
- Yang, W.; Guo, X.; Yao, T.; Yang, K.; Zhao, L.; Li, S.; Zhu, M. Summertime Surface Energy Budget and Ablation Modeling in the Ablation Zone of a Maritime Tibetan Glacier. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
| Sensor Type | Variable | Height (m) |
|---|---|---|
| Rotronic Hydroclip SC2 | Air temperature Relative humidity | 2.0 |
| Kipp & Zonen CNR4 | Incoming solar and longwave radiations | 2.0 |
| RM Young 015043 | Wind speed | 2.0 |
| Ott Pluvio 400 | Precipitation | 2.0 |
| Year | 2011–12 | 2012–13 | 2013–14 | 2014–15 | 2015–16 | 2016–17 | Mean | SD |
|---|---|---|---|---|---|---|---|---|
| Winter (m w.e.) | - | 0.01 | 0.21 | 0.22 | 0.2 | 0.24 | 0.18 | 0.09 |
| Summer (m w.e.) | - | −0.32 | −0.8 | −0.91 | −0.91 | −1.97 | −0.98 | 0.60 |
| Ba (m w.e.) | −0.85 | −0.31 | −0.59 | −0.69 | −0.71 | −1.73 | −0.81 | 0.48 |
| ELA (m) | 5441 | 5412 | 5417 | 5463 | 5451 | 5555 | 5457 | 52.07 |
| db/dz (m w.e. (100 m)−1) | 1.33 | 0.86 | 1.4 | 1.06 | 0.87 | 0.96 | 1.08 | 0.23 |
| AAR | 0.27 | 0.42 | 0.38 | 0.31 | 0.23 | 0.06 | 0.28 | 0.13 |
| Stake | QR (%) | QH (%) | QG (%) | QM (MJ m−2) |
|---|---|---|---|---|
| 2 (5260) | 65.65 | 34.25 | 0.10 | 991 |
| 3 (5279) | 64.48 | 34.96 | 0.56 | 922 |
| 4 (5315) | 62.90 | 36.29 | 0.80 | 819 |
| 5 (5358) | 61.15 | 37.65 | 1.20 | 727 |
| 7 (5450) | - | 90.77 | 9.23 | 218 |
| 8 (5482) | - | 90.35 | 9.65 | 215 |
| Season | Summer 2012 | Summer 2013 | Summer 2014 | |||
|---|---|---|---|---|---|---|
| Observed (m w.e.) | Modelled (m w.e.) | Observed (m w.e.) | Modelled (m w.e.) | Observed (m w.e.) | Modelled (m w.e.) | |
| Glacier wide mass balance (m w.e.) | - | −0.55 | −0.32 | −0.31 | −0.80 | −0.77 |
| ELA (m a.s.l.) | - | 5449 | 5412 | 5411 | 5438 | 5440 |
| Elevation (m a.s.l.) | Summer 2013 | Summer 2014 | ||
|---|---|---|---|---|
| Observed (m w.e.) | Modelled (m w.e.) | Observed (m w.e.) | Modelled (m w.e.) | |
| 5179 (Stake 1) | −2.01 | −1.99 | - | - |
| 5260 (Stake 2) | - | - | −2.4 | −2.2 |
| 5279 (Stake 3) | −1.69 | −1.62 | −1.86 | −1.96 |
| 5315 (Stake 4) | −0.82 | −0.85 | −1.64 | −1.59 |
| 5458 (Stake 5) | −0.304 | −0.32 | −1.59 | −1.26 |
| 5451 (Stake 7) | 0.446 | 0.494 | 0.447 | 0.38 |
| 5482 (Stake 8) | 0.576 | 0.547 | 0.579 | 0.43 |
| Input Parameters/Processes | Reference Case Mass Balance (m w.e.) 0.54 |
|---|---|
| Surface Parameters | Difference from reference case |
| Snow density increased by 50 kg m−3 | −15.4% |
| Ice density increased by 10 kg m−3 | −1.1% |
| Snow albedo increased by 0.1 | −18.3% |
| Ice albedo increased by 0.1 | −2.9% |
| All roughness length increased by 25% | +3.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acharya, A.; Kayastha, R.B. Mass and Energy Balance Estimation of Yala Glacier (2011–2017), Langtang Valley, Nepal. Water 2019, 11, 6. https://doi.org/10.3390/w11010006
Acharya A, Kayastha RB. Mass and Energy Balance Estimation of Yala Glacier (2011–2017), Langtang Valley, Nepal. Water. 2019; 11(1):6. https://doi.org/10.3390/w11010006
Chicago/Turabian StyleAcharya, Anushilan, and Rijan Bhakta Kayastha. 2019. "Mass and Energy Balance Estimation of Yala Glacier (2011–2017), Langtang Valley, Nepal" Water 11, no. 1: 6. https://doi.org/10.3390/w11010006
APA StyleAcharya, A., & Kayastha, R. B. (2019). Mass and Energy Balance Estimation of Yala Glacier (2011–2017), Langtang Valley, Nepal. Water, 11(1), 6. https://doi.org/10.3390/w11010006





