Fuzzy Solution to the Unconfined Aquifer Problem
Abstract
1. Introduction
2. Materials and Methods
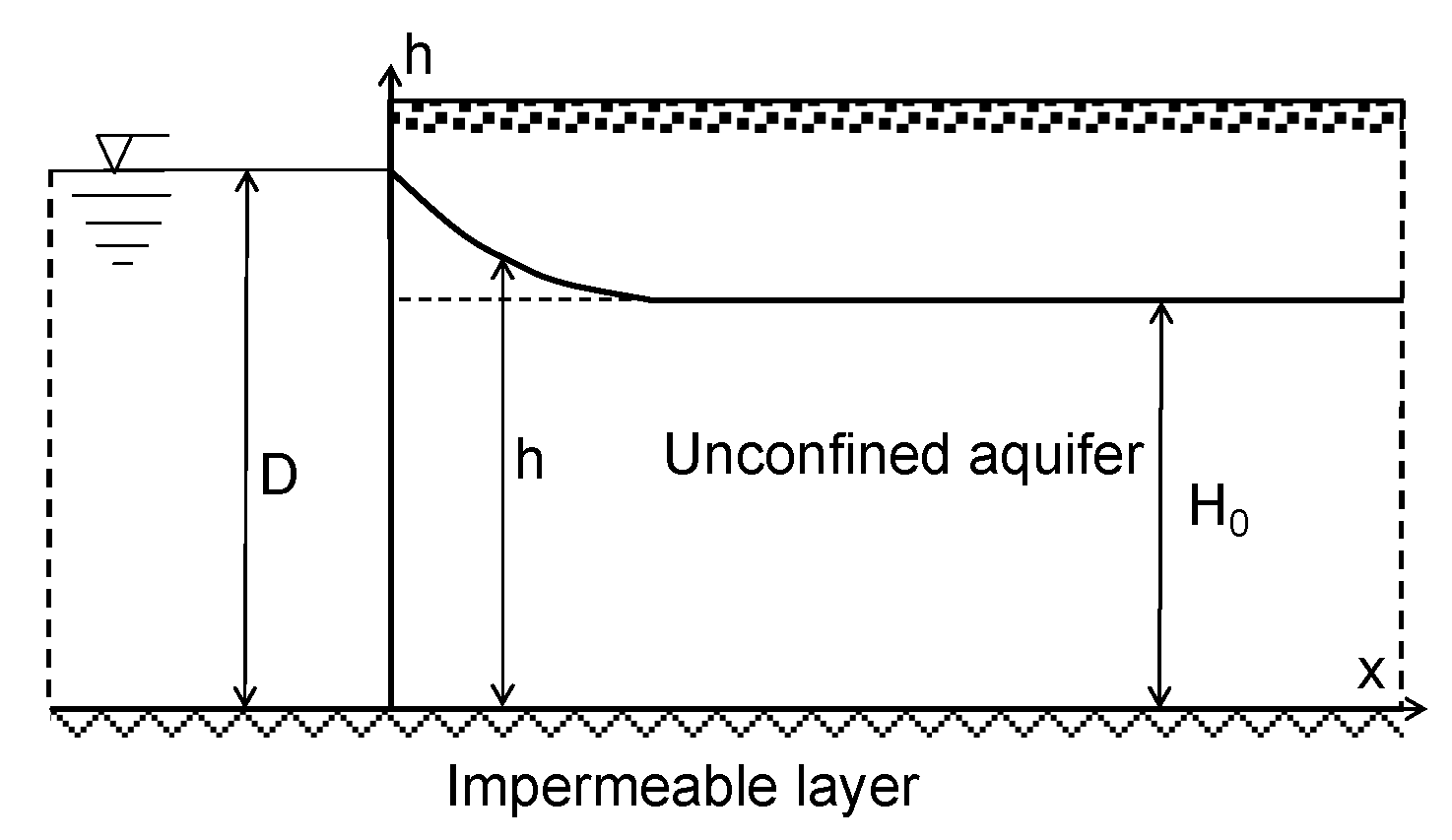
2.1. Physical Problems
Aquifer Recharging from the Lake
Crisp Case
Fuzzy Case
2.2. Mathematical Model
2.2.1. Definitions
2.2.2. Transform of the Fuzzy Problem
Systems of Crisp Problems
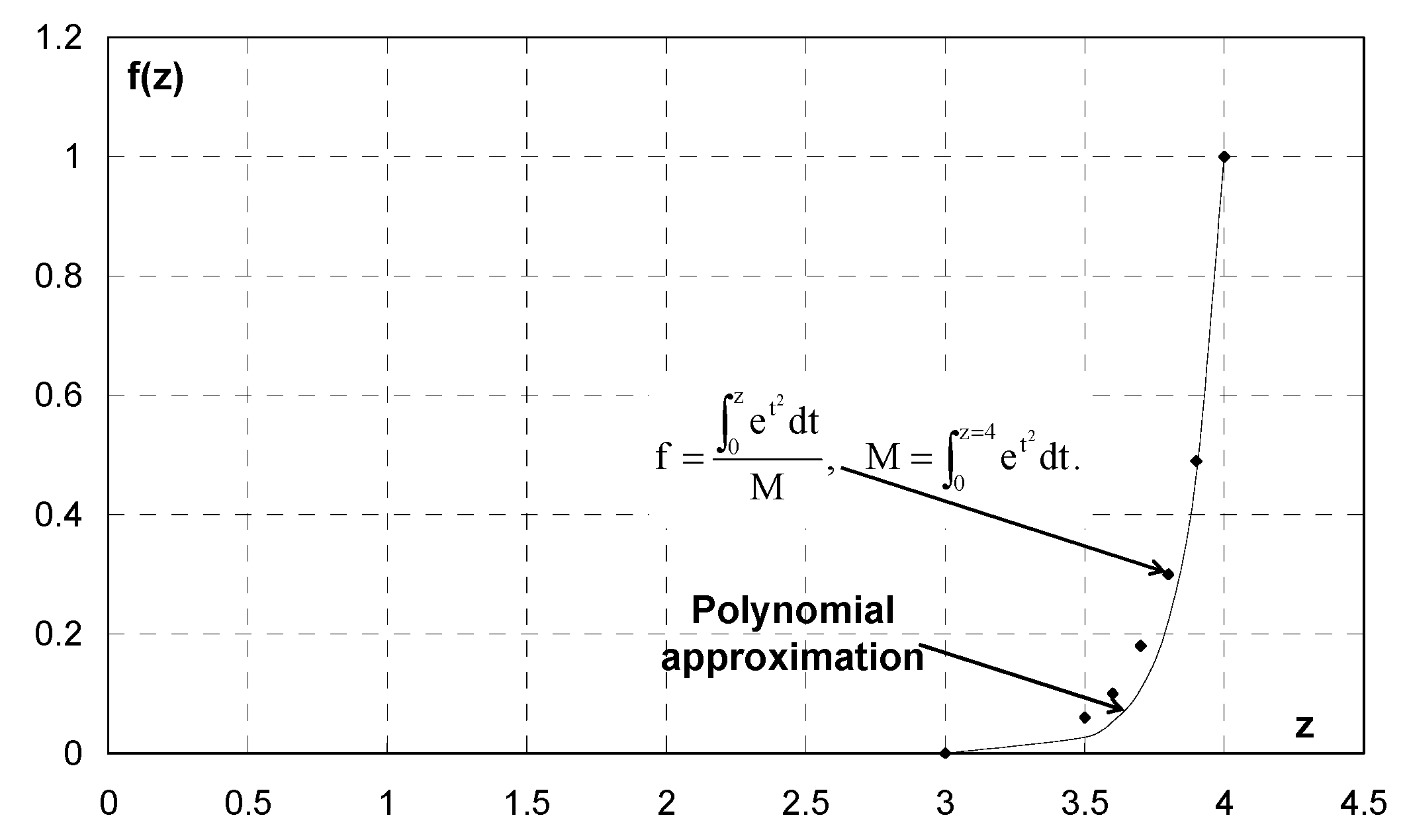
2.2.3. Solution of the (1.1)-System
First Equation of (1.1)
Second Equation of (1.1)
2.2.4. Solution of the (1.2)-System
Solution
2.2.5. Solution of the (2.1)-System
2.2.6. Solution of the (2.2)-System
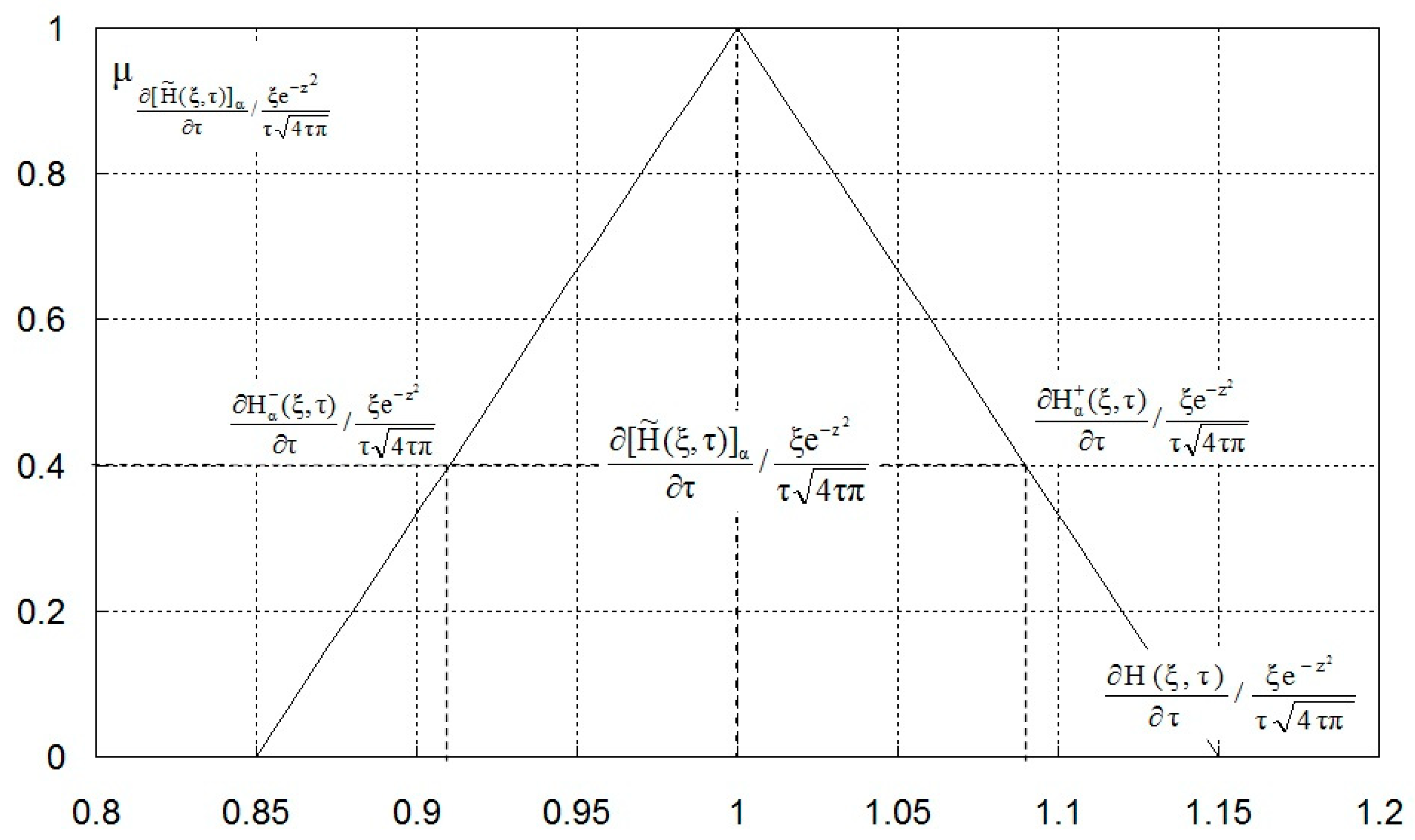
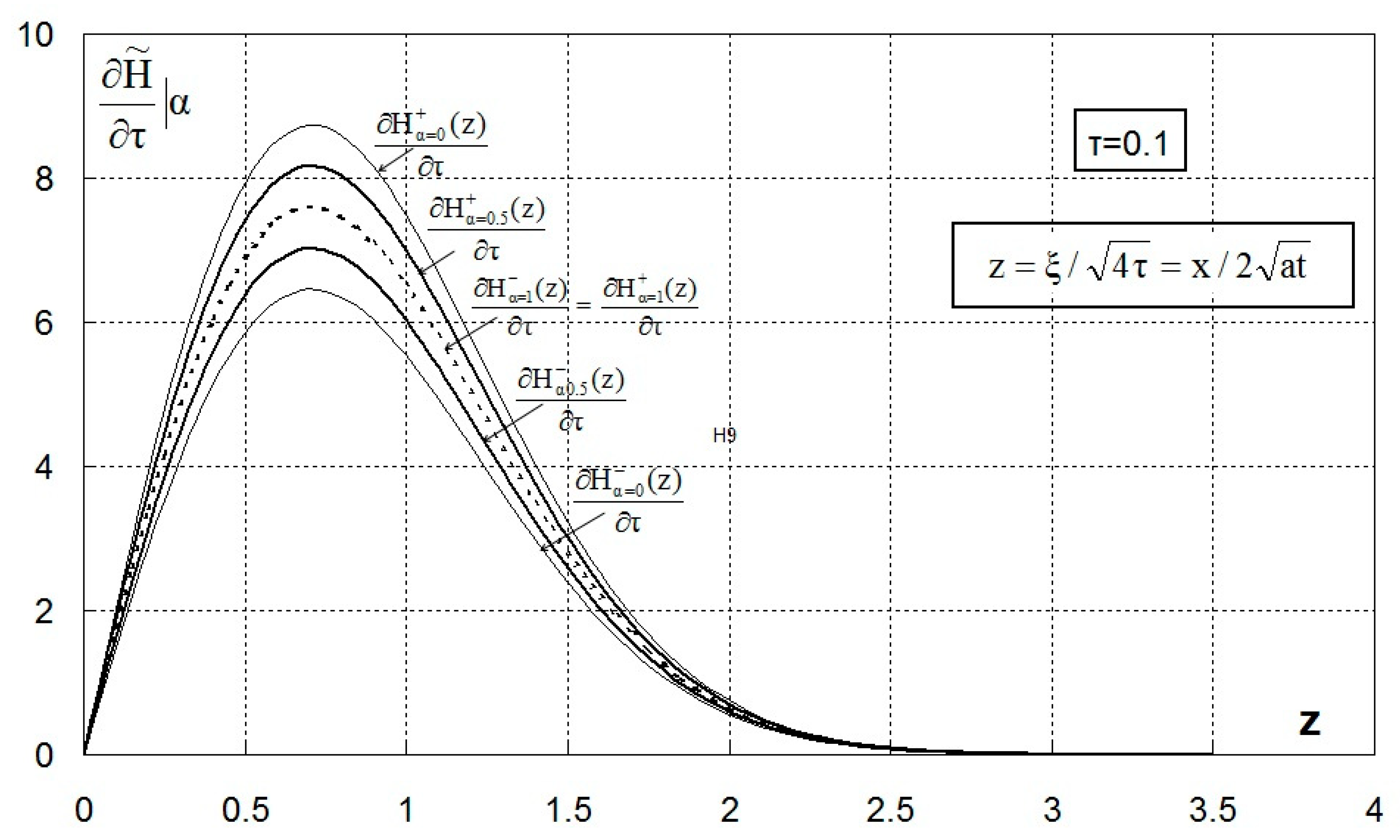
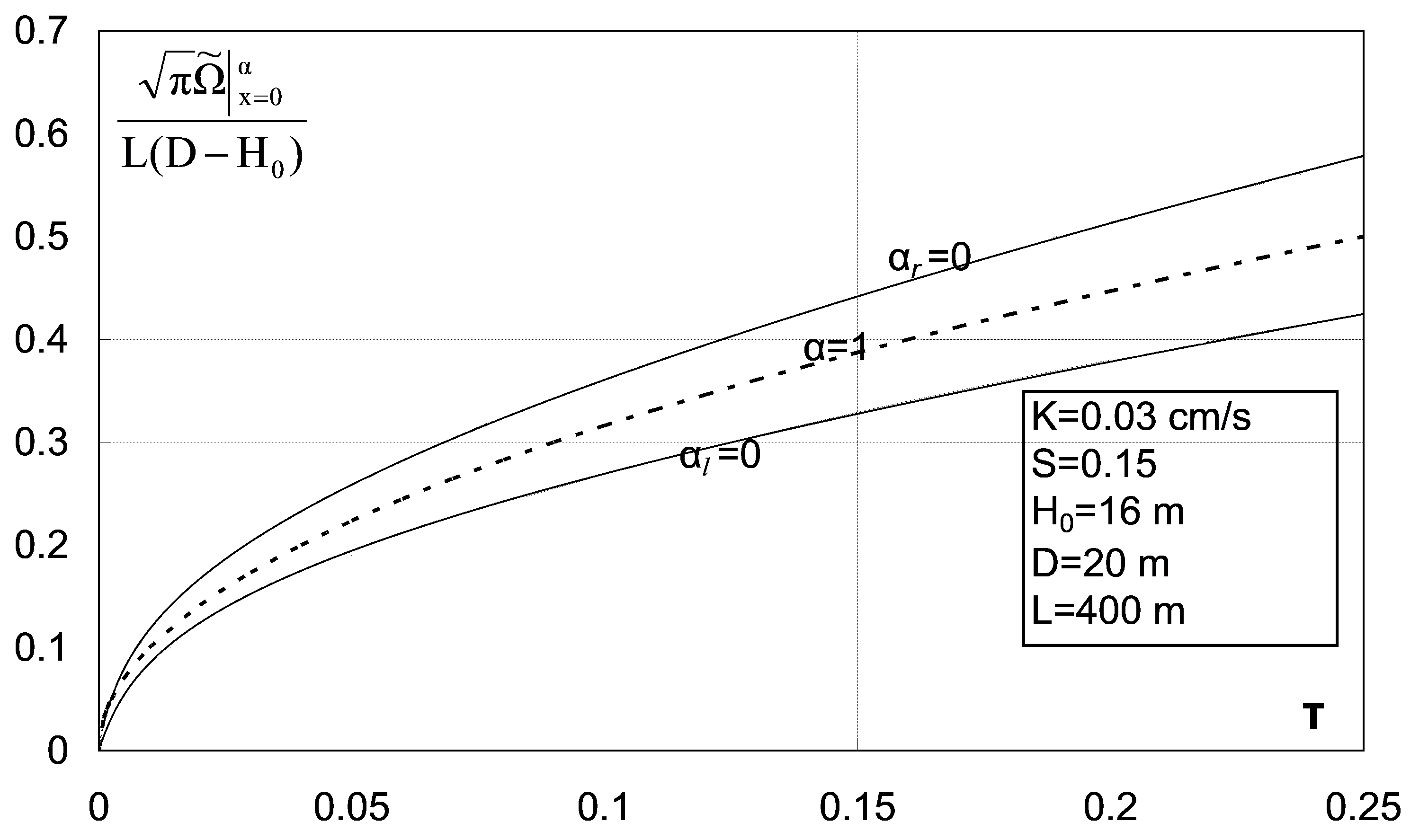
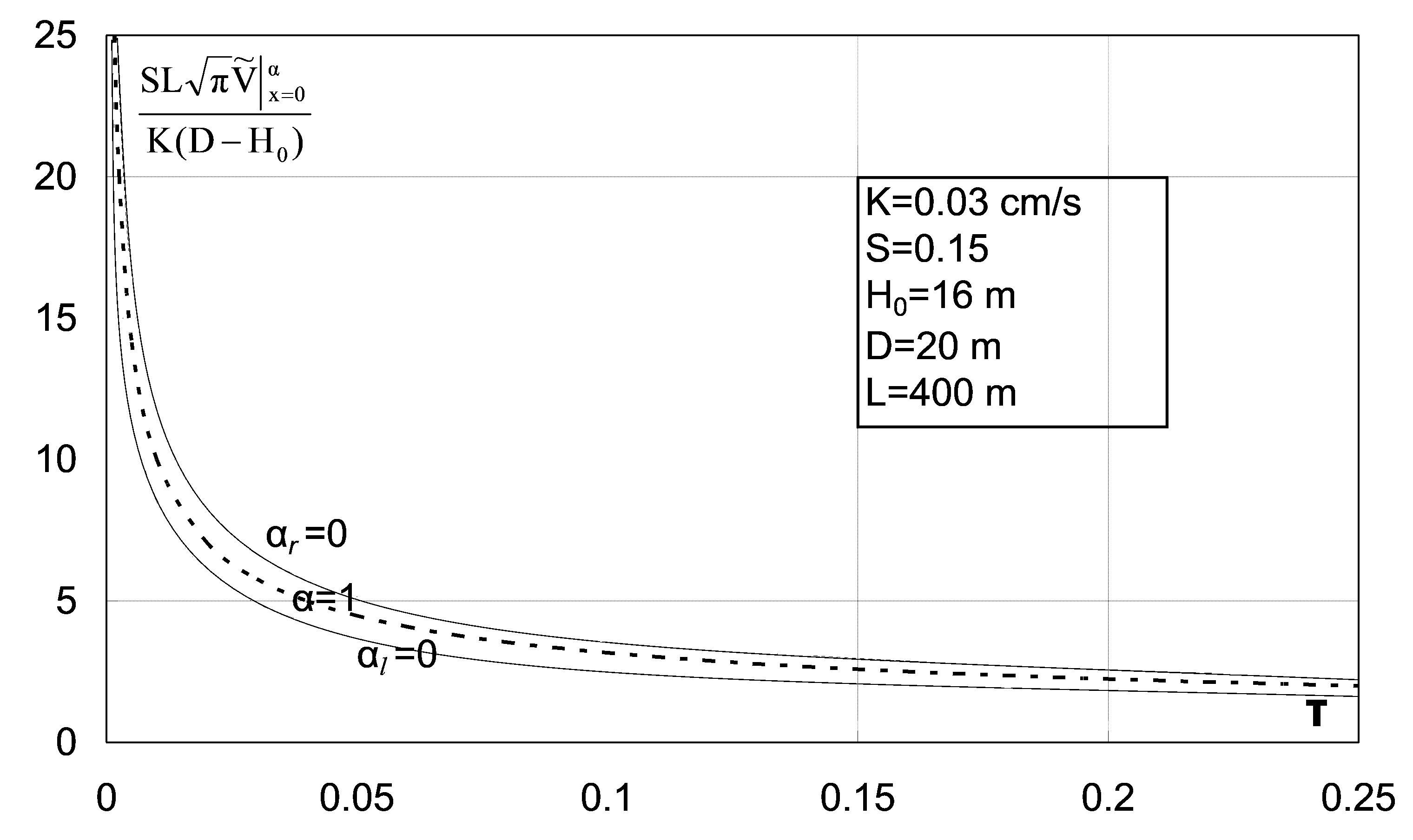
2.2.7. Darcy Velocity, Water Flow Recharging Volume
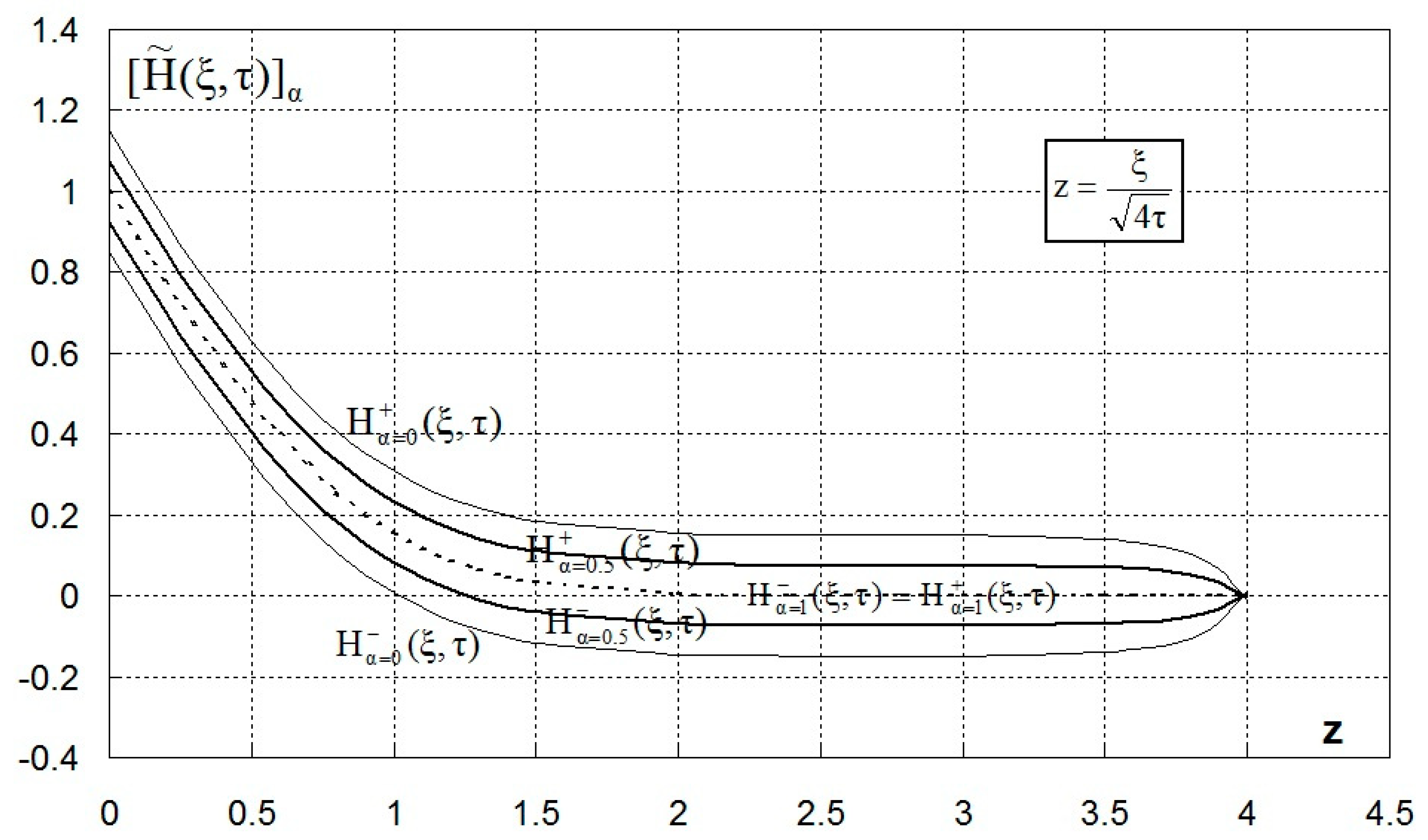
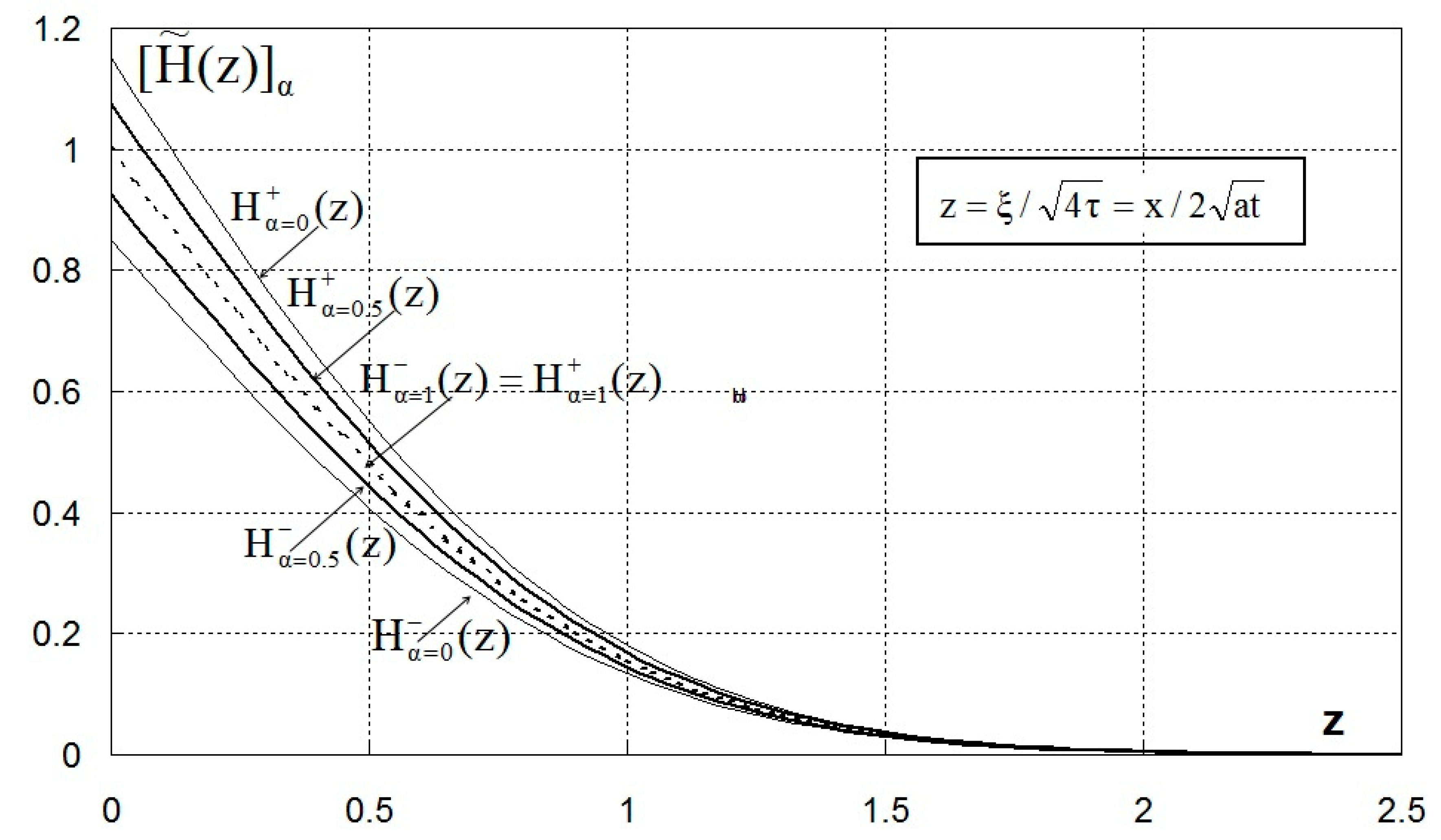
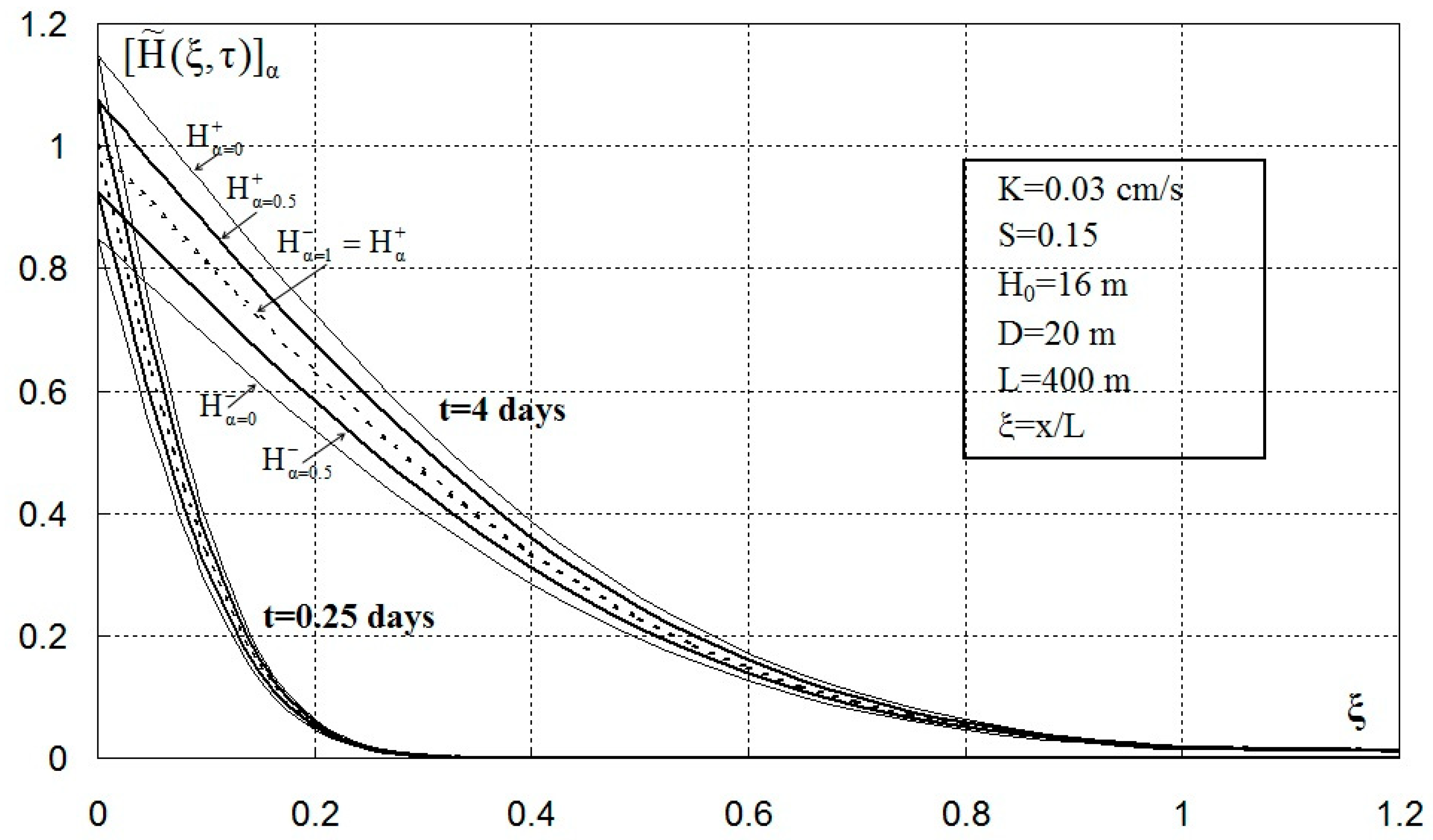
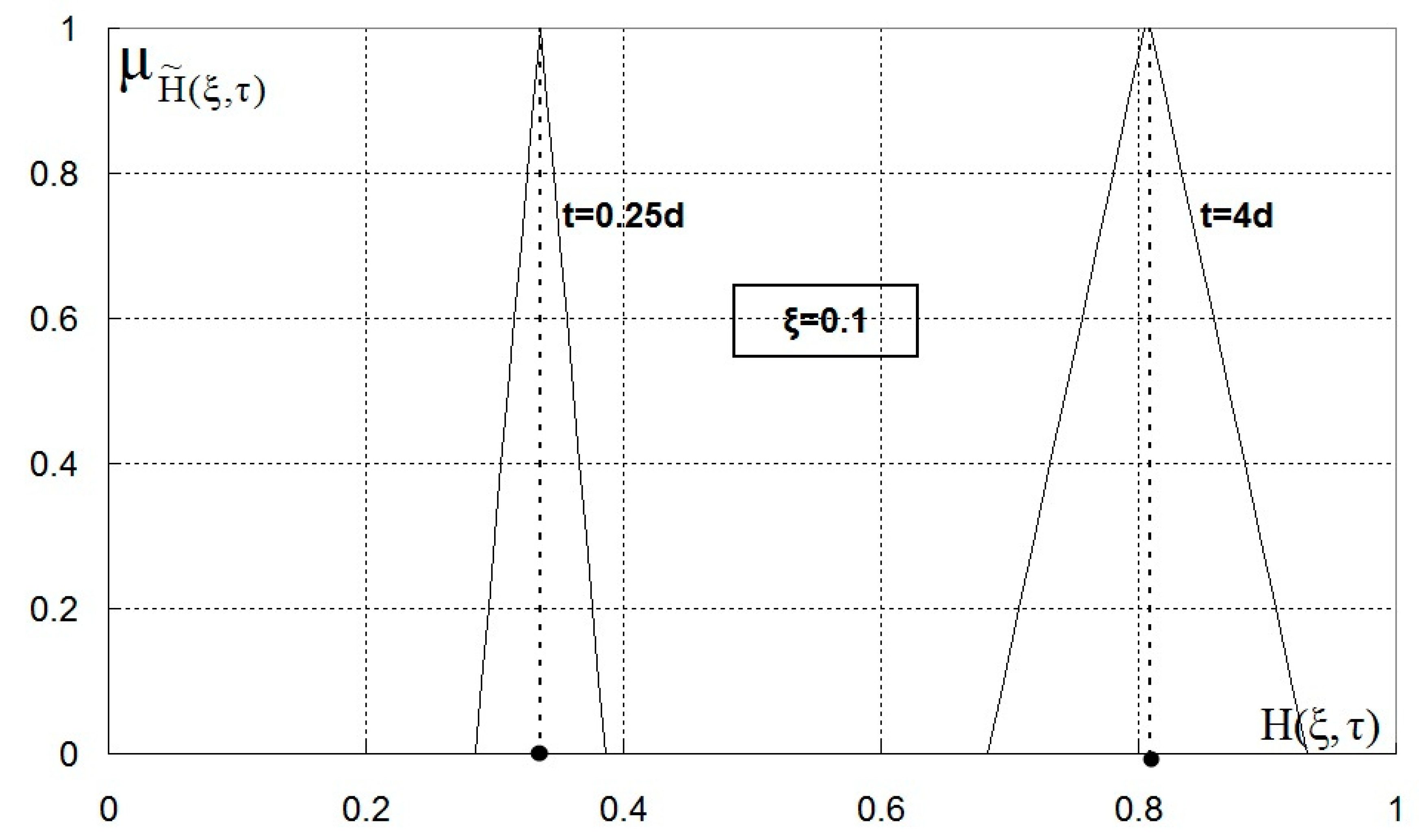
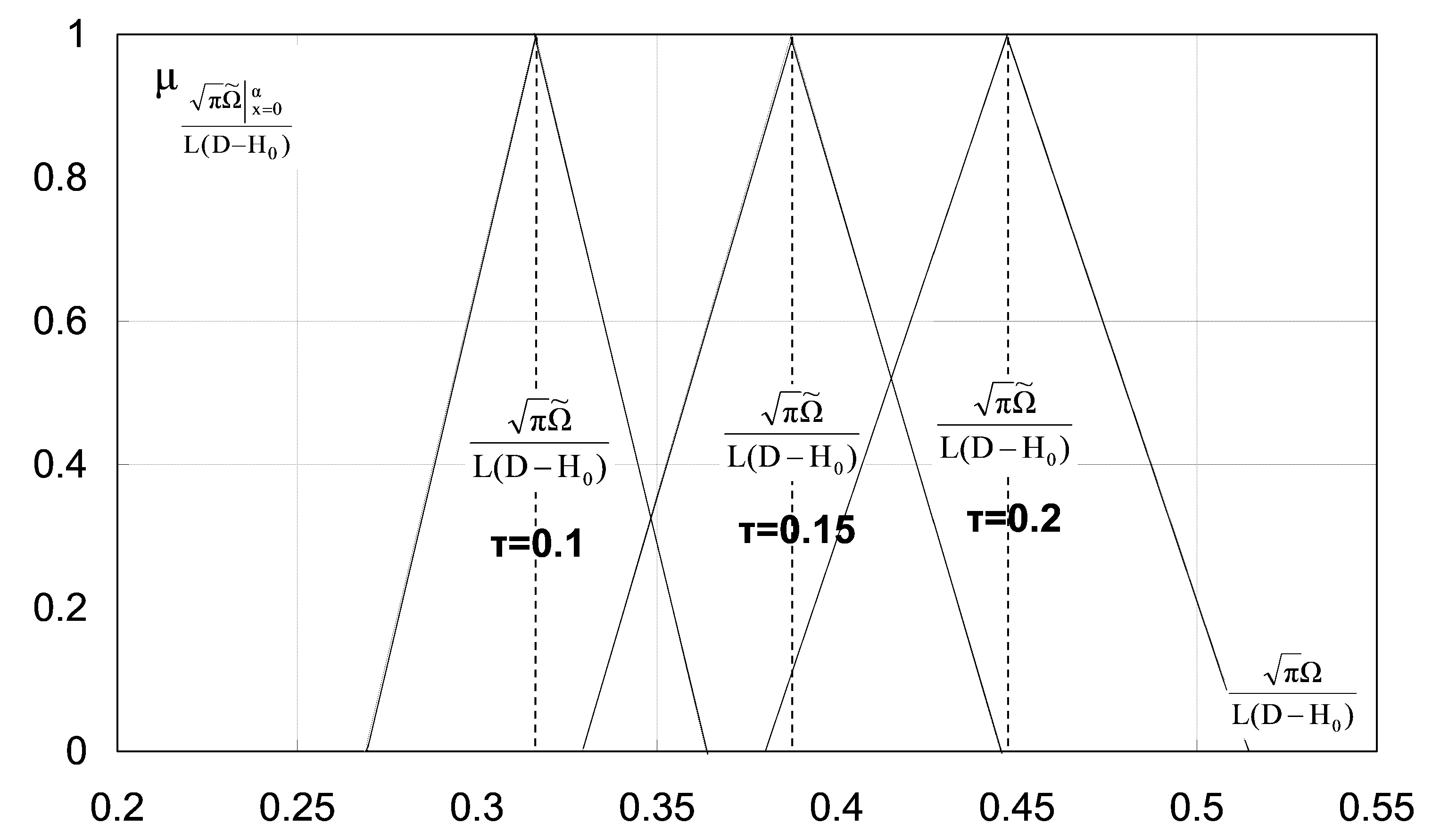
3. Results and Discussion
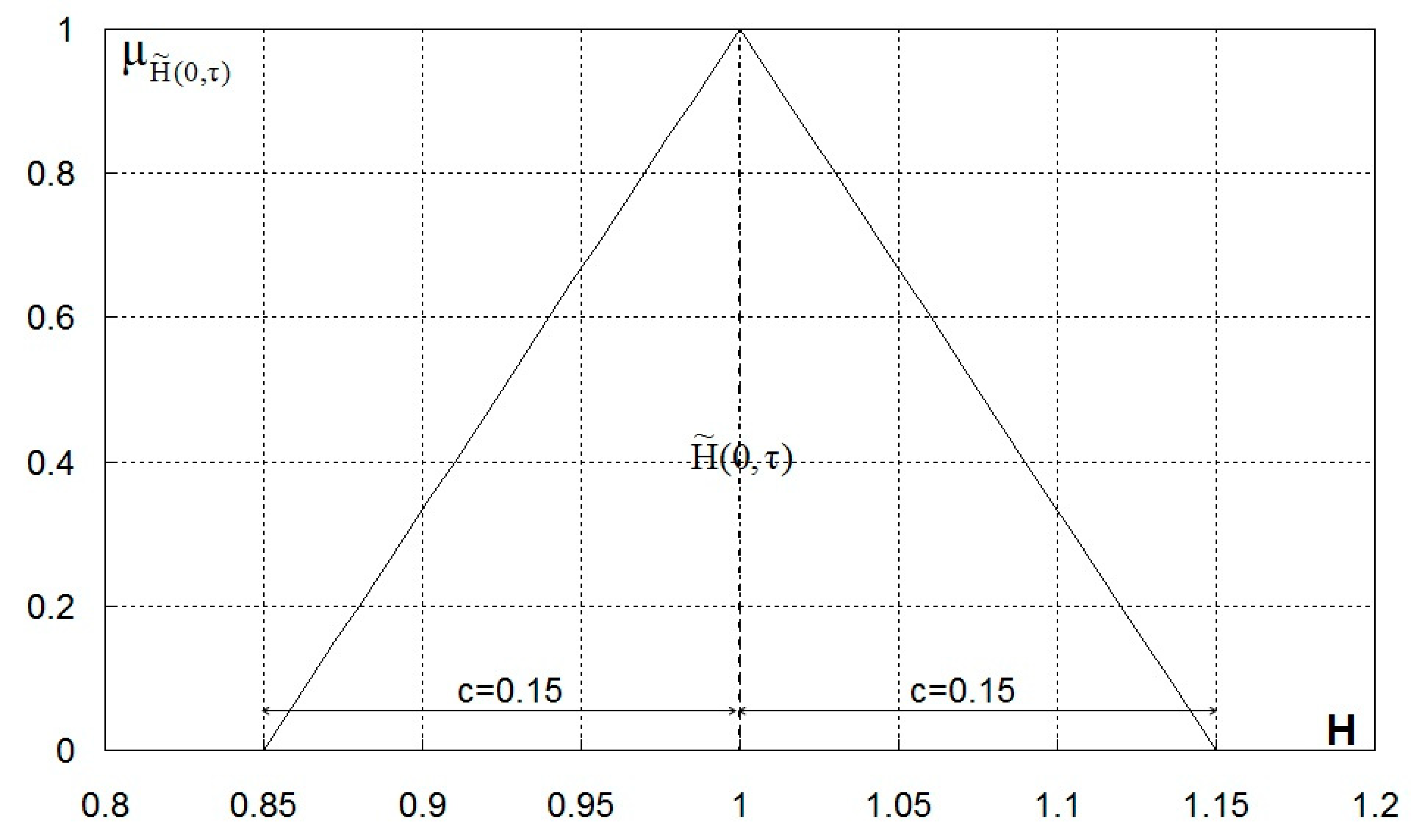
3.1. Parameters of the Problem
- t1 = 4.63 d( = 485,281 m3 ± 85,638 m3),
- t2 = 6.94 d( = 594346 m3 ± 104,884 m3),
- t3 = 9.26 d ( = 682,292 m3 ± 121,110 m3).
3.2. Remark
3.2.1. Trapezoidal Membership Function
3.2.2. Gaussian Membership Function
3.3. Remark Concerning the Uncertainties of the Parameters
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Boussinesq, J. Recherches théoriques sur l’écoulement des nappes d’eau infiltrées dans le sol et sur le débit des sources. J. Math. Pures Appl. 1904, 10, 5–78. [Google Scholar]
- Polubarinova-Cochina, P.Y. On unsteady motions of groundwater during seepage from water reservoirs. P.M.M. (Prinkladaya Matematica I Mekhanica) 1949, 13, 2. [Google Scholar]
- Werner, P.W. On non-artesian groundwater flow. Geofis. Pura Appl. 1953, 25, 37–43. [Google Scholar] [CrossRef]
- Dumm, L.D. New formula for determining depth and spacing of subsurface drains in irrigated lands. Agric. Eng. 1954, 35, 726–730. [Google Scholar]
- Dumm, L.D. Validity and use of the transient flow concept in subsurface drainage. Paper No 60-717 Presented at Asae Meeting, Memphis, TN, USA, 4–7 December 1960; pp. 4–7. [Google Scholar]
- Maasland, M. Water Table Fluctuations Induced by Intermittent Recharge. J. Geophys. Res. 1959, 64, 549–559. [Google Scholar] [CrossRef]
- Van Schilfgaarde, J.; Kirkham, D.; Frevert, R.K. Physical and Mathematical Theories Of Tile and Ditch Drainage And Their Usefulness in Design. In Research Bulletin 436; Agricultural Experiment Station, Iowa State College: Ames, IA, USA, 1956. [Google Scholar]
- Polubarinova-Cochina, P.Y. On a non-linear differential equation occurring in seepage theory. DAN 1948, 36, 82. [Google Scholar]
- Polubarinova-Cochina, P.Y. Theory of Groundwater Movement, 2015th ed.; Princeton University Press: Princeton, NJ, USA, 2015; p. 613. [Google Scholar]
- Aravin, V.I.; Numerov, S.N. Theory of Fluid Flow in Deformable Porous Media; Israel Program for Scientific Translation: Jerusalem, Israel, 1965; p. 511. [Google Scholar]
- Glover, R.E. Transient Groundwater Hydraulics, 2nd ed.; Water Resources Publications LLC: Fordt Collins, CO, USA, 1978; p. 413. [Google Scholar]
- Hálek, V.; Švek, J. Ground Water Hydraulics, 1979th ed.; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands; Oxford, UK, 1979; p. 620. [Google Scholar]
- De Ridder, N.A.; Zijlstra, G. Seepage and Groundwater Flow. In Drainage Principles and Applications, 2nd ed.; Ritzema, H.P., Ed.; ILRI Publication 16: Wageningen, The Netherlands, 1994; pp. 305–340. [Google Scholar]
- Serrano, S.E.; Workman, S.R.; Srivastava, K.; Miller-Van Cleave, B. Models of nonlinear stream aquifer transients. J. Hydrol. 2007, 336, 199–205. [Google Scholar] [CrossRef]
- Parlange, J.-Y.; Hogarth, W.L.; Govindaraju, R.S.; Parlange, M.B.; Lockington, D. On an Exact Analytical Solution of the Boussinesq Equation. Transp. Porous Media 2000, 39, 339–345. [Google Scholar] [CrossRef]
- Srivastava, K.; Serrano, S.E.; Workman, S.R. Stochastic modelling of transient stream–aquifer interaction with the nonlinear Boussinesq equation. J. Hydrol. 2006, 328, 538–547. [Google Scholar] [CrossRef]
- Serrano, S.; Workman, S.R. Modeling transient stream/aquifer interaction with the non-linear Boussinesq equation and its analytical solution. J. Hydrol. 1998, 206, 245–255. [Google Scholar] [CrossRef]
- Aminikhah, H. Approximate analytical solution for the one-dimensional nonlinear Boussinesq equation. Int. J. Numer. Method Heat 2015, 25, 831–840. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Bhaskar, T.; Lakshmikantham, V.; Devi, V. Revisiting fuzzy differential equations. Nonlinear Anal. 2004, 58, 351–358. [Google Scholar] [CrossRef]
- Kaleva, O. A note on fuzzy differential equations. Nonlinear Anal. 2006, 64, 895–900. [Google Scholar] [CrossRef]
- Nieto, J.J.; Rodríguez-López, R. Bounded solutions for fuzzy differential and integral equations. Chaos Solitons Fractals 2006, 27, 1376–1386. [Google Scholar] [CrossRef]
- Guo, M.; Xue, X.; Li, R. The oscillation of delay differential inclusion and fuzzy biodynamics models. Math. Comput. Model. 2003, 37, 651–658. [Google Scholar] [CrossRef]
- Guo, M.; Xue, X.; Li, R. Impulsive functional differential inclusion and fuzzy population models. Fuzzy Sets Syst. 2003, 138, 601–615. [Google Scholar] [CrossRef]
- Puri, M.L.; Ralescu, D.A. Differentials of Fuzzy Functions. J. Math. Anal. Appl. 1983, 91, 552–558. [Google Scholar] [CrossRef]
- Hukuhara, M. Intégration des Applications Mesurables dont la Valeur est un Compact Convexe. Funkc. Ekvacioj 1967, 10, 205–233. [Google Scholar]
- Kaleva, O. Fuzzy differential equations. Fuzzy Sets Syst. 1987, 24, 301–317. [Google Scholar] [CrossRef]
- Seikkala, S. On the fuzzy initial problem. Fuzzy Sets Syst. 1987, 24, 319–330. [Google Scholar] [CrossRef]
- Vorobiev, D.; Seikkala, S. Towards the theory of fuzzy differential equations. Fuzzy Sets Syst. 2002, 125, 231–237. [Google Scholar] [CrossRef]
- O’Regan, D.; Lakshmikantham, V.; Nieto, J.J. Initial and boundary value problem for fuzzy differential equations. Nonlinear Anal. 2003, 54, 405–415. [Google Scholar] [CrossRef]
- Diamond, P. Brief note on the variation of constants formula for fuzzy differential equations. Fuzzy Sets Syst. 2002, 129, 65–71. [Google Scholar] [CrossRef]
- Bede, B.; Gal, S.G. Generalizations of the differentiability of fuzzy-number-valued functions with applications to fuzzy differential equations. Fuzzy Sets Syst. 2005, 151, 581–599. [Google Scholar] [CrossRef]
- Bede, B. A note on two-point boundary value problems associated with non-linear fuzzy differential equations. Fuzzy Sets Syst. 2006, 157, 986–989. [Google Scholar] [CrossRef]
- Stefanini, L. A generalization of Hukuhara difference and division for interval and fuzzy Arithmetic. Fuzzy Sets Syst. 2010, 161, 1564–1584. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Gouyandeh, Z.; Armand, A.; Hasanoglu, A. On fuzzy solutions for heat equation based on generalized Hukuhara differentiability. Fuzzy Sets Syst. 2015, 265, 1–23. [Google Scholar] [CrossRef]
- Negoita, C.V.; Ralescu, D.A. Representation theorems for fuzzy concepts. Kybernetes 1975, 4, 169–174. [Google Scholar] [CrossRef]
- Goetschel, R.; Voxman, W. Elementary fuzzy calculus. Fuzzy Sets Syst. 1986, 18, 31–43. [Google Scholar] [CrossRef]
- Bede, B.; Stefanini, L. Generalized differentiability of fuzzy-valued functions. Fuzzy Sets Syst. 2013, 230, 119–141. [Google Scholar] [CrossRef]
- Khastan, A.; Nieto, J.J. A boundary value problem for second order fuzzy differential equations. Nonlinear Anal. 2010, 72, 3583–3593. [Google Scholar] [CrossRef]
- Mondal, S.P.; Roy, T.K. Solution of second order linear differential equation in fuzzy Environment. Ann. Fuzzy Math. Inform. 2015, x, 1–25. [Google Scholar]
- Bede, B.; Stefanini, L. Solution of Fuzzy Differential Equations with generalized differentiability using LU-parametric representation. In Proceedings of the 7th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT-11), Advances in Intelligent Systems Research, Aix-les-Bains, France, 18–22 July 2011; pp. 785–790. [Google Scholar] [CrossRef]
- Meyer zur Capellen, W. Integraltafeln: Sammlung unbestimmter Integrale elementarer Funktionen, 1950th ed.; Springer: Aachen, Germany, 1950; p. 292. [Google Scholar]
- Hanss, M.; Willner, K. On Using Fuzzy Arithmetic to Solve Problems with Uncertain Model Parameters. Int. J. Proj. Manag. 2000, 20, 1–8. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzimopoulos, C.; Papadopoulos, K.; Evangelides, C.; Papadopoulos, B. Fuzzy Solution to the Unconfined Aquifer Problem. Water 2019, 11, 54. https://doi.org/10.3390/w11010054
Tzimopoulos C, Papadopoulos K, Evangelides C, Papadopoulos B. Fuzzy Solution to the Unconfined Aquifer Problem. Water. 2019; 11(1):54. https://doi.org/10.3390/w11010054
Chicago/Turabian StyleTzimopoulos, Christos, Kyriakos Papadopoulos, Christos Evangelides, and Basil Papadopoulos. 2019. "Fuzzy Solution to the Unconfined Aquifer Problem" Water 11, no. 1: 54. https://doi.org/10.3390/w11010054
APA StyleTzimopoulos, C., Papadopoulos, K., Evangelides, C., & Papadopoulos, B. (2019). Fuzzy Solution to the Unconfined Aquifer Problem. Water, 11(1), 54. https://doi.org/10.3390/w11010054






