Classification of Stable Isotopes and Identification of Water Replenishment in the Naqu River Basin, Qinghai-Tibet Plateau
Abstract
1. Introduction
2. Description of the Study Area
3. Materials and Methods
3.1. Sampling and Analytical Methods
3.2. Methods
3.2.1. The Definition of Variable Fuzzy Sets
3.2.2. The Relative Membership Degree of Indices
3.2.3. Variable Fuzzy Evaluation Model (VFEM) for Classification of Stable Isotopes
3.2.4. Determination of the Weight of Index
4. Results
4.1. Classification of Stable Isotopes in the Naqu River Basin Based on the Variable Fuzzy Evaluation Method
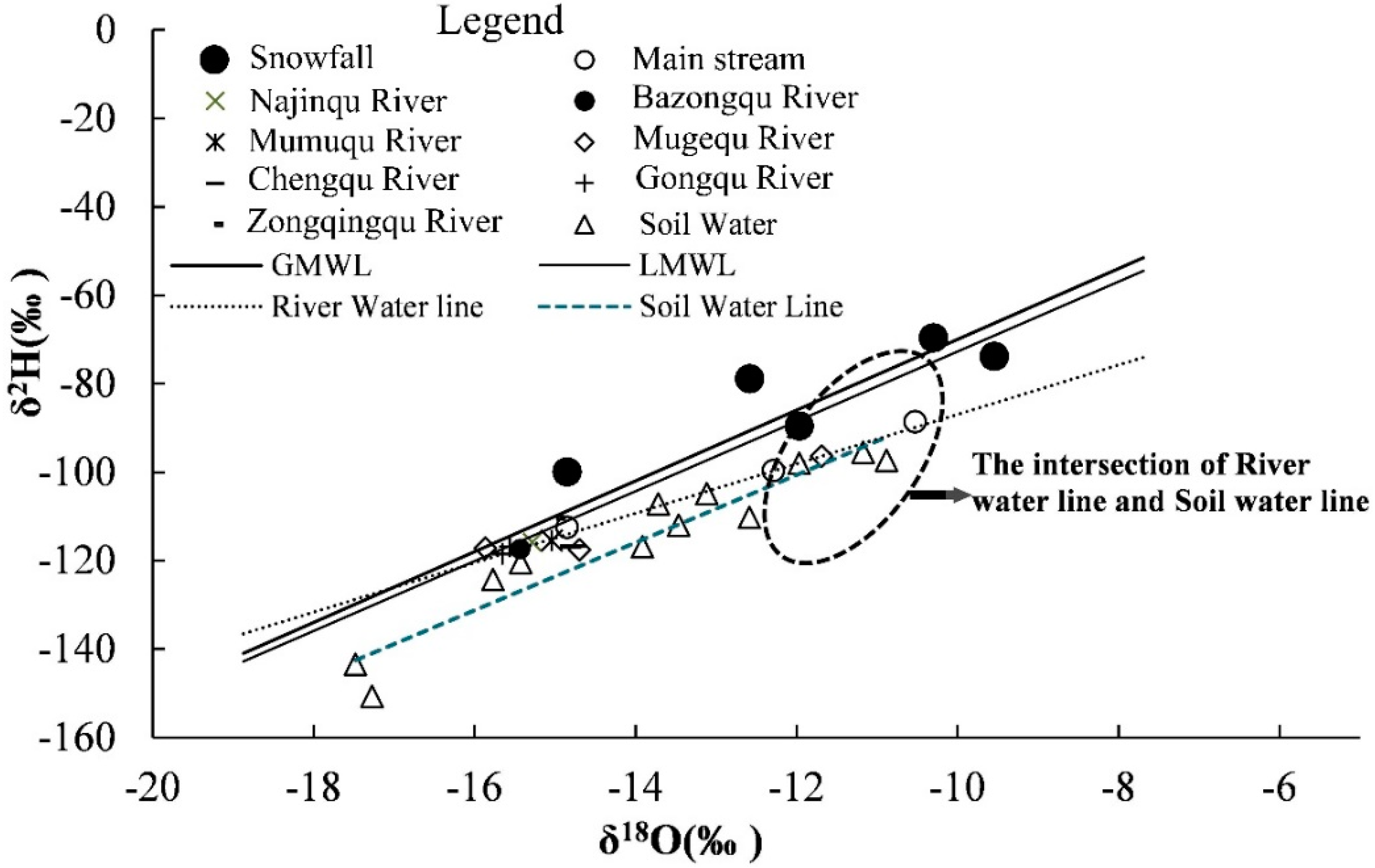
4.2. Local Meteoric Water Line (LMWL) in the Naqu River Basin
4.3. Stable Isotopic Composition of Surface Water, Soil Water and Snowfall
5. Discussion
5.1. Analysis of Stable Isotopic Composition of Surface Water, Soil Water and Snowfall
5.2. Estimation in Classification of Stable Isotopes in the Naqu River Basin Based on the Variable Fuzzy Evaluation Method
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Edwards, T.W.D.; Bursey, G.G.; Prowse, T.D. Estimating Evaporation Using Stable Isotopes: Quantitative Results and Sensitivity Analysis for Two Catchments in Northern Canada. Hydrol. Res. 1993, 24, 79–94. [Google Scholar]
- Buttle, J.M. Fundamentals of Small Catchment Hydrology. In Isotope Tracers in Catchment Hydrology; Elsevier Science: Amsterdam, The Netherlands, 1998; Chapter 1; pp. 1–49. [Google Scholar]
- Barbieri, M.; Boschetti, T.; Petitta, M.; Tallini, M. Stable isotope (2H, 18O and 87Sr/86Sr) and hydrochemistry monitoring for groundwater hydrodynamics analysis in a karst aquifer (Gran Sasso, Central Italy). Appl. Geochem. 2005, 20, 2063–2081. [Google Scholar] [CrossRef]
- Clark, I.D.; Fritz, P. Environmental Isotopes in Hydrogeology; Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 148–154, 172–186. [Google Scholar]
- Antúnez Contreras, S.P. Hydrogeological conceptual model of groundwater from carbonate aquifers using environmental isotopes (18O, 2H) and chemical tracers: A case study in southern Latium region, central Italy. J. Water Resour. Prot. 2012, 4, 695–716. [Google Scholar]
- Calligaris, C.; Mezga, K.; Slejko, F.; Urbanc, J.; Zini, L. Groundwater Characterization by Means of Conservative (δ18O and δ2H) and Non-Conservative (87Sr/86Sr) Isotopic Values: The Classical Karst Region Aquifer Case (Italy–Slovenia). Geosciences 2018, 8, 321. [Google Scholar] [CrossRef]
- Rank, D.; Wyhlidal, S.; Schott, K.; Weigand, S.; Oblin, A. Temporal and spatial distribution of isotopes in river water in Central Europe: 50 years experience with the Austrian network of isotopes in rivers. Isot. Environ. Health Stud. 2018, 54, 115–136. [Google Scholar] [CrossRef] [PubMed]
- Gibson, J.J.; Edwards, T.W.D.; Birks, S.J.; St Amour, N.A.; Buhay, W.M.; McEachern, P.; Wolfe, B.B.; Peters, D.L. Progress in isotope tracer hydrology in Canada. Hydrol. Process. 2005, 19, 303–327. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Li, X.; Li, G.; Huang, Y. Seasonal variations of deuterium and oxygen-18 isotopes and their response to moisture source for precipitation events in the subtropical monsoon region. Hydrol. Process. 2015, 29, 90–102. [Google Scholar] [CrossRef]
- Han, G.; Lv, P.; Tang, Y.; Song, Z. Spatial and temporal variation of H and O isotopic compositions of the Xijiang River system, Southwest China. Isot. Environ. Health Stud. 2018, 54, 137–146. [Google Scholar] [CrossRef]
- Qu, S.; Wang, Y.; Zhou, M.; Liu, H.; Shi, P.; Yu, Z.; Xiang, L. Temporal 18O and deuterium variations in hydrologic components of a small watershed during a typhoon event. Isot. Environ. Health Stud. 2017, 53, 172–183. [Google Scholar] [CrossRef]
- Meredith, K.T.; Hollins, S.E.; Hughes, C.E.; Cendón, D.I.; Chisari, R.; Griffiths, A.; Crawford, J. Evaporation and concentration gradients created by episodic river recharge in a semi-arid zone aquifer: Insights from Cl−, δ18O, δ2H, and 3H. J. Hydrol. 2015, 529, 1070–1078. [Google Scholar] [CrossRef]
- Biggs, T.W.; Lai, C.; Chandan, P.; Lee, R.M.; Messina, A.; Lesher, R.S.; Khatoon, N. Evaporative fractions and elevation effects on stable isotopes of high elevation lakes and streams in arid western Himalaya. J. Hydrol. 2015, 522, 239–249. [Google Scholar] [CrossRef]
- Yang, Y.; Xiao, H.; Qin, Z.; Zou, S. Hydrogen and oxygen isotopic records in monthly scales variations of hydrological characteristics in the different landscape zones of alpine cold regions. J. Hydrol. 2013, 499, 124–131. [Google Scholar] [CrossRef]
- Edirisinghe, E.A.; Pitawala, H.M.; Dharmagunawardhane, H.A.; Wijayawardane, R.L. Spatial and temporal variation in the stable isotope composition (δ18O and δ2H) of rain across the tropical island of Sri Lanka. Isot. Environ. Health Stud. 2017, 53, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Murillo, R.; Esquivel-Hernandez, G.; Saenz-Rosales, O.; Piedra-Marin, G.; Fonseca-Sanchez, A.; Madrigal-Solis, H.; Ulloa-Chaverri, F.; Rojas-Jimenez, L.D.; Vargas-Viquez, J.A. Isotopic composition in precipitation and groundwater in the northern mountainous region of the Central Valley of Costa Rica. Isot. Environ. Health Stud. 2017, 53, 1–17. [Google Scholar] [CrossRef]
- Jin, L.; Siegel, D.I.; Lautz, L.K.; Lu, Z. Identifying streamflow sources during spring snowmelt using water chemistry and isotopic composition in semi-arid mountain streams. J. Hydrol. 2012, 470–471, 289–301. [Google Scholar] [CrossRef]
- Wassenaar, L.I.; Athanasopoulos, P.; Hendry, M.J. Isotope hydrology of precipitation, surface and ground waters in the Okanagan Valley, British Columbia, Canada. J. Hydrol. 2011, 411, 37–48. [Google Scholar] [CrossRef]
- Rock, L.; Mayer, B. Isotope hydrology of the Oldman River basin, southern Alberta, Canada. Hydrol. Process. 2007, 21, 3301–3315. [Google Scholar] [CrossRef]
- Yao, Z.; Liu, J.; Huang, H.; Song, X.; Dong, X.; Liu, X. Characteristics of isotope in precipitation, river water and lake water in the Manasarovar basin of Qinghai–Tibet Plateau. Environ. Geol. 2009, 57, 551–556. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, W.X.; Zhang, Q.L. The distribution of deuterium and heavy oxygen in snow and ice, in the Jolmo Lungma regions of the southern Tibet. Sci. China B 1973, 4, 430–433. [Google Scholar]
- Zhang, X.P.; Zhong, W.Z.Y.; Yao, T.D.; Han, J.K.; Xie, Z.C. The stable isotope transformation of space-time in meteoric water in Qinghai–Tibet Plateau and its adjacent region. Sci. China D 2001, 31, 353–361. [Google Scholar]
- Tian, L.D.; Yao, T.D.; Shen, Y.P.; Yang, M.X.; Bai-Sheng, Y.E.; Tsujimura, M. Study on stable isotope in river water and precipitation in Naqu River basin, Tibetan Plateau. Adv. Water Sci. 2002, 13, 206–210. [Google Scholar]
- Pang, H.; He, Y.; Lu, A.; Zhao, J.; Ning, B.; Yuan, L.; Song, B.; Zhang, N. Comparisons of stable isotopic fractionation in winter and summer at Baishui Glacier No. 1, Mt. Yulong, China. J. Geogr. Sci. 2006, 16, 306–314. [Google Scholar]
- Chen, S.Y.; Hu, J.M. Variable fuzzy assessment method and its application in assessing water resources carrying capacity. J. Hydraul. Eng. 2006, 37, 264–277. [Google Scholar]
- Chen, S.Y. Theory and model of engineering variable fuzzy sets—Mathematical basis for fuzzy hydrology and water resources (in Chinese). J. Dalian Univ. Technol. 2005, 45, 308–312. [Google Scholar]
- Wang, W.; Xu, D.; Chau, K.; Lei, G. Assessment of river water quality based on theory of variable fuzzy sets and fuzzy binary comparison method. Water Resour. Manag. 2014, 28, 4183–4200. [Google Scholar] [CrossRef]
- Zou, Z.; Zhou, C.; Song, L.X.; Guo, J. Comprehensive flood risk assessment based on set pair analysis-variable fuzzy sets model and fuzzy AHP. Stoch. Environ. Res. Risk Assess. 2013, 27, 525–546. [Google Scholar] [CrossRef]
- Price, R.M.; Swart, P.K.; Willoughby, H.E. Seasonal and spatial variation in the stable isotopic composition (δ18O and δ2H) of precipitation in south Florida. J. Hydrol. 2008, 358, 193–205. [Google Scholar] [CrossRef]
- Craig, H. Isotopic variations in meteoric waters. Science 1961, 133, 1702–1703. [Google Scholar]
- Li, S.G.; Romero-Saltos, H.; Tsujimura, M.; Sugimoto, A.; Sasaki, L.; Davaa, G.; Oyunbaatar, D. Plant water sources in the cold semiarid ecosystem of the upper Kherlen River catchment in Mongolia: A stable isotope approach. J. Hydrol. 2007, 333, 109–117. [Google Scholar] [CrossRef]
- Šturm, M.B.; Ganbaatar, O.; Voigt, C.C.; Kaczensky, P. First field-based observations of δ2H and δ18O values of event-based precipitation, rivers and other water bodies in the Dzungarian Gobi, SW Mongolia. Isot. Environ. Health Stud. 2017, 53, 157–171. [Google Scholar]
- Tian, L.D.; Yao, T.D.; Sun, W.Z.; Stievenard, M.; Jouzel, J. Relationship between δ2H and δ18O and water vapour circulation in the precipitation of the Qinghai-Tibet plateau. Sci. Sin. Terrae 2001, 31, 214–220. [Google Scholar]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Clark, I.; Fritz, P. Environmental Isotopes in Hydrogeology; Lewis Publishers: Boca Raton, FL, USA, 1964; 328p. [Google Scholar]
- Wu, J.K.; Ding, Y.J.; Yang, J.H.; Liu, S.W.; Chen, J.Z.; Zhou, J.X.; Qin, X. Spatial variation of stable isotopes in different waters during melt season in the Laohugou Glacial Catchment, Shule River basin. J. Mt. Sci. 2016, 13, 1453–1463. [Google Scholar] [CrossRef]
- Jeelani, G.; Saravana Kumar, U.; Kumar, B. Variation of δ18O and δ2H in precipitation and stream waters across the Kashmir Himalaya (India) to distinguish and estimate the seasonal sources of stream flow. J. Hydrol. 2013, 481, 157–165. [Google Scholar] [CrossRef]
- Mayr, C.; Lücke, A.; Stichler, W.; Trimborn, P.; Ercolano, B.; Oliva, G.; Ohlendorf, C.; Soto, J.; Fey, M.; Haberzettl, T.; et al. Precipitation origin and evaporation of lakes in semi-arid Patagonia (Argentina) inferred from stable isotopes (δ18O, δ2H). J. Hydrol. 2007, 334, 53–63. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Li, W. Temporal and spatial variation of water stable isotopes (18O and 2H) in the Kaidu River basin, Northwestern China. Hydrol. Process. 2014, 28, 653–661. [Google Scholar] [CrossRef]

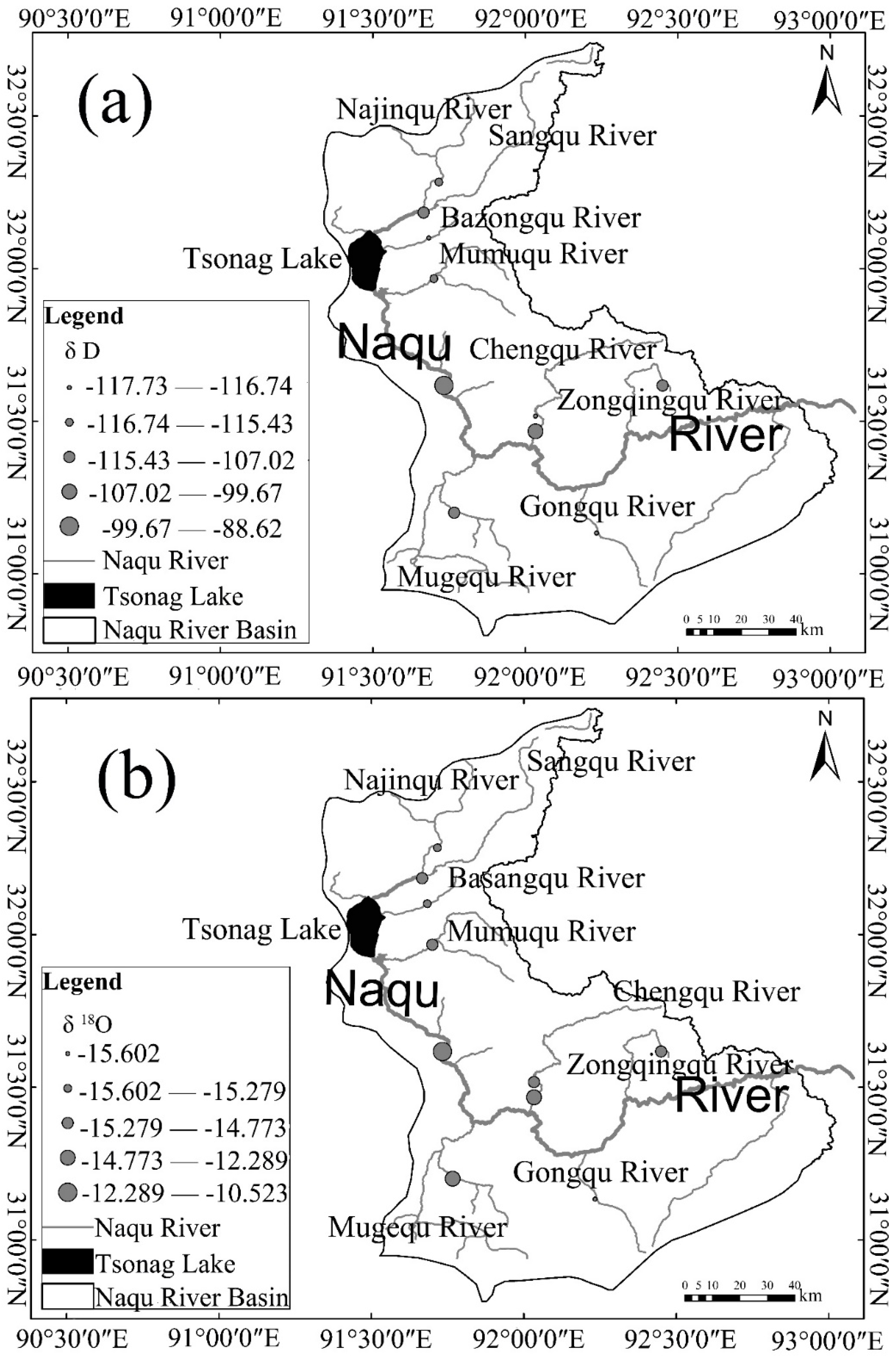
| The Evaluation Index | Evaluation of Regional (‰) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Najinqu River | Sangqu River | Bazongqu River | Mumuqu River | Middle Stream | Mugequ River | Chengqu River | The Downstream | Gongqu River | Zongqingqu River | |
| δ18O | −15.3 | −14.9 | −15.4 | −15.0 | −10.5 | −13.2 | −14.8 | −12.3 | −15.6 | −15.0 |
| δ2H | −116 | −113 | −117 | −115 | −89 | −107 | −117 | −100 | −118 | −110 |
| The Evaluation Index | Index Standard Value (‰) | |||
|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | Level 4 | |
| δ18O δ2H | ≤−14.6 ≤−111 | (−14.6) to (−13.6) (−111) to (−104) | (−13.6) to (−12.6) (−104) to (−97) | 0 ≥ −12.6 ≥−97 |
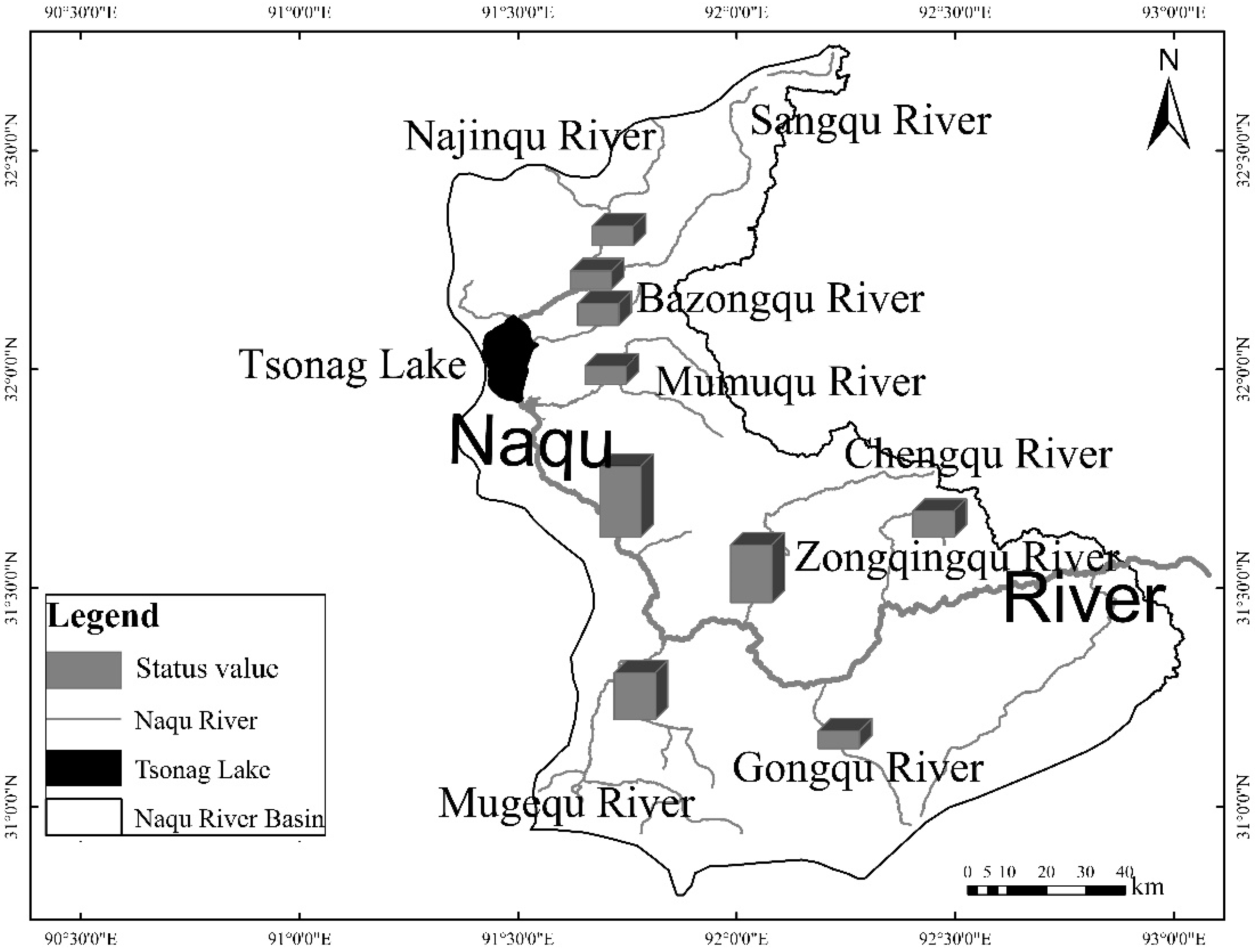
| Evaluation of Regional | Status Value | Rating |
|---|---|---|
| Najinqu River | 1.089 | 1 |
| Sangqu River | 1.03 | 1 |
| Bazongqu River | 1.264 | 1 |
| Mumuqu River | 1.005 | 1 |
| Middle stream | 4 | 4 |
| Mugequ River | 2.624 | 2 |
| Chengqu River | 1.151 | 1 |
| The downstream | 3.248 | 3 |
| Gongqu River | 1 | 1 |
| Zongqingqu River | 1.455 | 1 |
| Time | Samples | Range of Variation (‰) | |
|---|---|---|---|
| δ18O | δ2H | ||
| August | Surface water | −15.6 to 10.5 | −118 to −89 |
| January | Surface water | −16.6 to −9.1 | −122 to −81 |
| August | Soil water | −17.3 to −11.2 | −151 to −96 |
| January | Snowfall | −15.0 to −7.6 | −101 to −63 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wang, G.; Wang, F. Classification of Stable Isotopes and Identification of Water Replenishment in the Naqu River Basin, Qinghai-Tibet Plateau. Water 2019, 11, 46. https://doi.org/10.3390/w11010046
Chen X, Wang G, Wang F. Classification of Stable Isotopes and Identification of Water Replenishment in the Naqu River Basin, Qinghai-Tibet Plateau. Water. 2019; 11(1):46. https://doi.org/10.3390/w11010046
Chicago/Turabian StyleChen, Xi, Guoli Wang, and Fuqiang Wang. 2019. "Classification of Stable Isotopes and Identification of Water Replenishment in the Naqu River Basin, Qinghai-Tibet Plateau" Water 11, no. 1: 46. https://doi.org/10.3390/w11010046
APA StyleChen, X., Wang, G., & Wang, F. (2019). Classification of Stable Isotopes and Identification of Water Replenishment in the Naqu River Basin, Qinghai-Tibet Plateau. Water, 11(1), 46. https://doi.org/10.3390/w11010046





