A Novel ArcGIS Toolbox for Estimating Crop Water Demands by Integrating the Dual Crop Coefficient Approach with Multi-Satellite Imagery
Abstract
1. Introduction
2. Materials and Methods
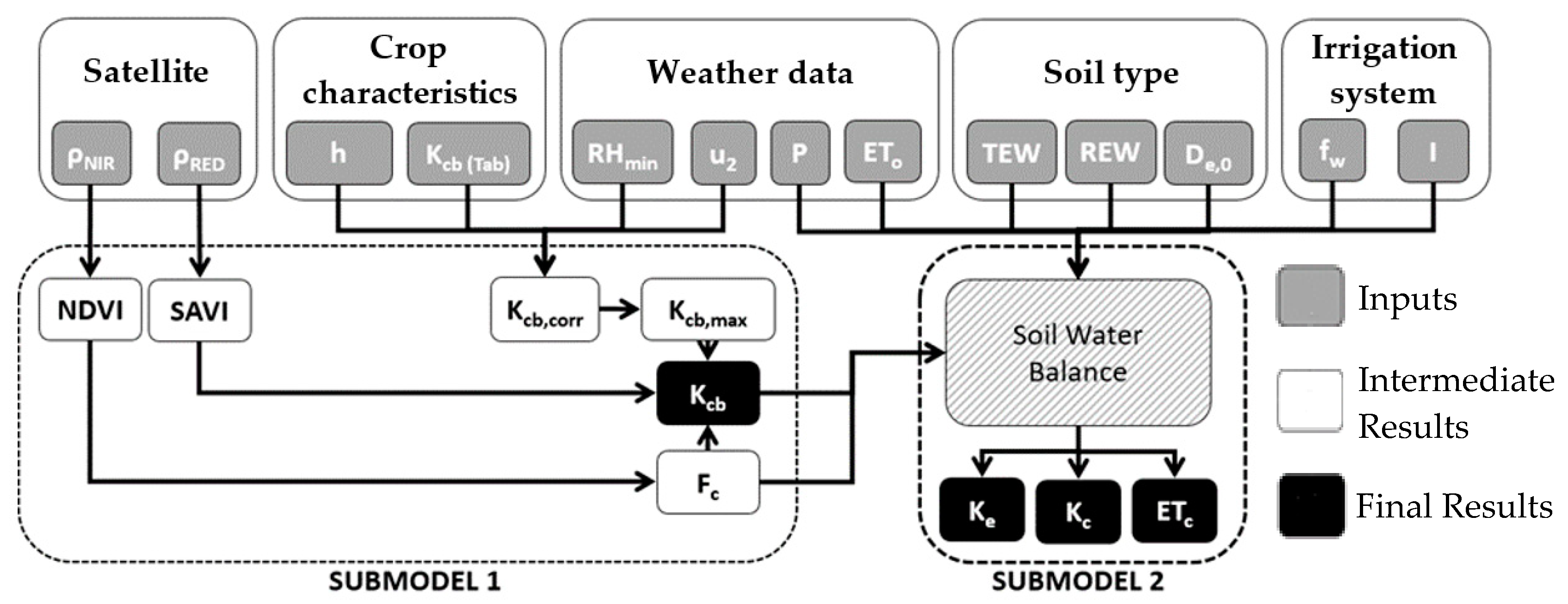
2.1. Model Theorical Framework
2.2. Model Implementation
2.3. Model Validation
2.4. Statistical Analyses
3. Results
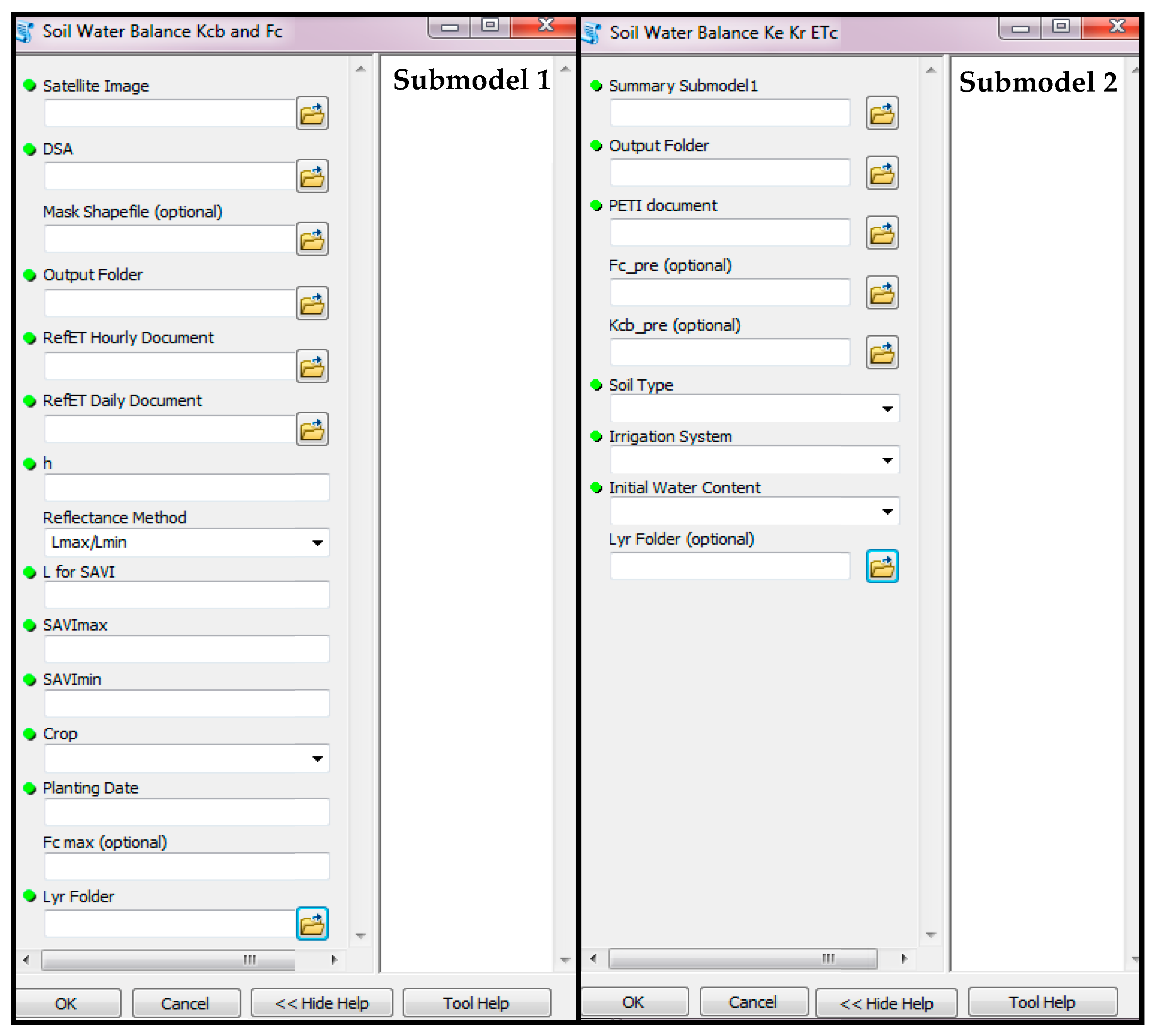
3.1. Model Interface
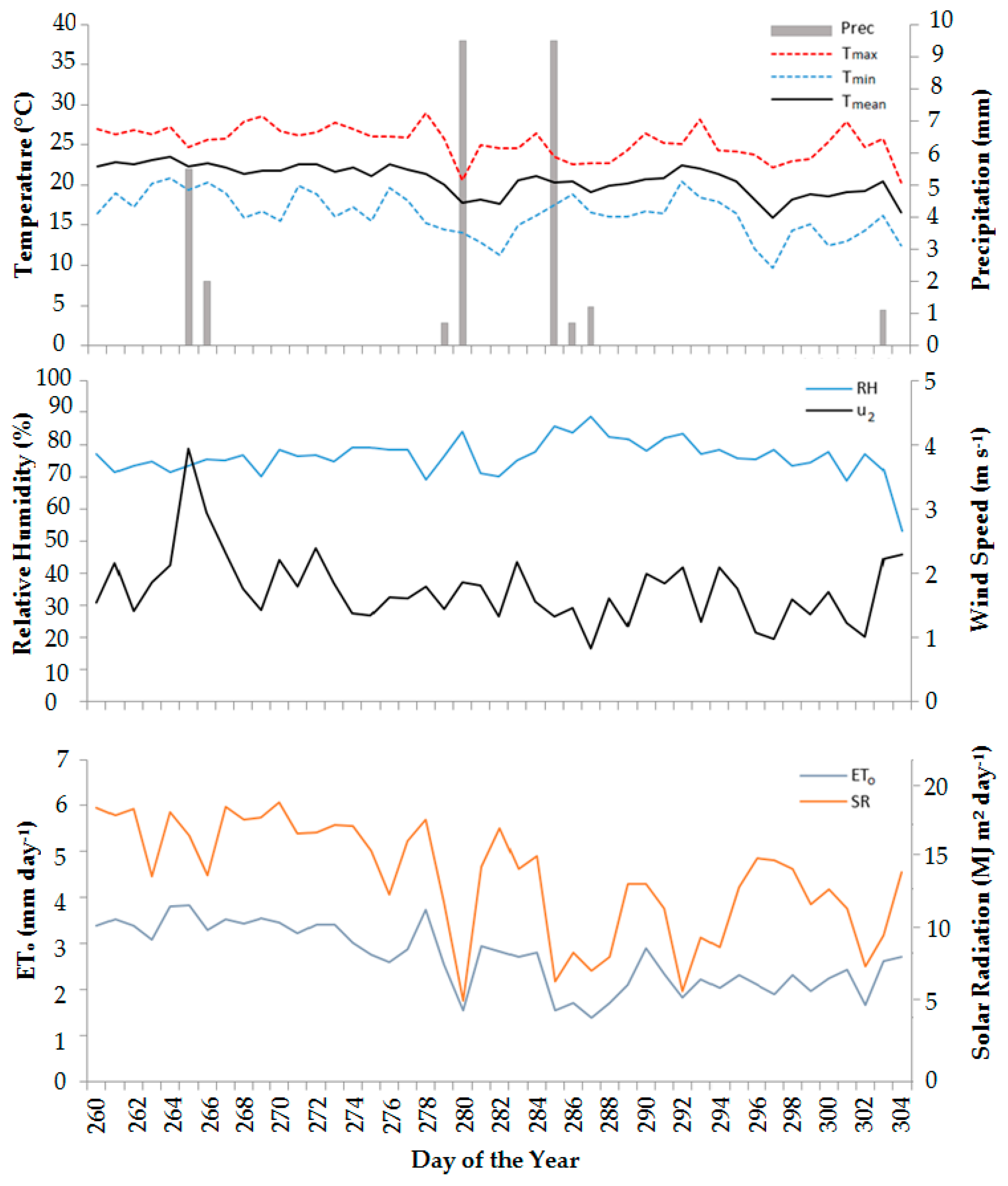
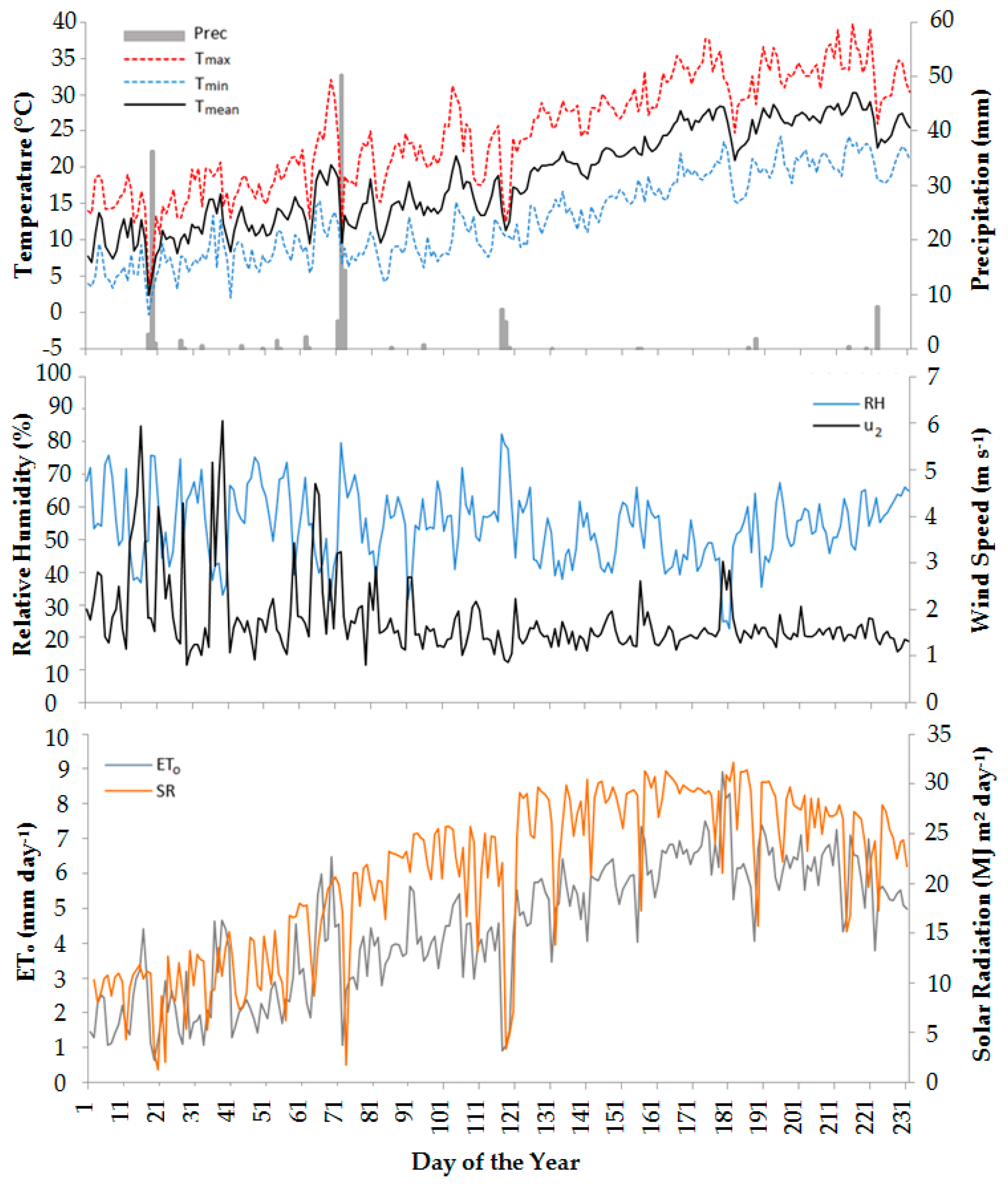
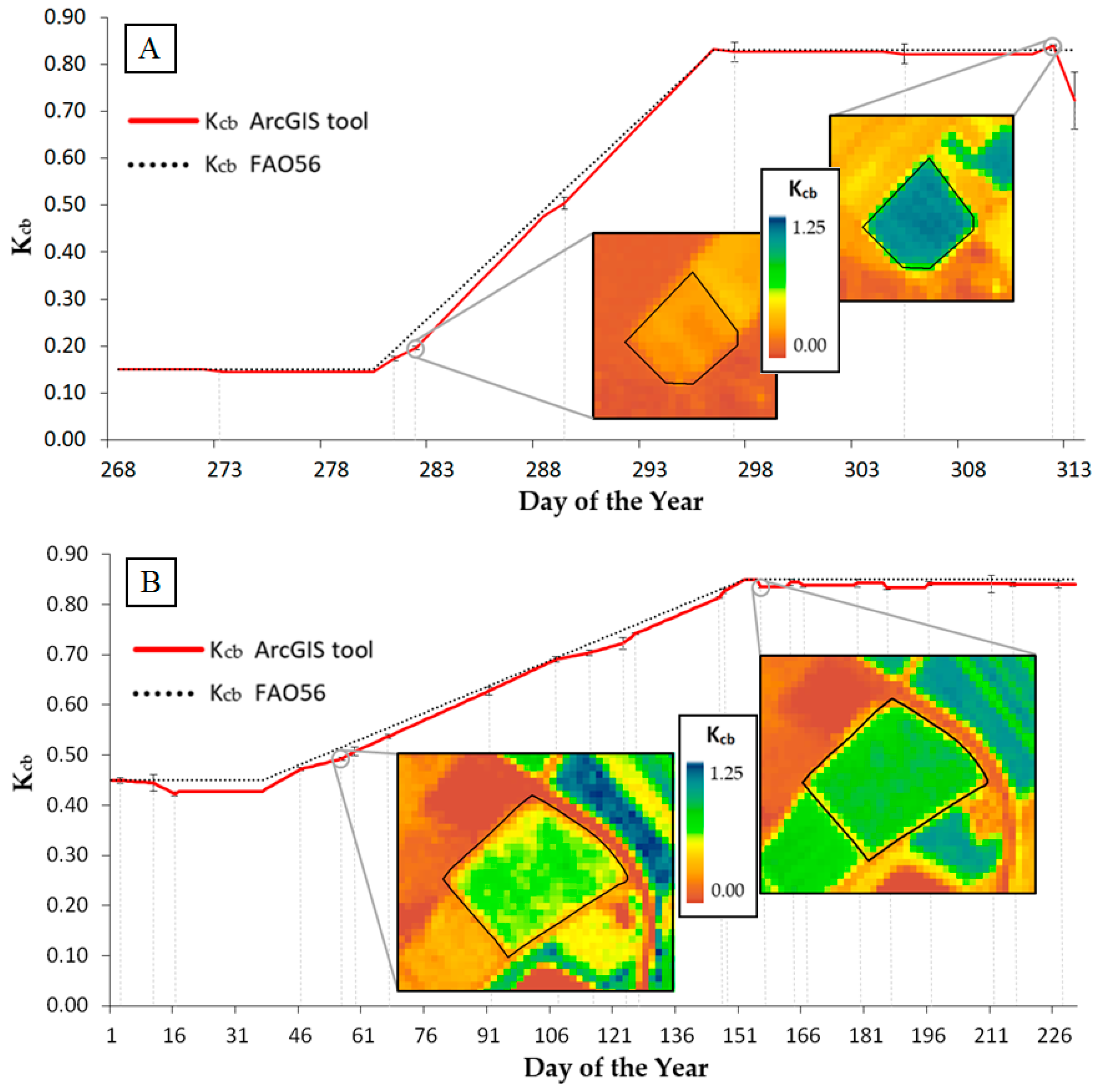
3.2. Practical Validation
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Antle, J.M.; Jones, J.W.; Rosenzweig, C. Towards a new generation of agricultural system models, data, and knowledge products: Introduction. Agric. Syst. 2017, 155, 186–190. [Google Scholar] [CrossRef] [PubMed]
- Donatelli, M.; Magarey, R.D.; Bregaglio, S.; Willocquet, L.; Whish, J.P.M.; Savary, S. Modelling the impacts of pests and diseases on agricultural systems. Agric. Syst. 2017, 155, 213–224. [Google Scholar] [CrossRef] [PubMed]
- Zarco-Tejada, P.J.; Camino, C.; Beck, P.S.A.; Calderon, R.; Hornero, A.; Hernández-Clemente, R.; Kattenborn, T.; Montes-Borrego, M.; Susca, L.; Morelli, M.; et al. Previsual symptoms of Xylella fastidiosa infection revealed in spectral plant-trait alterations. Nat. Plants 2018, 4, 432–439. [Google Scholar] [CrossRef] [PubMed]
- Le Bot, J.; Adamowicz, S.; Robin, P. Modelling plant nutrition of horticultural crops: A review. Sci. Hortic. 1998, 74, 47–82. [Google Scholar] [CrossRef]
- Ransom, K.M.; Nolan, B.T.; Traum, J.A.; Faunt, C.C.; Bell, A.M.; Gronberg, J.A.M.; Wheeler, D.C.; Rosecrans, C.Z.; Jurgens, B.; Schwarz, G.E.; et al. A hybrid machine learning model to predict and visualize nitrate concentration throughout the Central Valley aquifer, California, USA. Sci. Total Environ. 2017, 601–602, 1160–1172. [Google Scholar] [CrossRef] [PubMed]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Alves, I.; Fernando, R.M.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software. 1. Background and computational strategy. Agric. Water Manag. 2012, 103, 8–24. [Google Scholar] [CrossRef]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop: The FAO Crop Model to Simulate Yield Response to Water: I. Concepts and Underlying Principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Janssen, J.C.; Porter, C.H.; Moore, A.D.; Athanasiadis, I.N.; Foster, I.; Jones, J.W.; Antle, J.M. Towards a new generation of agricultural system data, models and knowledge products: Information and communication technology. Agric. Syst. 2017, 155, 200–212. [Google Scholar] [CrossRef]
- Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Brief history of agricultural systems modeling. Agric. Syst. 2016, 155, 240–254. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Wang, L.; Li, Y.; Li, D. Model predictive control and its application in agriculture: A review. Comput. Electron. Agric. 2018, 151, 104–117. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M. Upscaling and downscaling—A regional view of the Soil-Plant-Atmosphere continuum. Agron. J. 2003, 95, 1408–1423. [Google Scholar] [CrossRef]
- Ramírez-Cuesta, J.M.; Allen, R.G.; Zarco-Tejada, P.J.; Kilic, A.; Santos, C.; Lorite, I.J. Impact of the spatial resolution on the energy balance components on an open-canopy olive orchard. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 88–102. [Google Scholar] [CrossRef]
- Crago, R.D.; Brutsaert, W. Conservation and variability of the evaporative fraction during the daytime. J. Hydrol. 1996, 180, 173–194. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)-Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Aguilar, A.L.; Flores, H.; Crespo, G.; Marín, M.I.; Campos, I.; Calera, A. Performance assessment of MOD16 in evapotranspiration evaluation in Northwestern Mexico. Water 2018, 10, 901. [Google Scholar] [CrossRef]
- Mateos, L.; González-Dugo, M.P.; Testi, L.; Villalobos, F.J. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. I. Method validation. Agric. Water Manag. 2013, 125, 81–91. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper No. 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Er-Raki, S.; Chehbouni, A.; Boulet, G.; Williams, D.G. Using the dual approach of FAO-56 for partitioning ET into soil and plant components for olive orchards in a semi-arid region. Agric. Water Manag. 2010, 97, 1769–1778. [Google Scholar] [CrossRef]
- Paço, T.A.; Ferreira, M.I.; Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Conceição, N.; Pacheco, C.A.; Pereira, L.S. The dual crop coefficient approach using a density factor to simulate the evapotranspiration of a peach orchard: SIMDualKc model vs. eddy covariance measurements. Irrig. Sci. 2012, 30, 115–126. [Google Scholar] [CrossRef]
- Consoli, S.; Vanella, D. Mapping crop evapotranspiration by integrating vegetation indices into a soil water balance model. Agric. Water Manag. 2014, 143, 71–81. [Google Scholar] [CrossRef]
- Katerji, N.; Rana, G. FAO-56 methodology for determining water requirement of irrigated crops: Critical examination of the concepts, alternative proposals and validation in Mediterranean region. Theor. Appl. Climatol. 2014, 116, 515–536. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. FAO-56 Dual Crop Coefficient Method for Estimating Evaporation from Soil and Application Extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef]
- Fernández-Pacheco, D.G.; Escarabajal-Henajeros, D.; Ruiz Canales, A.; Conesa, J.; Molina-Martínez, J.M. A digital image-processing-based method for determining the crop coefficient of lettuce crops in the southeast of Spain. Biosyst. Eng. 2014, 117, 23–34. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT Cropping System Model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Moreno-Rivera, J.M.; Calera, A.; Osann, A. SPIDER—An Open GIS application use case. In Proceedings of the Open GIS UK Conference, Nottingham, UK, 22 June 2009. [Google Scholar]
- Navarro-Hellín, H.; Martínez-del-Rincon, J.; Domingo-Miguel, R.; Soto-Valles, F.; Torres-Sánchez, R. A decision support system for managing irrigation in agriculture. Comput. Electron. Agric. 2016, 124, 121–131. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Shen, Y.; Zhang, X.; Lei, Y. Web-based irrigation decision support system with limited inputs for farmers. Agric. Water Manag. 2018, 210, 279–285. [Google Scholar] [CrossRef]
- Huete, A.R.; Jackson, R.D.; Post, D.F. Spectral response of a plant canopy with different soil backgrounds. Remote Sens. Environ. 1985, 17, 37–53. [Google Scholar] [CrossRef]
- Ormsby, J.P.; Choudhury, B.J.; Owe, M. Vegetation spatial variability and its effect on vegetation indices. Int. J. Remote Sens. 1987, 8, 1301–1306. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A Comparison of Operational Remote Sensing-Based Models for Estimating Crop Evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- ESRI. ArcGIS for Desktop; Version 10.2; Environmental Systems Research Institute: Redlands, CA, USA, 2014; Available online: http://www.esri.com/ (accessed on 23 December 2018).
- Allen, R.G. Ref-ET: Reference Evapotranspiration Calculation Software for FAO and ASCE Standardized Equations; University of Idaho: Kimberly, ID, USA, 2010. [Google Scholar]
- Huete, A.R. A soil adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Reichert, P.; Omlin, M. On the usefulness of overparameterized ecological models. Ecol. Model. 1997, 95, 289–299. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Does a large number of parameters enhance model performance? Comparative assessment of common catchment model structures on 429 catchments. J. Hydrol. 2001, 242, 275–301. [Google Scholar] [CrossRef]
- Loague, K.M.; Freeze, R.A. A comparison of rainfall-runoff modelling techniques on small upland catchments. Water Resour. Res. 1985, 21, 229–248. [Google Scholar] [CrossRef]
- Bastidas, L.A.; Hogue, T.S.; Sorooshian, S.; Gupta, H.V.; Shuttleworth, W.J. Parameter sensitivity analysis for different complexity land surface models using multicriteria methods. J. Geophys. Res. 2006, 111, D20101. [Google Scholar] [CrossRef]
- Belaqziz, S.; Khabba, S.; Er-Raki, S.; Jarlan, L.; Le Page, M.; Kharrou, M.H.; El Adnani, M.; Chehbouni, A. A new irrigation priority index based on remote sensing data for assessing the networks irrigation scheduling. Agric. Water Manag. 2013, 119, 1–9. [Google Scholar] [CrossRef]
- González-Dugo, V.; Zarco-Tejada, P.J.; Nicolás, E.; Nortes, P.A.; Alarcón, J.J.; Intrigliolo, D.S.; Fereres, E. Using high resolution UAV thermal imagery to assess the variability in the water status of five fruit tree species within a commercial orchard. Precis. Agric. 2013, 14, 660–678. [Google Scholar] [CrossRef]
- Bellvert, J.; Zarco-Tejada, P.J.; Marsal, J.; Girona, J.; González-Dugo, V.; Fereres, E. Vineyard irrigation scheduling based on airborne thermal imagery and water potential thresholds. Aust. J. Grape Wine Res. 2016, 22, 307–315. [Google Scholar] [CrossRef]
- Romero, M.; Luo, Y.; Su, B.; Fuentes, S. Vineyard water status estimation using multispectral imagery from an UAV platform and machine learning algorithms for irrigation scheduling management. Comput. Electron. Agric. 2018, 147, 109–117. [Google Scholar] [CrossRef]
- Verrelst, J.; Romijn, E.; Kooistra, L. Mapping vegetation density in a heterogeneous river floodplain ecosystem using pointable CHRIS/PROBA data. Remote Sens. 2012, 4, 2866–2889. [Google Scholar] [CrossRef]
- Lorite, I.J.; García-Vila, M.; Santos, C.; Ruiz-Ramos, M.; Fereres, E. AquaData and AquaGIS: Two Computer Utilities for Temporal and Spatial Simulations of Water-Limited Yield with AquaCrop. Comput. Electron. Agric. 2013, 96, 227–237. [Google Scholar] [CrossRef]
- Simionesei, L.; Galvão, P.; Ramos, T.B.; Leitão, P.C.; Silva, A.; Neves, R. A plataforma FIGARO no apoio à gestão da rega. In Proceedings of the Livro de Actas do VII Congresso Ibérico das Ciências do Solo e do VI Congresso de Rega e Drenagem Solos e Água: Fontes (esgotáveis) de vida e de desenvolvimento, Beja, Portugal, 13–15 September 2016; pp. 309–312. (In Portuguese). [Google Scholar]
- Tsakmakis, I.; Kokkos, N.; Pisinaras, V.; Papaevangelou, V.; Hartzigiannakis, E.; Arampatzis, G.; Gikas, G.D.; Linker, R.; Zoras, S.; Evagelopoulos, V.; et al. Operational precise irrigation for cotton cultivation through the coupling of meteorological and crop growth models. Water Resour. Manag. 2017, 31, 563–580. [Google Scholar] [CrossRef]
- Thysen, I.; Detlefsen, N.K. Online decision support for irrigation for farmers. Agric. Water Manag. 2006, 86, 269–276. [Google Scholar] [CrossRef]
- Giusti, E.; Marsili-Libelli, S. A Fuzzy Decision Support System for irrigation and water conservation in agriculture. Environ. Model. Softw. 2015, 63, 73–86. [Google Scholar] [CrossRef]
- Yang, G.; Liu, L.; Guo, P.; Li, M. A flexible decision support system for irrigation scheduling in an irrigation district in China. Agric. Water Manag. 2017, 179, 378–389. [Google Scholar] [CrossRef]
- Corbari, C.; Bissolati, M.; Mancini, M. Multi-scales and multi-satellites estimates of evapotranspiration with a residual energy balance model in the Muzza agricultural district in Northern Italy. J. Hydrol. 2015, 524, 243–254. [Google Scholar] [CrossRef]
- Mousivand, A.; Menenti, M.; Gorte, B.; Verhoef, W. Multi-temporal, multi-sensor retrieval of terrestrial vegetation properties from spectral–directional radiometric data. Remote Sens. Environ. 2015, 158, 311–330. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef]
- Fieuzal, R.; Baup, F. Forecast of wheat yield throughout the agricultural season using optical and radar satellite images. Int. J. Appl. Earth Obs. Geoinf. 2017, 59, 147–156. [Google Scholar] [CrossRef]
- González-Esquiva, J.M.; García-Mateos, G.; Escarabajal-Henajeros, D.; Hernández-Hernández, J.L.; Ruiz-Canales, A.; Molina-Martínez, J.M. A new model for water balance estimation on lettuce crops using effective diameter obtained with image analysis. Agric. Water Manag. 2017, 183, 116–122. [Google Scholar] [CrossRef]
- Ayars, J.E.; Johnson, R.S.; Phene, C.J.; Trout, T.J.; Clark, D.A.; Mead, R.M. Water use by drip-irrigated late-season peaches. Irrig. Sci. 2003, 22, 187–194. [Google Scholar] [CrossRef]
- Abrisqueta, I.; Abrisqueta, J.M.; Tapia, L.M.; Munguía, J.P.; Conejero, W.; Vera, J.; Ruiz-Sánchez, M.C. Basal crop coefficients for early-season peach trees. Agric. Water Manag. 2013, 121, 158–163. [Google Scholar] [CrossRef]
- Lee, W.S.; Alchanatis, V.; Yang, C.; Hirafuji, M.; Moshou, D.; Li, C. Sensing technologies for precision specialty crop production. Comput. Electron. Agric. 2010, 74, 2–33. [Google Scholar] [CrossRef]
- Gago, J.; Douthe, C.; Coopman, R.E.; Gallego, P.P.; Ribas-Carbo, M.; Flexas, J.; Escalona, J.; Medrano, H. UAVs challenge to assess water stress for sustainable agriculture. Agric. Water Manag. 2015, 153, 9–19. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Shearer, S. An overview of current and potential applications of thermal remote sensing in precision agriculture. Comput. Electron. Agric. 2017, 139, 22–32. [Google Scholar] [CrossRef]
- Sørensen, C.; Pesonen, L.; Bochtis, D.; Vougioukas, S.; Suomi, P. Functional requirements for a future farm management information system. Comput. Electron. Agric. 2011, 76, 266–276. [Google Scholar] [CrossRef]
- Tan, L. Cloud-based decision support and automation for precision agriculture in orchards. IFAC-PapersOnLine 2016, 49, 330–335. [Google Scholar] [CrossRef]
- Cabelguenne, M.; Debaeke, Ph.; Puech, J.; Bose, N. Real time irrigation management using the EPIC-PHASE model and weather forecasts. Agric. Water Manag. 1997, 32, 227–238. [Google Scholar] [CrossRef]
- Bergez, J.E.; Garcia, F. Is it worth using short-term weather forecasts for irrigation management? Eur. J. Agron. 2010, 33, 175–181. [Google Scholar] [CrossRef]
- Lorite, I.J.; Ramírez-Cuesta, J.M.; Cruz-Blanco, M.; Santos, C. Using weather forecast data for irrigation scheduling under semi-arid conditions. Irrig. Sci. 2015, 33, 411–427. [Google Scholar] [CrossRef]
- Zhao, R.-X.; Kou, Y.-T.; Xian, G.-J.; Mao, G.-W. Study on Technologies for Information Monitoring and Quick Response of Agricultural Focuses and Significant Events. Agric. Sci. China 2010, 9, 764–770. [Google Scholar] [CrossRef]
| Date | Day of the Year | Satellite |
|---|---|---|
| 29 September 2016 | 273 | Landsat 8 |
| 7 October 2016 | 281 | Landsat 7 |
| 8 October 2016 | 282 | Sentinel 2A |
| 15 October 2016 | 289 | Landsat 8 |
| 23 October 2016 | 297 | Landsat 7 |
| 31 October 2016 | 305 | Landsat 8 |
| 7 November 2016 | 312 | Sentinel 2A |
| 8 November 2016 | 313 | Landsat 7 |
| Date | Day of the Year | Satellite |
|---|---|---|
| 3 January 2017 | 3 | Landsat 8 |
| 11 January 2017 | 11 | Landsat 7 |
| 16 January 2017 | 16 | Sentinel 2A |
| 15 February 2017 | 46 | Sentinel 2A |
| 25 February 2017 | 56 | Sentinel 2A |
| 28 February 2017 | 59 | Landsat 7 |
| 8 March 2017 | 67 | Landsat 8 |
| 1 April 2017 | 91 | Landsat 7 |
| 17 April 2017 | 107 | Landsat 7 |
| 25 April 2017 | 115 | Landsat 8 |
| 3 May 2017 | 123 | Landsat 7 |
| 6 May 2017 | 126 | Sentinel 2A |
| 26 May 2017 | 146 | Sentinel 2A |
| 27 May 2017 | 147 | Landsat 8 |
| 5 June 2017 | 156 | Sentinel 2A |
| 12 June 2017 | 163 | Landsat 8 |
| 15 June 2017 | 166 | Sentinel 2A |
| 28 June 2017 | 179 | Landsat 8 |
| 5 July 2017 | 186 | Sentinel 2A |
| 15 July 2017 | 196 | Sentinel 2A |
| 30 July 2017 | 211 | Landsat 8 |
| 4 August 2017 | 216 | Sentinel 2A |
| 15 August 2017 | 227 | Landsat 8 |
| 24 August 2017 | 236 | Sentinel 2A |
| Date | Day of the Year | Height (cm) ± SE |
|---|---|---|
| 29 September 2016 | 273 | 5.4 ± 0.18 |
| 6 October 2016 | 280 | 5.6 ± 0.13 |
| 13 October 2016 | 287 | 8.8 ± 0.12 |
| 20 October 2016 | 294 | 15.4 ± 0.16 |
| 27 October 2016 | 301 | 19.0 ± 0.18 |
| 3 November 2016 | 308 | 20.4 ± 0.25 |
| 9 November 2016 | 314 | 21.4 ± 0.26 |
| Sub-model | Input | Description |
|---|---|---|
| Sub-model 1 | Satellite Image | Folder containing the satellite image |
| DSA | Three-band image where band 1 is digital elevation model; band 2 is slope; and band 3 is terrain aspect | |
| Mask Shapefile | Mask polygon delimitating the study area | |
| Output Folder | Folder where sub-model 1 outputs will be saved | |
| RefET Hourly Document | Hourly weather data as outputted by RefET software [34] | |
| RefET Daily Document | Daily weather data as outputted by RefET software [34] | |
| h | Crop height | |
| Reflectance Method | Method for calculating reflectance from radiance (for Landsat satellite images) | |
| L for SAVI | L parameter for SAVI calculation [35]. As default, this value is set to 0.5 | |
| SAVImax | SAVI value corresponding with a high LAI surface | |
| SAVImin | SAVI value corresponding with a bare surface | |
| Crop | Crop under study | |
| Planting Date | Date when the crop was planted | |
| Fcmax | Vegetated covered fraction for which Kcb reaches its maximum value | |
| Lyr Folder | Folder containing the symbology for sub-model 1 outputs | |
| Sub-model 2 | Summary Submodel1 | Text document automatically generated just after sub-model 1 has been run successfully |
| Output Folder | Folder where sub-model 2 outputs will be saved | |
| PETI document | Text document including the daily irrigation amount applied to the crop | |
| Fc pre | Folder containing the vegetated covered fraction images of the previous days | |
| Kcb pre | Folder containing the Kcb images of the previous days | |
| Soil Type | Soil type category as defined in the FAO-56 document | |
| Irrigation System | Irrigation system as defined in the FAO-56 document | |
| Initial Water Content | Soil water content at the initialization of the soil water balance | |
| Lyr Folder | Folder containing the symbology for sub-model 2 outputs |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Cuesta, J.M.; Mirás-Avalos, J.M.; Rubio-Asensio, J.S.; Intrigliolo, D.S. A Novel ArcGIS Toolbox for Estimating Crop Water Demands by Integrating the Dual Crop Coefficient Approach with Multi-Satellite Imagery. Water 2019, 11, 38. https://doi.org/10.3390/w11010038
Ramírez-Cuesta JM, Mirás-Avalos JM, Rubio-Asensio JS, Intrigliolo DS. A Novel ArcGIS Toolbox for Estimating Crop Water Demands by Integrating the Dual Crop Coefficient Approach with Multi-Satellite Imagery. Water. 2019; 11(1):38. https://doi.org/10.3390/w11010038
Chicago/Turabian StyleRamírez-Cuesta, Juan Miguel, José Manuel Mirás-Avalos, José Salvador Rubio-Asensio, and Diego S. Intrigliolo. 2019. "A Novel ArcGIS Toolbox for Estimating Crop Water Demands by Integrating the Dual Crop Coefficient Approach with Multi-Satellite Imagery" Water 11, no. 1: 38. https://doi.org/10.3390/w11010038
APA StyleRamírez-Cuesta, J. M., Mirás-Avalos, J. M., Rubio-Asensio, J. S., & Intrigliolo, D. S. (2019). A Novel ArcGIS Toolbox for Estimating Crop Water Demands by Integrating the Dual Crop Coefficient Approach with Multi-Satellite Imagery. Water, 11(1), 38. https://doi.org/10.3390/w11010038








