Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook
Abstract
1. Introduction
2. Numerical Methods for Hydraulic Jump Research
2.1. Overview
2.2. One- and Two-Dimensional Modeling
2.3. Three-Dimensional Modeling
2.3.1. RANS Approach
- The Spalart–Allmaras model [30] solves a transport equation for an auxiliary turbulent viscosity .
- The standard [31,32] and the RNG [33,34] solve transport equations for k and another for . The former is the most widely-used engineering turbulence model for industrial applications because of its robustness and reasonable accuracy for a wide range of flows. It is a two-equation transport model for k and , their coefficients being empirically derived. The RNG version adds a term for the equation, which is known to be responsible for differences in its performance [8]. It is oftentimes mentioned that accuracy for rapidly-swirling flows is improved, despite fewer validations having been conducted [1].
- Standard (2008) and SST [35] solve transport equations for k and . The model is a two-equation transport model based on solving equations for k and . The original version was known to be excessively sensitive to free stream quantities, which is an undesired feature [36], while the revised version of Wilcox [37] attempts to solve this issue. The SST is a variant of the former. The SST model uses a blending function to transition gradually from the standard model near the wall to a high Reynolds number version of the model in the outer portion of the boundary layer [35].
2.3.2. LES and DES Approach
2.3.3. DNS Approach
2.4. Best Practices for CFD Modeling of Environmental Flows
3. Hydraulic Jump Numerical Modeling Studies
3.1. General Comments
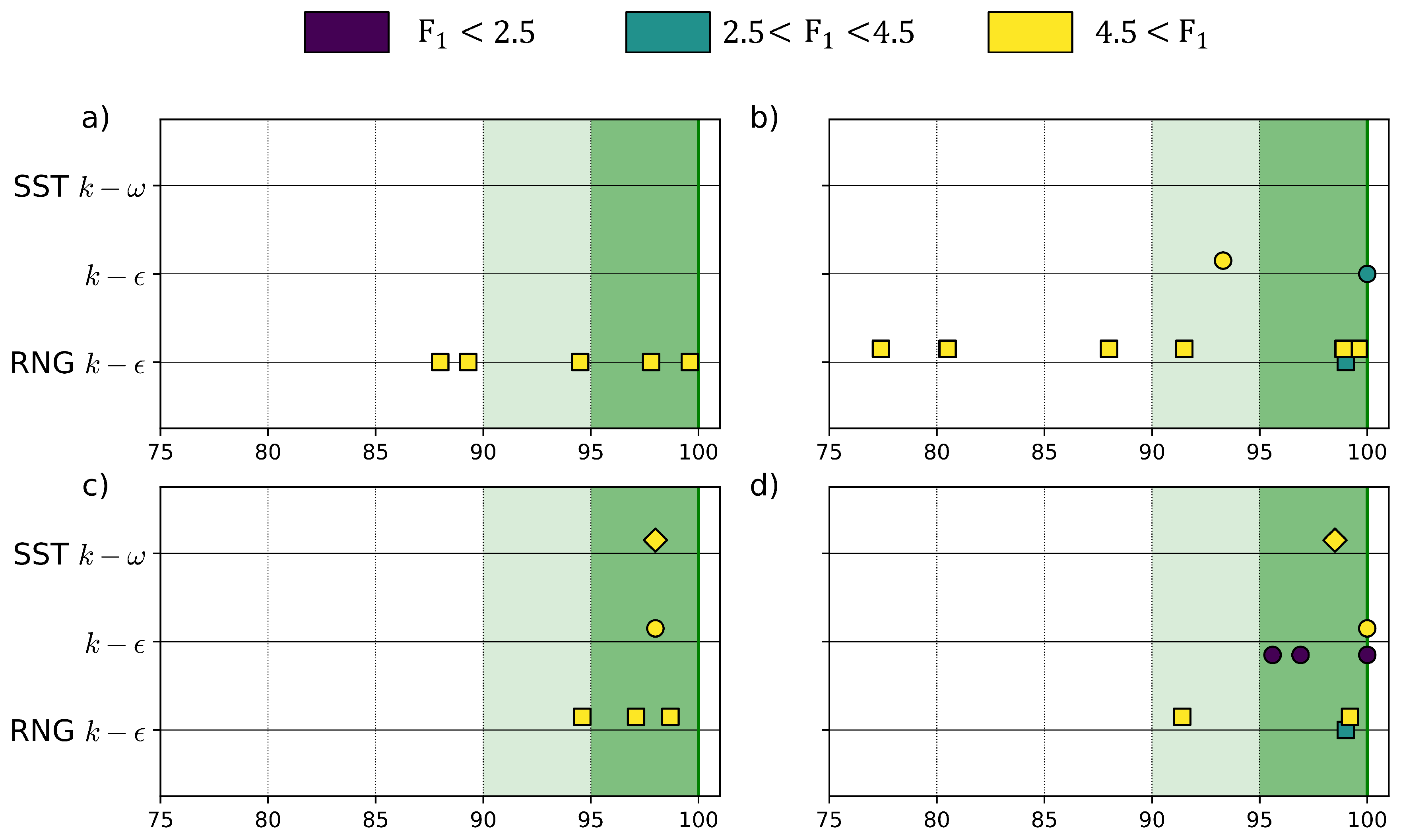
3.2. Reynolds-Averaged Navier–Stokes Approach
3.3. Detached Eddy Simulation and Large Eddy Simulation
3.4. Direct Numerical Simulation
3.5. Smoothed Particle Hydrodynamics
4. Conclusions
5. Future Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature and Abbreviations
Nomenclature
| inlet Froude number | |
| f | fraction of fluid |
| k | turbulence kinetic energy |
| mean pressure | |
| Reynolds stress tensor | |
| sub-grid scale stresses | |
| T | time interval |
| t | time |
| characteristic time-scale of the velocity fluctuations | |
| characteristic time-scale of the unsteadiness | |
| T | time interval |
| U | convection velocity |
| u | instantaneous velocity |
| mean velocity | |
| velocity fluctuation | |
| velocity fluctuation covariance | |
| coordinates () | |
| turbulence dissipation rate | |
| dynamic viscosity | |
| turbulent viscosity | |
| turbulent viscosity () | |
| fluid density | |
| specific dissipation rate |
Abbreviations
| ASME | American Society of Mechanical Engineers |
| CFD | Computational Fluid Dynamics |
| DES | Detached Eddy Simulation |
| DNS | Direct Numerical Simulation |
| FAVOR | Fractional Area-Volume Obstacle Representation |
| LES | Large Eddy Simulation |
| N-S | Navier Stokes |
| PDE | Partial Differential Equations |
| RANS | Reynolds-Averaged Navier Stokes |
| SPH | Smoothed Particles Hydrodynamics |
| USBR | United States Bureau of Reclamation |
| VOF | Volume of Fluid |
References
- Bradshaw, P.; Launder, B.E.; Lumley, J.L. Collaborative testing of turbulence models. J. Fluids Eng. 1996, 118, 243–247. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada Flintridge, CA, USA, 2006. [Google Scholar]
- Valero, D.; Viti, N.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 1: Experimental Data for Modelling Performance Assessment. Water 2018, in press. [Google Scholar]
- Valero, D.; Fullana, O.; Gacía-Bartual, R.; Andrés-Domenech, I.; Valles, F. Analytical formulation for the aerated hydraulic jump and physical modeling comparison. In Proceedings of the 3rd IAHR Europe Congress, Porto, Portugal, 14–16 April 2014. [Google Scholar]
- Bayon, A.; Valero, D.; García-Bartual, R.; Vallés-Morán, F.J.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Valero, D.; Bung, D.B.; Crookston, B.M. Energy dissipation of a Type III basin under design and adverse conditions for stepped and smooth spillways. J. Hydraul. Eng. 2018, 144, 04018036. [Google Scholar] [CrossRef]
- Frizell, K.W.; Svoboda, C.D. Performance of Type III Stilling Basins-Stepped Spillway Studies: Do Stepped Spillways Affect Traditional Design Parameters? US Department of the Interior, Bureau of Reclamation: Denver, CO, USA, 2012.
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Hirsch, C. Numerical Computation of Internal and External Flows: The Fundamentals of Computational Fluid Dynamics, 2nd ed.; Butterworth-Heinemann, Elsevier: Oxford, UK, 2007. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Prentice Hall: Englewood Cliffs, NJ, USA, 2007. [Google Scholar]
- Prosperetti, A.; Tryggvason, G. Computational Methods for Multiphase Flow; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Bombardelli, F. Computational multi-phase fluid dynamics to address flows past hydraulic structures. In Proceedings of the 4th IAHR International Symposium on Hydraulic Structures, Porto, Portugal, 9–11 February 2012. [Google Scholar]
- Carvalho, R.; Lemos, C.; Ramos, C. Numerical computation of the flow in hydraulic jump stilling basins. J. Hydraul. Res. 2008, 46, 739–752. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 2008, 39, 201–225. [Google Scholar] [CrossRef]
- Lemos, C.M. Wave Breaking: A Numerical Study; Brebbia, C.A., Orszag, S.A., Eds.; Lecture Notes in Engineering; Springer: New York, NY, USA, 1992. [Google Scholar]
- Qingchao, L.; Drewes, U. Turbulence characteristics in free and forced hydraulic jumps. J. Hydraul. Res. 1994, 32, 877–898. [Google Scholar] [CrossRef]
- Ubbink, O. Numerical Prediction of Two Fluid Systems with Sharp Interfaces. Ph.D. Thesis, Department of Mechanical Engineering, Imperial College of Science, Technology and Medicine, London, UK, 1997. [Google Scholar]
- Mortazavi, M.; Le Chenadec, V.; Moin, P.; Mani, A. Direct numerical simulation of a turbulent hydraulic jump: Turbulence statistics and air entrainment. J. Fluid Mech. 2016, 797, 60–94. [Google Scholar] [CrossRef]
- Fuster, D.; Bagué, A.; Boeck, T.; Le Moyne, L.; Leboissetier, A.; Popinet, S.; Ray, P.; Scardovelli, R.; Zaleski, S. Simulation of primary atomization with an octree adaptive mesh refinement and VOF method. Int. J. Multiph. Flow 2000, 35, 550–565. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 1999, 31, 567–603. [Google Scholar] [CrossRef]
- Madsen, P.A.; Svendsen, I.A. Turbulent bores and hydraulic jumps. J. Fluid Mech. 1983, 129, 1–25. [Google Scholar] [CrossRef]
- Valiani, A. Linear and angular momentum conservation in hydraulic jump. J. Hydraul. Res. 1997, 35, 323–354. [Google Scholar] [CrossRef]
- Madsen, P.A.; Simonsen, H.J.; Pan, C.H. Numerical simulation of tidal bores and hydraulic jumps. Coast. Eng. 2005, 52, 409–433. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Hager, W.H. Classical hydraulic jump: Basic flow features. J. Hydraul. Res. 2009, 47, 744–754. [Google Scholar] [CrossRef]
- Richard, G.L.; Gavrilyuk, S.L. The classical hydraulic jump in a model of shear shallow-water flows. J. Fluid Mech. 2013, 725, 492–521. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Hager, W.H. Non-Hydrostatic Free Surface Flows; Advances in Geophysical and Environmental Mechanics and Mathematics Book Series (AGEM); Springer: New York, NY, USA, 2017. [Google Scholar]
- Rodi, W. Turbulence Models and Their Application in Hydraulics, 3rd ed.; IAHR Monograph; Taylor & Francis: New York, NY, USA, 1993. [Google Scholar]
- Davidson, P. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Spalart, P.R.; Allmaras, S.R. A One-Equation Turbulence Model for Aerodynamic Flows. Rech. Aerosp. 1994, 1, 5–21. [Google Scholar]
- Jones, W.P.; Launder, B.E. The Prediction of Laminarization with a Two-Equation Model of Turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Launder, B.E.; Sharma, B.I. Application of the Energy Dissipation Model of Turbulence to the Calculation of Flow Near a Spinning Disc. Lett. Heat Mass Transf. 1974, 1, 131–138. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A Fluid Dyn. 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Spalart, P.R. Strategies for turbulence modeling and simulations. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the kw turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; NASA/CR-2014–218178, NF1676L-18332; NASA: Pasadena, CA, USA, 2014.
- Rodi, W.; Constantinescu, G.; Stoesser, T. Large-Eddy Simulation in Hydraulics; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Spalart, P.R.; Jou, W.-H.; Strelets, M.; Allmaras, S.R. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach. In Proceedings of the 1st AFOSR International Conference on Advances in DNS/LES, DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Alfonsi, G. On direct numerical simulation of turbulent flows. Appl. Mech. Rev. 2011, 64, 020802. [Google Scholar] [CrossRef]
- Moin, P.; Mahesh, K. Direct numerical simulation: A tool in turbulence research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Blocken, B.; Gualtieri, C. Ten iterative steps for model development and evaluation applied to Computational Fluid Dynamics for Environmental Fluid Mechanics. Environ. Model. Softw. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1998, 29, 123–160. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: Validation—What does it mean? J. Fluids Eng. 2009, 131, 034503. [Google Scholar] [CrossRef]
- Knight, D.W.; Wright, N.G.; Morvan, H.P. Guidelines for Applying Commercial CFD Software to Open Channel Flow; Report Based on Research Work Conducted under EPSRC Grants GR/R43716/01 and GR/R43723/01; EPSRC: Swindon, UK, 2005. [Google Scholar]
- Lane, S.N.; Hardy, R.J.; Ferguson, R.I.; Parsons, D.R. A framework for model verification and validation of CFD schemes in natural open channel flows. In Computational Fluid Dynamics: Applications in Environmental Hydraulics; Bates, P.D., Lane, S.N., Ferguson, R.I., Eds.; John Wiley & Sons: Chichester, UK, 2005. [Google Scholar]
- ASME. Perspective: Journal of Fluids Engineering Editorial Policy Statement on the Control of Numerical Accuracy. J. Fluids Eng. 2009, 115, 339–340. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Violeau, D. Fluid Mechanics and the SPH Method: Theory and Applications; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Violeau, D.; Rogers, B.D. Smoothed particle hydrodynamics (SPH) for free-surface flows: Past, present and future. J. Hydraul. Res. 2016, 54, 1–26. [Google Scholar] [CrossRef]
- Reynolds, O. On the dynamical theory of incompressible viscous fluids and the determination of the criterion. Philos. Trans. R. Soc. Lond. A 1895, 186, 123–164. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 1999, 41, 181–202. [Google Scholar] [CrossRef]
- Labourasse, E.; Lacanette, D.; Toutant, A.; Lubin, P.; Vincent, S.; Lebaigue, O.; Caltagirone, J.-P.; Sagaut, P. Towards large eddy simulation of isothermal two-phase flows: Governing equations and a priori tests. Int. J. Multiph. Flow 2007, 33, 1–39. [Google Scholar] [CrossRef]
- López, D.; Marivela, R.; Garrote, L. Smoothed particle hydrodynamics model applied to hydraulic structures: A hydraulic jump test case. J. Hydraul. Res. 2010, 48, 142–158. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S.; Torti, E. 3D SPH modeling of hydraulic jump in a very large channel. J. Hydraul. Res. 2010, 51, 158–173. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH numerical investigation of characteristics of hydraulic jumps. Environ. Fluid Mech. 2018, 18, 849–870. [Google Scholar] [CrossRef]
- Chippada, S.; Ramaswamy, B.; Wheeler, M.F. Numerical simulation of hydraulic jump. Int. J. Numer. Meth. Eng. 1994, 37, 1381–1397. [Google Scholar] [CrossRef]
- Zhao, Q.; Misra, S.K.; Svendsen, I.A.; Kirby, J.T. Numerical study of a turbulent hydraulic jump. In Proceedings of the 17th Engineering Mechanics Division Conference, Newark, DE, USA, 13–16 June 2004. [Google Scholar]
- Gonzalez, A.; Bombardelli, F. Two-phase-flow theoretical and numerical models for hydraulic jumps, including air entrainment. In Proceedings of the 31st IAHR Congress, Beijing, China, 16–21 September 2005. [Google Scholar]
- Abbaspour, A.; Farsadizadeh, D.; Hosseinadeh, A.D.; Sadraddini, A.A. Numerical study of hydraulic jumps on corrugated beds using turbulence models. Turk. J. Eng. Environ. Sci. 2009, 33, 61–72. [Google Scholar] [CrossRef]
- Ma, J.; Oberai, A.A.; Lahey, R.T.; Drew, D.A. Modeling air entrainment and transport in a hydraulic jump using two-fluid RANS and DES turbulence models. Heat Mass Transf. 2011, 47, 911. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Salmasi, F.; Abbaspour, A. Numerical Study of Hydraulic Jump on Rough Beds Stilling Basins. J. Civ. Eng. Urban. 2013, 3, 19–24. [Google Scholar]
- Bayon-Barrachina, A.; Lopez-Jimenez, P.A. Numerical analysis of hydraulic jumps using OpenFOAM. J. Hydroinform. 2015, 17, 662–678. [Google Scholar] [CrossRef]
- Witt, A.; Gulliver, J.; Shen, L. Simulating air entrainment and vortex dynamics in a hydraulic jump. Int. J. Multiph. Flow 2015, 72, 165–180. [Google Scholar] [CrossRef]
- Witt, A.; Gulliver, J.; Shen, L. Numerical investigation of vorticity and bubble clustering in an air entraining hydraulic jump. Comput. Fluids 2018, 172, 162–180. [Google Scholar] [CrossRef]
- Harada, S.; Li, S.S. Modeling hydraulic jump using the bubbly two-phase flow method. Environ. Fluid Mech. 2018, 18, 335–356. [Google Scholar] [CrossRef]
- Jesudhas, V.; Balachandar, R.; Roussinova, V.; Barron, R. Turbulence Characteristics of Classical Hydraulic Jump Using DES. J. Hydraul. Eng. 2018, 144, 04018022. [Google Scholar] [CrossRef]
- Lubin, P.; Glockner, S.; Chanson, H. Numerical Simulation of Air Entrainment and Turbulence in a Hydraulic Jump. In Proceedings of the Colloque SHF Modèles Modèles Physiques Hydrauliques, Lyon, France, 24–25 November 2009. [Google Scholar]
- Kothe, D.B.; Mjolsness, R.C.; Torrey, M.D. RIPPLE: A Computer Program for Incompressible Flows with Free Surfaces; Los Alamos Report, LA-72007-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 1994.
- Bakunin, J. Experimental Study of Hydraulic Jumps in Low Froude Number Range. Ph.D. Thesis, Department of Civil and Environmental Engineering, University of Delaware, Newark, DE, USA, 1995. [Google Scholar]
- Svendsen, I.A.; Veeramony, J.; Bakunin, J.; Kirby, J.T. The flow in weak turbulent hydraulic jumps. J. Fluid Mech. 2000, 418, 25–57. [Google Scholar] [CrossRef]
- Liu, M.; Rajaratnam, N.; Zhu, D.Z. Turbulence structure of hydraulic jumps of low Froude numbers. J. Hydraul. Eng. 2004, 130, 511–520. [Google Scholar] [CrossRef]
- Hager, W.H. Energy Dissipators and Hydraulic Jump; Water Science and Technology Library; Springer: New York, NY, USA, 1992; Volume 8, ISBN 978-90-481-4106-7. [Google Scholar]
- Darwish, M.S.; Moukalled, F. The Normalized Weighting Factor Method: A Novel Technique for Accelerating the Convergence of High-Resolution Convective Schemes. Numer. Heat Transf. Fundam. 1996, 30, 217–237. [Google Scholar] [CrossRef]
- Rider, W.J.; Kothe, D.B. Reconstructing Volume Tracking. J. Comput. Phys. 1998, 141, 112–152. [Google Scholar] [CrossRef]
- Hirt, C.W.; Sicilian, J.M. A porosity technique for the definition of obstacles in rectangular cell meshes. In Proceedings of the 4th International Conference on Ship Hydrodynamics, National Academy of Science, Washington, DC, USA, 24–27 September 1985. [Google Scholar]
- Ead, S.A.; Rajaratnam, N. Hydraulic jumps on corrugated beds. J. Hydraul. Eng. 2002, 128, 656–663. [Google Scholar] [CrossRef]
- Murzyn, F.; Mouaze, D.; Chaplin, J.R. Optical fibre probe measurements of bubbly flow in hydraulic jumps. Int. J. Multiph. Flow 2005, 31, 141–154. [Google Scholar] [CrossRef]
- Elsebaie, I.H.; Shabayek, S. Formation of Hydraulic Jumps on Corrugated Beds. Int. J. Civ. Environ. Eng. 2005, 10, 37–47. [Google Scholar]
- Wu, S.; Rajaratnam, N. Transition from Hydraulic Jump to Open Channel Flow. J. Hydraul. Eng. 1996, 122, 158–173. [Google Scholar] [CrossRef]
- Lin, C.; Hsieh, S.C.; Lin, I.J.; Chang, K.A.; Raikar, R.V. Flow property and self-similarity in steady hydraulic jumps. Exp. Fluids 2012, 53, 1591–1616. [Google Scholar] [CrossRef]
- Bakhmeteff, B.A.; Matzke, A.E. The hydraulic jump in terms of dynamic similarity. ASCE Trans. 1936, 101, 630–680. [Google Scholar]
- Hager, W.H.; Sinniger, R. Flow characteristics of the hydraulic jump in a stilling basin with an abrupt bottom rise. J. Hydraul. Res. 1985, 23, 101–113. [Google Scholar] [CrossRef]
- Hager, W.H.; Bremen, R. Classical hydraulic jump: Sequent depths. J. Hydraul. Res. 1989, 27, 565–585. [Google Scholar] [CrossRef]
- Chanson, H.; Carvalho, R. Hydraulic jumps and stilling basins. In Energy Dissipation in Hydraulic Structures; Chanson, H., Ed.; CRC Press: Leiden, The Netherlands, 2015; pp. 65–104. ISBN 978-1-138-02755-8. [Google Scholar]
- Wang, H.; Chanson, H. Experimental study of turbulent fluctuations in hydraulic jumps. J. Hydraul. Eng. 2015, 141, 04015010. [Google Scholar] [CrossRef]
- Bombardelli, F. Integral turbulent length and time scales in hydraulic jumps: An experimental investigation at large Reynolds numbers. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Kucukali, S.; Chanson, H. Turbulence in Hydraulic Jumps: Experimental Measurements; CH62/07; Department of Civil Engineering, The University of Queensland: Brisbane, Australia, 2007. [Google Scholar]
- Bradley, J.N.; Peterka, A.J. Hydraulic Design of Stilling Basins. ASCE J. Hydraul. Div. 1957, 83, 1401–1406. [Google Scholar]
- Chanson, H.; Brattberg, T. Experimental study of the air-water shear flow in a hydraulic jump. Int. J. Multiph. Flow 2000, 26, 583–607. [Google Scholar] [CrossRef]
- Murzyn, F.; Chanson, H. Free-surface fluctuations in hydraulic jumps: Experimental observations. Exp. Therm. Fluid Sci. 2018, 33, 1055–1064. [Google Scholar] [CrossRef]
- Murzyn, F.; Chanson, H. Free Surface, Bubbly Flow and Turbulence Measurements in Hydraulic Jumps; CH63/07; Department of Civil Engineering, The University of Queensland: Brisbane, Australia, 2007. [Google Scholar]
- Mossa, M. On the oscillating characteristics of hydraulic jumps. J. Hydraul. Res. 1999, 34, 541–558. [Google Scholar] [CrossRef]


| Dimensional Scale | Unit | Equation |
|---|---|---|
| Turbulent kinetic energy | L/T | |
| Turbulence dissipation rate | L/T | |
| Specific dissipation rate | 1/T |
| RANS | DES | LES | DNS | |
|---|---|---|---|---|
| Modeling approach | Reynolds-averaged | RANS-LES coupling | Sub-grid scale | Not necessary |
| Large scales/inertial Subrange/dissipation scale | M/M/M | R/M/M | R/R/M | R/R/R |
| Expected accuracy | Mean variables | Allow inertial’ modeling | Allow inertial’ modeling | Up to the Kolmogorov scale |
| Computational cost | Low | High | High | Extremely high |
| Flow Field Description | Approach | References |
|---|---|---|
| Lagrangian | Smoothed Particle Hydrodynamics | Gingold and Monhagan [50] |
| Monaghan [51] | ||
| Violeau [52] | ||
| Violeau and Rogers [53] | ||
| Eulerian | Reynolds-Averaged Navier–Stokes | Reynolds [54] |
| Rodi [28] | ||
| Spalart [36] | ||
| Wilcox [2] | ||
| Detached Eddy Simulation Large Eddy Simulation | Spalart [55] | |
| Labourasse et al. [56] | ||
| Rodi et al. [39] | ||
| Direct Numerical Simulation | Moin and Mahesh [42] | |
| Prosperetti and Tryggvason [11] | ||
| Alfonsi [41] |
| Turbulence Model | References |
|---|---|
| Standard | Jones and Launder [31] |
| Launder and Sharma [32] | |
| RNG | Yakhot and Orszag [33] |
| Yakhot et al. [34] | |
| Wilcox [2] | |
| Wilcox [37] | |
| SST | Menter [35] |
| Flow Field Description | References | Year | Numerical Approach | Turbulence Model | Resolution Dependence Study | |
|---|---|---|---|---|---|---|
| Lagrangian Methods | Lopez et al. [57] | 2010 | SPH | Meshless method | 3.25, 3.41, 3.58, 3.61, 3.64, 4.12, 4.45, 4.88, 5.13, 5.24, 6.62, 7.06, 7.16 | |
| De Padova et al. [58] | 2013 | XSPH | mixing length and | Meshless method | 3.90, 8.30 | |
| De Padova et al. [59] | 2018 | XSPH | mixing length and | Meshless method | 2.58, 2.66, 2.70, 3.89, 4.99, 5.11 | |
| Eulerian Methods | Chippada et al. [60] | 1994 | RANS | STD | − | 2.00, 4.00 |
| Zhao et al. [61] | 2004 | RANS | STD , | − | 1.46 | |
| Gonzalez and Bombardelli [62] | 2005 | RANS | STD | √ | 2.00, 2.50, 3.32 | |
| Carvalho et al. [14] | 2008 | RANS | RNG | − | 6.00 | |
| Abbaspour et al. [63] | 2009 | RANS | STD RNG | − | 4.00, 4.70, 5.00, 5.70, 5.80, 6.10, 7.00, 7.20, 8.00 | |
| Ma et al. [64] | 2011 | RANS | SST | − | 1.98 | |
| Ebrahimi et al. [65] | 2013 | RANS | STD | − | 3.00, 3.30, 3.60, 3.60, 5.00, 5.70, 6.70, 8.00 | |
| Bayon-Barrachina and [66] | 2015 | RANS RANS | STD RNG SST | √ | 6.10 | |
| Witt et al. [67] | 2015 | RANS | realizable | √ | 2.43, 3.65, 4.82 | |
| Bayon et al. [5] | 2016 | RANS | RNG | √ | 6.50 | |
| Witt et al. [68] | 2018 | RANS | realizable | √ | 2.43, 3.65, 4.82 | |
| Harada and Li [69] | 2018 | RANS | , | √ | 5.80 | |
| Valero et al. [6] | 2018 | RANS | RNG , | √ | 3.12, 3.88, 4.20, 6.17, 6.37, 6.47, 8.27, 9.52 | |
| Ma et al. [64] | 2011 | DES | √ | 1.98 | ||
| Jesudhas et al. [70] | 2018 | DES | √ | 8.5 | ||
| Gonzalez and Bombardelli [62] | 2005 | LES | √ | 2.00, 2.50, 3.32 | ||
| Lubin et al. [71] | 2009 | LES | − | 5.09 | ||
| Mortazavi et al. [19] | 2016 | DNS | Full solution of all the scales | √ | 2.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viti, N.; Valero, D.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook. Water 2019, 11, 28. https://doi.org/10.3390/w11010028
Viti N, Valero D, Gualtieri C. Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook. Water. 2019; 11(1):28. https://doi.org/10.3390/w11010028
Chicago/Turabian StyleViti, Nicolò, Daniel Valero, and Carlo Gualtieri. 2019. "Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook" Water 11, no. 1: 28. https://doi.org/10.3390/w11010028
APA StyleViti, N., Valero, D., & Gualtieri, C. (2019). Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook. Water, 11(1), 28. https://doi.org/10.3390/w11010028






