Improving the Performance of Vegetable Leaf Wetness Duration Models in Greenhouses Using Decision Tree Learning
Abstract
1. Introduction
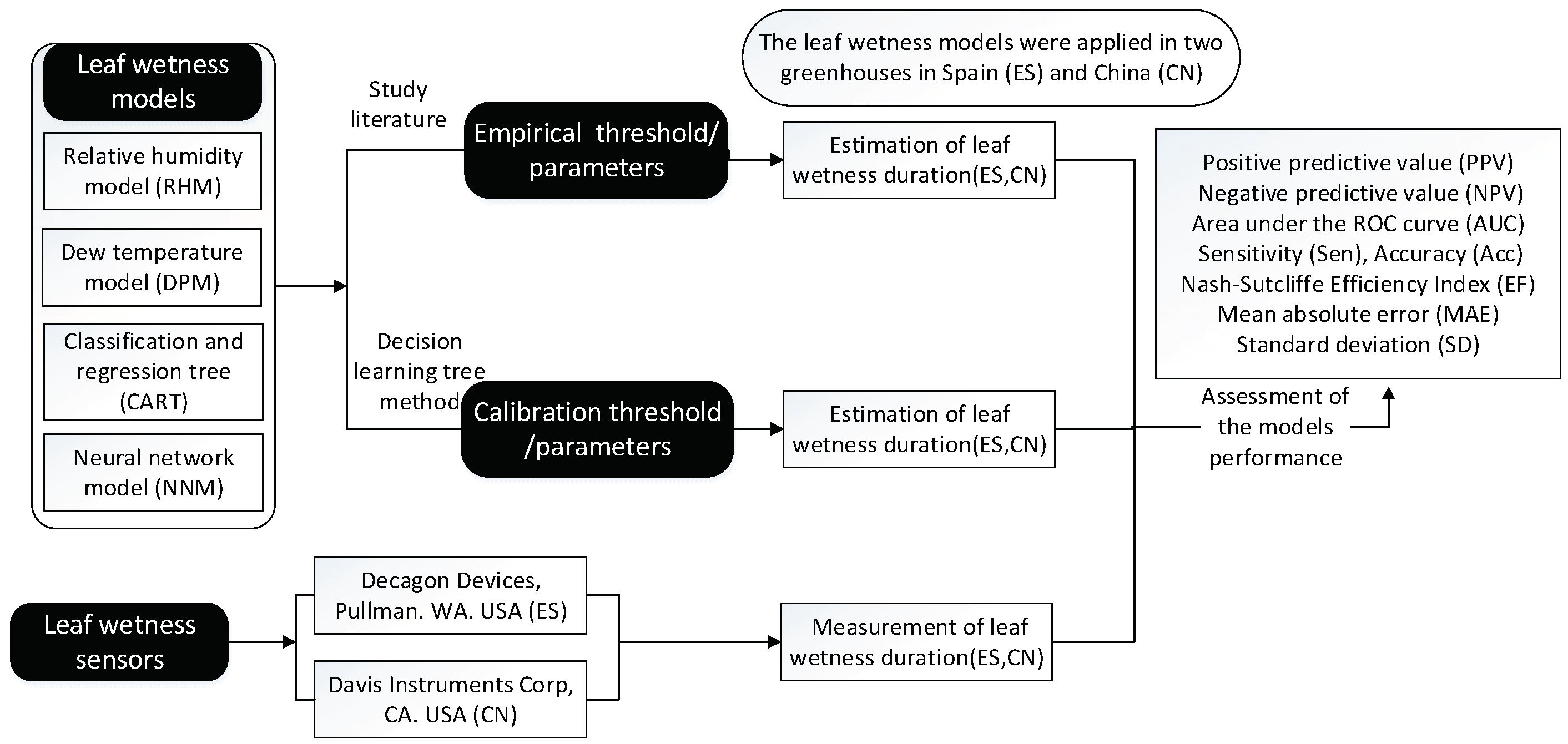
2. Materials and Methods
2.1. Greenhouse Facilities and Leaf Wetness Duration Monitoring
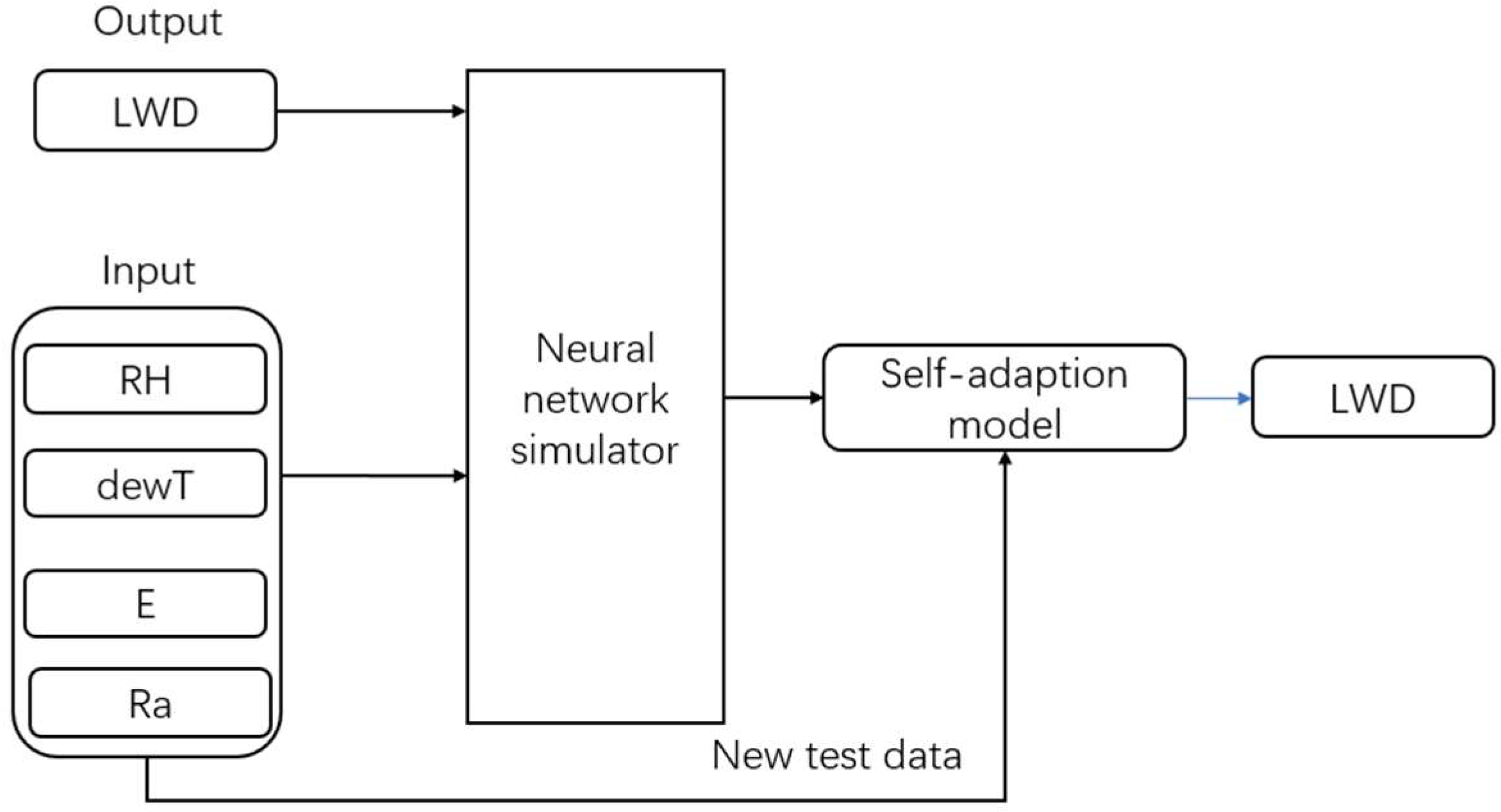
2.2. Model Description
- 1
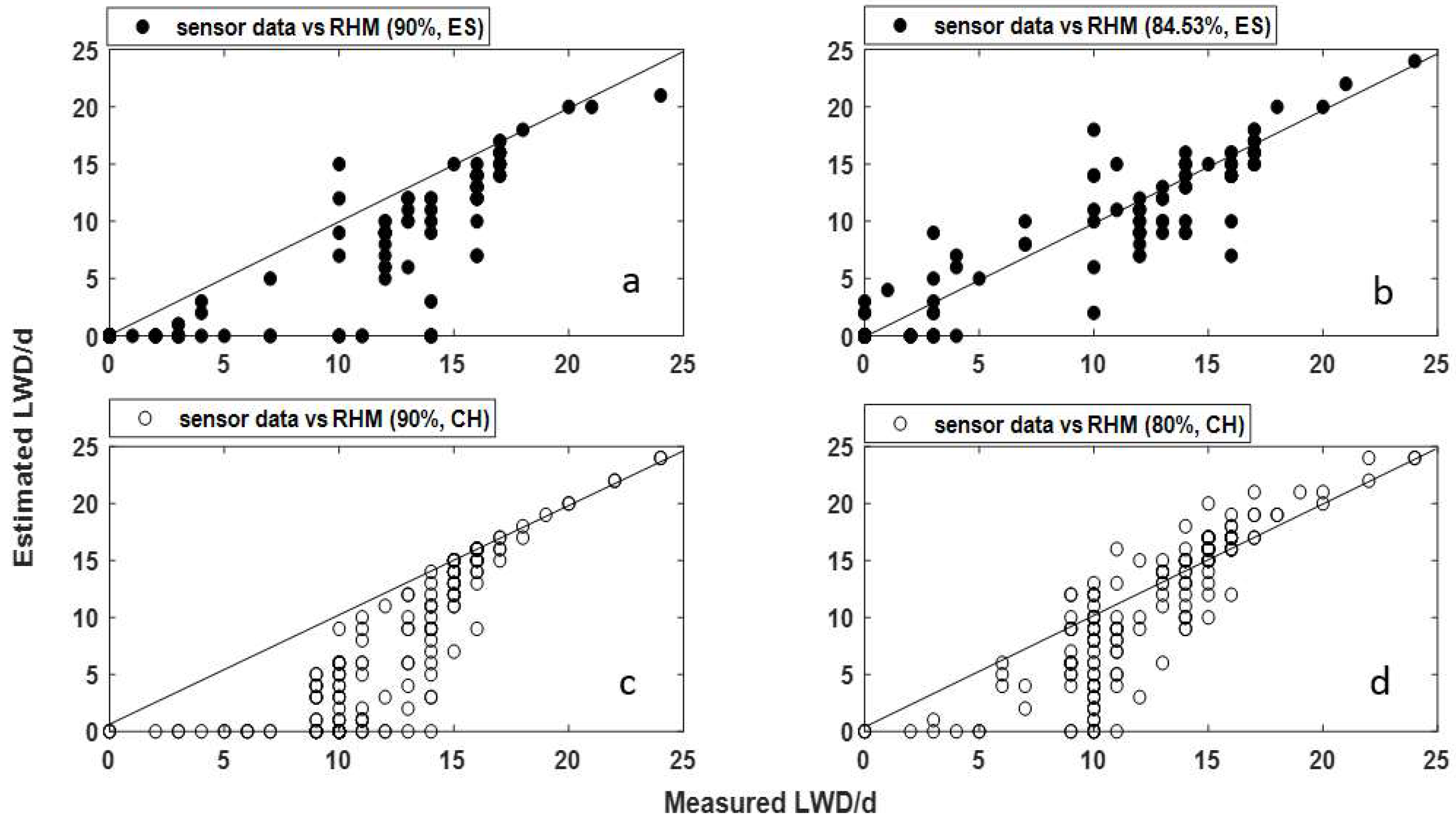
- The RHM assumes the LWD is equal to the number of hours that RH is greater than or equal to a constant threshold. If the RH is below that threshold, the leaves are assumed to be dry; conversely, if the RH is above the threshold, the leaves are assumed to be wet. In this case, we set the empirical threshold to 90% according to the cases of the relative humidity model application in disease warning systems; an optimal RHM threshold (RH ≥ 90%) was used in an existing cucumber downy mildew warning system [11], a strawberry disease-warning systems in four US states [30], and a potato late blight model [31].
- 2
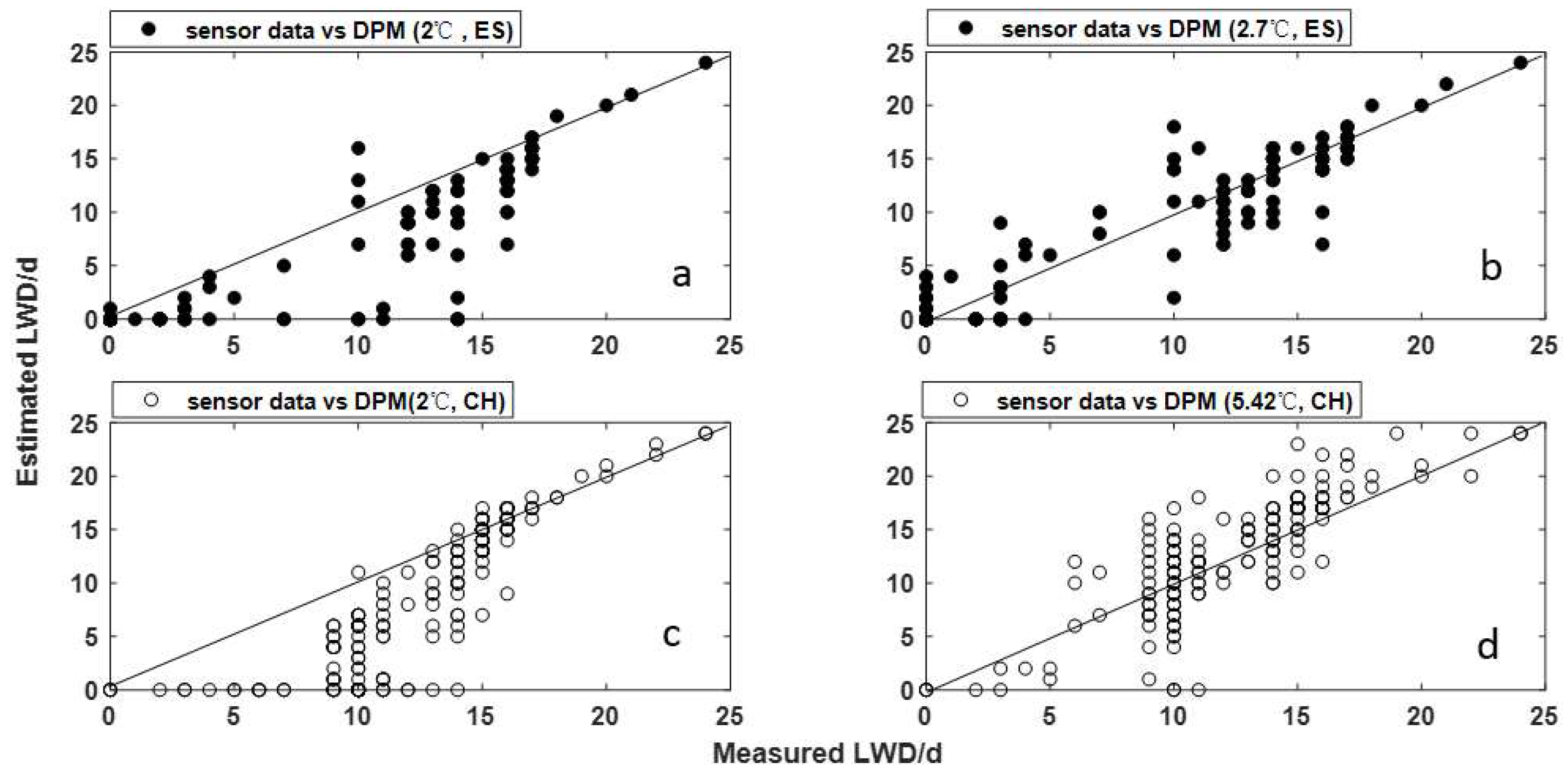
- The DPM is based on the difference value (DPD) between the air temperature (T) and the dew point temperature (dewT) [4]. Dew occurs only when the difference is below a certain threshold (2 °C) [32]. This model was used by Huber and Gillespie [4] and by Gillespie et al. [16]. The same model was also applied in other studies on leaf wetness estimation [13,32]. In this study, we kept the dew point threshold to 2 °C to determine dew presence in the two greenhouse systems.
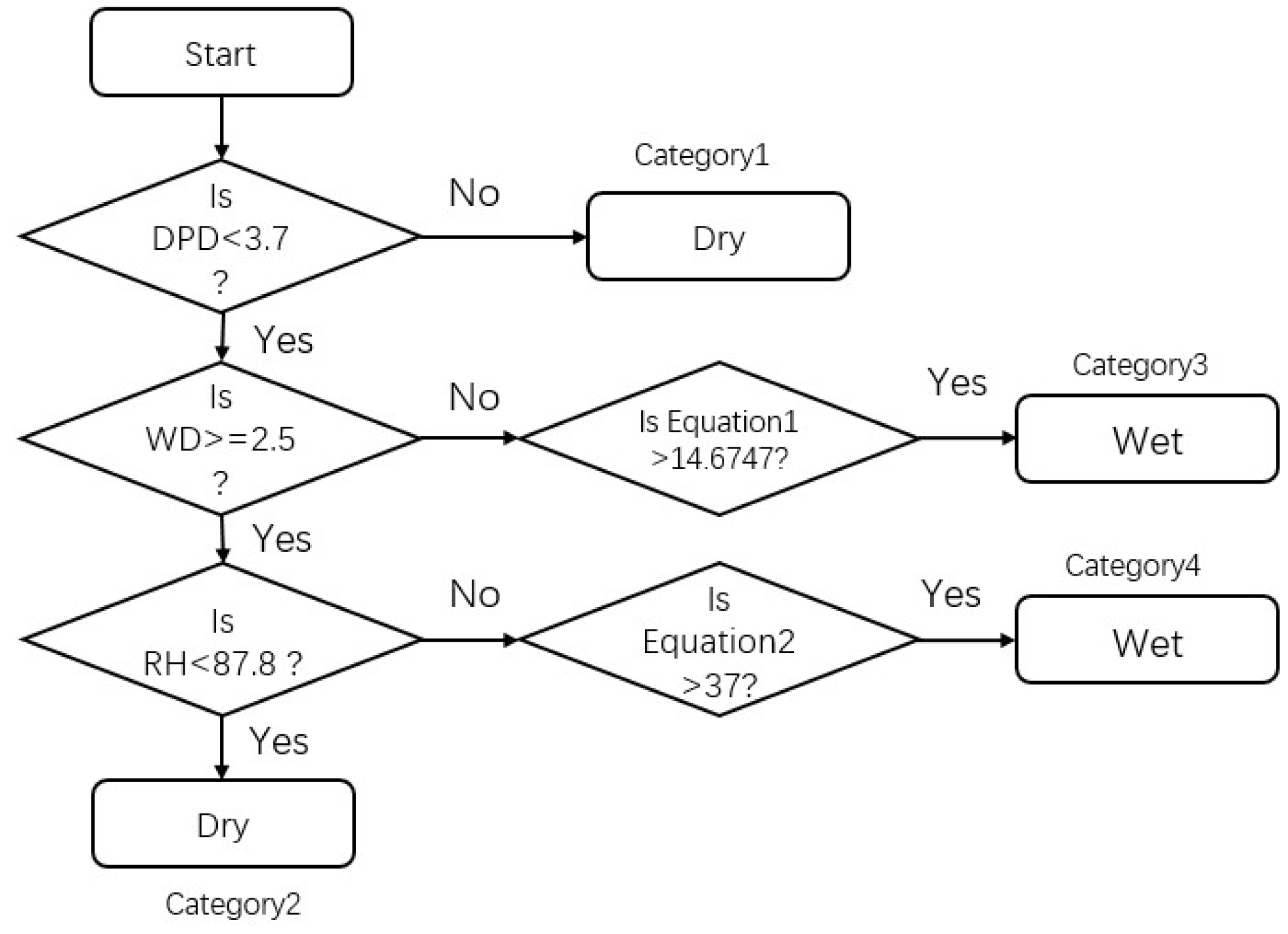
- 3
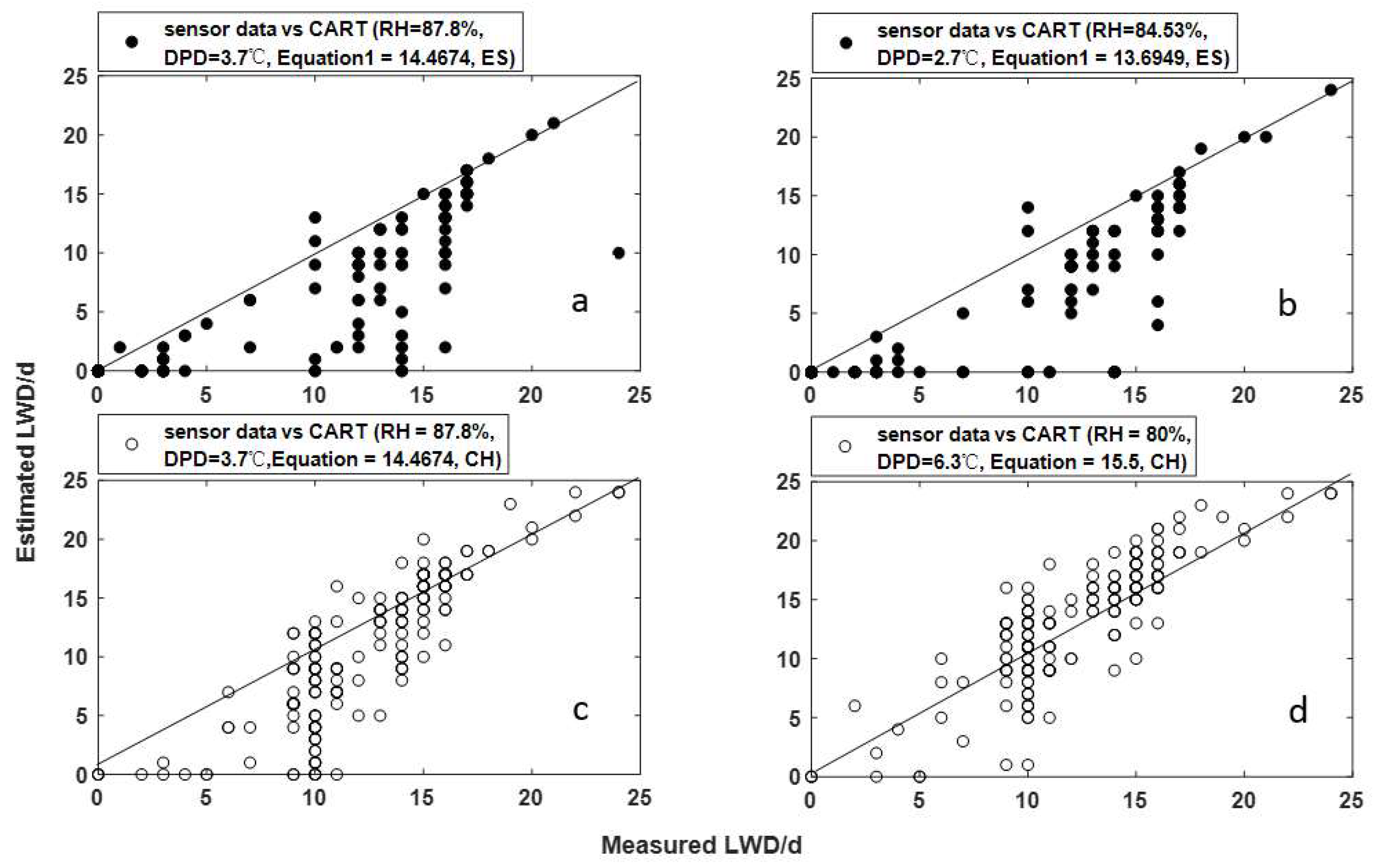
- The CART model [33] has four category conditions to identify whether leaves are dry or wet (Figure 4); these are the hours considered dry if either the hourly different value (DPD) is equal or greater than 3.7 °C (category 1) or if the relative humidity (RH) is less than 87.8% and the hourly wind speed (WD) is equal or greater than 2.5 m s−1 (category 2). The hours in category 3 (Equation (1)) and category 4 (Equation (2)) are classified as either dry or wet by a subsequent stepwise linear discriminant analysis.
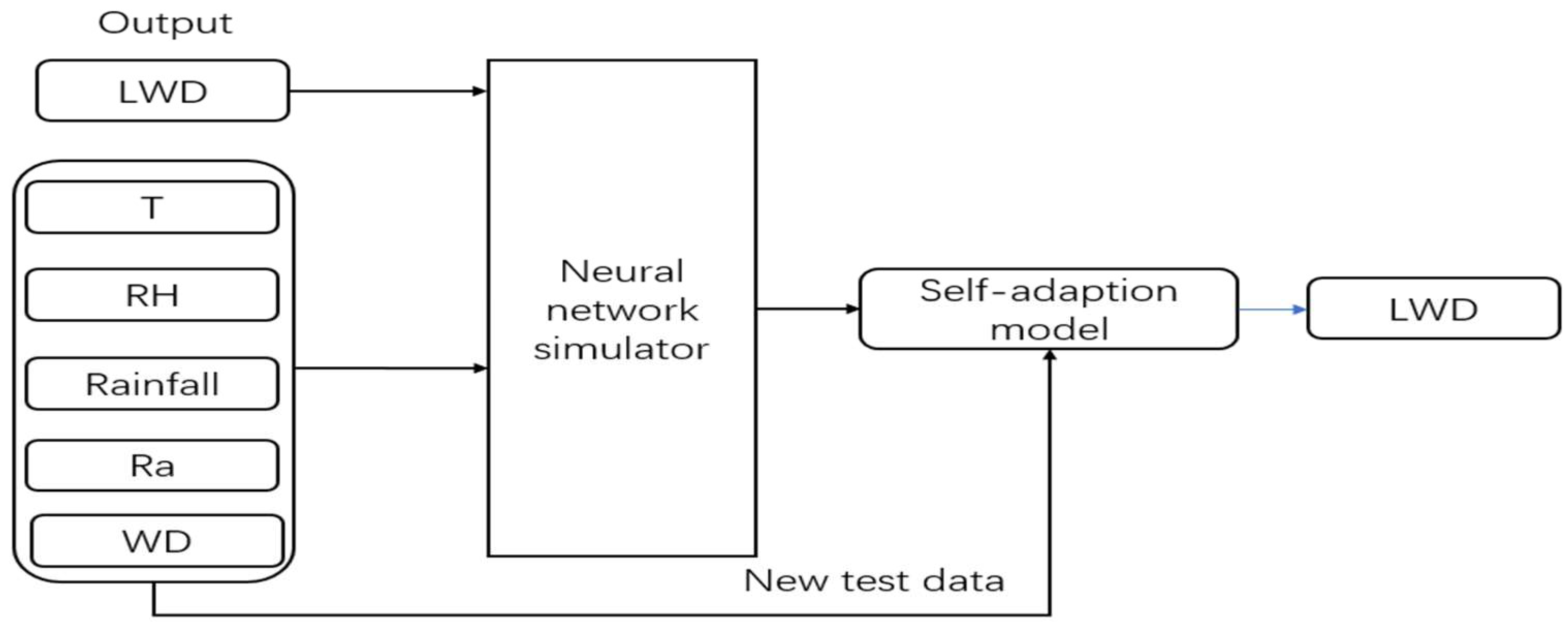
- 4
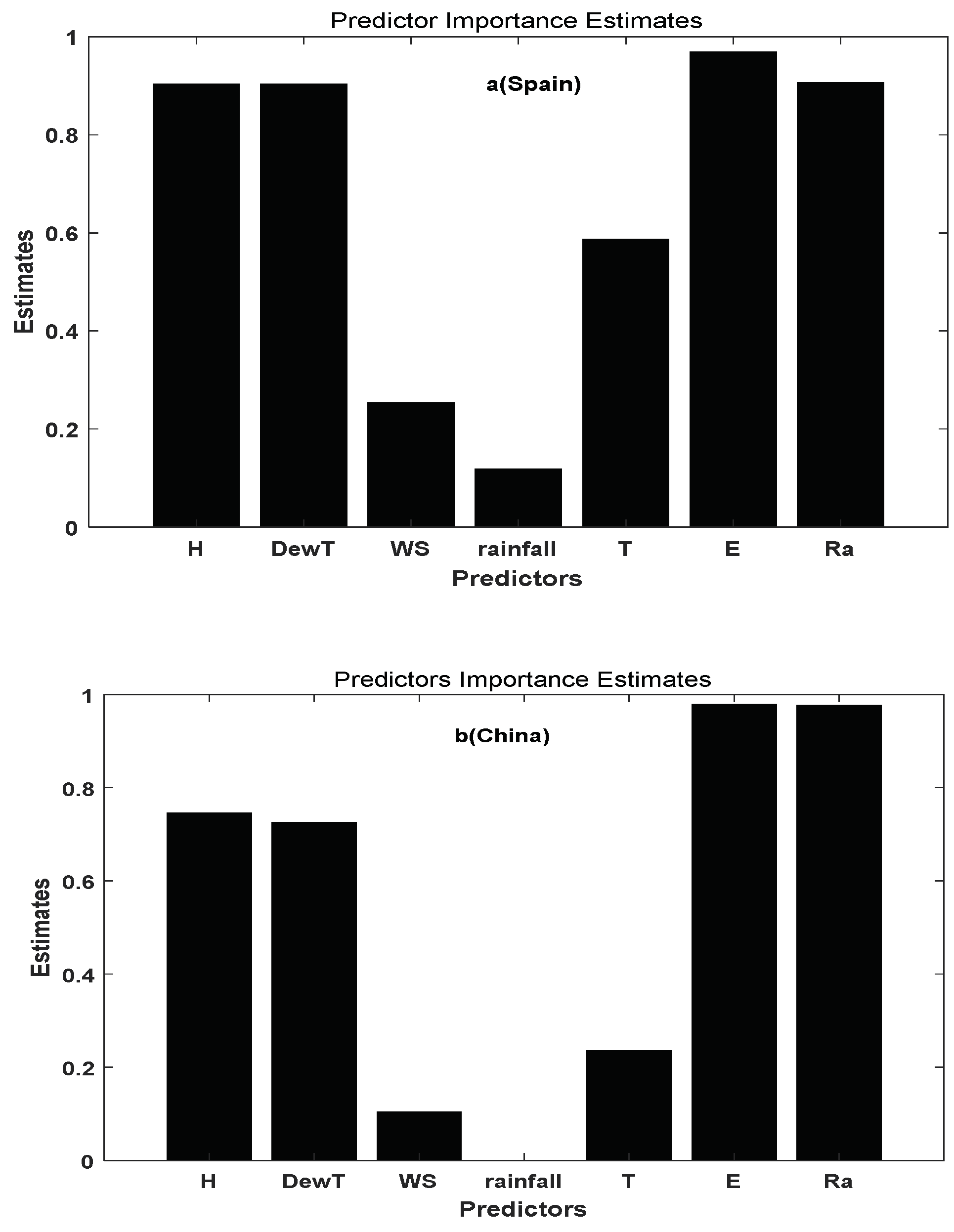
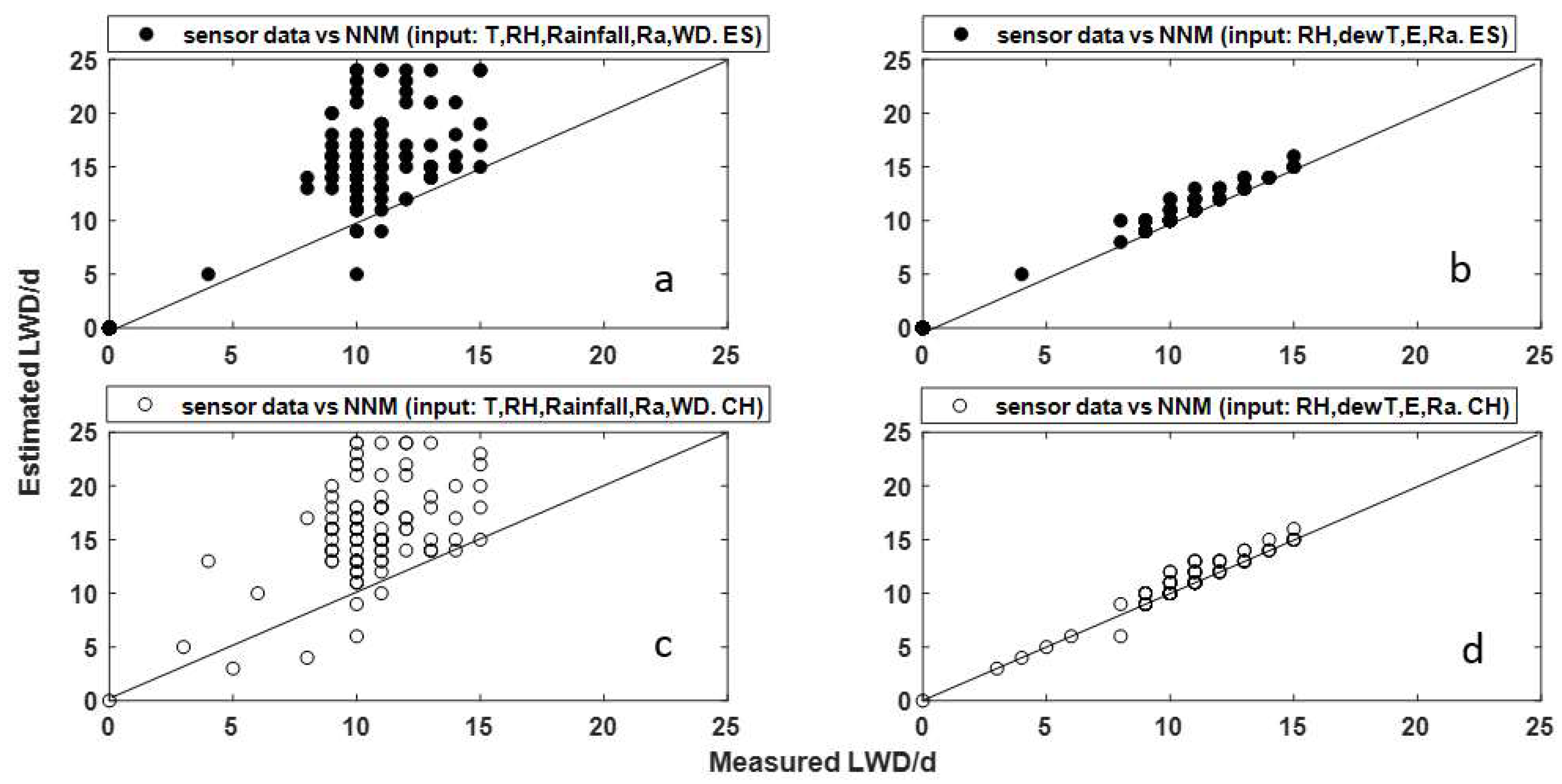
- A neural network model (NNM) is a method to predict a set of outputs from a set of input patterns [34]. It is like a central nervous system that can learn tasks by considering examples. Leaf wetness is the output of a neural network-based leaf wetness model [14]. Francl et al. estimated wheat leaf wetness using the inputs of temperature, relative humidity, solar radiation, precipitation, wind direction, and wind speed [24]. Marta et al. carried out the model in 47 weather stations, and its input parameters were rainfall, vapor pressure deficit, wind speed and solar global radiation [29]. Stella et al. [25] used the inputs (temperature, relative humidity, rainfall, wind speed and solar radiation) in a neural network model for estimating apple leaf wetness. We chose the empirical input parameters of NNM that are shown in Figure 5, in which T is temperature (°C); RH is relative humidity (%); DPD is dew point depression (°C); WD is wind speed (m/s) and Ra is global radiation (W2).
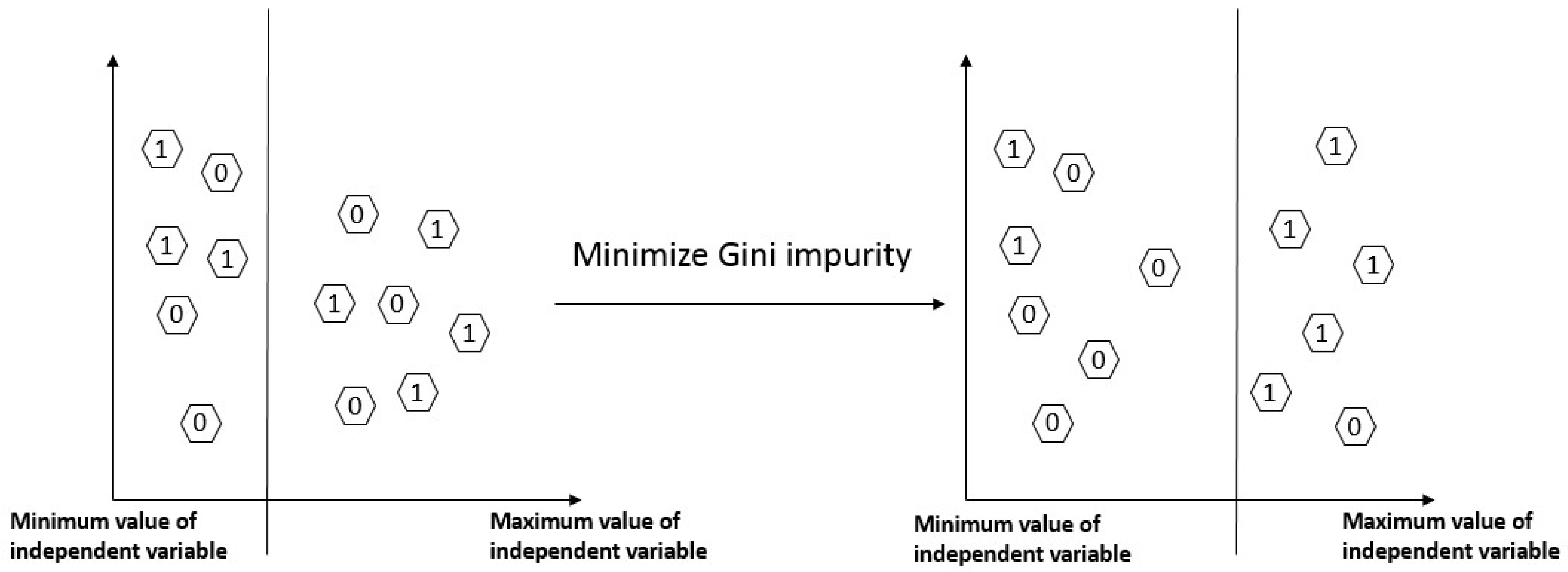
2.3. Decision Learning Tree (DLT) Method
2.4. Evaluation Criteria
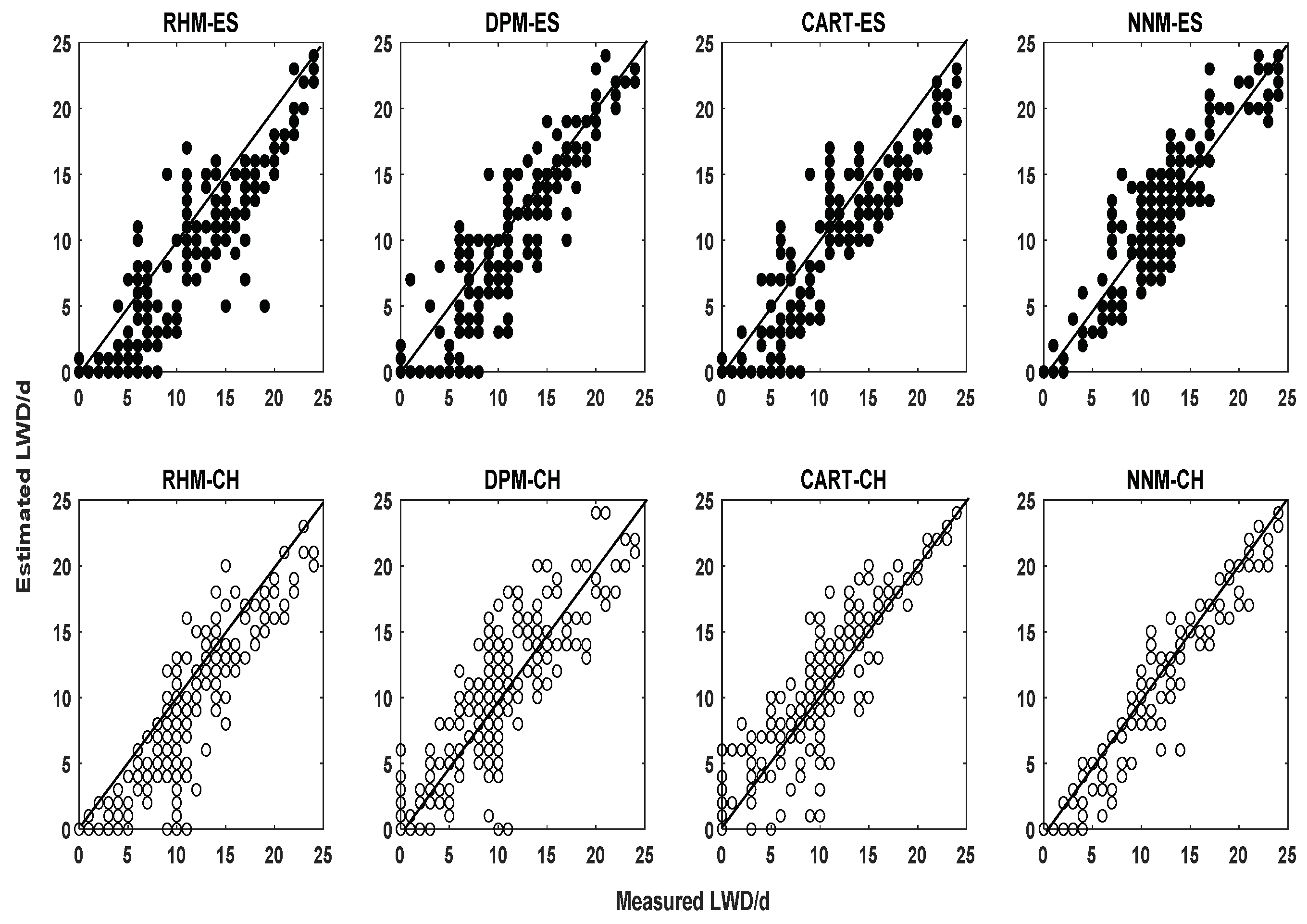
3. Results
4. Discussion
5. Conclusions
- The calibration of the parameters of leaf wetness models is effective for reducing the error between estimated LWD and measured LWD, and thus has the potential to greatly improve the model accuracy.
- Humidity, dew temperature, transpiration and radiation are the variables mostly contributing to the precision of a neural network model (NNM) for LWD estimation.
- Evaluation results showed that NNM was the most accurate in estimating LWD both in Spanish and Chinese greenhouses, with low error between estimated and measured LWD. All the other models obtained similar results in the two tested conditions.
Author Contributions
Funding
Conflicts of Interest
References
- Magarey, R.D.; Russo, J.M.; Seem, R.C.; Gadoury, D.M. Surface wetness duration under controlled environmental conditions. Agric. For. Meteorol. 2005, 128, 111–122. [Google Scholar] [CrossRef]
- Emilio, M.; Franco, E.; Troncozo, M.I.; Marianela, S.; López, Y.; Lucentini, G.; Medina, R.; Carlos, M.; Saparrat, N.; Ronco, L.B.; et al. A survey on tomato leaf grey spot in the two main production areas of Argentina led to the isolation of Stemphylium lycopersici representatives which were genetically diverse and differed in their virulence. Eur. J. Plant Pathol 2017, 149, 983–1000. [Google Scholar] [CrossRef]
- Ward, J.M.; Stromberg, E.L.; Nowell, D.C.; Nutter Jr, F.W. Gray leaf spot: a disease of global importance in maize production. Plant Dis. 1999, 83, 884–895. [Google Scholar] [CrossRef]
- Huber, L.; Gillespie, T.J. Modeling leaf wetness in relation to plant disease epidemiology. Ann. Rev. Phytopathol 1992, 30, 553–577. [Google Scholar] [CrossRef]
- Magarey, R.D.; Sutton, T.B.; Thayer, C.L. A Simple Generic Infection Model for Foliar Fungal Plant Pathogens. Phytopathology 2005, 95, 92–100. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, F.; Berenguel, M.; Guzmán, J.L.; Ramírez-Arias, A. Modeling and Control of Greenhouse Crop Growth; Springer: London, UK, 2015; ISBN 978-3-319-11133-9. [Google Scholar]
- Sánchez-Molina, J.A.; Rodríguez, F.; Guzmán, J.L.; Arahal, M.R. Virtual sensors for designing irrigation controllers in greenhouses. Sensors 2012, 12, 15244–15266. [Google Scholar] [CrossRef]
- Sentelhas, P.C.; Gillespie, T.J.; Santos, E.A. Evaluation of FAO Penman–Monteith and alternative methods for estimating reference evapotranspiration with missing data in Southern Ontario, Canada. Agric. Water Manag. 2010, 97, 635–644. [Google Scholar] [CrossRef]
- Magarey, R.D.; Russo, J.M.; Seem, R.C. Simulation of surface wetness with a water budget and energy balance approach. Agric. For. Meteorol. 2006, 139, 373–381. [Google Scholar] [CrossRef]
- Bregaglio, S.; Frasso, N.; Pagani, V.; Stella, T.; Francone, C.; Cappelli, G.; Acutis, M.; Balaghi, R.; Ouabbou, H.; Paleari, L.; et al. New multi-model approach gives good estimations of wheat yield under semi-arid climate in Morocco. Agron. Sustain. Dev. 2015, 35, 157–167. [Google Scholar] [CrossRef]
- Zhao, C.J.; Li, M.; Yang, X.T.; Sun, C.H.; Qian, J.P.; Ji, Z.T. A data-driven model simulating primary infection probabilities of cucumber downy mildew for use in early warning systems in solar greenhouses. Comput. Electron. Agric. 2011, 76, 306–315. [Google Scholar] [CrossRef]
- Mashonjowa, E.; Ronsse, F.; Mubvumac, M.; Milford, J.R.; Pieters, J.G. Estimation of leaf wetness duration for greenhouse roses using a dynamic greenhouse climate model in Zimbabwe. Comput. Electron. Agric. 2013, 95, 70–81. [Google Scholar] [CrossRef]
- Sentelhas, P.C.; Dalla Marta, A.; Orlandini, S.; Santos, E.A.; Gillespie, T.J.; Gleason, M.L. Suitability of relative humidity as an estimator of leaf wetness duration. Agric. For. Meteorol. 2008, 148, 392–400. [Google Scholar] [CrossRef]
- Bassimba, D.D.M.; Intrigliolo, D.S.; Dalla Marta, A.; Orlandini, S.; Vicent, A. Leaf wetness duration in irrigated citrus orchards in the Mediterranean climate conditions. Agric. For. Meteorol. 2017, 234, 182–195. [Google Scholar] [CrossRef]
- Kim, K.S.; Taylor, S.E.; Gleason, M.L.; Villalobos, R.; Arauz, L.F. Estimation of leaf wetness duration using empirical models in northwestern Costa Rica. Agric. For. Meteorol. 2005, 129, 53–67. [Google Scholar] [CrossRef]
- Gillespie, T.J.; Srivastava, B.; Pitblado, R.E. Using operational weather data to schedule fungicide sprays on tomatoes in southern Ontario, Canada. J. Appl. Meteorol. 1993, 32, 567–573. [Google Scholar] [CrossRef]
- Nury, A.H.; Hasan, K.; Alam, M.J.B. Comparative study of wavelet-ARIMA and wavelet-ANN models for temperature time series data in northeastern Bangladesh. J. King Saud Univ. 2017, 29, 47–61. [Google Scholar] [CrossRef]
- Wang, H.; Sánchez-Molina, J.A.; Li, M.; Berenguel, M.; Yang, X.T.; Bienvenido, J.F. Leaf area index estimation for a greenhouse transpiration model using external climate conditions based on genetics algorithms, back-propagation neural networks and nonlinear autoregressive exogenous models. Agric. Water Manag. 2017, 183, 107–115. [Google Scholar] [CrossRef]
- Paul, P.A.; Munkvold, G.P. Regression and artificial neural network modeling for the prediction of gray leaf spot of maize. Phytopathology 2005, 95, 388–396. [Google Scholar] [CrossRef]
- Tsakiri, K.; Marsellos, A.; Kapetanakis, S. Artificial Neural Network and Multiple Linear Regression for Flood Prediction in Mohawk River, New York. Water 2018, 10, 1158. [Google Scholar] [CrossRef]
- Mackenzie, S.J.; Peres, N.A. Use of Leaf Wetness and Temperature to Time Fungicide Applications to Control Anthracnose Fruit Rot of Strawberry in Florida. Plant Dis. 2012, 96, 529–536. [Google Scholar] [CrossRef]
- Gil, R.; Bojacá, C.R.; Schrevensc, E. Suitability evaluation of four methods to estimate leaf wetness duration in a greenhouse rose crop. Acta Hortic. 2011, 893, 797–804. [Google Scholar] [CrossRef]
- Braun, M.T.; Oswald, F.L. Exploratory regression analysis: A tool for selecting models and determining predictor importance. Behav. Res. Methods 2011, 43, 331–339. [Google Scholar] [CrossRef] [PubMed]
- Francl, L.J.; Panigrahi, S. Artificial neural network models of wheat leaf wetness. Agric. For. Meteorol. 1997, 88, 57–65. [Google Scholar] [CrossRef]
- Stella, A.; Caliendo, G.; Melgani, F.; Goller, R.; Barazzuol, M.; La Porta, N. Leaf Wetness Evaluation Using Artificial Neural Network for Improving Apple Scab Fight. Environments 2017, 4, 42. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Su, J.; Zhang, H. A Fast Decision Tree Learning Algorithm. In Proceedings of the 21st National Conference on Artificial Intelligence, Boston, MA, USA, 16–20 July 2006; Volume 1, pp. 500–505. [Google Scholar]
- Li, M. Early Warning Method and System for Cucumber downy Mildew (Pseudoperonospora cubensis) in Solar Greenhouse. Ph.D. Thesis, China Agriculture University, Beijing, China, 2010. [Google Scholar]
- Marta, A.D.; De Vincenzi, M.; Dietrich, S.; Orlandini, S. Neural network for the estimation of leaf wetness duration: application to a Plasmopara viticola infection forecasting. Phys. Chem. Earth, Parts A/B/C 2005, 30, 91–96. [Google Scholar] [CrossRef]
- Montone, V.O.; Fraisse, C.W.; Peres, N.A.; Sentelhas, P.C.; Gleason, M.; Ellis, M.; Schnabel, G. Evaluation of leaf wetness duration models for operational use in strawberry disease-warning systems in four US states. Int. J. Biometeorol. 2016, 60, 1761–1774. [Google Scholar] [CrossRef] [PubMed]
- Wilks, D.S.; Shen, K.W. Threshold relative humidity duration forecasts for plant disease prediction. J. Appl. Meteorol. 1991, 30, 463–477. [Google Scholar] [CrossRef]
- Rao, P.S.; Gillespie, T.J.; Schaafsma, A.W. Estimating wetness duration on maize ears from meteorological observations. Can. J. soil Sci. 1998, 78, 149–154. [Google Scholar] [CrossRef]
- Gleasom, M.L.; Taylor, S.E.; Loughin, T.M.; Koehler, K.J. Development and validation of an empirical model to estimate the duration of dew periods. Plant Dis. 1994, 78, 1011–1016. [Google Scholar]
- Beucher, A.; Møller, A.B.; Greve, M.H. Artificial neural networks and decision tree classification for predicting soil drainage classes in Denmark. Geoderma 2017. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Pham, B.T.; Pradhan, B.; Bui, D.T.; Prakash, I.; Dholakia, M.B. A comparative study of different machine learning methods for landslide susceptibility assessment: a case study of Uttarakhand area (India). Environ. Model. Softw. 2016, 84, 240–250. [Google Scholar] [CrossRef]
- Tien, D.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide susceptibility assessment in vietnam using support vector machines, decision tree, and nave bayes models. Math. Probl. Eng. 2012. [Google Scholar] [CrossRef]
- Dalla Marta, A.; Magarey, R.D.; Orlandini, S. Modelling leaf wetness duration and downy mildew simulation on grapevine in Italy. Agric. For. Meteorol. 2005, 132, 84–95. [Google Scholar] [CrossRef]
- Kim, K.S.; Taylor, S.E.; Gleason, M.L. Development and validation of a leaf wetness duration model using a fuzzy logic system. Agric. For. Meteorol. 2004, 127, 53–64. [Google Scholar] [CrossRef]
- Ferentinos, K.P.; Katsoulas, N.; Tzounis, A.; Bartzanas, T.; Kittas, C. Wireless sensor networks for greenhouse climate and plant condition assessment. Biosyst. Eng. 2017, 153, 70–81. [Google Scholar] [CrossRef]




| Location and Plant | Greenh-Ouse Type | Area | Plant Density | Leaf Wetness Sensor (Numbers/Series) | Experiment Data | T (°C) | RH (%) | LWD (h) |
|---|---|---|---|---|---|---|---|---|
| Tomato, Almeria, Spain | ‘Parral’ greenhou-se | 37.8 m × 23.2 m | 2.01 plants/m2 | 2/Decagon Devices, Pullman, WA, USA | April 2016–February 2018 | 22.91 | 59.86 | 4.39 |
| Cucumber, Beijing, China | Solar greenhou-se | 30 m × 7 m | 2.4 plants/m2 | 5/#6420, Davis Instruments Corp, Hayward CA, USA | April 2014–October 2015 | 20.35 | 67.33 | 6.06 |
| Models | Relative Humidity Model (RHM) | Dew Temperature Model (DPM) | Classification and Regression Tree (CART) | Neural Network Model (NNM) |
|---|---|---|---|---|
| Calibration parameters | Relative humidity (RH) | The difference of temperature and dew temperature (DPD) | DPD, Wind speed (WD), RH, the node splitting of Equations (1) and (2) | Input parameters |
| Inputs/Locations | Accuracy on Test Data | Accuracy on Validation Data | ||
|---|---|---|---|---|
| Spain | China | Spain | China | |
| Relative humidity (H) | 0.73 | 0.83 | 0.60 | 0.72 |
| Dew temperature (dewT) | 0.73 | 0.83 | 0.65 | 0.71 |
| Transpiration (E) | 0.93 | 0.87 | 0.70 | 0.74 |
| Radiation (Ra) | 0.85 | 0.88 | 0.70 | 0.74 |
| (H, Ra) | 0.88 | 0.89 | 0.76 | 0.78 |
| (H, dewT, E, Ra) | 0.82 | 0.98 | 0.88 | 0.92 |
| Location. | RHM | PPV | NPV | Sen | Acc | AUC | EF | MAE (h) | SD (h) |
|---|---|---|---|---|---|---|---|---|---|
| Spain | Experiential threshold (RH > 90%) | 0.63 | 0.82 | 0.30 | 0.80 | 0.83 | 1.14 | 7.12 | 8.12 |
| Calibrated threshold (RH > 84.53%) | 0.67 | 0.87 | 0.53 | 0.83 | 0.84 | 0.95 | 5.31 | 6.42 | |
| China | Experiential threshold (RH > 90%) | 0.55 | 0.89 | 0.39 | 0.78 | 0.83 | 0.79 | 6.12 | 7.45 |
| Calibrated threshold (RH > 80%) | 0.77 | 0.84 | 0.85 | 0.80 | 0.82 | 0.97 | 2.73 | 3.81 |
| Location | DPM | PPV | NPV | Sen | Acc | AUC | EF | MAE (h) | SD (h) |
|---|---|---|---|---|---|---|---|---|---|
| Spain | Experiential threshold (DPD < 2 °C) | 0.64 | 0.83 | 0.38 | 0.81 | 0.84 | 1.08 | 7.84 | 8.87 |
| Calibrated threshold (DPD < 2.7 °C) | 0.67 | 0.87 | 0.56 | 0.83 | 0.85 | 0.94 | 5.16 | 6.33 | |
| China | Experiential threshold (DPD < 2 °C) | 0.59 | 0.87 | 0.41 | 0.77 | 0.81 | 0.81 | 4.55 | 5.93 |
| Calibrated threshold (DPD < 5.42 °C) | 0.79 | 0.81 | 0.83 | 0.80 | 0.82 | 0.93 | 2.30 | 3.04 |
| Location | CART | PPV | NPV | Sen | Acc | AUC | EF | MAE (h) | SD (h) |
|---|---|---|---|---|---|---|---|---|---|
| Spain | Experiential threshold (RH < 87.8%, DPD < 3.7 °C, Equation (1) > 14.4674) | 0.63 | 0.83 | 0.36 | 0.80 | 0.84 | 1.11 | 6.19 | 7.38 |
| Calibrated threshold (RH < 84.53%, DPD < 2.7 °C, Equation (1) > 13.6949) | 0.63 | 0.89 | 0.62 | 0.83 | 0.88 | 0.96 | 4.60 | 5.29 | |
| China | Experiential threshold (RH < 87.8%, DPD < 3.7 °C, Equation (1) > 14.4674) | 0.73 | 0.88 | 0.49 | 0.80 | 0.78 | 0.82 | 3.18 | 4.49 |
| Calibrated threshold (RH < 80%, DPD < 6.3 °C, Equation (1) > 15.5) | 0.83 | 0.80 | 0.83 | 0.82 | 0.91 | 1.09 | 2.13 | 2.84 |
| Location | NNM | PPV | NPV | Sen | Acc | AUC | EF | MAE (h) | SD (h) |
|---|---|---|---|---|---|---|---|---|---|
| Spain | Experiential Inputes (T, RH, Rainfall, Ra, WD) | 0.92 | 0.68 | 0.56 | 0.75 | 0.87 | 1.36 | 5.10 | 6.25 |
| Calibrated Inputes (RH, dewT, E, Ra) | 0.92 | 0.77 | 0.64 | 0.82 | 0.88 | 1.05 | 0.23 | 0.65 | |
| China | Experiential Inputes (T, RH, Rainfall, Ra, WD) | 0.89 | 0.54 | 0.62 | 0.70 | 0.75 | 1.09 | 5.38 | 6.57 |
| Calibrated Inputes (RH, dewT, E, Ra) | 0.99 | 0.88 | 0.88 | 0.98 | 0.97 | 0.97 | 0.34 | 0.67 |
| Location | Spain | China | ||||||
|---|---|---|---|---|---|---|---|---|
| Index/Mode | RHM | DPM | CART | NNM | RHM | DPM | CART | NNM |
| PPV | 0.71 | 0.71 | 0.77 | 0.82 | 0.85 | 0.86 | 0.84 | 0.90 |
| NPV | 0.72 | 0.71 | 0.76 | 0.87 | 0.80 | 0.78 | 0.87 | 0.92 |
| Sen | 0.62 | 0.64 | 0.68 | 0.85 | 0.75 | 0.80 | 0.81 | 0.89 |
| Acc | 0.73 | 0.73 | 0.76 | 0.88 | 0.87 | 0.86 | 0.86 | 0.92 |
| AUC | 0.73 | 0.74 | 0.77 | 0.90 | 0.79 | 0.83 | 0.84 | 0.94 |
| EF | 0.83 | 0.83 | 0.85 | 0.92 | 0.85 | 0.86 | 0.88 | 0.94 |
| MAE | 5.45 | 5.46 | 3.46 | 1.85 | 3.42 | 3.29 | 2.75 | 1.30 |
| SD | 6.11 | 6.11 | 4.11 | 2.25 | 4.43 | 4.20 | 3.51 | 1.62 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Sanchez-Molina, J.A.; Li, M.; Rodríguez Díaz, F. Improving the Performance of Vegetable Leaf Wetness Duration Models in Greenhouses Using Decision Tree Learning. Water 2019, 11, 158. https://doi.org/10.3390/w11010158
Wang H, Sanchez-Molina JA, Li M, Rodríguez Díaz F. Improving the Performance of Vegetable Leaf Wetness Duration Models in Greenhouses Using Decision Tree Learning. Water. 2019; 11(1):158. https://doi.org/10.3390/w11010158
Chicago/Turabian StyleWang, Hui, Jorge Antonio Sanchez-Molina, Ming Li, and Francisco Rodríguez Díaz. 2019. "Improving the Performance of Vegetable Leaf Wetness Duration Models in Greenhouses Using Decision Tree Learning" Water 11, no. 1: 158. https://doi.org/10.3390/w11010158
APA StyleWang, H., Sanchez-Molina, J. A., Li, M., & Rodríguez Díaz, F. (2019). Improving the Performance of Vegetable Leaf Wetness Duration Models in Greenhouses Using Decision Tree Learning. Water, 11(1), 158. https://doi.org/10.3390/w11010158







