Evaluation of Hydrological Application of CMADS in Jinhua River Basin, China
Abstract
1. Introduction
2. Materials and Methodology
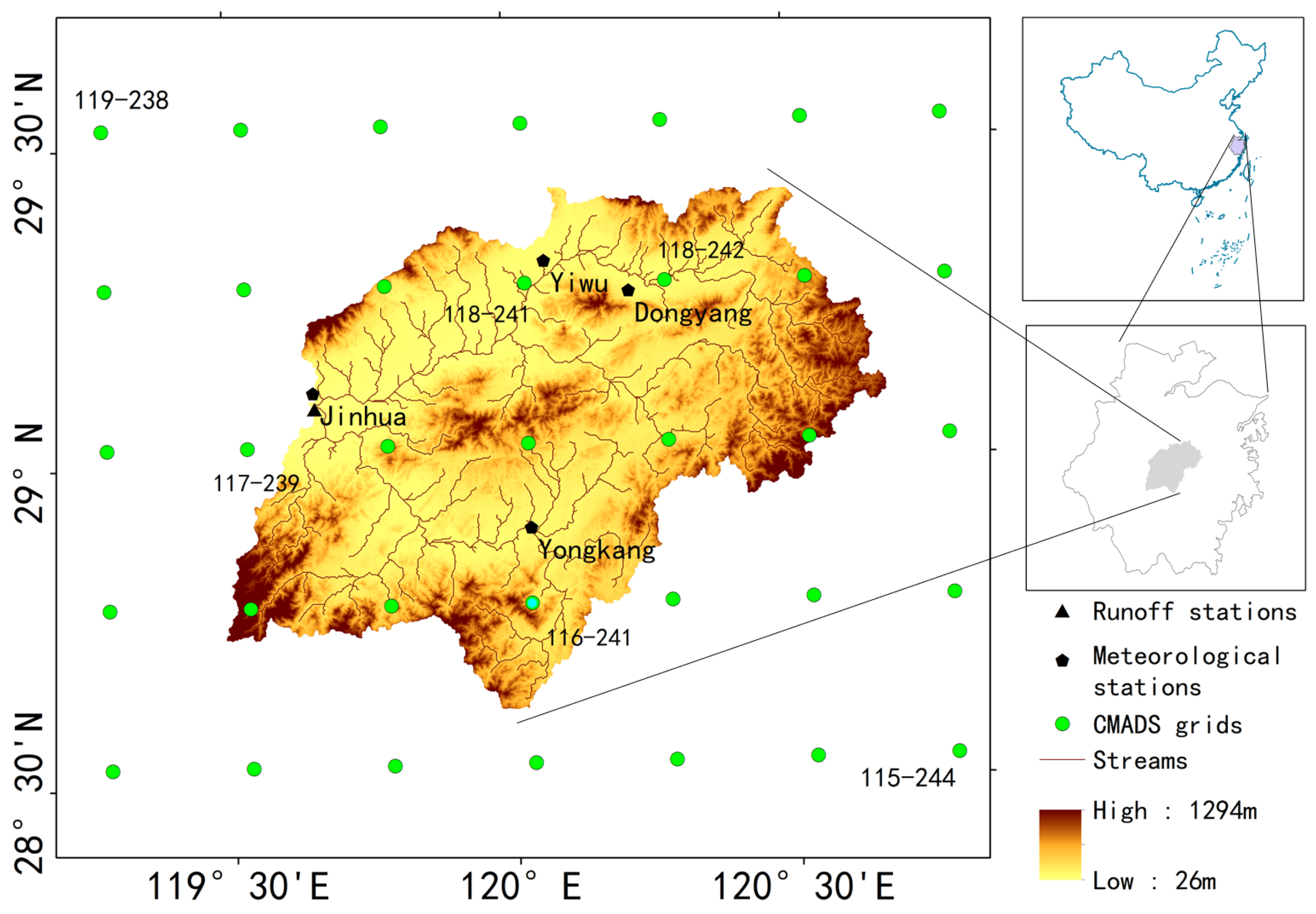
2.1. Study Area
2.2. Data
2.3. Straightforward Comparison
Diagnostic Statistics
2.4. Distributed Hydrological Model
2.5. Model Calibration and Validation
3. Results
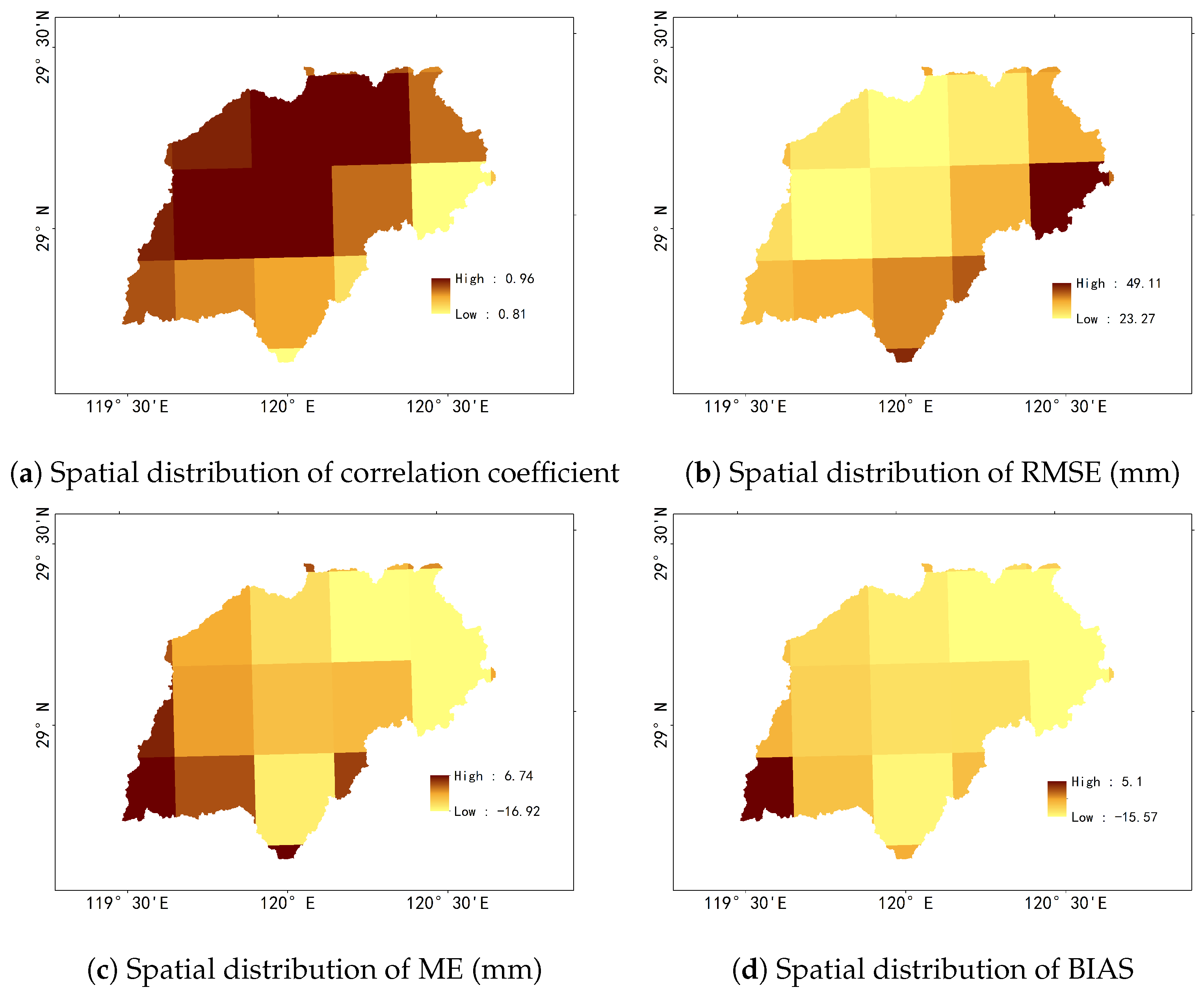
3.1. Straightforward Comparison between CMADS and Gauge Observations
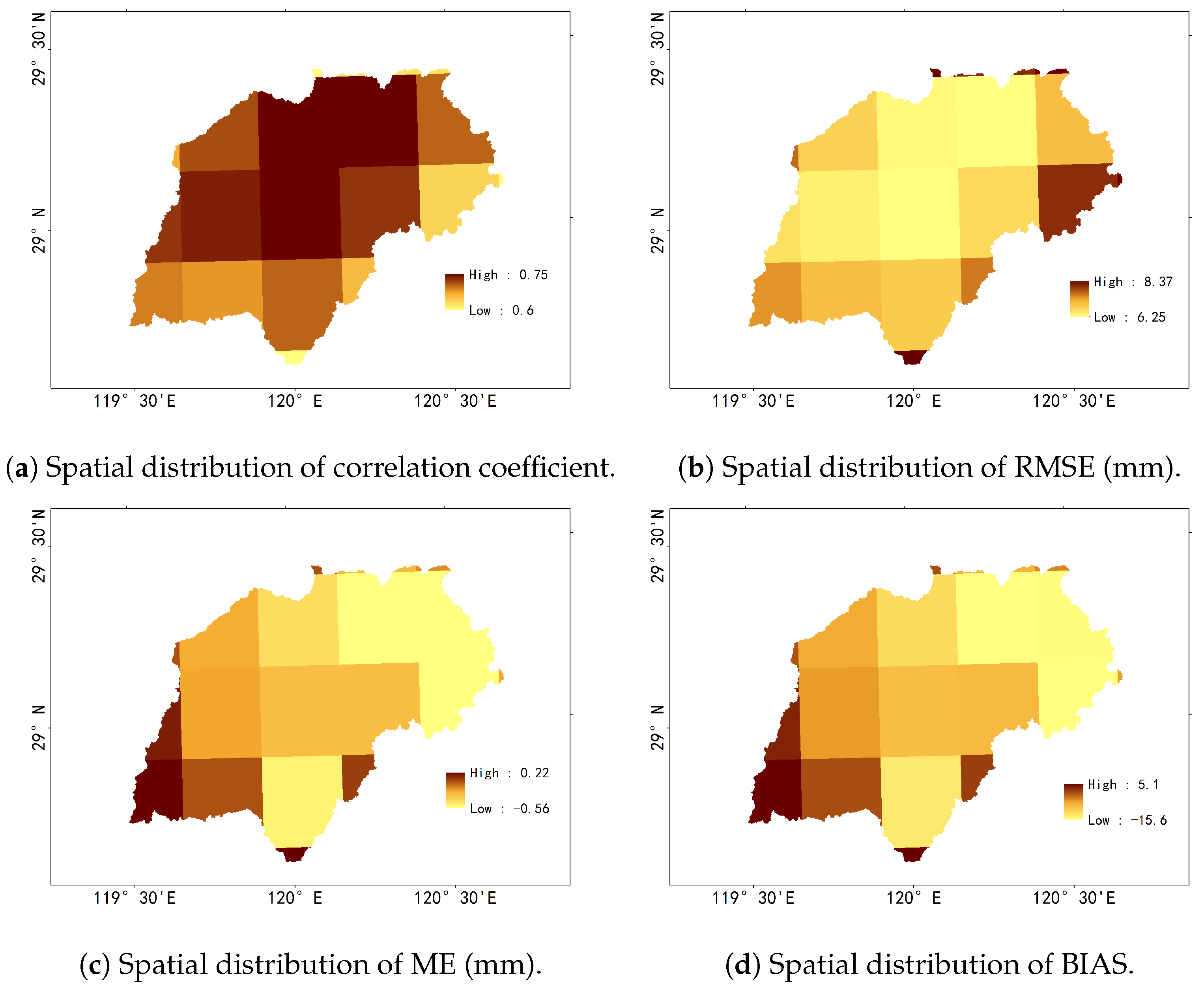
3.1.1. Comparison at Daily Scale
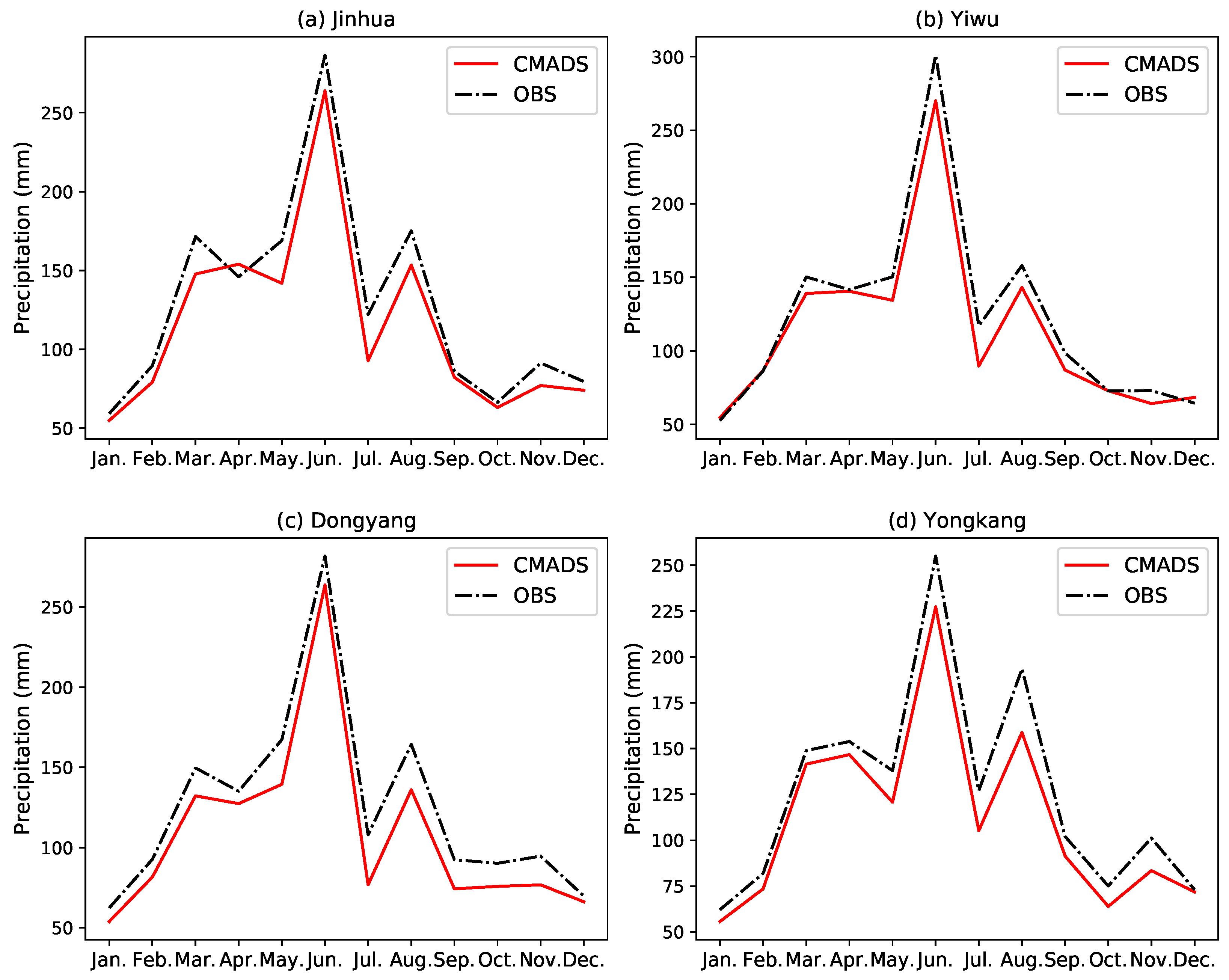
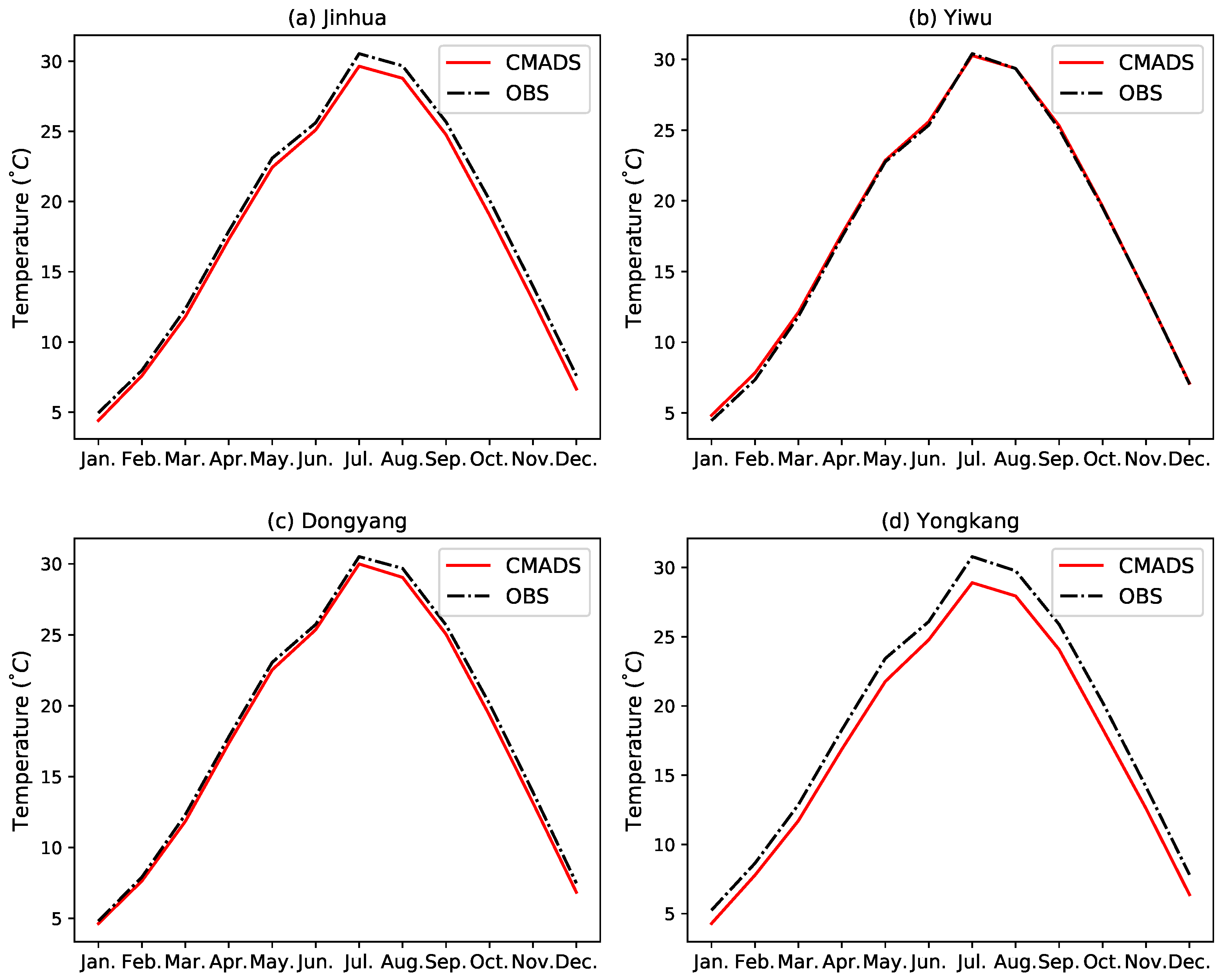
3.1.2. Comparison at Monthly Scale
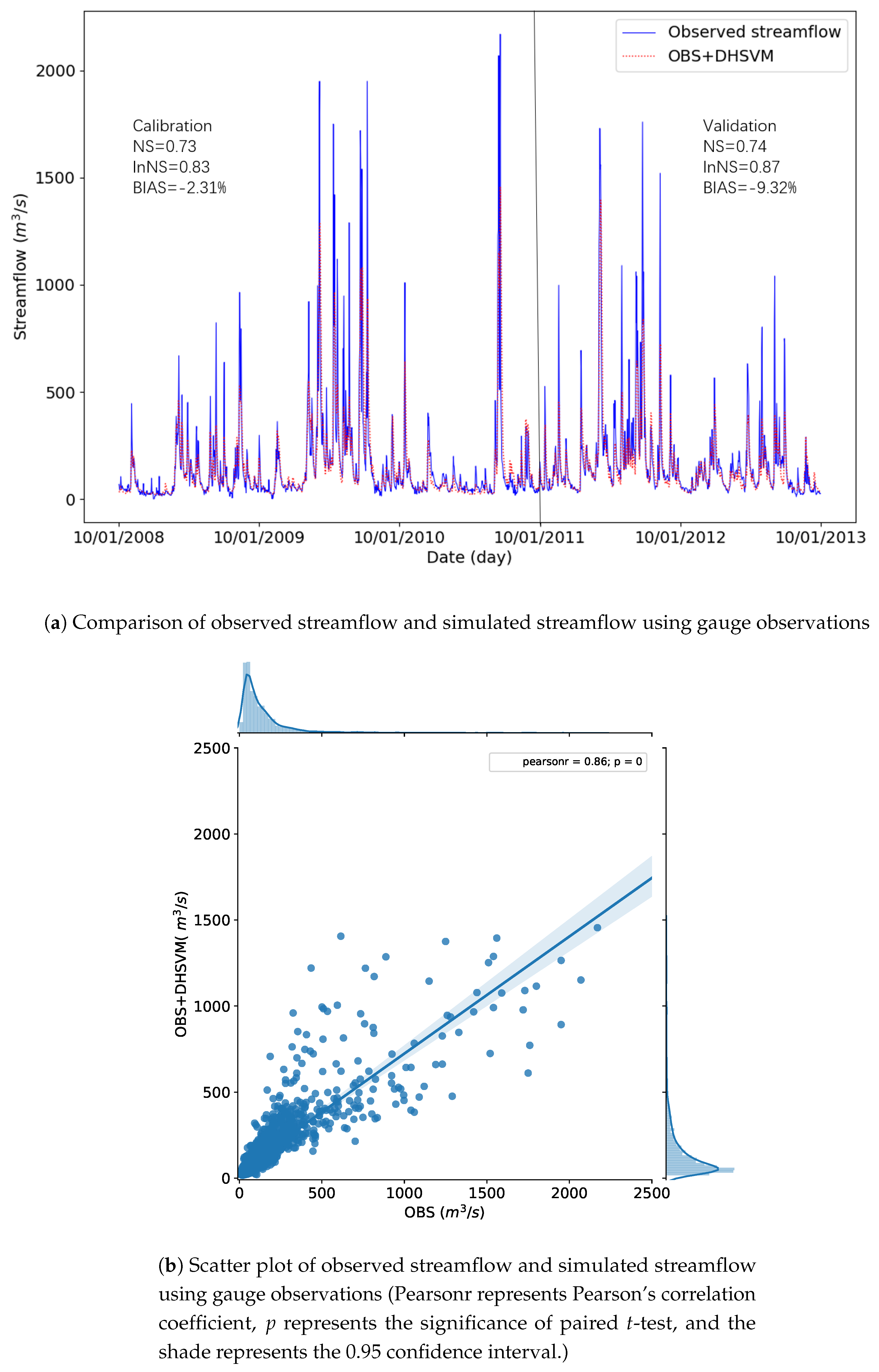
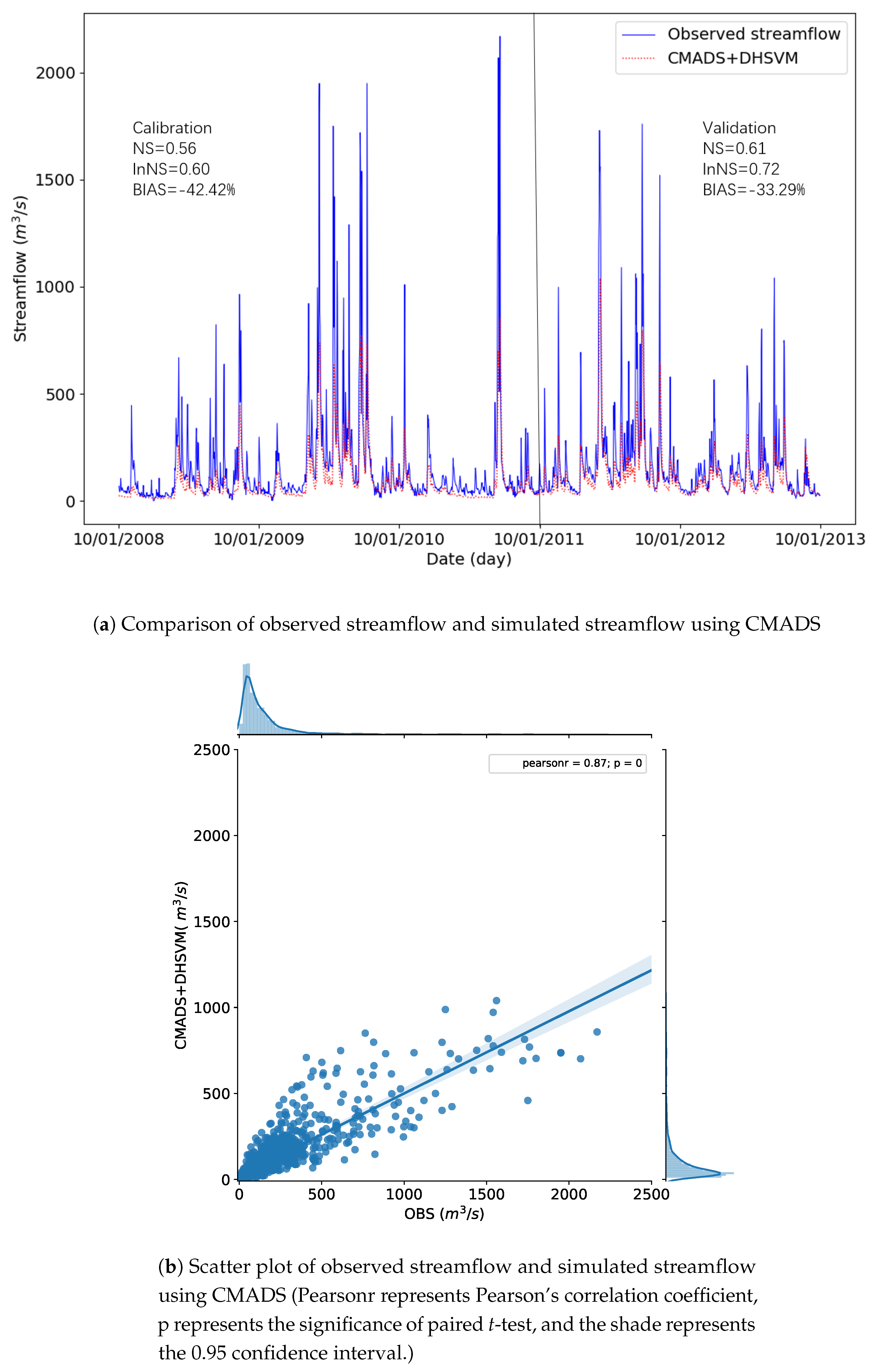
3.2. Results of Model Calibration and Validation
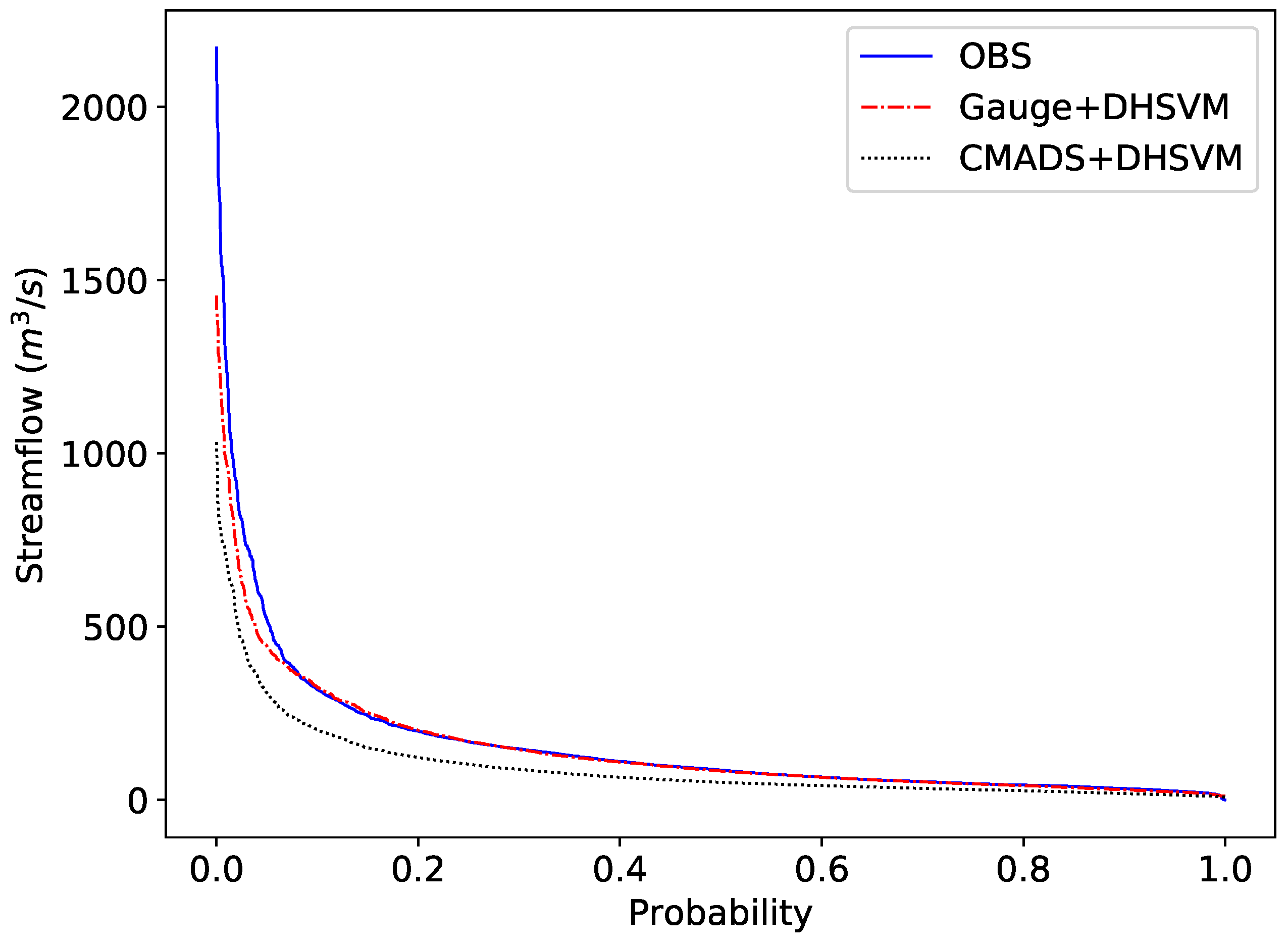
3.3. Comparison of Streamflow Simulations
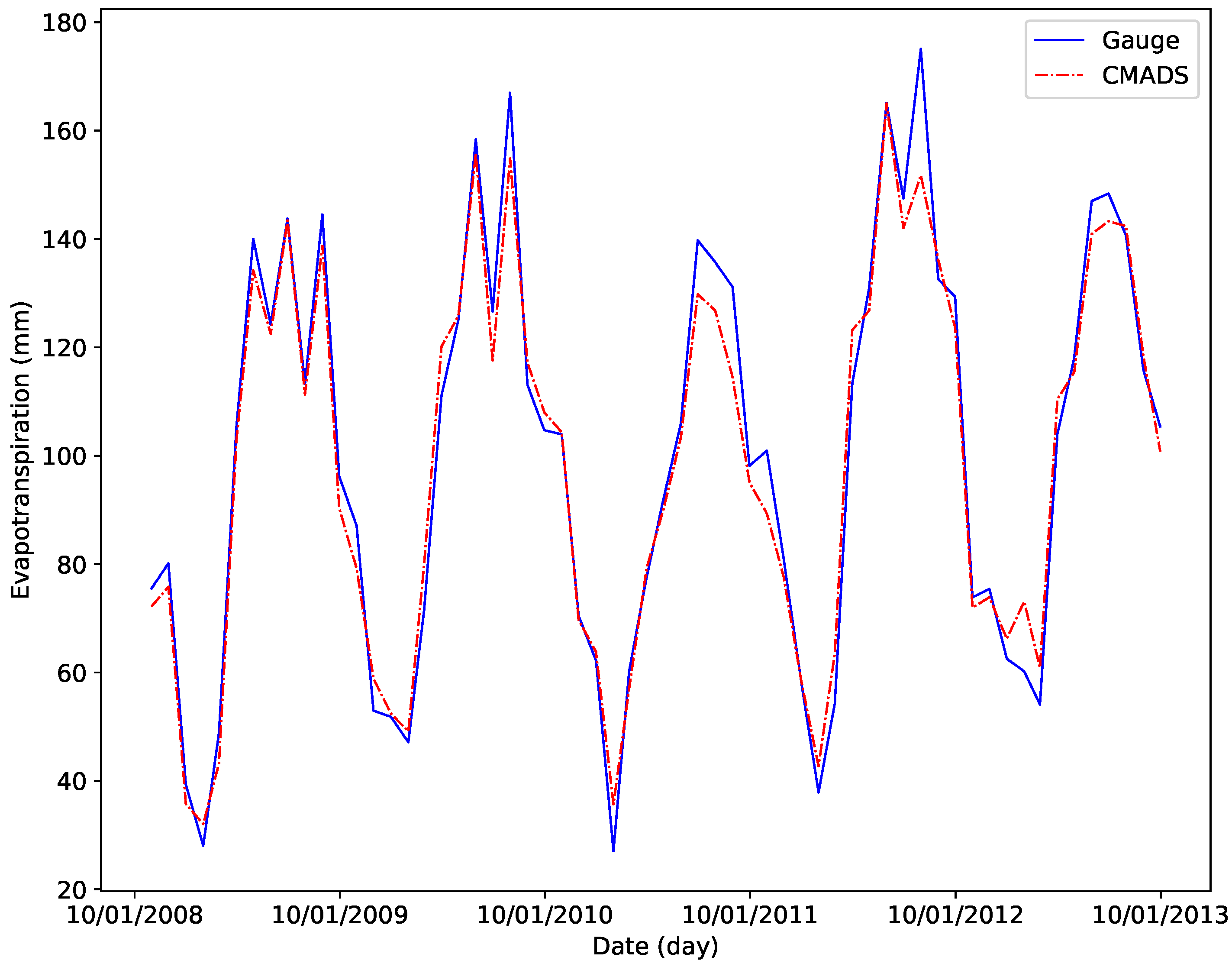
3.4. Comparison of Evapotranspiration
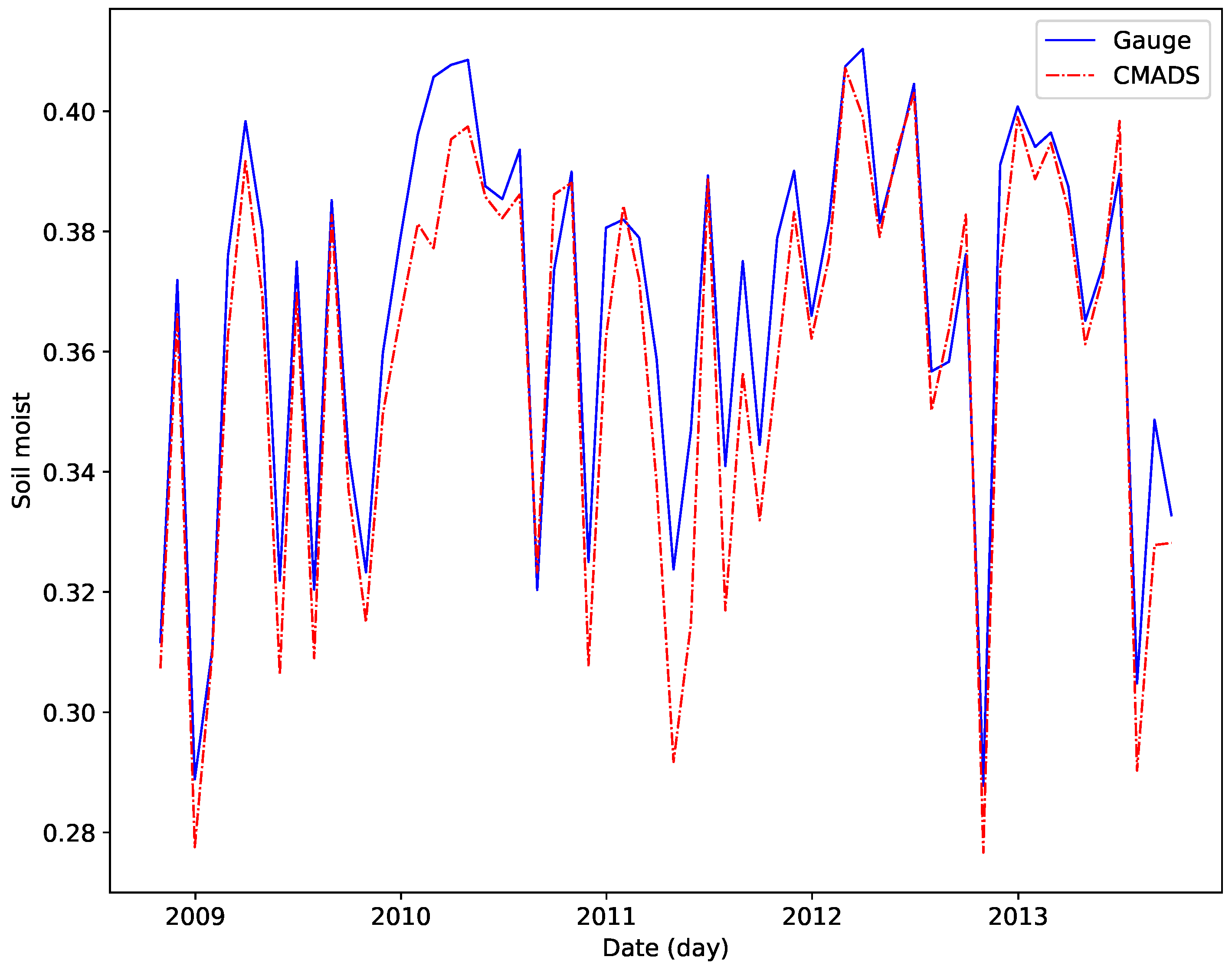
3.5. Comparison of Soil Moisture Content
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baldassarre, G.D.; Montanari, A.; Lins, H.; Koutsoyiannis, D.; Brandimarte, L.; Blöschl, G. Flood fatalities in Africa: From diagnosis to mitigation. Geophys. Res. Lett. 2010, 37, 707–716. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Aerts, J.C.J.H.; Beek, L.P.H.V.; Bierkens, M.F.P.; Bouwman, A.; Jongman, B.; Kwadijk, J.C.J.; Ligtvoet, W.; Lucas, P.L.; Vuuren, D.P.V. Global drivers of future river flood risk. Nat. Clim. Chang. 2016, 6, 381. [Google Scholar] [CrossRef]
- Ma, F.; Ye, A.; You, J.; Duan, Q. 2015–16 floods and droughts in China, and its response to the strong El Niño. Sc. Total Environ. 2018, 627, 1473–1484. [Google Scholar] [CrossRef]
- Kite, G. Modelling the Mekong: Hydrological simulation for environmental impact studies. J. Hydrol. 2001, 253, 1–13. [Google Scholar] [CrossRef]
- Bellos, V.; Tsakiris, G. A hybrid method for flood simulation in small catchments combining hydrodynamic and hydrological techniques. J. Hydrol. 2016, 540, 331–339. [Google Scholar] [CrossRef]
- Schumacher, M.; Forootan, E.; Dijk, A.I.J.M.V.; Schmied, H.M.; Crosbie, R.S.; Kusche, J.; Döll, P. Improving drought simulations within the Murray-Darling Basin by combined calibration/assimilation of GRACE data into the WaterGAP Global Hydrology Model. Remote Sens. Environ. 2017, 204, 212–228. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Nijssen, B.; Storck, P.; Singh, V.P.; Frevert, D. The distributed hydrology soil vegetation model. Hydrol. Process. 2002, 22, 4205–4213. [Google Scholar]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Griensven, A.V.; Liew, M.W.V. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1345–1352. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Vail, L.W.; Lettenmaier, D.P. A distributed hydrology-vegetation model for complex terrain. Water Resour. Res. 1994, 30, 1665–1679. [Google Scholar] [CrossRef]
- Abbott, M.B.; Refsgaard, J.C. Distributed Hydrological Modelling; Springer: Berlin/Heidelberg, Germany, 1996; pp. 289–305. [Google Scholar]
- Zhang, W.C.; Ogawa, K.; Ye, B.S.; Yamaguchi, Y. A monthly stream flow model for estimating the potential changes of river runoff on the projected global warming. Hydrol. Process. 2015, 14, 1851–1868. [Google Scholar]
- Chen, J.M.; Chen, X.; Ju, W.; Geng, X. Distributed hydrological model for mapping evapotranspiration using remote sensing inputs. J. Hydrol. 2005, 305, 15–39. [Google Scholar] [CrossRef]
- Wang, A.; Zeng, X. Evaluation of multireanalysis products with in situ observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2012, 117, D0512. [Google Scholar] [CrossRef]
- Janowiak, J.E.; Gruber, A.; Kondragunta, C.R.; Livezey, R.E.; Huffman, G.J. A Comparison of the NCEP-NCAR Reanalysis Precipitation and the GPCP Rain Gauge-Satellite Combined Dataset with Observational Error Considerations. J. Clim. 1998, 11, 2960–2979. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-Year High-Resolution Global Dataset of Meteorological Forcings for Land Surface Modeling. J. Clim. 2005, 19, 3088–3111. [Google Scholar] [CrossRef]
- Tang, M.S.Y.; Chenoli, S.N.; Samah, A.A.; Hai, O.S. An assessment of historical Antarctic precipitation and temperature trend using CMIP5 models and reanalysis datasets. Polar Sci. 2018, 15, 1–12. [Google Scholar] [CrossRef]
- Maurer, E.P.; Lettenmaier, D.P. Predictability of seasonal runoff in the Mississippi River basin. J. Geophys. Res. Atmos. 2003, 108, D16. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Hong, Y. Cross-Evaluation of Ground-based, Multi-Satellite and Reanalysis Precipitation Products: Applicability of the Triple Collocation Method across Mainland China. J. Hydrol. 2018, 562, 71–83. [Google Scholar] [CrossRef]
- Smith, S.R. Quantifying uncertainties in NCEP reanalyses using high-quality research vesses observations. J. Clim. 2001, 14, 4062–4072. [Google Scholar] [CrossRef]
- Hodges, K.I.; Lee, R.W.; Bengtsson, L. A Comparison of Extratropical Cyclones in Recent Reanalyses ERA-Interim, NASA MERRA, NCEP CFSR, and JRA-25. J. Clim. 2011, 24, 4888–4906. [Google Scholar] [CrossRef]
- Ebisuzaki, W.; Zhang, L. Assessing the performance of the CFSR by an ensemble of analyses. Clim. Dyn. 2011, 37, 2541–2550. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Smith, C.A.; Compo, G.P.; Hooper, D.K. Web-Based Reanalysis Intercomparison Tools (WRIT) for analysis and comparison of reanalyses and other datasets. Bull. Am. Meteorol. Soc. 2014, 95, 1671–1678. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Meng, X.; Wang, H. Significance of the China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS) of East Asia. Water 2017, 9, 765. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, Y.; Qiu, L.; Sun, Y.; Sun, L.; Li, Q.; Niu, J.; Wang, G. Parameter Uncertainty Analysis of the SWAT Model in a Mountain-Loess Transitional Watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef]
- Thom, V.; Li, L.; Jun, K.S. Evaluation of Multi-Satellite Precipitation Products for Streamflow Simulations: A Case Study for the Han River Basin in the Korean Peninsula, East Asia. Water 2018, 10, 642. [Google Scholar]
- Meng, X.; Long, A.; Wu, Y.; Yin, G.; Wang, H.; Ji, X. Simulation and spatiotemporal pattern of air temperature and precipitation in Eastern Central Asia using RegCM. Sci. Rep. 2018, 8, 3639. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.Y.; Yu, D.L.; Liu, Z.H. Energy balance-based SWAT model to simulate the mountain snowmelt and runoff—Taking the application in Juntanghu watershed (China) as an example. J. Mt. Sci. 2015, 12, 368–381. [Google Scholar] [CrossRef]
- Meng, X.; Sun, Z.; Zhao, H.; Ji, X.; Wang, H.; Xue, L.; Wu, H.; Zhu, Y. Spring Flood Forecasting Based on the WRF-TSRM Mode. Tehnički Vjesnik 2018, 25, 27–37. [Google Scholar]
- Meng, X.; Wang, H.; Lei, X.; Cai, S.; Wu, H.; Ji, X.; Wang, J. Hydrological modeling in the manas river basin using soil and water assessment tool driven by CMADS. Tehnički Vjesnik 2017, 24, 525–534. [Google Scholar]
- Meng, X.; Wang, H.; Wu, Y.; Long, A.; Wang, J.; Shi, C.; Ji, X. Investigating spatiotemporal changes of the land-surface processes in Xinjiang using high-resolution CLM3.5 and CLDAS: Soil temperature. Sci. Rep. 2017, 7, 13286. [Google Scholar] [CrossRef]
- Liu, J.; Shanguan, D.; Liu, S.; Ding, Y. Evaluation and Hydrological Simulation of CMADS and CFSR Reanalysis Datasets in the Qinghai-Tibet Plateau. Water 2018, 10, 513. [Google Scholar] [CrossRef]
- Wang, Y.J.; Meng, X.Y.; Liu, Z.H.; Ji, X.N. Snowmelt Runoff Analysis under Generated Climate Change Scenarios for the Juntanghu River Basin, in Xinjiang, China. Water Sci. Technol. 2016, 7, 41–54. [Google Scholar]
- Xu, Y.P.; Gao, X.; Zhu, Q.; Zhang, Y.; Kang, L. Coupling a Regional Climate Model and a Distributed Hydrological Model to Assess Future Water Resources in Jinhua River Basin, East China. J. Hydrol. Eng. 2015, 20, 04014054. [Google Scholar] [CrossRef]
- Chen, H.; Xu, C.Y.; Guo, S. Comparison and evaluation of multiple GCMs, statistical downscaling and hydrological models in the study of climate change impacts on runoff. J. Hydrol. 2012, 434, 36–45. [Google Scholar] [CrossRef]
- Gao, X.; Zhu, Q.; Yang, Z.; Wang, H. Evaluation and Hydrological Application of CMADS against TRMM 3B42V7, PERSIANN-CDR, NCEP-CFSR, and Gauge-Based Datasets in Xiang River Basin of China. Water 2018, 10, 1225. [Google Scholar] [CrossRef]
- Caracciolo, D.; Francipane, A.; Viola, F.; Noto, L.V.; Deidda, R. Performances of GPM satellite precipitation over the two major Mediterranean islands. Atmos. Res. 2018, 213, 309–322. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of Near-Real-Time Precipitation Estimates from Satellite Observations and Numerical Models. Bull. Am. Meteorol. Soc. 2010, 88, 47. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Z.; Ye, B.; Qin, Y.; Wei, Z.; Fang, S. A snowmelt runoff forecasting model coupling WRF and DHSVM. Hydrol. Earth Syst. Sci. 2009, 13, 233–246. [Google Scholar] [CrossRef]
- Du, E.; Link, T.E.; Gravelle, J.A.; Hubbart, J.A. Validation and sensitivity test of the distributed hydrology soil-vegetation model (DHSVM) in a forested mountain watershed. Hydrol. Process. 2015, 28, 6196–6210. [Google Scholar] [CrossRef]
- Alvarenga, L.A.; Mello, C.R.D.; Colombo, A.; Cuartas, L.A.; Bowling, L.C. Assessment of land cover change on the hydrology of a Brazilian headwater watershed using the Distributed Hydrology-Soil-Vegetation Model. CATENA 2016, 143, 7–17. [Google Scholar] [CrossRef]
- Pan, S.; Fu, G.; Chiang, Y.M.; Ran, Q.; Xu, Y.P. A two-step sensitivity analysis for hydrological signatures in Jinhua River Basin, East China. Hydrol. Sci. J. 2017, 62, 2511–2530. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115, D02114. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef]
- Safeeq, M.; Fares, A. Hydrologic response of a Hawaiian watershed to future climate change scenarios. Hydrol. Process. 2012, 26, 2745–2764. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Krogh, S.A.; Pomeroy, J.W.; McPhee, J. Physically Based Mountain Hydrological Modeling Using Reanalysis Data in Patagonia. J. Hydrometeorol. 2015, 16, 172–193. [Google Scholar] [CrossRef]
- Dile, Y.T.; Srinivasan, R. Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: an application in the Blue Nile River Basin. JAWRA J. Am. Water Resour. Assoc. 2014, 50, 1226–1241. [Google Scholar] [CrossRef]
- Bastola, S.; Misra, V. Evaluation of dynamically downscaled reanalysis precipitation data for hydrological application. Hydrol. Process. 2014, 28, 1989–2002. [Google Scholar] [CrossRef]
- Maurer, E.P.; O’Donnell, G.M.; Lettenmaier, D.P.; Roads, J.O. Evaluation of the land surface water budget in NCEP/NCAR and NCEP/DOE reanalyses using an off-line hydrologic model. J. Geophys. Res. Atmos. 2001, 106, 17841–17862. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Yang, X.; Yong, B.; Hong, Y.; Chen, S.; Zhang, X. Error analysis of multi-satellite precipitation estimates with an independent raingauge observation network over a medium-sized humid basin. Hydrol. Sci. J. 2016, 61, 1813–1830. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, W.; Liu, L.; Xu, Y. Evaluation and hydrological application of precipitation estimates derived from PERSIANN-CDR, TRMM 3B42V7, and NCEP-CFSR over humid regions in China. Hydrol. Process. 2016, 30, 3061–3083. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, J.; Xu, T.; Croke, B.; Jakeman, A.; Song, Y.; Yang, Q.; Lei, X.; Liao, W. Applicability Assessment and Uncertainty Analysis of Multi-Precipitation Datasets for the Simulation of Hydrologic Models. Water 2018, 10, 1611. [Google Scholar] [CrossRef]
| Parameter | Unit | Range |
|---|---|---|
| Rain LAI multiplier | m | |
| Lateral conductivity for clay loam | m/s | |
| Porosity for clay loam | 1 | |
| Field capacity for clay loam | 1 | |
| Wilting point for clay loam | 1 | |
| Understory monthly LAI for cropland | 1 | |
| Understory minimum resistance for cropland | s/m | |
| Root zone depth | m |
| Daily Precipitation | |||||||
| Gauges | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| Jinhua | 0.71 | 7.74 | 0.72 | 0.13 | 0.65 | ||
| Yiwu | 0.71 | 7.27 | 0.73 | 0.16 | 0.64 | ||
| Dongyang | 0.75 | 6.74 | 0.73 | 0.15 | 0.64 | ||
| Yongkang | 0.72 | 6.90 | 0.74 | 0.14 | 0.66 | ||
| Basin average | 0.77 | 7.18 | 0.74 | 0.16 | 0.65 | ||
| Daily Temperature | |||||||
| Gauges | CC | RMSE (°C) | ME (°C) | BIAS (%) | |||
| Jinhua | 0.99 | 1.18 | −0.75 | −4.24 | |||
| Yiwu | 1.00 | 0.88 | 0.15 | 0.85 | |||
| Dongyang | 0.99 | 1.16 | −0.52 | −2.94 | |||
| Yongkang | 0.99 | 1.84 | −1.47 | −8.57 | |||
| Basin average | 0.99 | 1.15 | −0.51 | −2.75 | |||
| Daily Wind Speed | |||||||
| Gauges | CC | RMSE (m/s) | ME (m/s) | ||||
| Jinhua | 0.66 | 1.42 | −1.31 | ||||
| Yiwu | 0.73 | 1.98 | −1.82 | ||||
| Dongyang | 0.46 | 1.11 | −0.97 | ||||
| Yongkang | 0.60 | 0.96 | −0.87 | ||||
| Basin average | 0.63 | 1.24 | −1.10 | ||||
| Daily Relative Humidity | |||||||
| Gauges | CC | RMSE | ME | BIAS (%) | |||
| Jinhua | 0.94 | 6.59 | 4.61 | 6.51 | |||
| Yiwu | 0.95 | 4.95 | 2.10 | 2.98 | |||
| Dongyang | 0.94 | 7.00 | 5.15 | 7.11 | |||
| Yongkang | 0.93 | 8.61 | 7.16 | 9.86 | |||
| Basin average | 0.94 | 8.28 | 7.06 | 9.61 | |||
| Monthly Precipitation | ||||
| Gauges | CC | RMSE (mm) | ME (mm) | BIAS (%) |
| Jinhua | 0.94 | 32.78 | −13.18 | −11.42 |
| Yiwu | 0.95 | 29.21 | −9.65 | −8.57 |
| Dongyang | 0.97 | 26.54 | −17.01 | −15.65 |
| Yongkang | 0.94 | 29.20 | −14.31 | −12.81 |
| Basin average | 0.96 | 22.62 | −7.90 | −6.67 |
| Monthly Temperature | ||||
| Gauges | CC | RMSE (°C) | ME (°C) | BIAS (%) |
| Jinhua | 1.00 | 0.80 | −0.75 | −4.26 |
| Yiwu | 1.00 | 0.29 | 0.16 | 0.88 |
| Dongyang | 1.00 | 0.59 | −0.52 | −2.96 |
| Yongkang | 1.00 | 1.54 | −1.48 | −8.66 |
| Basin average | 1.00 | 1.10 | −0.55 | −5.15 |
| Monthly Wind Speed | ||||
| Gauges | CC | RMSE (m/s) | ME (m/s) | |
| Jinhua | 0.71 | 1.32 | −1.31 | |
| Yiwu | 0.62 | 1.83 | −1.82 | |
| Dongyang | 0.28 | 1.01 | −0.97 | |
| Yongkang | 0.59 | 0.88 | −0.87 | |
| Basin average | 0.55 | 1.17 | −1.16 | |
| Monthly Relative Humidity | ||||
| Gauges | CC | RMSE | ME | BIAS (%) |
| Jinhua | 0.92 | 5.12 | 4.61 | 6.50 |
| Yiwu | 0.94 | 2.92 | 2.10 | 2.97 |
| Dongyang | 0.90 | 5.82 | 5.14 | 7.10 |
| Yongkang | 0.92 | 7.50 | 7.15 | 9.85 |
| Basin average | 0.93 | 7.35 | 7.05 | 9.60 |
| Period | NS | lnNS | BIAS (%) |
|---|---|---|---|
| Calibration | 0.73 | 0.83 | −2.31 |
| Validation | 0.74 | 0.87 | −9.32 |
| Dry Seasons | |||
| Period | NS | lnNS | BIAS (%) |
| Calibration | 0.81 | 0.82 | −3.30 |
| Validation | 0.80 | 0.88 | −4.11 |
| Wet seasons | |||
| Period | NS | lnNS | BIAS (%) |
| Calibration | 0.70 | 0.84 | −1.82 |
| Validation | 0.69 | 0.86 | −12.98 |
| Period | NS | lnNS | BIAS (%) |
|---|---|---|---|
| Calibration | 0.56 | 0.60 | −42.42 |
| Validation | 0.61 | 0.72 | −33.29 |
| Dry Seasons | |||
| Period | NS | lnNS | BIAS (%) |
| Calibration | 0.53 | 0.55 | −48.40 |
| Validation | 0.67 | 0.66 | −32.72 |
| Wet Seasons | |||
| Period | NS | lnNS | BIAS (%) |
| Calibration | 0.56 | 0.61 | −39.41 |
| Validation | 0.57 | 0.76 | −33.68 |
| Period | NS | lnNS | BIAS (%) |
|---|---|---|---|
| Calibration | 0.97 | 0.97 | −2.01 |
| Validation | 0.96 | 0.96 | −0.54 |
| Period | NS | lnNS | BIAS (%) |
|---|---|---|---|
| Calibration | 0.81 | 0.80 | −2.85 |
| Validation | 0.91 | 0.91 | −1.39 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Gao, X.; Yang, Z.; Feng, J.; Meng, C.; Xu, Z. Evaluation of Hydrological Application of CMADS in Jinhua River Basin, China. Water 2019, 11, 138. https://doi.org/10.3390/w11010138
Zhou Z, Gao X, Yang Z, Feng J, Meng C, Xu Z. Evaluation of Hydrological Application of CMADS in Jinhua River Basin, China. Water. 2019; 11(1):138. https://doi.org/10.3390/w11010138
Chicago/Turabian StyleZhou, Zhenghui, Xichao Gao, Zhiyong Yang, Jie Feng, Chao Meng, and Zhi Xu. 2019. "Evaluation of Hydrological Application of CMADS in Jinhua River Basin, China" Water 11, no. 1: 138. https://doi.org/10.3390/w11010138
APA StyleZhou, Z., Gao, X., Yang, Z., Feng, J., Meng, C., & Xu, Z. (2019). Evaluation of Hydrological Application of CMADS in Jinhua River Basin, China. Water, 11(1), 138. https://doi.org/10.3390/w11010138





