Dynamic Variation Characteristics of Seawater Intrusion in Underground Water-Sealed Oil Storage Cavern under Island Tidal Environment
Abstract
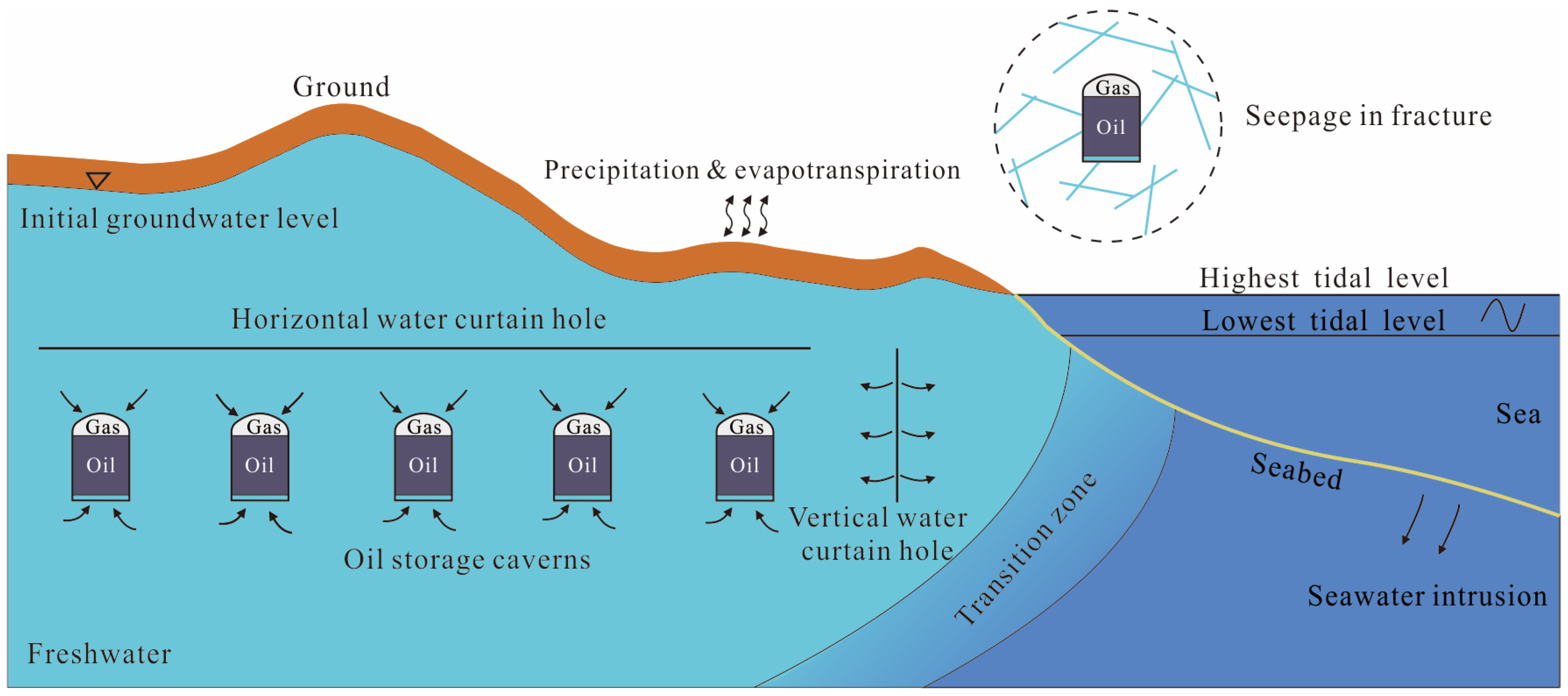
1. Introduction
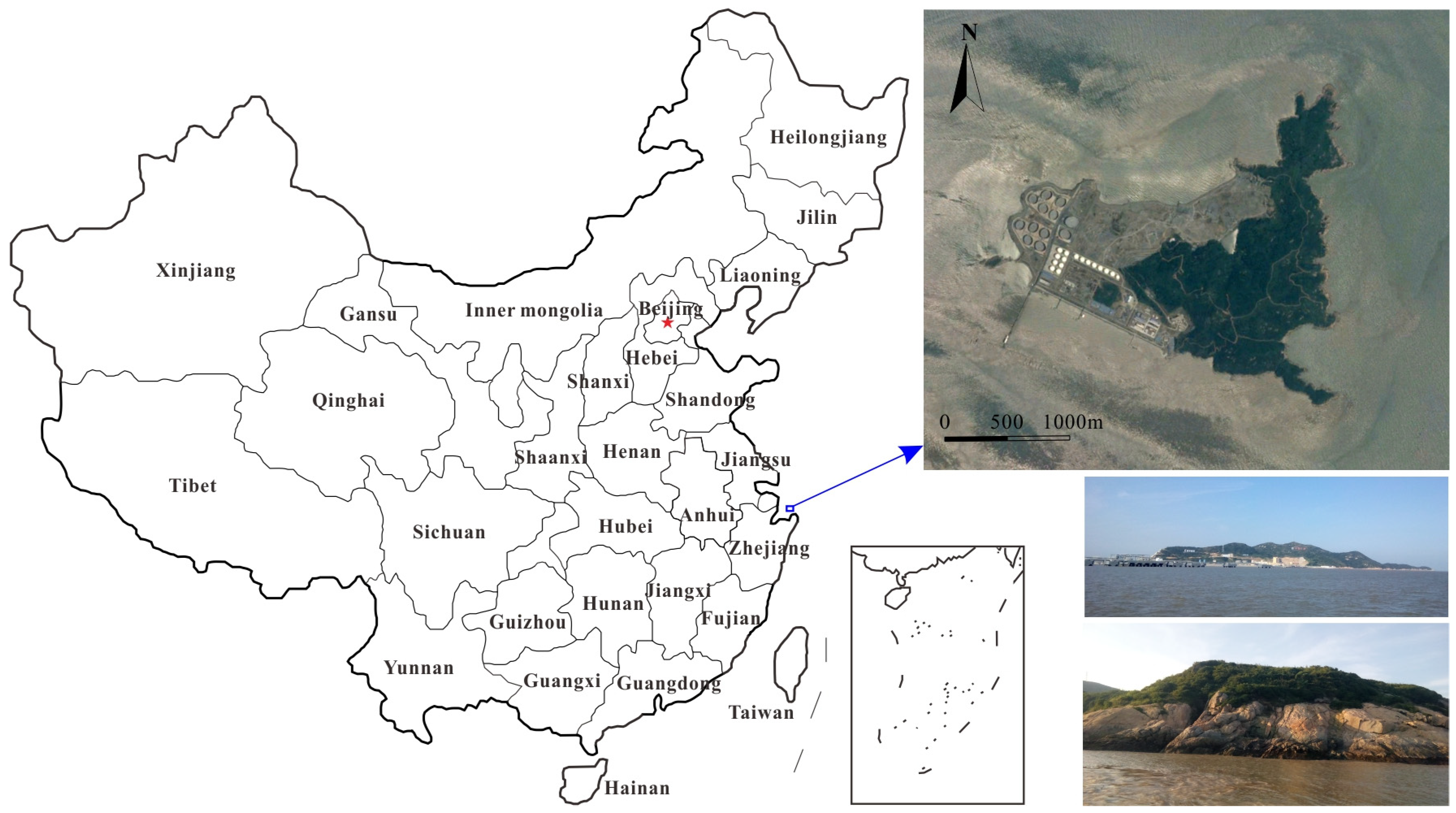
2. Research Area
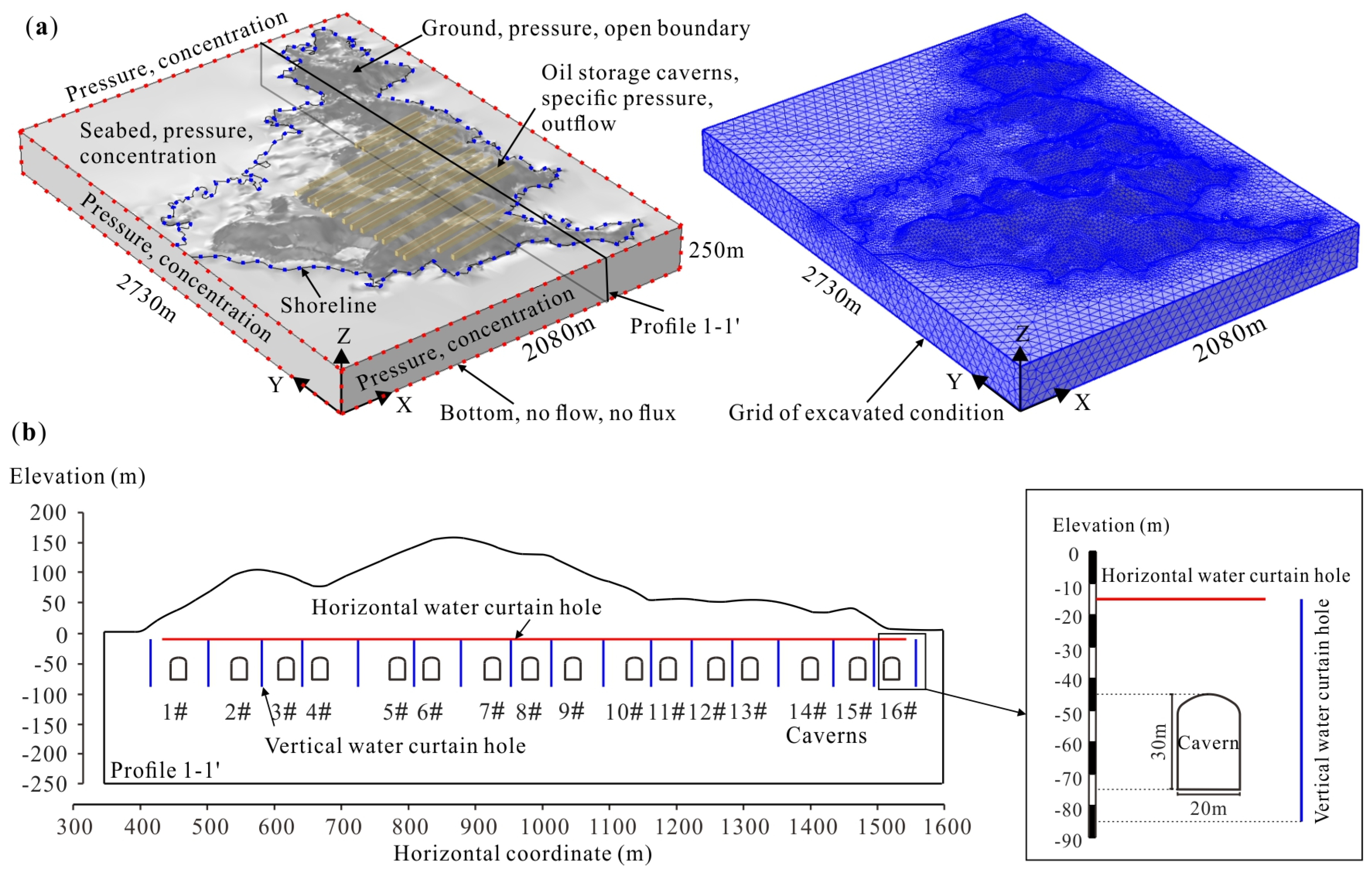
2.1. Project Overview
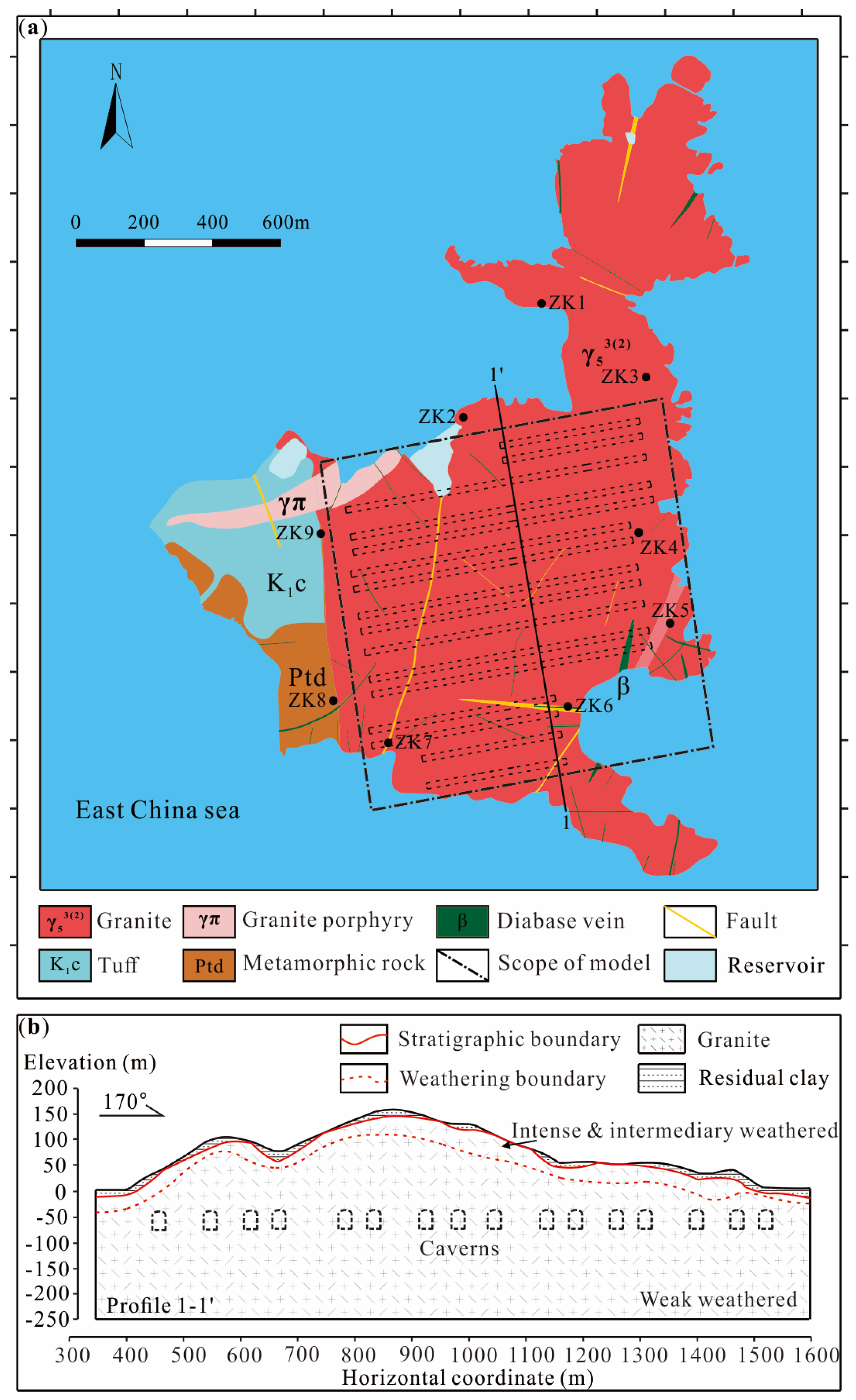
2.2. Engineering Geology
2.3. Hydrogeology
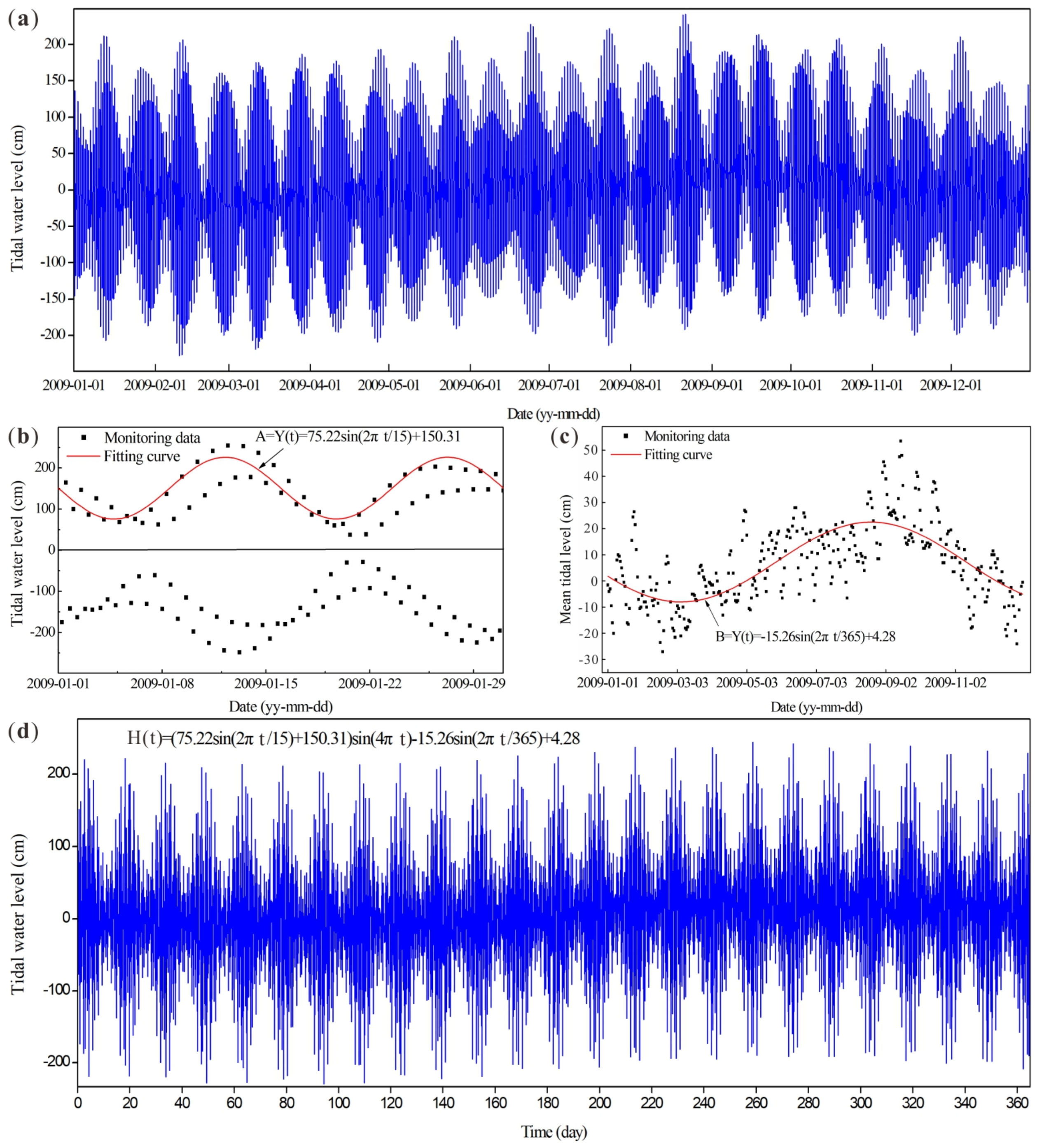
3. Simulation Method
3.1. Numerical Model
3.2. Governing Equation
- (1)
- The underground seepage field is subject to the seepage continuity equation (Equation (6)) and Darcy’s law (Equation (7)) and [41]:where k is the hydraulic conductivity (m/s), n is the porosity, is the rate of recharge to the water table per unit volume of the aquifer (kg/s), v is the Darcy’s flux (m/s), p is the pore water pressure (Pa), z is the vertical coordinate (m), g is the gravitational acceleration (m/s2), is the density of water (kg/m3), is the density of freshwater (kg/m3), is the density of seawater (kg/m3), is the concentration of chlorine ions in water (kg/m3) and is the concentration of chlorine ions in seawater (kg/m3).
- (2)
- In the three-dimensional numerical model, the solute transport equation can be described as follows [42]:where is the concentration of chlorine ions (mol/kg), the concentration of solute in recharged water (mol/kg), x is the flow direction, and y and z are vertical to the flow direction, D is the hydrodynamic dispersion coefficient tensor (m2/s), Dii and Dij are the components of the hydrodynamic dispersion coefficient tensor (m2/s), D* is the diffusion coefficient (m2/s), is the longitudinal dispersity (m), is the transversal dispersity (m), , and are the three components of the seepage velocity (m/s).
3.3. Model Parameters
3.4. Boundary and Initial Conditions
- 1
- There are several types of boundary and initial conditions for the transient seepage of groundwater:
- (1)
- Initial conditions:
- (2)
- The first boundary condition is:
- (3)
- The second boundary condition is:where H* is the hydraulic head (m), q* is the quantity of flow, and is the boundary.
- 2
- The boundary conditions of the solute transport field mainly include the following:
- (1)
- Initial conditions:
- (2)
- The first boundary condition, also known as the Dirichlet boundary condition, where the solute concentration is known:
- (3)
- The second boundary condition, also called Neumann boundary condition, which describes the change rate of the solute concentration in normal direction at the boundary:
- (4)
- Input boundary condition. Under the effect of groundwater flow and hydrodynamic dispersion, the solute flux across the boundary is known:where q is the flux through the boundary (kgm−2s−1).
4. Results
4.1. Validation of the Numerical Model
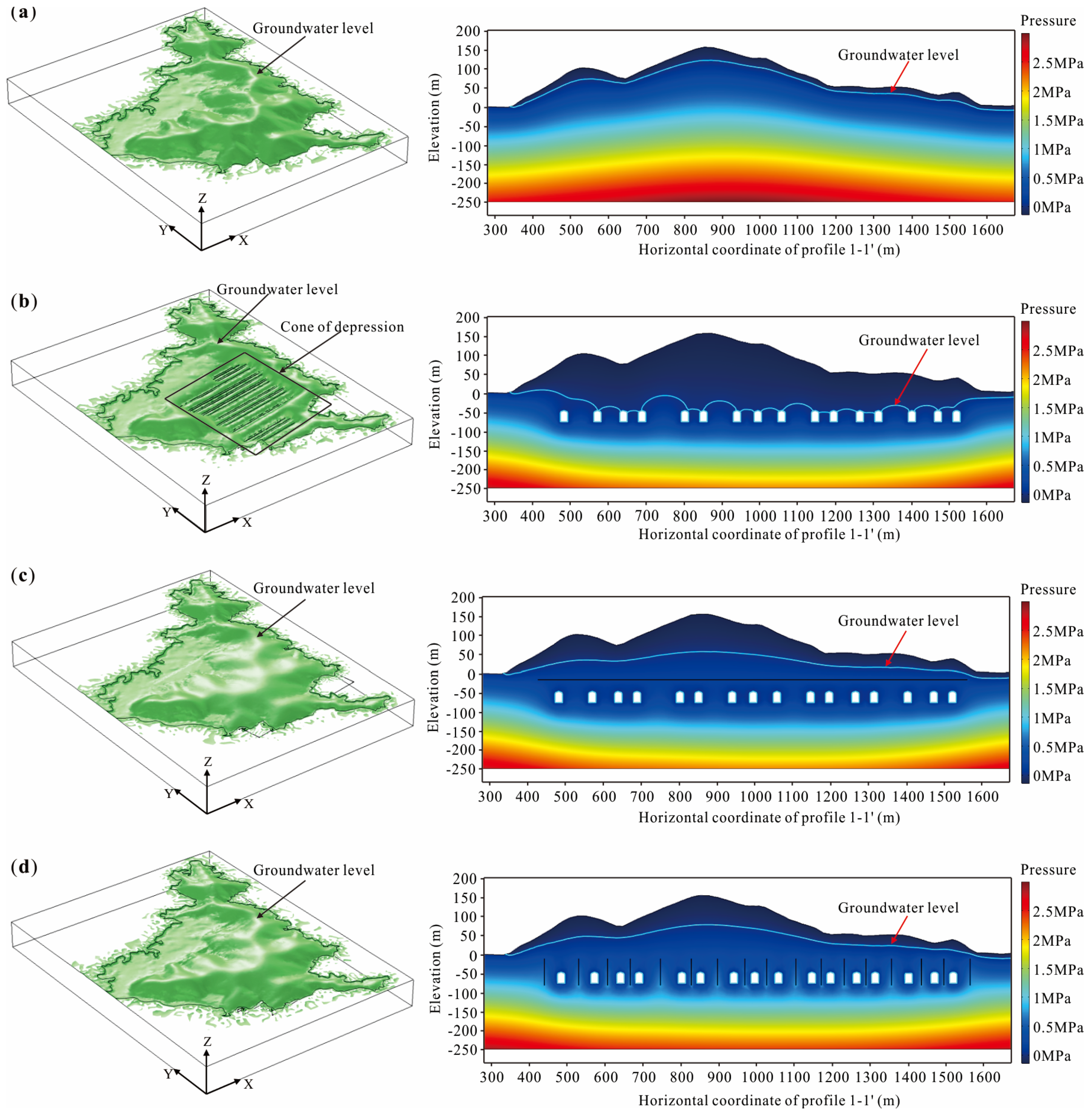
4.2. Characteristics of Groundwater Seepage
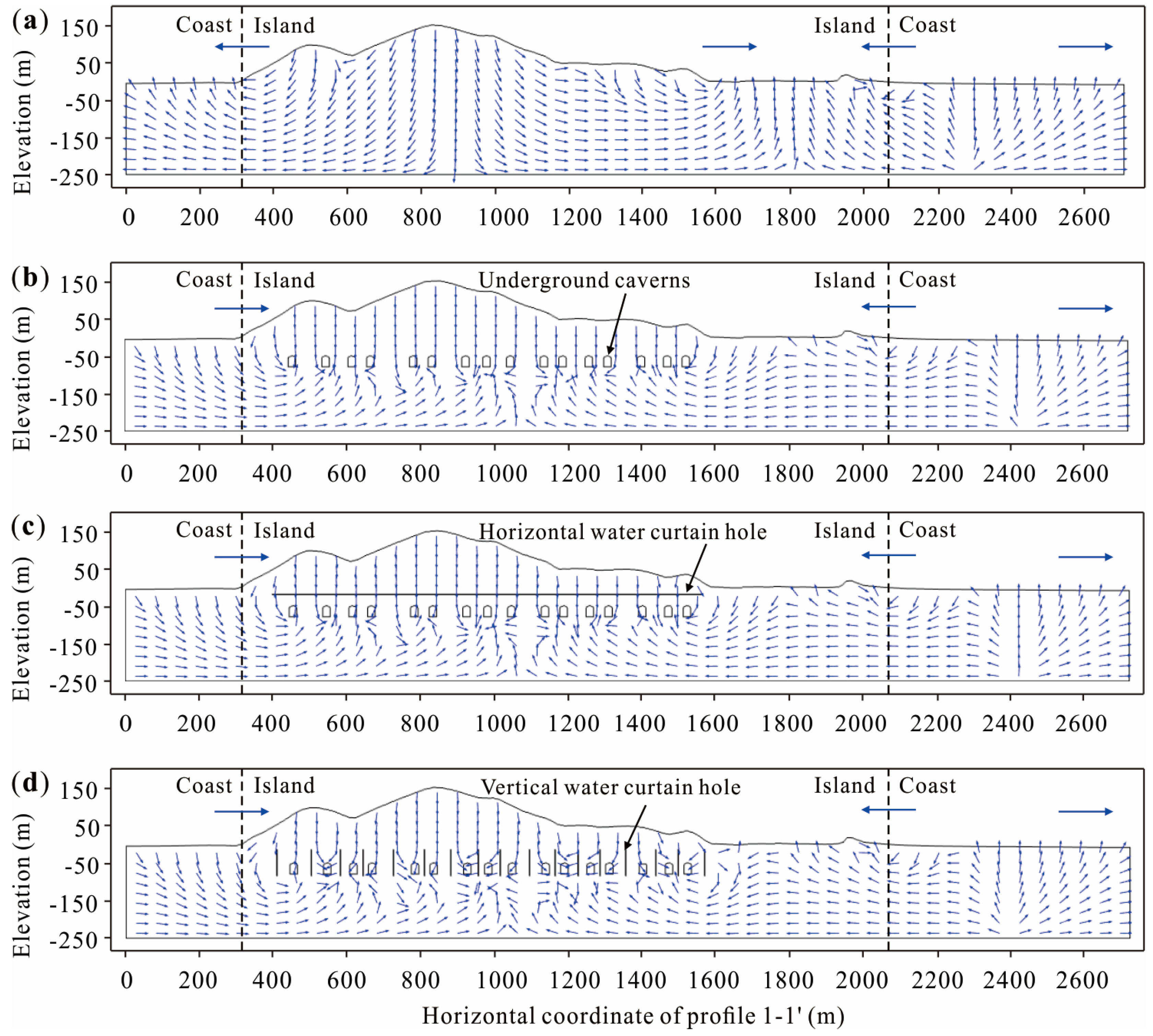
4.2.1. Groundwater Seepage Direction
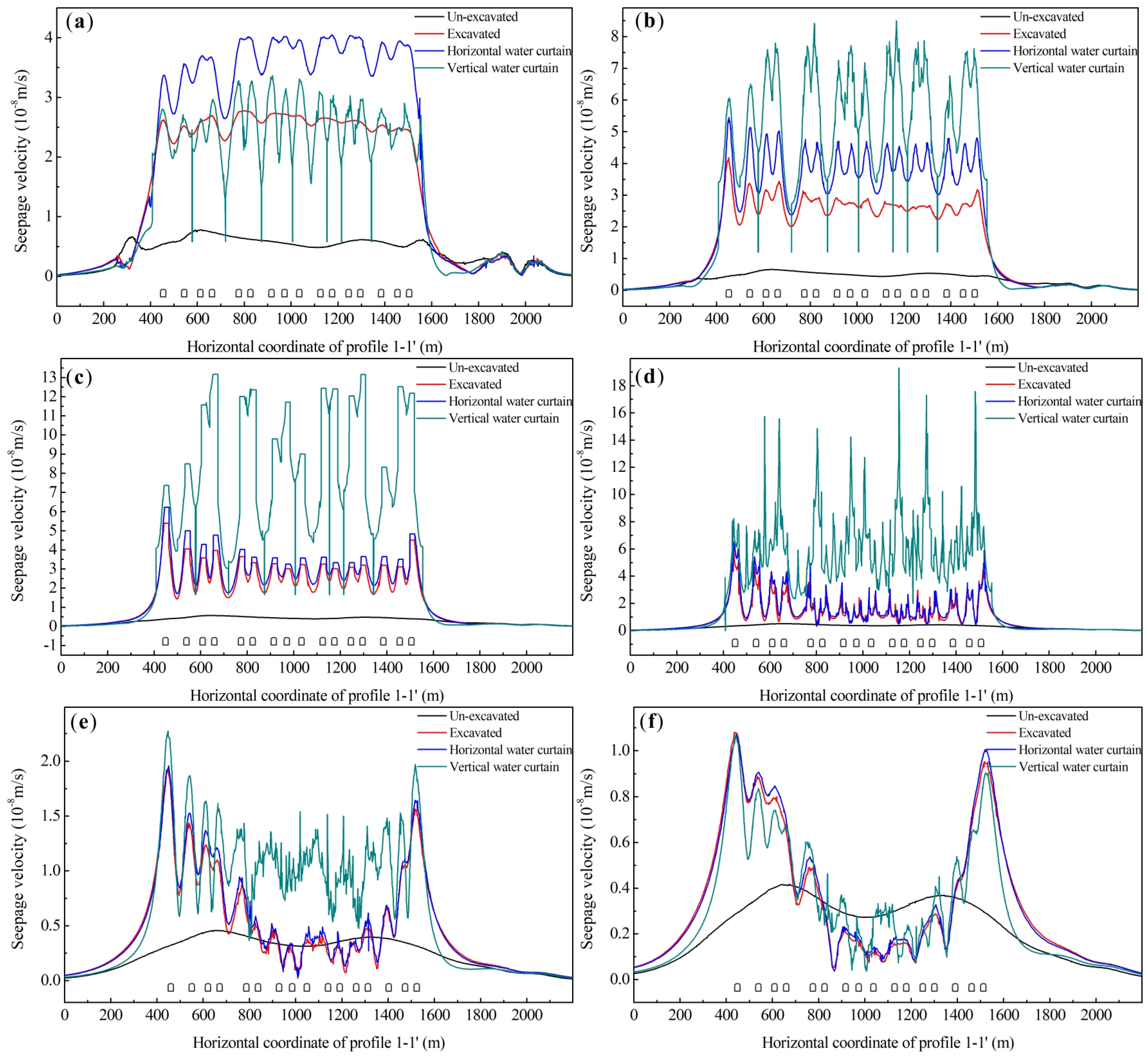
4.2.2. Groundwater Seepage Velocity
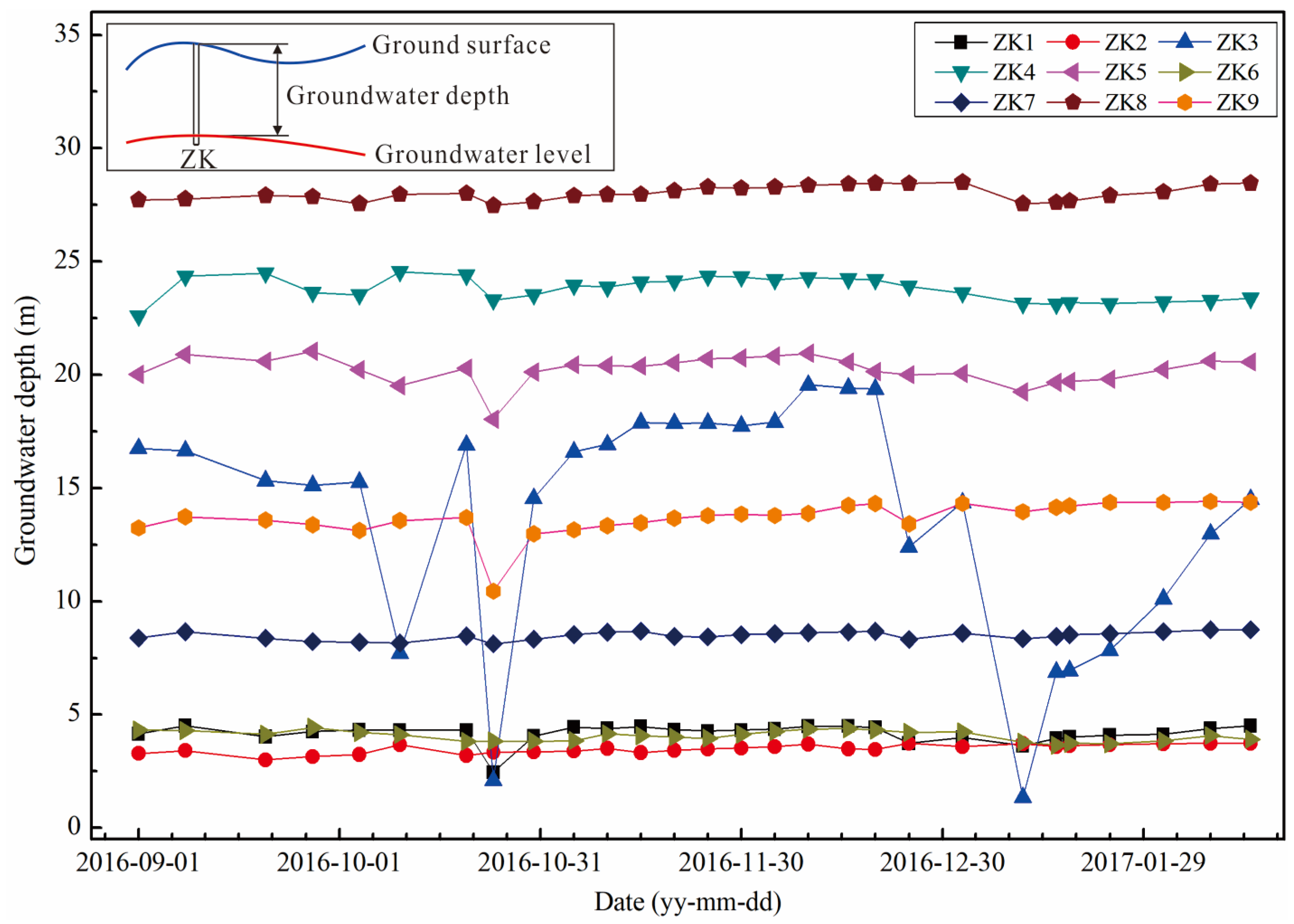
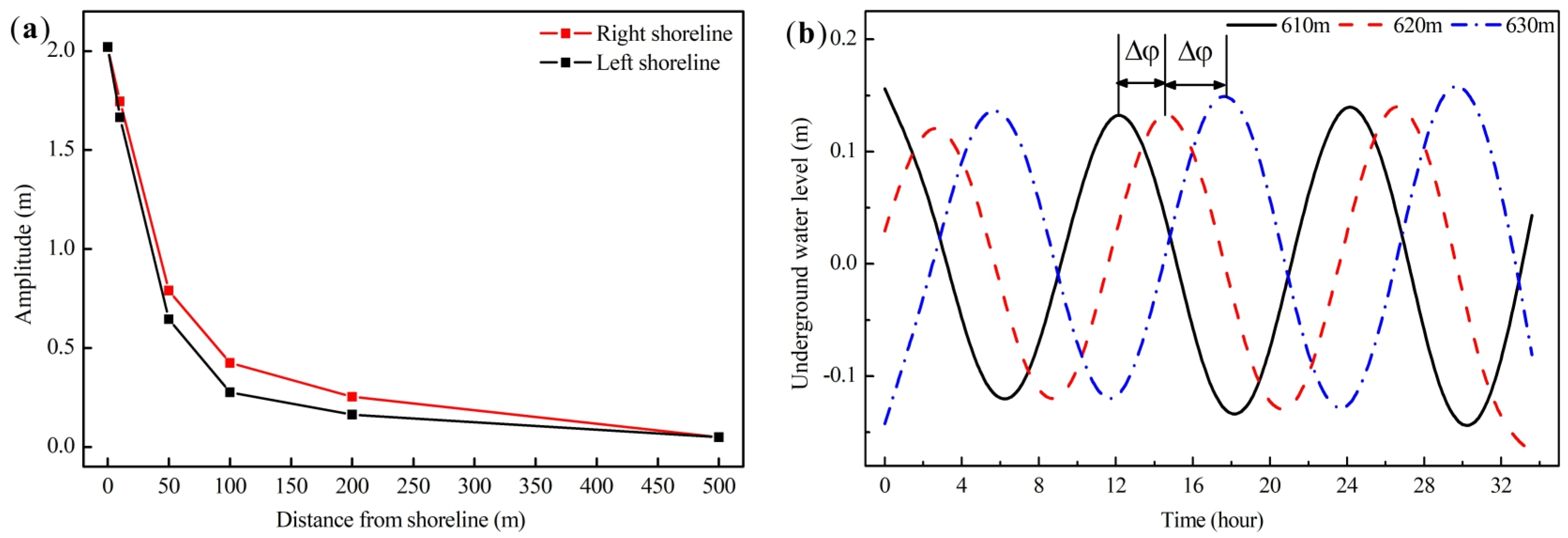
4.2.3. Groundwater Level
4.3. Characteristics of Seawater Intrusion
4.3.1. Temporal-Spatial Variations of Seawater Intrusion
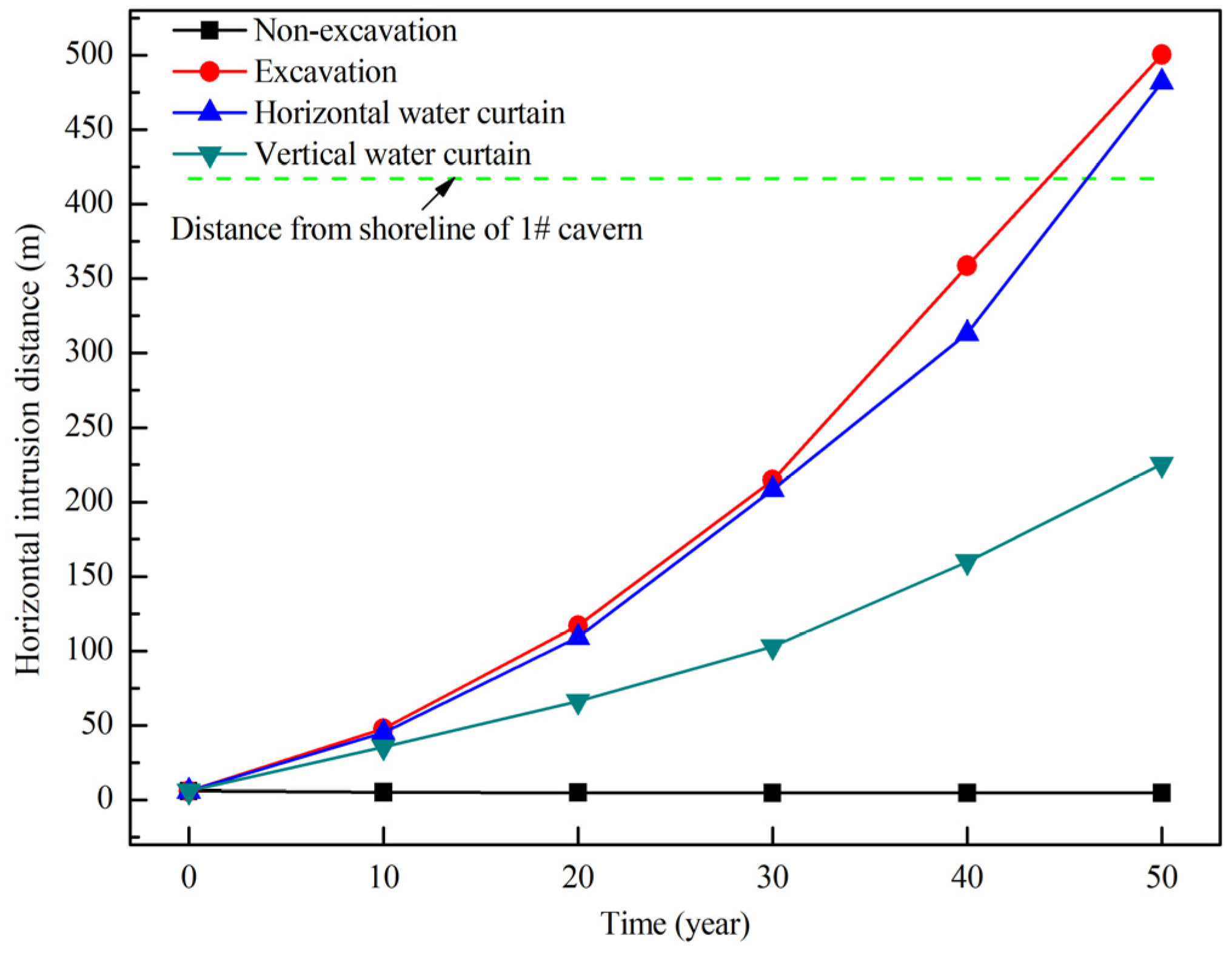
4.3.2. Influence of Water Curtain System on Seawater Intrusion
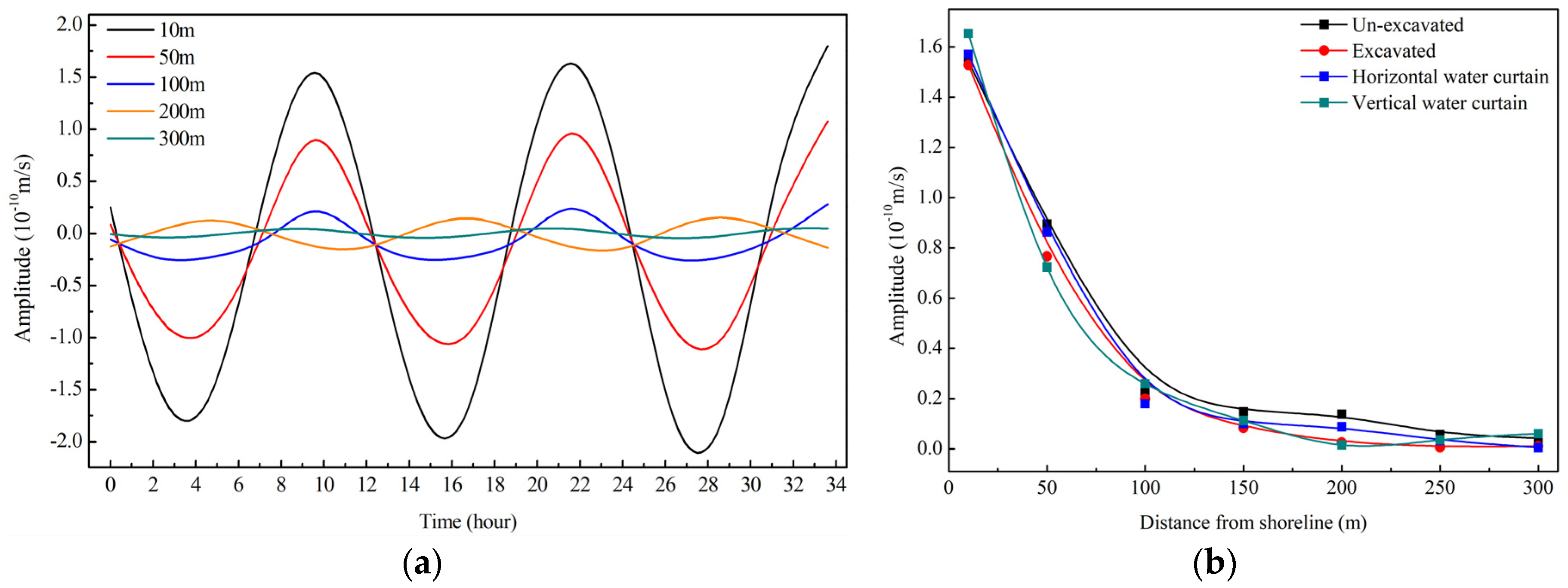
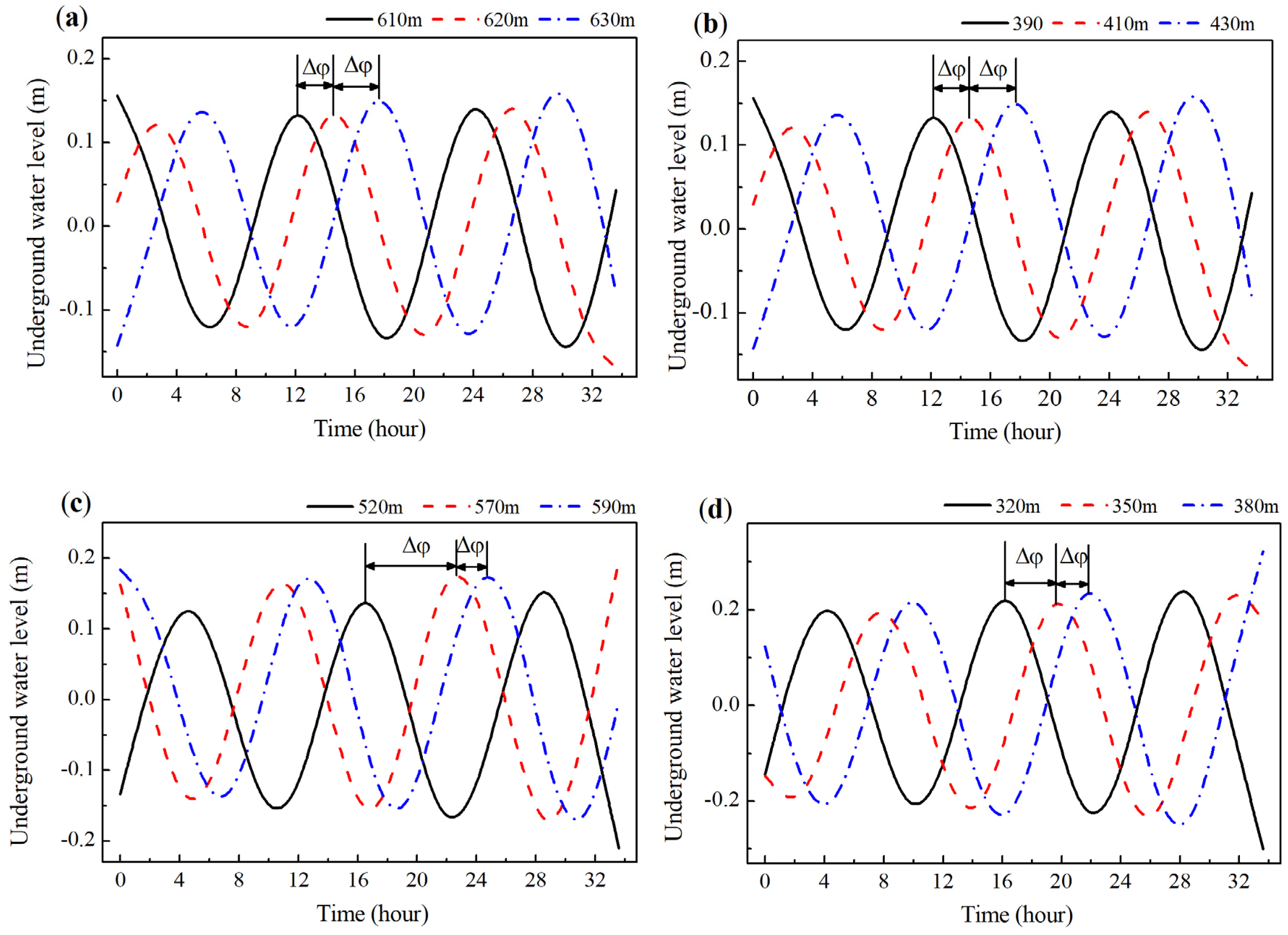
4.3.3. Tidal Influence on Seawater Intrusion
5. Discussion
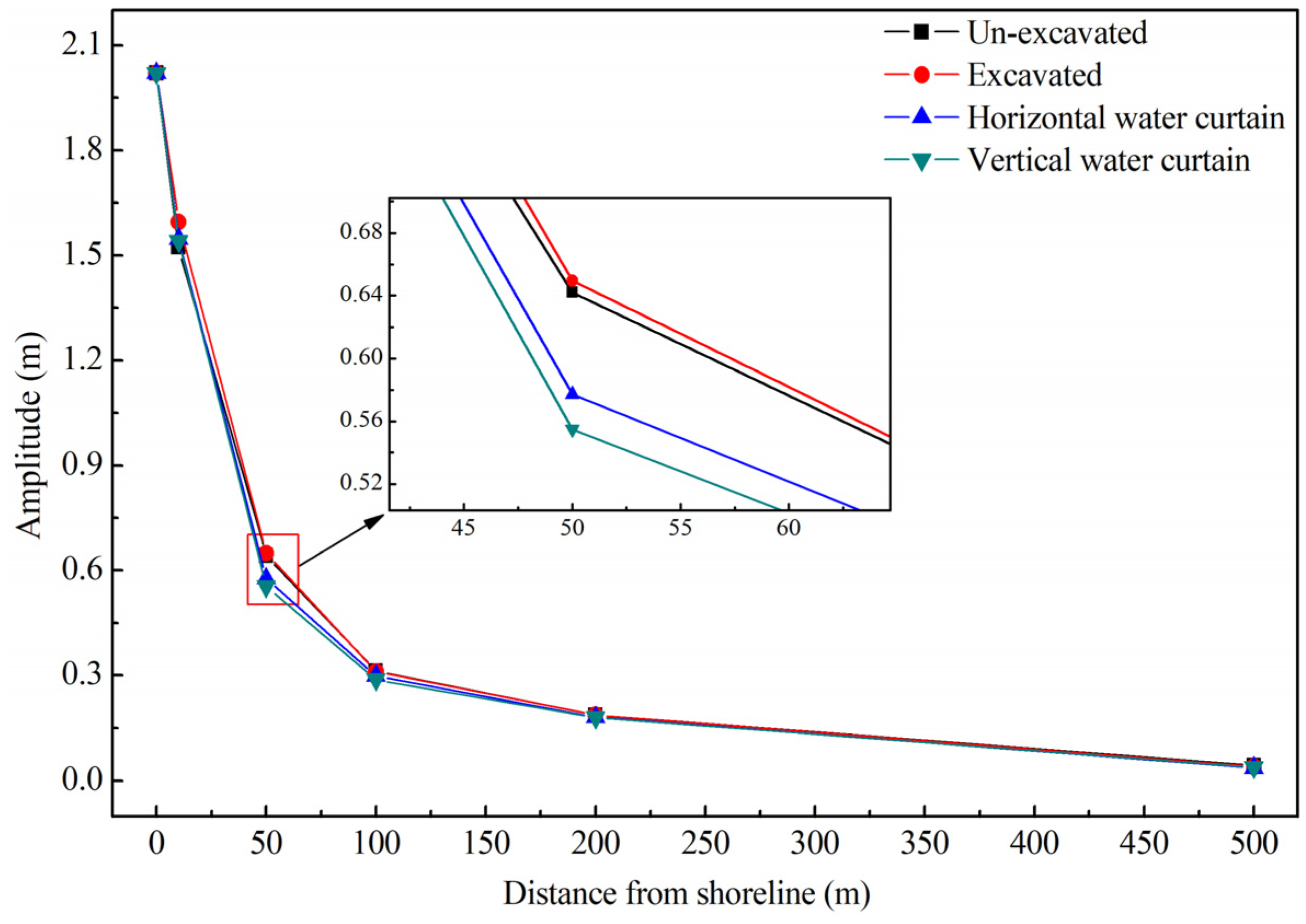
- (1)
- Under the island tidal environment, the groundwater level within the island is affected by tidal fluctuations, which show fluctuation characteristics. When the underground water-sealed oil storage cavern is built in the island, the fluctuation amplitude damping rate of the groundwater level can be successively sorted from low to high: excavated, un-excavated, with a horizontal water curtain system and with a vertical water curtain system (as shown in Figure 13). The tidal wave is transmitted from the shoreline to the island, and the wave energy decreases continually in the process of transmission, so the amplitude damping is generated. After the underground cavern is excavated, the groundwater seeps into the underground cavern, which accelerates the velocity of groundwater flow. Therefore, the amplitude damping velocity of the groundwater level is smaller than that of the un-excavated condition. After the water curtain system is set, the water curtain system recharges the groundwater, and the groundwater seepage around the island is restrained, so the amplitude of the groundwater level damps faster than that without the water curtain system. The amplitude damping velocity under the influence of a vertical water curtain system is greater than that of a horizontal water curtain system, which indicates that the vertical water curtain system has a greater barrier effect on the seepage flow of groundwater into the island. This phenomenon reveals the advantages of vertical water curtain systems in the construction of underground water-sealed oil storage caverns in island tidal environments.
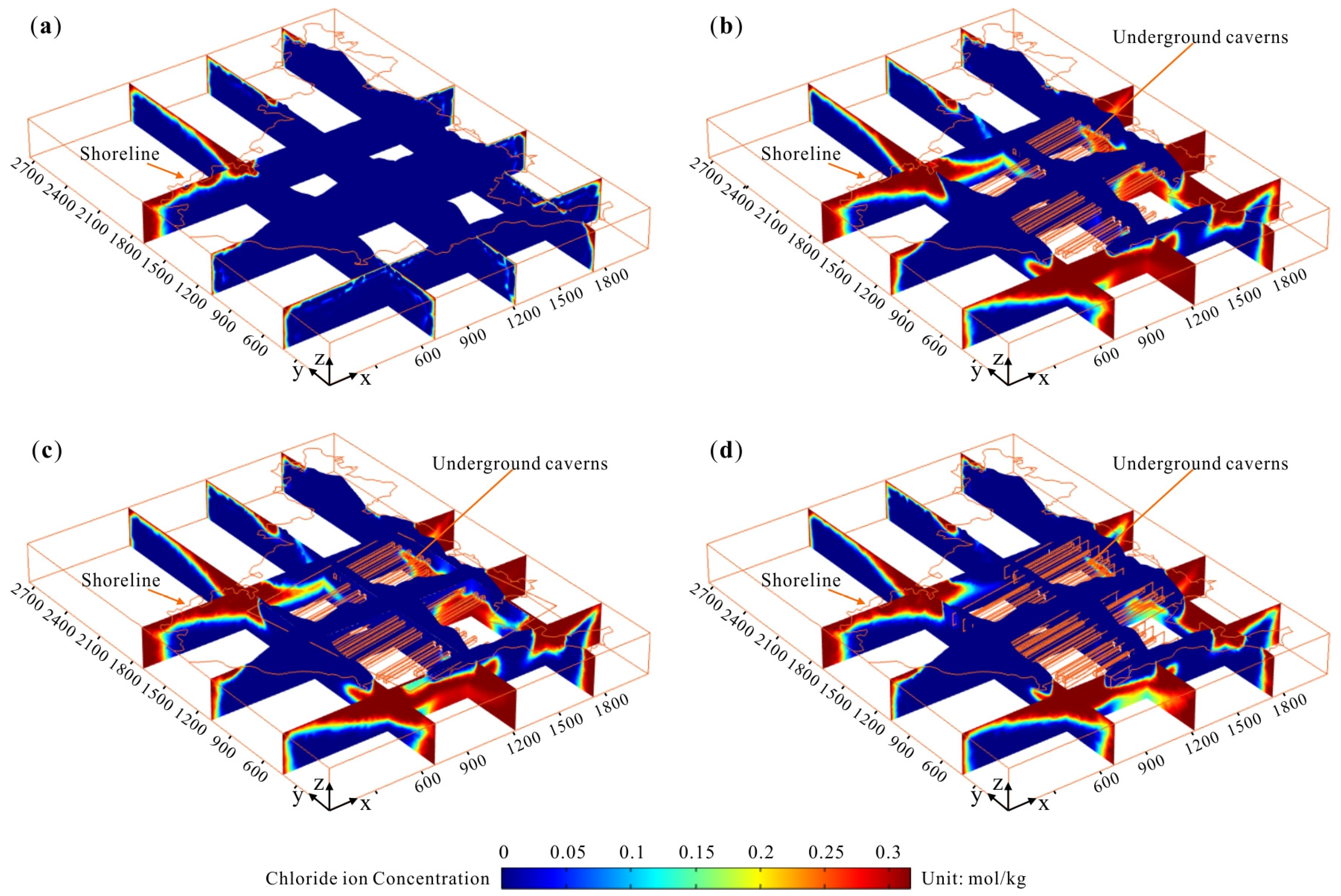
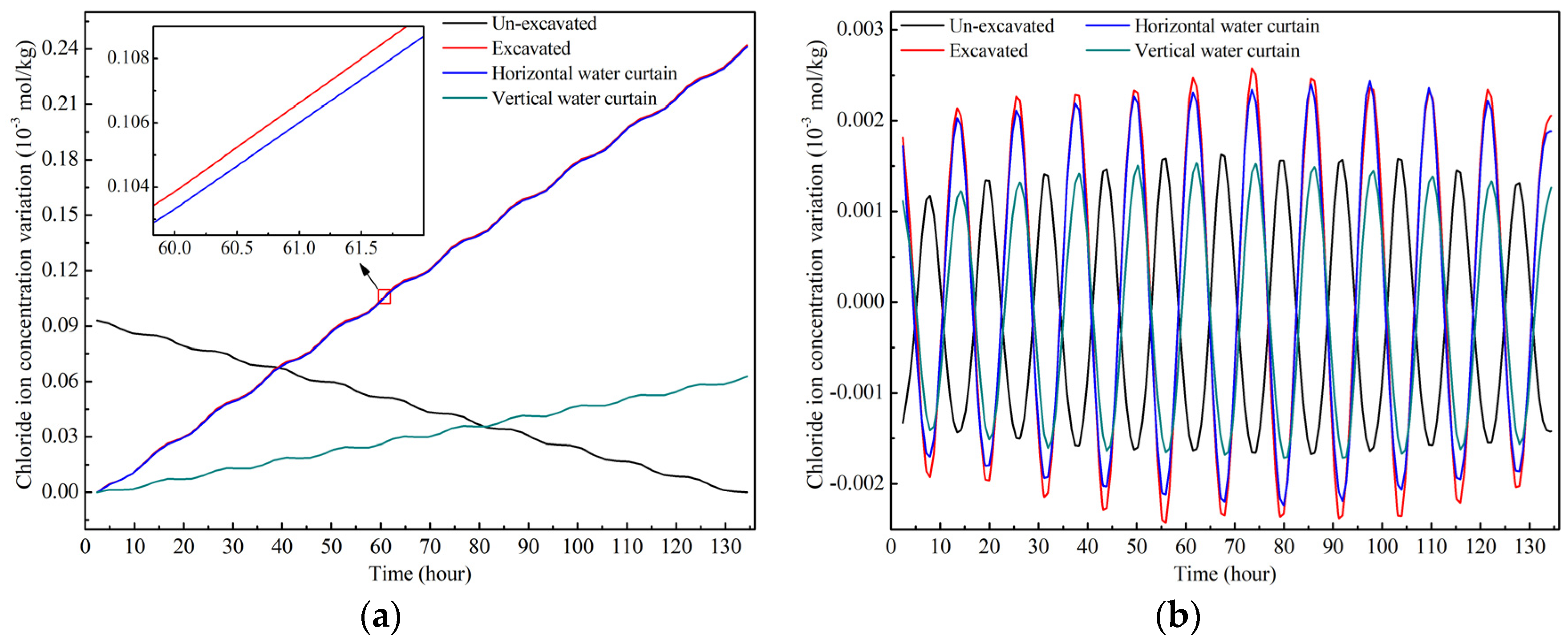
- (2)
- Before the excavation of the underground cavern (as shown in Figure 17a), the chloride ion concentration at the monitoring point shows a decreasing trend. According to the governing equation, seawater intrusion is affected by the groundwater flow and the hydrodynamic dispersion of solute ions. In the case of an un-excavated island, groundwater seeps from the island to the shoreline (as shown in Figure 8). In contrast, solute diffusion is affected by its concentration, from high concentration to low concentration, that is, it diffuses from the shoreline to the island interior. It can be seen from the results that at the location of the monitoring point, the influence of the groundwater flow on seawater intrusion is greater than that of hydrodynamic dispersion.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Morfeldt, C.O. Storage of petroleum products in man-made caverns in Sweden. Bull. Eng. Geol. Environ. 1983, 28, 17–30. [Google Scholar] [CrossRef]
- Lu, M. Finite element analysis of a pilot gas storage in rock cavern under high pressure. Eng. Geol. 1998, 49, 353–361. [Google Scholar] [CrossRef]
- Makita, T.; Miyanaga, Y.; Iguchi, K.; Hatano, T. Underground oil storage facilities in japan. Eng. Geol. 1993, 35, 191–198. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.F.; Zhang, G.J.; Liu, Y.; Zhou, C.B. A numerical procedure for modeling the seepage field of water-sealed underground oil and gas storage caverns. Tunn. Undergr. Space Technol. 2017, 66, 56–63. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, B.; Wang, L.; Wang, H.X.; Zhang, H.J. Functional efficiency assessment of the water curtain system in an underground water-sealed oil storage cavern based on time-series monitoring data. Eng. Geol. 2018, 239, 79–95. [Google Scholar] [CrossRef]
- Xue, Y.G.; Li, S.C.; Qiu, D.H.; Wang, Z.C.; Li, Z.Q.; Tian, H.; Su, M.X.; Yang, W.M.; Lin, C.J.; Zhu, J.Y. A new evaluation method for site selection of large underground water-sealed petroleum storage depots. Sci. China Technol. Sci. 2015, 58, 967–978. [Google Scholar] [CrossRef]
- Lim, J.W.; Lee, E.; Moon, H.S.; Lee, K.K. Integrated investigation of seawater intrusion around oil storage caverns in a coastal fractured aquifer using hydrogeochemical and isotopic data. J. Hydrol. 2013, 486, 202–210. [Google Scholar] [CrossRef]
- Lee, J.Y.; Cho, B.W. Submarine groundwater discharge into the coast revealed by water chemistry of man-made undersea liquefied petroleum gas cavern. J. Hydrol. 2008, 360, 195–206. [Google Scholar] [CrossRef]
- Huyakorn, P.S.; Andersen, P.F.; Mercer, J.W.; White, H.O. Saltwater intrusion in aquifers: Development and testing of a three-dimensional finite element model. Water Resour. Res. 1987, 23, 293–312. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.H.; Kim, H.M.; Chang, H.W. Statistical approach to determine the salinized ground water flow path and hydrogeochemical features around the underground LPG cavern, Korea. Hydrol. Process. 2010, 21, 3615–3626. [Google Scholar] [CrossRef]
- Mas-Pla, J.; Rodríguez-Florit, A.; Zamorano, M.; Roqué, C.; Menció, A.; Brusi, D. Anticipating the effects of groundwater withdrawal on seawater intrusion and soil settlement in urban coastal areas. Hydrol. Process. 2013, 27, 2352–2366. [Google Scholar] [CrossRef]
- Werner, A.D.; Bakker, M.; Post, V.E.A.; Vandenbohede, A.; Lu, C.H.; Ataie-Ashtiani, B.; Simmons, C.T.; Barry, D.A. Seawater intrusion processes, investigation and management: Recent advances and future challenges. Adv. Water Resour. 2013, 51, 3–26. [Google Scholar] [CrossRef]
- Boschetti, T.; Awaleh, M.O.; Barbieri, M. Waters from the Djiboutian Afar: A Review of Strontium Isotopic Composition and a Comparison with Ethiopian Waters and Red Sea Brines. Water 2018, 10, 1700. [Google Scholar] [CrossRef]
- Sreekanth, J.; Datta, B. Review: Simulation-optimization models for the management and monitoring of coastal aquifers. Hydrogeol. J. 2015, 23, 1155–1166. [Google Scholar] [CrossRef]
- Nocchi, M.; Salleolini, M. Prediction of pollutant remediation in a heterogeneous aquifer in Israel: Reducing uncertainty by incorporating lithological, head and concentration data. J. Hydrol. 2018, 564, 651–666. [Google Scholar] [CrossRef]
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- Sebben, M.L.; Werner, A.D.; Graf, T. Seawater intrusion in fractured coastal aquifers: A preliminary numerical investigation using a fractured Henry problem. Adv. Water Resour. 2015, 85, 93–108. [Google Scholar] [CrossRef]
- Arfib, B.; Marsily, G.D. Modeling the salinity of an inland coastal brackish karstic spring with a conduit-matrix model. Water Resour. Res. 2004, 40, 417–427. [Google Scholar] [CrossRef]
- Liu, W.C.; Liu, H.M. Assessing the Impacts of Sea Level Rise on Salinity Intrusion and Transport Time Scales in a Tidal Estuary, Taiwan. Water 2014, 6, 324–344. [Google Scholar] [CrossRef]
- Petti, M.; Bosa, S.; Pascolo, S. Lagoon Sediment Dynamics: A Coupled Model to Study a Medium-Term Silting of Tidal Channels. Water 2018, 10, 569. [Google Scholar] [CrossRef]
- Oberle, F.K.J.; Swarzenski, P.W.; Storlazzi, C.D. Atoll Groundwater Movement and Its Response to Climatic and Sea-Level Fluctuations. Water 2017, 9, 650. [Google Scholar] [CrossRef]
- Taniguchi, M. Tidal effects on submarine groundwater discharge into the ocean. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Li, L.; Barry, D.A.; Parlange, J.Y.; Pattiaratchi, C.B. Beach water table fluctuations due to wave run-up: Capillarity effects. Water Resour. Res. 1997, 33, 817–824. [Google Scholar] [CrossRef]
- Jeng, D.S.; Li, L.; Barry, D.A. Analytical solution for tidal propagation in a coupled semi-confined/phreatic coastal aquifer. Adv. Water Resour. 2002, 25, 577–584. [Google Scholar] [CrossRef]
- Teo, H.T.; Jeng, D.S.; Seymour, B.R.; Barry, D.A.; Li, L. A new analytical solution for water table fluctuations in coastal aquifers with sloping beaches. Adv. Water Resour. 2003, 26, 1239–1247. [Google Scholar] [CrossRef]
- Huang, F.K.; Chuang, M.H.; Wang, G.S.; Yeh, H.D. Tide-induced groundwater level fluctuation in a u-shaped coastal aquifer. J. Hydrol. 2015, 530, 291–305. [Google Scholar] [CrossRef]
- Levanon, E.; Shalev, E.; Yechieli, Y.; Gvirtzman, H. Fluctuations of fresh-saline water interface and of water table induced by sea tides in unconfined aquifers. Adv. Water Resour. 2016, 96, 34–42. [Google Scholar] [CrossRef]
- Nielsen, P. Tidal dynamics of the water table in beaches. Water Resour. Res. 1990, 26, 2127–2134. [Google Scholar] [CrossRef]
- Siarkos, I.; Latinopoulos, D.; Mallios, Z.; Latinopoulos, P. A methodological framework to assess the environmental and economic effects of injection barriers against seawater intrusion. J. Environ. Manag. 2017, 193, 532–540. [Google Scholar] [CrossRef]
- Huang, P.S.; Chiu, Y.C. A simulation-optimization model for seawater intrusion management at pingtung coastal area, Taiwan. Water 2018, 10, 251. [Google Scholar] [CrossRef]
- Lee, E.; Lim, J.W.; Moon, H.S.; Lee, K.K. Assessment of seawater intrusion into underground oil storage cavern and prediction of its sustainability. Environ. Earth Sci. 2015, 73, 1179–1190. [Google Scholar] [CrossRef]
- Ivars, D.M. Water inflow into excavations in fractured rock—A three-dimensional hydro-mechanical numerical study. Int. J. Rock Mech. Min. 2006, 43, 705–725. [Google Scholar] [CrossRef]
- Li, S.C.; Wang, Z.C.; Ping, Y.; Zhou, Y.; Zhang, L. Discrete element analysis of hydro-mechanical behavior of a pilot underground crude oil storage facility in granite in china. Tunn. Undergr. Space Technol. 2014, 40, 75–84. [Google Scholar] [CrossRef]
- Wang, Z.C.; Li, S.C.; Qiao, L.P.; Zhang, Q.S. Finite element analysis of the hydro-mechanical behavior of an underground crude oil storage facility in granite subject to cyclic loading during operation. Int. J. Rock Mech. Min. 2015, 73, 70–81. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.W.; Wang, Y.; Fan, L.F. Pipe network model for unconfined seepage analysis in fractured rock masses. Int. J. Rock Mech. Min. 2016, 88, 183–196. [Google Scholar] [CrossRef]
- Wang, Z.C.; Li, W.; Li, S.C.; Qiu, W.G.; Ding, W.T. Development of an optimum forepole spacing (OFS) determination method for tunnelling in silty clay with a case study. Tunn. Undergr. Space Technol. 2018, 74, 20–32. [Google Scholar] [CrossRef]
- Louis, C. Rock Hydraulics; Springer Vienna: New York, NY, USA, 1972; p. 59. ISBN 978-3-7091-4109-0. [Google Scholar]
- Navigation Guarantee Department of Chinese Navy Headquarters. Tide Table: 2009, East China Sea; China Navigation Publications Press: Beijing, China, 2008; pp. 100–102. ISBN 978-7-80224-554-9. [Google Scholar]
- Chen, Z.Y. Ocean Tide; Science Press: Beijing, China, 1979; pp. 18–24. ISBN 13031-946. [Google Scholar]
- Chun, J.A.; Lim, C.; Kim, D.; Kim, J.S. Assessing Impacts of Climate Change and Sea-Level Rise on Seawater Intrusion in a Coastal Aquifer. Water 2018, 10, 357. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of fluids in porous media. Eng. Geol. 1972, 7, 174–175. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Xie, C.H. Transport in Subsurface Flow; China Architecture & Building Press: Beijing, China, 1990; pp. 214–219. ISBN 7-112-01092-6. [Google Scholar]
- Gelhar, L.W.; Welty, C.; Rehfeldt, K.R. A critical review of data on field-scale dispersion in aquifers. Water Resour. Res. 1992, 28. [Google Scholar] [CrossRef]
- Harrison, W.; Fang, C.S.; Wang, S.N. Groundwater flow in a sandy tidal beach: One dimensional finite element analysis. Water Resour. Res. 1971, 7, 1313–1322. [Google Scholar] [CrossRef]
- Li, L.; Barry, D.A.; Pattiaratchi, C.B. Numerical modelling of tide-induced beach water table fluctuations. Coast. Eng. 1997, 30, 105–123. [Google Scholar] [CrossRef]
- Liu, H.J.; Zhang, X.H.; Lu, X.B.; Liu, Q.J. Study on flow in fractured porous media using pore-fracture network modeling. Energies 2017, 10, 17. [Google Scholar] [CrossRef]
- Xu, S.Y.; Zhang, Y.B.; Shi, H.; Wang, K.; Geng, Y.P.; Chen, J.F. Physical Simulation of Strata Failure and Its Impact on Overlying Unconsolidated Aquifer at Various Mining Depths. Water 2018, 10, 650. [Google Scholar] [CrossRef]
| Items | Four Conditions | |||
|---|---|---|---|---|
| Un-Excavated | Excavated | Horizontal Water Curtain | Vertical Water Curtain | |
| Number of elements | 440,710 | 970,463 | 1,083,967 | 3,054,415 |
| Minimum element size (m) | 9.45 | 4.26 | 1.54 | 1.29 |
| Maximum element size (m) | 94.75 | 91.65 | 80.72 | 92.452 |
| Average element size (m) | 51.22 | 46.98 | 44.39 | 44.59 |
| Granite Density | Freshwater Density | Seawater Density | Porosity n | Diffusion Coefficients D* (m2/s) | Longitudinal Dispersity | Transversal Dispersity |
|---|---|---|---|---|---|---|
| 2600 | 1000 | 1025 | 0.015 | 21.3 | 4.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, B.; Shi, L.; Ye, Y. Dynamic Variation Characteristics of Seawater Intrusion in Underground Water-Sealed Oil Storage Cavern under Island Tidal Environment. Water 2019, 11, 130. https://doi.org/10.3390/w11010130
Li Y, Zhang B, Shi L, Ye Y. Dynamic Variation Characteristics of Seawater Intrusion in Underground Water-Sealed Oil Storage Cavern under Island Tidal Environment. Water. 2019; 11(1):130. https://doi.org/10.3390/w11010130
Chicago/Turabian StyleLi, Yutao, Bin Zhang, Lei Shi, and Yiwei Ye. 2019. "Dynamic Variation Characteristics of Seawater Intrusion in Underground Water-Sealed Oil Storage Cavern under Island Tidal Environment" Water 11, no. 1: 130. https://doi.org/10.3390/w11010130
APA StyleLi, Y., Zhang, B., Shi, L., & Ye, Y. (2019). Dynamic Variation Characteristics of Seawater Intrusion in Underground Water-Sealed Oil Storage Cavern under Island Tidal Environment. Water, 11(1), 130. https://doi.org/10.3390/w11010130





