Colloid Transport in a Single Fracture–Matrix System: Gravity Effects, Influence of Colloid Size and Density

Abstract

A numerical model was developed to investigate the influence of gravitational force on the transport of colloids in a single horizontal fracture–matrix system. Along with major transport phenomena, prominence was given to study the mass flux at the fracture–matrix interface, and colloid penetration within the rock matrix. Results suggest that the gravitational force significantly alters and controls the velocity of colloids in the fracture. Further, it was shown that the colloid density and size play a vital part in determining the extent that gravity may influence the transport of colloids in both fracture and rock matrix. The mass flux transfer across the fracture–matrix interface is predominantly dependent on the colloidal size. As large as 80% reduction in penetration of colloids in the rock matrix was observed when the size of the colloid was increased from 50–600 nm. Similarly, the farther the density of colloid from that of the fluid in the fracture (water), then the higher the mitigation of colloids in the fracture and the rock matrix. Finally, a non-dimensional parameter “Rock Saturation Factor” has been presented in the present study, which can offer a straightforward approach for evaluating the extent of penetration of colloids within the rock matrix.

1. Introduction

Colloids are an integral part of fractured porous media. Studies [1,2] have established that colloids act as carriers, and enhance the migration of contaminants, which have leached into the subsurface water system, thereby, enhancing their sweep through the system. Significant advancements have been made in understanding the prediction of colloid behavior in fractured media. The knowledge imparted by these studies has been critical in understanding colloid advection, dispersion, adsorption, biodegradation and other transport phenomena [1,2,3,4,5]. However, apart from conventionally studied transport phenomena, an understanding of various forces acting on the colloids stability and migration is essential for predicting the near to actual spreading or migration of colloids. Forces such as the electric double layer, van der Waals, shear forces (lift and drag), and gravitational forces acting on colloids are the primary contributors to the stability of colloids [6,7,8]. In the present numerical experiment, forces such as lift, drag, electric double layer, and van der Waals forces acting on colloids are neglected, and the principal objective is to understand the influence of the gravitational force on the stability, and hence, the transport of the colloids in the fractured matrix-system. Equation (1) represents the force acting on the colloids due to gravitation (F_g) [6]. It can be noted from Equation (1) that the F_g is a function of the size and density of the colloids, and does not depend on the charge of the particle or its distance from another particle. Therefore, the influence of the double layer and van der Waals force arising due to these two factors on gravity can be eliminated. Hence, the assumption of selecting gravity as an isolated phenomenon influencing the stability of colloids would be valid. The gravitational force is a potential driver of retention, thus has a strong influence on the velocity of the colloid through the fracture. The gravitational force acts as normal to the flow direction of the colloids, inducing a component of colloidal velocity normal to its flow direction [4]. Due to the normal component, the colloids drift towards the fracture wall, into the region of relatively low axial velocity.

Colloid density and size are the two parameters that contribute to the influence of the gravitational force on the transport of colloids in a fractured porous system. Stokes–Einstein’s equation (Equation (4)) representing the diffusion of colloids show that diffusion is inversely a function of colloid size (diameter/radius). Further, the dispersion, which is a predominant phenomenon of transport in the fracture, is a function of velocity, which in turn is sensitive to the size of the colloid [9]. The axial velocity of colloid is sensitive to the size of colloid, under the gravitational force the reasonably large colloids tend to migrate towards the fracture wall due to reduced axial velocity [10]. Hence, it becomes critical to include the influence of colloidal size in the analysis of colloidal transport.

Few studies have been carried out that have examined the impact of the gravitational force on the transport of colloids in the fractured porous medium [11,12,13]. However, a majority of them consider gravity as an outcome of the change in potential energy (height) by carrying out either vertical or inclined column/fracture experiments. In such experiments, the gravity is a forced effect of the change in potential (height), which causes a change in the velocity of the colloid. The change in velocity of the colloid is not due to gravity alone, but may additionally be attributed to acceleration or deceleration of fluid (suspension) in which colloids are suspended, due to change in potential energy (height). In order to have a clear analysis of the impact of gravitational force on the colloids, the change in velocity of the fluid due to change in potential energy has to be isolated, and the experiment has to be carried out at zero potential energy change. Not many studies have considered the influence of gravity on the transport of colloids at zero potential energy change. The number of studies is even fewer when the system, in consideration for the analysis, is a multi-continuum fractured porous media. Some studies have come close enough, by analyzing the influence of external forces in a system that resembles that similar to fracture, sans the surrounding rock matrix [14]. Unni and Yang [15] and James and Chrysikopoulos [12] analyzed the influence of the external force on colloids flowing in a constant width channel, which was horizontal and inclined respectively. The channel represents the high permeability fracture zone, however, without the surrounding porous rock matrix (no mass flux transfer to the surrounding porous media). Jen and Li [16] in their study on performance assessment of high-level radioactive waste disposal in a fractured porous media proposed a theoretical model to include the external forces acting on the colloids in a fracture–matrix system. However, the primary focus of Jen and Li [16] was to understand the colloid assisted radionuclide transport and here a mathematical model for inclusion of gravity has been presented, and the detailed numerical analysis has not been carried out. Therefore, the current knowledge and the methods used in understanding the influence of the gravitational force on the stability are inadequate to accurately predict the colloid migration in fractured porous media under the influence of gravity. Additionally, the combined influence of gravitational force, size and density of colloids has received relatively minimal attention, especially in the multi continuum fracture–matrix system.

The focus of the current work is to investigate the influence of the gravitational force, along with different colloid size and density on the transport of colloids in a single horizontal multi-continuum fracture–matrix system. The influence of gravitational force on colloids is introduced through the velocity of the colloids into the transport equation. Apart from the analysis of major transport phenomena, prominence is given to analyzing the mass flux transfer at the fracture–matrix interface, and the diffusive transport in the porous rock matrix when gravitational force, different colloid size and density are taken into consideration. Finally, a novel non-dimensional parameter (Rock Saturation Factor) has been developed as a simple approach for evaluating the extent of penetration of colloids within the rock matrix.

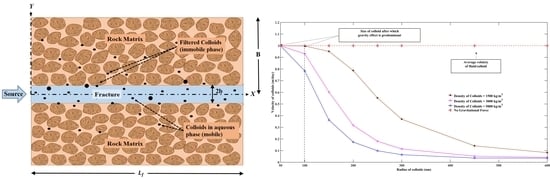
2. Physical System

Figure 1 illustrates the conceptual model depicting the cross-section of a simplified single horizontal fracture–matrix system, which forms the fraction of the complete fracture network at large field scale. In Figure 1, b is the average half fracture aperture representing the fracture, B is the half fracture spacing, and L_f is the length of the fracture. Colloid enters into the fracture–matrix system from the left boundary (fracture inlet at left end, X = 0), then the injected colloids transport through the fracture, and some of them diffuse into the rock matrix. In Figure 1 the colloids, which are adsorbed onto the porous rock matrix or fracture, are termed as “immobile colloids” (filtered colloids onto the surface), and the colloids which are being transported are termed “mobile colloids”. The fracture and matrix geometry repeat itself, and each fracture is symmetrical. Therefore, only one-half of a fracture and one-half of the rock matrix system is considered in the present analysis [17] (Figure 1).

Assumptions made regarding the geometry and hydrodynamic properties of the system.

• Transport in the fracture is 1D with fluid flowing horizontally.
• Transport within the rock matrix is 1D with the transport of the fluid orthogonal to the direction of flow in the fracture.
• The fracture aperture is smaller than the length of the fracture (2b << L_f) [17].
• Transport along the fracture is faster compared to that within the porous rock matrix.
• Colloids can be transported in fracture and within rock matrix [4].
• Diffusion is the only transport mechanism within the rock matrix. Diffusion within the rock matrix is in the transverse direction (Y-axis) to that of the fracture axis (along with the X-axis) [4].
• Transverse diffusion and dispersion ensure complete mixing at all times across the fracture, and a concentration gradient does not occur across the width of the fracture [16].

In the modeling of the transport of colloids in the single horizontal fracture–matrix system, the following transport phenomena and forces were considered:

• Colloids in the aqueous phase were transported advectively and dispersed in the fracture.
• Colloids were filtered (adsorbed) onto the walls of the fracture and mobile colloids may attach on to the walls of the fracture [4].
• Irreversible deposition of colloids on rock surface may occur [3].
• Colloids diffuse into the porous rock matrix from the fracture [3].
• The clogging of colloids on the fracture–matrix interface is taken care of by the percentage of matrix diffusion of colloids (ε), which is constant throughout the analysis [4].
• Gravitational force act on colloids.

3. Mathematical Model

3.1. Model for the Inclusion of the Gravitational Force

The force due to gravity operates on the mass of the colloid, influencing the colloidal velocity along the fracture, and eventually, on the transport in the fracture, the gravitational acceleration acts transverse to the fracture axis. Equation (1) represents the force acting on the colloids due to gravitation (F_g) [6].

$$F_g=\frac{4}{3}\pi a_p{}^3({\rho }_f-{\rho }_P)g,$$

(1)

where a_P the radius (size) of the colloid (m); g is the acceleration due to gravity (m/s²); ρ_f and ρ_P are the density of the fluid (suspension) and the density of colloid in fluid respectively (kg/m³). The effect of gravitational force on the transverse velocity of colloids is modeled based on the expression given by Jen and Li [16].

$$u_g=-2·a_P{}^2·\left({\rho }_P-{\rho }_F\right)\frac{g}{9·\mu },$$

(2)

where u_g (m/s) is the velocity of colloids in transverse direction due to gravitational force. It is clear from Equation (2) that the velocity due to the gravitational force is a function of the square of the size of the colloids (a_P).

The transverse velocity of colloids obtained from Equation (2) is substituted into Equation (3) [16], to obtain the velocity of the colloids in the longitudinal direction through the fracture. The first step in applying the model is to carry out the following integration:

$$E(y,a_P)=\frac{{\displaystyle \underset{0}{\overset{b}{\int }}{u}_g(y,a_P)}}{D_B}dy,$$

(3)

where E is the integral term representing the summation of transverse velocities. The limits (0 to b) represents the integration over the entire fracture aperture. D_B is the Brownian diffusion coefficient and is given by Stokes–Einstein relation:

$$D_B=\frac{K_B·T}{6\pi ·a_P·\mu },$$

(4)

In the Equation (4), K_B (J K⁻¹) is Boltzmann’s constant; T (K) is the temperature.

The expression that captures the effect of the transverse velocity on the longitudinal velocity of colloids through the fracture is represented by Equation (5).

$$V_c=\frac{{\displaystyle {\int }_{-(b-a_P)}^{(b-a_P)}w(y)·e^{E(y,a_P)}dy}}{{\displaystyle {\int }_{-(b-a_P)}^{(b-a_P)}{e}^{E(y,a_P)}}dy},$$

(5)

where b is the half fracture aperture, and w(y) is the velocity distribution of the fluid in the fracture aperture (Equation (6)). Since a parallel plate model is assumed, the velocity distribution for a fully developed creeping flow will be parabolic and is incorporated into the model using Equation (6):

$$w(y)=\frac{3}{2}(V_f·R)(1-\frac{y^2}{b^2}),$$

(6)

where V_f (m/day) is the averaged fluid velocity through the fracture. Equation (5) computes the velocity of the colloids (V_c) in the fracture taking into account the influence of the gravitational force.

3.2. Governing Equations for the Transport in Fracture–Matrix System

A fractured porous media consists of a high permeability fracture surrounded by a region of relatively low permeability porous rock. The rock and fluid properties in both these regions of fluid flow are distinct. Therefore, mathematically each of these regions has to be considered as a separate continuum and represented by a separate mass transport equation. Then both of these equations are coupled to capture the mass flux transfer across the fracture–matrix interface. From the assumptions, and transport phenomena considered, the physics of the colloidal transport in a single fracture–matrix system is represented by two coupled partial differential equations derived from mass balance considerations. The partial differential equations governing the transport of colloids in fracture and the rock matrix have been adopted from Abdel-Salam and Chrysikopoulos [3] and Li et al. [4]. Equations (7) and (8) represent the transport of mobile and immobile colloids respectively in the fracture:

$$\frac{\partial }{\partial t}(C_f+\frac{{\sigma }_f}{b})=-V_c\frac{\partial C_f}{\partial x}+D_f\frac{{\partial }^2{C}_f}{\partial x^2}+\frac{\epsilon ·{\theta }_m·D_e}{b}\frac{\partial C_m}{\partial y},$$

(7)

$$\frac{\partial {\sigma }_f}{\partial t}={\lambda }_f·V_c·C_f·b,$$

(8)

where x and y represent the longitudinal axis and transverse axis respectively, and t represents time (day). C_f (kg/m³), σ_f (kg/m²), and C_m (kg/m³) are the concentration of mobile, immobile colloids, and concentration of colloids within the rock matrix respectively. D_f and D_e are the hydrodynamic dispersion coefficient (m²/day) and diffusion coefficient (m²/day) of rock matrix respectively. V_c is the velocity of colloids in fracture (m/day) which has been calculated using Equation (5). θ_m, ε, and λ_f are porosity of rock matrix, the percentage of matrix diffusion of colloids, and the filtration coefficient of colloids in fracture (m⁻¹) respectively. Experimental studies have shown that the release rate of the deposited particles is negligible for the case of the smooth parallel surface [18] and hence, colloid deposition can be assumed irreversible (Equation (8)).

Colloids migrate in the fracture, and some of them may be adsorbed on to the solid surface. The irreversible adsorption process considered in the present study can be represented by the Equation (8). In Equation (7), the first and second term on the RHS (Right Hand Side) represents the advection and dispersive transport phenomena of colloids in fracture respectively. The third term on RHS of Equation (7) represents the mass flux transfer of colloids from the fracture into the rock matrix. The rock matrix, which forms the wall of the fracture, is permeable, making it possible for the colloids to transport (perpendicular to fluid flow in fracture) into the rock matrix by process of diffusion. The loss of mass from a fracture is equal to the diffusive flux, which crosses the fracture–matrix interface, and represented by the coupling term of the Equation (7) (third term on RHS) (modeled on the Fick’s first law) [17,19]. The pores of the rock matrix may block the colloids from entering the rock matrix from the fracture. The blockage may be small or total depending on the size of the colloids. Some of the filtered colloids on the fracture wall may further act as a hindrance for the mass flux transfer from fracture to the rock matrix. The parameter ε (percentage of diffusion flux of colloids into the rock matrix) in the final term of Equation (7) on RHS is a function of both sizes of colloids and filter colloids on the fracture wall that could hinder the mass flux transfer process. The value of ε varies from ε = 0 to 1, with ε = 0 being no flux transfer and ε = 1 being 100% flux transfer. In the present article, ε is constant (

Table 1. Transport parameters used for analysis of the transport of colloids in a single fracture–matrix system with variable fracture aperture.

Parameter	Value	Reference
Spatial grid size along the fracture, ∆x (m)	0.006	Calculated
Time step size. ∆t (days)	0.005	Calculated
Length of fracture, L (m)	20	Assumed
Thickness of rock matrix, B (m)	0.25	Assumed
Total time of simulation, T (days)	100	Assumed
Half fracture aperture (Parallel Plate Model), b (μm)	50	Assumed
Sorption partition coefficient for colloids in rock matrix, Kdm	0.2	[4]
Percentage of matrix diffusion flux of colloids, ε (0–1)	0.1	[4]
Porosity of rock matrix, θ	0.03	[4]
Hydrodynamic dispersion coefficient of colloids suspended in fracture, $D_f$(m2/day)	0.013	[4]
Density of water, ${\rho }_w$(kg/m3)	1000
Average velocity of the colloids’ particles, $V_c$ (absence of gravity) (m/day)	1	Assumed
Fluid flow rate, Q (m3/day)	50 × 10−6	Q = A·Vc
Filtration coefficient of the colloids in fracture, ${\lambda }_f$, (L/m)	0.3	[4]
Density of colloids, ρc (kg/m3)	1500–5000	[4]
Radius of colloids, $a_P$(nm)	50–600	[4]
Boltzmann’s constant, $k_B$(J/K)	1.38 × 10−23	[4]

).

Equation (9) represents the diffusive transport of colloids within the porous rock matrix.

$$(1+K_{dm})\frac{\partial C_m}{\partial t}=D_m\frac{{\partial }^2{C}_m}{\partial y^2},$$

(9)

where K_dm is the sorption partition coefficient for colloids within the rock matrix.

Equations (10)–(14) represent the set of initial and boundary conditions described for the colloidal transport within a single fracture–matrix system. Initial conditions are represented by Equation (10):

$$C_f(x,t=0)=C_m(x,y\ge b,t=0)=0.$$

(10)

$$C_f(x=0,t>0)=C_o$$

(11)

Equation (7) is the boundary condition at fracture and matrix interface (y = b).

$$C_m(x,y=b,t>0)=C_f(x,t>0)$$

(12)

$$C_f(x=L_f,t>0)=0$$

(13)

$$\frac{\partial C_m(x,y=B,t>0)}{\partial y}=0$$

(14)

The data used to solve above numerical model is listed in Table 1.

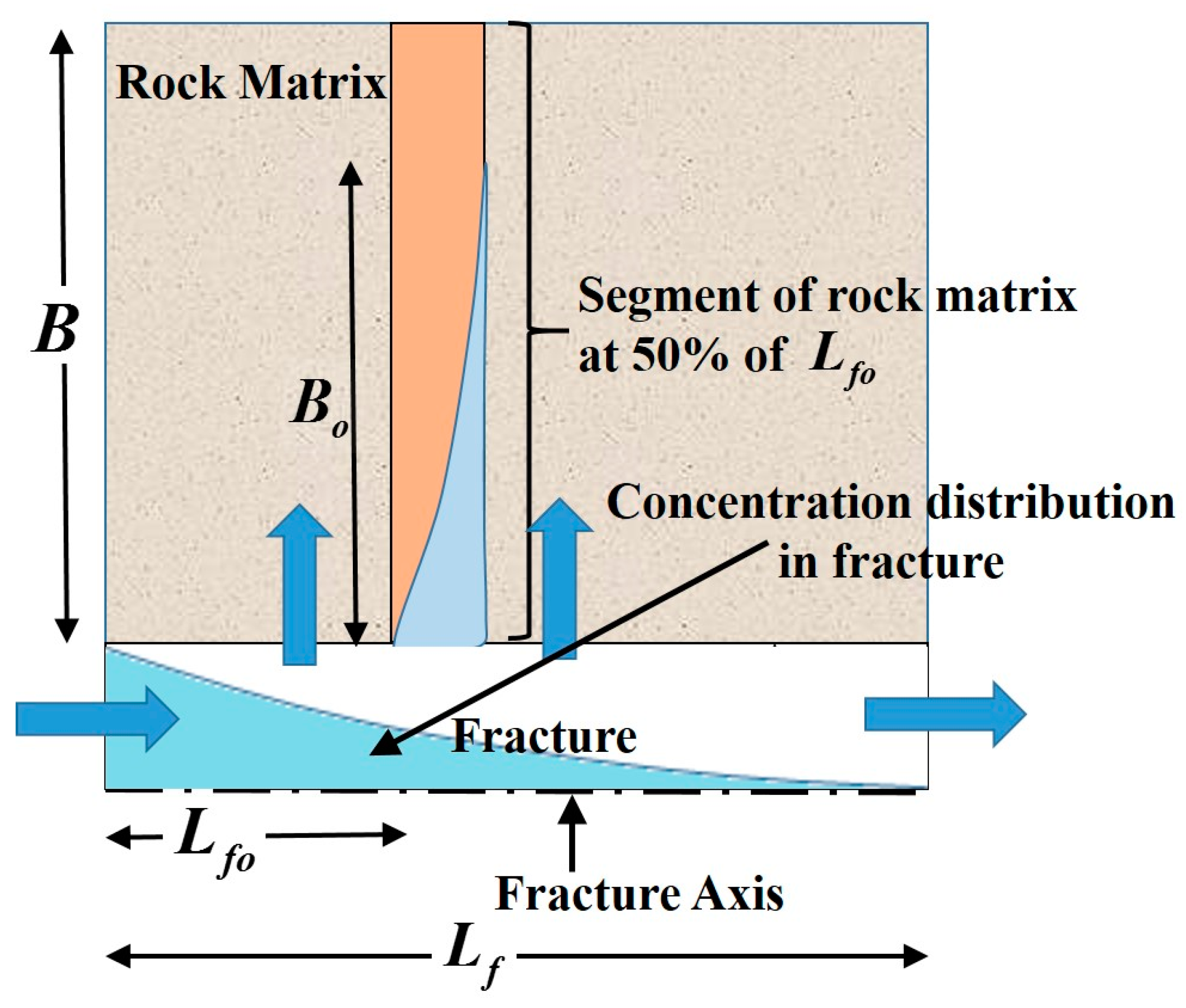
3.3. Rock Penetration Length and Rock Saturation Factor

The information of the extent of colloid penetration (diffusion) within the rock matrix from the fracture is vital to many areas of study. The extent of colloid penetration would help in accessing the level of contamination of colloid assisted radionuclides transport into the subsurface system. Nanoparticles which are one form of colloids are finding great applications in the field of petroleum (enhanced oil recovery), and the knowledge of the extent of penetration or spreading of nanoparticles within the rock matrix is vital. The higher the nanoparticles diffuse into the rock matrix, the better will be the oil recovery [20] from the fractured reservoir.

Effective and easy computation of the extent of penetration of colloids within the rock matrix is not an easy job. The transport of colloids (mass transfer) into the rock matrix from the fracture to the end of rock matrix is primarily attributed to two processes, the diffusion (Equation (4)), and the flux transfer at the fracture–matrix interface (coupling term, final term on the RHS of Equation (7)). It is evident from Equations (7)–(9) that a considerable number of parameters influence the diffusion or transport of particles from the fracture into the surrounding rock matrix (ε, D_m, D_f, V_c, b, λ_f). Therefore, it becomes tedious to accurately, and quickly evaluate the extent of penetration of colloids into the rock matrix. Hence, there is a need for a single measurable tool for determining the colloid or contaminant penetration within the rock matrix. The tool should be such that it considers all the parameters involved, and estimates the actual extent of diffusion of suspended particles within the rock matrix in a simple manner. One such measuring tool can be “Rock Saturation Factor” (RSF) developed in the present study. RSF effectively measures the extent of penetration/diffusion of suspended particles/colloids within the porous rock matrix (developed based on Bagalkot et al. [21]). RSF gives the information on the extent of the diffusion for various size and density of colloids or any suspended particle or solute within the rock matrix from the fracture. In Figure 2, B_o is the maximum rock penetration length (m), which is the maximum depth of penetration of colloids in rock matrix at a section of rock matrix, which is at 50% of L_fo. L_fo is the length measured along the fracture from the inlet to the point at which the concentration of colloid dies down to zero in the fracture, indicating the direct dependency of B_o on the value of L_fo. Equation (15) represents the Maximum rock penetration length.

B_o = f (L_fo).

(15)

Equation (16) shows the relationship of L_fo and other parameters considered in the analysis.

$$L_{fo}=f(\epsilon ,D_m,D_f,D_e,V_c,b,{\lambda }_f),$$

(16)

where D = f(a_P) and V_c = f(a_P, ρ_P, g) . Substituting these two equations in Equation (16), we get.

$$L_{fo}=f(\epsilon ,a_p,{\rho }_P,g,D_f,D_m,b,{\lambda }_f).$$

(17)

Hence, L_fo not only dependent on the transport parameters, evidently, is a function of parameters (a_P, g, and ρ_P) that govern the gravitational force acting on colloids.

Using Equation (17) in Equation (15) gives a modified version of Equation (15) represented by Equation (18).

$$B_o=f(\epsilon ,a_p,{\rho }_P,g,D_f,D_m,b,{\lambda }_f).$$

(18)

From the relation presented by the Equation (18), it can be safely inferred that for the calculation of B_o all the parameters influencing colloid transport and the force of gravitation on the transport of colloids in a single horizontal fracture–matrix system has been considered. Hence, B_o is a reliable and suitable single measuring tool to quantify the extent of penetration of colloids in the porous rock matrix.

For a straightforward prediction of mitigation of contaminants, or the extent of penetration of suspended particles (nanoparticle, microbes, NAPLs or any suspended matter) a non-dimensional factor “Rock Saturation Factor” (RSF) is introduced in the present research. The work of Rock saturation factor gives the information about the extent of saturation of the rock at a section of rock matrix, which is at 50% of L_fo regarding colloids or any contaminant that has diffused into the rock matrix. The RSF is a non-dimensional form of maximum penetration length (B_o). Equation (19) represents the mathematical form of the RSF.

$$\mathrm{RSF}=\frac{B_o}{B},$$

(19)

where B_o (m) is the maximum depth of penetration of colloids within the rock matrix at a section of rock matrix which is at 50% of L_fo (Figure 2) and B (m) is the half fracture spacing. At B_o = B, the penetration (diffusion) of the colloids within the rock matrix is maximum. L_fo is the length measured along the fracture from the inlet to the point at which the concentration of colloid dies down to zero in the fracture (Figure 2). The schematics representing the penetration of colloids within the rock matrix, penetration length, and hence the RSF are shown in Figure 2. RSF = 1 indicates that the colloids/contaminants have penetrated the entire length of the rock matrix (B = B_o), signifying complete diffusion of colloids within the rock matrix. RSF = 0 symbolizes that the colloids were ineffective at penetrating the rock matrix, signifying no diffusion of colloids into the rock matrix. For the intermediate values of RSF (1 > RSF > 0) there is partial diffusion of colloids within the rock matrix (Figure 2).

3.4. Numerical Model

The governing Equations (7)–(9) are solved for the given set of initial and boundary conditions (Equations (10)−(14)), to investigate the influence of gravity on the transport of colloids in a single coupled horizontal fracture–matrix system. A semi-implicit finite difference formulation is adopted to discretize the governing coupled partial differential equations. A first-order fully implicit backward (upwind) difference is employed to discretize the advection terms (first term on the RHS of Equation (7)). The Crank–Nicolson discretization scheme is used for the second order terms representing hydrodynamic dispersion (second term on the RHS (Right Hand Side) of Equation (7)) in fracture and diffusion in the rock matrix (first term on the RHS of Equation (10)). A two-point backwards differencing is used to discretize all the temporal terms (source terms). The iterations were carried out at each time step to satisfy the continuity at the fracture–matrix interface. A uniform grid spacing is adopted along the length of the fracture (X-axis), and a geometrically varying (increasing) grid space is applied to the rock matrix perpendicular to the flow in fracture (Y-axis). The grid size of the rock matrix increases geometrically, with the size of the first grid equal to half of the fracture aperture (y₁ = b). A smaller grid size is used in the first grid, which represents the interface of the fracture–matrix to capture the mass flux transfer occurring at the interface effectively.

Figure 3 provides the comparison of the present numerical model with that of analytical solution given by Abdel-Salam and Chrysikopoulos [3]. The present numerical model is in close agreement with the model presented by Abdel-Salam and Chrysikopoulos [3] establishing the credibility of the numerical model.

4. Results and Discussion

Figure 4 shows the dependency of the velocity of colloid in fracture (V_c) (Equation (5)) on the gravitational force, colloid density (1500, 3000, and 5000 kg/m³) and colloid size (50–600 nm). Figure 4 also depicts the longitudinal velocity of colloid (V_c) if the gravitational force is neglected (hashed horizontal line). It may be observed in Figure 4 that when the gravitational force is applied the V_c is sensitive to change in both density and size of the colloid, indicating that the gravitational force is influential on the colloid velocity in the fracture. Further, for a fixed colloid density (ρ_P > ρ_F), the colloid velocity reduces exponentially, as the colloid size (radius) increases. At 1500 kg/m³ the V_c diminishes by one order from 1m/day to around 0.1 m/day. The reduction in velocity due to gravity is amplified with the increase in the colloid density (1500 to 5000 kg/m³). The observations in Figure 4 makes sense as previous studies have shown that the higher the density of the particles (colloids), the larger will be the effect of the gravity on the colloids [9,13,22]. When the colloid density (1500 kg/m³) is near to that of fluid (suspension) (1000 kg/m³), there exists a spectrum of a size of colloids (0–100 nm) over which there is a negligible influence of gravity and colloid velocity remains constant. Once the threshold is crossed the velocity of colloid drops exponentially with the increase in the colloid size. The size of the colloid does not exclusively influence the velocity of the colloid, but the density equally plays an important part. As the colloid density shifts away from the fluid density of 1000 kg/m³ (3000 and 5000 kg/m³), the range of spectrum becomes small (0–50 nm), indicating the increased influence of gravity. This behavior of colloid in the presence of gravity is consistent with the previously presented conceptual models [9,16], which predicted a more significant loss for the larger particles and negligible loss for smaller particle leading to faster transport.

Figure 5 depicts the spatial distribution of the relative concentration of colloids in the fracture for three different colloid densities (1500 kg/m³, 3000 kg/m³ and 5000 kg/m³) and at a fixed colloid size of 300 nm (radius). There is a contrast in the relative concentration of the colloids in the fracture, among the considered density values, especially compared to the values that are near (1500 kg/m³), and away (3000 and 5000 kg/m³), from the density of the fluid (1000 kg/m³). The distance traversed by colloid along fracture is more significant (>8m) for colloid density values (1500 kg/m³) near to that of fluid density compared to the colloid densities (3000 kg/m³ and 5000 kg/m³) significantly higher than fluid density (<6 m). The influence of gravitational force on the transport of colloids in fracture becomes dominant as the density of colloid shifts away from that of the fluid density (1000 kg/m³), and the gravity effects lead to more substantial retardation of colloids. As noted from Figure 4, for a colloid size of 300 nm, as the density is increased the velocity reduces considerably from 0.4 m/day for 1500 kg/m³ to 0.08 m/day for 5000 kg/m³ (80% reduction). Advection and dispersion phenomena in the fracture are closely related to the velocity of colloid, and an increase in colloid density will give rise to a reduction in velocity, leading to the weakening of advection and dispersion transport phenomena. Hence, a decrease in distance transported by colloid in fracture as density increases can be attributed to the decrease in the influence of advection and dispersion phenomena on the transport.

Figure 6A–C show the contour representing the penetration of colloids within the rock matrix for 1500 kg/m³, 3000 kg/m³, and 5000 kg/m³ respectively for 300 nm size colloid. Figure 6D shows the case when gravitational force is not considered at size of 300 nm. It may be observed from Figure 6C (colloid density of 5000 kg/m³) that there is a diminished penetration (diffusion) of colloids (maximum 0.003 m along the rock matrix and maximum 2 m along the fracture). Slightly deeper penetration is observed when the density is brought down to 3000 kg/m³ (maximum 0.0035 m along the rock matrix and around 3 m along the fracture) (Figure 6B). A significant difference in penetration is observed when the colloid density is reduced to 1500 kg/m³ as observed in Figure 6A (above 0.0035 m along the rock matrix and around 9 m along fracture) when compared to other two colloidal densities (Figure 6B,C). The greater diffusion and hence penetration of colloids within the rock matrix for the case of 1500 kg/m³ is due to the presence of a higher concentration of colloids in the fracture compared to higher density (3000 and 5000 kg/m³). As seen in Figure 5 for the density of 1500 kg/m³ greater length of the fracture–matrix interface is exposed to colloids (>8 m) as compared to colloids of densities of 3000 and 5000 kg/m³ (<6 m) due to a more significant influence of the gravitational force. The longer length of colloids indicates the enhanced possibility of mass flux transfer of colloids into the rock matrix from fracture, which is precisely what is observed in Figure 6A. The high-density colloids (3000 and 5000 kg/m3) depreciate the diffusion within the rock matrix by approximately 80% when compared to the low-density colloids (1500 kg/m³). Interestingly, when the gravitational effect is neglected (Figure 6D) the penetration of colloids is significantly higher than when the gravitational force is considered (Figure 6A–C). Due to the absence of gravity affect the velocity of the colloids would not be altered, as may be seen in Figure 4, this would affect the advection and mass flux at the interface, hence the observed difference. Further, comparing Figure 6D with Figure 6A–C, it may be concluded that for the present system, neglecting the gravitational force on colloids would lead over estimation in the assessment of penetration of colloids within the rock matrix.

From Equation (4) it may be observed that the diffusion coefficient (D_e) is independent of mass, but is inversely related to the size of the colloid. Consequently, a decrease in particle size will be accompanied by an increase in diffusion (when the rest of the parameters are fixed in Equation (4)). In the present article, the diffusion term (D_e) has been viewed from another perspective. Rather than examining the influence of the colloidal size on diffusion within the porous rock matrix, the influence of colloidal size on the mass flux transfer at the fracture–matrix interface will be investigated. The diffusion coefficient is one of the parameters present in the coefficient of the coupling term $(\epsilon {\theta }_m{D}_e/b)$, that controls the mass flux transfer at the fracture–matrix interface. The coupling term at-large controls the mass of colloids that can diffuse into the surrounding porous rock matrix from the high permeability fracture. The larger the value of the coefficient of coupling term, the higher the mass flux transfer at the interface, and subsequent enhanced diffusion (colloid penetration) within the rock matrix.

Table 2. Measured coefficient of diffusion and coupling term (3rd term of RHS of Equation (7)) for various colloid size.

Size of Colloid (nm)	De (m2/day)	Coupling Coefficient $\left(\frac{\mathit{\theta }·{\mathit{D}}_{\mathit{e}}}{\mathit{b}}\right)$ (m/day)
50	3.29 × 10−7	6.57 × 10−4
300	0.65 × 10−7	1.31 × 10−4
600	0.27 × 10−7	0.54 × 10−4

provides the values of the diffusion coefficient and the magnitude coupling term for different size of colloids (radius). In the analysis, the porosity of the rock matrix (θ_m), the percentage of matrix diffusion of colloids (ε), and the half fracture aperture (b) are fixed. It can be noted from Table 2 that the strength of the coupling term for 50 nm, 300 nm and 600 nm is 6.57 × 10⁻⁴ m/day, 1.31 × 10⁻⁴ m/day, and 0.58 × 10⁻⁴ m/day, respectively. Therefore, as the colloidal size increases the coupling term becomes weaker, indicating that there will be a diminished diffusion of colloids within the rock matrix for larger colloids in comparison with smaller.

Figure 7 shows the influence of the size of colloids on the extent penetration (diffusion) of colloids within the rock matrix for three sizes 50 nm (Figure 7A), 300 nm (Figure 7B) and 600 nm (Figure 7C), and at a fixed density of 3000 kg/m³. Further, Figure 7D shows the case when the gravitational force has been neglected for 600 nm colloid size. Comparing Figure 7A–C, it may be observed that there is a significant penetration of colloids for 50 nm (around 0.004 m along the rock matrix and around 6 m along the fracture) (Figure 7A) compared to 300 nm (Figure 7B), and 600 nm (Figure 7C). A significantly lower diffusion is witnessed for 300 nm (around 0.002 m along the rock matrix and just above 2 m along the fracture) and 600 nm (around 0.0015 m along the rock matrix and around 2 m along the fracture) (Figure 7B,C). The reason for the difference in diffusion of colloids for different size of colloid may be derived from data presented in Table 2. From Table 2, it may be confirmed that for smaller size colloids the coupling term is stronger and a weaker coupling term is observed for large sized colloids. Stronger coupling term implies a possibility of greater mass flux transport across the interface and subsequently, deeper penetration of colloids within rock matrix. The observed results of Figure 7 serve as further confirmation of this concept. The strength of the coupling term for 50 nm, 300 nm, and 600 nm are 6.57 × 10⁻⁴ m/day, 1.31 × 10⁻⁴ m/day, and 0.58 × 10⁻⁴ m/day, respectively. Hence, there is an approximately 90% reduction in the strength of the coupling term when size is increased from 50 nm (negligible gravity) to 600 nm (high gravity) and around 80% from 50 nm to 300 nm. Hence, a greater diffusion observed in the Figure 7A for 50 nm compared to 300 and 600 nm may be attributed to the presence of stronger coupling term for 50 nm colloid. Similar to Figure 6, it may be observed that even in Figure 7, there is a considerable difference in the cases where gravity effect is considered (Figure 7A–C) and when the gravity effect is neglected (Figure 7D). It may be observed that even at large colloid size of 600 nm neglecting gravity effect would show a deeper and more uniform penetration, which is not realistic. Therefore, it is critical to include the influence of gravitational force on colloid transport in fractured porous media.

Figure 8 depicts the spatial distribution of relative concentration of colloids along the fracture for three different values of colloid size (50 nm, 300 nm and 600 nm) at a fixed density of 3000 kg/m³. At colloid density of 3000 kg /m³, for a colloid size of 50 nm the colloid velocity is 1m/day (Figure 4), which is same as that of fluid and 0.1 m/day for 300 nm and 0.04 m/day for 600 nm. Hence, 50 nm due its smaller size is not influenced by gravity, while the same cannot be said for 300 nm and 600 nm size colloids. The impact of gravitational force is dominant as the size of colloids increases, causing a greater retardation for large sized colloids by increasing the degree of gravitational settling. It is also observed that the distance traversed by the colloids from fracture inlet increases with the decrease in colloidal size. Thus, the gravitational force significantly reduces the colloidal migration downstream for large sized colloids, which indirectly implies that the colloid-facilitated radionuclide may not get migrated to a large distance downstream as anticipated using the concept of colloids as a typical contaminant carrier.

Table 3. Measured Rock Saturation Factor values for different colloid density and size.

Colloid Size (nm)	Colloid Density (kg/m3)
	1500	3000	5000
	Rock Saturation Factor	Rock Saturation Factor	Rock Saturation Factor
50	0.214	0.214	0.214
300	0.156	0.122	0.112
600	0.112	0.100	0.075

shows the values of non-dimensional parameter rock saturation factor (RSF) developed in the present study to assess the extent of penetration of colloids within the rock matrix for three different colloid size and densities. The greater the value of RSF (0 ≤ RSF≤ 1) the greater will the saturation of the rock matrix due to the diffusion of the colloids. For RSF = 1 implies 100% saturation of the rock matrix with the colloids or contaminants and for RSF = 0 implies no diffusion at all. The RSF data in Table 3 gives an insight into the influence of gravity, colloidal size and density put together with other influencing parameters (Equation (18)) on the extent of transport of colloids within the rock matrix. It can be noted from Table 3 that, as density increases from 1500 kg/m³ to 5000 kg/m³ except for 50 nm size for which there is negligible influence of gravity, there is a reduction RSF indicating lower saturation of the rock matrix by colloids for 300 and 600 nm size. Further, it can be noticed that there is hardly any penetration of colloids at 5000 kg/m³ for 600 nm and 300 nm. At 5000 kg/m³ a meager 7.5% (RSF = 0.075) of the rock matrix is saturated with 600 nm and 11.5% (RSF = 0.112) at 300 nm, whereas, for 50 nm around 21.5% (RSF = 0.214) of the rock matrix is saturated by colloids. Hence, at 5000 kg/m³, there is approximately 65% for 600 nm and 45% for 300 nm lower diffusion is noted in comparison with 50 nm. A similar phenomenon is witnessed for 3000 kg/m³ and 1500 kg/m³ (Table 3) but at lesser impact. Few important observations can be made from Table 3. First, for 50 nm no change in the RSF value was noted at all densities, this could be attributed to the negligible influence of gravity for smaller size colloids. This shows that for 50 nm there is negligible influence of gravitational force as explained in the discussion of Figure 4. Second, for 300 nm or 600 nm as density increased from 1500 kg/m³ to 5000 kg/m³, the extent of saturation decreased significantly (approximately 28% for 300 nm (RSF = 0.156 to 0.112) and approximately 33% for 600 nm (RSF = 0.112 to 0.075)). This proves that the transport of larger size colloid is sensitive to the density and size of colloids as predicted by previous studies [9,16]. Therefore, there is an optimum range of colloid size present up to which the gravitational influence is negligible. The value of RSF will be helpful to gauge the extent of mitigation of hazardous chemical due to matrix diffusion, especially for the case of colloid assisted radionuclide transport (a possible practical application). RSF will further help in deciding the optimum size of the nanoparticle (petroleum EOR), for the nanoparticles to migrate extensively in rock matrix to create any impact. If the nanoparticles are too large and their density is greater than that of the fluid, then the nanoparticles will become unsuitable for Enhanced Oil Recovery applications.

5. Conclusions

A relatively new approach has been applied in the present study to understand the influence of gravitational force on the transport of colloids in a single fracture–matrix system using numerical experiments. The sensitivity of the transport phenomena on the size and density of colloids has been additionally included in the study. Based on the outcome of the developed numerical model the following conclusions can be drawn:

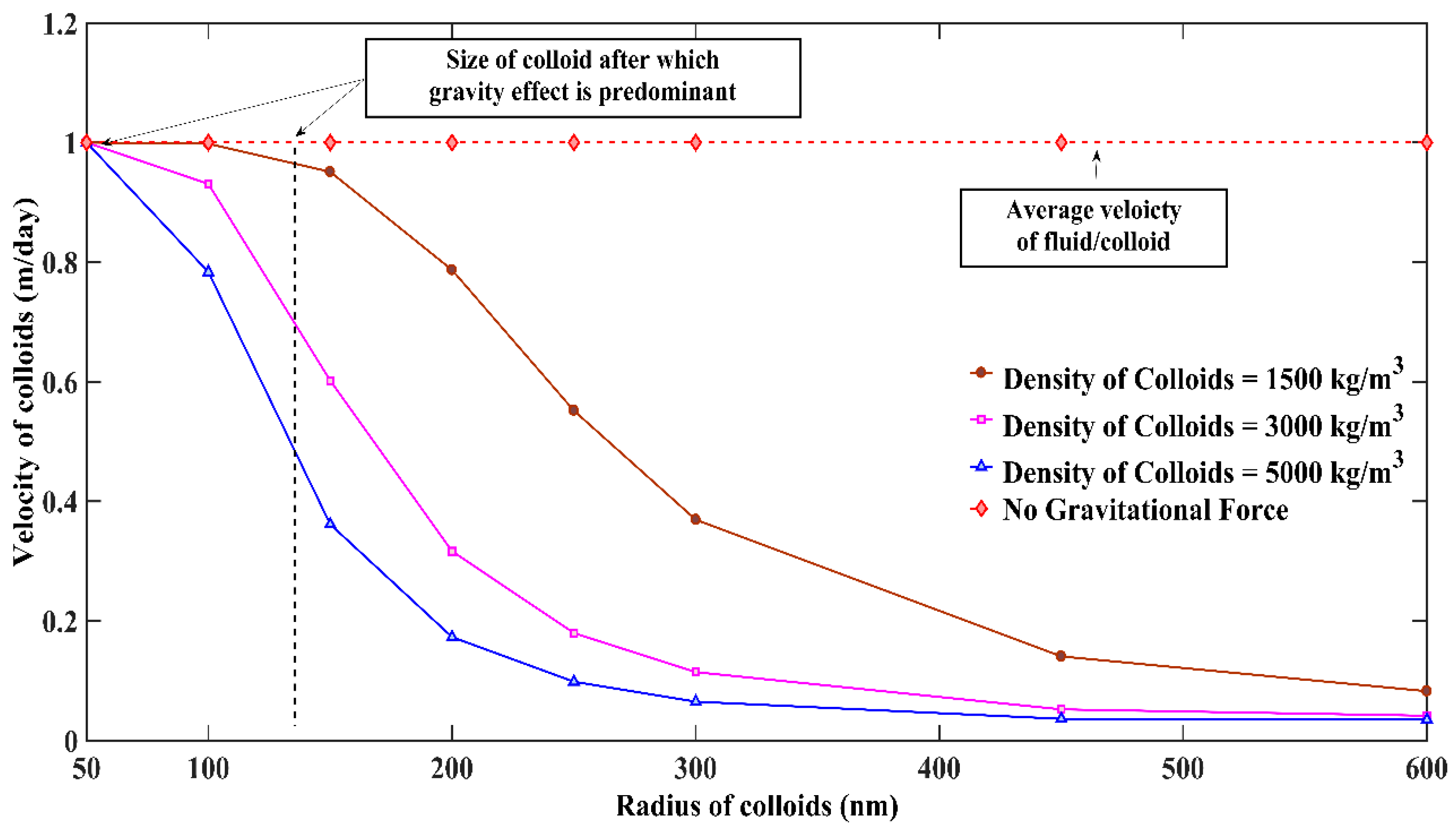
• The gravitational force manifests a powerful control on the transport of colloidal transport by directly altering the velocity of the colloid through the fluid, and hence, altering advection and diffusion phenomena. The colloidal velocity reduces as the size of the colloid increases in the presence of the gravitational force. The reduction of colloidal velocity with the increase in the radius of colloid follows an exponential decreasing profile. This is further enhanced by an increase in colloidal density while a lower colloidal density will experience a minimum difference between the velocities of colloid and fluid. However, it was found that for a certain range of size (<50 nm) and for relatively low values of density (around 1500 kg/m³) the velocity did not reduce indicating that influence of gravity would be negligible.
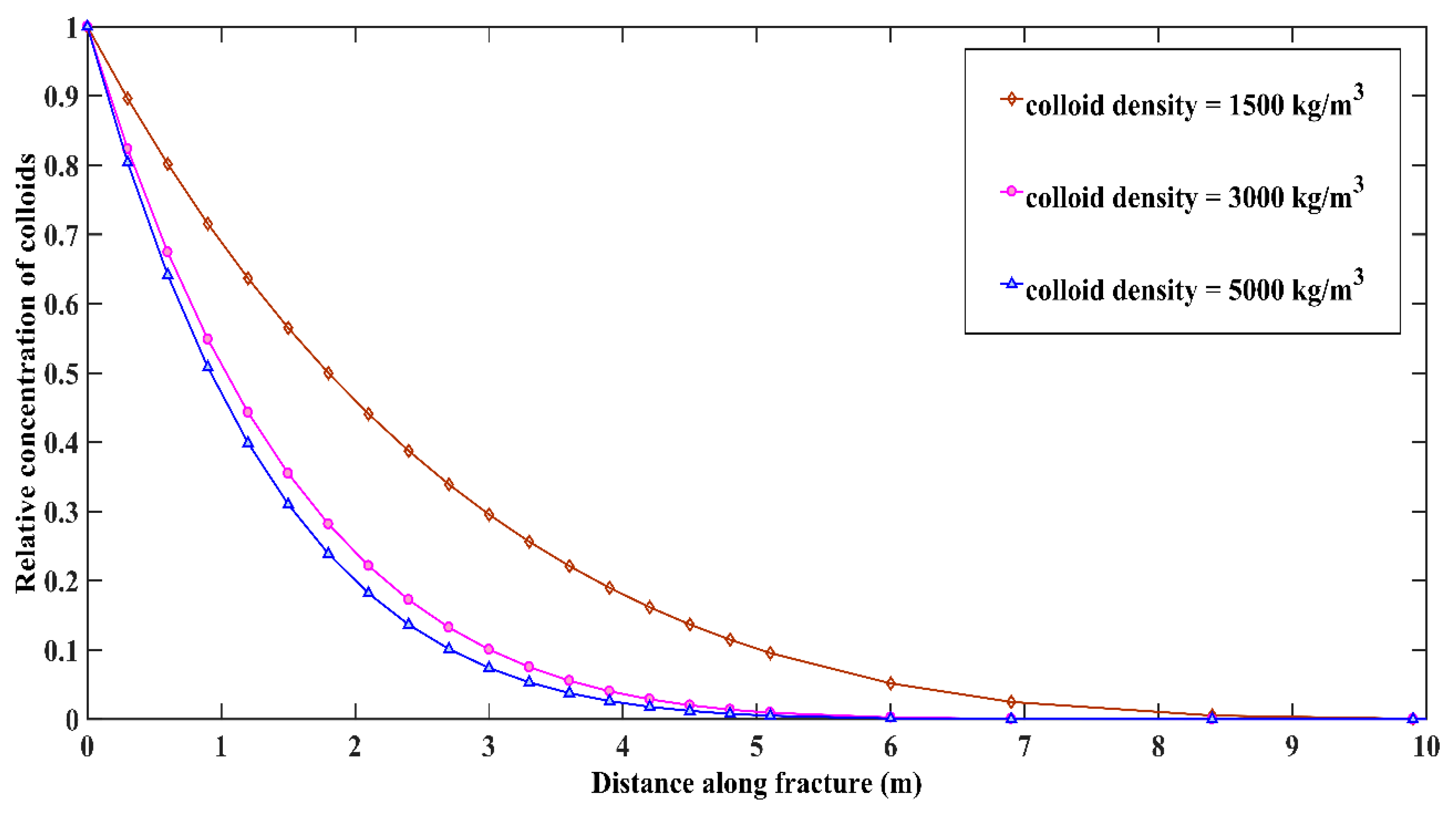
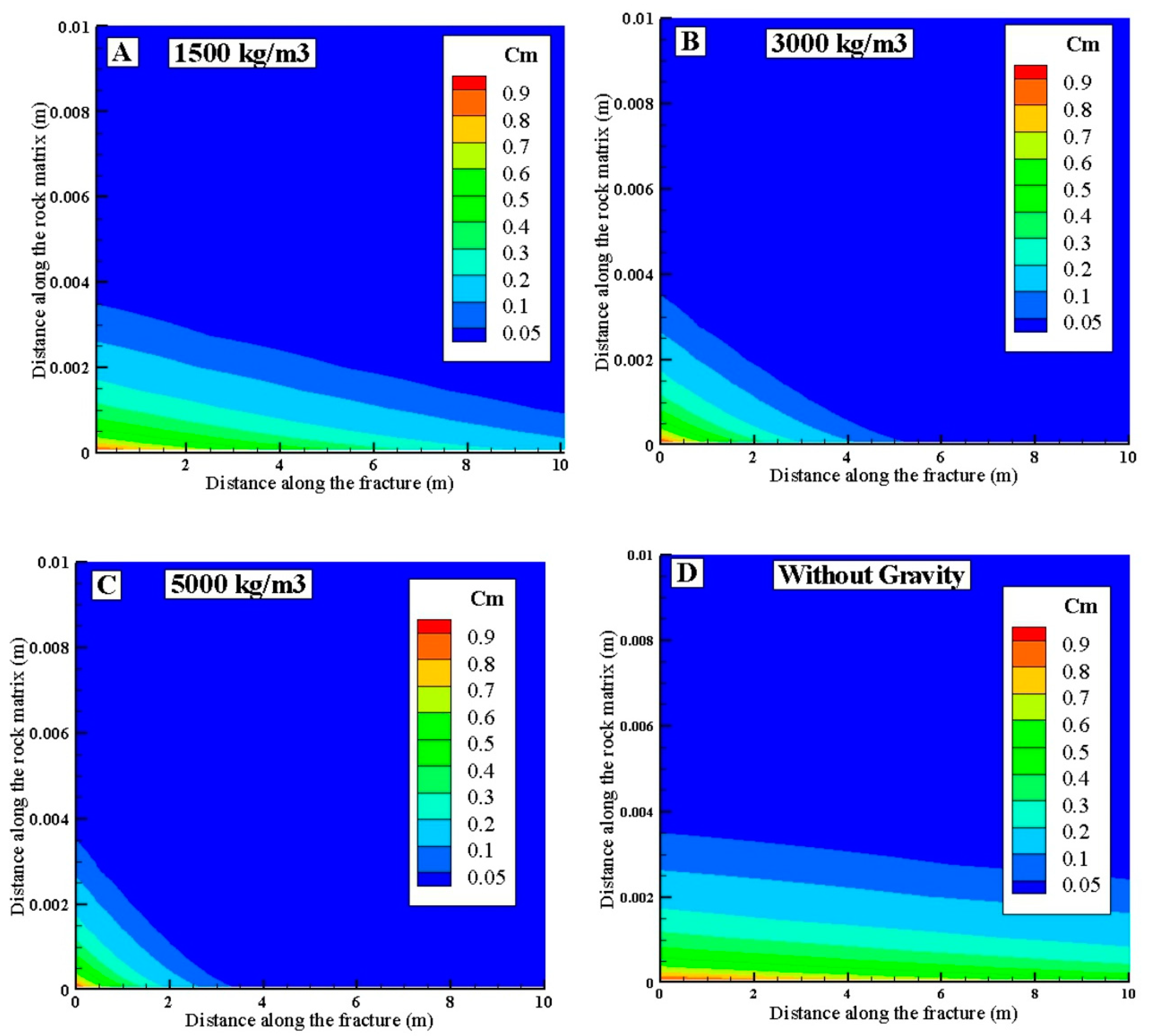
• The density of colloid determines the magnitude of the impact of gravitational force on the transport of colloids. There is a limited colloid transport by the denser colloids along the fracture and within rock matrix. The influence of gravity becomes dominant as the density of colloid shifts away from that of the flowing fluid, and the gravitational influence a larger retardation of colloids for greater colloid density, enhancing the degree of gravitational settling. Roughly, 80% decrease in diffusion within the rock matrix and about 30% reduction in spatial spreading in fracture was witnessed as density increased from 1500 kg/m³ to 5000 kg/m³.
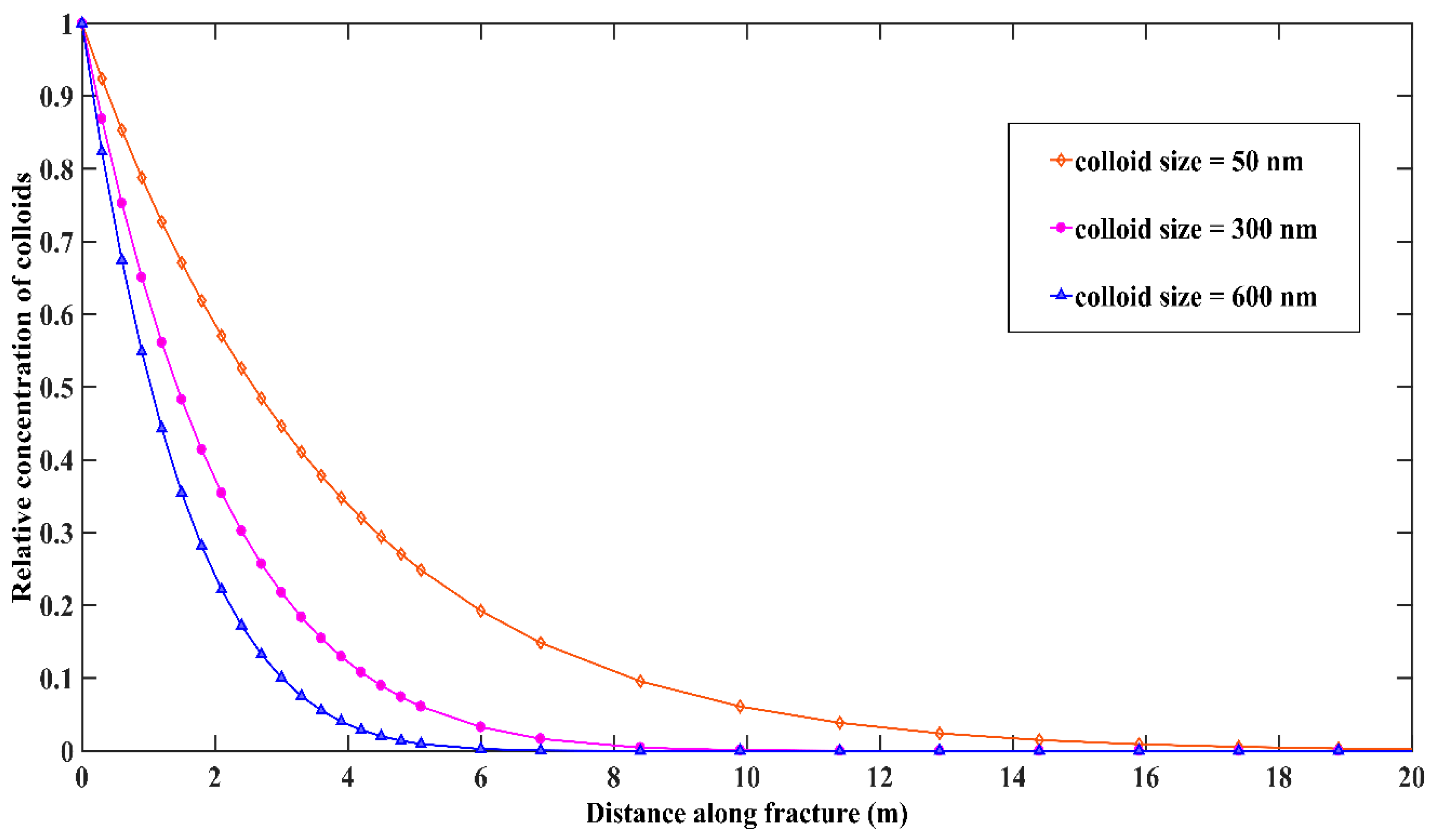
• The mass flux transfer across the fracture–matrix interface is predominantly dependent on the size of the colloid. Large size colloids face a greater obstacle at the fracture–matrix interface compared to the small size. The mass flux transfer across the interface reduces by approximately 80% when colloid size increase from 50 nm to 300 nm, and around 90% when increased from 50 nm to 600 nm. Higher mass flux transfer for 50 nm further leads to enhanced diffusion within the rock matrix compared to a scant diffusion for 300 nm and 600 nm size colloids.
• The developed non-dimensional parameter, Rock Saturation Factor (RSF) proved to be helpful in identifying the limits in terms of size and density of colloids that can penetrate deep into the rock matrix. RSF is an easy way to decide the optimum size that the colloids/suspended particle that can be transported within a fracture–matrix system to create a positive impact. The RSF will give an added advantage to the process of decision making with respect to size and density of particles before injecting in a fractured medium, especially in real-time applications such as petroleum and contamination remediation.