Temperature and Circulation Dynamics in a Small and Shallow Lake: Effects of Weak Stratification and Littoral Submerged Macrophytes
Abstract
1. Introduction
2. Materials and Methods
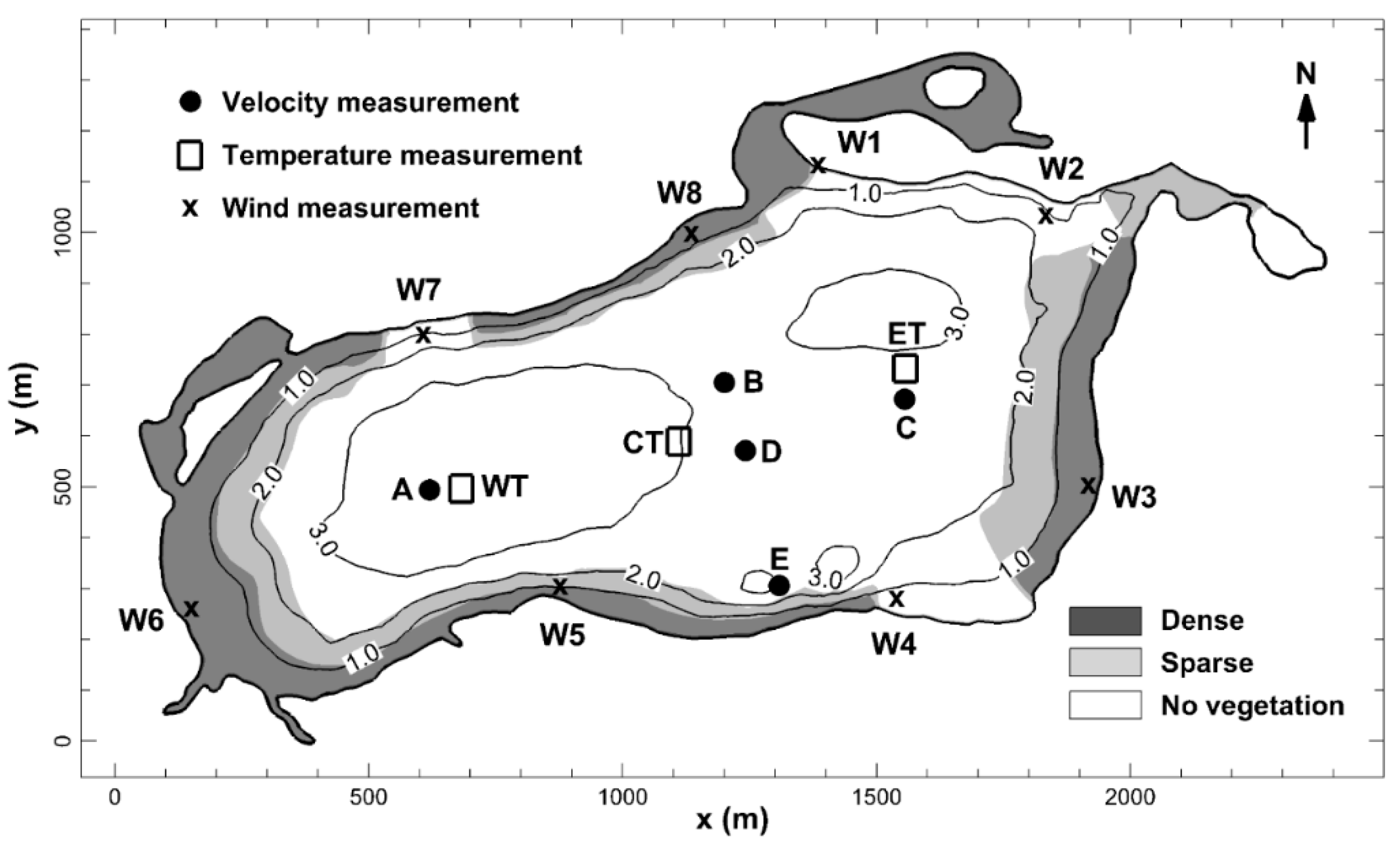
2.1. Study Site
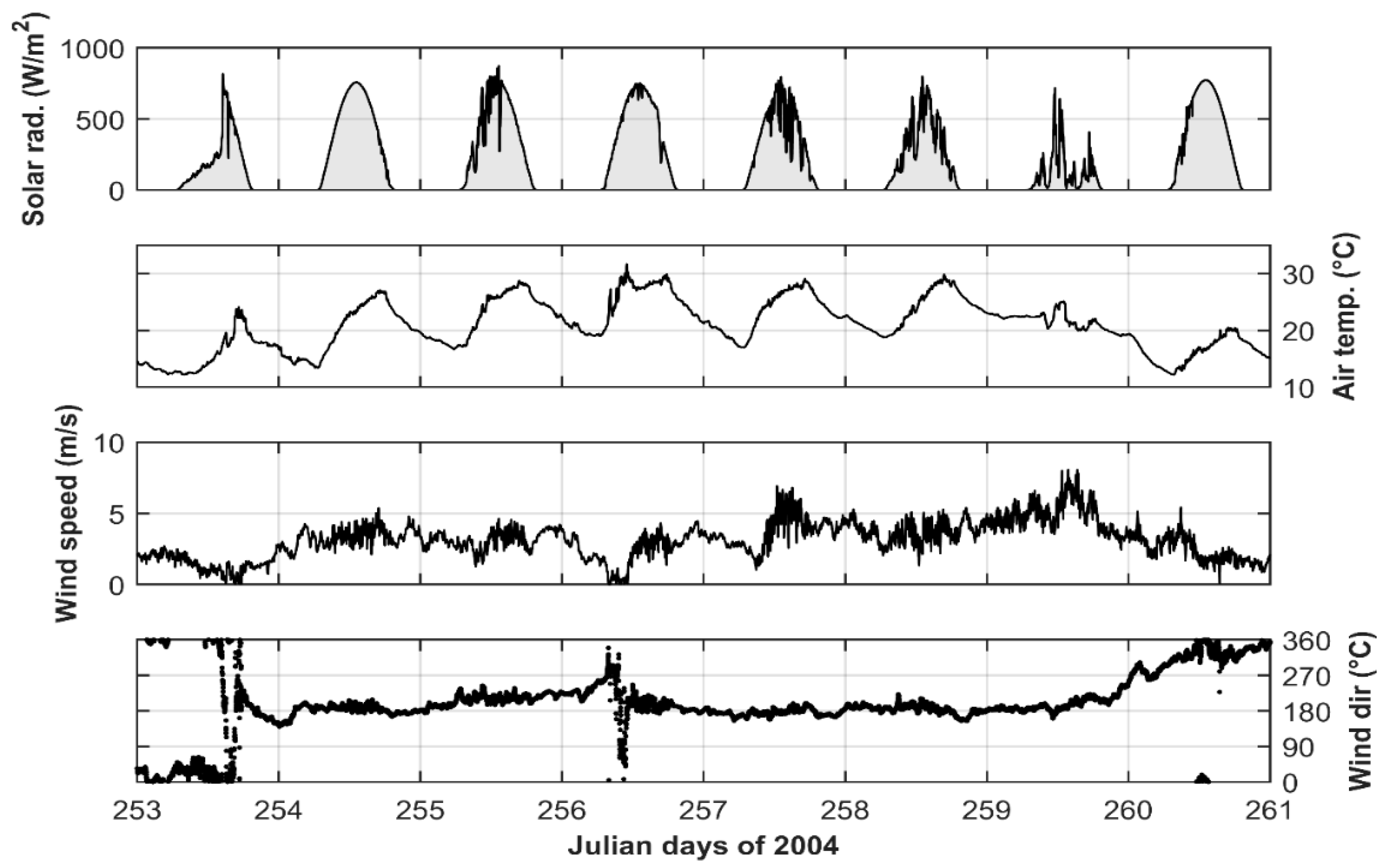
2.2. Field Observations
2.3. Hydrodynamic Model
2.4. Model Setup
3. Results and Discussion
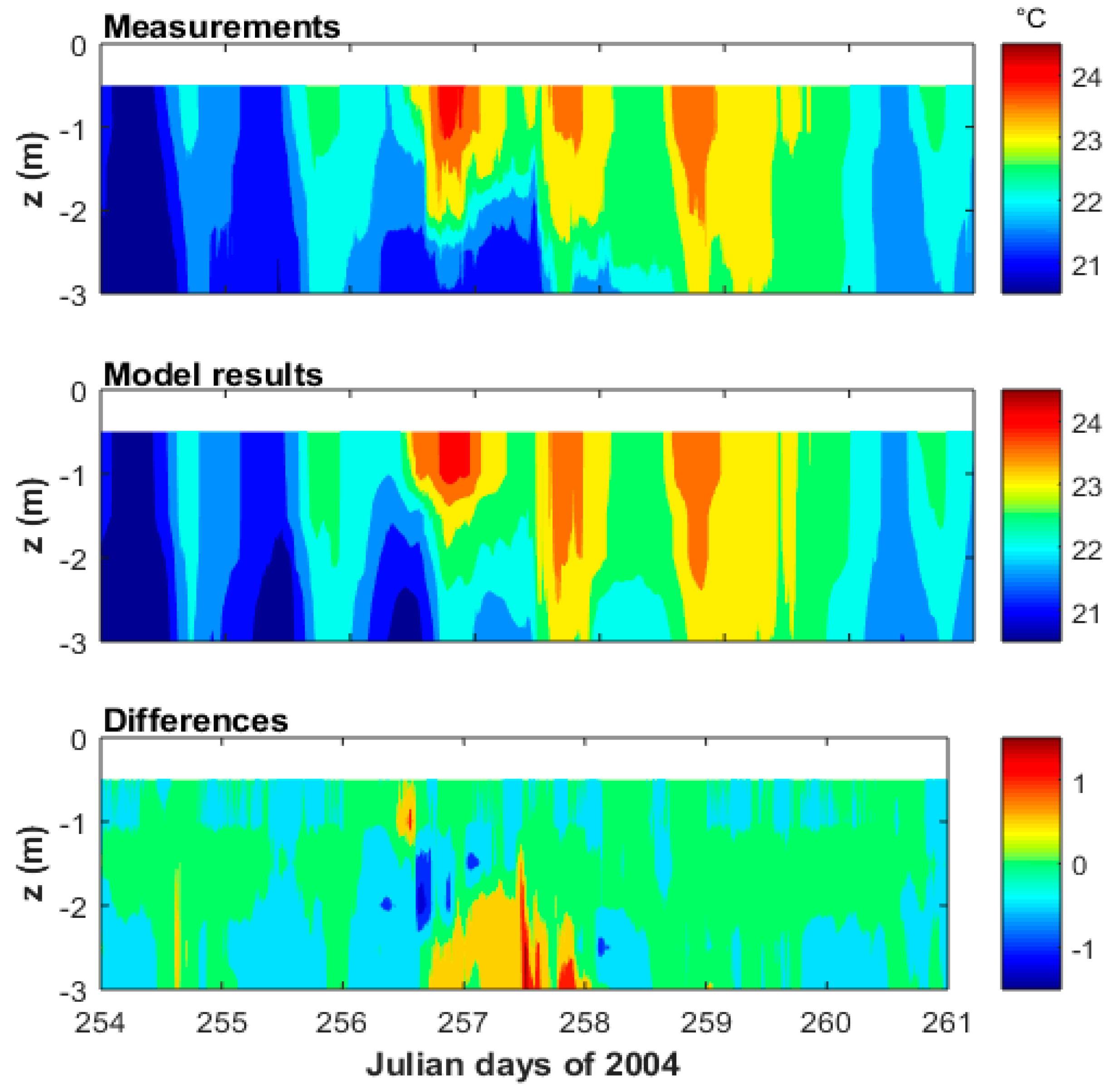
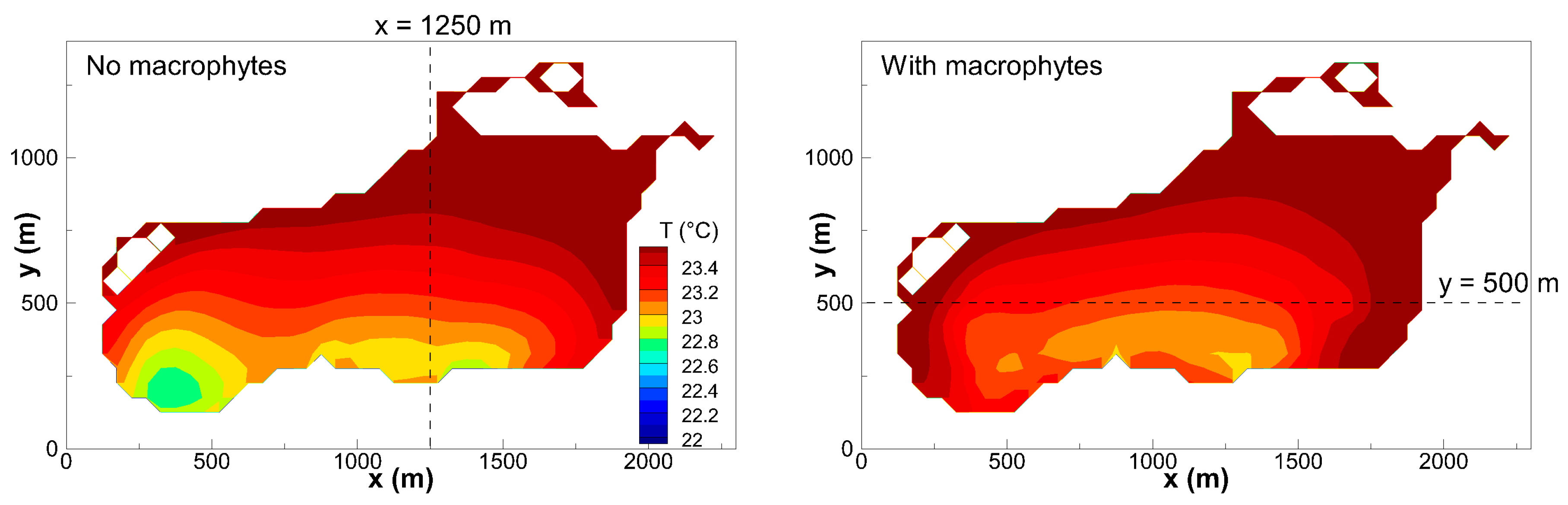
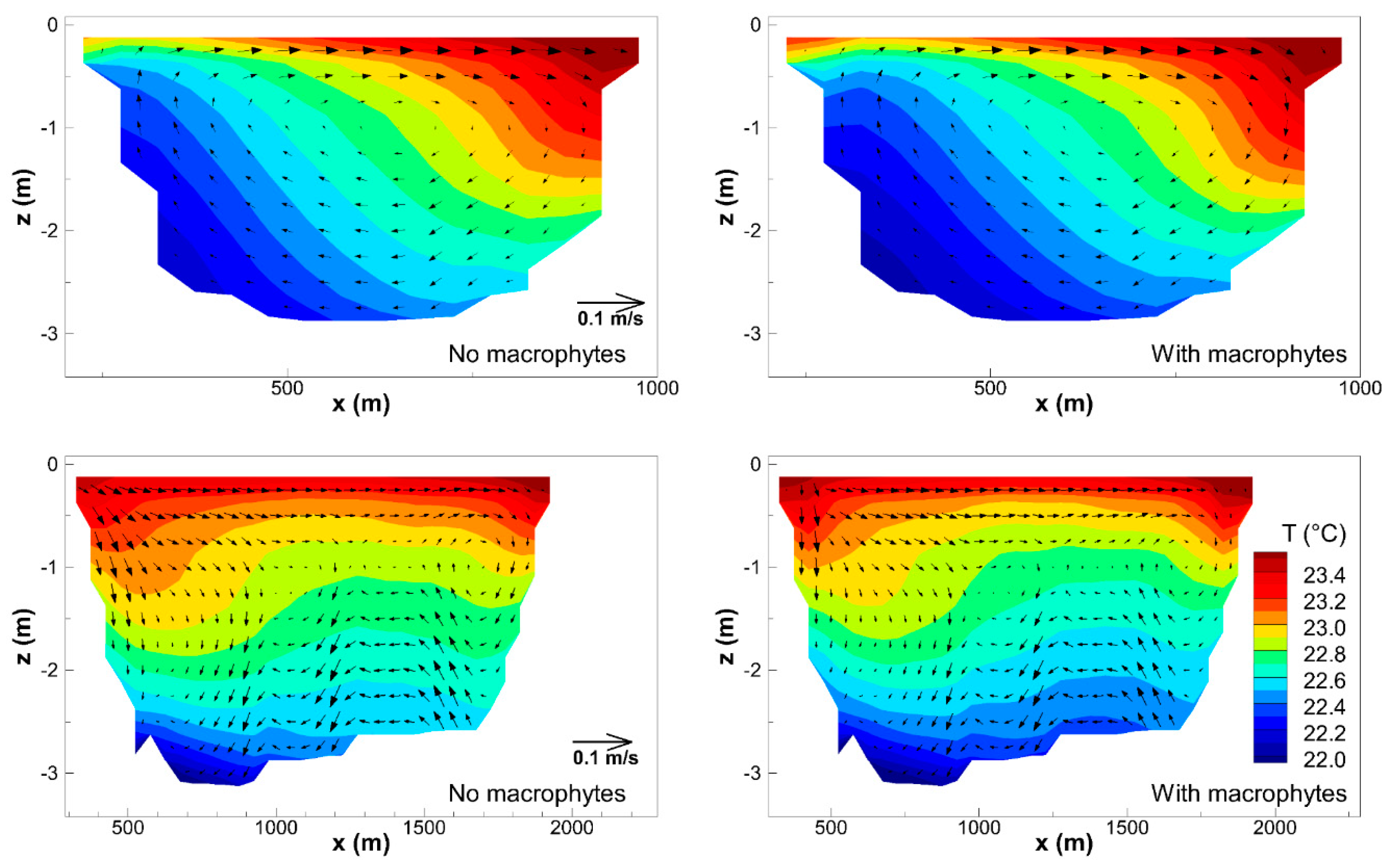
3.1. Temperature Structures
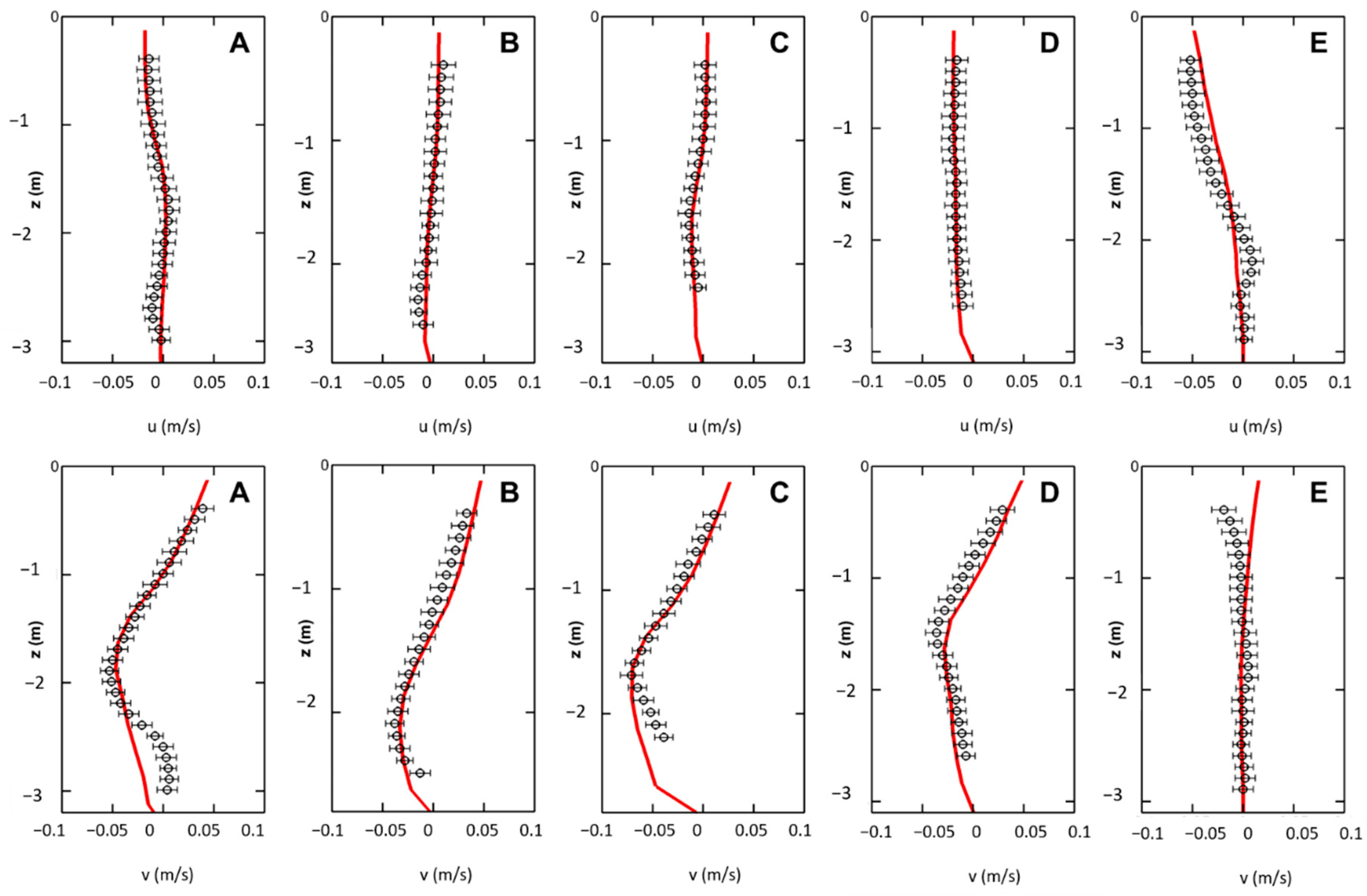
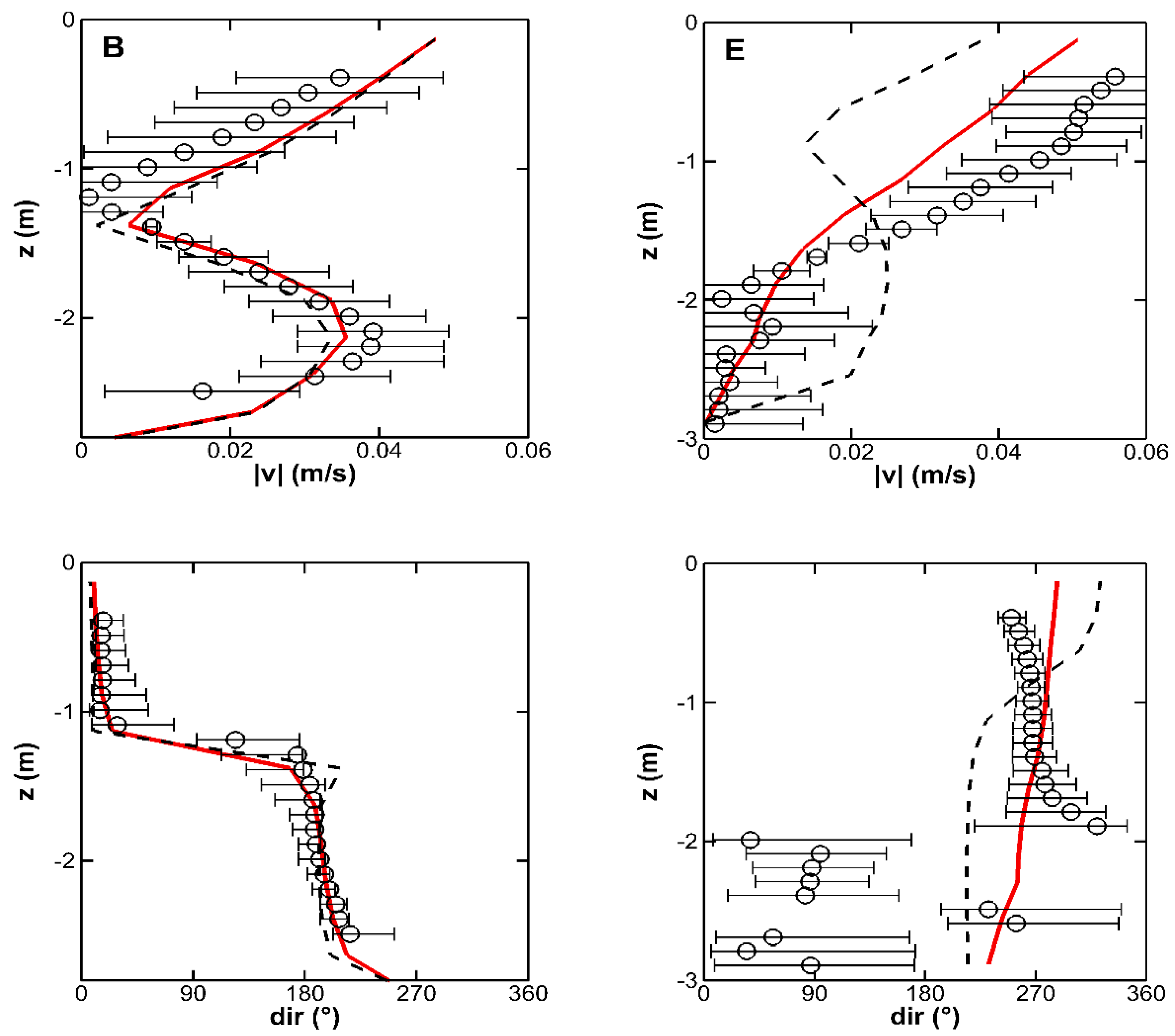
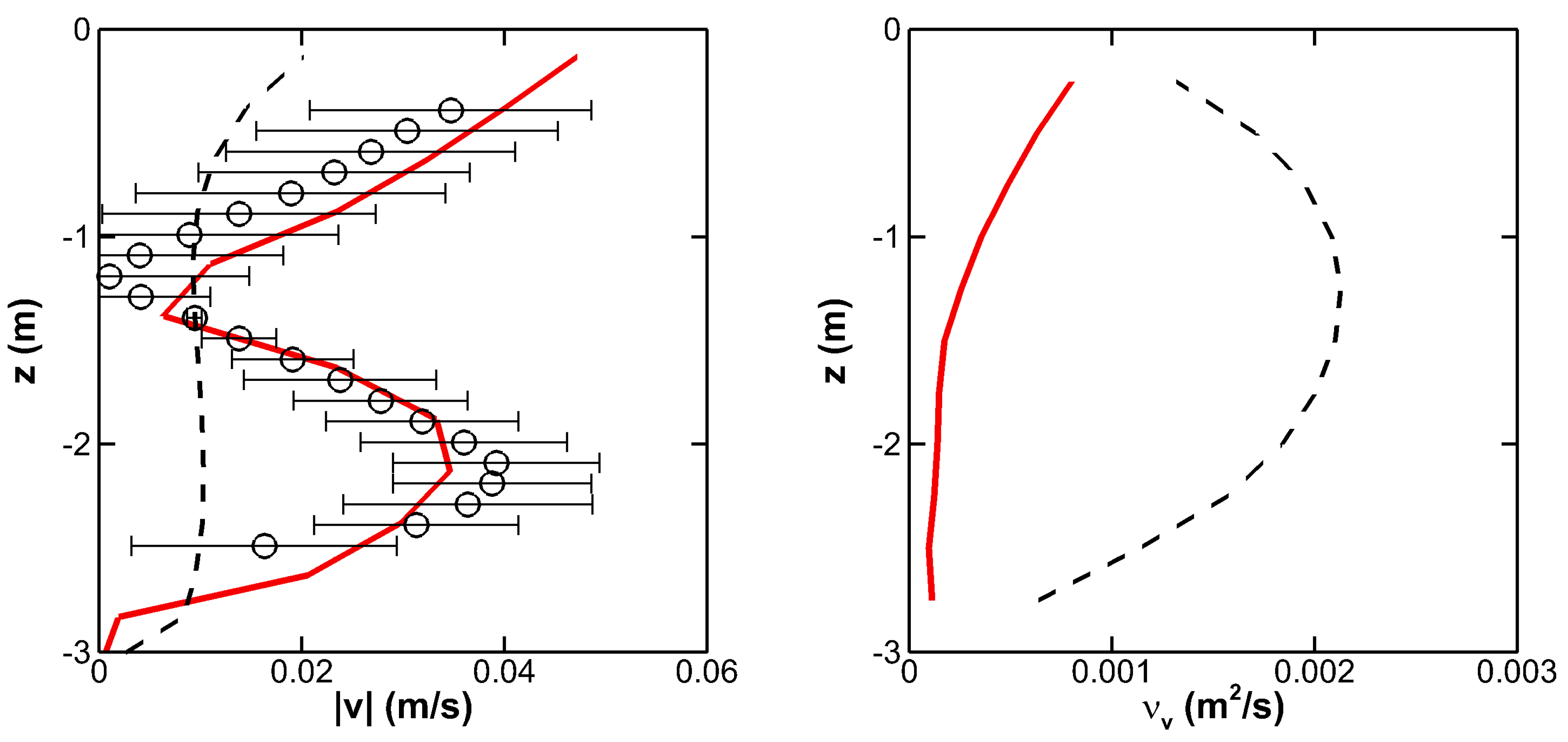
3.2. Velocity Prfoiles
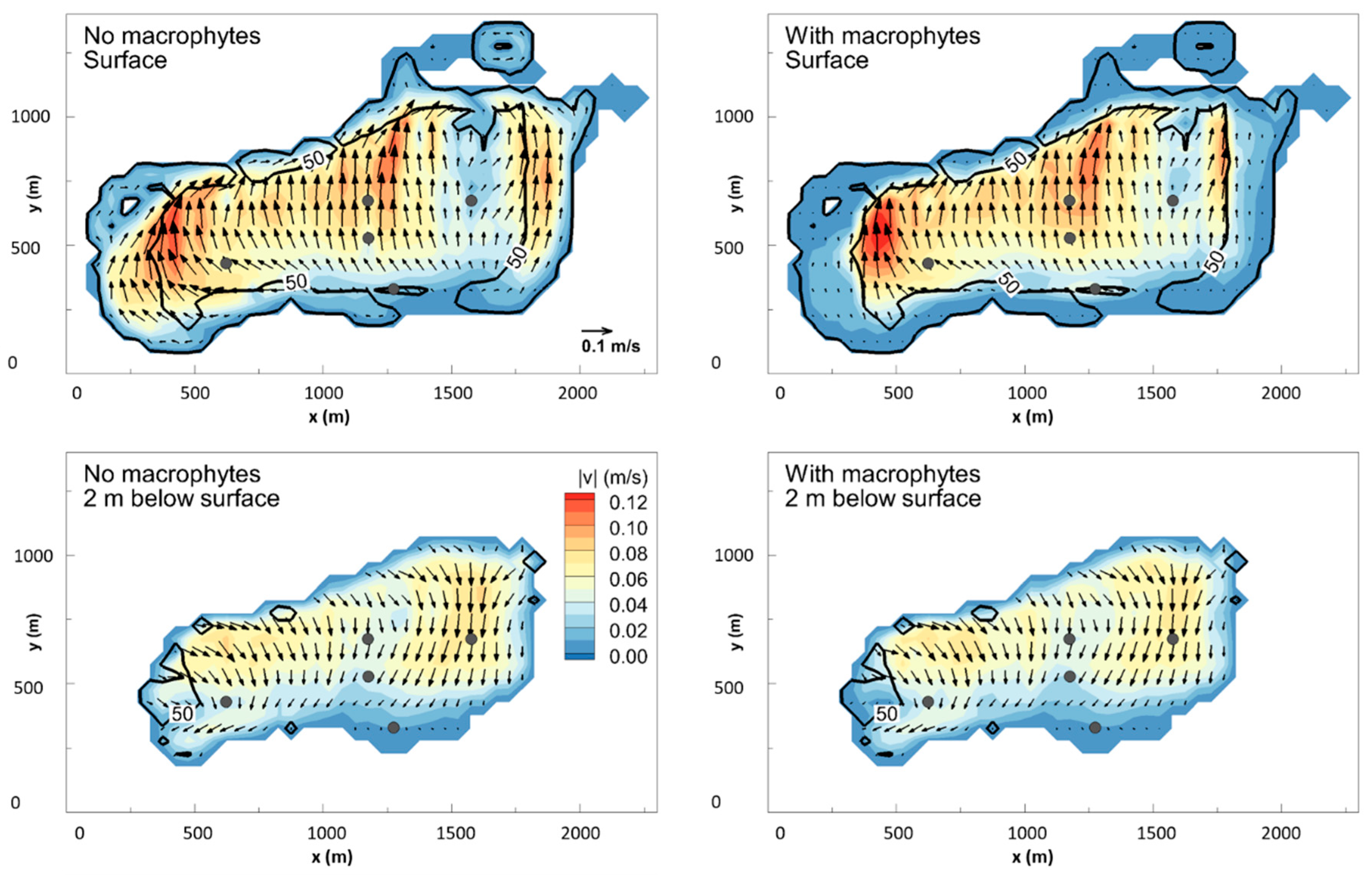
3.3. Effects of Macrophytes
3.4. Effects of Weak Stratification
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- George, D.G.; Heaney, S.I. Factors influencing the spatial distribution of phytoplankton in a small productive Lake. J. Ecol. 1978, 66, 133. [Google Scholar] [CrossRef]
- Schindler, D.W.; Mills, K.H.; Malley, D.F.; Findlay, D.L.; Shearer, J.A.; Davies, I.J.; Turner, M.A.; Linsey, G.A.; Cruikshank, D.R. Long-Term Ecosystem Stress: The effects of years of experimental acidification on a small lake. Science 1985, 228, 1395–1401. [Google Scholar] [CrossRef] [PubMed]
- Hilton, J.; Lishman, J.P.; Allen, P.V. The dominant processes of sediment distribution and focusing in a small, eutrophic, monomictic lake. Limnol. Oceanogr. 1986, 31, 125–133. [Google Scholar] [CrossRef]
- Fee, E.J.; Shearer, J.A.; DeBruyn, E.R.; Schindler, E.U. Effects of lake size on phytoplankton photosynthesis. Can. J. Fish. Aquat. Sci. 1992, 49, 2445–2459. [Google Scholar] [CrossRef]
- Carlsson, P.; Caron, D.A. Seasonal variation of phosphorus limitation of bacterial growth in a small lake. Limnol. Oceanogr. 2001, 46, 108–120. [Google Scholar] [CrossRef]
- Cole, J.J.; Carpenter, S.R.; Kitchell, J.F.; Pace, M.L. Pathways of organic carbon utilization in small lakes: Results from a whole-lake 13 C addition and coupled model. Limnol. Oceanogr. 2002, 47, 1664–1675. [Google Scholar] [CrossRef]
- Phillips, G.L. Eutrophication of shallow temperate lakes. In The Lakes Handbook; Blackwell Science Ltd.: Oxford, UK, 2005; Volume 2, pp. 261–278. [Google Scholar]
- Bengtsson, L.; Hellström, T. Wind-induced resuspension in a small shallow lake. Hydrobiologia 1992, 241, 163–172. [Google Scholar] [CrossRef]
- Lacroix, G.; Lescher-Moutou, F. Spatial patterns of planktonic microcrustaceans in a small shallow lake. Hydrobiologia 1995, 300–301, 205–217. [Google Scholar] [CrossRef]
- Scheffer, M. Ecology of Shallow Lakes, 1st ed.; Springer US: New York, NY, USA, 1998; ISBN 978-0-412-74920-9. [Google Scholar]
- Blindow, I.; Hargeby, A.; Meyercordt, J.; Schubert, H. Primary production in two shallow lakes with contrasting plant form dominance: A paradox of enrichment? Limnol. Oceanogr. 2006, 51, 2711–2721. [Google Scholar] [CrossRef]
- Barko, J.W.; Gunnison, D.; Carpenter, S.R. Sediment interactions with submersed macrophyte growth and community dynamics. Aquat. Bot. 1991, 41, 41–65. [Google Scholar] [CrossRef]
- Dixon, K.R.; Florian, J.D. Modeling mobility and effects of contaminants in wetlands. Environ. Toxicol. Chem. 1993, 12, 2281–2292. [Google Scholar] [CrossRef]
- Tanino, Y. Water exchange between littoral zone and open lake water. Encycl. Lakes Reserv. Encycl. Earth Sci. Ser. 2012, 869–872. [Google Scholar]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press, Elsevier: London, UK, 2013; ISBN 9780080511771. [Google Scholar]
- Pernica, P.; Wells, M. Frequency of episodic stratification in the near surface of Lake Opeongo and other small lakes. Water Qual. Res. J. Can. 2012, 47, 227. [Google Scholar] [CrossRef]
- McEnroe, N.A.; Buttle, J.M.; Marsalek, J.; Pick, F.R.; Xenopoulos, M.A.; Frost, P.C. Thermal and chemical stratification of urban ponds: Are they ‘completely mixed reactors’? Urban Ecosyst. 2013, 16, 327–339. [Google Scholar] [CrossRef]
- Pernica, P. Implications of Periodic Weak Thermal Stratification in the Epilimnion of Lake Opeongo; University of Toronto: Toronto, ON, Canada, 2014. [Google Scholar]
- Andersen, M.R.; Sand-Jensen, K.; Iestyn Woolway, R.; Jones, I.D. Profound daily vertical stratification and mixing in a small, shallow, wind-exposed lake with submerged macrophytes. Aquat. Sci. 2017, 79, 395–406. [Google Scholar] [CrossRef]
- Kimura, N.; Wu, C.H.; Hoopes, J.A.; Tai, A. Diurnal dynamics in a small shallow lake under spatially nonuniform wind and weak Stratification. J. Hydraul. Eng. 2016, 142, 04016047. [Google Scholar] [CrossRef]
- Torma, P.; Krámer, T. Modeling the effect of waves on the diurnal temperature stratification of a shallow lake. Period. Polytech. Civ. Eng. 2016, 61, 165–175. [Google Scholar] [CrossRef]
- Condie, S.A.; Webster, I.T. Stratification and circulation in a shallow turbid waterbody. Environ. Fluid Mech. 2002, 2, 177–196. [Google Scholar] [CrossRef]
- Podsetchine, V.; Schernewski, G. The influence of spatial wind inhomogeneity on flow patterns in a small lake. Water Res. 1999, 33, 3348–3356. [Google Scholar] [CrossRef]
- Honti, M.; Istvánovics, V.; Staehr, P.A.; Brighenti, L.S.; Zhu, M.; Zhu, G. Robust estimation of lake metabolism by coupling high frequency dissolved oxygen and chlorophyll fluorescence data in a Bayesian framework. Int. Waters 2016, 6, 608–621. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Darby, S.E. Effect of riparian vegetation on flow resistance and flood potential. J. Hydraul. Eng. 1999, 125, 443–454. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E.; Stoesser, T.; Bates, P.D.; Pinzen, A.B. Open channel flow through different forms of submerged flexible vegetation. J. Hydraul. Eng. 2003, 129, 847–853. [Google Scholar] [CrossRef]
- Mendez, F.J.; Losada, I.J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coast. Eng. 2004, 51, 103–118. [Google Scholar] [CrossRef]
- Coates, M.J.; Folkard, A.M. The effects of littoral zone vegetation on turbulent mixing in lakes. Ecol. Modell. 2009, 220, 2714–2726. [Google Scholar] [CrossRef]
- Abt, S.R.; Clary, W.P.; Thornton, C.I. Sediment deposition and entrapment in vegetated streambeds. J. Irrig. Drain. Eng. 1994, 120, 1098–1111. [Google Scholar] [CrossRef]
- Thorne, C.R. Effects of vegetation on riverbank erosion and stability. In Vegetation and Erosion: Processes and Environments; J. Wiley: Chichester, UK, 1990; pp. 128–144. [Google Scholar]
- Herb, W.R.; Stefan, H.G. Dynamics of vertical mixing in a shallow lake with submersed macrophytes. Water Resour. Res. 2005, 41, 1–14. [Google Scholar] [CrossRef]
- Herb, W.R.; Stefan, H.G. Model for wind-driven vertical mixing in a shallow lake with submersed Macrophytes. J. Hydraul. Eng. 2005, 131, 488–496. [Google Scholar] [CrossRef]
- Simons, T.J.; Lam, D.C.L. Documentation of a two-dimensional model package for computing lake circulation and pollutant transport. In Physics Based Modelling of Lakes, Reservoirs, and Impoundments; Gray, W.G., Ed.; ASCE: New York, NY, USA, 1986; pp. 258–308. [Google Scholar]
- Koutitas, C.; Gousidou-Koutita, M. A comparative study of three mathematical models for wind-generated circulation in coastal areas. Coast. Eng. 1986, 10, 127–138. [Google Scholar] [CrossRef]
- Wu, J.; Tsanis, I.K. A vertical/horizontal integration wind-induced circulation model (VH13D): A method for including surface and bottom logarithmic profiles. Adv. Water Resour. 1995, 18, 77–87. [Google Scholar] [CrossRef]
- Lin, Y.-T.; Wu, C.H. The role of rooted emergent vegetation on periodically thermal-driven flow over a sloping bottom. Environ. Fluid Mech. 2014, 14, 1303–1334. [Google Scholar] [CrossRef]
- Lin, Y.-T.; Wu, C.H. Effects of a sharp change of emergent vegetation distributions on thermally driven flow over a slope. Environ. Fluid Mech. 2015, 15, 771–791. [Google Scholar] [CrossRef]
- Lin, Y.-T. Wind effect on diurnal thermally driven flow in vegetated nearshore of a lake. Environ. Fluid Mech. 2015, 15, 161–178. [Google Scholar] [CrossRef]
- Botte, V.; Kay, A. A model of the wind-driven circulation in Lake Baikal. Dyn. Atmos. Ocean. 2002, 35, 131–152. [Google Scholar] [CrossRef]
- Koçyigit, M.B.; Falconer, R.A. Three-dimensional numerical modelling of wind-driven circulation in a homogeneous lake. Adv. Water Resour. 2004, 27, 1167–1178. [Google Scholar] [CrossRef]
- Vilas, M.P.; Marti, C.L.; Adams, M.P.; Oldham, C.E.; Hipsey, M.R. Invasive macrophytes control the spatial and temporal patterns of temperature and dissolved oxygen in a shallow lake: A Proposed Feedback Mechanism of Macrophyte Loss. Front. Plant Sci. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.H.; Yuan, H.; Young, C.-C. Non-hydrostatic modeling of vegetation effects on wave and flow motions. In Estuarine and Coastal Modeling (2007); American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 304–321. [Google Scholar]
- Kamarainen, A.M.; Yuan, H.; Wu, C.H.; Carpenter, S.R. Estimates of phosphorus entrainment in Lake Mendota: A comparison of one-dimensional and three-dimensional approaches. Limnol. Oceanogr. Methods 2009, 7, 553–567. [Google Scholar] [CrossRef]
- Baumann, P.; Kitchell, J.; Magnuson, J.; Kayes, T. Lake Wignra, 1837–1973: A case history of human impact. Trans. Wis. Acad. Sci. Arts Lett. 1974, 62, 57–94. [Google Scholar]
- Carpenter, S.R.; Benson, B.J.; Biggs, R.; Chipman, J.W.; Foley, J.A.; Golding, S.A.; Hammer, R.B.; Hanson, P.C.; Johnson, P.T.J.; Kamarainen, A.M.; et al. Understanding Regional Change: A comparison of two lake districts. Bioscience 2007, 57, 323–335. [Google Scholar] [CrossRef]
- Carpenter, S.R. Enrichment of Lake Wingra, Wisconsin, by Submersed Macrophyte Decay. Ecology 1980, 61, 1145–1155. [Google Scholar] [CrossRef]
- Trebitz, A.S.; Nichols, S.A.; Carpenter, S.R.; Lathrop, R.C. Patterns of vegetation change in Lake Wingra following a Myriophyllum spicatum decline. Aquat. Bot. 1993, 46, 325–340. [Google Scholar] [CrossRef]
- Lin, Y.-T.; Wu, C.H. Response of bottom sediment stability after carp removal in a small lake. Ann. Limnol. Int. J. Limnol. 2013, 49, 157–168. [Google Scholar] [CrossRef]
- Nichols, S.A. Factors influencing the distribution of eurasian watermilfoil (Myriophyllum spicatum L.) Biomass in Lake Wingra, Wisconsin. J. Freshw. Ecol. 1994, 9, 145–151. [Google Scholar] [CrossRef]
- Nichols, S.A.; Mori, S. Littoral macrophyte vegetation of Lake Wingra—An example of Myriophyllum-Spicatum invasion in a southern Wisconsin lake. Trans. Wis. Acad. Sci. Arts Lett. 1971, 59, 107–120. [Google Scholar]
- Irwin, J.S. A theoretical variation of the wind profile power-law exponent as a function of surface roughness and stability. Atmos. Environ. 1979, 13, 191–194. [Google Scholar] [CrossRef]
- Wüest, A.; Lorke, A. Small-scale hydrodynamics in lakes. Annu. Rev. Fluid Mech. 2003, 35, 373–412. [Google Scholar] [CrossRef]
- Wu, C.H.; Yuan, H. Efficiency and accuracy of non-hydrostatic modeling of free-surface flows. In Estuarine and Coastal Modeling (2005); American Society of Civil Engineers: Reston, VA, USA, 2006; pp. 434–447. [Google Scholar]
- Arakawa, A. Computational design for long-term numerical integration of the equations of fluid motion: Two-dimensional incompressible flow. Part I. J. Comput. Phys. 1966, 1, 119–143. [Google Scholar] [CrossRef]
- Pacanowski, R.C.; Gnanadesikan, A. transient resp onse in a Z-level ocean model that resolves topography with partial cells. Mon. Weather Rev. 1998, 126, 3248–3270. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, C.H. Fully Nonhydrostatic modeling of surface waves. J. Eng. Mech. 2006, 132, 447–456. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, C.H. An implicit three-dimensional fully non-hydrostatic model for free-surface flows. Int. J. Numer. Methods Fluids 2004, 46, 709–733. [Google Scholar] [CrossRef]
- Haidvogel, D.; Beckmann, A. Numerical models of the coastal ocean. In The Sea. The Global Coastal Ocean: Processes and Methods; Brink, K., Robinson, A., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Wu, C.H.; Yuan, H. Efficient non-hydrostatic modelling of surface waves interacting with structures. Appl. Math. Model. 2007, 31, 687–699. [Google Scholar] [CrossRef]
- Wu, C.H.; Young, C.-C.; Chen, Q.; Lynett, P.J. Efficient nonhydrostatic modeling of surface waves from deep to shallow Water. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 104–118. [Google Scholar] [CrossRef]
- Young, C.-C.; Wu, C.H.; Liu, W.-C.; Kuo, J.-T. A higher-order non-hydrostatic σ model for simulating non-linear refraction–diffraction of water waves. Coast. Eng. 2009, 56, 919–930. [Google Scholar] [CrossRef]
- Venayagamoorthy, S.K. Nonhydrostatic and nonlinear contributions to the energy flux budget in nonlinear internal waves. Geophys. Res. Lett. 2005, 32, L15603. [Google Scholar] [CrossRef]
- Vitousek, S.; Fringer, O.B. Physical vs. numerical dispersion in nonhydrostatic ocean modeling. Ocean Model. 2011, 40, 72–86. [Google Scholar] [CrossRef]
- García, M.H.; López, F.; Dunn, C.; Alonso, C.V. Flow, turbulence, and resistance in a flume with simulated vegetation. In Riparian Vegetation and Fluvial Geomorphology; American Geophysical Union: Washington, DC, USA, 2004; pp. 11–27. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Kantha, L.H.; Clayson, C.A. On the effect of surface gravity waves on mixing in the oceanic mixed layer. Ocean Model. 2004, 6, 101–124. [Google Scholar] [CrossRef]
- Fischer-Antze, T.; Stoesser, T.; Bates, P.; Olsen, N.R.B. 3D numerical modelling of open-channel flow with submerged vegetation. J. Hydraul. Res. 2001, 39, 303–310. [Google Scholar] [CrossRef]
- Nicholas, A.R.; McLelland, S.J. Computational fluid dynamics modelling of three-dimensional processes on natural river floodplains. J. Hydraul. Res. 2004, 42, 131–143. [Google Scholar] [CrossRef]
- Jin, K.-R.; Hamrick, J.H.; Tisdale, T. Application of three-dimensional hydrodynamic model for Lake Okeechobee. J. Hydraul. Eng. 2000, 126, 758–771. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows. Computational Methods for Inviscid and Viscous Flows; John Wiley & Sons, Ltd.: Chichester, UK, 1990. [Google Scholar]
- Woodward, B.L.; Marti, C.L.; Imberger, J.; Hipsey, M.R.; Oldham, C.E. Wind and buoyancy driven horizontal exchange in shallow embayments of a tropical reservoir: Lake Argyle, Western Australia. Limnol. Oceanogr. 2017, 62, 1636–1657. [Google Scholar] [CrossRef]
- Markfort, C.D.; Perez, A.L.S.; Thill, J.W.; Jaster, D.A.; Porté-Agel, F.; Stefan, H.G. Wind sheltering of a lake by a tree canopy or bluff topography. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Magee, M.R.; Wu, C.H. Effects of changing climate on ice cover in three morphometrically different lakes. Hydrol. Process. 2017, 31, 308–323. [Google Scholar] [CrossRef]
- Pan, H.; Avissar, R.; Haidvogel, D.B. Summer circulation and temperature structure of Lake Kinneret. J. Phys. Oceanogr. 2002, 32, 295–313. [Google Scholar] [CrossRef]
- Rueda, F.J.; Schladow, S.G. Dynamics of large polymictic lake. II: Numerical simulations. J. Hydraul. Eng. 2003, 129, 92–101. [Google Scholar] [CrossRef]
- Rosati, A.; Miyakoda, K. A general circulation model for upper ocean simulation. J. Phys. Oceanogr. 1988, 18, 1601–1626. [Google Scholar] [CrossRef]
- Imberger, J.; Patterson, J.C. Physical Limnology. In Advances in Applied Mechanics; Hutchinson, J.W., Wu, T.Y., Eds.; Academic Press: Cambridge, MA, USA, 1989; pp. 303–475. [Google Scholar]
- Horn, D.A.; Imberger, J.; Ivey, G.N. The degeneration of large-scale interfacial gravity waves in lakes. J. Fluid Mech. 2001, 434. [Google Scholar] [CrossRef]
- Dorostkar, A.; Boegman, L.; Pollard, A. Three-dimensional simulation of high-frequency nonlinear internal wave dynamics in Cayuga Lake. J. Geophys. Res. Ocean. 2017, 122, 2183–2204. [Google Scholar] [CrossRef]
- Meire, D.W.S.A.; Kondziolka, J.M.; Nepf, H.M. Interaction between neighboring vegetation patches: Impact on flow and deposition. Water Resour. Res. 2014, 50, 3809–3825. [Google Scholar] [CrossRef]
- Tsujimoto, T.; Kitamura, T. Lateral bed-load transport and sand-ridge formation near vegetation zone in an open channel. J. Hydrosci. Hydraul. Eng. 1995, 13, 35–45. [Google Scholar]
- Nezu, I.; Onitsuka, K. Turbulent structures in partly vegetated open-channel flows with LDA and PI V measurements. J. Hydraul. Res. 2001, 39, 629–642. [Google Scholar] [CrossRef]
- Nadaoka, K.; Yagi, H. Shallow-water turbulence modeling and horizontal large-eddy computation of river Flow. J. Hydraul. Eng. 1998, 124, 493–500. [Google Scholar] [CrossRef]
- Xiaohui, S.; Li, C.W. Large eddy simulation of free surface turbulent flow in partly vegetated open channels. Int. J. Numer. Methods Fluids 2002, 39, 919–937. [Google Scholar] [CrossRef]
- Davies, A.M.; Jones, J.E.; Xing, J. Review of recent developments in tidal hydrodynamic modeling. II: Turbulence energy models. J. Hydraul. Eng. 1997, 123, 293–302. [Google Scholar] [CrossRef]
- Chen, Y.; Lei, Z. A study of eddy viscosity coefficient in numerical tidal simulation. China Ocean Eng. 2001, 15, 241–252. [Google Scholar]
- Rubol, S.; Ling, B.; Battiato, I. Universal scaling-law for flow resistance over canopies with complex morphology. Sci. Rep. 2018, 8, 4430. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torma, P.; Wu, C.H. Temperature and Circulation Dynamics in a Small and Shallow Lake: Effects of Weak Stratification and Littoral Submerged Macrophytes. Water 2019, 11, 128. https://doi.org/10.3390/w11010128
Torma P, Wu CH. Temperature and Circulation Dynamics in a Small and Shallow Lake: Effects of Weak Stratification and Littoral Submerged Macrophytes. Water. 2019; 11(1):128. https://doi.org/10.3390/w11010128
Chicago/Turabian StyleTorma, Péter, and Chin H. Wu. 2019. "Temperature and Circulation Dynamics in a Small and Shallow Lake: Effects of Weak Stratification and Littoral Submerged Macrophytes" Water 11, no. 1: 128. https://doi.org/10.3390/w11010128
APA StyleTorma, P., & Wu, C. H. (2019). Temperature and Circulation Dynamics in a Small and Shallow Lake: Effects of Weak Stratification and Littoral Submerged Macrophytes. Water, 11(1), 128. https://doi.org/10.3390/w11010128





