Improving Alpine Summertime Streamflow Simulations by the Incorporation of Evapotranspiration Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Watersheds Examined
2.2. Datasets Used
2.3. SWAT Model Description
2.4. SWAT Model Set-Up and Evaluation
2.5. SUFI-2 Autocalibration Routine
2.6. Scenarios Executed
3. Results
3.1. ET
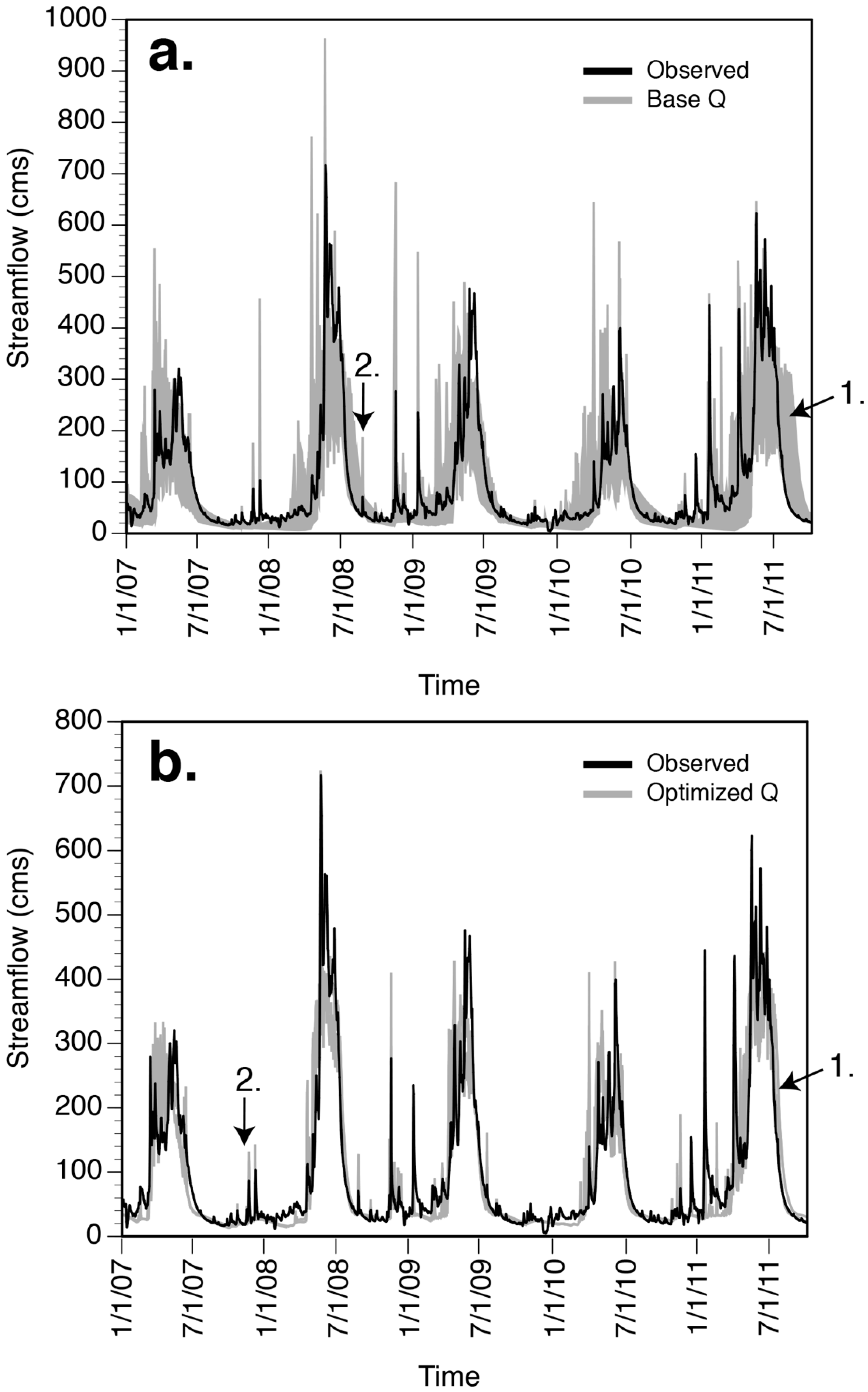
3.2. Streamflow
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ahl, R.S.; Woods, S.W.; Zuuring, H.R. Hydrologic calibration and validation of SWAT on a dominated Rocky Mountain watershed, Montana, U.S.A. J. Am. Water Resour. Assoc. 2008, 44, 1411–1430. [Google Scholar] [CrossRef]
- Chiang, L.-C.; Yuan, Y.; Mehaffey, M.; Jackson, M.; Chaubey, I. Assessing SWAT’s performance in the Kaskaskia River watershed as influenced by the number of calibration stations used. Hydrol. Process. 2014, 28, 676–687. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modeling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Tobin, K.J.; Bennett, M.E. Constraining SWAT calibration with remotely sensed evapotranspiration data. J. Am. Water Resour. Assoc. 2017, 53, 593–604. [Google Scholar] [CrossRef]
- Chen, Y.; Marek, G.W.; Marek, T.H.; Brauer, D.K.; Srinivasan, R. Assessing the Efficacy of the SWAT Auto-Irrigation Function to Simulate Irrigation, Evapotranspiration, and Crop Response to Management Strategies of the Texas High Plains. Water 2017, 9, 509. [Google Scholar] [CrossRef]
- Feng, Q.; Chaubey, I.; Cibin, R.; Engel, B.; Sudheer, K.P.; Volenec, J. Simulating Establishment Periods of Switchgrass and Miscanthus in the Soil and Water Assessment Tool (SWAT). Trans. ASABE 2017, 60, 1621–1632. [Google Scholar] [CrossRef]
- Rajib, M.A.; Merwade, V. Improving soil moisture accounting and streamflow prediction in SWAT by incorporating a modified time-dependent Curve Number method. Hydrol. Process. 2016, 30, 603–624. [Google Scholar]
- Seibert, J.; McDonnell, J.J. On the dialog between experimentalist and modeler in catchment hydrology: Use of soft data for multicriteria model calibration. Water Resour. Res. 2002, 38, WR000978. [Google Scholar] [CrossRef]
- Arnold, J.G.; Youssef, M.A.; Yen, H.; White, M.J.; Sheshukov, A.Y.; Sadeghi, A.M.; Moriasi, D.N.; Steiner, J.L.; Amatya, D.M.; Skaggs, R.W.; et al. Hydrological processes and model representation: Impact of soft data on calibration. Trans. ASABE 2015, 58, 1637–1660. [Google Scholar]
- Winsemius, H.C.; Schaefli, B.; Montanari, A.; Savenije, H.H.G. On the calibration of hydrological models in ungauged basins: A framework for integrating hard and soft hydrological information. Water Resour. Res. 2009, 45, W12422.1–W12422.15. [Google Scholar] [CrossRef]
- Kang, H.; Moon, J.; Shin, Y.; Ryu, J.; Kum, D.H.; Jang, C.; Choi, J.; Kong, D.S.; Lim, K.J. Modification of SWAT autocalibration for accurate flow estimation at all flow regimes. Paddy Water Environ. 2016, 14, 499–508. [Google Scholar] [CrossRef]
- Guse, B.; Reusser, D.E.; Fohrer, N. How to improve the representation of hydrologic processes in SWAT for a lowland catchment—Temporal analysis of parameter sensitivity and model performance. Hydrol. Process. 2014, 28, 2651–2670. [Google Scholar] [CrossRef]
- Omani, N.; Srinivasan, R.; Karthikeyan, R.; Smith, P.K. Hydrological modeling of highly glacierized basins (Andes, Alps, and Central Asia). Water 2017, 9, 111. [Google Scholar] [CrossRef]
- McNamara, J.; Chandler, D.; Seyfried, M.; Achet, S. Soil moisture states, lateral flow, and streamflow generation in a semi-arid, snowmelt-driven catchment. Hydrol. Process. 2005, 19, 4023–4038. [Google Scholar] [CrossRef]
- Clayton, J.A. Summer soil moisture loss at Utah SNOTEL sites and streamflow recession at nearby gauges: Variability in runoff generation and the potential for flow forecasting. Hydrol. Process. 2016, 30, 119–134. [Google Scholar] [CrossRef]
- Rahman, K.; Maringanti, C.; Beniston, M.; Widmer, F.; Abbaspour, K.; Lehmann, A. Streamflow modeling in a highly managed mountainous glacier watershed using SWAT: The Upper Rhone River Watershed case in Switzerland. Water Resour. Manag. 2013, 27, 323–339. [Google Scholar] [CrossRef]
- Knowles, J.F.; Harpold, A.A.; Cowie, R.; Zeliff, M.; Barnard, H.R.; Burns, S.P.; Blanken, P.D.; Morse, J.F.; Williams, M.W. The relative contributions of alpine and subalpine ecosystems to the water balance of a mountainous, headwater catchment. Hydrol. Process. 2015, 29, 4794–4808. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, Q.; Zou, S.; Yang, L. Assessing variation in water balance components in mountainous inland river basin experiencing climate change. Water 2016, 8, 472. [Google Scholar] [CrossRef]
- Maddox, R.A.; Hoxit, L.R.; Chappell, C.F.; Caracena, F. Comparison of meteorological aspects of the Big Thompson and Rapid City flash floods. Mon. Weather Rev. 1978, 106, 375–389. [Google Scholar] [CrossRef]
- Petersen, W.A.; Carey, L.D.; Rutledge, S.A.; Knievel, J.C.; Doesken, N.J.; Johnson, R.H.; McKee, T.B.; Haar, T.V.; Weaver, J.F. Mesoscale and radar observations of the Fort Collins flash flood of 28 July 1997. Bull. Am. Meteorol. Soc. 1999, 80, 197–216. [Google Scholar] [CrossRef]
- Gesch, D.; Oimoen, M.; Greenlee, S.; Nelson, C.; Steuck, M.; Tyler, D. The National Elevation Dataset. Photogramm. Eng. Remote Sens. 2002, 68, 5–32. [Google Scholar]
- Gesch, D.B. The National Elevation Dataset. In Digital Elevation Model Technologies and Applications: The DEM Users Manual, 2nd ed.; Maune, D., Ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2007; pp. 99–118. [Google Scholar]
- Fry, J.; Xian, G.; Jin, S.; Dewitz, J.; Homer, C.; Yang, L.; Barnes, C.; Herold, N.; Wickham, J. Completion of the 2006 National Land Cover Database for the conterminous United States. Photogramm. Eng. Remote Sens. 2011, 77, 858–864. [Google Scholar]
- Soil Survey Staff. Natural Resources Conservation Service, Web Soil Survey. 2016. Available online: http://websoilsurvey.nrcs.usda.gov/ (accessed on 1 July 2016).
- U.S. Geological Survey. National Water Information System Data Available on the World Wide Web (USGS Water Data for the Nation). Available online: http://waterdata.usgs.gov/nwis/ (accessed on 1 July 2016).
- PRISM Climate Group, Oregon State University. Available online: http://prism.oregonstate.edu (accessed on 1 July 2016).
- Didan, K. MOD16A2: MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500 m SIN Grid V006 Was Retrieved from the online Data Pool, Courtesy of the NASA Land Processes Distributed Active Archive Center (LP DAAC), USGS/Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mod16a2_v006 (accessed on 1 July 2016).
- Savoca, M.E.; Senay, G.B.; Maupin, M.A.; Kenny, J.F.; Perry, C.A. Actual Evapotranspiration Modeling Using the Operational Simplified Surface Energy Balance (SSEBop) Approach; U.S. Geological Survey Scientific Investigations Report 2013-5126; U.S. Geological Survey: Reston, VA, USA, 2013; 16p. Available online: http://pubs.usgs.gov/sir/2013/5126 (accessed on 1 July 2016).
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, V.P. Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Arnold, J.G.; Fohrer, N. SWAT2000: Current capabilities and research opportunities In applied watershed modeling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.; Arnold, J.G. The Soil and Water Assessment Tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Williams, J.R. Flood routing with variable travel time or variable storage coefficients. Trans. ASABE 1969, 12, 100–103. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil and Water Assessment Tool User’s Manual; Texas Water Resource Institute Report TR-192; Texas Water Resource Institute: College Station, TX, USA, 2002. [Google Scholar]
- Moriasi, D.N.; Starks, P.J.; Steiner, J.L.; Guzman, J.A.; Allen, P.B.; Naney, J.W. Upper Washita River Experimental Watersheds: Physiography data. J. Environ. Qual. 2014, 43, 1298–1309. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, L.; Siber, R.; Bogner, K. Modeling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for SWAT application to the Chaoche Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Wu, H.; Chen, B. Evaluating uncertainty estimates in distributed hydrological modeling for the Wenjing River watershed in China by GLUE, SUFI-2, and Para Sol methods. Ecol. Eng. 2015, 76, 110–121. [Google Scholar] [CrossRef]
- Uniyal, B.; Jha, M.K.; Verma, A.K. Parameter identification and uncertainty analysis for simulating streamflow in a river basin of Eastern India. Hydrol. Process. 2015, 29, 3744–3766. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and groundwater recharge from stream flow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Miralles, D.G.; Gash, J.H.; Holmes, T.R.H.; de Jeu, R.A.M.; Dolman, A.J. Global canopy interception from satellite observations. J. Geophys. Res. 2010, 115, D16122. [Google Scholar] [CrossRef]
- Afinowicz, J.D.; Munster, C.L.; Wilcox, B.P. Modeling effects of brush management on the rangeland water budget. Edwards Plateau, Texas. J. Am. Water Resour. Assoc. 2005, 41, 181–193. [Google Scholar] [CrossRef]
- Alemayehu, T.; van Griensven, A.; Bauwens, W. Evaluating CFSR and WATCH data as input to SWAT for the estimation of the potential evapotranspiration in a data-scarce Eastern-African Catchment. J. Hydrol. Eng. 2015, 21, 05015028. [Google Scholar] [CrossRef]
- Wolock, D.M. Base-Flow Index Grid for the Conterminous United States; U.S. Geological Survey Open-File Report 03-263; U.S. Geological Survey: Reston, VA, USA, 2003.
- Zhang, X.; Srinivasan, R.; Debele, B.; Hao, F. Runoff simulation of the headwaters of the Yellow River using the SWAT model with three snowmelt algorithms. J. Am. Water Resour. Assoc. 2008, 44, 48–61. [Google Scholar] [CrossRef]
- Debele, B.; Srinivasan, R.; Gosain, A.K. Comparison of process-based and temperature-index snowmelt modeling in SWAT. Water Resour. Manag. 2010, 24, 1065–1088. [Google Scholar] [CrossRef]
- Marek, G.; Gowda, P.; Evett, S.; Srinivasan, R. Calibration and validation of the SWAT model for predicting daily ET over irrigated crops in the Texas High Plains using lysimetric data. Trans. ASABE 2016, 59, 611–622. [Google Scholar] [CrossRef]
- Faramarzi, M.; Srinivasan, R.; Iravani, M.; Bladon, K.D.; Abbaspour, K.; Zehnder, A.J.B.; Goss, G.G. Setting up a hydrological model of Alberta: Data discrimination analyses prior to calibration. Environ. Model. Softw. 2015, 74, 48–65. [Google Scholar] [CrossRef]
- Abiodun, O.O.; Guan, H.; Post, V.E.A.; Batelaan, O. Comparison of MODIS and SWAT evapotranspiration over a complex terrain at different spatial scales. Hydrol. Earth Syst. Sci. 2018, 22, 2775–2794. [Google Scholar] [CrossRef]
- Parajuli, P.B.; Jayakody, P.; Ouyang, Y. Evaluation of Using Remote Sensing Evapotranspiration Data in SWAT. Water Resour. Manag. 2018, 32, 985–996. [Google Scholar] [CrossRef]
- Wambura, F.J.; Dietrich, O.; Lischeid, G. Improving a distributed hydrological model using evapotranspiration-related boundary conditions as additional constraints in a data-scarce river basin. Hydrol. Process. 2018, 32, 759–775. [Google Scholar] [CrossRef]
- Patil, A.; Ramsankaran, R.A.A.J. Improving streamflow simulations and forecasting performance of SWAT model by assimilating remotely sensed soil moisture observations. J. Hydrol. 2017, 555, 683–696. [Google Scholar] [CrossRef]
- Zhang, Y.; Hou, J.; Gu, J.; Huang, C.; Li, X. SWAT-Based hydrological data assimilation system (SWAT-HDAS): Description and case application to river basin-scale hydrological predictions. J. Adv. Model. Earth Syst. 2017, 9, 2863–2882. [Google Scholar] [CrossRef]
- Qiao, L.; Herrmann, R.B.; Pan, Z. Parameter Uncertainty Reduction for SWAT Using Grace, Streamflow, and Groundwater Table Data for Lower Missouri River Basin. J. Am. Water Resour. Assoc. 2013, 49, 343–358. [Google Scholar] [CrossRef]
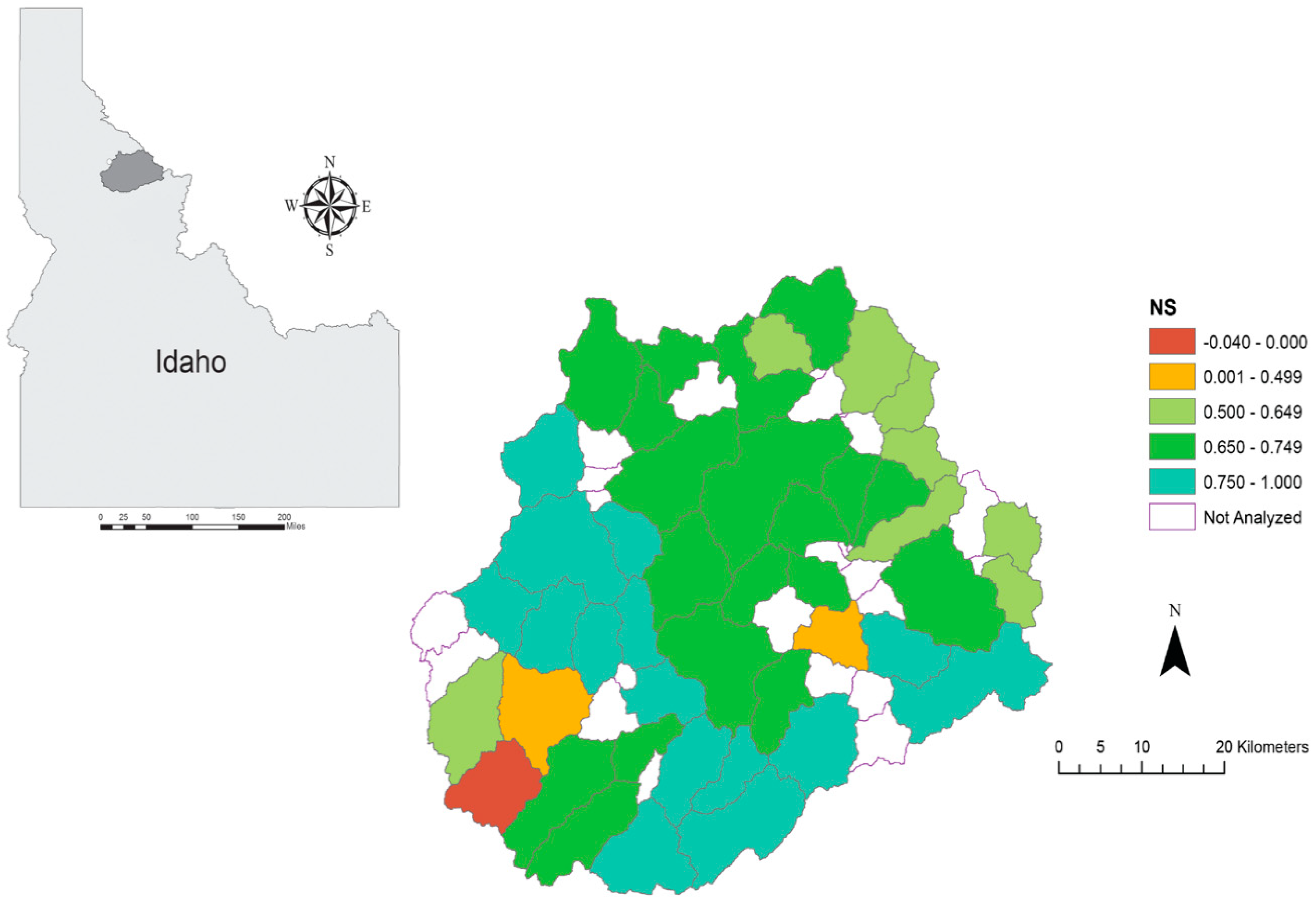
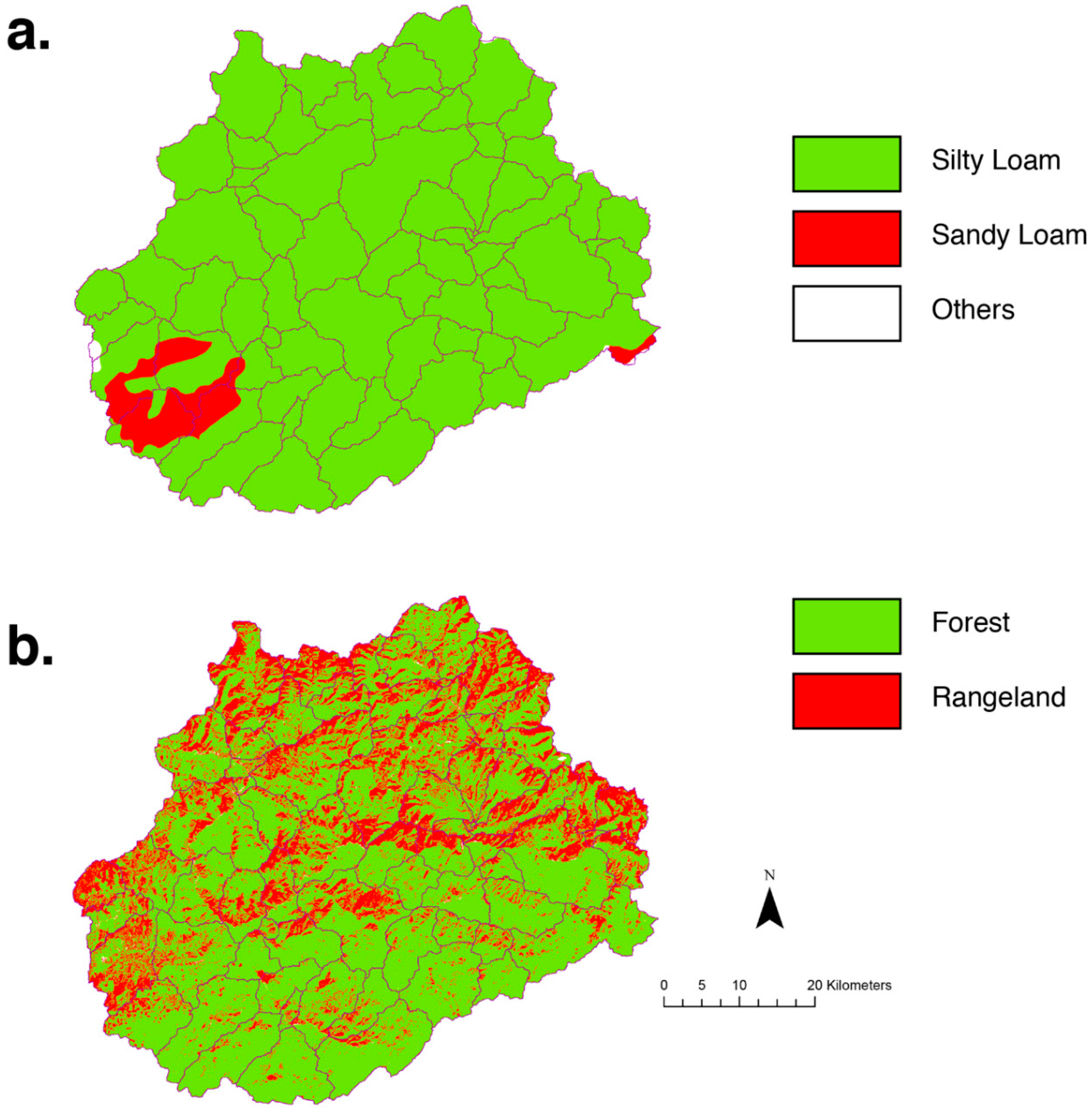
| Soil Name | Mukey | Texture | Areal Percentage |
|---|---|---|---|
| Vay | 662090 | Silty loam | 17.33 |
| Prospectors Variant | 661986 | Silty loam | 31.30 |
| Vay | 662085 | Silty loam | 10.89 |
| Buckhouse Family | 661824 | Silty loam | 12.89 |
| Nakama Family | 662086 | Silty loam | 10.10 |
| Honey jones | 661952 | Silty loam | 6.97 |
| Narnett | 662001 | Silty loam | 5.94 |
| Rubble Land (Latour-Honey Jones-Ahrs) | 661997 | Sandy loam | 4.51 |
| Parameters | Initial Parameters | Base Q Parameters | Final Parameters |
|---|---|---|---|
| CN2 (Initial SCS Runoff Curve Number for Moisture Condition II) | 35.0 to 58.1 | 36.5 to 56.5 | 51.85 to 51.89 |
| CH_N2 (Manning’s “n” Value for the Main Channel) | 0 to 0.3 | 0.826 to 0.2858 | 0.1360 to 0.1799 |
| CH_K2 (Hydraulic Conductivity of the Main Channel Alluvium, mm/h) | 0 to 500 | 36.7 to 183.2 | 61.99 to 63.15 |
| CH_N1 (R; Manning’s “n” Value for the Tributary Channel) | 0 to 0.3 | 0.0283 to 0.2749 | 0.0467 to 0.0822 |
| CH_K1 (R; Hydraulic Conductivity the Tributary Alluvium mm/h) | 0 to 300 | 26.5 to 261.1 | 95.9 to 119.5 |
| OV_N (Manning’s “n” Value for Overland Flow) | 0.01 to 0.6 | 0.0304 to 0.5832 | 0.0756 to 0.0908 |
| SURLAG (Surface Runoff Lag Coefficient) | 1 to 34 | 2.40 to 26.75 | 17.07 to 26.28 |
| ALPHA_BF (Baseflow Alpha Factor) | 0.0385 to 0.1075 | 0.0612 to 0.1051 | 0.0777 to 0.0952 |
| GW_DELAY (A; Groundwater Delay Time, days) | 30 to 450 | 108.7 to 413.7 | 150.9 to 213.6 |
| GW_REVAP (A; Groundwater “Reevap” Coefficient) | 0.02 to 0.2 | 0.0275 to 0.1961 | 0.0986 to 0.1448 |
| GWQMN (A; Threshold Depth of Shallow Aquifer Water Required for Return Flow to Occur, mm) | 0 to 5000 | 762 to 3572 | 1354 to 3321 |
| ESCO (Soil Evaporation Compensation Factor) | 0 to 1 | 0.1345 to 0.7605 | 0.8227 to 0.964 |
| REVAPMN (A; Depth to Shallow Aquifer for “Reevap” or Percolation to Deep Aquifer, mm) | 0 to 500 | 42.2 to 483.2 | 51.4 to 251.4 |
| CANMX (A; Maximum Canopy Storage, mm) | 0 to 100 | 33.95 to 86.95 | 1.738 to 1.931 |
| EPCO (Plant Uptake Compensation Factor) | 0 to 1 | 0.0315 to 0.9745 | 0.6120 to 0.6196 |
| SOL_AWC (R; Available Water Capacity of the Soil Layer (mm H2O/mm soil) | −0.2 to 0.4 | −0.1697 to 0.3631 | 0.2879 to 0.3852 |
| SOL_K (R; Saturated Hydraulic Conductivity, mm/h) | −0.8 to 0.8 | −0.6680 to 0.7480 | 0.2810 to 0.5638 |
| SOL_BD (R; Moisture Bulk Density, g/cm3) | −0.5 to 0.6 | −0.4159 to 0.5687 | −0.2916 to 0.3192 |
| SFTMP (Snowfall temperature, °C) | −5 to 5 | −0.835 to 4.895 | 1.118 to 1.358 |
| SMTMP (Snow melt base temperature, °C) | −5 to 5 | −3.205 to 4.895 | 3.613 to 4.407 |
| SMFMX (Melt factor for snow on June 21, mm H2O/°C-day) | 0 to 10 | 0.705 to 9.605 | 2.754 to 5.402 |
| SMFMN (Melt factor for snow December 21, mm H2O/°C-day) | 0 to 10 | 0.755 to 7.925 | 0.916 to 2.181 |
| TIMP (Snow pack temperature lag factor, °C) | 0.01 to 1 | 0.0362 to 0.9500 | 0.2089 to 0.3036 |
| Threshold | NS | Absolute MBE |
|---|---|---|
| Perfect | 1.00 | 0% |
| Very Good | 0.75 | 10% |
| Good | 0.65 | 15% |
| Satisfactory | 0.50 | 25% |
| Unacceptable | <0.50 | >25% |
| ESCO | CANMX | SOL_AWC | SOL_K | SOL_BD | Avg NS | Average Bias | |
|---|---|---|---|---|---|---|---|
| MODIS16A2 | 0.7435 to 0.9585 | 0.9789 to 2.320 | 0.2719 to 0.3985 | −0.7688 to 0.7656 | −0.3773 to 0.3244 | 0.6842 | 19.1% |
| Satisfactory | |||||||
| SSEBop | 0.4505 to 0.7885 | 1.146 to 2.250 | 0.3565 to 0.3913 | −0.7912 to 0.3448 | −0.4521 to 0.5786 | 0.6138 | 20.7% |
| Satisfactory | |||||||
| GLEAM 3.1a | 0.1525 to 0.5605 | 1.070 to 2.269 | 0.2557 to 0.3943 | −0.7832 to −0.6568 | −0.4951 to 0.1165 | 0.2637 | 38.0% |
| Unsatisfactory | |||||||
| a. Calibration | Base Q (n = 11) | Best Q (MODIS; n = 8) | Best Q (SSEBop; n = 2) | Optimized Q (n = 2) |
| Overall- NS | 0.51 to 0.73 | 0.51 to 0.69 | 0.53 to 0.66 | 0.77 to 0.82 |
| Overall- Bias | 5.5 to 24.4% | 0.2 to 17.7% | 5.5 to 16.7% | 3.3 to 6.1% |
| Baseflow Ratio | 0.627 to 0.772 | 0.716 to 0.766 | 0.736 to 0.766 | 0.739 to 0.762 |
| Recessional- NS | 0.54 to 0.77 | 0.56 to 0.72 | 0.51 to 0.62 | 0.77 to 0.86 |
| Recessional- Bias | 1.1 to 24.2% | 1.9 to 23.9% | 3.5 to 13.1% | 7.0 to 8.7% |
| Summer Peak- NS | 0.66 to 0.94 | 0.67 to 0.91 | 0.69 to 0.78 | 0.80 to 0.89 |
| Summer Peak- Bias | −24.3 to 19.1% | −22.8 to 24.7% | −22.6 to −23.9% | −5.1 to 2.4% |
| Performance Threshold | Satisfactory | Satisfactory | Satisfactory | Very Good |
| b. Validation | Base Q (n = 11) | Best Q (MODIS; n = 8) | Best Q (SSEBop; n = 2) | Optimized Q (n = 2) |
| Overall- NS | 0.36 to 0.77 | 0.42 to 0.72 | 0.58 to 0.75 | 0.78 to 0.79 |
| Overall- Bias | 9.0 to 27.9% | 6.1 to 21.2% | 7.5 to 22.2% | 8.8 to 10.6% |
| Baseflow Ratio | 0.608 to 0.770 | 0.708 to 0.761 | 0.739 to 0.758 | 0.737 to 0.758 |
| Recessional- NS | 0.33 to 0.79 | 0.59 to 0.75 | 0.60 to 0.78 | 0.80 to 0.81 |
| Recessional- Bias | 5.9 to 30.3% | 8.0 to 23.6% | 6.6 to 16.1% | 12.1 to 14.7% |
| Summer Peak- NS | −4.25 to 0.60 | −0.82 to 0.44 | −0.06 to 0.44 | 0.47 to 0.57 |
| Summer Peak- Bias | −98.7 to 27.2% | −34.6 to 23.1% | −28.6 to −30.3% | −2.2 to 1.8% |
| Performance Threshold | Unsatisfactory to Satisfactory | Unsatisfactory | Unsatisfactory | Unsatisfactory to Satisfactory |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tobin, K.J.; Bennett, M.E. Improving Alpine Summertime Streamflow Simulations by the Incorporation of Evapotranspiration Data. Water 2019, 11, 112. https://doi.org/10.3390/w11010112
Tobin KJ, Bennett ME. Improving Alpine Summertime Streamflow Simulations by the Incorporation of Evapotranspiration Data. Water. 2019; 11(1):112. https://doi.org/10.3390/w11010112
Chicago/Turabian StyleTobin, Kenneth J., and Marvin E. Bennett. 2019. "Improving Alpine Summertime Streamflow Simulations by the Incorporation of Evapotranspiration Data" Water 11, no. 1: 112. https://doi.org/10.3390/w11010112
APA StyleTobin, K. J., & Bennett, M. E. (2019). Improving Alpine Summertime Streamflow Simulations by the Incorporation of Evapotranspiration Data. Water, 11(1), 112. https://doi.org/10.3390/w11010112





