1. Introduction
Proper water management is a key global challenge. Indeed, there are already indicators that anthropogenic influences are impacting the flow rates of rivers and the winter recovery of glaciers [
1]. The energy, agricultural and domestic sectors are found worldwide, and even as relative water withdrawals in these sectors change, the overall global volume of extracted water is projected to increase. This becomes especially clear as factors such as population growth and improvements to the quality of life come into play [
2]. When the water needs of each sector are combined, it becomes clear that water must be managed systematically in order to ensure a sustainable supply for the future. Therefore, understanding how both natural and anthropogenic factors affect a watershed is key to the proper management of this resource.
Collaborative measures must be taken to manage limited water resources to meet the increasing water demands of every sector. Eco-hydro-geologic modelling can be useful in quantifying the resources and needs of specific areas and understanding the natural and anthropogenic factors affecting their distribution in time and space [
3,
4,
5]. Depending on the scope of the research studies, models can be applied to regions of significantly varying size and complexity. In order to make accurate forecasts, computer models that quantify water resources should be holistic, focusing on groundwater (GW) and surface water (SW) together instead of treating them individually. In the last two decades, the number of models that considered GW and SW together has increased [
6,
7,
8,
9]. Developing models that are consistently accurate is a key step toward more intelligent water management. To achieve this objective, considerations must be made during the selection process to ensure that the model is able to meet the demands of the study, including data availability, ease of use, desired accuracy of simulations and budget. Of those available, four coupled GW–SW models have been used in multiple published basin-scale studies. These include HydroGeoSphere [
8], MIKE SHE [
10], GSFLOW [
7] and SWAT–MODFLOW [
4,
6,
11,
12]. While the first two of these models are capable of incredibly complex simulations, they are both fully distributed and grid-based, therefore requiring significant amounts of high-resolution data and computing capacity. The latter two are semi-distributed, and incorporate the most important physical processes to efficiently simulate large-scale basins over longer timespans.
SWAT–MODFLOW is a coupled hydro(geo)logical model that employs both the Soil and Water Assessment Tool—SWAT [
13] and MODFLOW [
14] (SW and GW models, respectively) to yield an integrated output. Coupling the component models covers the limitations inherent in each component model to yield a solution that is more faithful to real-world hydro(geo)logy. SWAT covers processes associated with SW hydrology, such as precipitation, temperature, river flow, surface runoff, soil water, actual evapotranspiration and GW recharge, while MODFLOW is responsible for the GW processes, including saturated flow and GW discharge into rivers.
Although multiple SWAT–MODFLOW codes have been developed over the past twenty years for study areas of highly varying scale [
4,
6,
12,
15,
16], each study was carried out to overcome the shortcomings of each of its component models (SWAT and MODFLOW), and to evaluate SW and GW resources as one system. While SWAT simulates physical processes associated with soil, plants, water in the root zone and weather, MODFLOW is responsible for providing outputs for three-dimensional GW flow, as well as groundwater pumping simulations. Each SWAT–MODFLOW code follows the same general logic, in that MODFLOW is run as a subroutine of SWAT [
4,
11,
12], effectively replacing the GW module in SWAT to yield outputs at finer resolution than SWAT can achieve by itself for a given time step. Due to its ability to efficiently simulate multiple physical processes in a large region with no associated cost, this study uses the publicly available SWAT–MODFLOW tool developed by Bailey et al. [
4].
Models developed in previous studies covered smaller study areas with less complex hydrogeology, and were mainly intended for understanding local water changes [
4,
6,
11,
12]. Prior to this study, the Sprague River Watershed model [
4] was the largest at roughly 4100 km
2. Other models range in size to fit various goals, with some as small as 198 km
2 [
11], and most having study areas in the high hundreds to low thousands of square kilometers [
12]. In addition, the successfully implemented SWAT–MODFLOW models thus far have had hydrology and hydrogeology of low complexity, with each of the MODFLOW components focusing on shallow, local GW flow patterns [
11,
12].
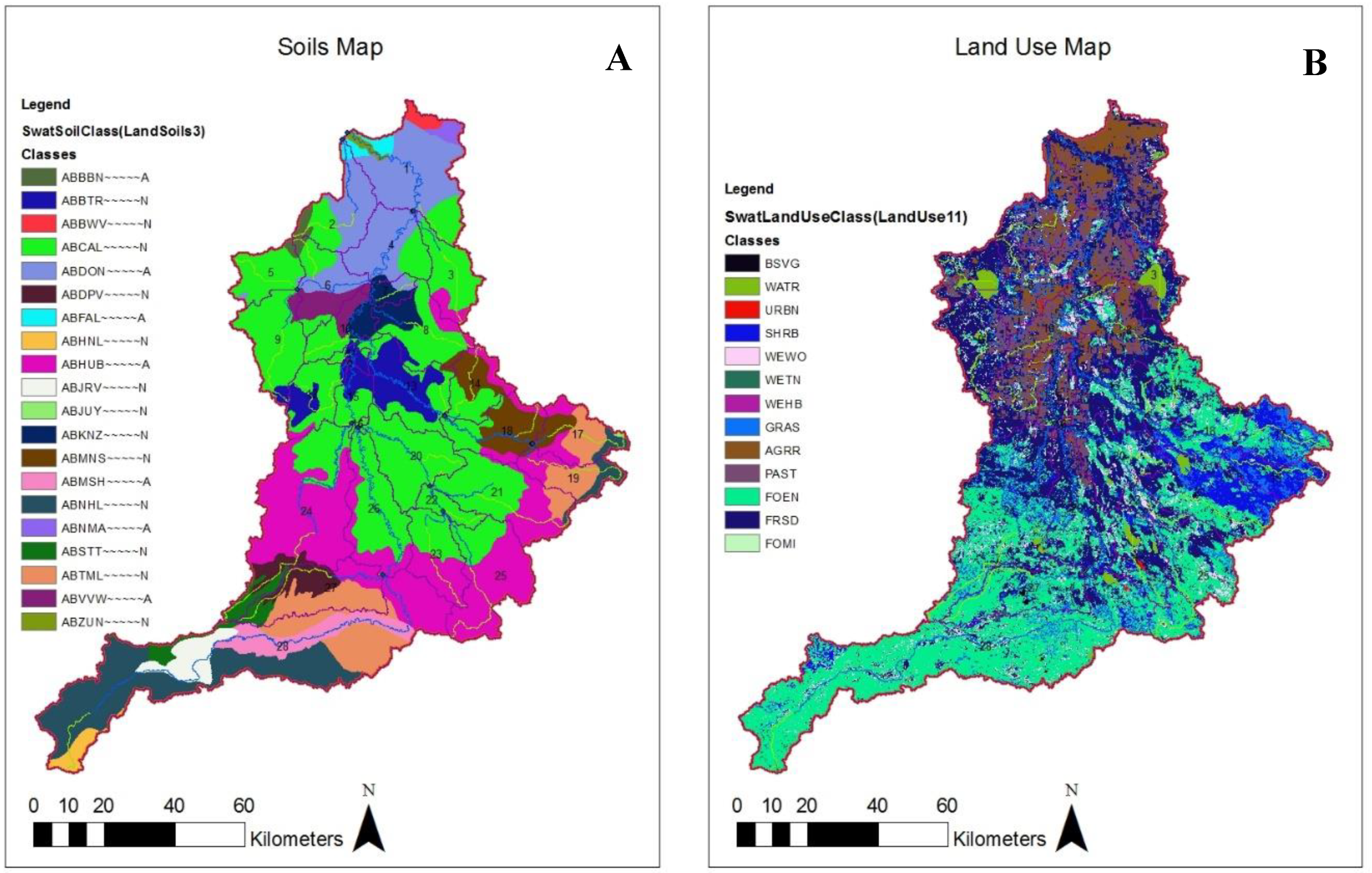
This study uses a portion of western Alberta, Canada as a case study to simulate a hydro(geo)logically variable watershed (Little Smoky River). Since the rise in the economic potential of hydraulic stimulation in combination with horizontal drilling to develop unconventional resources, the region has become a key area for Alberta’s oil and gas development [
17]. For many operators in the area, the Duvernay Formation is targeted for its unconventional resources, with wells using as much as 30,000 m
3 of water to effectively fracture the reservoir [
18], although this value can increase further when targeting formations elsewhere in western Canada [
19]. Historically, much of the fresh water required for operations was sourced from the rivers and streams in the region [
20], with occasional extraction of GW from freshwater (or near-fresh) aquifers. With increased unconventional resource development comes the potential to use GW to support hydraulic fracturing operations [
21,
22]. However, a lack of understanding of the total GW and SW availability, reliability and interactions, and limited available projections under future climate change scenarios, may restrict future increases in production of energy resources in the region. Therefore, the integration of both SW and GW supply-demand processes in the region is needed to systematically study the future opportunities and conflicts for industry. Due to similarly increasing water use trends in other semi-arid basins with strongly defined seasons, such as North Dakota [
23], the findings and workflows of this study can be applied to evaluate GW–SW interactions in many similar watersheds worldwide.
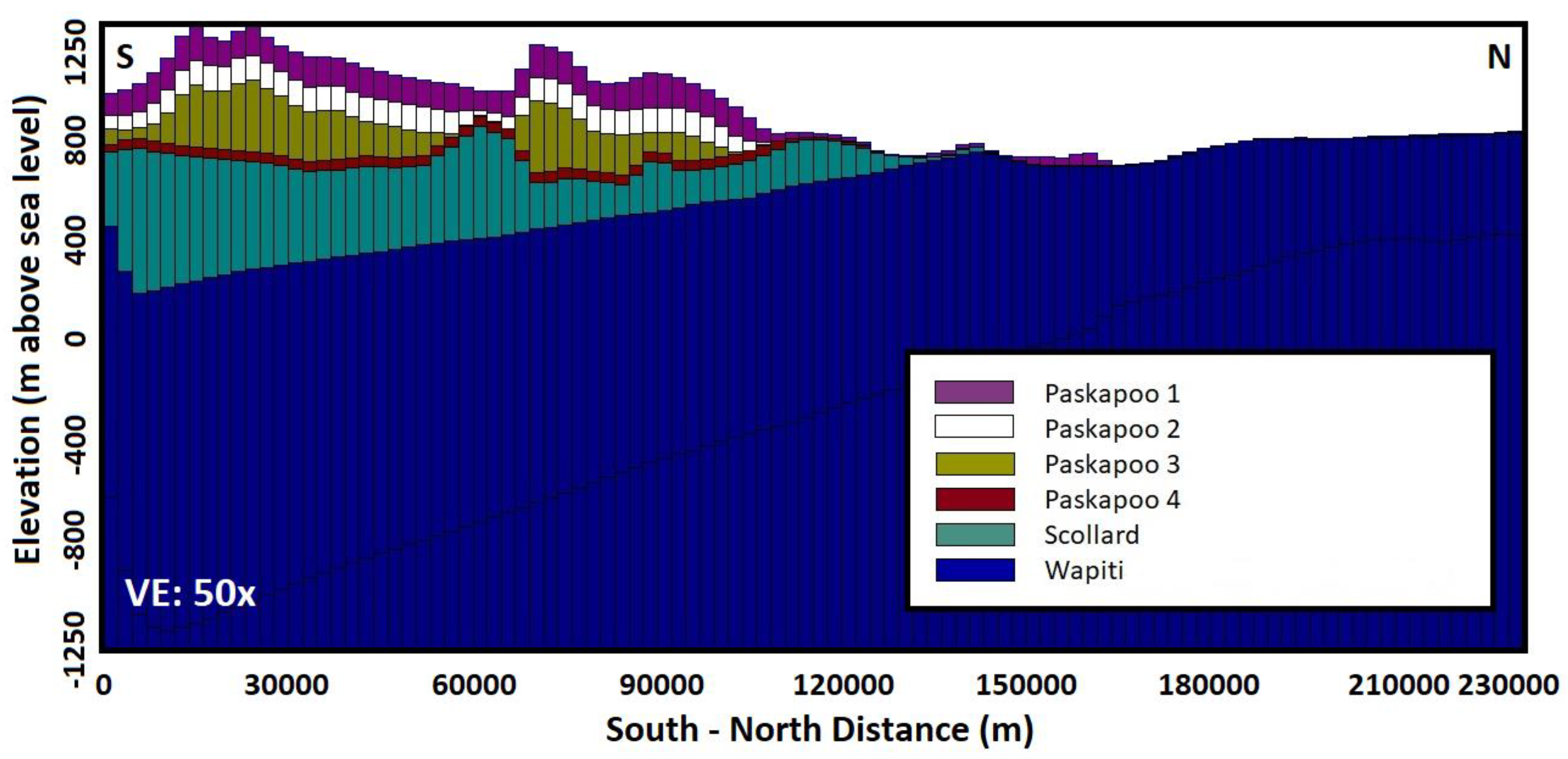
By virtue of being in western Alberta, the case study area is subjected to highly variable, yet predictable, climate patterns. Like most Canadian watersheds, the Little Smoky River experiences higher discharge during the spring and summer months, with next to no flow during the winter months. This, in turn, affects the hydrology of the basins in the study area. With the headwaters of the Little Smoky River located at elevations of more than 1200 m above sea level, snowfall is an influence that must be considered in this area for the most realistic representation of the climate. In addition, the underlying Western Canadian Sedimentary Basin (WCSB) is comprised of geological formations that dip upwards from west to east, creating a wedge-shape geological setting in the study area. Many of the formations are both thicker and deeper along the Rocky Mountains but become shallower and are exposed or only covered by a thin layer of sediments to the northeast. Combined with these dipping layers, variability of rock properties within a given geological formation also varies spatially, resulting in a complex hydrogeological environment with widely varying hydraulic conductivity and storage properties [
22,
24]. These complex but realistic hydrologic and hydrogeologic conditions and the importance of water to support unconventional resource development and sustain rivers, makes it an ideal case study to test the SWAT–MODFLOW model.
The primary objective of this study was to apply SWAT–MODFLOW to simulate a large region to study the regional hydrogeological conditions and the potential impacts of climate change and water withdrawal on GW–SW interactions. Our specific objectives were: (1) to calibrate, validate, and provide uncertainty analyses for both model components; (2) to assess the effects of future climate change on the GW–SW exchange pattern; and (3) to examine the impacts of groundwater use scenarios on GW–SW interactions for the interval of 2010–2034. This was done to achieve the goal of further understanding of the use of SWAT–MODFLOW as a planning tool to predict the effect of natural and anthropogenic influences on the watershed.
3. Results and Discussion
3.1. Sensitivity, Calibration, Validation and Uncertainty Analysis
3.1.1. SWAT
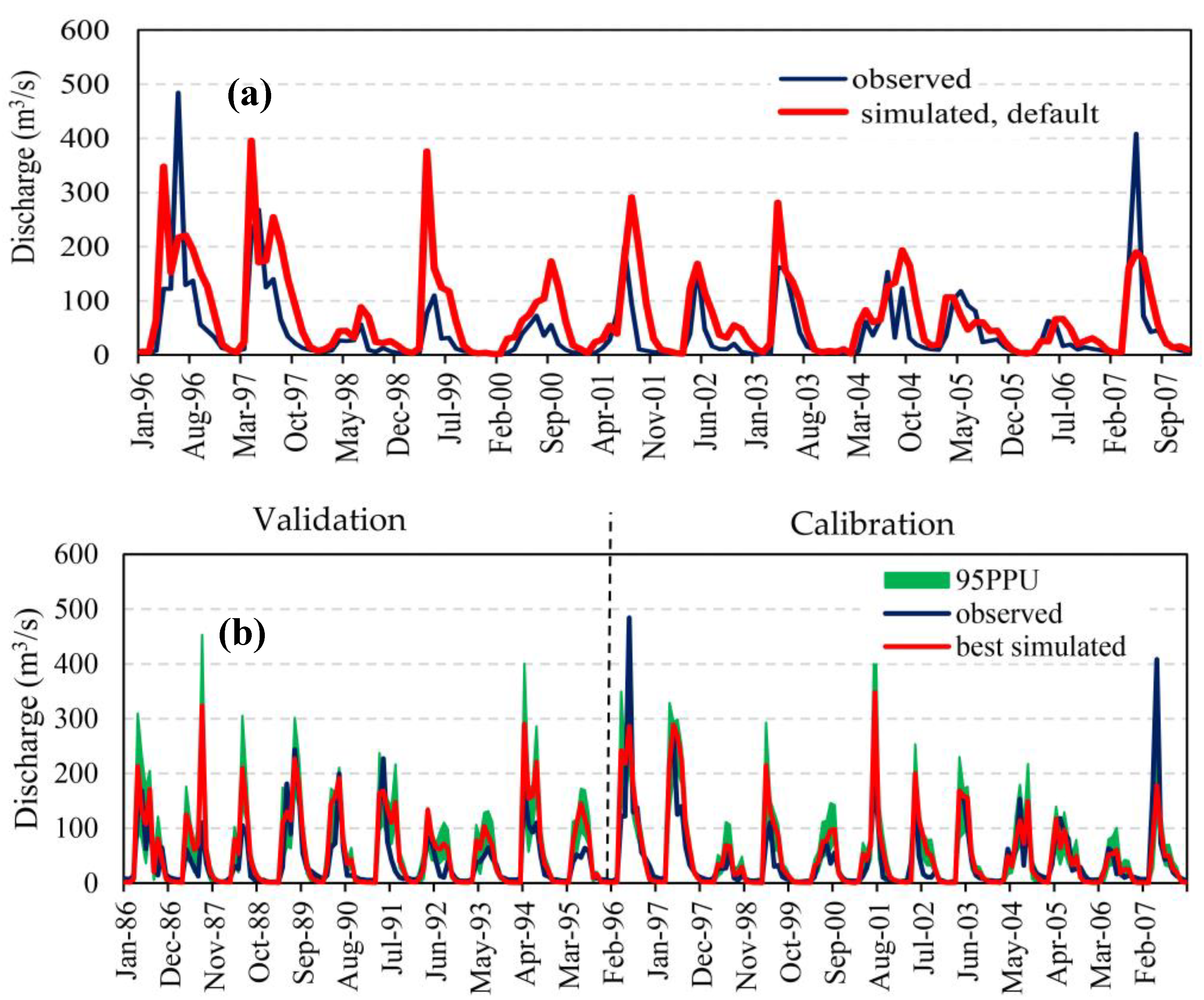
With a preliminary SWAT run prior to calibration, the simulated results overestimated river peak flows when compared to the observed values (
Figure 5a). For calibration purposes, a total of 21 physical parameters sensitive to river discharge were initially selected from literature [
3]. The parameters were further regionalized to capture a higher degree of spatial variability due to land use, soil, and hydrologic conditions for a total of 45 sensitive parameters. From these, a one-at-a-time, and then global sensitivity analysis was performed, evaluating model reactions to changes in single parameters and later to all parameter changes [
45]. The addition of elevation bands (PLAPS and TLAPS, allowing multiple temperature and precipitation values to capture the effects of orographic changes within a sub-basin) improved the overall calibration performance, particularly in Sub-basin 24, which was treated as its own system. Allowing for more water capacity in the soil (SOL_AWC), and less runoff (curve number; CN2) also decreased the overestimated peak flows. The final values were kept within the range provided by the soil input data, with a maximum water capacity of 0.333 mm H
2O and a curve number decrease of 20%. To further constrain this peak flow reduction, the soil hydraulic conductivity values were increased as well. In addition to the above, snow-related parameters (.sno) were altered so that the snowfall and snowmelt simulations occurred in the correct temperature range (−5 to 5 °C). A complete list of the parameters used and their initial and final value ranges, can be viewed in the
Appendix A (
Figure A4).
In
Figure 5b, the calibrated results can be seen for the outlet gauge. The data are shown on a monthly basis, and clearly outline the contrast between the peak flows of the summer and the low flows of the winter months. By changing the parameters as described above and in
Section 2.3.1 and
Section 2.3.2, the simulated overprediction of peak stream discharge was mitigated.
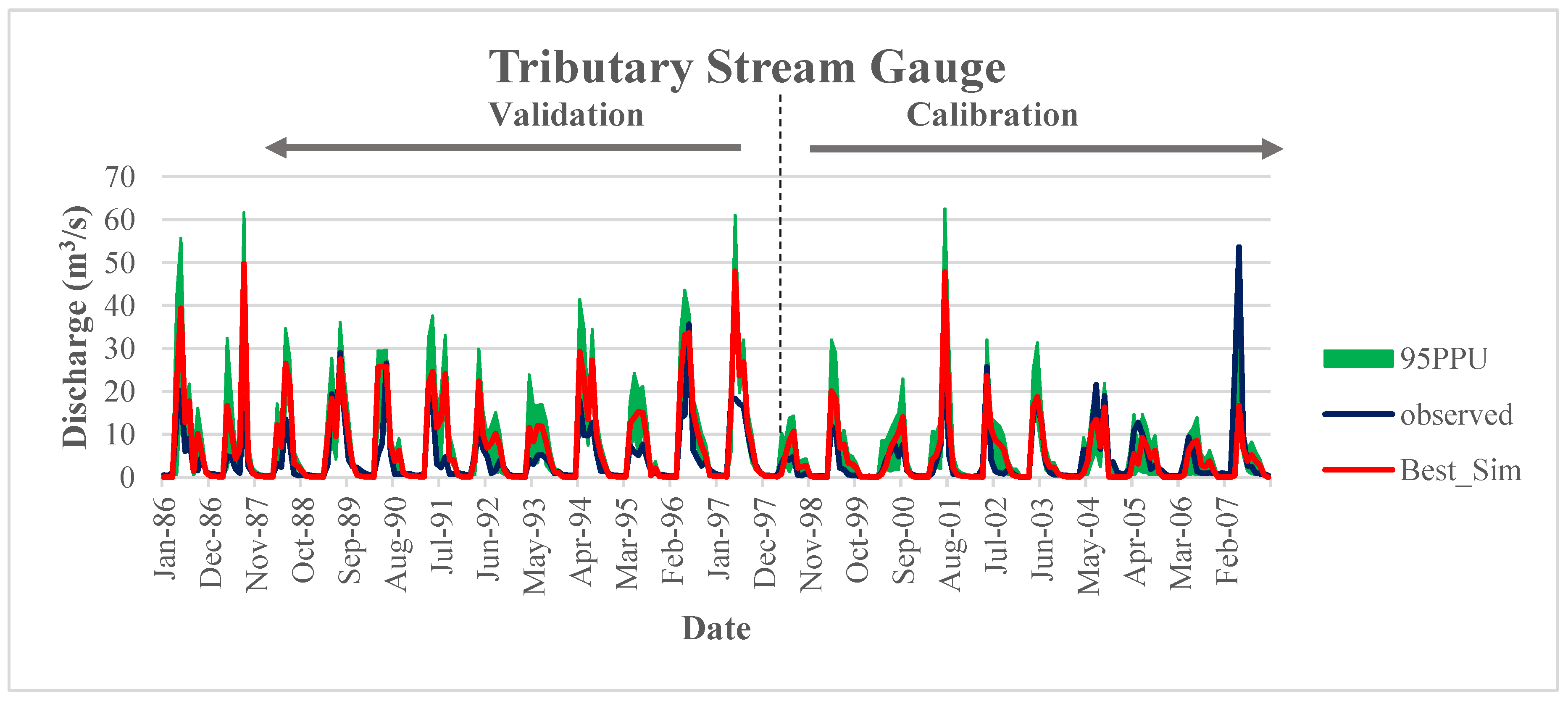
Validation of the model was performed by comparing the simulation to observed data for the 1986–1995 period. Overall, the model follows very similar trends, with the peak flows of some years being slightly overpredicted, and the low flows of the winter months falling to zero for most simulation years. Apart from not being the primary focus of calibration, the discrepancies between the simulated and observed curves for the validated timespan of the SWAT model may be due to the short period of calibration/validation. In general, model calibration in both the tributary and watershed outlets ensured proper apportioning of precipitation and soil water into surface runoff, actual evapotranspiration, and groundwater recharge. This improved model performance compared to the pre-calibration model (
Table 2,
Figure 5a). Overall, 48% of the observed river flow data were captured by the simulated 95PPU and the average r-factor was about 0.75 at the watershed scale. The final summary statistics for the SWAT calibration and validation process at each stream gauge are given below (
Table 2). The lower performance at the tributary gauge may be due to inadequate quality and quantity of input data, which is not representative at the study’s level of detail. The spatial and temporal quality and quantity of geospatial maps and climate time series are often not able to perform ideally for each individual sub-basin (including upstream tributaries with small drainage areas). This area of uncertainty has been addressed by earlier studies [
3,
44]. Due to the focus on applying new scenarios to a coupled SWAT–MODFLOW model, the summary statistics below were taken to be satisfactory for the purpose of coupling with the MODFLOW model.
3.1.2. MODFLOW
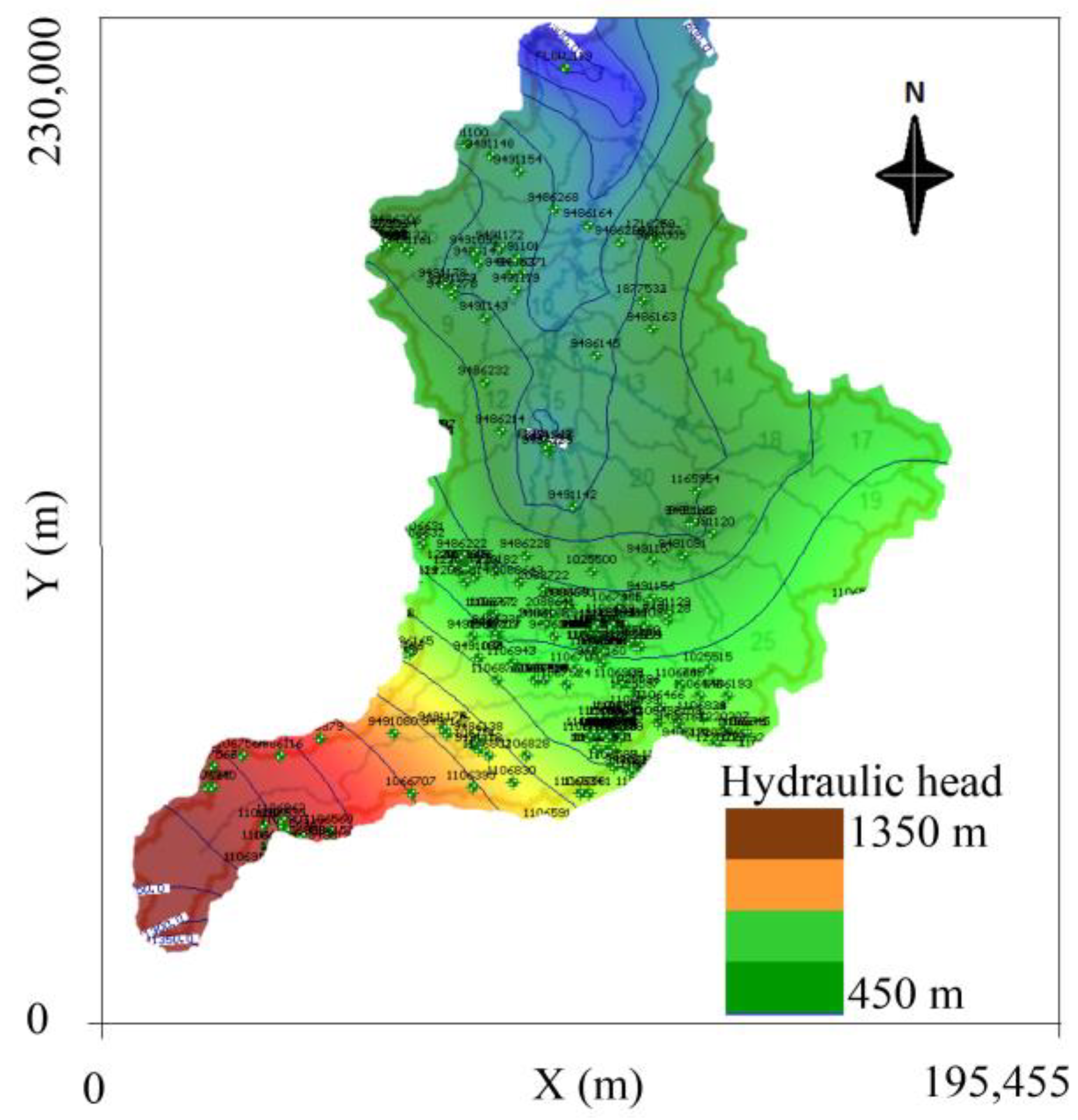
As outlined in
Section 2.3.2, the MODFLOW hydraulic head output was calibrated using 379 points, consisting of two groundwater observation wells, water wells and the two stream gauges used to calibrate the SWAT model. Throughout the calibration process, it was found that the most sensitive parameter of the model was hydraulic conductivity. While maintaining values that were realistic representative [
22], the hydraulic conductivity values were modified to create heterogeneous layers representative of the geological setting.
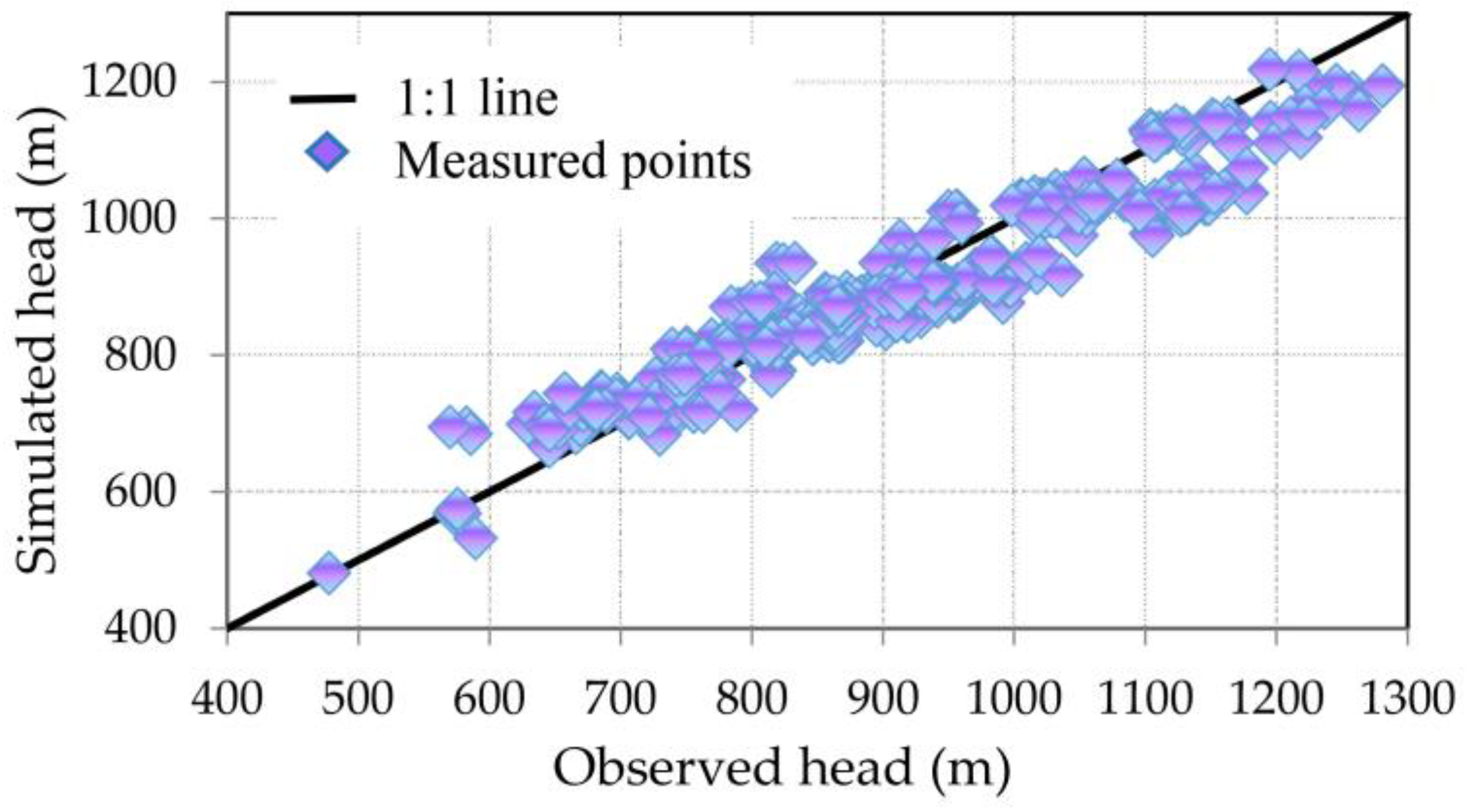
Calibration progress was measured by comparing the simulated hydraulic heads to observed hydraulic heads (
Figure 6), with several commonly used summary statistics for each time step including the normalized RMS, the correlation coefficient, the standard error and the residual mean. For most of these statistics, lower values indicate a more accurate calibration (with the exception of the correlation coefficient, where values closer to 1 indicate a better fit). As more detailed recharge data were added from the SWAT model to the MODFLOW model, the results of the calibration for each time step improved, demonstrating the positive reaction of the model to more variable recharge. The best performance statistics we obtained for the entire region, after many trials of manual parameter change, were 0.96, 6.5, and −21.3 for R
2, NRMS, and Rm, respectively. This proved that, even though these specific recharge values would be replaced by those of the SWAT model, the MODFLOW model performs well under the same conditions as are used in the SWAT model, and the Normalized root mean square (RMS) error remains relatively constant between 6% and 7%. Although the groundwater recharge output values from the SWAT model are used directly in the MODFLOW model, each model will yield slightly different results based on their governing flow mechanisms (HRU-based flow vs. grid-based Finite-Difference flow).
3.2. SWAT–MODFLOW
Using the calibrated component models, a coupled SWAT–MODFLOW model was created using a similar method as in Bailey et al. [
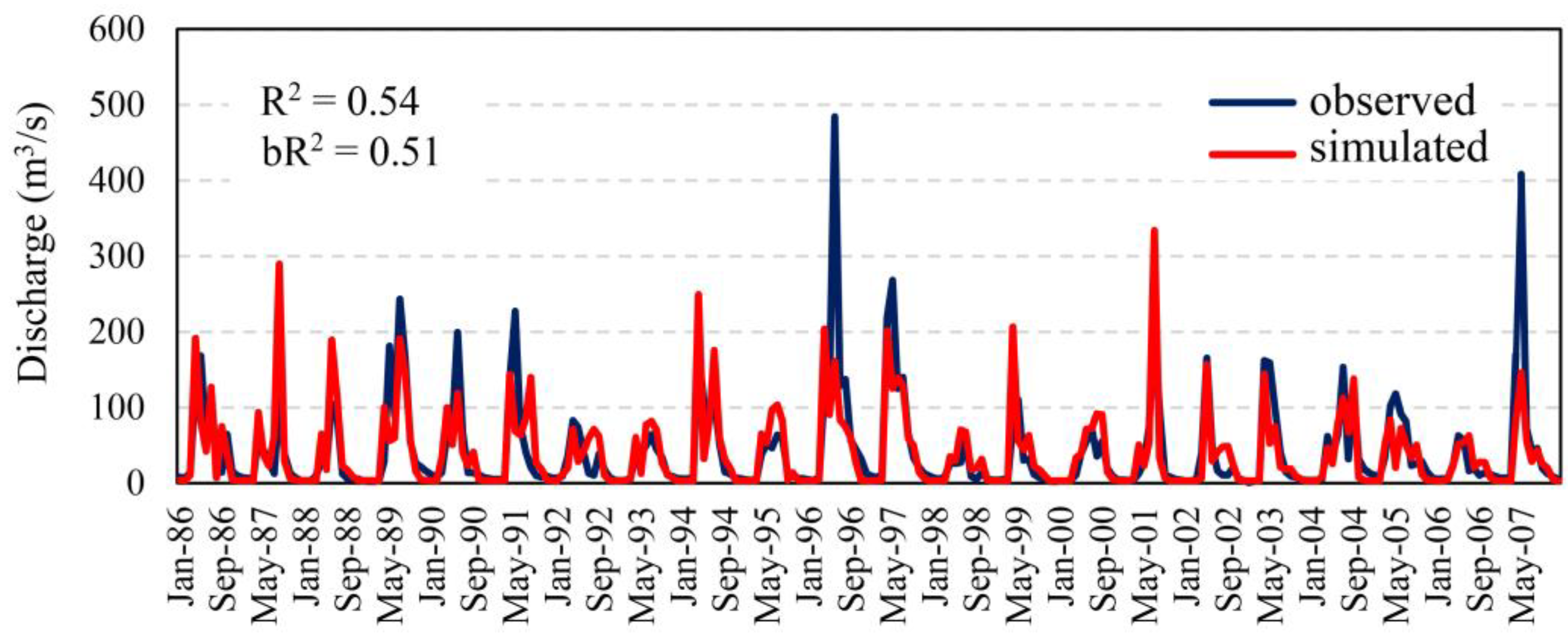
4]. The median SWAT-simulated 95PPU results were used, out of 100 runs from the best parameter ranges, to couple to the MODFLOW model. To ensure accuracy, the river flow results for the SWAT–MODFLOW model were compared to observed data at two hydrometric stations. We found that the calibrated SWAT model consistently under-predicted river discharge in low-flow periods (winter months), likely due to the limited ability of the model to take GW discharge into account, with flux values dropping to 0 m
3/s in most cases (
Figure 5). However, river flux values of above 0 m
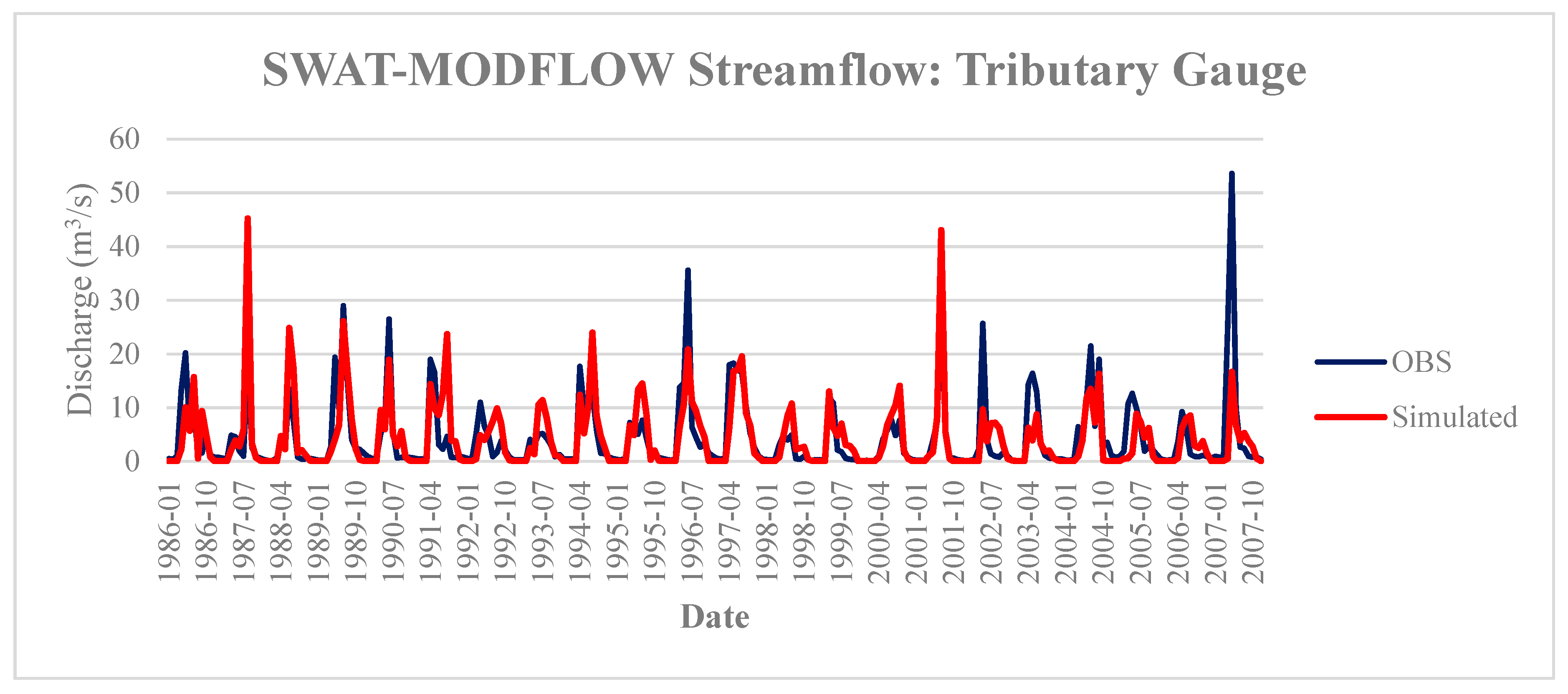
3/s were simulated after use of the SWAT–MODFLOW model, indicating influence from the GW system and necessity of incorporating the MODFLOW component. The simulated streamflow of the coupled model had similar accuracy to that of the SWAT model by itself at both stream gauges (
Figure 7), with the R
2 statistic at the outlet and tributary gauges for this run of SWAT–MODFLOW were 0.54 and 0.484 respectively.
The outputs produced by the coupled model fall within the acceptable range of values for the study area, as the simulated river flow values produced by the coupled SWAT–MODFLOW model faithfully reproduce the results of the calibrated SWAT model (
Figure 6). With regards to the GW–SW exchange flow rates, even MODFLOW grid cells with discharge values of over 50,000 m
3/d convert to m
3/s values of less than 1, which are minor in comparison to the river discharges in the area, particularly at the outlet gauge.
A key output of the SWAT–MODFLOW model is detailed GW–SW interaction for each MODFLOW river cell in the watershed (see
Table A5). This output is yielded at each time step (daily), with flux values recorded with respect to the GW system. As such, positive values indicate recharge into the GW system, and negative values indicate discharge from groundwater to rivers [
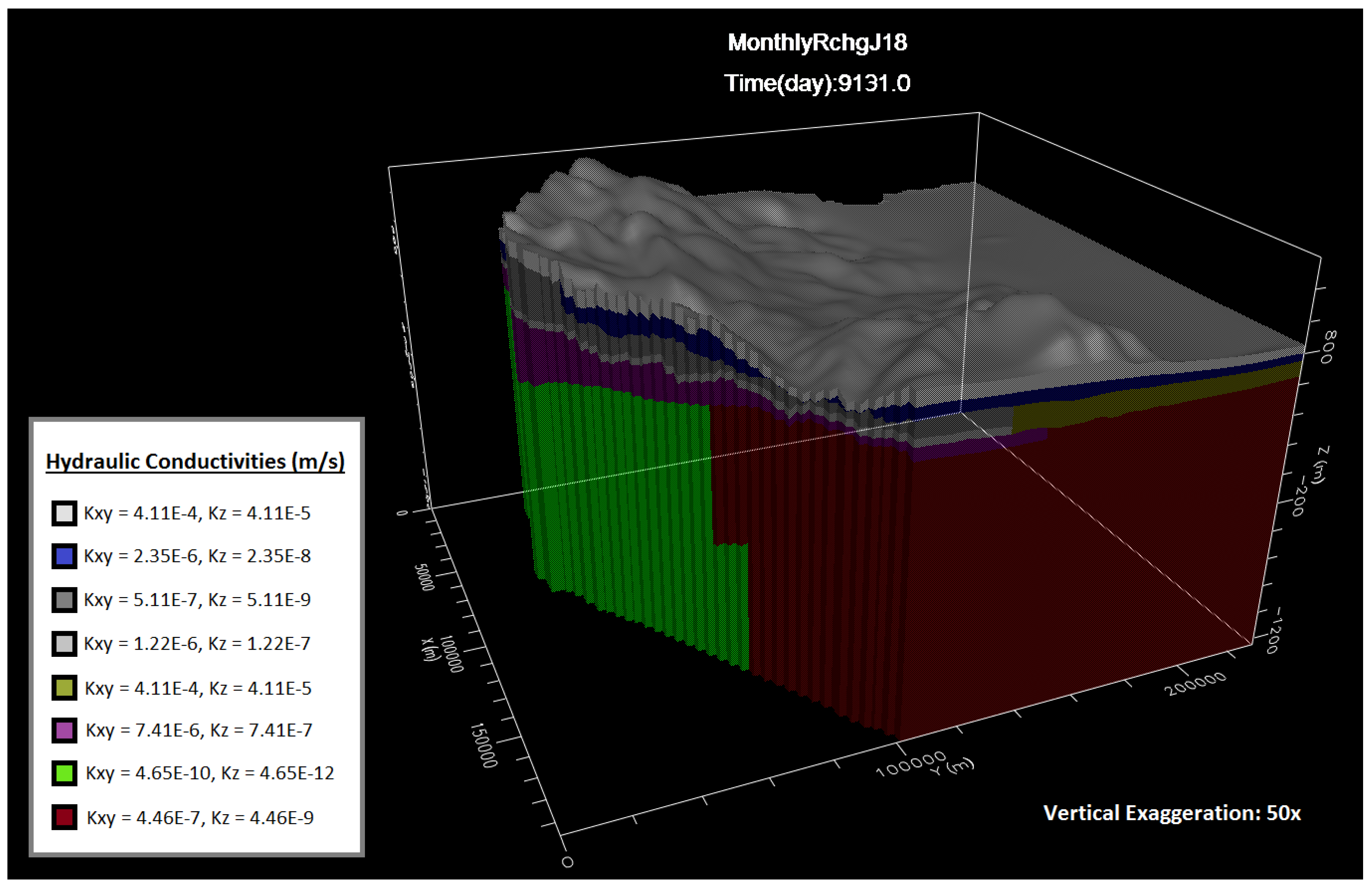
34]. For nearly every river cell in the study area, the magnitude of simulated discharge varied considerably. These variations were based on a multitude of factors, but primarily owe to the hydraulic head found at each of these river cells. The hydraulic conductivity of the aquifers can also affect the simulated discharge, especially in areas of variable conductivity (
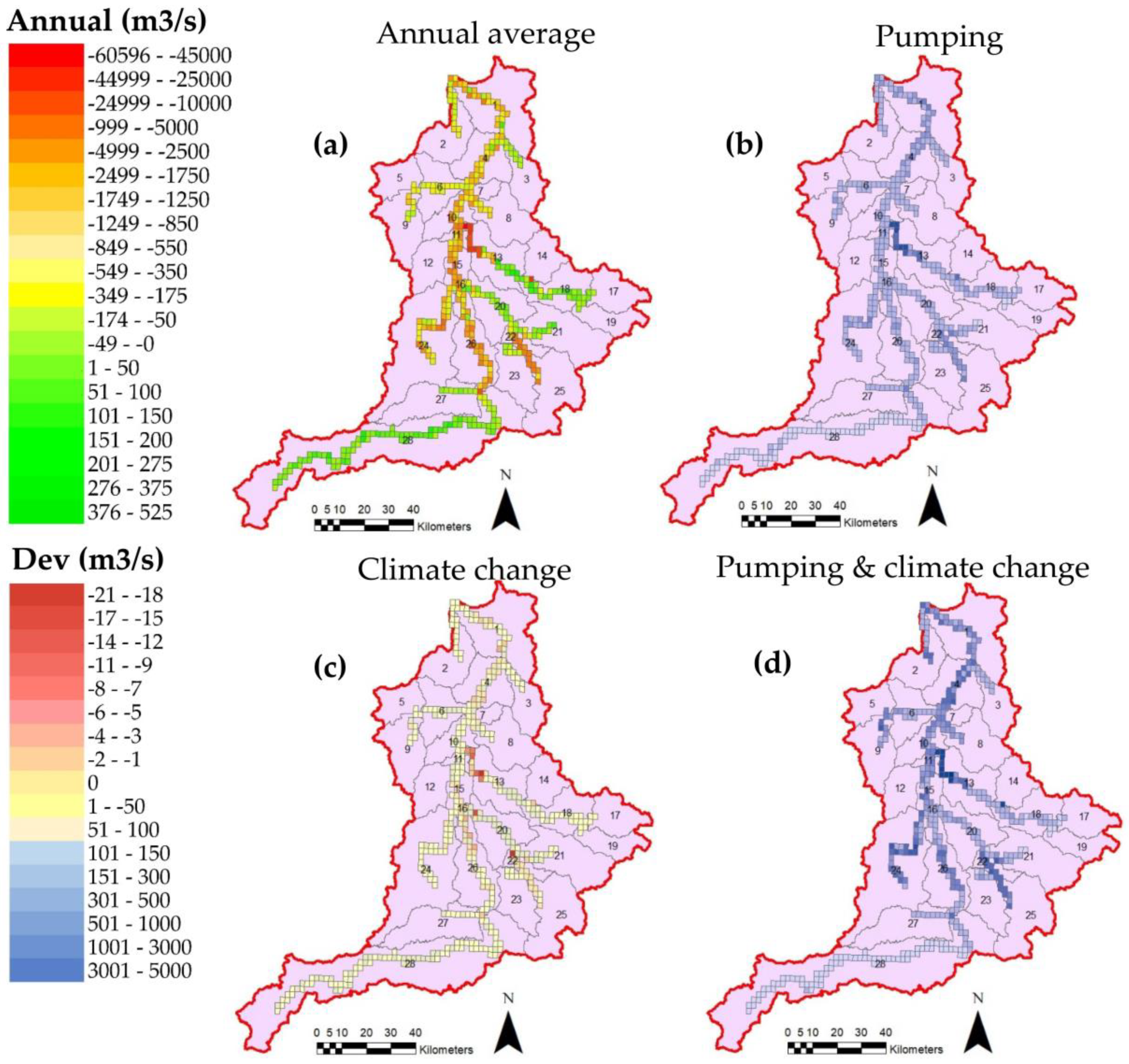
Figure 8).
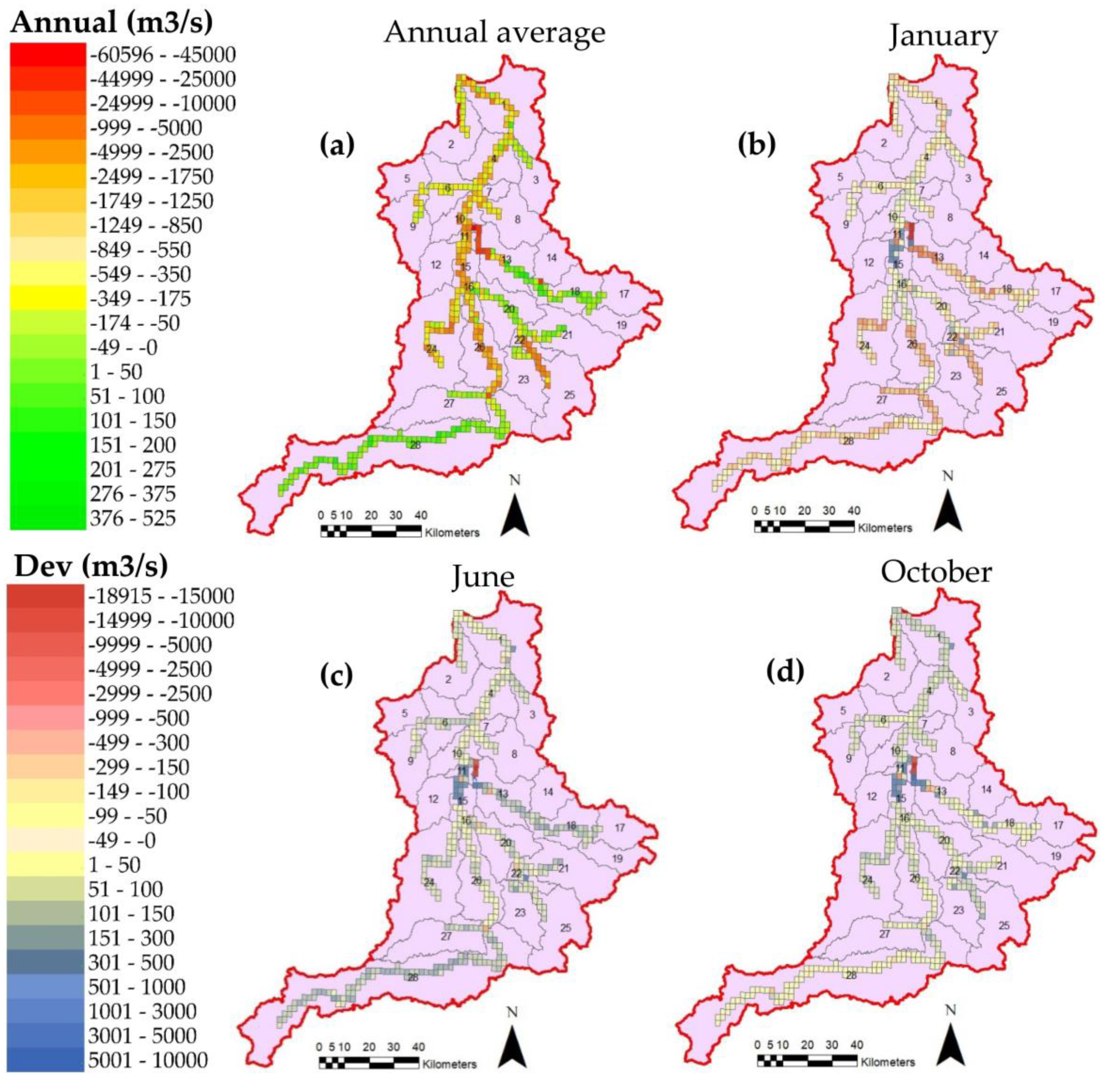
The simulated GW–SW exchange flux values varied spatially, but were primarily negative, indicating discharge from the aquifers. Positive values reached into the hundreds of cubic meters per day (to a maximum of 794 m3/d per grid cell), whereas negative values, in many grid cells and time steps, reached into the tens of thousands of cubic meters per day (to −62,479 m3/d per grid cell). This indicates a significant interaction occurring between the GW and SW systems of this watershed and will prove useful for providing dynamic data to future GW–SW projections using the workflows applied here.
The simulated GW–SW exchange data (
Figure 8) show that overall exchange trends remain fairly constant throughout the simulation period, while the southern (upstream) portion of the river showed the most pronounced fluctuation between the wet and dry months, with lower relative recharge from the river occurring during January, and more river seepage (i.e., less aquifer discharge) taking place in June. In addition, the tributary found within Sub-basin 13 of the study area consistently had the highest discharge rates observed. The reason for these simulated patterns may be due to the regional bedrock strata: more formations pinch out and outcrop to the north (see
Figure 3), so the changes in flow patterns may be partially caused by the hydraulic conductivity of layers that are close to the surface.
3.3. Model Application for Examining GW Pumping and Climate Change Scenarios
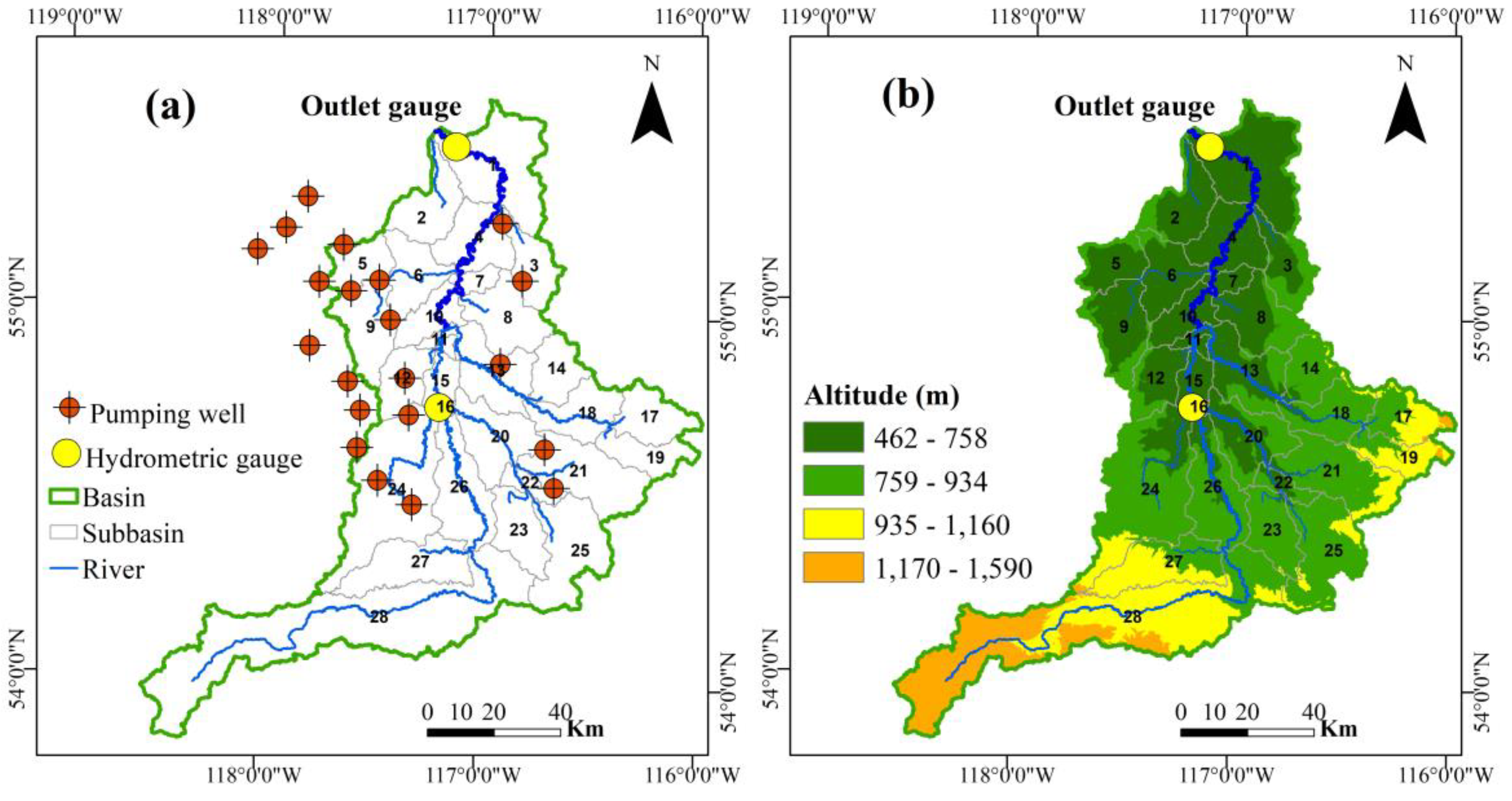
As is discussed in
Section 2.2, 21 wells were included in the SWAT–MODFLOW model (
Figure 2a), with pumping rates of 468 m
3/d. Screens for each well were assigned to one of the two aquifers in the study area: either the Paskapoo or the Wapiti formation, each already containing water wells. The pumping rate was taken from an example water extraction well drilled by an operator in the study area, and was active in the model for half of each year after the 3-year warm-up period, beginning at the start of each simulation year.
As expected, hydraulic heads in the regions with wells decrease, with a difference of up to 5 m of drawdown observed in comparison with the SWAT–MODFLOW model without pumping wells. In addition, the influence of water well pumping had an effect on the observed cell-by-cell GW–SW flow rates. On average, the aquifer discharge rate to the river decreased, with the simulated flow rate changing from −1294 m3/d to −1261 m3/d. This discharge rate decreased in 329 of the 405 river cells, and the maximum observed decrease in discharge was 938 m3/d.
The GW–SW interaction change observed is likely due to the fact that as water is extracted from the subsurface, less of the remaining water is available to provide baseflow to rivers. Depending on the rate and schedule of pumping (including the number of pumping wells), these results show that the effects of pumping are immediately observable, and may affect the discharge rates of associated rivers. However, at the tested pumping rate of 468 m3/d, the discharge decreases in terms of the overall discharge rates (~150 m3/s) of the Little Smoky River are relatively insignificant. This suggests that the bedrock aquifers within the study area could support water well pumping at rates similar to those tested.
A climate change run over the 2010–2034 period was the next scenario to be applied. The coupled SWAT–MODFLOW model was run five separate times, each with a different downscaled GCM dataset (see
Section 2.4). The results of each run were then averaged to yield one harmonized output, with the GW–SW exchange rates shown in
Figure 9. Immediately noticeable in the figure is that the long-term average annual historical results for GW–SW interaction patterns look similar to the results of the climate change scenarios. This is indeed the case, as the overall average historical flow rate was −1294.04 m
3/d, while that of the averaged climate change scenarios was −1294.14 m
3/d (both indicating overall discharge into the river). These results indicated that the effects of climate change on this watershed over the 2010–2034 period are negligible. A possible reason for the lack of influence of the climate change scenario is that the simulation period was quite short in terms of overall climate trends, with little change occurring in the predicted CO
2 concentration over this timespan for the RCP8.5 scenario, as well as all other scenarios (~375 to ~475 ppm; 41). Although the simulation used in this study for scenario analysis was an average, it should be noted that each individual coupled climate change model yielded relatively similar simulation results, again likely owing to the short-term future projection.
As the most complex scenario to be tested in this study, the five coupled climate change scenarios were run again with a MODFLOW model that included the higher pumping rate of 4680 m
3/d per well. The effects of the elevated pumping rates caused a more noticeable change in the GW–SW interaction pattern of the watershed for the 2010–2034 forecasts. The substantial increase in the volume of pumped water left less stored GW in the primary aquifers (i.e., the Paskapoo Fm.), as the overall discharge rates for each river cell are observed to decrease (
Figure 9). This storage trend can also be observed in the MODFLOW model before coupling, with model-wide fluxes from storage spiking to correspond with pumping intervals (from un-pumped totals of under 1 m
3/d up to total maximums of ~1,000,000 m
3/d). While the total average discharge into the rivers was 1294 m
3/d in the initial SWAT–MODFLOW model (1983–2007), this average was reduced to 1174 m
3/d after simulating with the RCP8.5 GCMs and the elevated pumping schedule, with cell-by-cell flowrate differences ranging from under 5 m
3/d to over 3000 m
3/d (discharge decreasing in 320 of 405 river cells). A comparison of the change in aquifer discharge under the tested simulation scenarios, i.e., with pumping and without pumping, indicates that anthropogenic influence can have more immediate effects on the watershed than those of climate change, even at the lower rate of 468 m
3/d.
Although water well pumping simulations were the only anthropogenic influence applied to this study, the change in the GW–SW exchange was measurable on a regional scale. However, the environmental footprint in the study area will only grow when considering additional sectors such as agriculture. The fact that the potential effects of these operations can now be quantified with respect to both GW and SW resources is a key benefit of using a coupled model.
The ability of SWAT–MODFLOW to simulate the hydro(geo)logy of a watershed is fully dependent on the accuracy of its component models. Due to much time being spent on the calibration of both the SW and GW models, the coupled result proves to be robust in terms of its representation of river discharges (
Figure 7). Similar to the Sprague River model built by Bailey et al. [
4], high spatial variation in GW–SW exchange rates can be seen in each SWAT–MODFLOW figure in
Section 3. The ability to gain information on these patterns may prove to be crucial for the informed management of both SW and GW resources in this watershed, as well as any other in which a GW–SW model has been applied. Moreover, when additional stressors such as climate change and pumping simulations are included, it yields more information from a risk management perspective, which can aid operators and regulators to better understand the effects of anthropogenic influence within a watershed.
3.4. Limitations
If each component model is built and calibrated effectively, SWAT–MODFLOW acts as a powerful tool for simulating integrated GW–SW interaction. Although this has been established in the current study and those previously done [
4,
6,
11,
12], the current novelty of the model and dependence on its components give rise to some limitations. The performance of a SWAT–MODFLOW model is governed by the quality and refinement of its components. Therefore, in study areas that may be lacking in either GW- or SW-related inputs or observational data, the ability to produce a faithful model may be limited. In addition, this coupled model encounters a limitation shared with all models: the trade-off between scientific accuracy and computational burden while keeping the study goal in mind. One has the flexibility with SWAT–MODFLOW to discretize both of its component models to any desired refinement [
4,
12]. However, the goals of the study (and lack of access to computational power/data) may limit the ability to produce models of such fine detail. In such cases, the limitations of SWAT and MODFLOW may, in fact, resurface. The coupled model used the best simulation results for SWAT, and the final results of manual calibration for MODFLOW, which were deemed to be satisfactory for the purposes of this study. As these components are subject to non-uniqueness, future studies using multiple calibration methods are an opportunity to address uncertainty in the coupled model. In addition, the SW component of SWAT–MODFLOW, SWAT, is primarily used for regional studies of hydrology due to its efficient HRU-based computational scheme [
3,
4]. Because of this, the ability of SWAT–MODFLOW to simulate short-term site-specific processes may be limited. It is therefore important for an adequate model selection process to occur so that the goals of the study are met.
Study-specific limitations of our SWAT–MODFLOW model include the fact that the component models were calibrated over a relatively brief period with respect to the overall hydro-climate. As the calibrated parameters reflect short-term dynamics over 25 years, large-scale temporal variations may not have been taken into consideration. In light of this, further studies are required to assess the robustness of this model when subjected to a wider range of natural climate variability, including the addition of more climate change scenarios. To more completely assess the various demands within the water–food–energy nexus, water conflicts between sectors will also be a growing area of study. As such, conducting research where the water extraction rates from the petroleum, agriculture and domestic sectors (in addition to the needs of ecosystems) are all considered under various climate change scenarios will increase the ability of decision-makers to quantify the interrelated demands on water as a holistic GW–SW system
4. Conclusions
It is becoming increasingly important to understand the interrelated nature of water resources, and to consider them in a unified manner. This is especially true in areas like Alberta, where significant demands are placed on these resources from multiple sectors. Hydro(geo)logic models can help us to forecast and visualize complex scenarios, as well as to make more informed decisions about the management of these resources. Coupled or integrated hydro(geo)logic models are one of the critical emerging tools for this purpose, as they track the interactions between both the vital components in the hydrologic system.
This study tested the robustness of one such model, SWAT–MODFLOW, in an area of diverse climate and hydrogeology, and included both pumping and climate change to determine the relative effects on the study watershed. Although some fully integrated models may offer a more faithful representation of the site conceptual model [
8], the relatively user-friendly and cost-effective code tested here performed successfully under highly variable hydro(geo)logic and weather conditions while incorporating a deeper, more complex bedrock system than any prior SWAT–MODFLOW model. The model also included additional factors, such as snow influence, that had not been included in previous SWAT–MODFLOW studies. The implementation of this SWAT–MODFLOW model proved that GW has a heavy influence on the hydrology of the Little Smoky River watershed, discharging significant volumes of water into the rivers and tributaries of the study area. This reinforces the importance of examining SW and GW as one system, as the demands placed on one have direct effects on the other.
The modelling workflows developed here can be used to apply new GW–SW interaction scenarios with a multitude of both natural and anthropogenic influences. Use of this model can help scientists track water resources more accurately, and can inform the decisions made by policymakers whose priority is to ensure that this vital resource can remain available to all who need it.