Collapsing Mechanisms of the Typical Cohesive Riverbank along the Ningxia–Inner Mongolia Catchment
Abstract
1. Introduction
2. Materials and Methods
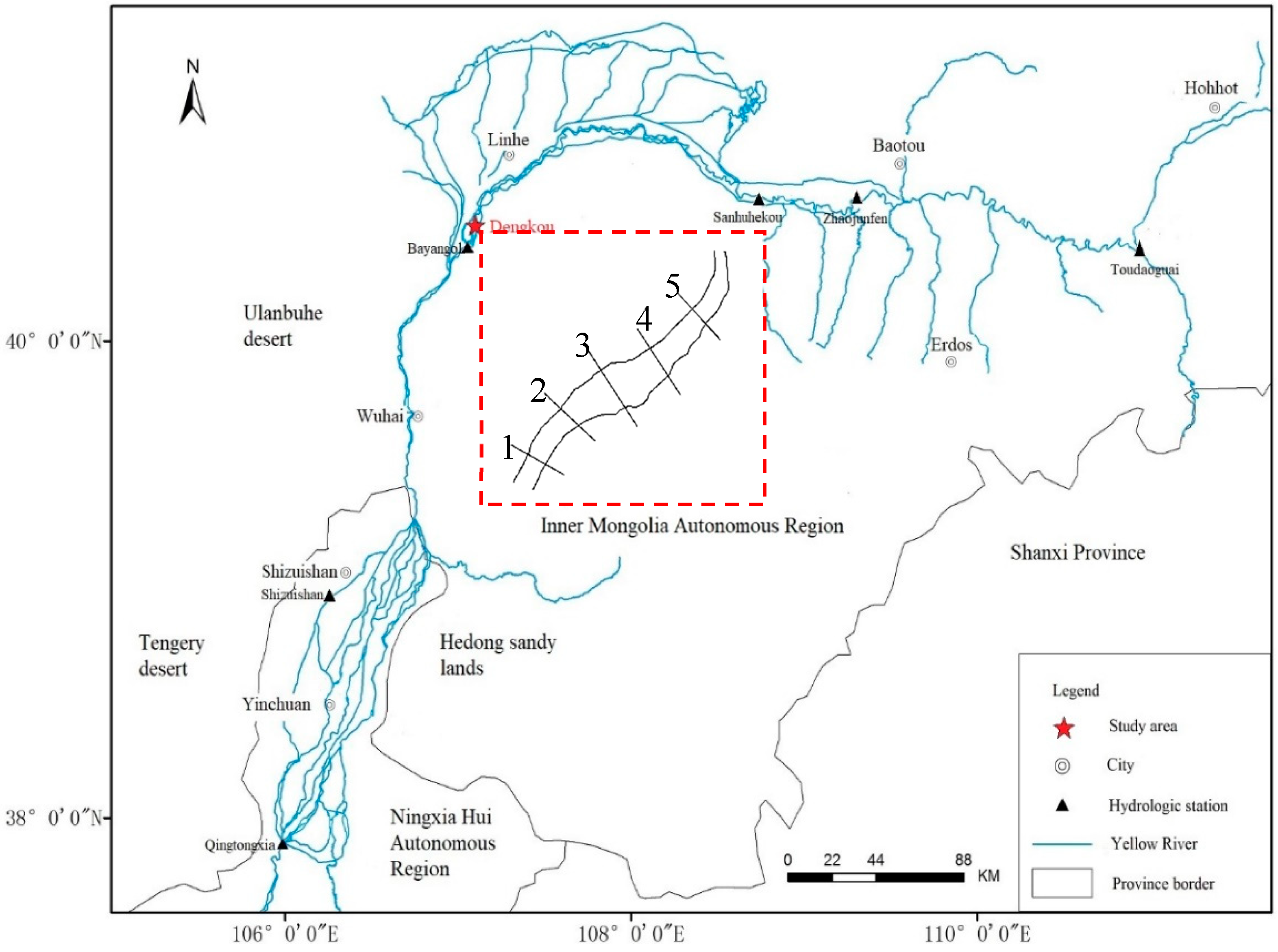
2.1. Case Study
2.2. Field Data
2.2.1. Hydrologic Data
2.2.2. Bank Characteristics of Each Section
2.3. Riverbank Collapse Characterisation
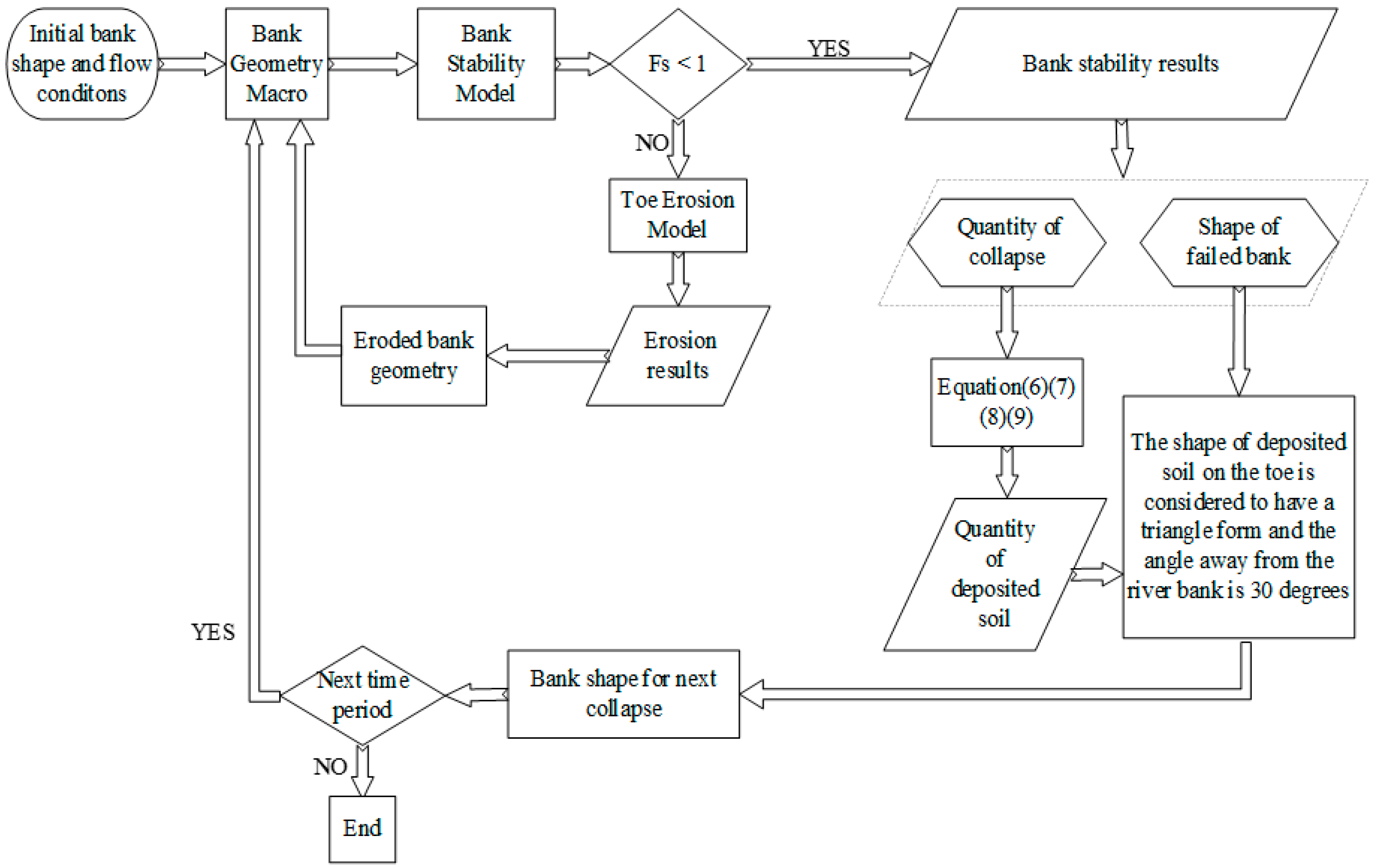
2.4. Numerical Modeling
2.4.1. BSTEM Method
2.4.2. BSTEM Method Modified
3. Results and Discussion
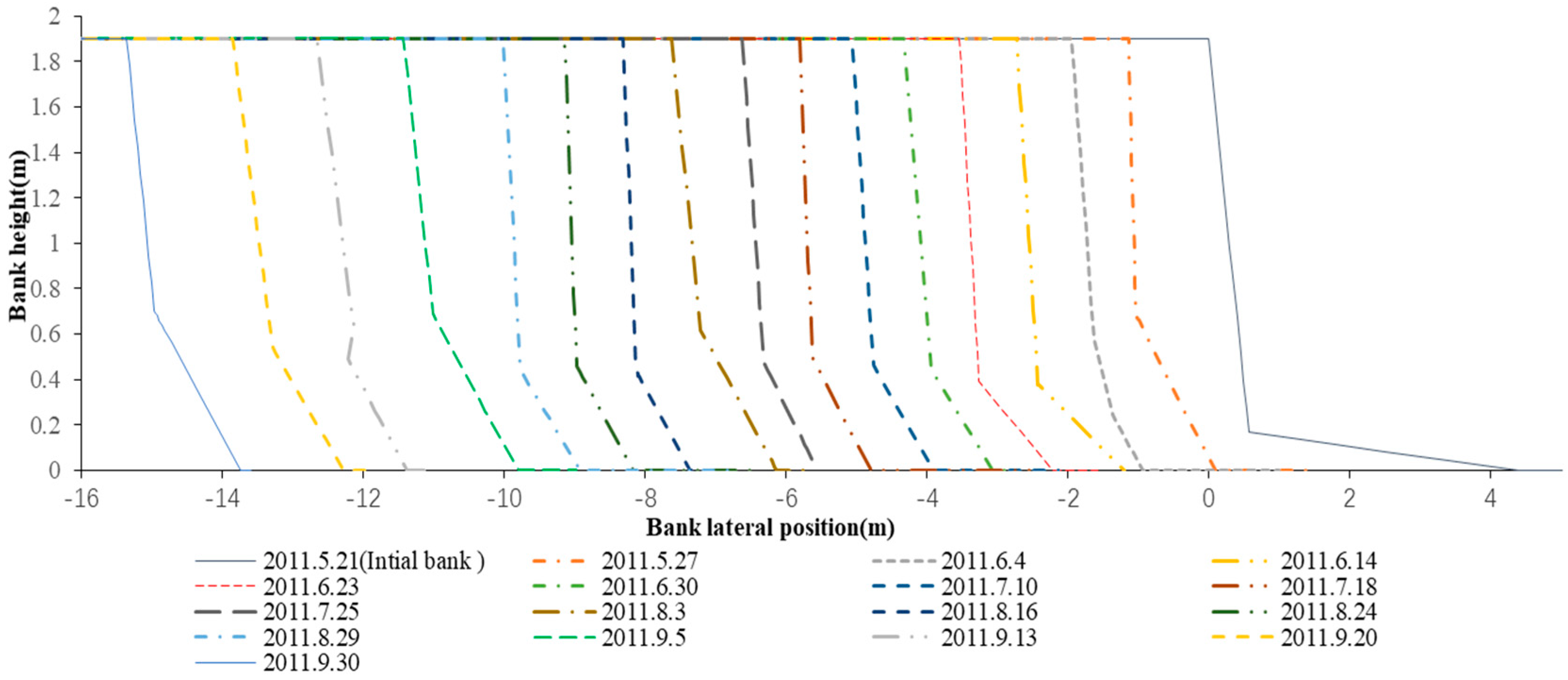
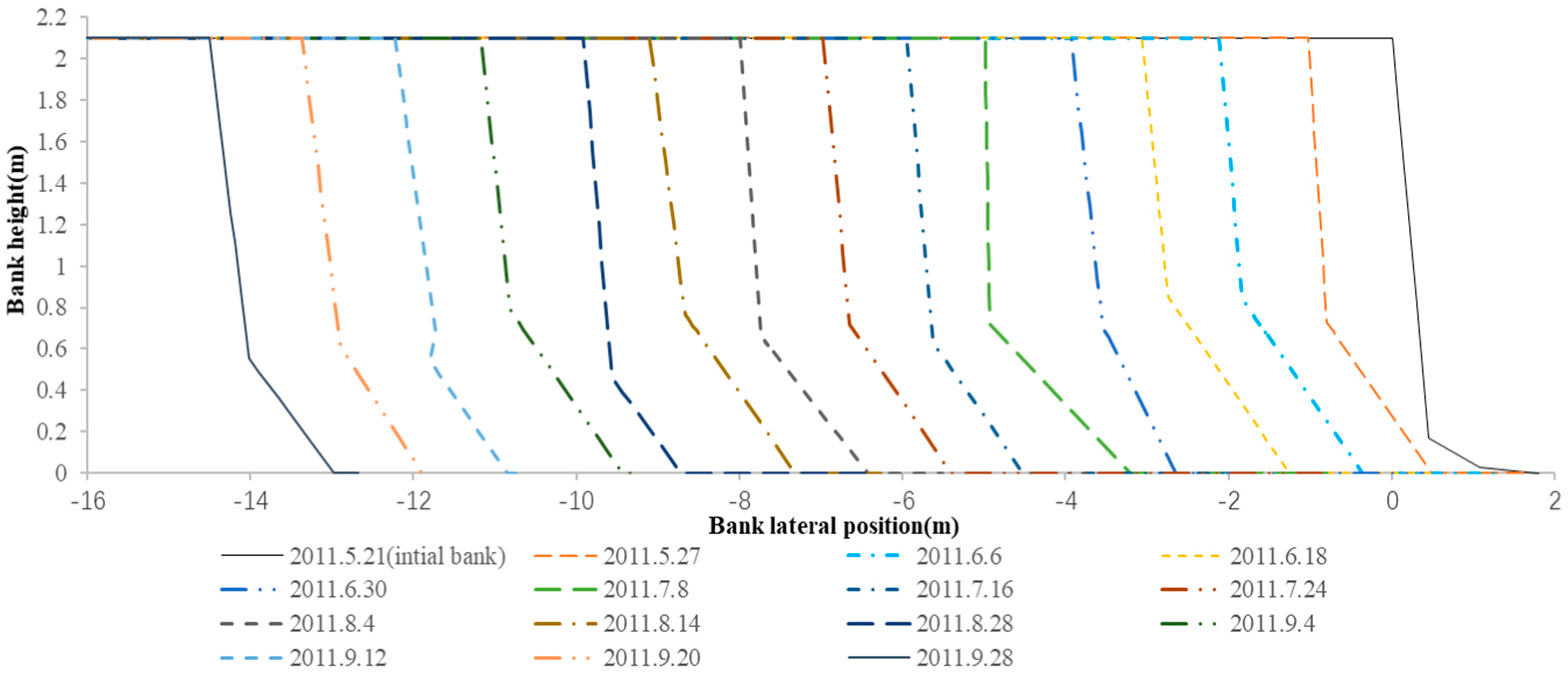
3.1. Collapse Processes Obtained through Numerical Simulations with the Modified BSTEM Model
3.2. Non Applicability of the Traditional BSTEM Method
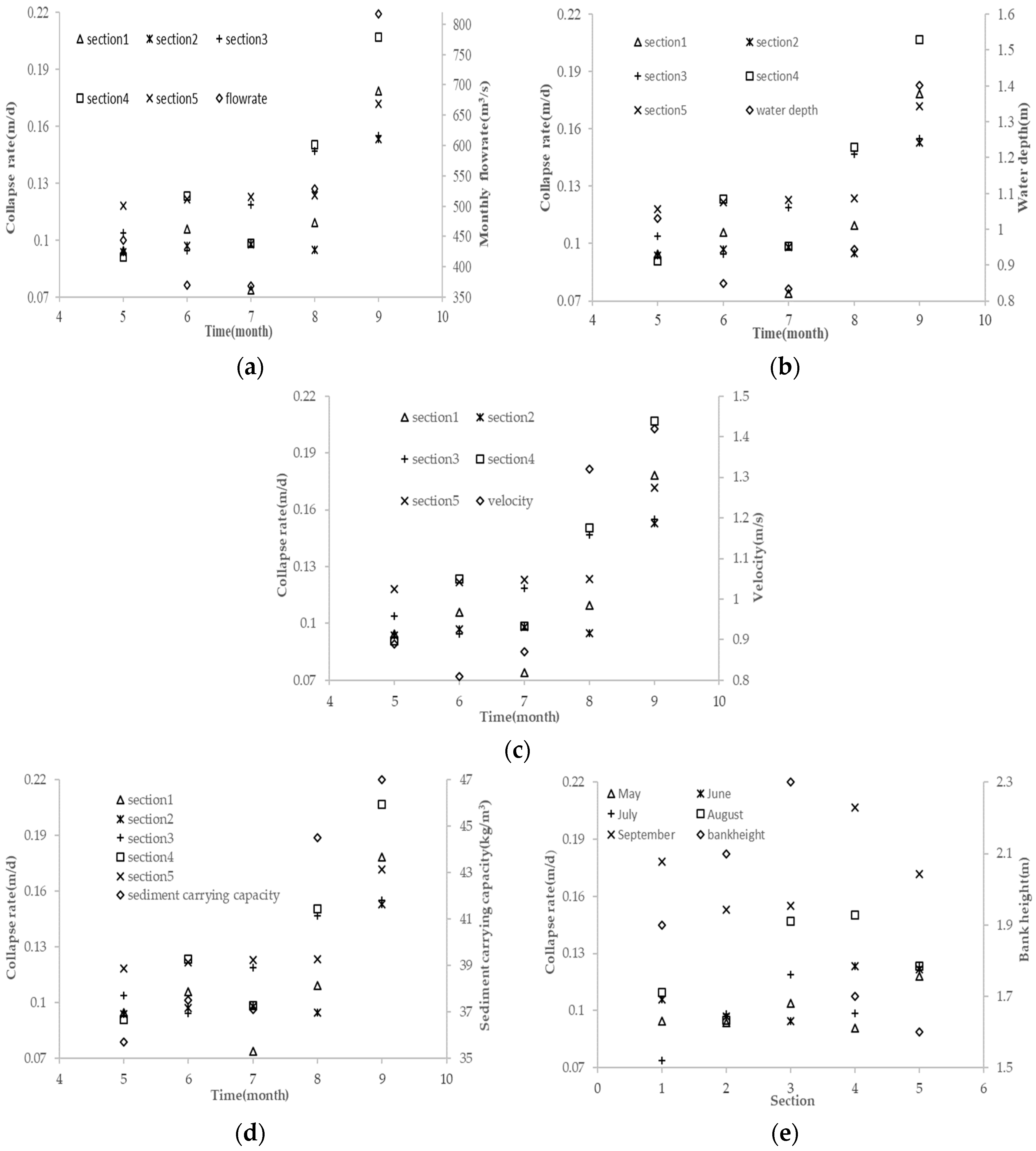
3.3. Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nanson, G.C.; Hickin, E.J. A statistical analysis of bank erosion and channel migration in western Canada. Geol. Soc. Am. Bull. 1986, 97, 497–504. [Google Scholar] [CrossRef]
- Shu, A.P.; Li, F.H.; Liu, H.F.; Duan, G.S.; Zhou, X. Characteristics of particle size distributions for the collapsed riverbank along the desert reach of the upper Yellow River. Int. J. Sediment. Res. 2016, 31, 291–298. [Google Scholar] [CrossRef]
- Yao, Z.Y.; Ta, W.Q.; Jia, X.P.; Xiao, J.H. Bank erosion and accretion along the Ningxia–Inner Mongolia reaches of the Yellow River from 1958 to 2008. Geomorphology 2011, 127, 99–106. [Google Scholar] [CrossRef]
- Hou, S. Analysis on recent channel evolution characteristics on Inner-Mongolia reaches of the Yellow River. Yellow River 1996, 18, 43–44. [Google Scholar]
- Hou, S.; Chang, W.; Wang, P. Characteristics and cause of formation of channel atrophy at Inner Mongolia section of the Yellow River. Yellow River 2007, 29, 25–29. [Google Scholar]
- Wu, J.M.; Wang, R.S.; Yao, J.H. Remote sensing monitoring and study on the change of the Yellow River course in Yinchuan plain sector. Remote Land Resour. 2006, 18, 36–40. [Google Scholar]
- Ta, W.Q.; Xiao, H.L.; Dong, Z.B. Long-term morphodynamic changes of a desert reach of the Yellow River following upstream large reservoirs’ operation. Geomorphology 2008, 7, 249–259. [Google Scholar] [CrossRef]
- Grabowski, R.C.; Droppo, I.G.; Wharton, G. Erodibility of cohesive sediment: The importance of sediment properties. Earth-Sci. Rev. 2011, 105, 101–120. [Google Scholar] [CrossRef]
- Thorne, C.R. Processes and mechanisms of river bank erosion. In Gravel-Bed Rivers; Bathurst, J.C., Thorne, C.R., Eds.; Wiley and Sons: Chichester, UK, 1982; pp. 227–259. [Google Scholar]
- ASCE Task Committee on Hydraulics; Bank Mechanics; Modeling of River Width Adjustment. River width adjustment. I: Processes and mechanisms. J. Hydraul. Eng. 1998, 124, 881–902. [Google Scholar] [CrossRef]
- Shields, A.; Ott, W.P.; Uchelen, J.C.V. Application of Similarity Principles and Turbulence Research to Bed-Load Movement; Soil Conservation Service Cooperative Laboratory California Institute of Technology: Pasadena, CA, USA, 1936. [Google Scholar]
- Buffington, J.M.; Montgomery, D.R. A systematic analysis of eight decades of incipient motion studies, with special reference to gravel-bedded rivers. Water Resour. Res. 1997, 33, 1993–2029. [Google Scholar] [CrossRef]
- Hooke, J.M. An analysis of the processes of riverbank erosion. J. Hydrol. 1979, 42, 39–62. [Google Scholar] [CrossRef]
- Grissinger, E.H. Bank erosion of cohesive materials. In Gravel-Bed Rivers; Thorne, C.R., Bathurst, J.C., Eds.; Wiley and Sons: Chichester, UK, 1982; pp. 273–287. [Google Scholar]
- Simon, A.; Collison, A.J.C. Pore-water pressure effects on the detachment of cohesive streambeds: Seepage forces and matric suction. Earth Surf. Process. Landf. 2001, 26, 1421–1442. [Google Scholar] [CrossRef]
- Julian, J.P.; Torres, R. Hydraulic erosion of cohesive riverbanks. Geomorphology 2006, 76, 193–206. [Google Scholar] [CrossRef]
- Twidale, C.R. Erosion of an alluvial bank at Birdwood, South Australia. Z. Geomorphol. 1964, 8, 189–211. [Google Scholar]
- Lawler, D.M. The measurement of river bank erosion and lateral channel change: A review. Earth Surf. Process. Landf. 1993, 18, 777–821. [Google Scholar] [CrossRef]
- Rinaldi, M.; Casagli, N. Stability of streambanks formed in partially saturated soils and effects of negative pore water pressures: The Sieve River (Italy). Geomorphology 1999, 26, 253–277. [Google Scholar] [CrossRef]
- Singer, M.J.; Munns, D.N. Soils: An Introduction; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1999; pp. 14–46. ISBN 9780131190191. [Google Scholar]
- Couper, P. Effects of silt–clay content on the susceptibility of riverbanks to subaerial erosion. Geomorphology 2003, 56, 95–108. [Google Scholar] [CrossRef]
- Musa, J.J.; Abdulwaheed, S.; Saidu, M. Effect of surface runoff on Nigerian rural roads (a case study of Offa local government area). AU J. Technol. 2010, 13, 242–248. [Google Scholar]
- Wolman, M.G. Factors influencing erosion of a cohesive river bank. Am. J. Sci. 1959, 257, 204–216. [Google Scholar] [CrossRef]
- Knighton, A.D. Riverbank erosion in relation to streamflow conditions, River Bollin-Dean, Cheshire. East Midl. Geogr. 1973, 5, 416–426. [Google Scholar]
- Albidin, R.Z.; Sulaiman, M.S.; Yusoff, N. Erosion risk assessment: A case study of the Langat Riverbank in Malaysia. Int. Soil Water Conserv. Res. 2017, 5, 26–35. [Google Scholar] [CrossRef]
- Yu, M.; Wei, H.; Wu, S. Experimental study on the bank erosion and interaction with near-bank bed evolution due to fluvial hydraulic force. Int. J. Sediment. Res. 2015, 1, 81–89. [Google Scholar] [CrossRef]
- Yang, G.S.; Tuo, W.Q.; Dai, F.N.; Liu, Y.X.; Jing, K.; Li, B.Y.; Zhang, O.Y.; Lu, R.; Hu, L.F.; Tao, Y. Contribution of sand sources to the silting of riverbed in Inner Mongolia section of Huanghe River. J. Desert Res. 2003, 23, 152–159. [Google Scholar]
- Feng, G. The coarse sediment of the Yellow River mainly from wind sand. J. Soil Water Conserv. 1992, 3, 45–47. [Google Scholar]
- Jing, K.; Li, J.; Li, F. Erosion yield from the middle Yellow River basin and tendency prediction. Acta Geogr. Sin. 1998, 53, 107–115. [Google Scholar]
- Jing, K.; Li, J.; Li, F. Study on delimitation of coarse sand area in the middle Yellow River. J. Soil Water Conserv. 1997, 3, 10–15. [Google Scholar]
- Xu, J.H.; Lv, G.C.; Zhang, S.L.; Gan, Z.M. Definition of the Source Area of Centralized Coarse Sediment and Sediment Yield and Transportation in the Middle Yellow River; Yellow River Press: Zhengzhou, China, 2000; pp. 11–36. ISBN 9787806214527. [Google Scholar]
- Bai, T.; Ma, R.; Ma, X.; Ha, Y.; Huang, Q. Threshold of water and sediment in desert wide valley reaches upper the Yellow River. J. Desert Res. 2018, 38, 645–650. [Google Scholar]
- Yu, M.; Shen, K.; Zhang, J.H. Preliminary investigation on bank properties and sediment source in Yellow River Ningmeng River Reach. Int. J. Sediment. Res 2014, 4, 39–42. [Google Scholar]
- Rijn, L.C.V. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications: Delft, The Netherlands, 1993; ISBN 90-800356-2-9. [Google Scholar]
- Catano, Y.; Passoni, G.; Pacheco, R.G.; Toro, F.M.; Naranjo, B.J. Comparison between different numerical solutions for the hydraulic dam-break wave. In Proceedings of the Iche 98-International Conference on Hydro-sciences and Engineering, Berlin, Germany, 31 August–3 September 1998. [Google Scholar]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley: New York, NY, USA, 2001; pp. 566–571. ISBN 9780471987666. [Google Scholar]
- Cao, Z.; Day, R.; Egashira, S. Coupled and decoupled numerical modeling of flow and morphological evolution in alluvial rivers. J. Hydraul. Eng. 2002, 128, 306–321. [Google Scholar] [CrossRef]
- Hudson, J.; Sweby, P.K. A high-resolution scheme for the equations governing 2D bed-load sediment transport. Int. J. Numer. Meth. 2005, 47, 1085–1091. [Google Scholar] [CrossRef]
- Simon, A.; Curini, A.; Darby, S.E.; Langendoen, E.J. Bank and near-bank processes in an incised channel. Geomorphology 2000, 35, 193–217. [Google Scholar] [CrossRef]
- Zong, Q.; Xia, J.; Deng, C.; Xu, Q.X. Modeling of the composite bank failure process using BSTEM. J. Sichuan Univ. 2013, 45, 69–78. [Google Scholar]
- Simon, A.; Pollen-Bankhead, N.; Mahacek, V.; Langendoen, E. Quantifying reductions of mass-failure frequency and sediment loadings from streambanks using toe protection and other means: Lake Tahoe, United States. J. Am. Water Resour. Assoc. 2009, 45, 170–186. [Google Scholar] [CrossRef]
- Lindow, N.; Fox, G.A.; Evans, R.O. Seepage erosion in layered stream bank material. Earth Surf. Process. Landf. 2009, 34, 1693–1701. [Google Scholar] [CrossRef]
- Wilson, G.V.; Perketi, R.K.; Fox, G.A.; Dabney, S.M.; Shields, F.D.; Cullum, R.F. Soil properties controlling seepage erosion contributions to streambank failure. Earth Surf. Process. Landf. 2007, 32, 447–459. [Google Scholar] [CrossRef]
- Cancienne, R.M.; Fox, G.A.; Simon, A. Influence of seepage undercutting on the stability of root-reinforced streambanks. Earth Surf. Process. Landf. 2008, 33, 1769–1786. [Google Scholar] [CrossRef]
- Xiao, C.; Hao, Y.; Liu, F. Analysis of climate change for Dengkou in recent 52 years. J. Arid Land Resour. Environ. 2008, 22, 90–93. [Google Scholar]
- Kolerski, T.; Shen, H.T. Possible effects of the 1984 St Clair River Ice jam on bed changes. Can. J. Civ. Eng. 2015, 42, 696–703. [Google Scholar] [CrossRef]
- Kolerski, T.; Shen, H.T. St. Clair River ice jam dynamics and possible effect on bed changes. In Proceedings of the 20th IAHR International Symposium on Ice, Lahti, Finland, 14–18 June 2010. [Google Scholar]
- Thorne, C.R.; Tovey, N.K. Stability of composite riverbanks. Earth Surf. Process. Landf. 1981, 6, 469–484. [Google Scholar] [CrossRef]
- Shu, A.P.; Gao, J.; Li, F.H. Lateral variation properties in river channels due to bank failure along the desert valley reach of upper Yellow River. Adv. Water Sci. 2014, 25, 77–82. [Google Scholar]
- Osman, A.M.; Thorne, C.R. Riverbank stability analysis. I: Theory. J. Hydraul. Eng. 1988, 114, 134–150. [Google Scholar] [CrossRef]
- Darby, S.E.; Thorne, C.R. Numerical simulation of widening and bed deformation of straight sand-bed rivers. I: Model development. J. Hydraul. Eng. 1996, 122, 184–193. [Google Scholar] [CrossRef]
- Midgley, T.L.; Fox, G.A.; Heeren, D.M. Evaluation of the bank stability and toe erosion model (BSTEM) for predicting lateral retreat on composite streambanks. Geomorphology 2012, 145, 107–114. [Google Scholar] [CrossRef]
- Garcia, M.H. Sedimentation Engineering; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 21–163. ISBN 9780784408148. [Google Scholar]
- Rinaldi, M.; Mengoni, B.; Luppi, L.; Darby, S.E.; Mosselman, E. Numerical simulation of hydrodynamics and bank erosion in a river bend. Water Resour. Res. 2008, 44, 303–312. [Google Scholar] [CrossRef]
- Hanson, G.J. Surface erodibility of earthen channels at high stresses. Part II—Developing an in-situ testing device. Trans. ASAE 1990, 33, 127–131. [Google Scholar] [CrossRef]
- Amiritokaldany, E.; Darby, S.E.; Tosswell, P. Bank stability for predicting reach-scale land loss and sediment yield. J. Am. Water Resour. Assoc. 2003, 39, 897–910. [Google Scholar] [CrossRef]
- Langendoen, E.J.; Simon, A. Modeling the evolution of incised streams. II: Streambank erosion. J. Hydraul. Eng. 2008, 134, 905–915. [Google Scholar] [CrossRef]
- Samadi, A.; Amiritokaldany, E.; Darby, S.E. Identifying the effects of parameter uncertainty on the reliability of riverbank stability modelling. Geomorphology 2009, 106, 219–230. [Google Scholar] [CrossRef]
- Taghavi, M.; Dovoudi, M.H.; Amiritokaldany, E.; Darby, S.E. An analytical method to estimate failure plane angle and tension crack depth for use in riverbank stability analyses. Geomorphology 2010, 123, 74–83. [Google Scholar] [CrossRef]
- Dodaro, G.; Tafarojnoruz, A.; Stefanucci, F.; Adduce, C.; Calomino, F.; Gaudio, R.; Sciortino, G. An experimental and numerical study on the spatial and temporal evolution of a scour hole downstream of a rigid bed. In Proceedings of the International Conference on Fluvial Hydraulics, Lausanne, Switzerland, 3–5 September 2014; pp. 1415–1422. [Google Scholar]
- Dodaro, G.; Tafarojnoruz, A.; Sciortino, G.; Adduce, C.; Calomion, F.; Gaudio, R. Modified Einstein sediment transport method to simulate the local scour evolution downstream of a rigid bed. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Wang, X.K.; Shao, X.J.; Li, D.X. Fundamental River Mechanics; China Water and Power Press: Beijing, China, 2002; pp. 54–98. ISBN 7-5084-1093-9. [Google Scholar]
- Gaudio, R.; Tafarojnoruz, A.; Calomino, F. Combined flow-altering countermeasures against bridge pier scour. J. Hydraul. Res. 2012, 50, 35–43. [Google Scholar] [CrossRef]
- Tafarojnoruz, A.; Gaudio, R.; Calomino, F. Bridge pier scour mitigation under steady and unsteady flow conditions. Acta Geophys. 2012, 60, 1076–1097. [Google Scholar] [CrossRef]
- Tang, C.B. Laws of sediment incipient motion. J. Hydraul. Eng. 1963, 2, 3–14. [Google Scholar]



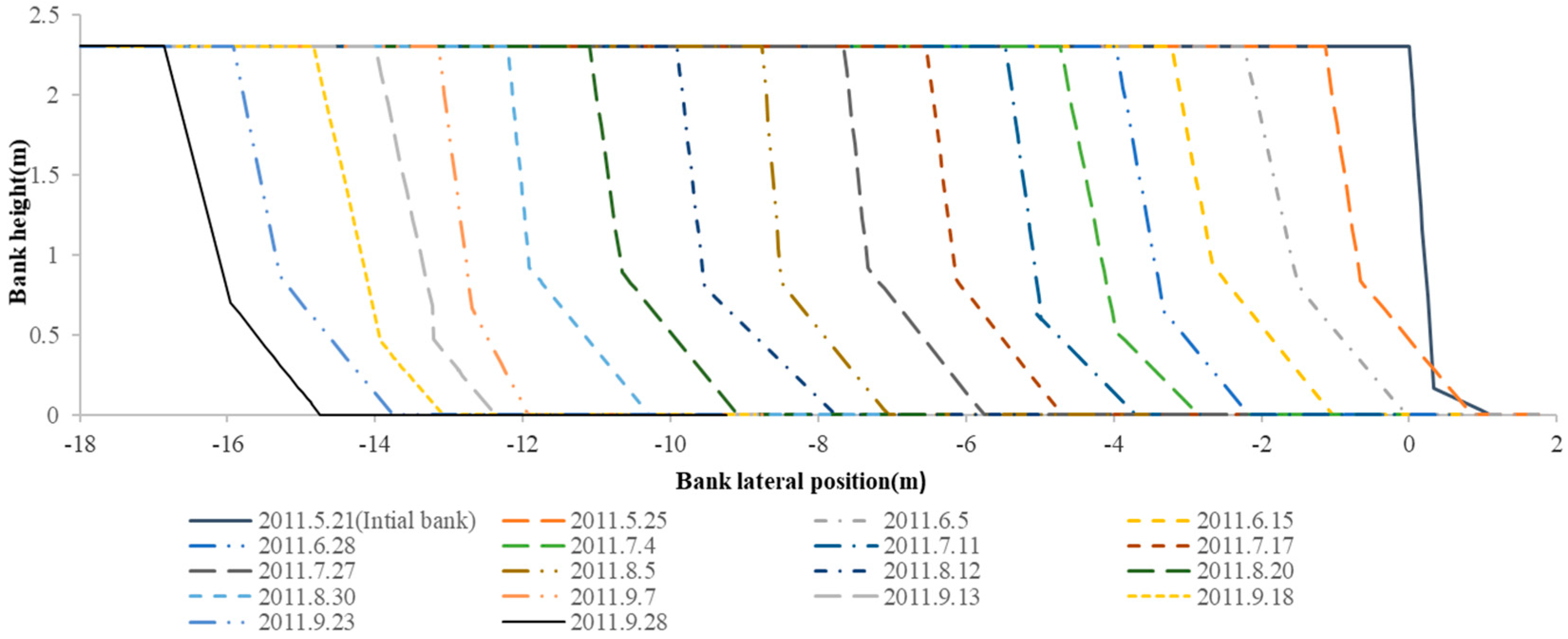
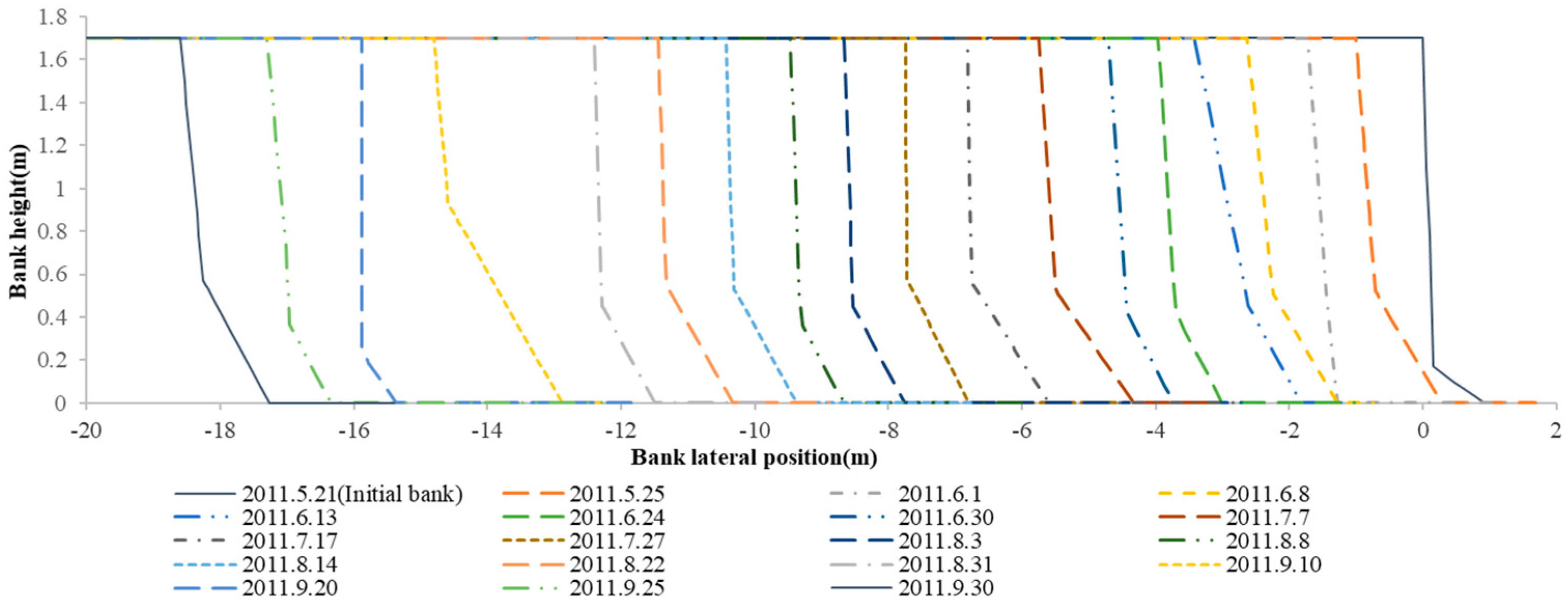
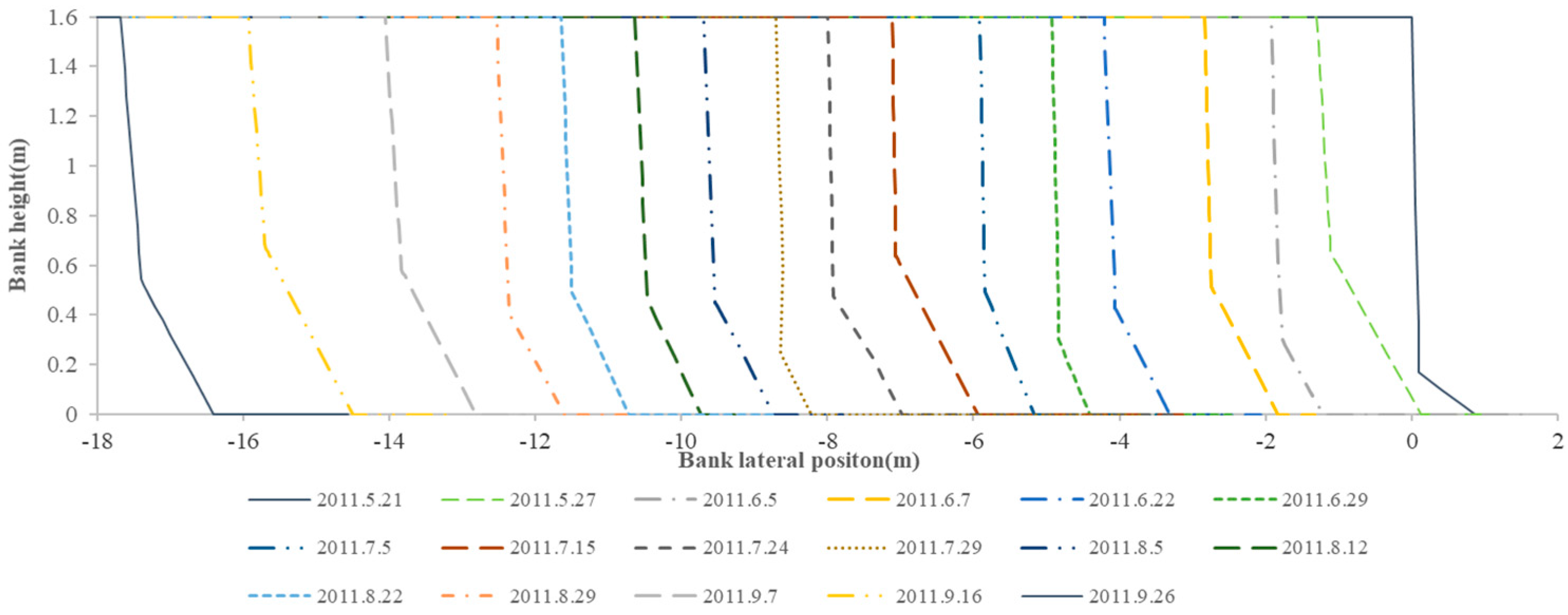
| Bank Shape | Soil Composition | Mechanical Properties | |
|---|---|---|---|
| Parameter monitored | Bank height (m) | Median diameter (μm) | Critical shear stress (kPa) |
| Bank gradient (°) | Unit weight (g/cm3) | Internal friction angle (°) | |
| Length of bank toe (m) | Moisture content (%) | / | |
| Equipment utilized for the monitoring | Gradometer (±1°), Tape (±1 cm) | Scale, Laser particle sizer (±5 μm) | Direct shear apparatus |
| Time Scale | Section 1 | Section 2 | Section 3 | Section 4 | Section 5 |
|---|---|---|---|---|---|
| 21 May–13 July | 4.60 | 4.50 | 5.80 | 5.30 | 5.60 |
| 13 July–9 August | 3.05 | 2.80 | 3.10 | 3.95 | 3.60 |
| 9 August–23 September | 5.25 | 5.08 | 6.80 | 6.20 | 6.50 |
| 23 September–30 September | 1.68 | 1.45 | 1.10 | 2.40 | 1.45 |
| Total | 14.58 | 13.81 | 16.80 | 17.85 | 17.15 |
| Month | Flow (m3/s) | Velocity (m/s) | Water Depth (m) | Sediment Concentration (kg/m3) | Sediment Transport Rate (kg/s) |
|---|---|---|---|---|---|
| 1 | 494.23 | 0.68 | 3.09 | 0.21 | 102 |
| 2 | 568.11 | 0.74 | 3.02 | 0.22 | 123 |
| 3 | 495.58 | 1.06 | 1.94 | 1.23 | 615 |
| 4 | 684.77 | 1.08 | 1.34 | 2.16 | 1480 |
| 5 | 444.00 | 0.89 | 1.03 | 0.64 | 283 |
| 6 | 369.60 | 0.81 | 0.85 | 0.59 | 217 |
| 7 | 368.35 | 0.87 | 0.83 | 0.77 | 283 |
| 8 | 528.00 | 1.32 | 0.94 | 3.20 | 1690 |
| 9 | 817.30 | 1.42 | 1.40 | 1.95 | 1590 |
| 10 | 612.48 | 1.37 | 0.99 | 1.27 | 779 |
| 11 | 495.90 | 1.18 | 0.62 | 1.17 | 580 |
| 12 | 592.52 | 0.95 | 2.00 | 2.58 | 1530 |
| Section | Bank Height (m) | Bank Gradient (°) | Toe Length (m) | Median Diameter (μm) | Wet Unit Weight (g/cm3) | Critical Shear Stress (kPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|---|---|
| 1 | 1.9 | 82 | 0.85 | 33 | 1.55 | 7.2 | 32 |
| 2 | 2.1 | 77 | 0.9 | 35 | 1.48 | 7.5 | 31 |
| 3 | 2.3 | 81 | 0.95 | 32 | 1.50 | 7.3 | 32 |
| 4 | 1.7 | 84 | 0.8 | 37 | 1.46 | 7.5 | 30 |
| 5 | 1.6 | 86 | 0.75 | 30 | 1.52 | 7.2 | 31 |
| Time Scale | Calculating Collapse Distance (m) | Monitoring Collapse Distance (m) | Error (%) |
|---|---|---|---|
| 21 May–13 July | 4.96 | 4.60 | 7.83 |
| 14 July–9 August | 3.24 | 3.05 | 6.23 |
| 10 August–23 September | 5.55 | 5.25 | 5.71 |
| 23 September–30 September | 1.50 | 1.68 | 10.71 |
| Total collapse | 15.25 | 14.58 | 4.60 |
| Time Scale | Calculating Collapse Distance (m) | Monitoring Collapse Distance (m) | Error (%) |
|---|---|---|---|
| 21 May–13 July | 4.99 | 4.50 | 10.89 |
| 14 July–9 August | 3.01 | 2.80 | 7.5 |
| 10 August–23 September | 5.38 | 5.08 | 5.91 |
| 23 September–30 September | 1.13 | 1.45 | 22.06 |
| Total collapse | 14.51 | 13.81 | 5.07 |
| Time Scale | Calculating Collapse Distance (m) | Monitoring Collapse Distance (m) | Error (%) |
|---|---|---|---|
| 21 May–13 July | 5.46 | 5.80 | 5.9 |
| 14 July–9 August | 3.30 | 3.10 | 6.5 |
| 10 August–23 September | 7.15 | 6.80 | 5.1 |
| 23 September–30 September | 0.94 | 1.10 | 14.5 |
| Total collapse | 16.85 | 16.80 | 0.3 |
| Time Scale | Calculating Collapse Distance (m) | Monitoring Collapse Distance (m) | Error (%) |
|---|---|---|---|
| 21 May–13 July | 5.75 | 5.3 | 8.5 |
| 14 July–9 August | 3.72 | 3.95 | 5.8 |
| 10 August–23 September | 6.41 | 6.2 | 3.4 |
| 23 September–30 September | 2.73 | 2.4 | 13.8 |
| Total collapse | 18.61 | 17.85 | 4.3 |
| Time Scale | Calculating Collapse Distance (m) | Monitoring Collapse Distance (m) | Error (%) |
|---|---|---|---|
| 21 May–13 July | 5.93 | 5.6 | 5.9 |
| 14 July–9 August | 3.82 | 3.6 | 6.1 |
| 10 August–23 September | 6.24 | 6.5 | 4 |
| 23 September–30 September | 1.75 | 1.45 | 20.7 |
| Total collapse | 17.74 | 17.15 | 3.4 |
| Month | Section 1 | Section 2 | Section 3 | Section 4 | Section 5 |
|---|---|---|---|---|---|
| 5 | 0.095 | 0.094 | 0.104 | 0.091 | 0.118 |
| 6 | 0.106 | 0.097 | 0.094 | 0.123 | 0.122 |
| 7 | 0.074 | 0.098 | 0.119 | 0.098 | 0.123 |
| 8 | 0.109 | 0.095 | 0.147 | 0.150 | 0.124 |
| 9 | 0.178 | 0.153 | 0.155 | 0.207 | 0.172 |
| Time Scale | BSTEM Method Results (m) | Monitoring Collapse Distance (m) | Error (%) |
| 21 May–13 July | 7.80 | 4.60 | 69.6 |
| 14 July–9 August | 7.18 | 3.05 | 135.4 |
| 10 August–23 September | 9.98 | 5.25 | 89.3 |
| 23 September–30 September | 2.08 | 1.68 | 23.8 |
| Total collapse | 27 | 14.58 | 85.2 |
| Time Scale | BSTEM Method Results (m) | Monitoring Collapse Distance(m) | Error (%) |
| 21 May–13 July | 7.70 | 4.50 | 71.1 |
| 14 July–9 August | 5.94 | 2.80 | 112.1 |
| 10 August–23 September | 8.48 | 5.08 | 67.2 |
| 23 September–30 September | 1.73 | 1.45 | 19.1 |
| Total collapse | 23.84 | 13.81 | 72.6 |
| Time Scale | BSTEM Method Results (m) | Monitoring Collapse Distance (m) | Error (%) |
| 21 May–13 July | 9.63 | 5.80 | 66.1 |
| 14 July–9 August | 6.85 | 3.10 | 121.1 |
| 10 August–23 September | 11.83 | 6.80 | 73.9 |
| 23 September–30 September | 1.36 | 1.10 | 24.1 |
| Total collapse | 29.68 | 16.80 | 76.6 |
| Time Scale | BSTEM Method Results(m) | Monitoring Collapse Distance (m) | Error (%) |
| 21 May–13 July | 8.9 | 5.3 | 68.1 |
| 14 July–9 August | 9.13 | 3.95 | 131.1 |
| 10 August–23 September | 11.35 | 6.2 | 83.2 |
| 23 September–30 September | 2.9 | 2.4 | 21 |
| Total collapse | 32.28 | 17.85 | 80.8 |
| Time Scale | BSTEM Method Results (m) | Monitoring Collapse Distance (m) | Error (%) |
| 21 May–13 July | 9.63 | 5.6 | 71.9 |
| 14 July–9 August | 7.85 | 3.6 | 118.1 |
| 10 August–23 September | 12.02 | 6.5 | 85 |
| 23 September–30 September | 1.77 | 1.45 | 22 |
| Total collapse | 31.27 | 17.15 | 82.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, G.; Shu, A.; Rubinato, M.; Wang, S.; Zhu, F. Collapsing Mechanisms of the Typical Cohesive Riverbank along the Ningxia–Inner Mongolia Catchment. Water 2018, 10, 1272. https://doi.org/10.3390/w10091272
Duan G, Shu A, Rubinato M, Wang S, Zhu F. Collapsing Mechanisms of the Typical Cohesive Riverbank along the Ningxia–Inner Mongolia Catchment. Water. 2018; 10(9):1272. https://doi.org/10.3390/w10091272
Chicago/Turabian StyleDuan, Guosheng, Anping Shu, Matteo Rubinato, Shu Wang, and Fuyang Zhu. 2018. "Collapsing Mechanisms of the Typical Cohesive Riverbank along the Ningxia–Inner Mongolia Catchment" Water 10, no. 9: 1272. https://doi.org/10.3390/w10091272
APA StyleDuan, G., Shu, A., Rubinato, M., Wang, S., & Zhu, F. (2018). Collapsing Mechanisms of the Typical Cohesive Riverbank along the Ningxia–Inner Mongolia Catchment. Water, 10(9), 1272. https://doi.org/10.3390/w10091272






