Evaporation from (Blue-)Green Roofs: Assessing the Benefits of a Storage and Capillary Irrigation System Based on Measurements and Modeling
Abstract
1. Introduction
2. Materials and Methods
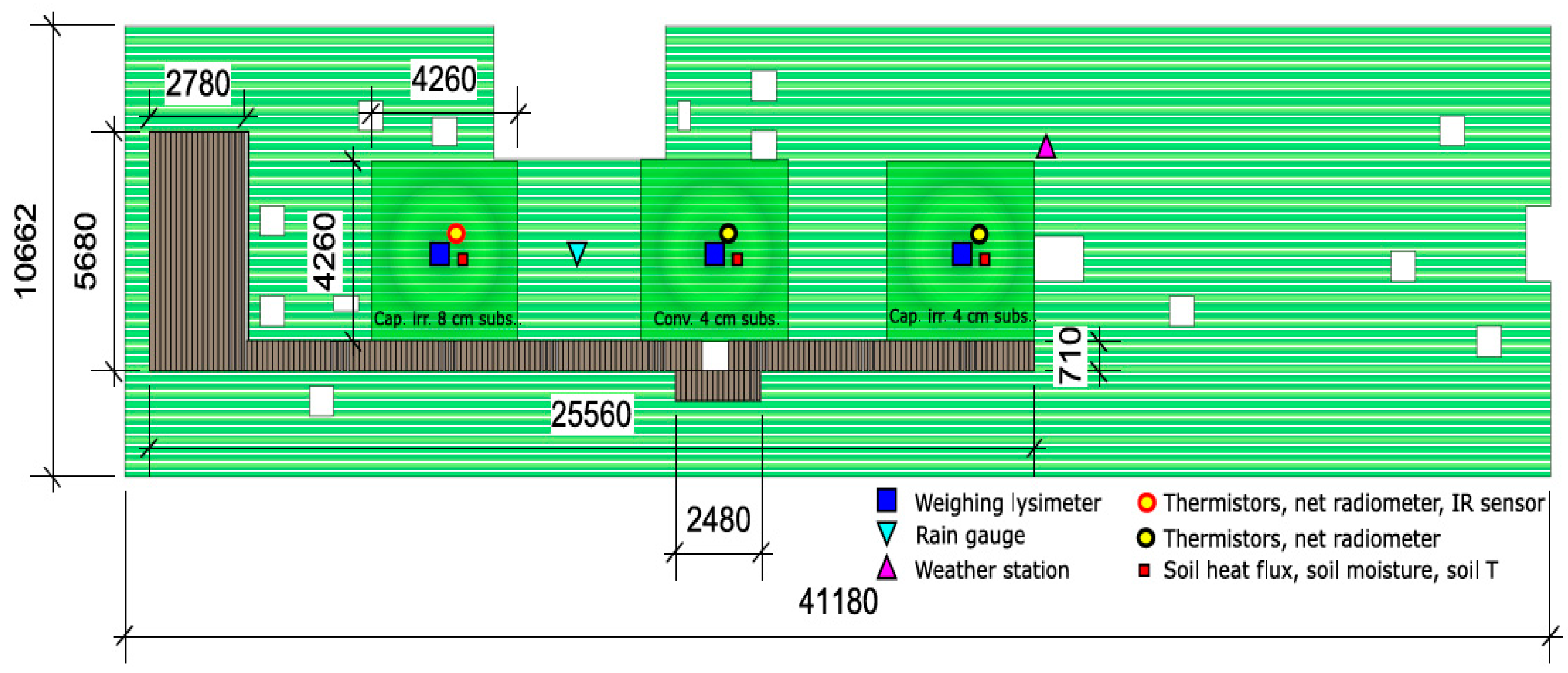
2.1. General Setup
2.2. Hydrometeorological Measurements
2.3. Parameterization of the Penman–Monteith Equation
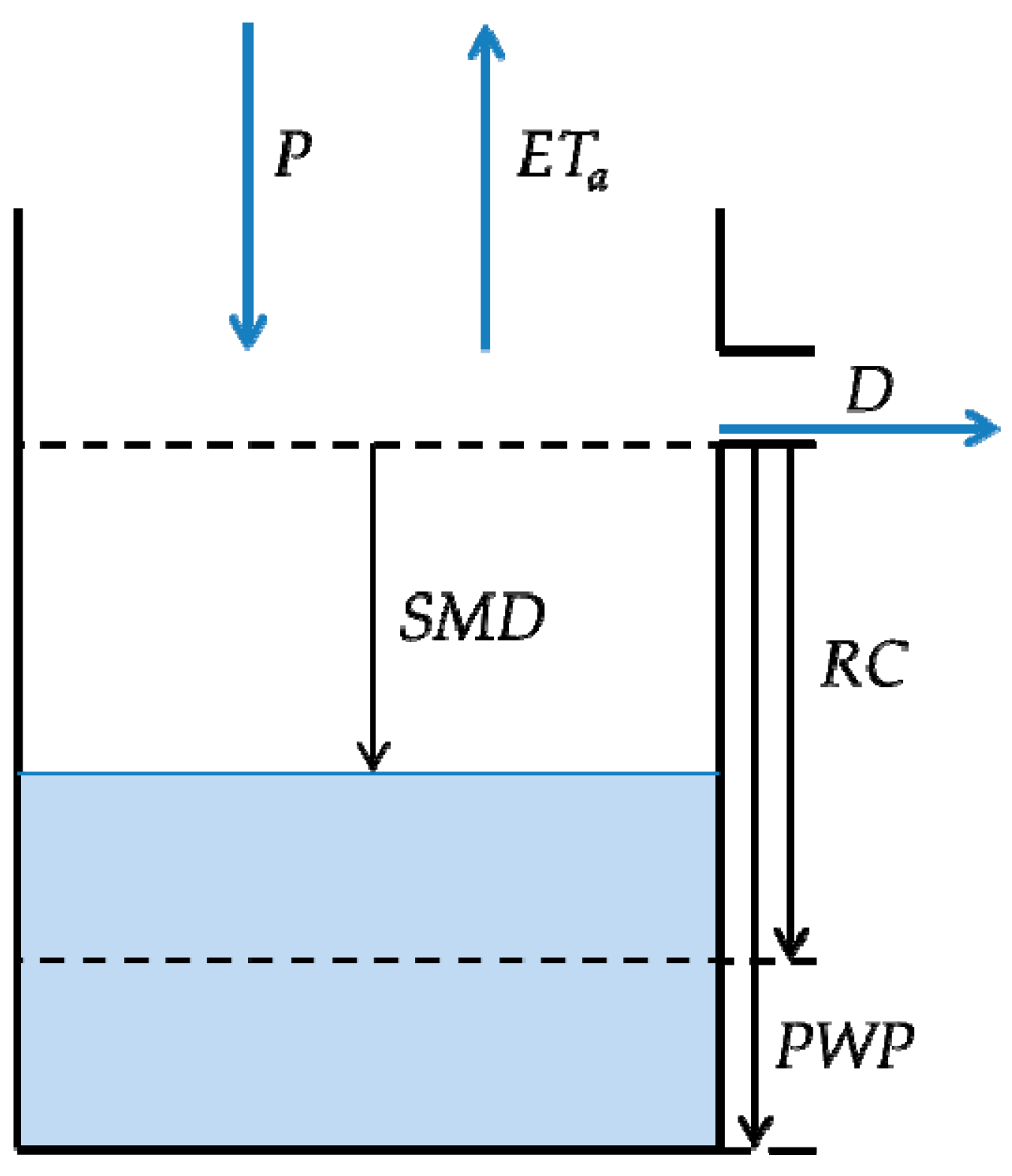
2.4. Model Simulation of Ea
3. Results
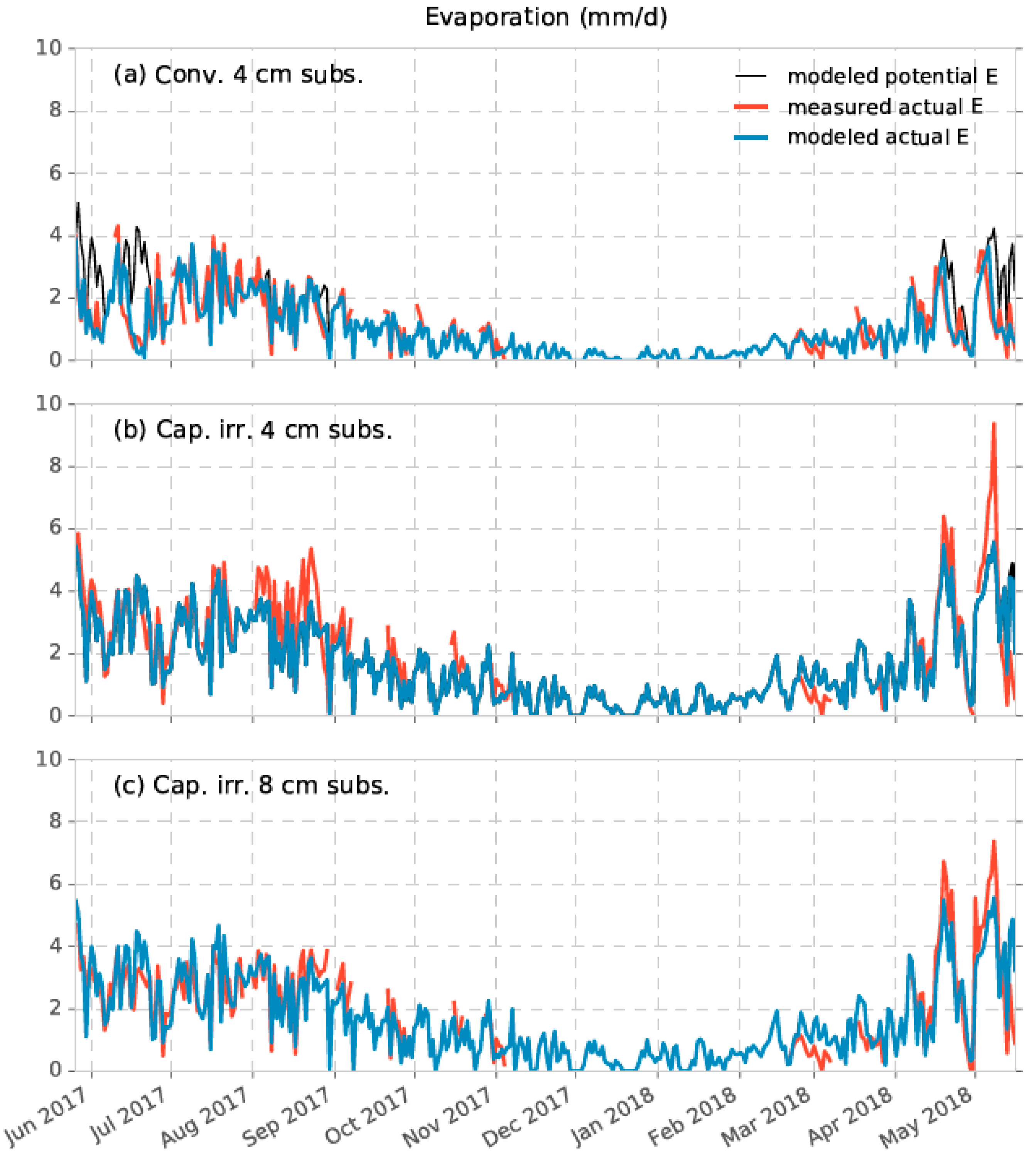
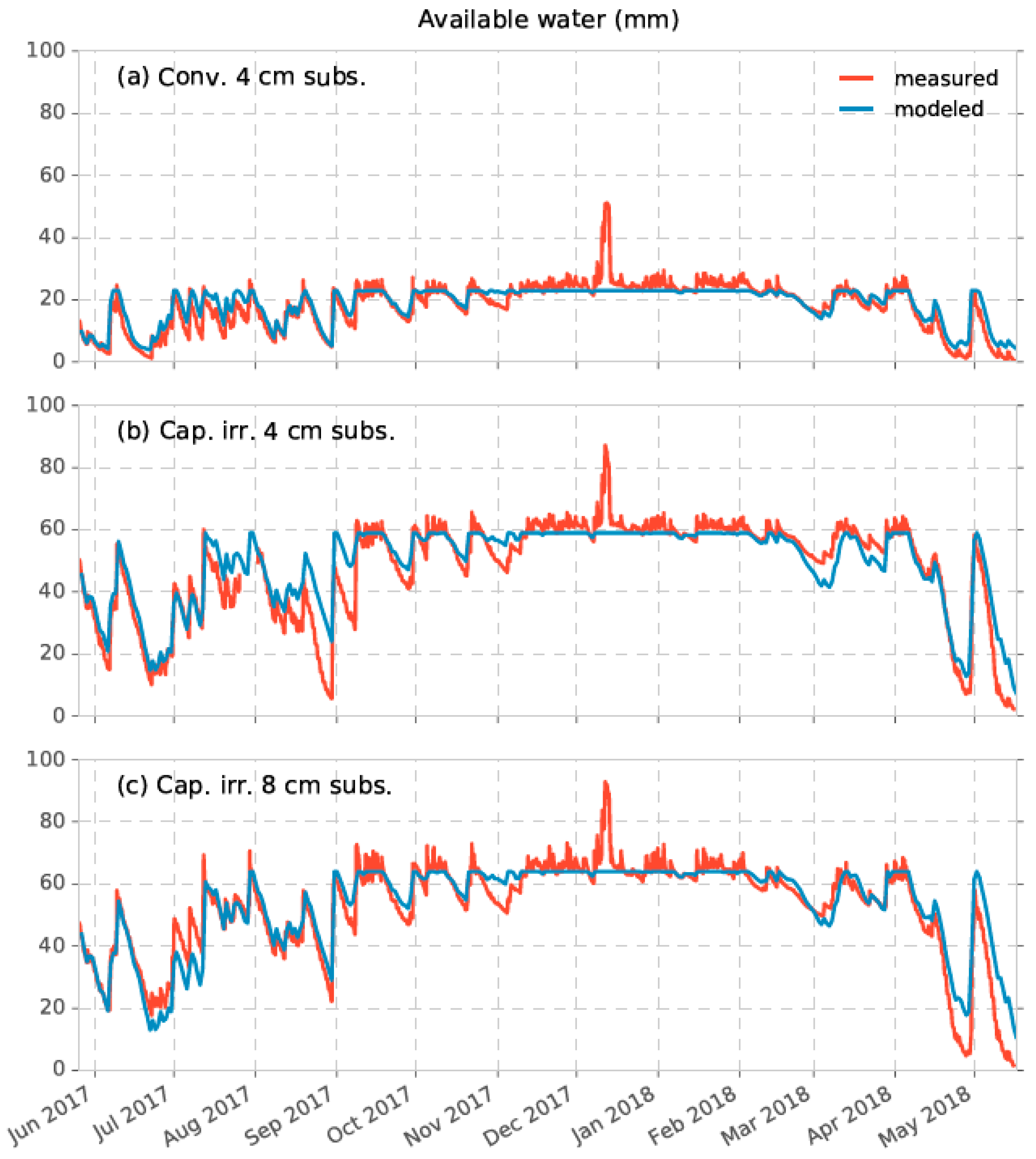
3.1. Measured vs. Modeled Evaporation
3.2. Long-Term Evaporation Fluxes From Six Different Roof Setups
3.3. Energy Considerations
4. Discussion
5. Conclusions
- A combination of Penman–Monteith estimates of potential evaporation, and a simple bucket model for evaporation reduction results in good estimates of actual evaporation of green roof vegetations (i.e., NSE > 0.73, Pearson’s r > 0.86).
- Storing precipitation water and passive capillary irrigation significantly increases the evaporation and delays the evaporation reduction and decrease of latent heat flux during hot dry periods.
- Storing precipitation water and passive capillary irrigation decreases the number of days with high Bowen ratios. Storage and capillary irrigation thus strongly reduces the sensible heat flux.
- Sedum had a remarkably large evaporation rate and showed predominantly daytime evaporation, pointing at a shift from CAM to C3 when water is abundantly available.
- Although well-watered Sedum vegetation has a lower evaporation rate compared to grass/herbs vegetation, day-to-day evaporation still remains substantial. Moreover, due to the higher water efficiency of a Sedum vegetation, it takes longer before the water runs out in the system and evaporative cooling declines.
- In the case of stormwater reduction and biodiversity as additional objectives, a grass/herb vegetation might provide extra benefits due to the higher evaporation and the earlier emptying of the system, and a more diverse native vegetation. However, under the Dutch climatic conditions, additional irrigation is needed for the survival of such a vegetation during dry spells.
- To assess the potential effects on UHI, our findings need to be extrapolated to the city scale and other climates with regional climate models. Our measurements, parameterizations, and simulations can help to improve the implementation of water availability effects in these models.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Notation | Description |
| E | Evaporation from a vegetated surface (mm/day) |
| Et | Plant transpiration (mm/day) |
| Es | Soil evaporation (mm/day) |
| Ei | Evaporation of intercepted water (mm/day) |
| Ep | Potential evaporation (mm/day) |
| Ea | Actual evaporation (mm/day) |
| LE | Latent heat flux (MJm−2/day) |
| H | Sensible heat flux (MJm−2/day) |
| Rn | Net radiation (MJm−2/day) |
| Rs | Incoming shortwave radiation (MJm−2/day) |
| G | Soil heat flux (MJm−2/day) |
| ρa | Air density (kg m−3) |
| cp | Specific heat of moist air (J·kg−1 °C−1) |
| es | Saturation vapour pressure of the air (kPa) |
| ea | Actual vapour pressure of the air (kPa) |
| ra | Aerodynamic resistance to turbulent heat and vapour transfer (s·m−1) |
| rs | Surface resistance (s·m−1) |
| γ | Psychrometric constant (kPa·°C−1) |
| λ | Latent heat of vaporization (J·kg−1) |
| ρw | Density of liquid water (kg·m−3) |
| θ | Soil moisture content (−) |
| Tsoil | Soil temperature (°C) |
| Ta | Ambient air temperature (°C) |
| P | Precipitation (mmd−1) |
| RH | Relative humidity (-) |
| zm | Height of wind measurements (m) |
| zh | Height of humidity measurements (m) |
| d | Zero plane displacement height (m) |
| zom | Roughness length governing momentum transfer (m) |
| zoh | Roughness length governing transfer of heat and vapour (m) |
| k | Von Karman’s constant (0.41 (-)) |
| uz | Wind speed at height zm (ms−1) |
| V | Vegetation height (m) |
| β | Bowen ratio (-) |
| RC | Root Constant in simple bucket model (mm) |
| PWP | Permanent Wilting Point in simple bucket model (mm) |
| D | Drainage in simple bucket model (mm/day) |
Appendix A. Linear Regressions between Rn and G, and between Rs and Rn
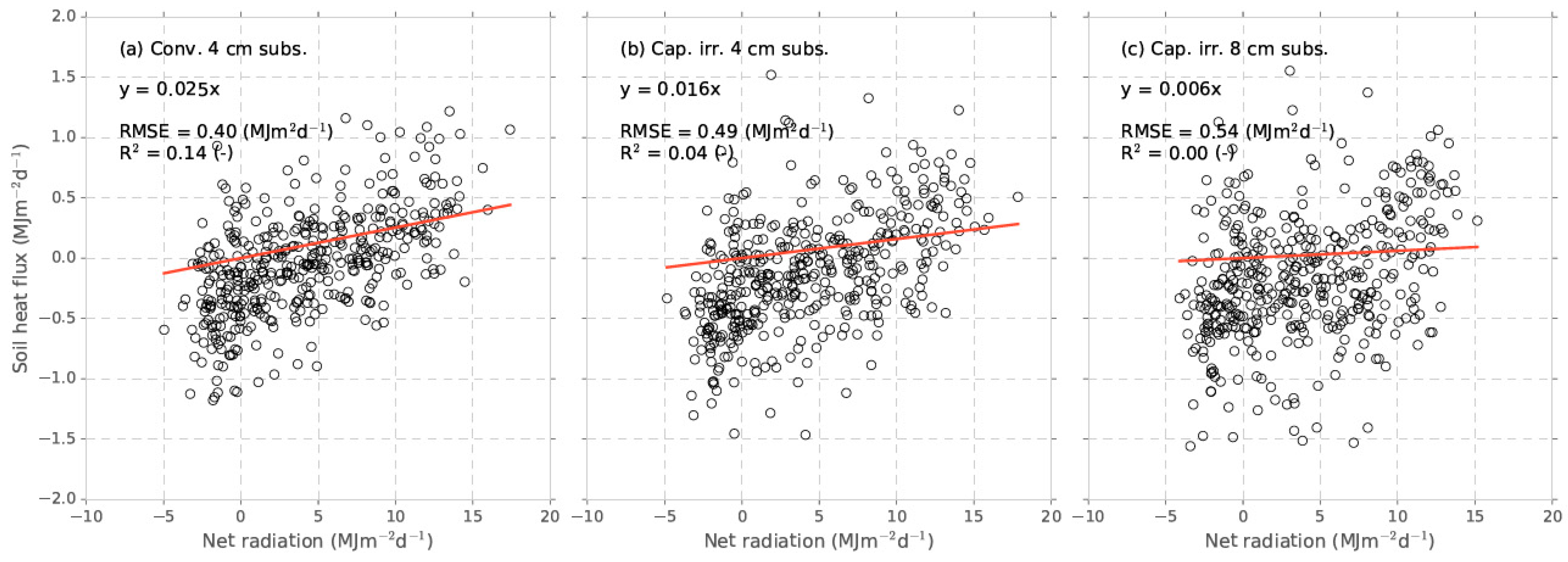
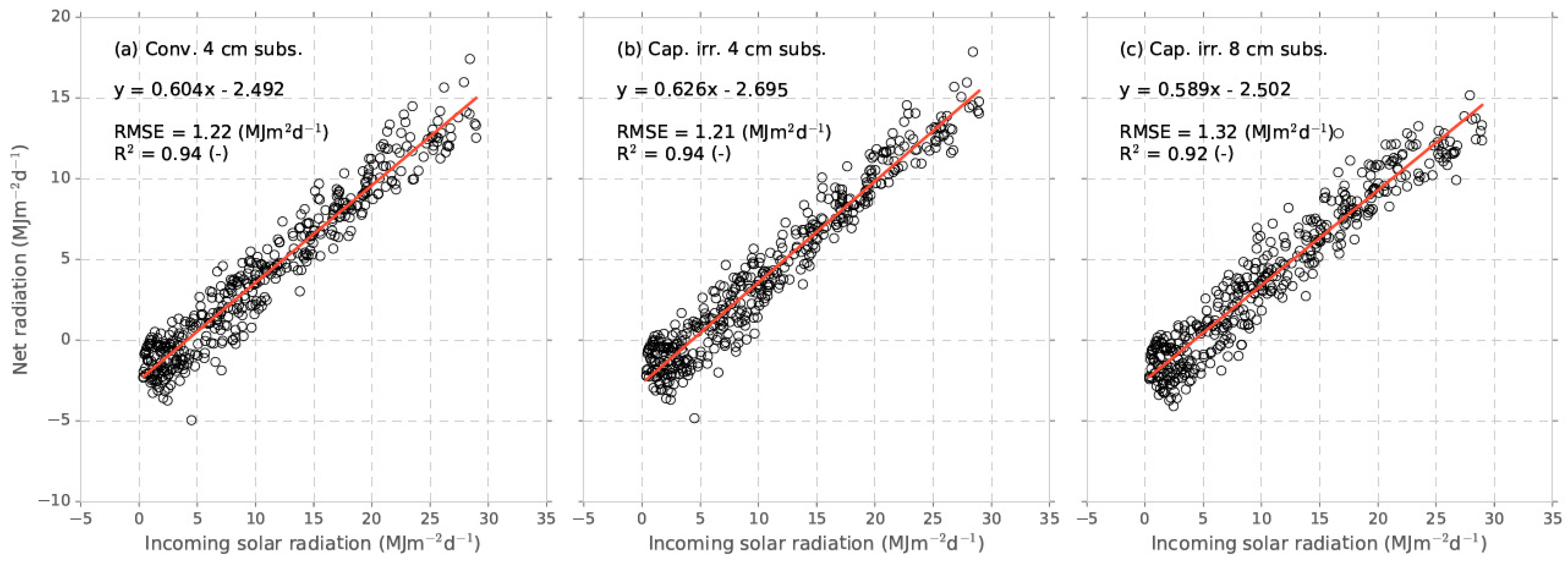
Appendix B. List of Sown Plant Species
| Species Name | Species Name (Continued) |
|---|---|
| Achillea millefolium | Koeleria glauca |
| Allium schoenoprasum | Linaria vulgaris |
| Anthoxanthum odoratum | Linum usitatissimum |
| Armeria maritima | Lotus corniculatus subsp. corniculatus |
| Bromus tectorum | Melica ciliata |
| Campanula rotundifolia | Origanum vulgare |
| Dianthus armeria | Phleum boehmeri |
| Dianthus carthusianorum | Plantago media |
| Dianthus deltoides | Potentilla argentea |
| Dianthus superbus | Prunella grandiflora |
| Erigeron acer | Prunella vulgaris |
| Erodium cicutarium | Rumex acetosella |
| Festuca ovina subsp. cinerea | Satureja vulgaris |
| Festuca ovina subsp. ovina | Sedum acre |
| Festuca rubra subsp. arenaria | Sedum album |
| Galium verum | Sedum rupestre |
| Geranium robertianum | Sedum spurium |
| Helichrysum arenarium | Silene vulgaris |
| Hieracium pilosella | Thymus pulegioides |
| Jasione montana | Trifolium arvense |
Appendix C. Wind Speed Correction
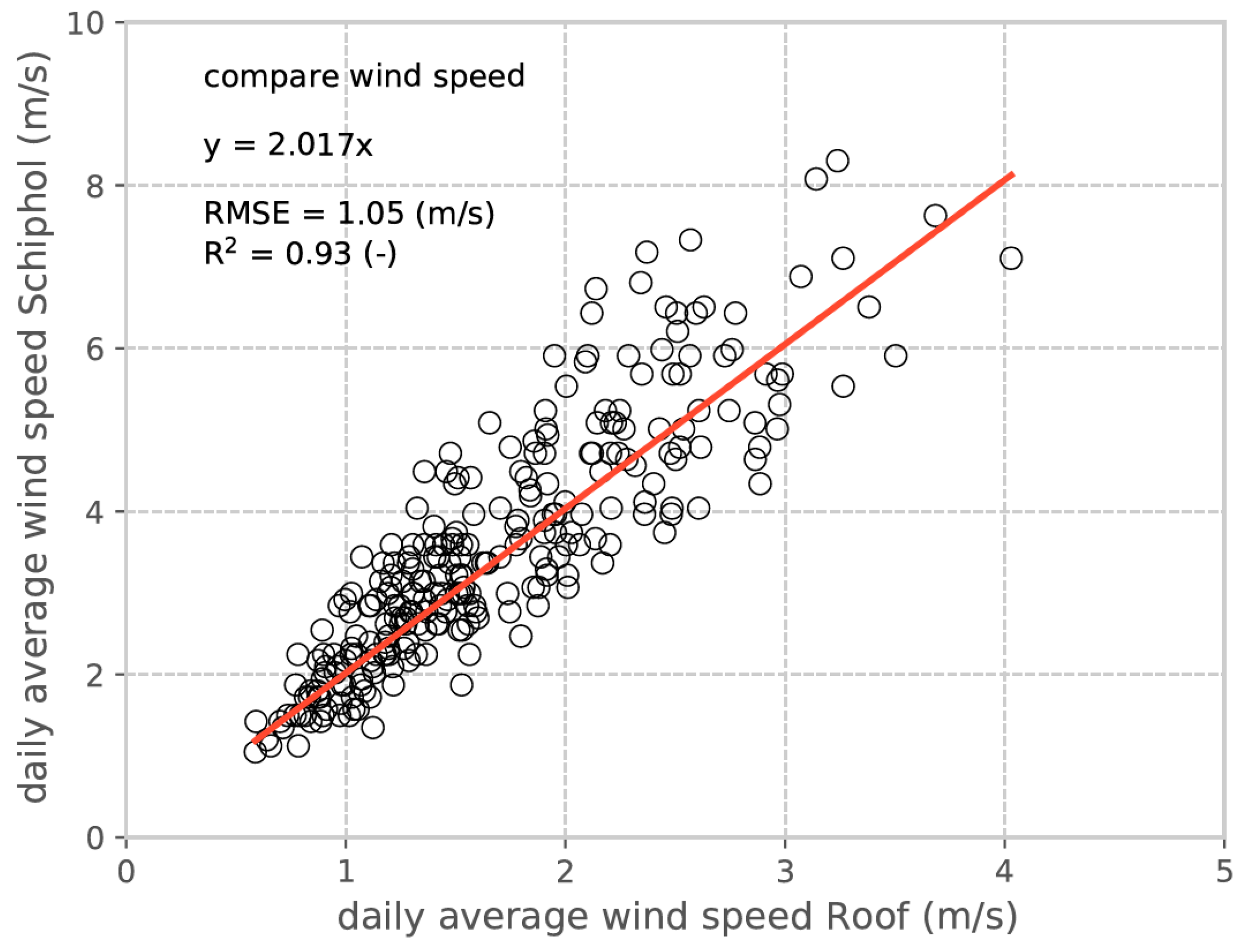
References
- Kleerekoper, L.; Van Esch, M.; Salcedo, T.B. How to make a city climate-proof, addressing the urban heat island effect. Resour. Conserv. Recycl. 2012, 64, 30–38. [Google Scholar] [CrossRef]
- Santamouris, M. Cooling the cities—A review of reflective and green roof mitigation technologies to fight heat island and improve comfort in urban environments. Sol. Energy 2014, 103, 682–703. [Google Scholar] [CrossRef]
- Scholz, M. Case study: Design, operation, maintenance and water quality management of sustainable storm water ponds for roof runoff. Bioresour. Technol. 2004, 95, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.V.; Paddon, A.; Jimenez, A. Review of world urban heat islands: Many linked to increased mortality. J. Energy Resour. Technol. 2013, 135, 022101. [Google Scholar] [CrossRef]
- Tan, J.; Zheng, Y.; Tang, X.; Guo, C.; Li, L.; Song, G.; Zhen, X.; Yuan, D.; Kalkstein, A.J.; Li, F. The urban heat island and its impact on heat waves and human health in shanghai. Int. J. Biometeorol. 2010, 54, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Konopacki, S.; Akbari, H. Energy Savings for Heat-Island Reduction Strategies in Chicago and Houston (Including Updates for Baton Rouge, Sacramento, and Salt Lake City). Available online: http://repositories.cdlib.org/lbnl/LBNL-49638 (accessed on 14 September 2018).
- Rosenfeld, A.H.; Akbari, H.; Romm, J.J.; Pomerantz, M. Cool communities: Strategies for heat island mitigation and smog reduction. Energy Build. 1998, 28, 51–62. [Google Scholar] [CrossRef]
- Tosca, M.G.; Campbell, J.; Garay, M.; Lolli, S.; Seidel, F.; Marquis, J.; Kalashnikova, O. Attributing accelerated summertime warming in the southeast united states to recent reductions in aerosol burden: Indications from vertically-resolved observations. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Lenderink, G.; Van Meijgaard, E. Increase in hourly precipitation extremes beyond expectations from temperature changes. Nat. Geosci. 2008, 1, 511–514. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Lenderink, G. Klimaatverandering in Nederland; Aanvullingen op de knmi’06 Scenario’s; KNMI: De Bilt, The Netherlands, 2009. [Google Scholar]
- Attema, J.; Bakker, A.; Beersma, J.; Bessembinder, J.; Boers, R.; Brandsma, T.; van den Brink, H.; Drijfhout, S.; Eskes, H.; Haarsma, R. Knmi’14: Climate change scenarios for the 21st century—A netherlands perspective; KNMI: De Bilt, The Netherlands, 2014. [Google Scholar]
- Foster, J.; Lowe, A.; Winkelman, S. The Value of Green Infrastructure for Urban Climate Adaptation; Center Clean Air Policy: Washington, DC, USA, 2011; pp. 1–52. [Google Scholar]
- Gill, S.E.; Handley, J.F.; Ennos, A.R.; Pauleit, S. Adapting cities for climate change: The role of the green infrastructure. Built Environ. 2007, 33, 115–133. [Google Scholar] [CrossRef]
- Costanzo, V.; Evola, G.; Marletta, L. Energy savings in buildings or uhi mitigation? Comparison between green roofs and cool roofs. Energy Build. 2016, 114, 247–255. [Google Scholar] [CrossRef]
- Ran, J.; Tang, M. Passive cooling of the green roofs combined with night-time ventilation and walls insulation in hot and humid regions. Sustain. Cities Soc. 2018, 38, 466–475. [Google Scholar] [CrossRef]
- Karteris, M.; Theodoridou, I.; Mallinis, G.; Tsiros, E.; Karteris, A. Towards a green sustainable strategy for mediterranean cities: Assessing the benefits of large-scale green roofs implementation in thessaloniki, northern greece, using environmental modelling, gis and very high spatial resolution remote sensing data. Renew. Sustain. Energy Rev. 2016, 58, 510–525. [Google Scholar] [CrossRef]
- Gregoire, B.G.; Clausen, J.C. Effect of a modular extensive green roof on stormwater runoff and water quality. Ecol. Eng. 2011, 37, 963–969. [Google Scholar] [CrossRef]
- Coutts, A.M.; Daly, E.; Beringer, J.; Tapper, N.J. Assessing practical measures to reduce urban heat: Green and cool roofs. Build. Environ. 2013, 70, 266–276. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E.; Oppenheimer, M. The effectiveness of cool and green roofs as urban heat island mitigation strategies. Environ. Res. Lett. 2014, 9, 055002. [Google Scholar] [CrossRef]
- Solcerova, A.; van de Ven, F.; Wang, M.; Rijsdijk, M.; van de Giesen, N. Do green roofs cool the air? Build. Environ. 2017, 111, 249–255. [Google Scholar] [CrossRef]
- Jim, C.Y.; Peng, L.L.H. Weather effect on thermal and energy performance of an extensive tropical green roof. Urban For. Urban Green. 2012, 11, 73–85. [Google Scholar] [CrossRef]
- Bartholomeus, R.; Stagge, J.; Tallaksen, L.; Witte, J. How over 100 years of climate variability may affect estimates of potential evaporation. HESSD 2014, 11, 10787–10828. [Google Scholar] [CrossRef]
- Voyde, E.; Fassman, E.; Simcock, R.; Wells, J. Quantifying evapotranspiration rates for New Zealand green roofs. J. Hydrol. Eng. 2010, 15, 395–403. [Google Scholar] [CrossRef]
- Tabares-Velasco, P.C.; Srebric, J. The role of plants in the reduction of heat flux through green roofs: Laboratory experiments. Ashrae Trans. 2009, 115, 793–802. [Google Scholar]
- DiGiovanni, K.; Montalto, F.; Gaffin, S.; Rosenzweig, C. Applicability of classical predictive equations for the estimation of evapotranspiration from urban green spaces: Green roof results. J. Hydrol. Eng. 2012, 18, 99–107. [Google Scholar] [CrossRef]
- Sims, A.W.; Robinson, C.E.; Smart, C.C.; Voogt, J.A.; Hay, G.J.; Lundholm, J.T.; Powers, B.; O’Carroll, D.M. Retention performance of green roofs in three different climate regions. J. Hydrol. 2016, 542, 115–124. [Google Scholar] [CrossRef]
- Marasco, D.E.; Hunter, B.N.; Culligan, P.J.; Gaffin, S.R.; McGillis, W.R. Quantifying evapotranspiration from urban green roofs: A comparison of chamber measurements with commonly used predictive methods. Environ. Sci. Technol. 2014, 48, 10273–10281. [Google Scholar] [CrossRef] [PubMed]
- Johannessen, B.G.; Hanslin, H.M.; Muthanna, T.M. Green roof performance potential in cold and wet regions. Ecol. Eng. 2017, 106, 436–447. [Google Scholar] [CrossRef]
- Makkink, G.F. Testing the penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Voeten, J.G.; van de Werken, L.; Newman, A.P. Demonstrating the use of below-substrate water storage as a means of maintaining green roofs-performance data and a novel approach to achieving public understanding. In World Environmental and Water Resources Congress; ASCE Library: West Palm Beach, FL, USA, 2016; pp. 12–21. [Google Scholar]
- Optigrün. Properties of the m-l Substrate; Optigrün International: Krauchenwies-Göggingen, Germany, 2013. [Google Scholar]
- Voortman, B.; Bartholomeus, R.; Van Der Zee, S.; Bierkens, M.; Witte, J. Quantifying energy and water fluxes in dry dune ecosystems of the netherlands. HESS 2015, 19, 3787–3805. [Google Scholar]
- Jarraud, M. Guide to Meteorological Instruments and Methods of Observation (wmo-no. 8); World Meteorological Organisation: Geneva, Switzerland, 2008. [Google Scholar]
- Peters, A.; Nehls, T.; Schonsky, H.; Wessolek, G. Separating precipitatin and evapotranspiration from noise—A new filter routine for high-resolution lysimeter data. HESS 2014, 18, 1189–1198. [Google Scholar]
- Irmak, S.; Mutiibwa, D.; Payero, J.O. Net radiation dynamics: Performance of 20 daily net radiation models as related to model structure and intricacy in two climates. Trans. ASABE 2010, 53, 1059–1076. [Google Scholar] [CrossRef]
- Sabziparvar, A.; Mirgaloybayat, R.; Marofi, S.; Zare-Abyaneh, H.; Khodamorad Pour, M. Evaluation of some net radiation models for improving daily reference evapotranspiration estimation in iran. J. Irrig. Drain. Eng. 2016, 142, 04016051. [Google Scholar] [CrossRef]
- Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics, 2nd ed.; Edward Arnold: London, UK, 1990; p. 291. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines For Computing Crop Water Requirements; FAO—Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Volume 56. [Google Scholar]
- Ireson, A.; Butler, A. A critical assessment of simple recharge models: Application to the UK chalk. HESS 2013, 17, 2083–2096. [Google Scholar]
- Gravatt, D.A.; Martin, C.E. Comparative ecophysiology of five species of Sedum (crassulaceae) under well-watered and drought-stressed conditions. Oecologia 1992, 92, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Kuronuma, T.; Watanabe, H. Photosynthetic and transpiration rates of three Sedum species used for green roofs. Environ. Control Biol. 2017, 55, 137–141. [Google Scholar] [CrossRef]
- Pilon-Smits, E.A.H.; Hart, H.T.; Meesterburrie, J.A.N.; Naber, P.; Kreuler, R.; Van Brederode, J. Variation in crassulacean acid metabolism within the genus sedum: Carbon isotope composition and water status dependent phosphoenolpyruvate carboxylase activity. J. Plant Physiol. 1991, 137, 342–346. [Google Scholar] [CrossRef]
- Castillo, F. Antioxidative protection in the inducible cam plant Sedum album l. Following the imposition of severe water stress and recovery. Oecologia 1996, 107, 469–477. [Google Scholar] [CrossRef] [PubMed]
- Sayed, O.; Earnshaw, M.; Cooper, M. Growth, water relations, and cam induction in Sedum Album in response to water stress. Biol. Plant. 1994, 36, 383. [Google Scholar] [CrossRef]
- Kluge, M. Is Sedum Acre L. A cam plant? Oecologia 1977, 29, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Starry, O.; Lea-Cox, J.; Kim, J.; Van Iersel, M. Photosynthesis and water use by two Sedum species in green roof substrate. Environ. Exp. Bot. 2014, 107, 105–112. [Google Scholar] [CrossRef]
- Monterusso, M.A.; Rowe, D.B.; Rugh, C.L. Establishment and persistence of sedum spp. And native taxa for green roof applications. Hortscience 2005, 40, 391–396. [Google Scholar]
- Van der Linden, E.C.; Haarsma, R.J.; van der Schrier, G. Resolution-dependence of future european soil moisture droughts. Hydrol. Earth Syst. Sci. Discuss. 2018, 2018, 1–31. [Google Scholar] [CrossRef]
- Getter, K.L.; Rowe, D.B. Media depth influences Sedum green roof establishment. Urban Ecosyst. 2008, 11, 361. [Google Scholar] [CrossRef]
- Sun, T.; Bou-Zeid, E.; Ni, G.-H. To irrigate or not to irrigate: Analysis of green roof performance via a vertically-resolved hygrothermal model. Build. Environ. 2014, 73, 127–137. [Google Scholar] [CrossRef]
- Zuurbier, K.G.; Raat, K.J.; Paalman, M.; Oosterhof, A.T.; Stuyfzand, P.J. How subsurface water technologies (swt) can provide robust, effective, and cost-efficient solutions for freshwater management in coastal zones. Water Resour. Manag. 2017, 31, 671–687. [Google Scholar] [CrossRef]
- Fowdar, H.S.; Hatt, B.E.; Breen, P.; Cook, P.L.; Deletic, A. Designing living walls for greywater treatment. Water Res. 2017, 110, 218–232. [Google Scholar] [CrossRef] [PubMed]
- Morakinyo, T.E.; Dahanayake, K.K.C.; Ng, E.; Chow, C.L. Temperature and cooling demand reduction by green-roof types in different climates and urban densities: A co-simulation parametric study. Energy Build. 2017, 145, 226–237. [Google Scholar] [CrossRef]
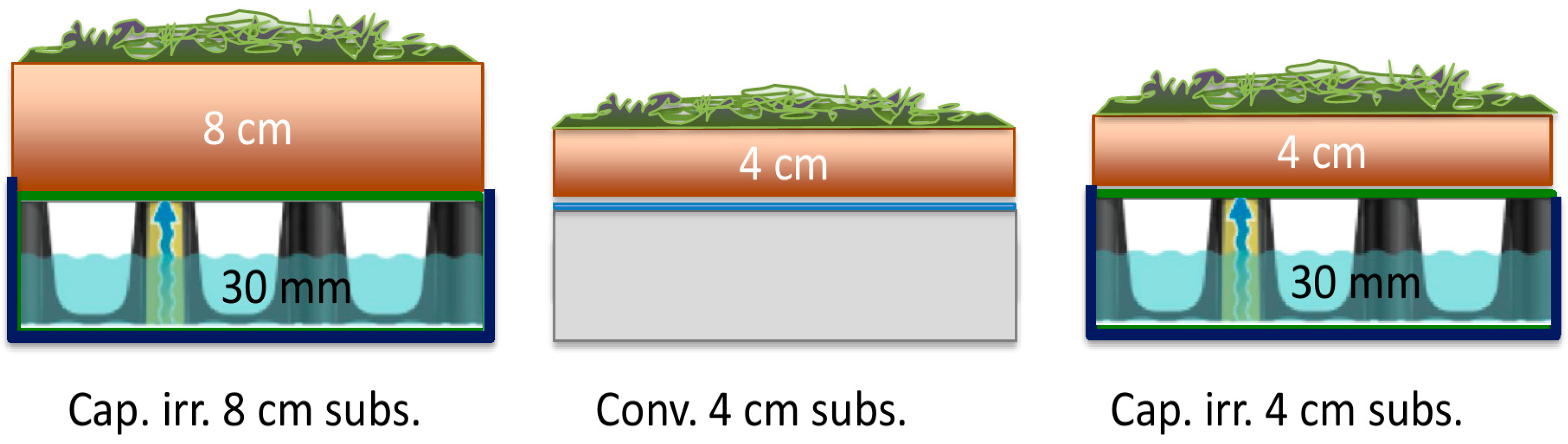
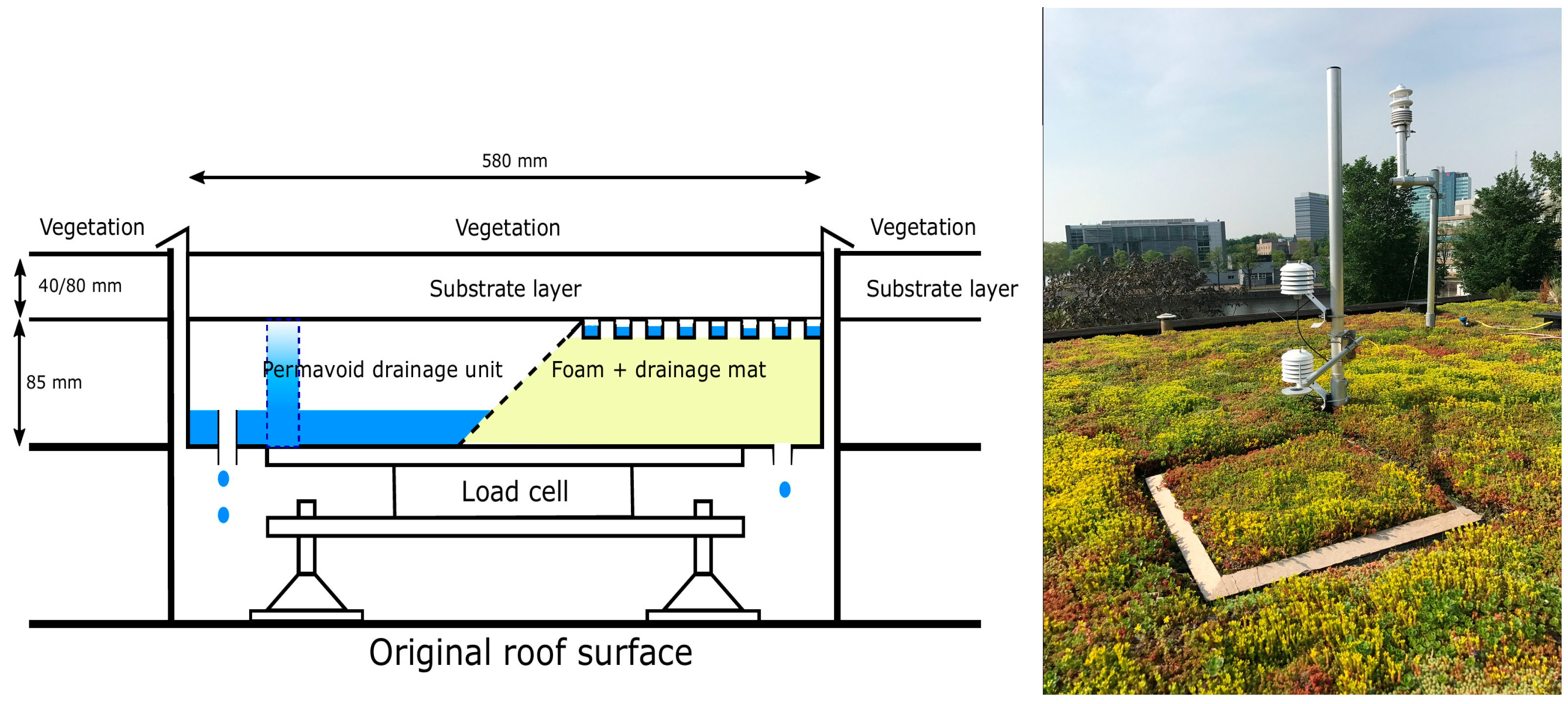

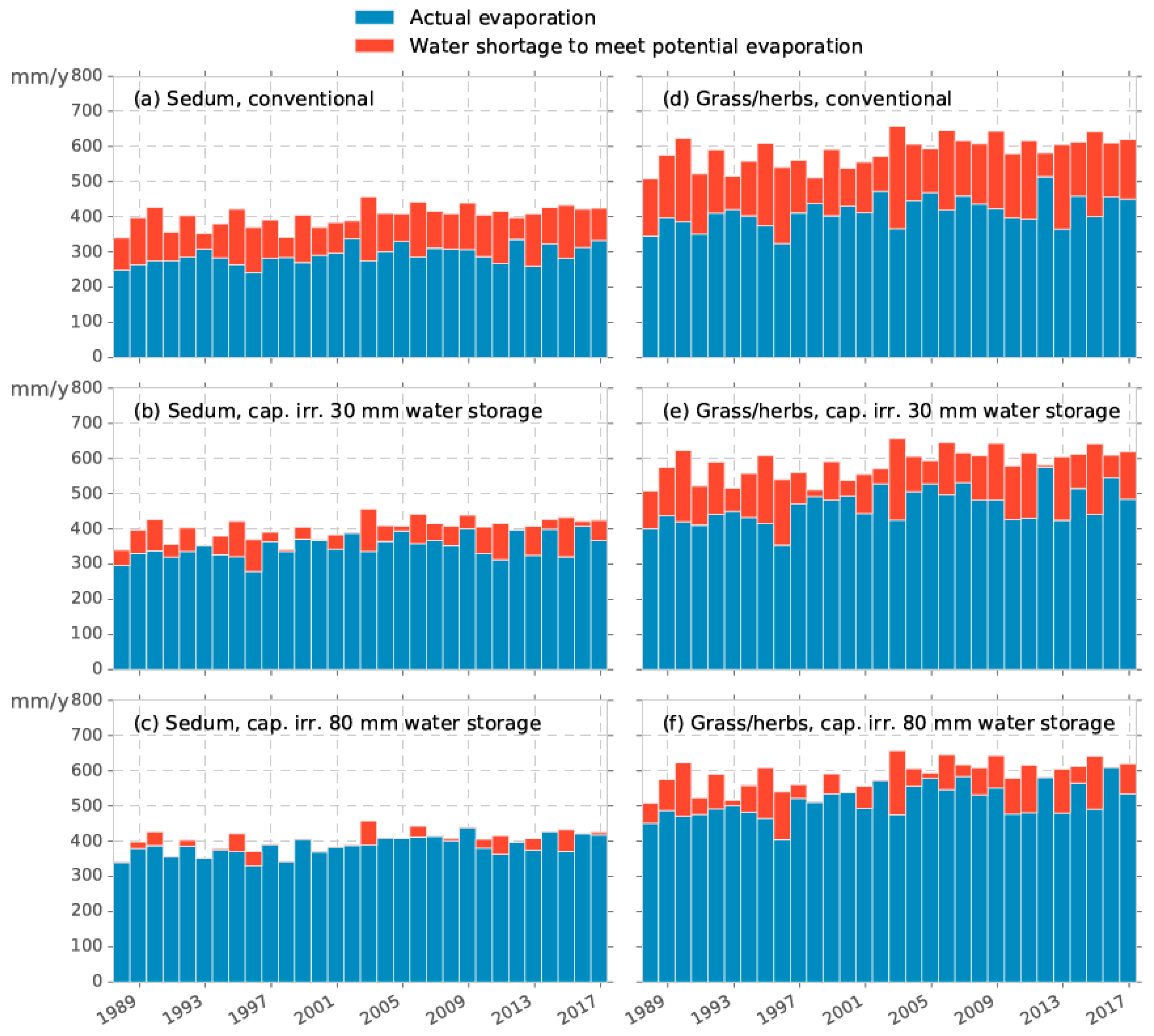
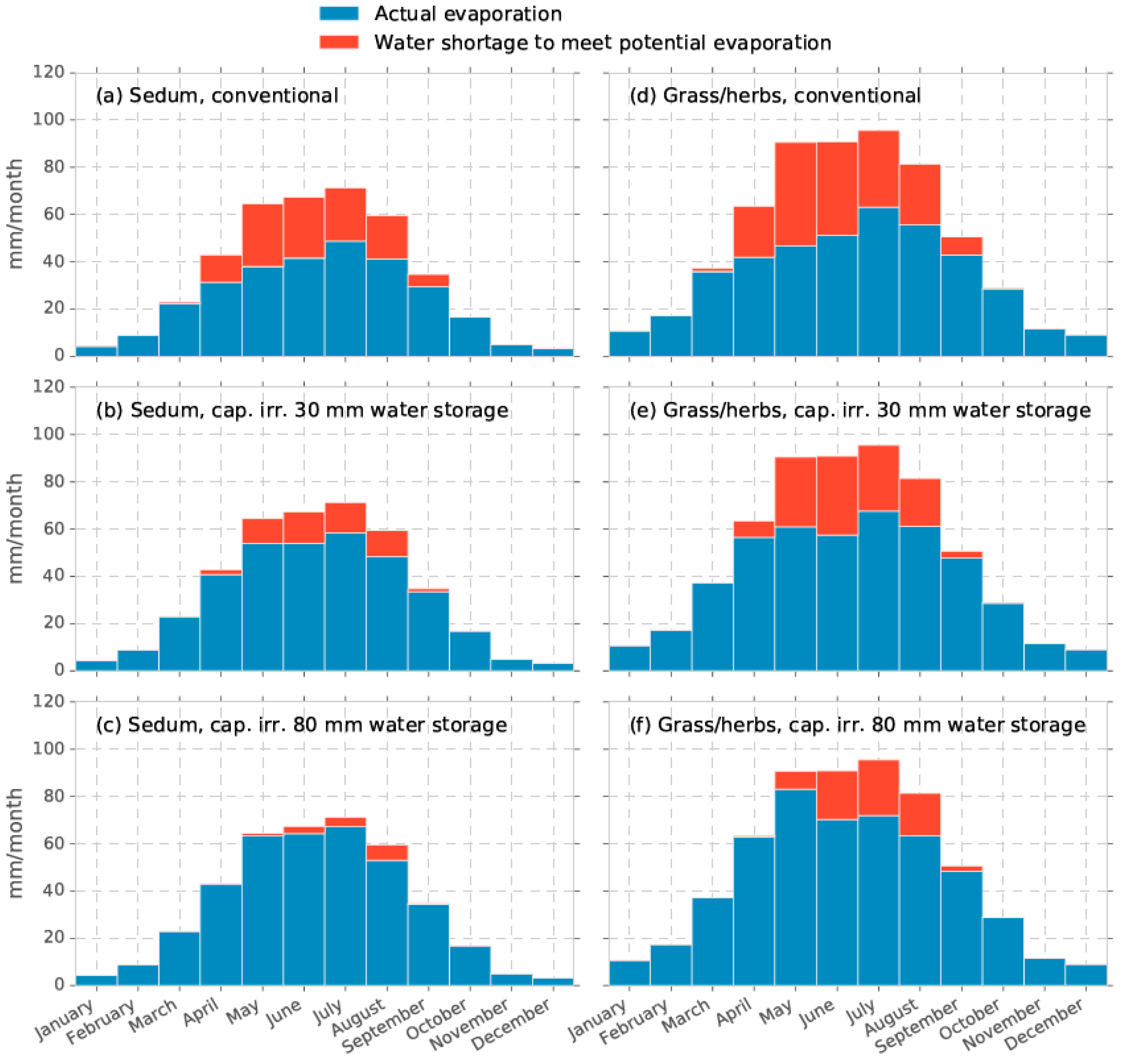
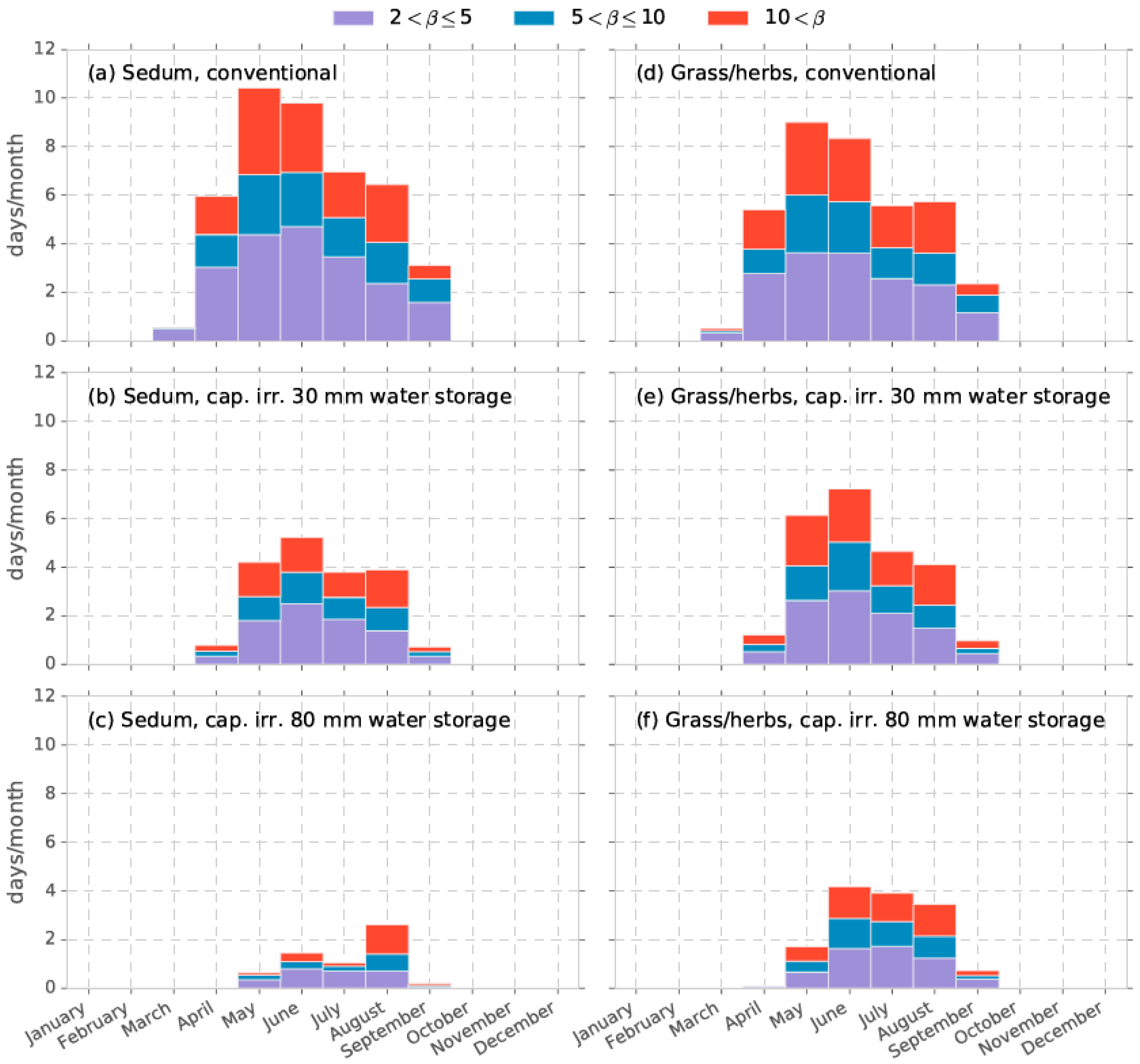
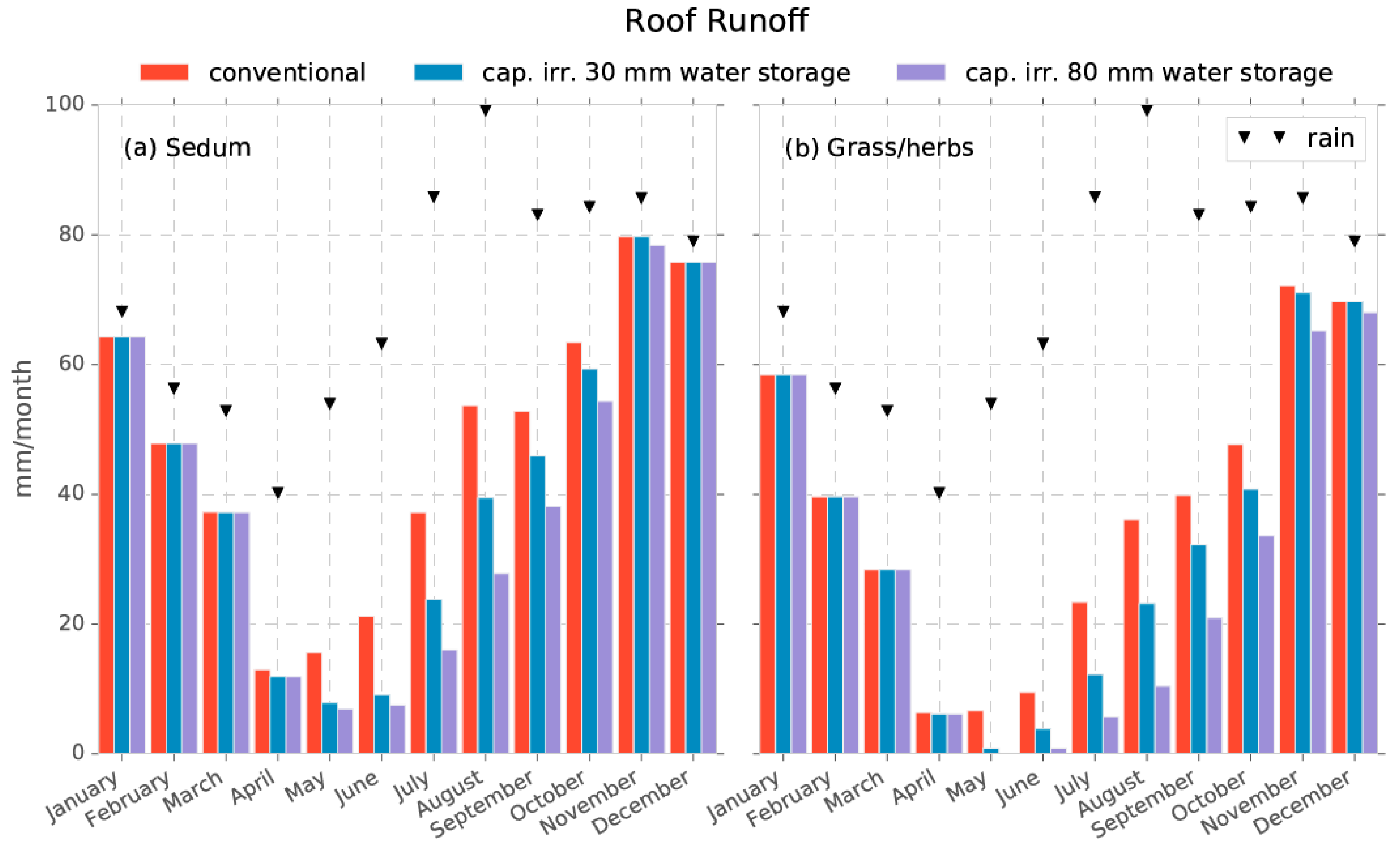
| Roof System | Vegetation | Water Storage (mm) | Ep (mm/year) | Ea (mm/year) | Water Shortage (mm) |
|---|---|---|---|---|---|
| Conventional | Sedum | - | 401 | 290 | 111 |
| Conventional | Grass/herbs | - | 587 | 414 | 173 |
| Capillary irrigation | Sedum | 30 | 401 | 350 | 51 |
| Capillary irrigation | Sedum | 80 | 401 | 386 | 15 |
| Capillary irrigation | Grass/herbs | 30 | 587 | 466 | 121 |
| Capillary irrigation | Grass/herbs | 80 | 587 | 515 | 72 |
| Roof System | Vegetation | Water Storage (mm) | Fraction LE of Rn (-) | Bowen Ratio β (-) |
|---|---|---|---|---|
| Conventional | Sedum | - | 0.54 | 0.87 |
| Conventional | Grass/herbs | - | 0.65 | 0.55 |
| Capillary irrigation | Sedum | 30 | 0.71 | 0.41 |
| Capillary irrigation | Sedum | 80 | 0.76 | 0.31 |
| Capillary irrigation | Grass/herbs | 30 | 0.86 | 0.16 |
| Capillary irrigation | Grass/herbs | 80 | 0.95 | 0.05 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cirkel, D.G.; Voortman, B.R.; Van Veen, T.; Bartholomeus, R.P. Evaporation from (Blue-)Green Roofs: Assessing the Benefits of a Storage and Capillary Irrigation System Based on Measurements and Modeling. Water 2018, 10, 1253. https://doi.org/10.3390/w10091253
Cirkel DG, Voortman BR, Van Veen T, Bartholomeus RP. Evaporation from (Blue-)Green Roofs: Assessing the Benefits of a Storage and Capillary Irrigation System Based on Measurements and Modeling. Water. 2018; 10(9):1253. https://doi.org/10.3390/w10091253
Chicago/Turabian StyleCirkel, Dirk Gijsbert, Bernard R. Voortman, Thijs Van Veen, and Ruud P. Bartholomeus. 2018. "Evaporation from (Blue-)Green Roofs: Assessing the Benefits of a Storage and Capillary Irrigation System Based on Measurements and Modeling" Water 10, no. 9: 1253. https://doi.org/10.3390/w10091253
APA StyleCirkel, D. G., Voortman, B. R., Van Veen, T., & Bartholomeus, R. P. (2018). Evaporation from (Blue-)Green Roofs: Assessing the Benefits of a Storage and Capillary Irrigation System Based on Measurements and Modeling. Water, 10(9), 1253. https://doi.org/10.3390/w10091253






