Coupling of Ultrasonic and Photometric Techniques for Synchronous Measurements of Unconfined Turbidity Currents
Abstract
1. Introduction
Effect of Confinement and Obstacles on Flow
2. Experimental Methodology
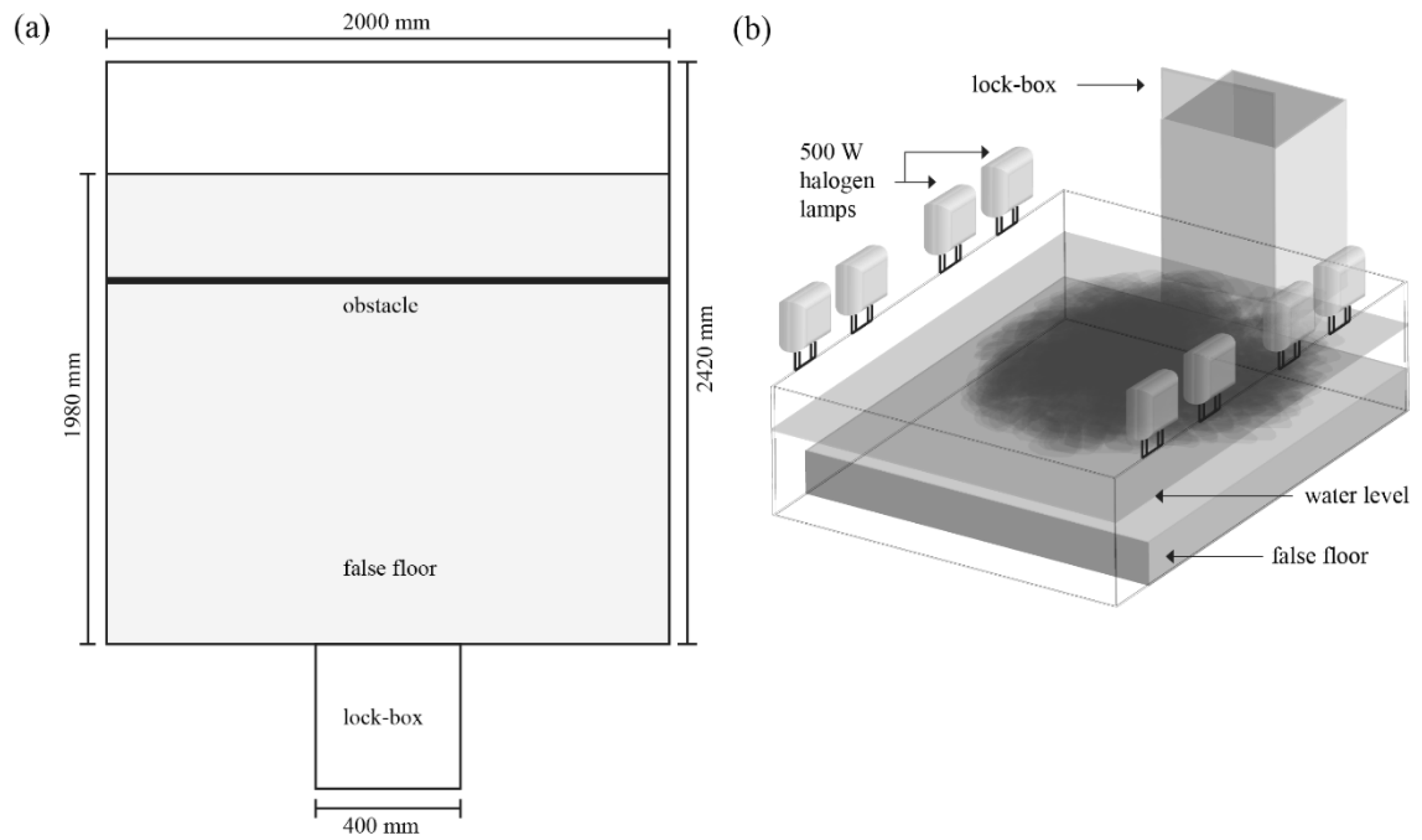
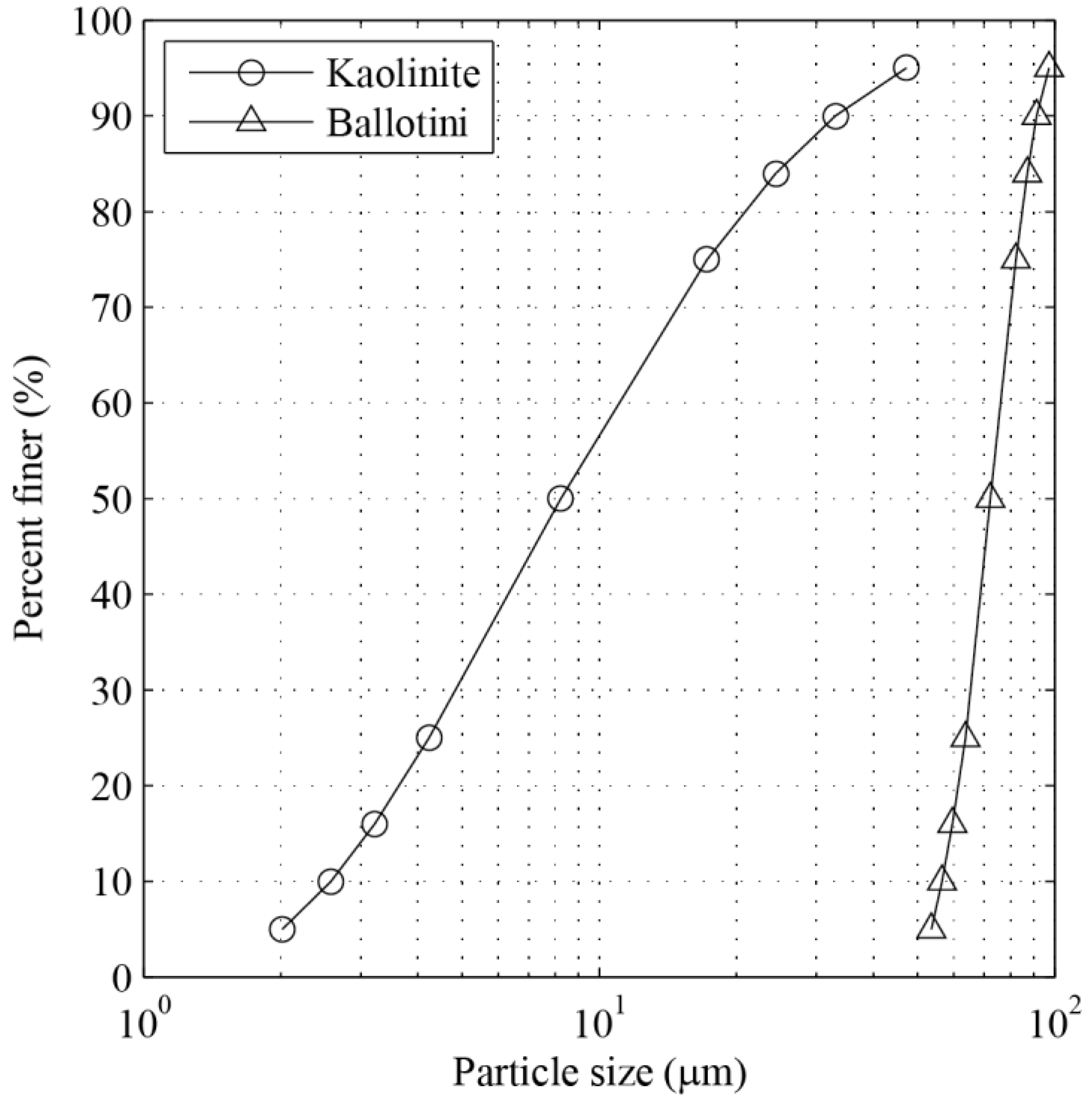
2.1. Basin and Material
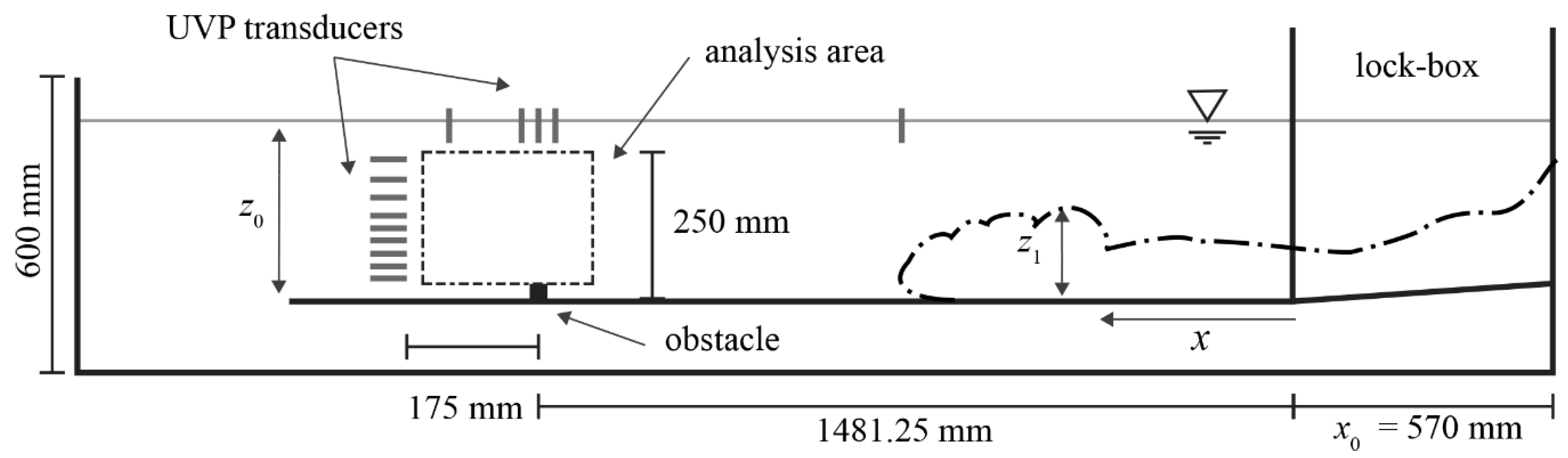
2.2. Flow Measurements
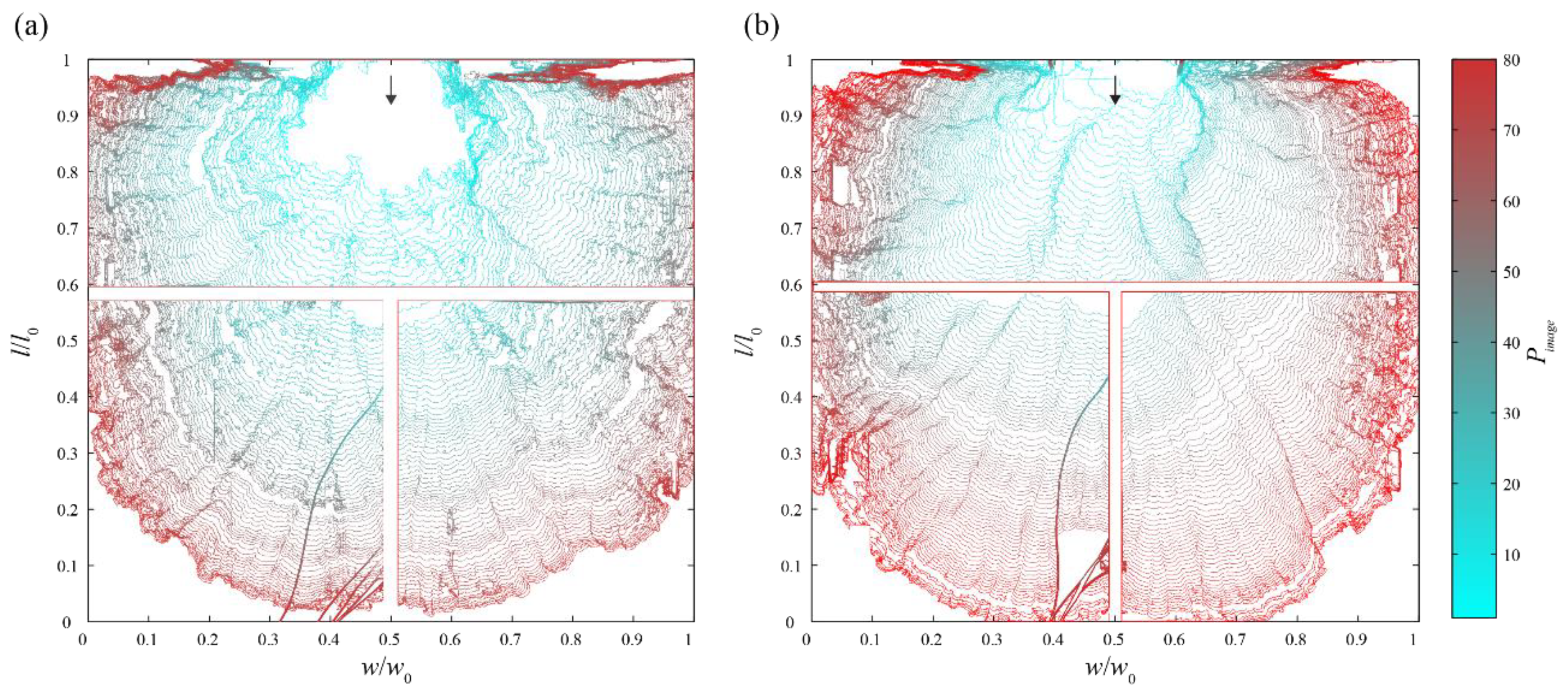
2.3. Photometric Measurements
2.4. Experimental Procedure
3. Analytical Methodology
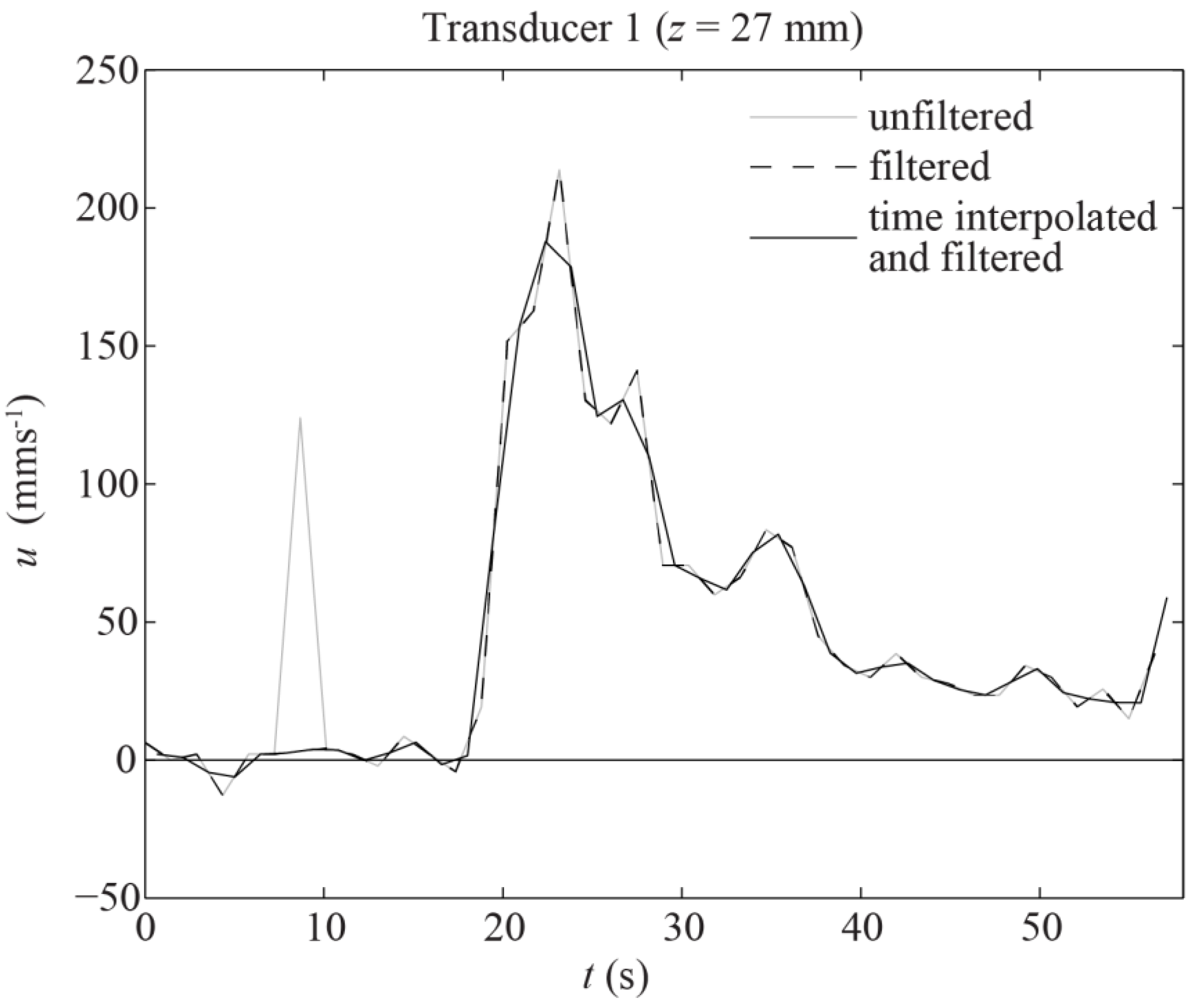
3.1. Flow Data
3.2. Photometric Data
4. Results and Discussion
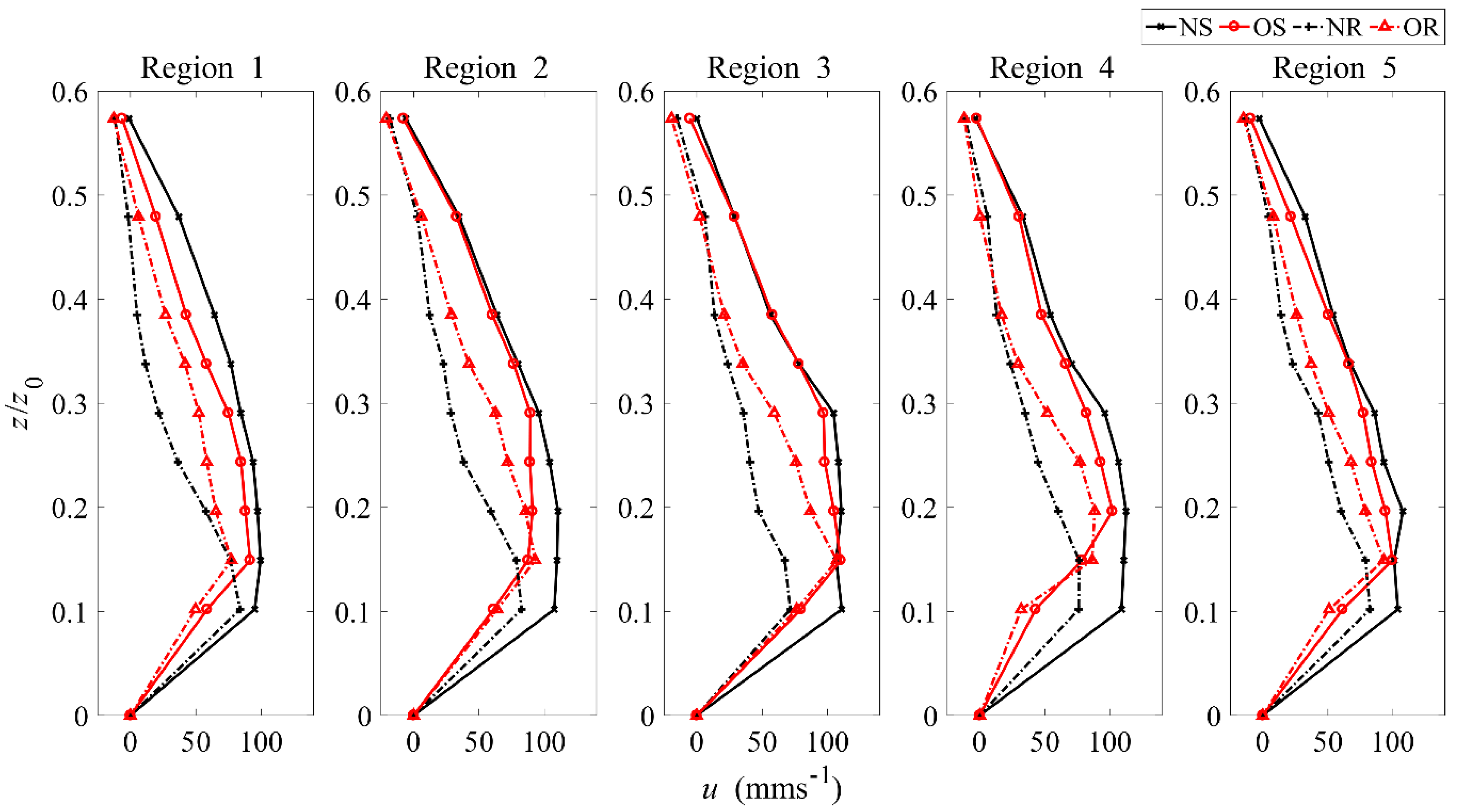
4.1. Velocity Profile Development
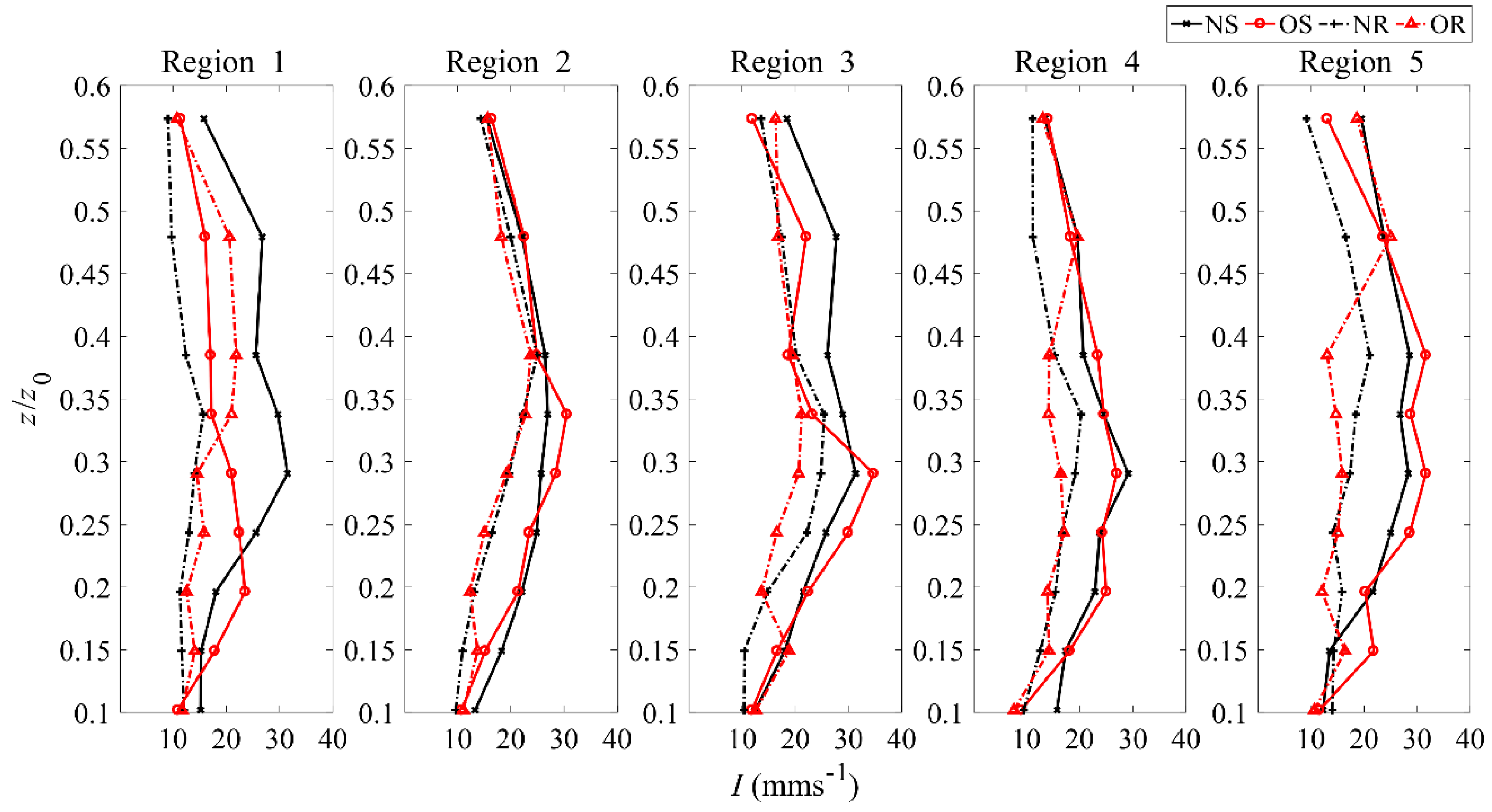
4.2. Turbulence Intensities
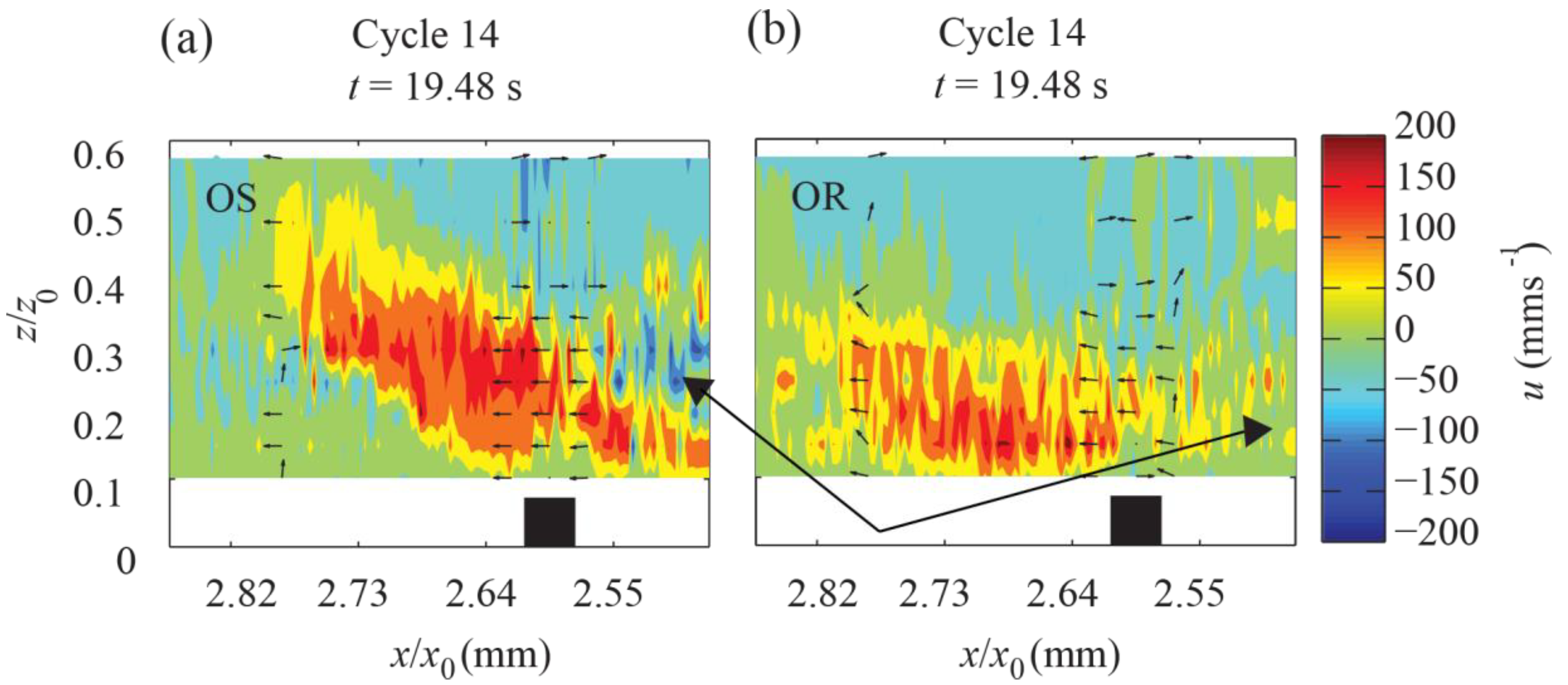
4.3. Future Potential of the Coupled Approach
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kneller, B.; Buckee, C. The structure and fluid mechanics of turbidity currents: A review of some recent studies and their geological implications. Sedimentology 2000, 47, 62–94. [Google Scholar] [CrossRef]
- Meiburg, E.; Kneller, B. Turbidity currents and their deposits. Annu. Rev. Fluid Mech. 2010, 42, 135–156. [Google Scholar] [CrossRef]
- Middleton, G.V. Sediment deposition from turbidity currents. Annu. Rev. Earth Planet. Sci. 1993, 21, 89–114. [Google Scholar] [CrossRef]
- Weimer, P.; Link, M.H. Global petroleum occurrences in submarine fans and turbidite systems. In Seismic Facies and Sedimentary Processes of Submarine Fans and Turbidite Systems; Weimer, P., Link, M.H., Eds.; Springer: New York, NY, USA, 1991; pp. 9–67. [Google Scholar]
- Felix, M.; Sturton, S.; Peakall, J. Combined measurements of velocity and concentration in experimental turbidity currents. Sediment. Geol. 2005, 179, 31–47. [Google Scholar] [CrossRef]
- Altinakar, M.S.; Graf, W.H.; Hopfinger, E.J. Flow structure in turbidity currents. J. Hydraul. Res. 1996, 34, 713–718. [Google Scholar] [CrossRef]
- Kneller, B.; Bennett, S.; McCaffrey, W.D. Velocity structure, turbulence and fluid stresses in experimental gravity currents. J. Geophys. Res. Oceans 1999, 104, 5381–5391. [Google Scholar] [CrossRef]
- Eggenhuisen, J.T.; McCaffrey, W.D. The vertical turbulence structure of experimental turbidity currents encountering basal obstructions: Implications for vertical suspended sediment distribution in non-equilibrium currents. Sedimentology 2012, 59, 1101–1120. [Google Scholar] [CrossRef]
- Nogueira, H.I.S.; Adduce, C.; Alves, E.; Franca, M.J. Dynamics of the head of gravity currents. Environ. Fluid Mech. 2014, 14, 519–540. [Google Scholar] [CrossRef]
- Gladstone, C.; Pritchard, D. Patterns of deposition from experimental turbidity currents with reversing buoyancy. Sedimentology 2010, 57, 53–84. [Google Scholar] [CrossRef]
- Heezen, B.C.; Ewing, M. Turbidity currents and submarine slumps, and 1929 grand banks earthquake. Am. J. Sci. 1952, 250, 849–873. [Google Scholar] [CrossRef]
- Gonzalez-Juez, E.; Meiburg, E.; Constantinescu, G. Gravity currents impinging on bottom-mounted square cylinders: Flow fields and associated forces. J. Fluid Mech. 2009, 631, 65–102. [Google Scholar] [CrossRef]
- Nogueira, H.I.S.; Adduce, C.; Alves, E.; Franca, M.J. Analysis of lock-exchange gravity currents over smooth and rough beds. J. Hydraul. Res. 2013, 51, 417–431. [Google Scholar] [CrossRef]
- Cenedese, C.; Nokes, R.; Hyatt, J. Lock-exchange gravity currents over rough bottoms. Environ. Fluid Mech. 2018, 18, 59–73. [Google Scholar] [CrossRef]
- Bursik, M.I.; Woods, A.W. The effects of topography on sedimentation from particle-laden turbulent density currents. J. Sediment. Res. 2000, 70, 53–63. [Google Scholar] [CrossRef]
- Nasr-Azadani, M.M.; Meiburg, E. Turbidity currents interacting with three-dimensional seafloor topography. J. Fluid Mech. 2014, 745, 409–443. [Google Scholar] [CrossRef]
- Lane-Serff, G.F.; Beal, L.M.; Hadfield, T.D. Gravity current flow over obstacles. J. Fluid Mech. 1995, 292, 39–53. [Google Scholar] [CrossRef]
- Rottman, J.W.; Simpson, J.E.; Hunt, J.C.R.; Britter, R.E. Unsteady gravity current flows over obstacles: Some observations and analysis related to the phase ii trials. J. Hazard. Mater. 1985, 11, 325–340. [Google Scholar] [CrossRef]
- Asghari Pari, S.A.; Kashefipour, S.M.; Ghomeshi, M. An experimental study to determine the obstacle height required for the control of subcritical and supercritical gravity currents. Eur. J. Environ. Civ. Eng. 2017, 21, 1080–1092. [Google Scholar] [CrossRef]
- Ermanyuk, E.; Gavrilov, N. Interaction of internal gravity current with an obstacle on the channel bottom. J. Appl. Mech. Tech. Phys. 2005, 46, 489–495. [Google Scholar] [CrossRef]
- Ermanyuk, E.; Gavrilov, N. Interaction of an internal gravity current with a submerged circular cylinder. J. Appl. Mech. Tech. Phys. 2005, 46, 216–223. [Google Scholar] [CrossRef]
- Gonzalez-Juez, E.; Constantinescu, G.; Meiburg, E. A study of the interaction of a gravity current with a square cylinder using two-dimensional numerical simulations. In Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2017; ASME: San Diego, CA, USA, 2007; Volume 2007, pp. 861–870. [Google Scholar]
- Gonzalez-Juez, E.; Meiburg, E. Shallow-water analysis of gravity-current flows past isolated obstacles. J. Fluid Mech. 2009, 635, 415–438. [Google Scholar] [CrossRef]
- Tokyay, T.; Constantinescu, G. The effects of a submerged non-erodible triangular obstacle on bottom propagating gravity currents. Phys. Fluids 2015, 27, 056601. [Google Scholar] [CrossRef]
- Oshaghi, M.R.; Afshin, H.; Firoozabadi, B. Experimental investigation of the effect of obstacles on the behavior of turbidity currents. Can. J. Civ. Eng. 2013, 40, 343–352. [Google Scholar] [CrossRef]
- Oehy, C.; Schleiss, A.J. Control of turbidity currents in reservoirs by solid and permeable obstacles. J. Hydraul. Eng. 2007, 133, 637–648. [Google Scholar] [CrossRef]
- Janocko, M.; Cartigny, M.; Nemec, W.; Hansen, E. Turbidity current hydraulics and sediment deposition in erodible sinuous channels: Laboratory experiments and numerical simulations. Mar. Pet. Geol. 2013, 41, 222–249. [Google Scholar] [CrossRef]
- Stagnaro, M.; Bolla Pittaluga, M. Velocity and concentration profiles of saline and turbidity currents flowing in a straight channel under quasi-uniform conditions. Earth Surf. Dyn. 2014, 2, 167–180. [Google Scholar] [CrossRef]
- Chowdhury, M.R.; Testik, F.Y. Laboratory testing of mathematical models for high-concentration fluid mud turbidity currents. Ocean Eng. 2011, 38, 256–270. [Google Scholar] [CrossRef]
- Jacobson, M.R.; Testik, F.Y. Turbulent entrainment into fluid mud gravity currents. Environ. Fluid Mech. 2014, 14, 541–563. [Google Scholar] [CrossRef]
- Hallworth, M.A.; Huppert, H.E.; Phillips, J.C.; Sparks, R.S.J. Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 1996, 308, 289–311. [Google Scholar] [CrossRef]
- Marleau, L.J.; Flynn, M.R.; Sutherland, B.R. Gravity currents propagating up a slope in a two-layer fluid. Phys. Fluids 2015, 27, 036601. [Google Scholar] [CrossRef]
- Mirajkar, H.N.; Tirodkar, S.; Balasubramanian, S. Experimental study on growth and spread of dispersed particle-laden plume in a linearly stratified environment. Environ. Fluid Mech. 2015, 1241–1262. [Google Scholar] [CrossRef]
- Choi, S.-U.; Garcia, M.H. Spreading of gravity plumes on an incline. Coast. Eng. J. 2001, 43, 221. [Google Scholar] [CrossRef]
- La Rocca, M.; Adduce, C.; Sciortino, G.; Pinzon, A.B. Experimental and numerical simulation of three-dimensional gravity currents on smooth and rough bottom. Phys. Fluids 2008, 20, 106603. [Google Scholar] [CrossRef]
- Sahuri, R.M.; Kaminski, A.K.; Flynn, M.R.; Ungarish, M. Axisymmetric gravity currents in two-layer density-stratified media. Environ. Fluid Mech. 2015, 15, 1035–1051. [Google Scholar] [CrossRef]
- Alexander, J.; Morris, S.A. Observations on experimental, nonchannelized, high-concentration turbidity currents and variations in deposits around obstacles. J. Sediment. Res. 1994, 64, 899–909. [Google Scholar]
- Morris, S.A.; Alexander, J. Changes in flow direction at a point caused by obstacles during passage of a density current. J. Sediment. Res. 2003, 73, 621–629. [Google Scholar] [CrossRef]
- Choux, C.M.A.; Baas, J.H.; McCaffrey, W.D.; Haughton, P.D.W. Comparison of spatio-temporal evolution of experimental particulate gravity flows at two different initial concentrations, based on velocity, grain size and density data. Sediment. Geol. 2005, 179, 49–69. [Google Scholar] [CrossRef]
- Gray, T.E.; Alexander, J.; Leeder, M.R. Longitudinal flow evolution and turbulence structure of dynamically similar, sustained, saline density and turbidity currents. J. Geophys. Res. 2006, 111, C08015. [Google Scholar] [CrossRef]
- Gray, T.E.; Alexander, J.; Leeder, M.R. Quantifying velocity and turbulence structure in depositing sustained turbidity currents across breaks in slope. Sedimentology 2005, 52, 467–488. [Google Scholar] [CrossRef]
- Keevil, G.M.; Peakall, J.; Best, J.L.; Amos, K.J. Flow structure in sinuous submarine channels: Velocity and turbulence structure of an experimental submarine channel. Mar. Geol. 2006, 229, 241–257. [Google Scholar] [CrossRef]
- Sequeiros, O.E.; Spinewine, B.; Garcia, M.H.; Beaubouef, R.T.; Sun, T.; Parker, G. Experiments on wedge-shaped deep sea sedimentary deposits in minibasins and/or on channel levees emplaced by turbidity currents. Part I. Documentation of the flow. J. Sediment. Res. 2009, 79, 593–607. [Google Scholar] [CrossRef]
- Jacobson, M.R.; Testik, F.Y. On the concentration structure of high-concentration constant-volume fluid mud gravity currents. Phys. Fluids 2013, 25, 016602. [Google Scholar] [CrossRef]
- Nogueira, H.I.S.; Adduce, C.; Alves, E.; Franca, M.J. Image analysis technique applied to lock-exchange gravity currents. Meas. Sci. Technol. 2013, 24, 047001. [Google Scholar] [CrossRef]
- Wilson, R.I.; Friedrich, H.; Stevens, C. Image thresholding process for combining photometry with intrusive flow instruments. J. Hydraul. Res. 2018, 56, 282–290. [Google Scholar] [CrossRef]




| Transducer # | x/x0 | z/z0 | Transducer # | x/x0 | z/z0 |
|---|---|---|---|---|---|
| 1 | 2.91 | 0.10 | 8 | 2.91 | 0.48 |
| 2 | 2.91 | 0.15 | 9 | 2.91 | 0.57 |
| 3 | 2.91 | 0.20 | 10 | 2.78 | 0.94 |
| 4 | 2.91 | 0.24 | 11 | 2.63 | 0.94 |
| 5 | 2.91 | 0.29 | 12 | 2.60 | 0.94 |
| 6 | 2.91 | 0.34 | 13 | 2.57 | 0.94 |
| 7 | 2.91 | 0.38 | 14 | 1.73 | 0.94 |
| Met-Flow UVP-DUO | |
| Sampling frequency (MHz) | 4 |
| Number of Bins | 128 |
| Bin width (mm) | 1.48 |
| Distance between bin centres (mm) | 1.67 |
| Measurement window (mm) | 25.9–237.36 |
| Speed of sound (ms−1) | 1480 |
| Velocity resolution (mms−1) | 2.138 |
| Velocity bandwidth (mms−1) | 547.3 |
| Cycles per pulse | 8 |
| Repetitions per profile | 32 |
| Sampling period (ms) | 15 |
| Full cycle time (s) | 1.45 |
| RF gain—US voltage (V) | 90 |
| Nikon D90 | |
| Lens | AF-S DX NIKKOR 18–105 mm |
| Camera mode | Manual |
| Capture mode | Continuous high-speed |
| Frame Rate (Hz) | 4.5 |
| Distance from free surface (m) | 2.045 |
| Shutter speed (s) | 1/200 |
| Aperture | f/3.5 |
| ISO | 200 |
| Image resolution (pixels) | 4288 × 2848 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilson, R.I.; Friedrich, H. Coupling of Ultrasonic and Photometric Techniques for Synchronous Measurements of Unconfined Turbidity Currents. Water 2018, 10, 1246. https://doi.org/10.3390/w10091246
Wilson RI, Friedrich H. Coupling of Ultrasonic and Photometric Techniques for Synchronous Measurements of Unconfined Turbidity Currents. Water. 2018; 10(9):1246. https://doi.org/10.3390/w10091246
Chicago/Turabian StyleWilson, Richard I., and Heide Friedrich. 2018. "Coupling of Ultrasonic and Photometric Techniques for Synchronous Measurements of Unconfined Turbidity Currents" Water 10, no. 9: 1246. https://doi.org/10.3390/w10091246
APA StyleWilson, R. I., & Friedrich, H. (2018). Coupling of Ultrasonic and Photometric Techniques for Synchronous Measurements of Unconfined Turbidity Currents. Water, 10(9), 1246. https://doi.org/10.3390/w10091246





