Study of Hydrodynamic Interference of Vertical-Axis Tidal Turbine Array
Abstract
1. Introduction
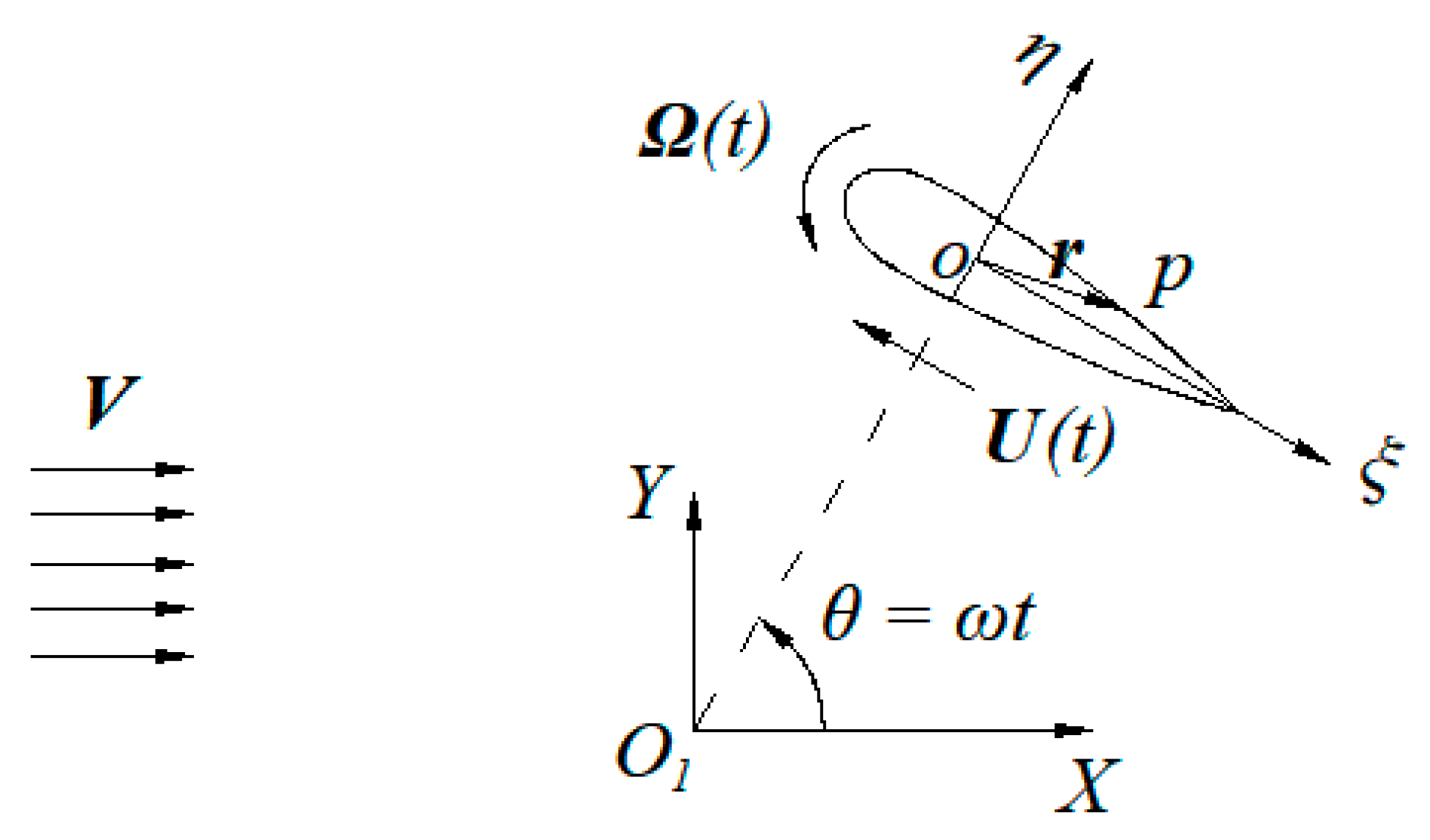
2. Methods
3. Results
3.1. Issues of Turbine Array
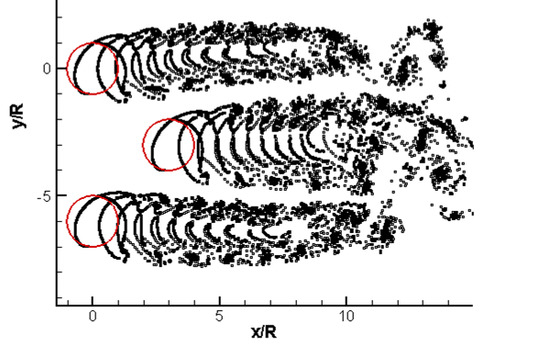
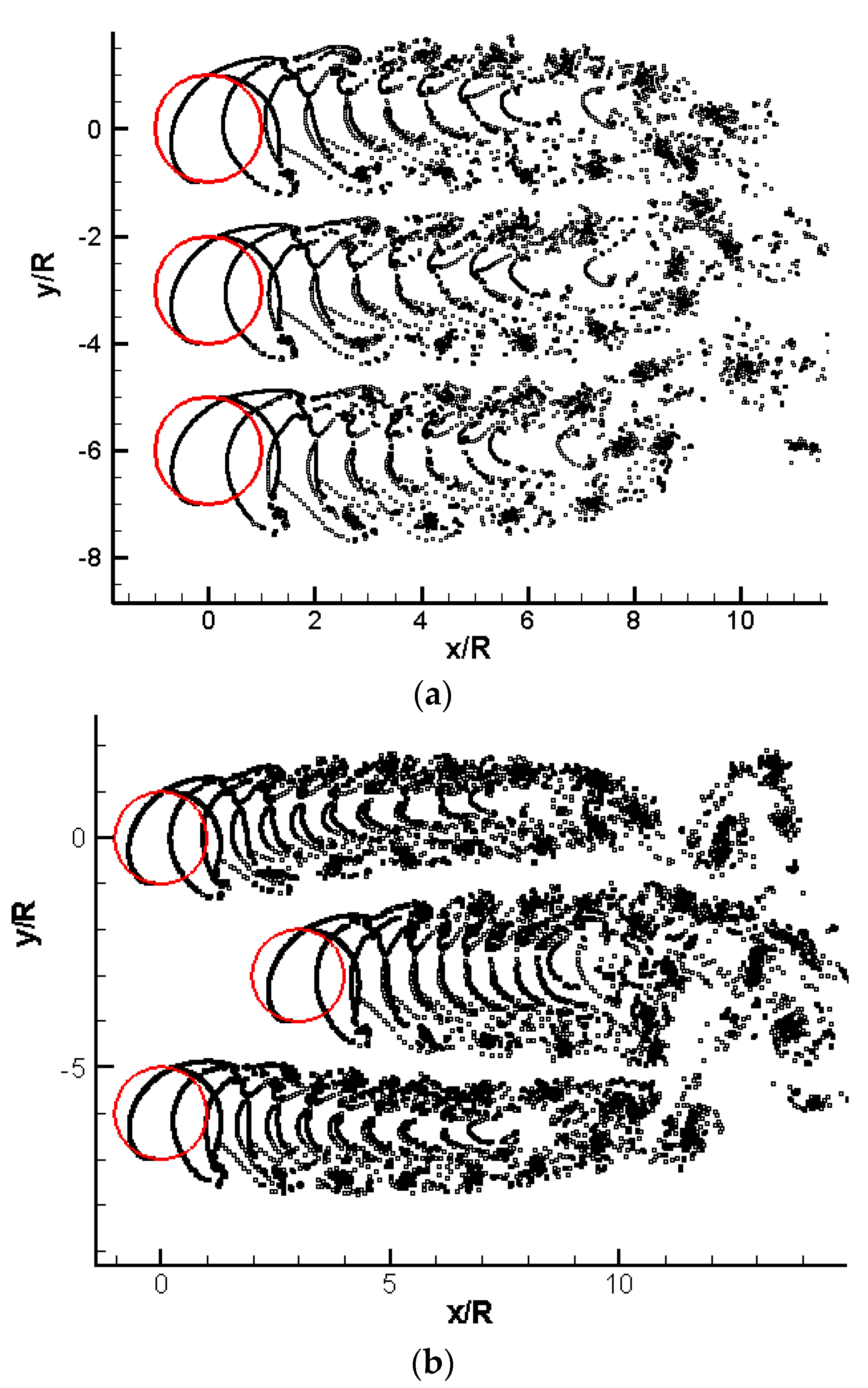
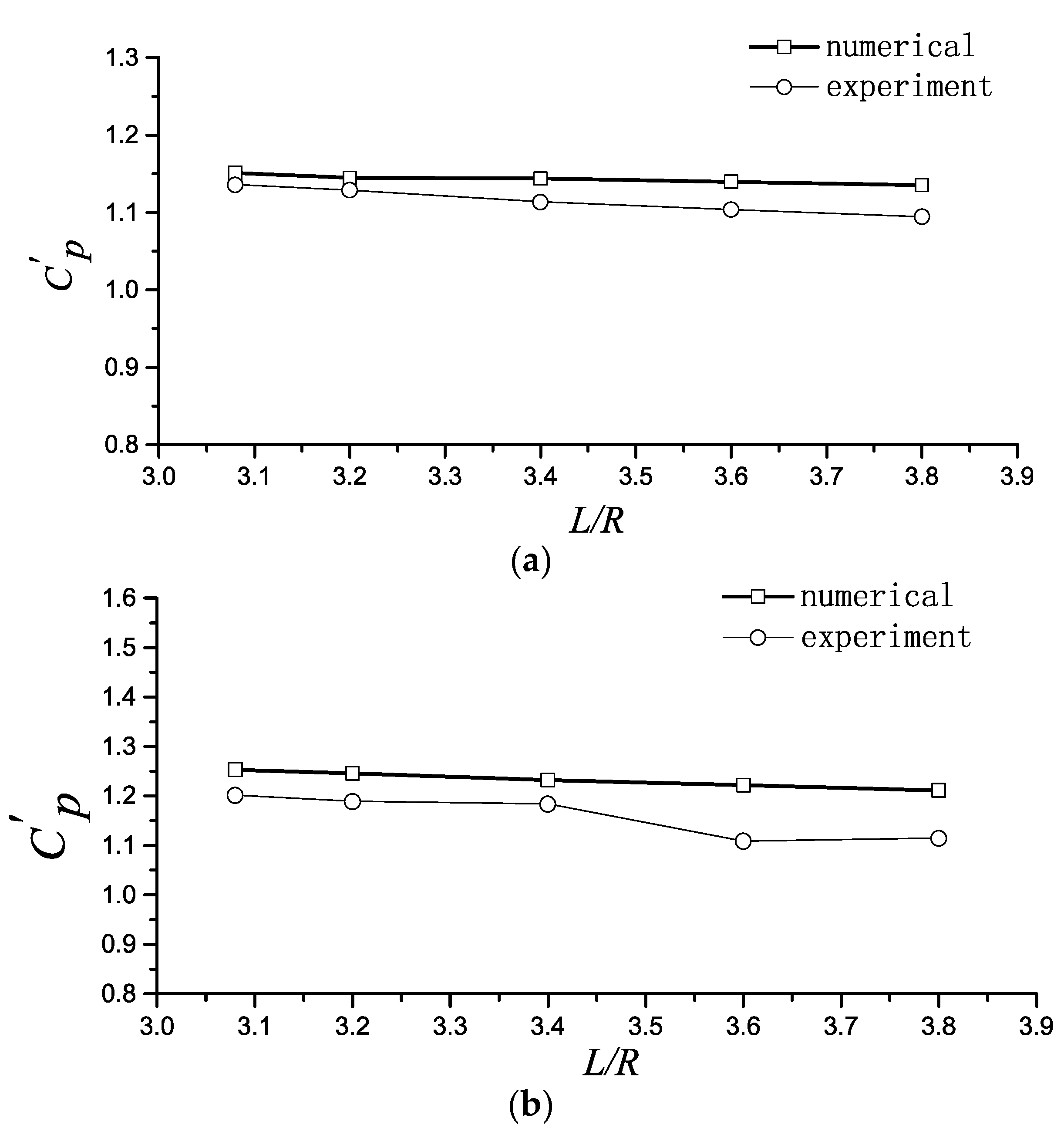
3.2. Validation of the Method
3.3. Analysis of Results
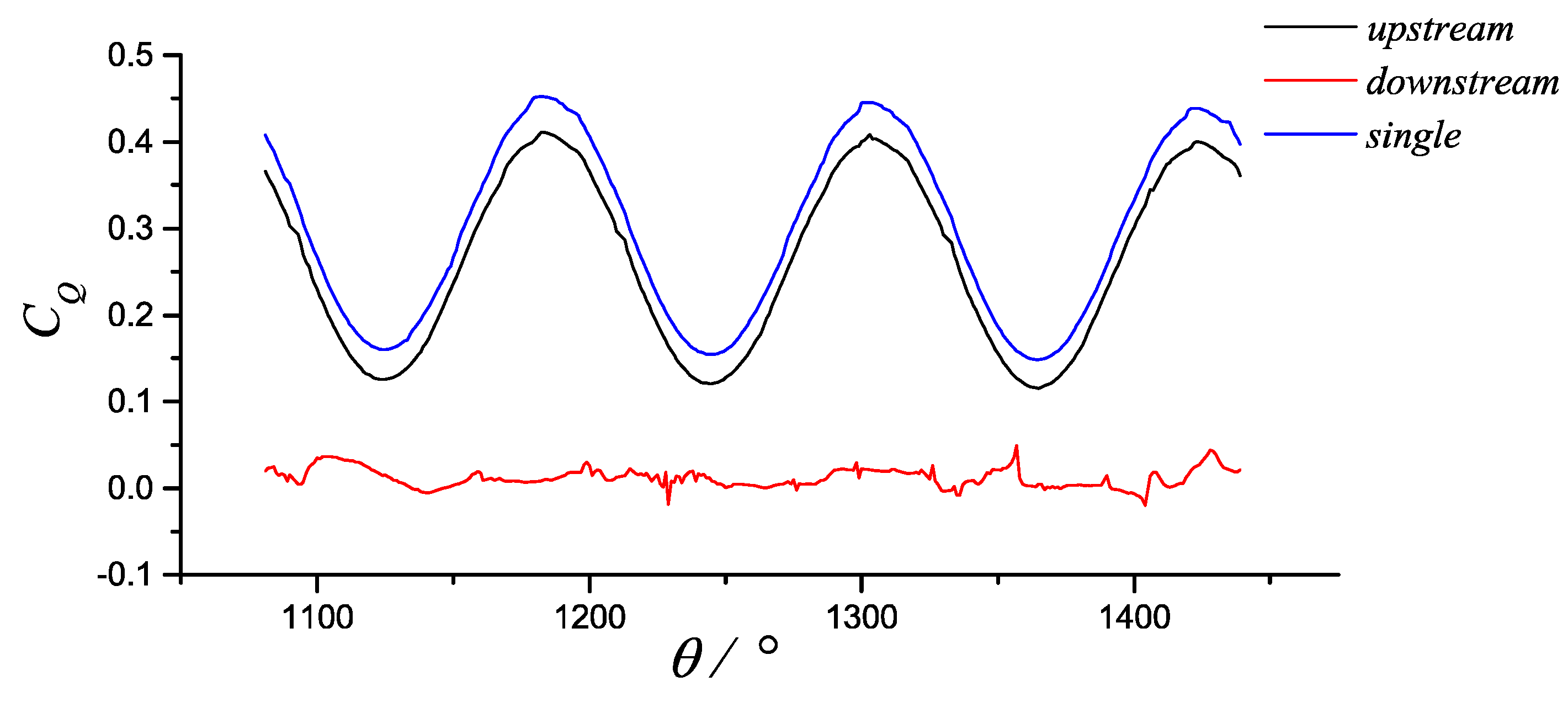
3.3.1. Cases of Ψ = 0°
3.3.2. Cases of Ψ = 90°
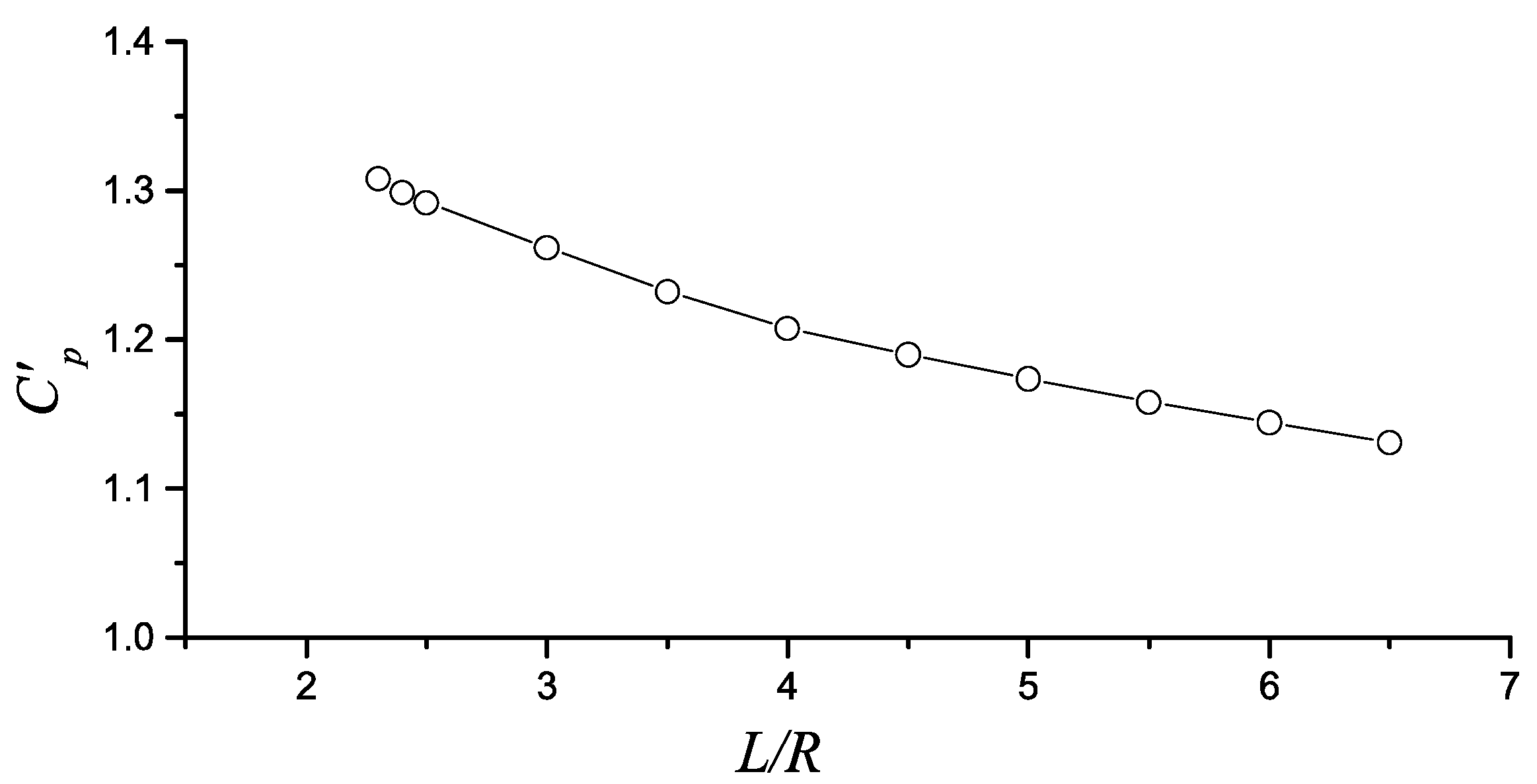
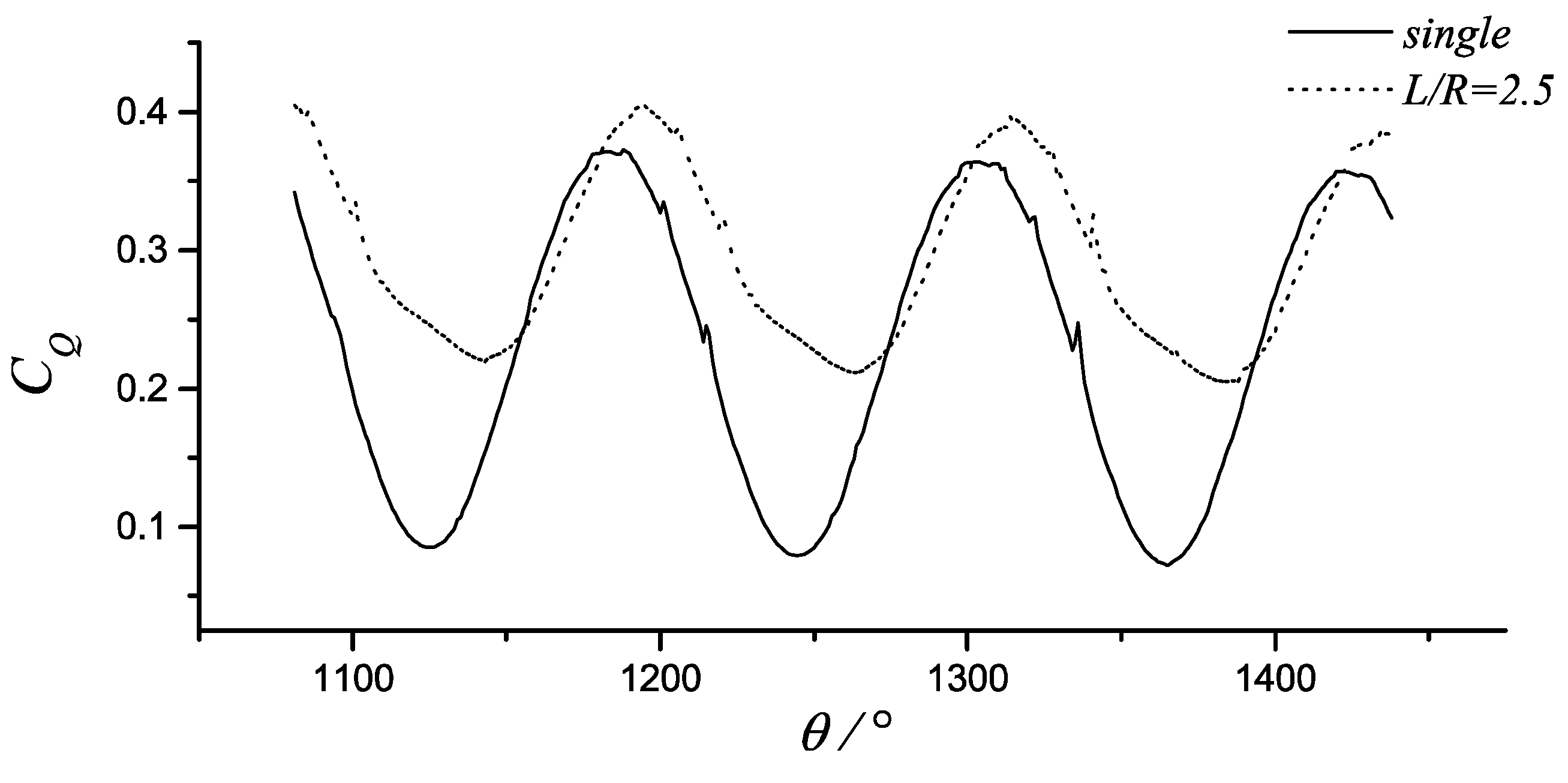
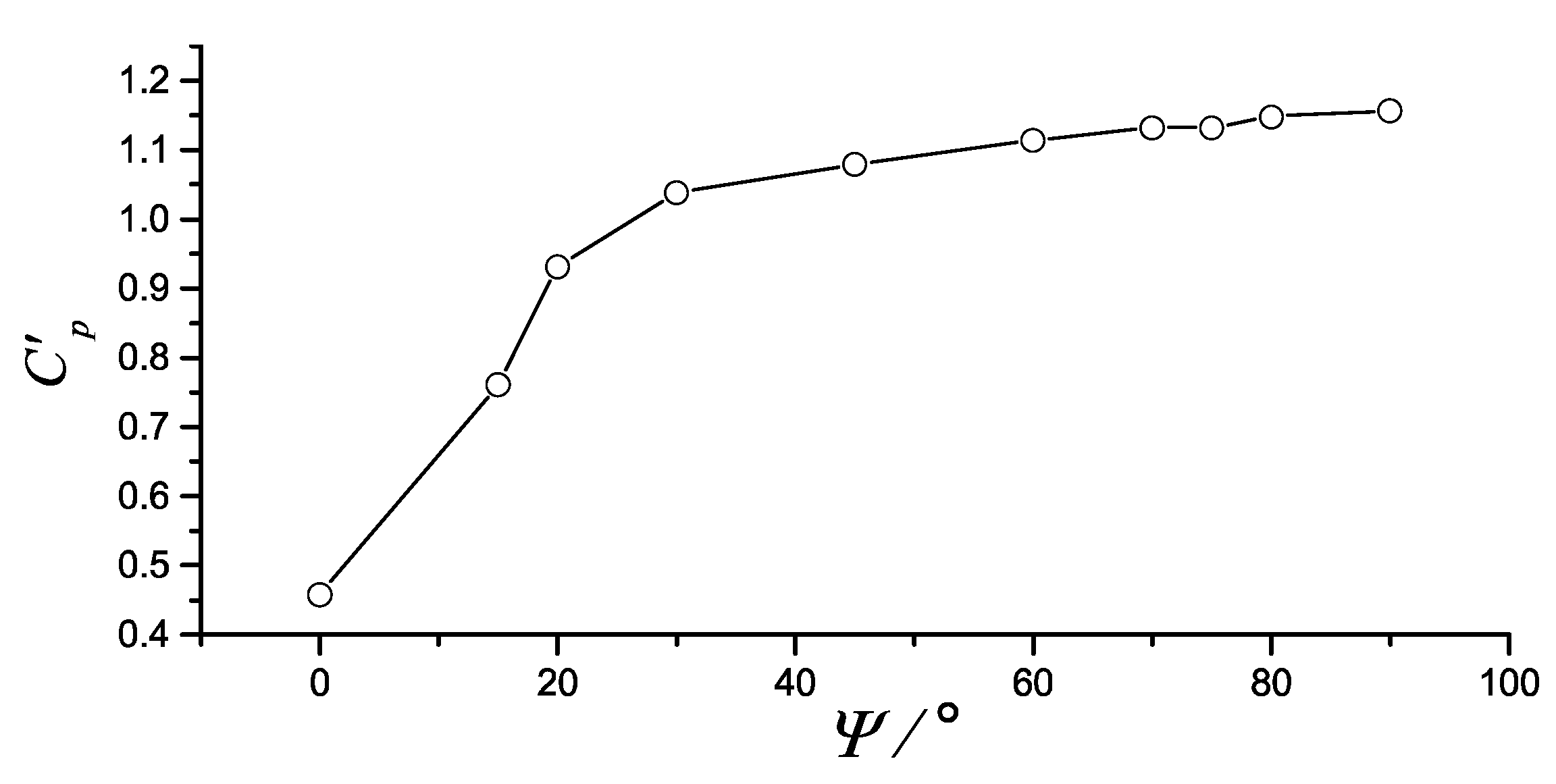
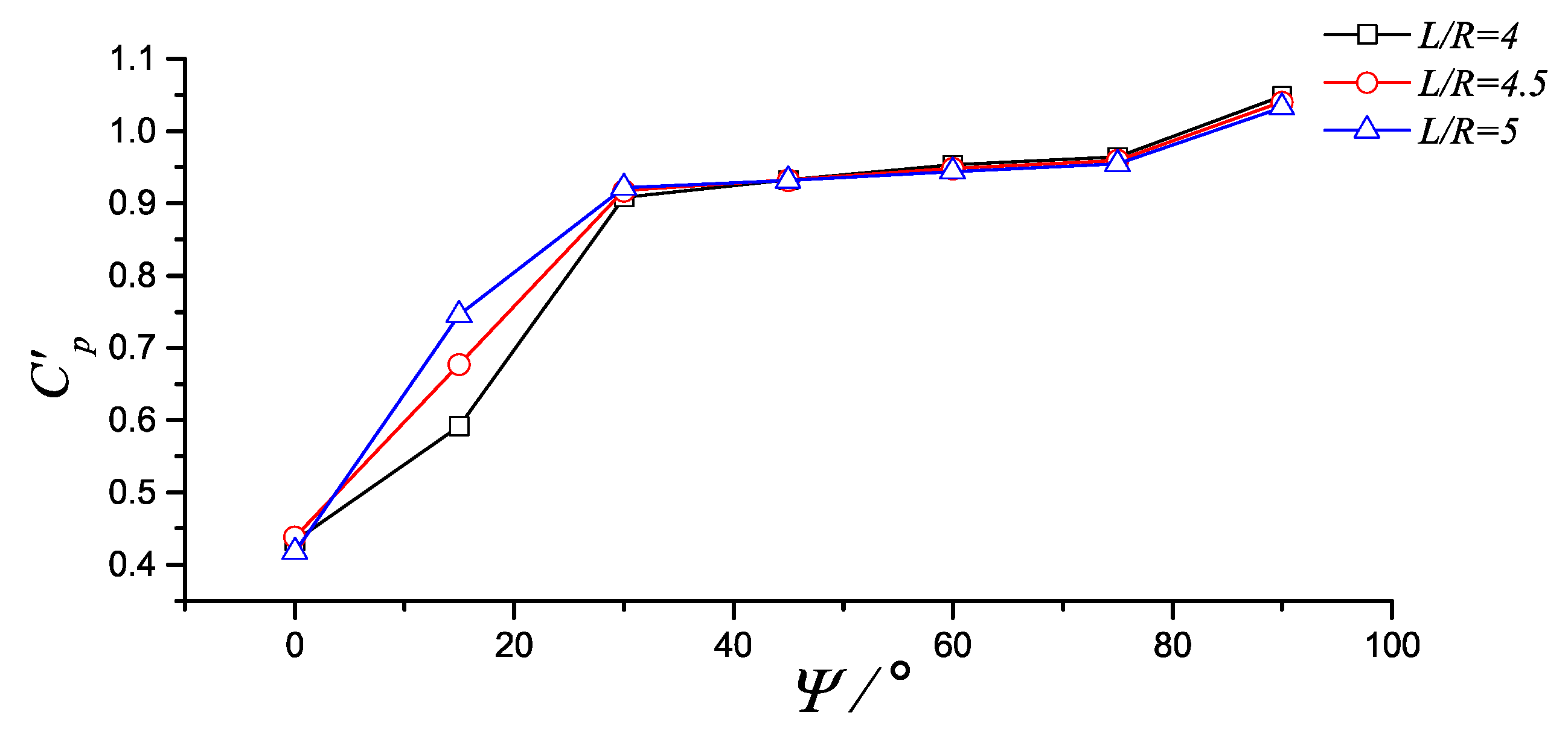
3.3.3. Case of Arbitrary Ψ
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| BEMT | Blade Element Momentum Theory |
| CFD | Computational Fluid Dynamics |
| LES | Large Eddy Simulation |
| RANS | Reynolds Average Navier-Stokes |
| BEMT | Blade Element Momentum Theory |
| Xd, Yd | coordinate spacing of the rotation centers of turbines in twin-turbine system |
| angle between the connection of the rotation centers of turbines and the X axis | |
| L | distance of the rotation centers of turbines |
| t | time |
| t0 | initial time |
| Ω | rotating angular velocity about the origin o |
| U | translational velocity of the origin o |
| V | velocity of uniform incoming flow at infinity |
| θ | azimuthal angle |
| rotating angular velocity about the rotation center of turbine | |
| velocity potential | |
| fluid domain | |
| perturbation velocity potential | |
| P | pressure on the blade surface |
| f | force on the blade |
| q | moment of the blade |
| Cq | moment coefficient of a single blade on turbine |
| F | hydrodynamic force acting on the turbine |
| Q | hydrodynamic torque acting on the turbine rotor shaft |
| resultant force coefficient of the turbine | |
| CQ | average torque coefficient of the turbine rotor shaft |
| CP | power coefficient of the turbine |
| D | diameter of turbine |
| R | radius of turbine |
| b | wingspan length of blade |
| C | chord length of blade |
| Z | blade number of a single turbine |
| λ | tip speed ratios |
| relative power coefficient of double turbines array |
References
- Yang, M.; Pation-Echeverri, D.; Yang, F. Wind power generation in China: Understanding the mismatch between capacity and generation. Renew. Energy 2012, 41, 145–151. [Google Scholar] [CrossRef]
- Yu, J.; Ji, F.; Zhang, L. An over painted oriental arts: Evaluation of the development of the Chinese renewable energy market using the wind power market as a model. Energy Policy 2009, 37, 5221–5225. [Google Scholar] [CrossRef]
- Li, Z. Numerical Simulation and Experimental Study on Hydrodynamic Characteristic of Vertical Axis Tidal Turbine. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2011. [Google Scholar]
- Bahaj, A.S. Generating electricity from the oceans. Renewable Sustainable Energy Rev. 2011, 15, 3399–3416. [Google Scholar] [CrossRef]
- Westwood, A. SeaGen installation moves forward. Renew. Energy Focus 2008, 9, 26–27. [Google Scholar] [CrossRef]
- Westwood, A. Ocean power: Wave and tidal energy review. Refocus 2004, 5, 50–55. [Google Scholar] [CrossRef]
- Open Centre Turbine. Available online: http://www.openhydro.com/Technology/Open-Centre-Turbine (accessed on 7 May 2017).
- Ocean energy technology: The Davis Hydro Turbine. Refocus 2001, 2, 44–47. [CrossRef]
- Lago, L.I.; Ponta, F.L.; Chen, L. Advances and trends in hydrokinetic turbine systems. Energy Sustainable Dev. 2010, 14, 287–296. [Google Scholar] [CrossRef]
- Sathit, P.; Chaiwat, K.; Yodchai, T. Experimental investigation of helical tidal turbine characteristics with different twists. Energy Procedia 2015, 79, 409–414. [Google Scholar]
- Zhou, Z.; Benbouzid, M.; Charpentiera, J.F. Developments in large marine current turbine technologies—A review. Renewable Sustainable Energy Rev. 2017, 71, 852–858. [Google Scholar] [CrossRef]
- Coiro, D.P.; Nicolosi, F.; De Marco, A.; Melone, S.; Montella, F. Dynamic behavior of the patented kobold tidal current turbine: Numerical and experimental aspects. Acta Polythecnica Int. J. 2005, 45, 77–84. [Google Scholar]
- Guo, F. Performance Analysis of Vertical-Axis Tidal Current Turbines and Optimizing Turbines Array. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2013. [Google Scholar]
- Bai, L.; Spence, R.R.G.; Dudziak, G. Investigation of the influence of array arrangement and spacing on Tidal Energy Converter (TEC) performance using a 3-dimensional CFD model. In Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009. [Google Scholar]
- Churchfield, M.J.; Li, Y.; Moriarty, P.J. A large-eddy simulation study of wake propagation and power production in an array of tidal-current turbines. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southhampton, UK, 4–9 September 2011. [Google Scholar]
- Turnock, S.R.; Phillips, A.B.; Banks, J. Modelling tidal current turbine wakes using a coupled RANS-BEMT approach as a tool for analyzing power capture of arrays of turbines. Ocean Eng. 2011, 38, 1300–1307. [Google Scholar] [CrossRef]
- Antheaume, S.; Maitre, T.; Achard, J.L. Hydraulic Darrieus turbines efficiency for free fluid flow conditions versus power farms conditions. Renew. Energy 2008, 33, 2186–2198. [Google Scholar] [CrossRef]
- Li, Y.; Calisal, S.M. Preliminary investigation of power output of two typical two-turbine tidal current systems. In Proceedings of the ASME Conference, New York, NY, USA, 31 May–5 June 2009. [Google Scholar]
- Goude, A.; Agren, O. Numerical simulation of a farm of vertical axis marine current turbines. In Proceedings of the ASME 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010. [Google Scholar]
- Gebreslassie, M.G.; Tabor, G.R.; Belmont, M.R. Investigation of the performance of a staggered configuration of tidal turbines using CFD. Renew. Energy 2015, 80, 690–698. [Google Scholar] [CrossRef]
- Zanforlin, S.; Burchi, F.; Bitossi, N. Hydrodynamic interactions between three closely-spaced Vertical Axis Tidal Turbines. Energy Procedia 2016, 101, 520–527. [Google Scholar] [CrossRef]
- Giorgetti, S.; Pellegrini, G.; Zanforlin, S. CFD investigation on the aerodynamic interferences between medium-solidity Darrieus Vertical Axis Wind Turbines. Energy Procedia 2015, 81, 227–239. [Google Scholar] [CrossRef]
- Li, G.; Wu, W.; Xie, Y. Analysis of hydrodynamic performance of vertical-axis tidal-current turbine with experiment in towing tank. Shipbuild. Chin. 2014, 55, 143–148. [Google Scholar]
- Xie, Y.; Li, G.; Zhang, Z. Experimental analysis on arrangement rule of the twin-turbine systems with vertical axis tidal current turbines. Acta Energiae Solaris Sin. 2017, 38, 537–542. [Google Scholar]








© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Chen, Q.; Gu, H. Study of Hydrodynamic Interference of Vertical-Axis Tidal Turbine Array. Water 2018, 10, 1228. https://doi.org/10.3390/w10091228
Li G, Chen Q, Gu H. Study of Hydrodynamic Interference of Vertical-Axis Tidal Turbine Array. Water. 2018; 10(9):1228. https://doi.org/10.3390/w10091228
Chicago/Turabian StyleLi, Guangnian, Qingren Chen, and Hanbin Gu. 2018. "Study of Hydrodynamic Interference of Vertical-Axis Tidal Turbine Array" Water 10, no. 9: 1228. https://doi.org/10.3390/w10091228
APA StyleLi, G., Chen, Q., & Gu, H. (2018). Study of Hydrodynamic Interference of Vertical-Axis Tidal Turbine Array. Water, 10(9), 1228. https://doi.org/10.3390/w10091228