Quantitative Agricultural Flood Risk Assessment Using Vulnerability Surface and Copula Functions
Abstract
1. Introduction
2. Materials and Methods
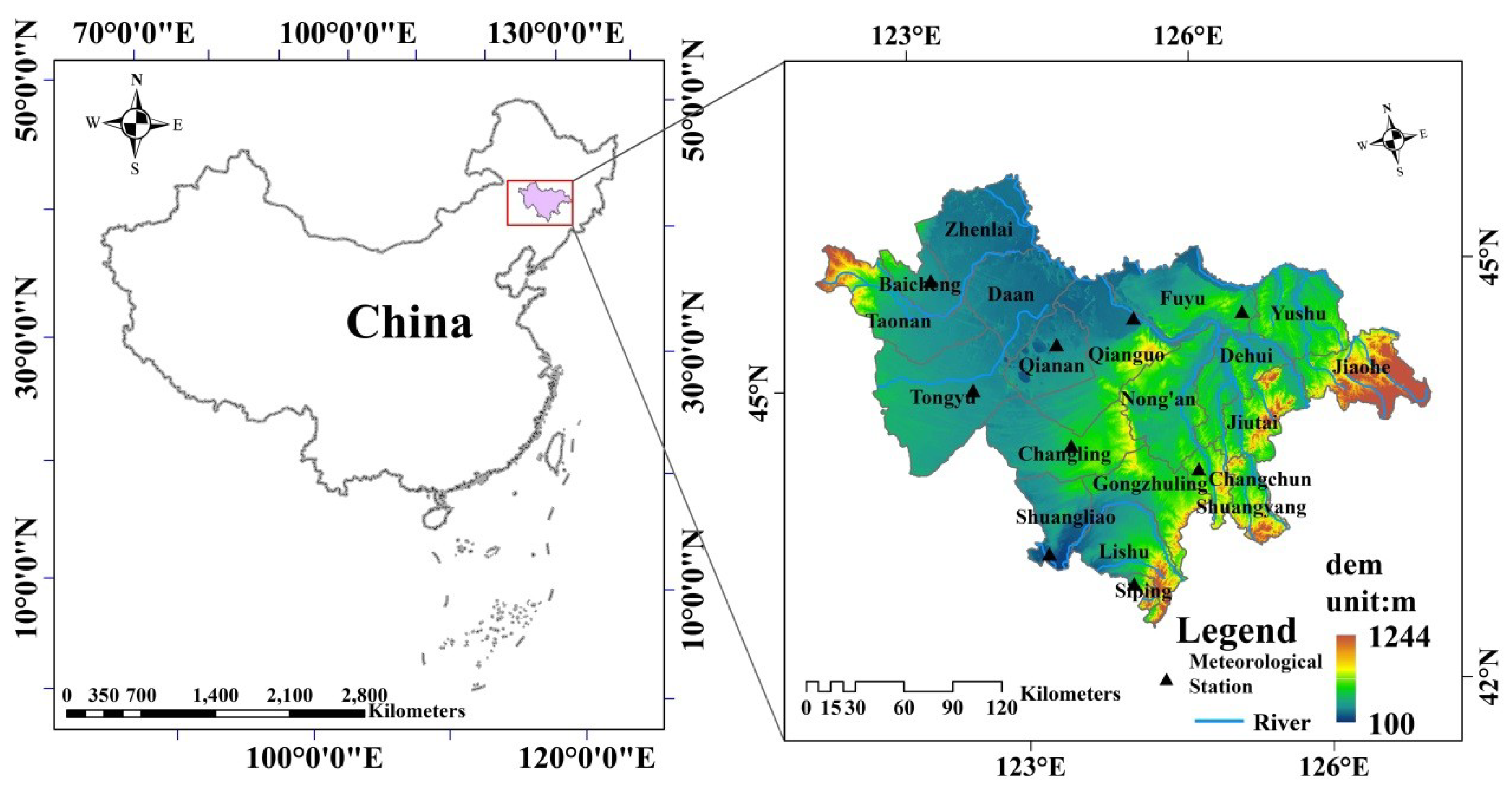
2.1. Study Region
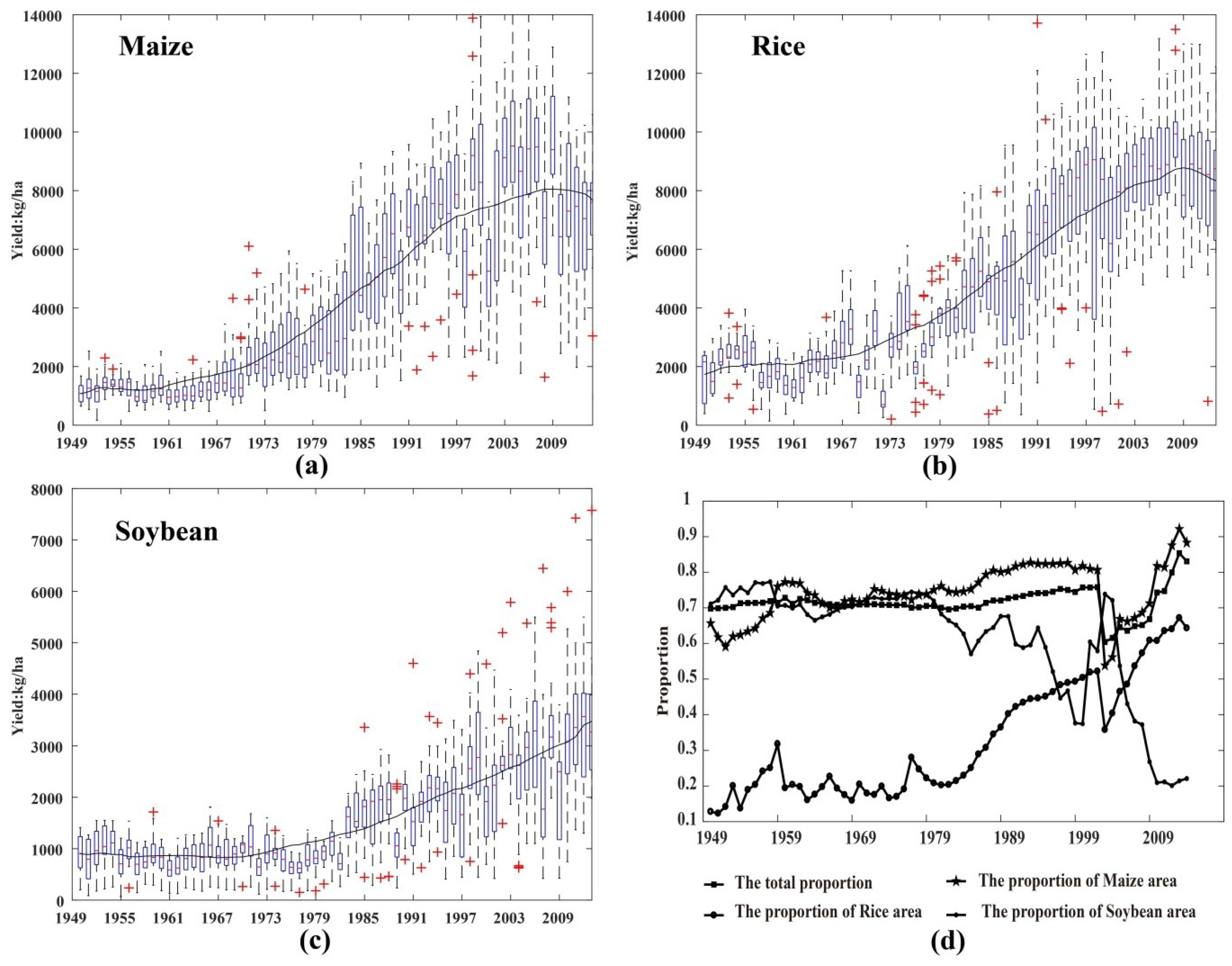
2.2. Data Source and Processing
2.2.1. Multifractal Detrended Fluctuation Analysis Method
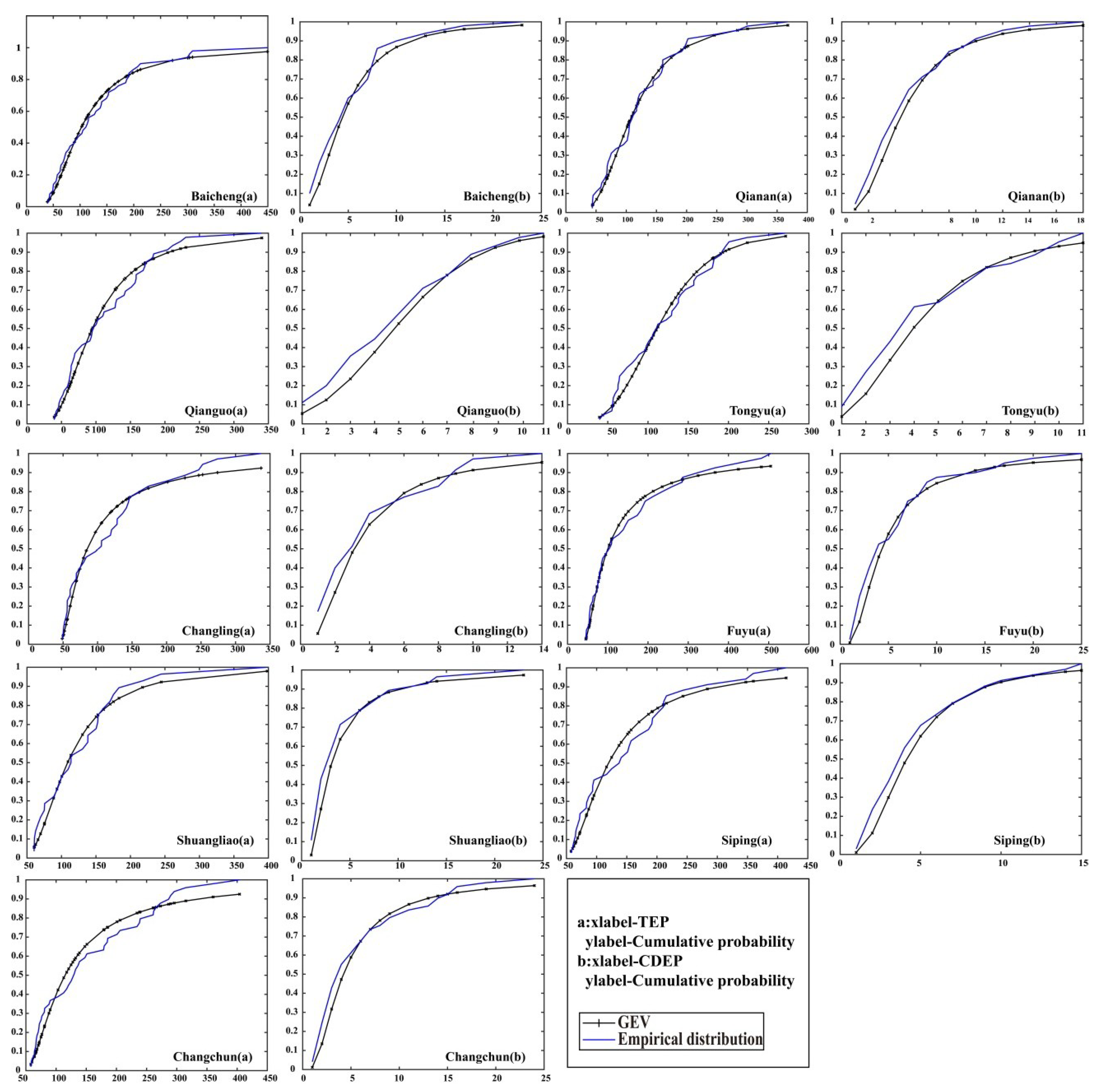
2.2.2. Marginal Distribution Functions
2.2.3. Joint Distribution Function of the Flood Indicators
2.2.4. Joint Return Period of Flood Indicators
2.2.5. The Vulnerability Surface Model
2.2.6. Quantitative Agricultural Flood Risk Assessment
3. Results
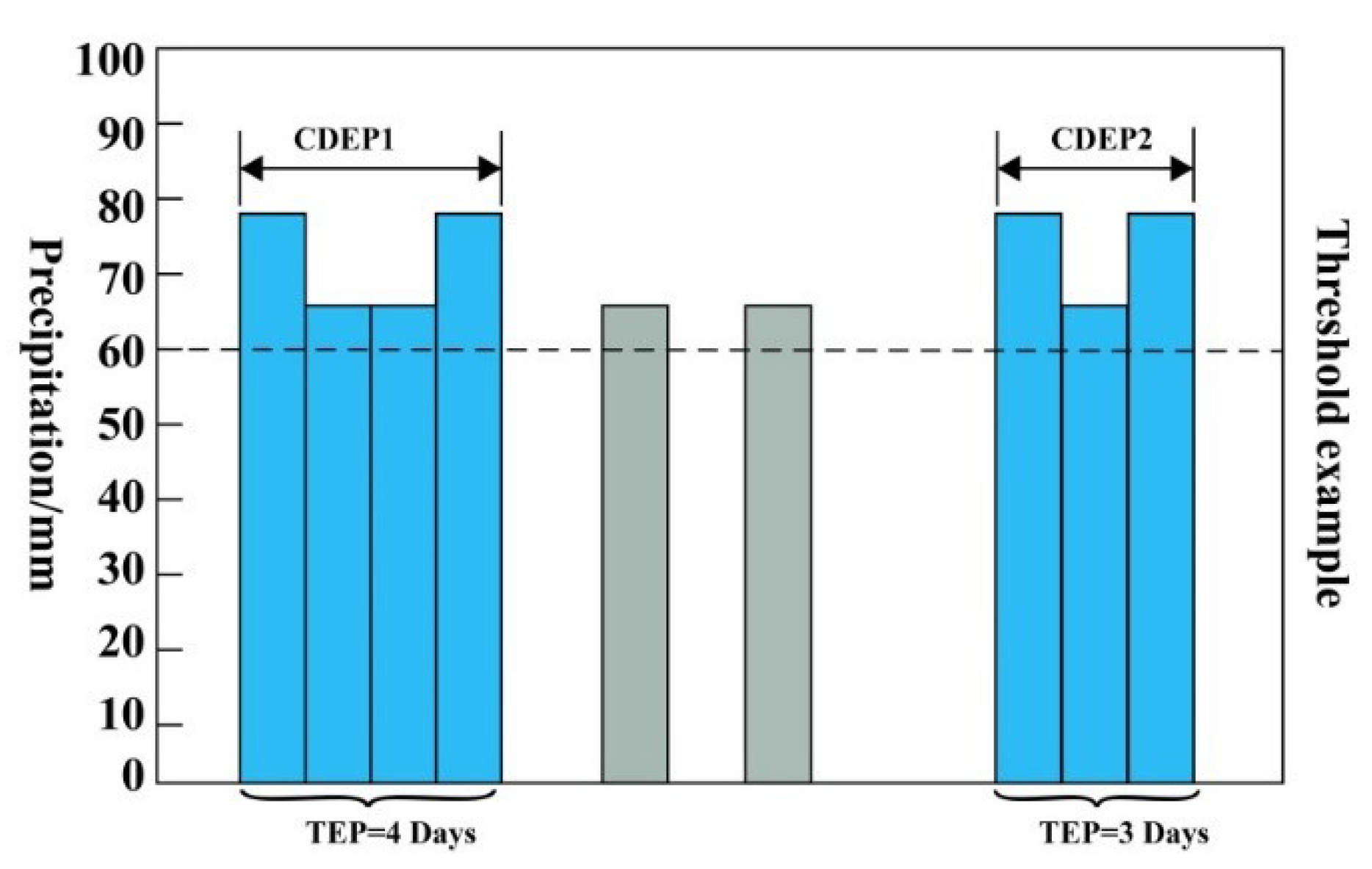
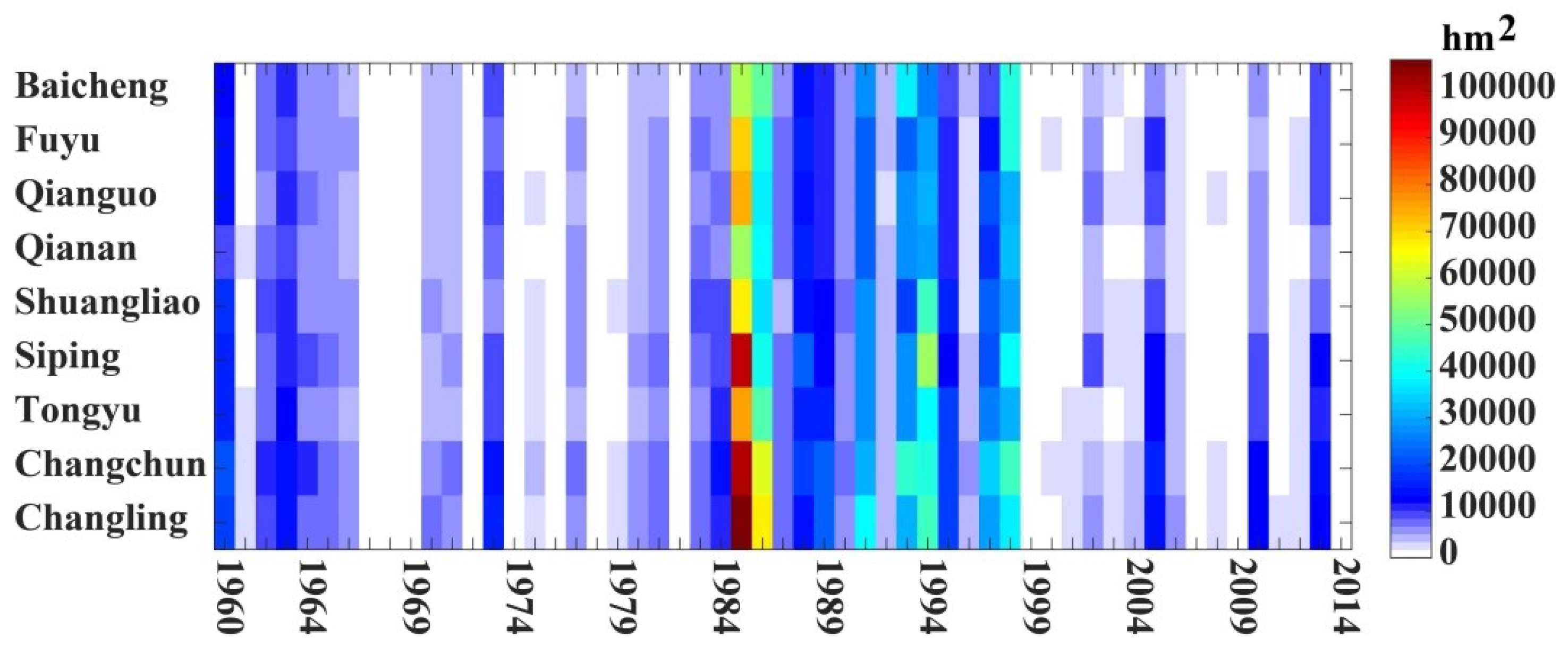
3.1. Determining the Threshold of Extreme Precipitation Events
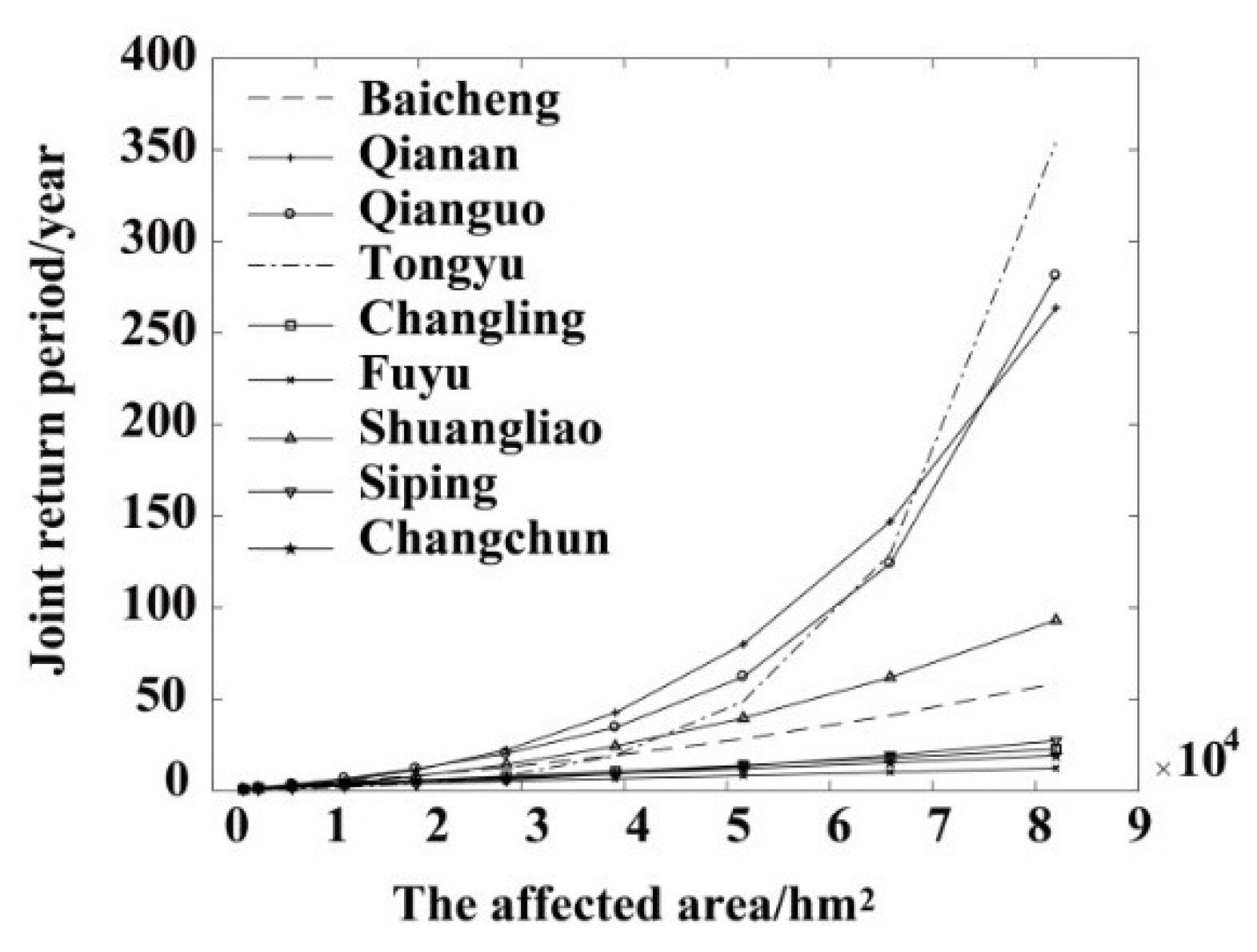
3.2. Joint Return Period of Flood Hazards
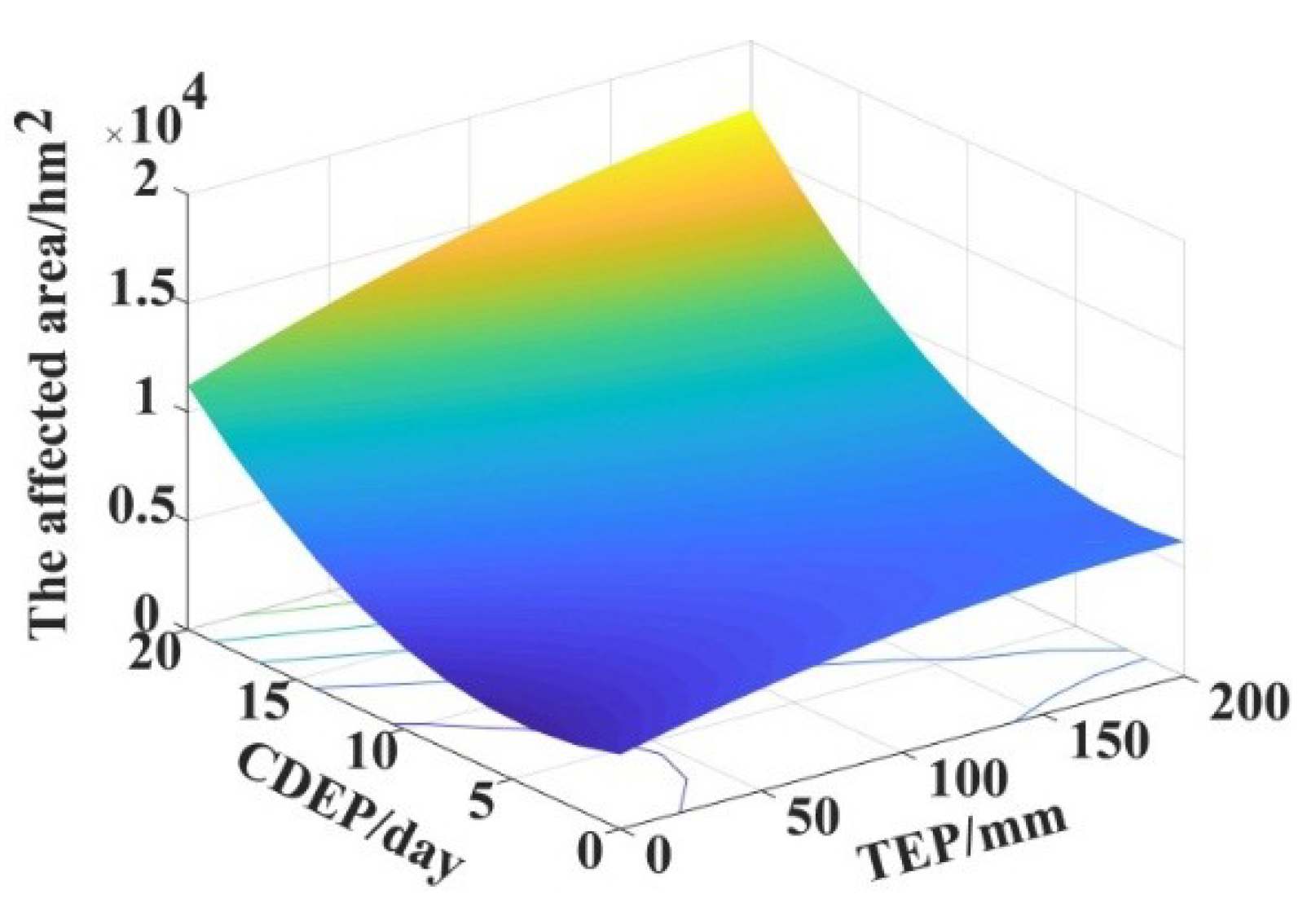
3.3. Vulnerability Surface Model
3.4. Risk Curves
4. Discussion
5. Conclusions
- (1)
- The CDEP and TEP both had a tendency of increase in the MJP. The threshold of extreme precipitation events gradually decreases from east to west, and their spatial distribution is similar to that of the precipitation in this region. The CDEP highly correlates with the TEP at each station and all correlation coefficients pass the 0.05 significance test;
- (2)
- The shortest joint return period was determined for Fuyu and Changchun, which indicates that the flood hazard level of the two regions is higher. On contrary, the longest joint return period was obtained for Tongyu and Qianguo at the same intensity of flood indicators; and
- (3)
- We found that the agricultural flood risk of the MJP gradually decreases from east to west, and the spatial distribution of risk in the area with the same spatial pattern of that of the flood hazard, which further illustrates that the amount and duration of extreme precipitation are the important factors affecting agricultural losses in the region.
Author Contributions
Funding
Conflicts of Interest
References
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Change, C. Mitigation of Climate Change; Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Wang, Y.; Zhang, Q.; Singh, V.P. Spatiotemporal Patterns of Precipitation Regimes in the Huai River Basin, China, and Possible Relations with ENSO Events. Nat. Hazards 2016, 82, 2167–2185. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Singh, V.P.; Gu, X.; Kong, D.; Xiao, M. Impacts of ENSO and ENSO Modoki+A Regimes on Seasonal Precipitation Variations and Possible Underlying Causes in the Huai River Basin, China. J. Hydrol. 2016, 533, 308–319. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood Hazard Risk Assessment Model Based on Random Forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Jonkman, S.N.; Kok, M.; Vrijling, J.K. Flood Risk Assessment in the Netherlands: A Case Study for Dike Ring South Holland. Risk Anal. 2008, 28, 1357–1374. [Google Scholar] [CrossRef] [PubMed]
- Tapia-Silva, F.O.; Itzerott, S.; Foerster, S.; Kuhlmann, B.; Kreibich, H. Estimation of Flood Losses to Agricultural Crops Using Remote Sensing. Phys. Chem. Earth 2011, 36, 253–265. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Carisi, F.; Castellarin, A.; Brath, A. Evolution of Flood Risk over Large Areas: Quantitative Assessment for the Po River. J. Hydrol. 2015, 527, 809–823. [Google Scholar] [CrossRef]
- Ma, L. Design and Implementation of Multi-Scale Flood Disaster Risk Assessment Model Based on GIS; Capital Normal University: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Yan, S. National Flood Disaster in 2013. China Flood Drought Manag. 2014, 20, 18–19. (In Chinese) [Google Scholar]
- National Flood Control and Drought Relief Headquarters. China Water and Drought Disaster Bulletin in 2013; China Water Conservancy and Hydropower Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Gao, F.; Dong, L.; Zhang, B. Characteristics Analysis of Flood Disasters in Jilin Province in the 1990s. Meteorol. Disaster Prev. 2002, 10, 14–17. (In Chinese) [Google Scholar]
- Li, J.; Ren, H.; Liu, S.; Tang, X. Quantitative Analysis of Remote Sensing Monitoring Information of Heavy Rain and Flood Disasters in Jilin Province in Summer of 2010. Meteorol. Disaster Prev. 2012, 19, 38–41. (In Chinese) [Google Scholar]
- Förster, S.; Kuhlmann, B.; Lindenschmidt, K.E.; Bronstert, A. Assessing Flood Risk for a Rural Detention Area. Nat. Hazard. Earth Syst. 2008, 8, 311–322. [Google Scholar] [CrossRef]
- Lei, X.; Zhang, Q.; Zhou, A.L.; Ran, H. Assessment of Flood Catastrophe Risk for Grain Production at the Provincial Scale in China Based on the BMM Method. J. Integr. Agric. 2013, 12, 2310–2320. [Google Scholar]
- Sun, Z.; Liu, X.; Zhu, X.; Pan, Y. Agriculture Flood Risk Assessment Based on Information Diffusion. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 4391–4394. [Google Scholar]
- Gain, A.K.; Mojtahed, V.; Biscaro, C.; Balbi, S.; Giupponi, C. An Integrated Approach of Flood Risk Assessment in the Eastern Part of Dhaka city. Nat. Hazards 2015, 79, 1499–1530. [Google Scholar] [CrossRef]
- Duan, H.L.; Wang, C.L.; Tang, L.S.; Chen, H. Risk Assessments of Late Rice Flood Disaster in South China. Chin. J. Ecol. 2014, 33, 1368–1373. (In Chinese) [Google Scholar]
- Ghosh, A.; Kar, S.K. Application of Analytical Hierarchy Process (AHP) for Flood Risk Assessment: A Case Study in Malda District of West Bengal, India. Nat. Hazards 2018, 1–20. [Google Scholar] [CrossRef]
- Guo, E.; Zhang, J.; Ren, X.; Zhang, Q.; Sun, Z. Integrated Risk Assessment of Flood Disaster Based on Improved Set Pair Analysis and the Variable Fuzzy Set Theory in Central Liaoning Province, China. Nat. Hazards 2014, 74, 947–965. [Google Scholar] [CrossRef]
- Derdous, O.; Djemili, L.; Bouchehed, H.; Tachi, S.E. A GIS Based Approach for the Prediction of the Dam Break Flood Hazard—A Case Study of Zardezas Reservoir “Skikda, Algeria”. J. Water Land Dev. 2015, 7, 15–20. [Google Scholar] [CrossRef]
- Luu, C.; Meding, J.V.; Kanjanabootra, S. Assessing Flood Hazard Using Flood Marks and Analytic Hierarchy Process Approach: A Case Study for the 2013 Flood Event in Quang Nam, Vietnam. Nat. Hazards 2018, 90, 1031–1050. [Google Scholar] [CrossRef]
- Wu, F.; Sun, Y.; Sun, Z.; Wu, S.; Zhang, Q. Assessing Agricultural System Vulnerability to Floods: A Hybrid Approach Using Emergy and a Landscape Fragmentation Index. Ecol. Indic. 2017. [Google Scholar] [CrossRef]
- Paprotny, D.; Sebastian, A.; Morales-Nápoles, O.; Jonkman, S.N. Trends in Flood Losses in Europe over the Past 150 Years. Nat. Commun. 2018, 9, 1985. [Google Scholar] [CrossRef] [PubMed]
- Salman, A.M.; Li, Y. Flood Risk Assessment, Future Trend Modeling, and Risk Communication: A Review of Ongoing Research. Nat. Hazards Rev. 2018, 19, 04018011. [Google Scholar] [CrossRef]
- Hsu, W.K.; Huang, P.C.; Chang, C.C.; Chen, C.W.; Hung, D.M.; Chiang, W.L. An Integrated Flood Risk Assessment Model for Property Insurance Industry in Taiwan. Nat. Hazards 2011, 58, 1295–1309. [Google Scholar] [CrossRef]
- Papathoma-Koehle, M.; Keiler, M.; Totschnig, R.; Glade, T. Improvement of Vulnerability Curves Using Data from Extreme Events: Debris Flow Event in South Tyrol. Nat. Hazards 2012, 64, 2083–2105. [Google Scholar] [CrossRef]
- Zischg, A.P.; Felder, G.; Weingartner, R.; Quinn, N.; Coxon, G.; Neal, J.; Freer, J.; Bates, P. Effects of Variability in Probable Maximum Precipitation Patterns on Flood Losses. Hydrol. Earth Syst. Sci. 2018, 22, 2759–2773. [Google Scholar] [CrossRef]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T.R. Review of Trend Analysis and Climate Change Projections of Extreme Precipitation and Floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef]
- Ming, X.; Xu, W.; Li, Y.; Du, J.; Liu, B.; Shi, P. Quantitative Multi-Hazard Risk Assessment with Vulnerability Surface and Hazard Joint Return Period. Stoch. Environ. Res. Risk Assess. 2015, 29, 35–44. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, J.; Xu, Y.; Mu, J. Effects of Climate Change on Cultivation Patterns of Spring Maize and Its Climatic Suitability in Northeast China. Agric. Ecosyst. Environ. 2015, 202, 178–187. [Google Scholar] [CrossRef]
- Guo, E.; Zhang, J.; Wang, Y.; Alu, S.; Wang, R.; Li, D.; Ha, S. Assessing Non-Linear Variation of Temperature and Precipitation for Different Growth Periods of Maize and their Impacts on Phenology in the Midwest of Jilin Province, China. Theor. Appl. Climatol. 2018, 132, 685–699. [Google Scholar] [CrossRef]
- Wen, K. Chinese Meteorological Disasters Ceremony (Jilin Volume); China Meteorological Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Du, H.; Wu, Z.; Zong, S.; Meng, X.; Wang, L. Assessing the Characteristics of Extreme Precipitation over Northeast China Using the Multifractal Detrended Fluctuation Analysis. J. Geophys. Res. 2013, 118, 6165–6174. [Google Scholar] [CrossRef]
- Du, H.; Wu, Z.; Li, M.; Jin, Y.; Zong, S.; Meng, X. Characteristics of Extreme Daily Minimum and Maximum Temperature over Northeast China, 1961–2009. Theor. Appl. Climatol. 2013, 111, 161–171. [Google Scholar] [CrossRef]
- Baranowski, P.; Krzyszczak, J.; Slawinski, C.; Hoffmann, H.; Kozyra, J.; Nieróbca, A.; Gluza, A. Multifractal Analysis of Meteorological Time Series to Assess Climate Impacts. Clim. Res. 2015, 65, 39–52. [Google Scholar] [CrossRef]
- Guo, E.; Zhang, J.; Si, H.; Dong, Z.; Cao, T.; Lan, W. Temporal and Spatial Characteristics of Extreme Precipitation Events in the Midwest of Jilin Province Based on Multifractal Detrended Fluctuation Analysis Method and Copula Functions. Theor. Appl. Climatol. 2016, 130, 597–607. [Google Scholar] [CrossRef]
- Timonina, A.; Hochrainer-Stigler, S.; Pflug, G.; Jongman, B.; Rojas, R. Structured Coupling of Probability Loss Distributions: Assessing Joint Flood Risk in Multiple River Basins. Risk Anal. 2015, 35, 2102–2119. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Liu, X.; Xie, W.; Wu, J.; Zhang, P. The Return Period Analysis of Natural Disasters with Statistical Modeling of Bivariate Joint Probability Distribution. Risk Anal. 2013, 33, 134–145. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ren, X.; Li, Y. Analysis of Extreme Precipitation Characteristics in Low Mountain Areas Based on Three-dimensional Copulas—Taking Kuandian County as an Example. Theor. Appl. Climatol. 2015, 128, 169–179. [Google Scholar] [CrossRef]
- Murray, A.T. Quantitative geography. J. Reg. Sci. 2010, 50, 143–163. [Google Scholar] [CrossRef]
- Bernaola-Galván, P.; Ivanov, P.C.; Amaral, L.A.N.; Stanley, H.E. Scale Invariance in the Nonstationarity of Human Heart Rate. Phys. Rev. Lett. 2001, 87, 168105. [Google Scholar] [CrossRef] [PubMed]
- Ren, B.; Zhang, J.; Li, X.; Fan, X.; Dong, S.; Liu, P.; Zhao, B. Effects of Waterlogging on the Yield and Growth of Summer Maize under Field Conditions. Can. J. Plant. Sci. 2014, 94, 23–31. [Google Scholar] [CrossRef]
- International Strategy for Disaster Reduction. Living with Risk: A Global Review of Disaster Reduction Initiatives; United Nations Press: New York, NY, USA, 2004. [Google Scholar]
- Liu, X.; Zhang, J.; Ma, D.; Bao, Y.; Tong, Z.; Liu, X. Dynamic Risk Assessment of Drought Disaster for Maize Based on Integrating Multi-sources Data in the Region of the Northwest of Liaoning Province, China. Nat. Hazards 2013, 65, 1393–1409. [Google Scholar] [CrossRef]
- Sun, J. Risk Assessment of Rainstorm and Flood Disaster in Jilin Province Based on GIS and RS Technology; Northeast Normal University: Changchun, China, 2010. (In Chinese) [Google Scholar]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Dai, Y.; Watanabe, S.; Kim, H.; Kanae, S. Global flood risk under climate change. Nat. Clim. Chang. 2013, 3, 816–821. [Google Scholar] [CrossRef]
- Jung, Y.; Shin, Y.; Jang, C.H.; Kum, D.; Kim, Y.S.; Lim, K.J.; Kim, H.B.; Park, T.S.; Lee, S.O. Estimation of Flood Risk Index Considering the Regional Flood Characteristics: A Case of South Korea. Paddy Water Environ. 2014, 12, 41–49. [Google Scholar] [CrossRef]
- Shaikh, M.S.; Shariot-Ullah, M.; Ali, M.A.; Adham, A.K.M. Flood Disaster Risk Reduction and Adaptation around the Coastal Area of Bangladesh. J. Environ. Sci. Nat. Resour. 2015, 6, 53–57. [Google Scholar] [CrossRef]
- Ying, X.U.; Zhang, B.; Zhou, B.T.; Dong, S.Y.; Li, Y.U.; Rou-Ke, L.I. Projected Flood Risks in China Based on Cmip5. Adv. Clim. Chang. Res. 2014, 5, 57–65. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; McIntyre, P.B.; Gessner, M.O.; Dudgeon, D.; Prusevich, A.; Green, P.; Davies, P.M. Global Threats to Human Water Security and River Biodiversity. Nature 2010, 467, 555–561. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Han, S.; Xu, Q. The Application Intention and Driving Factors of Agricultural Low-Carbon Technology: Based on the Investigation of Scale Farmers in Jiangxi. Chin. J. Ecol. Econ. 2018, 34, 54–60. (In Chinese) [Google Scholar]
- Norse, D. Low Carbon Agriculture: Objectives and Policy Pathways. Environ. Dev. 2012, 1, 25–39. [Google Scholar] [CrossRef]
| Copula Function | Parameter Space | |
|---|---|---|
| Frank Copula | ||
| Clayton Copula | ||
| Gumbel Copula |
| Stations | Changchun | Tongyu | Changling | Qianan | Qianguo | Shuangliao | Fuyu | Baicheng | Siping |
|---|---|---|---|---|---|---|---|---|---|
| threshold | 47.8 | 38.3 | 48.2 | 38.4 | 37.1 | 58.5 | 43 | 38.5 | 56.6 |
| Indicators | Parameters | Changchun | Tongyu | Changling | Qianan | Qianguo | Shuangliao | Fuyu | Baicheng | Siping |
|---|---|---|---|---|---|---|---|---|---|---|
| TEP | k | 0.375 | 0.200 | 0.295 | −0.026 | 0.844 | 0.808 | 0.337 | 0.498 | 0.674 |
| s | 45.635 | 45.170 | 39.520 | 44.960 | 29.917 | 44.423 | 37.930 | 47.953 | 45.413 | |
| m | 84.566 | 91.208 | 79.495 | 94.979 | 71.990 | 81.112 | 94.069 | 100.317 | 96.017 | |
| CDEP | k | 0.302 | 0.250 | −0.183 | 0.171 | 0.469 | 0.527 | 0.606 | 0.319 | 0.539 |
| s | 2.464 | 2.149 | 2.485 | 2.039 | 1.709 | 2.241 | 1.577 | 1.967 | 2.248 | |
| m | 3.433 | 3.545 | 3.946 | 3.187 | 2.425 | 3.407 | 2.387 | 3.363 | 3.302 |
| Stations | Copula Functions | RMSE | AIC | Parameter |
|---|---|---|---|---|
| Baicheng | Clayton | 0.0653 | −116.9052 | 1.4973 |
| Frank | 0.0533 | −125.8407 | 7.1460 | |
| Gumbel | 0.0501 | −128.6466 | 2.4672 | |
| Qianan | Clayton | 0.0679 | −115.1339 | 0.9138 |
| Frank | 0.0529 | −126.1794 | 4.8031 | |
| Gumbel | 0.0500 | −128.6915 | 1.8931 | |
| Qianguo | Clayton | 0.0541 | −125.2456 | 2.0720 |
| Frank | 0.0530 | −126.1135 | 7.4039 | |
| Gumbel | 0.0521 | −126.8485 | 2.5475 | |
| Tongyu | Clayton | 0.0617 | −119.3877 | 1.8507 |
| Frank | 0.0627 | −118.6967 | 6.7939 | |
| Gumbel | 0.0712 | −113.0363 | 2.0599 | |
| Changling | Clayton | 0.0603 | −120.4239 | 1.8507 |
| Frank | 0.0520 | −126.9380 | 6.7939 | |
| Gumbel | 0.0511 | −127.7760 | 2.0599 | |
| Fuyu | Clayton | 0.0547 | −124.7080 | 2.2624 |
| Frank | 0.0510 | −127.7962 | 9.1288 | |
| Gumbel | 0.0506 | −128.1797 | 2.8739 | |
| Shuangliao | Clayton | 0.0652 | −116.9382 | 0.9143 |
| Frank | 0.0566 | −123.1843 | 4.4784 | |
| Gumbel | 0.0540 | −125.2837 | 1.8775 | |
| Siping | Clayton | 0.0615 | −119.5317 | 1.5214 |
| Frank | 0.0578 | −122.2900 | 6.6635 | |
| Gumbel | 0.0542 | −125.0960 | 2.4773 | |
| Changchun | Clayton | 0.0738 | −111.4586 | 1.3408 |
| Frank | 0.0568 | −123.0482 | 7.4784 | |
| Gumbel | 0.0551 | −124.3642 | 2.6622 |
| Coefficient | a | b | C | d | e | f |
|---|---|---|---|---|---|---|
| Estimated Value | 3421 | −32.14 | 292.9 | 0.3552 | 0.7325 | −7.738 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, G.; Guo, E.; Yun, X. Quantitative Agricultural Flood Risk Assessment Using Vulnerability Surface and Copula Functions. Water 2018, 10, 1229. https://doi.org/10.3390/w10091229
Wang Y, Liu G, Guo E, Yun X. Quantitative Agricultural Flood Risk Assessment Using Vulnerability Surface and Copula Functions. Water. 2018; 10(9):1229. https://doi.org/10.3390/w10091229
Chicago/Turabian StyleWang, Yongfang, Guixiang Liu, Enliang Guo, and Xiangjun Yun. 2018. "Quantitative Agricultural Flood Risk Assessment Using Vulnerability Surface and Copula Functions" Water 10, no. 9: 1229. https://doi.org/10.3390/w10091229
APA StyleWang, Y., Liu, G., Guo, E., & Yun, X. (2018). Quantitative Agricultural Flood Risk Assessment Using Vulnerability Surface and Copula Functions. Water, 10(9), 1229. https://doi.org/10.3390/w10091229






