An Integrated Statistical Method to Generate Potential Future Climate Scenarios to Analyse Droughts
Abstract
1. Introduction
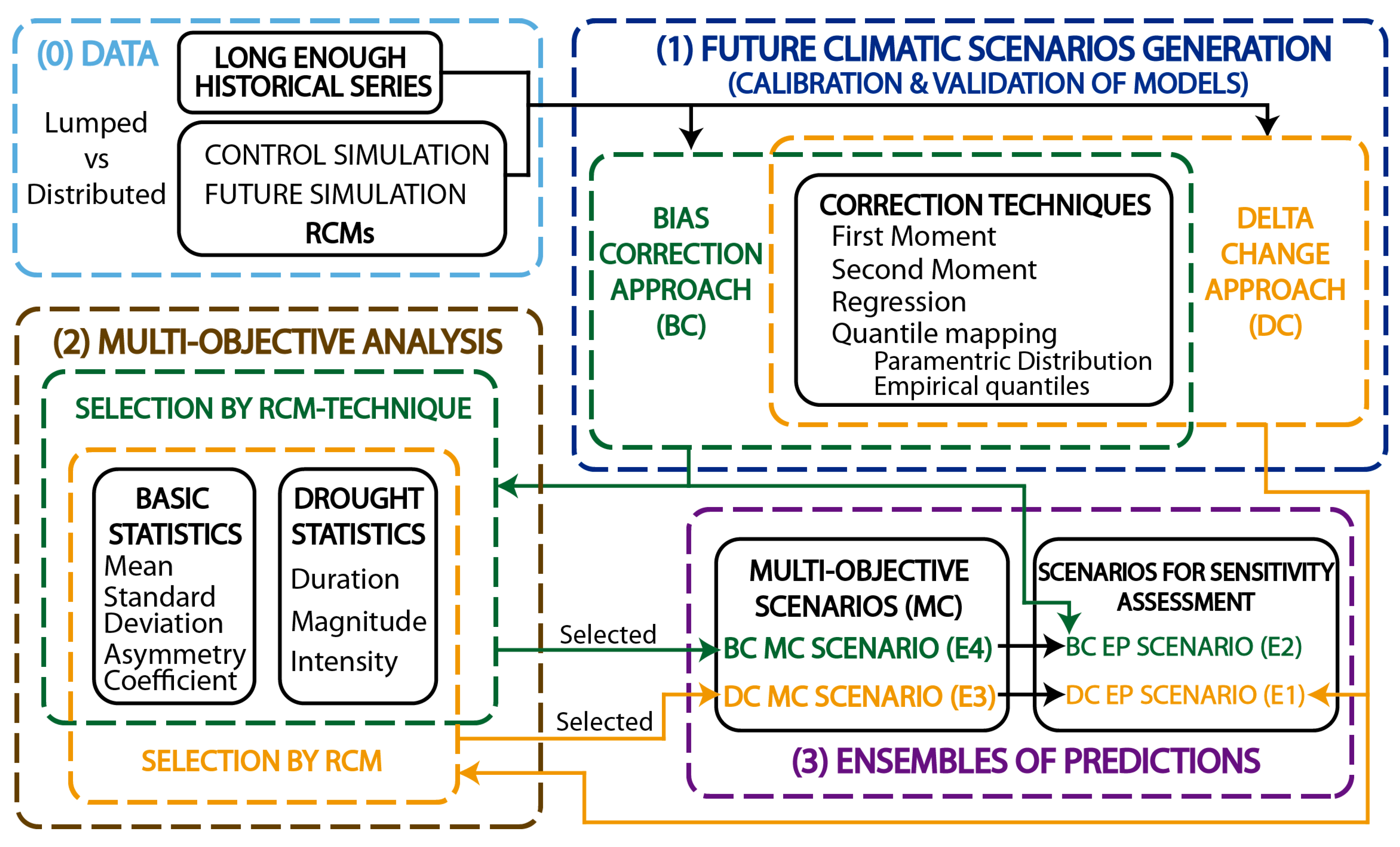
2. Method
2.1. Generation of Future Individual Projections
- (1)
- For each RCM model, we can represent the differences between the statistics (basic and drought statistics) of the control scenarios simulations and the “historical” values. These usually reveal significant bias, which justifies correcting them. The set of techniques to address this issue are known as bias correction approaches, since they apply a perturbation to the control series with the aim of forcing some of their statistics to get closer to the historical ones. In order to generate future series, they assume that the bias between the statistics of real data and model scenarios (control scenarios) will remain invariant into the future (e.g., [22,32]).
- (2)
- We can also represent and analyse the relative differences between control and future scenario statistics for the climatic model simulation for specific emission scenarios. Based on this information, future scenarios can be also generated by assuming that the RCMs provide accurate assessment of the relative changes in the statistics between present and future scenarios, but that they do not adequately assess the absolute values. These approaches, known as delta change solutions, use the relative difference in the statistics of control and future simulations to create a perturbation in the historical series, in accordance with these estimated changes (e.g., [25,26,27]).
2.2. Multi-Objective Analysis of the Main Statistics (Basic and Drought Statistics)
2.3. Ensembles of Predictions to Define More Representative Future Climate Scenarios
3. Study Area: Description and Available Data
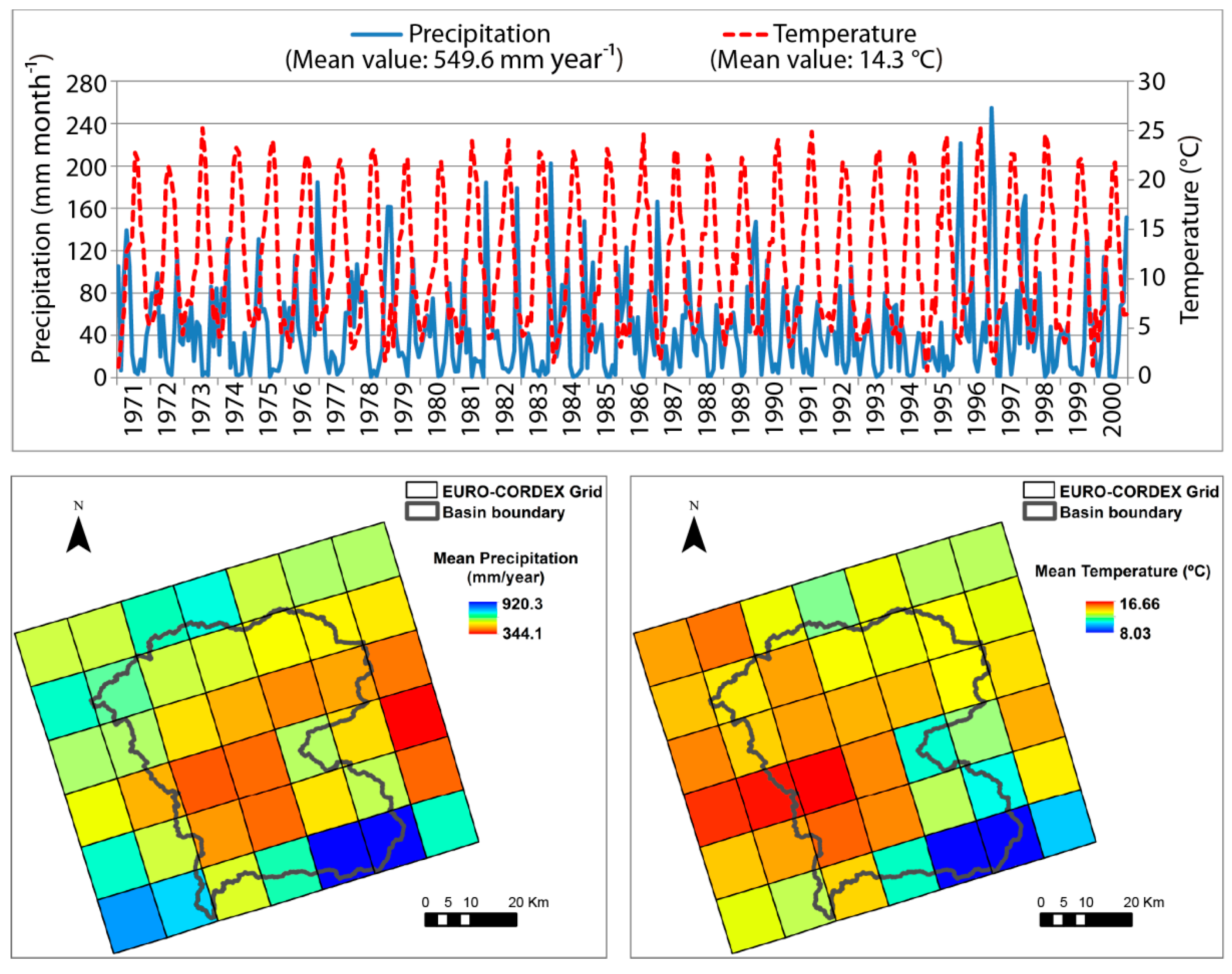
3.1. Location and Description of the Alto Genil Basin
3.2. Historical Climate Data
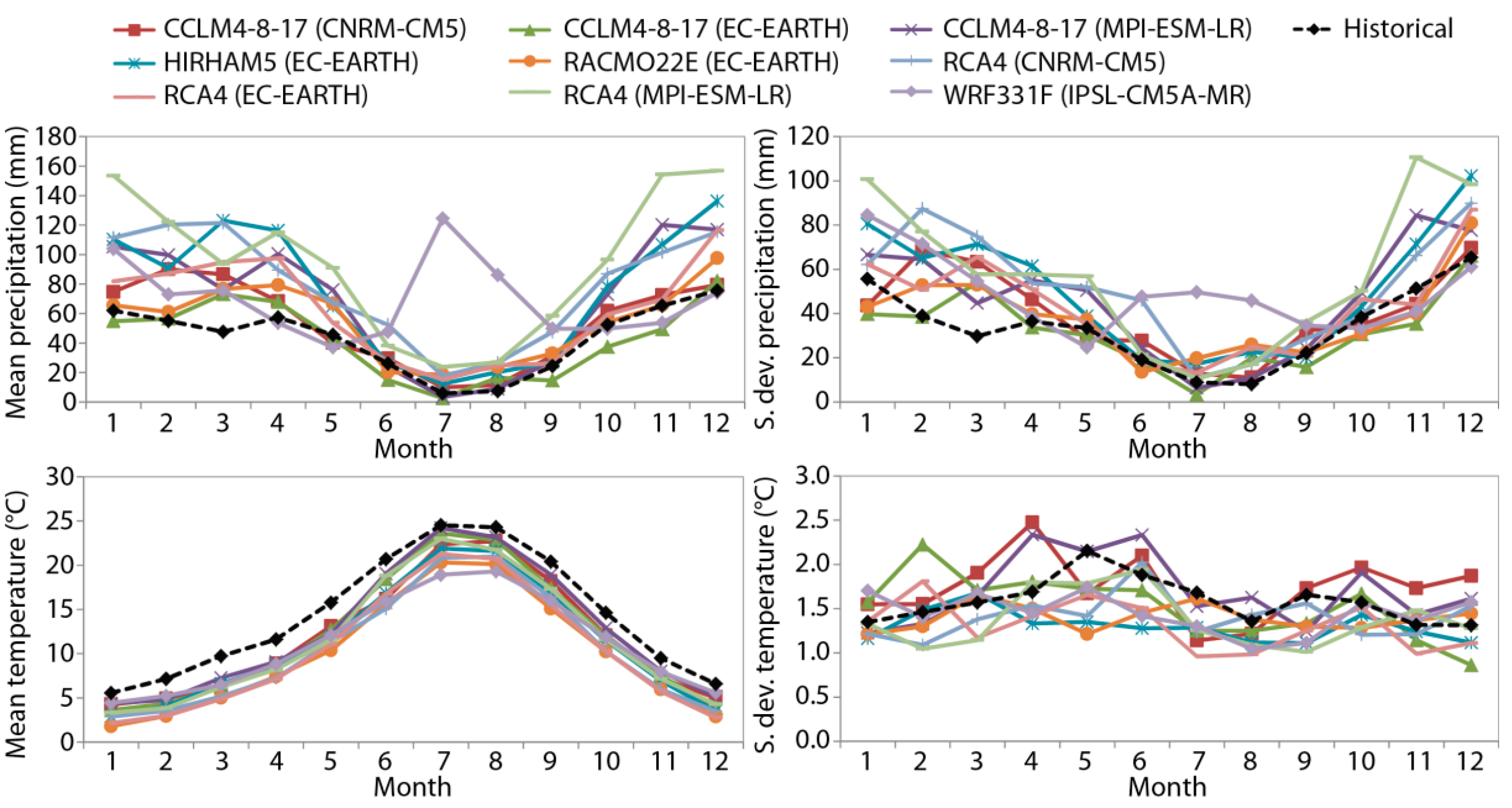
3.3. Climate Model Simulation Data. Control and Future Scenarios
4. Results and Discussion
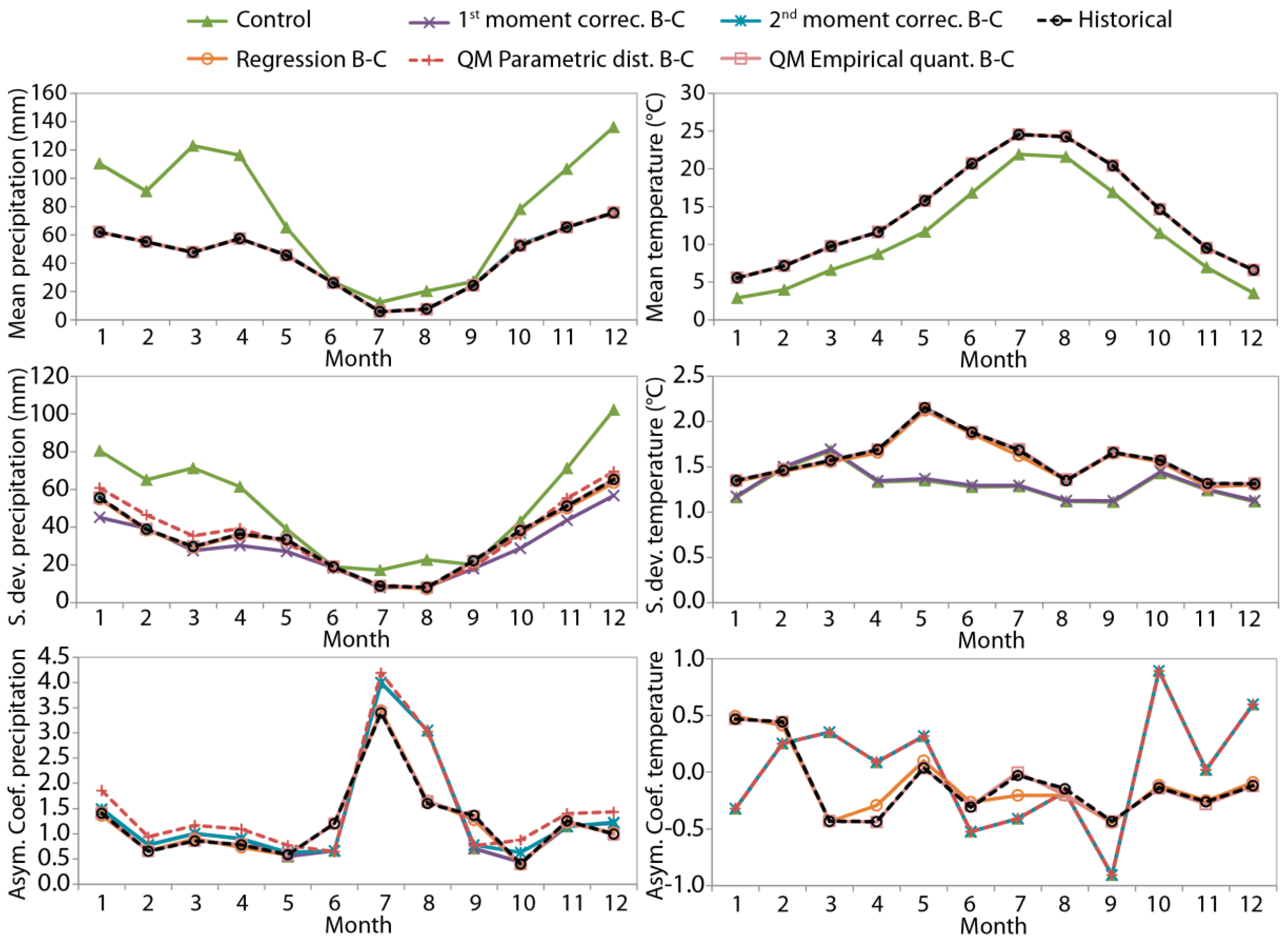
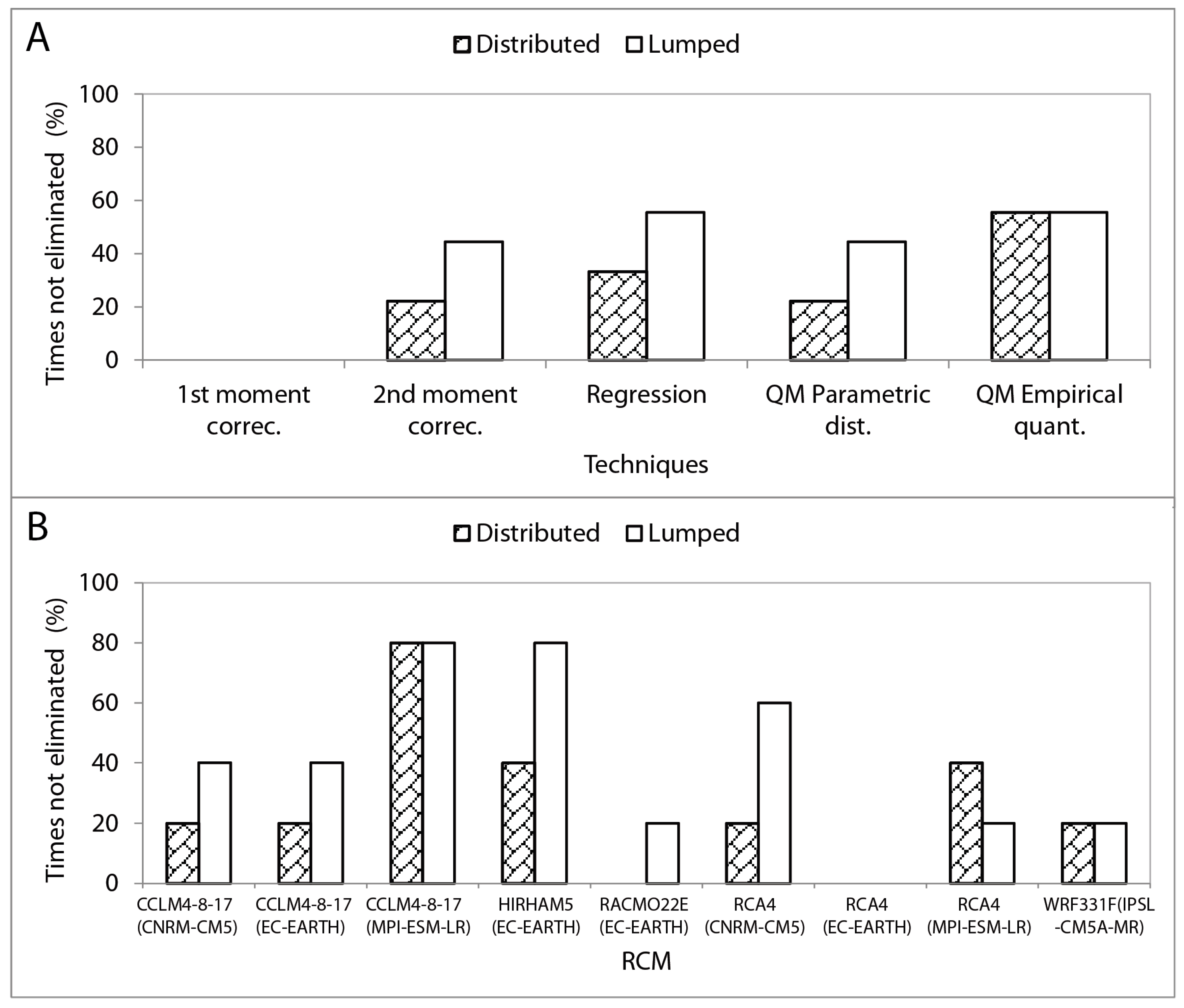
4.1. Application of Different Correction Techniques
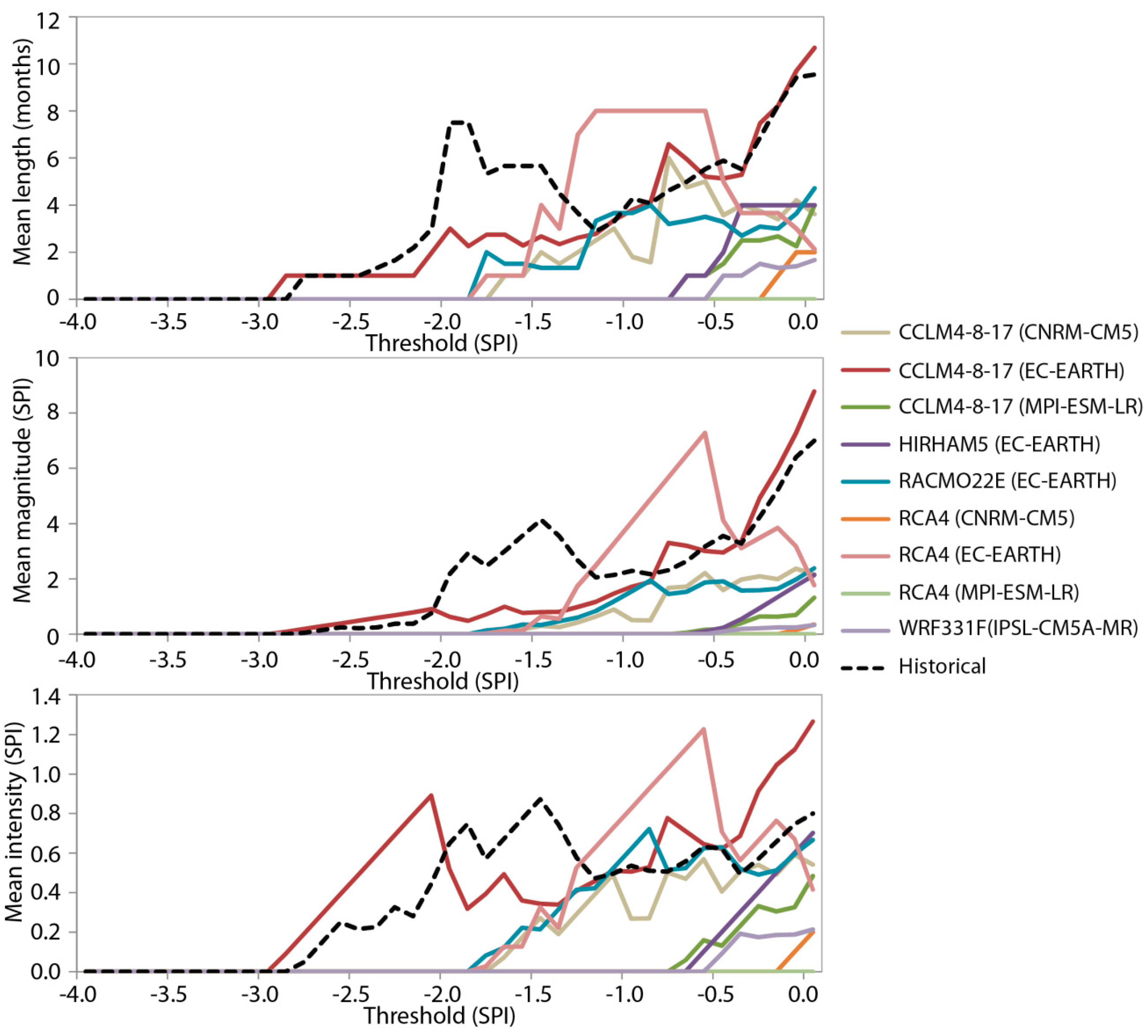
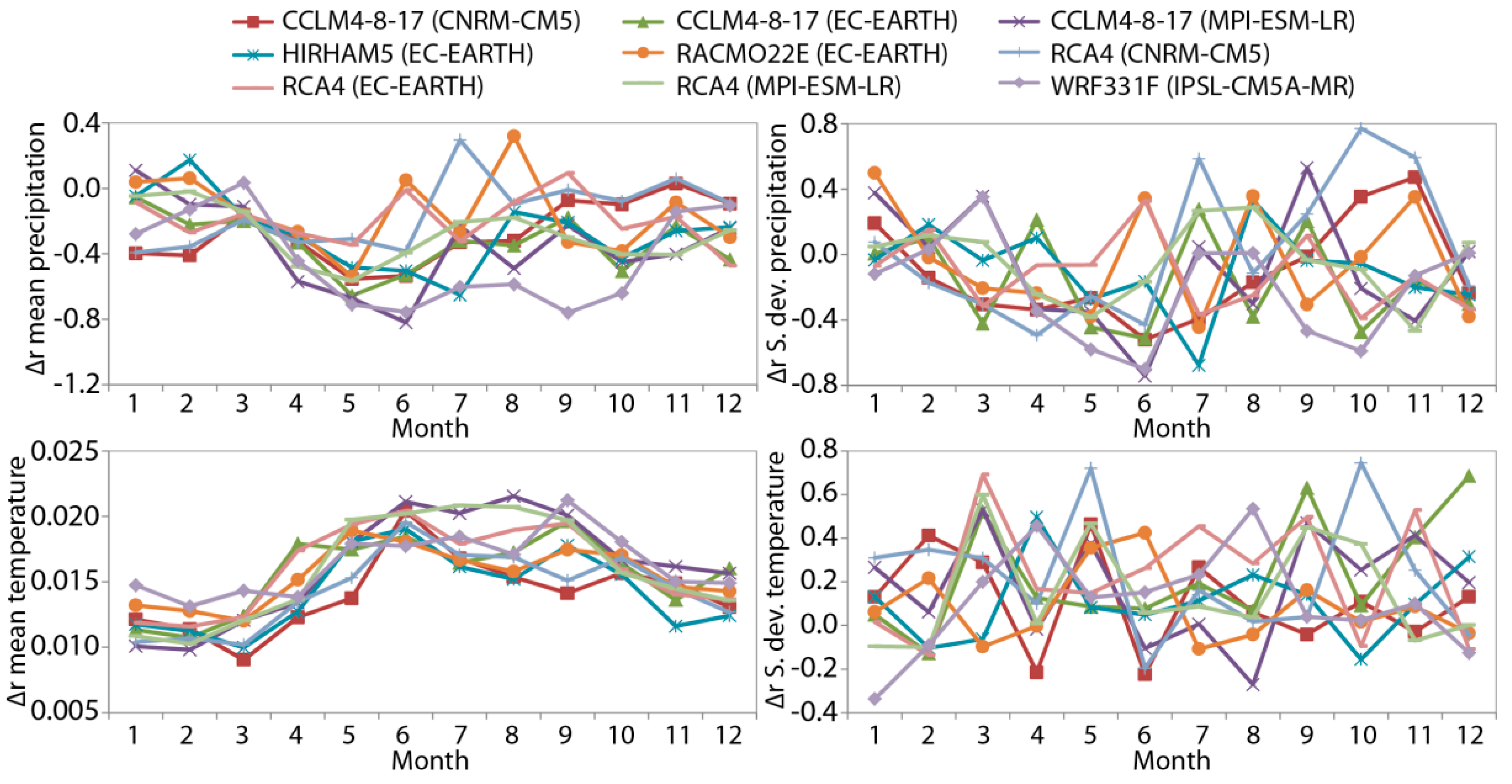
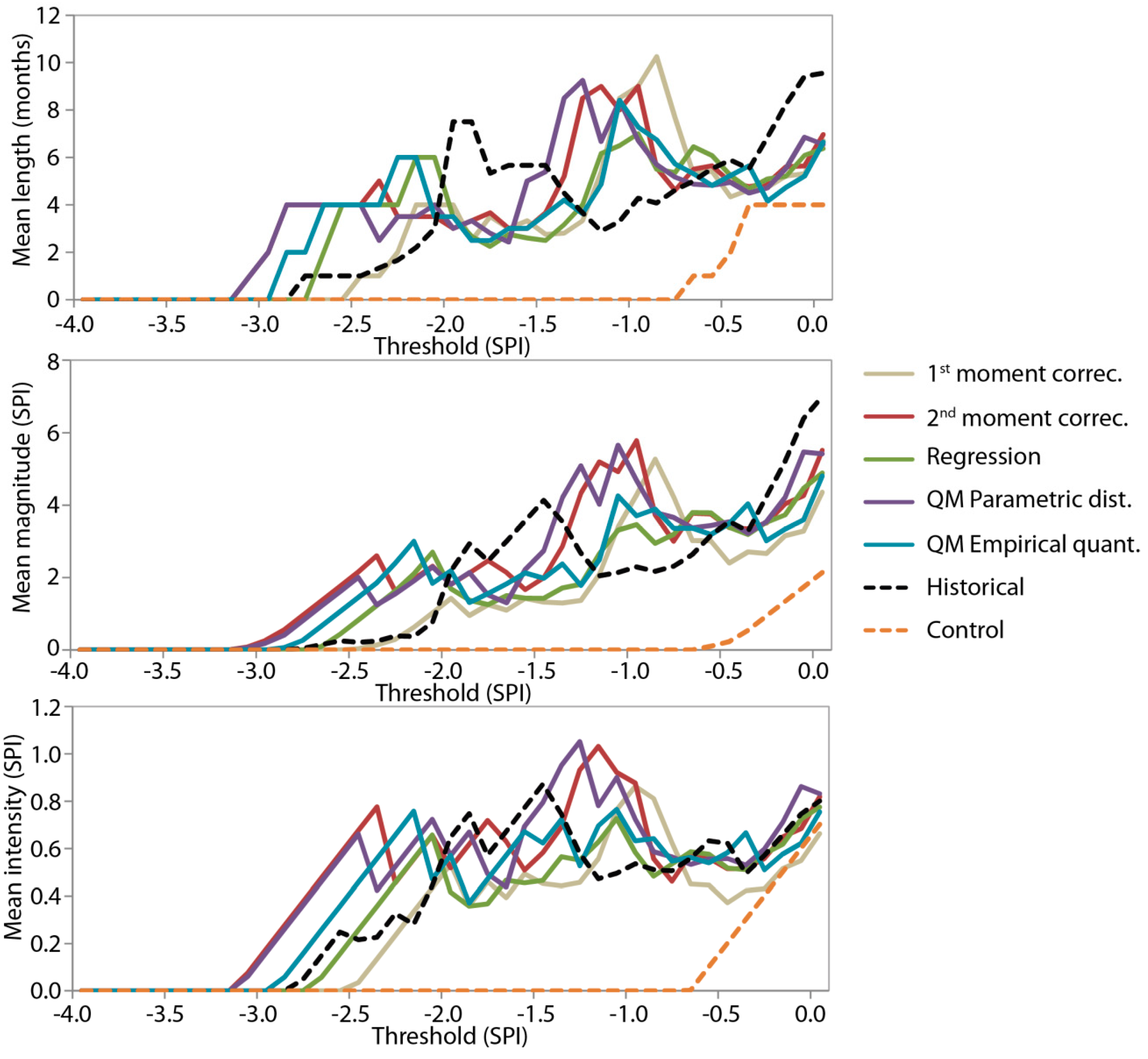
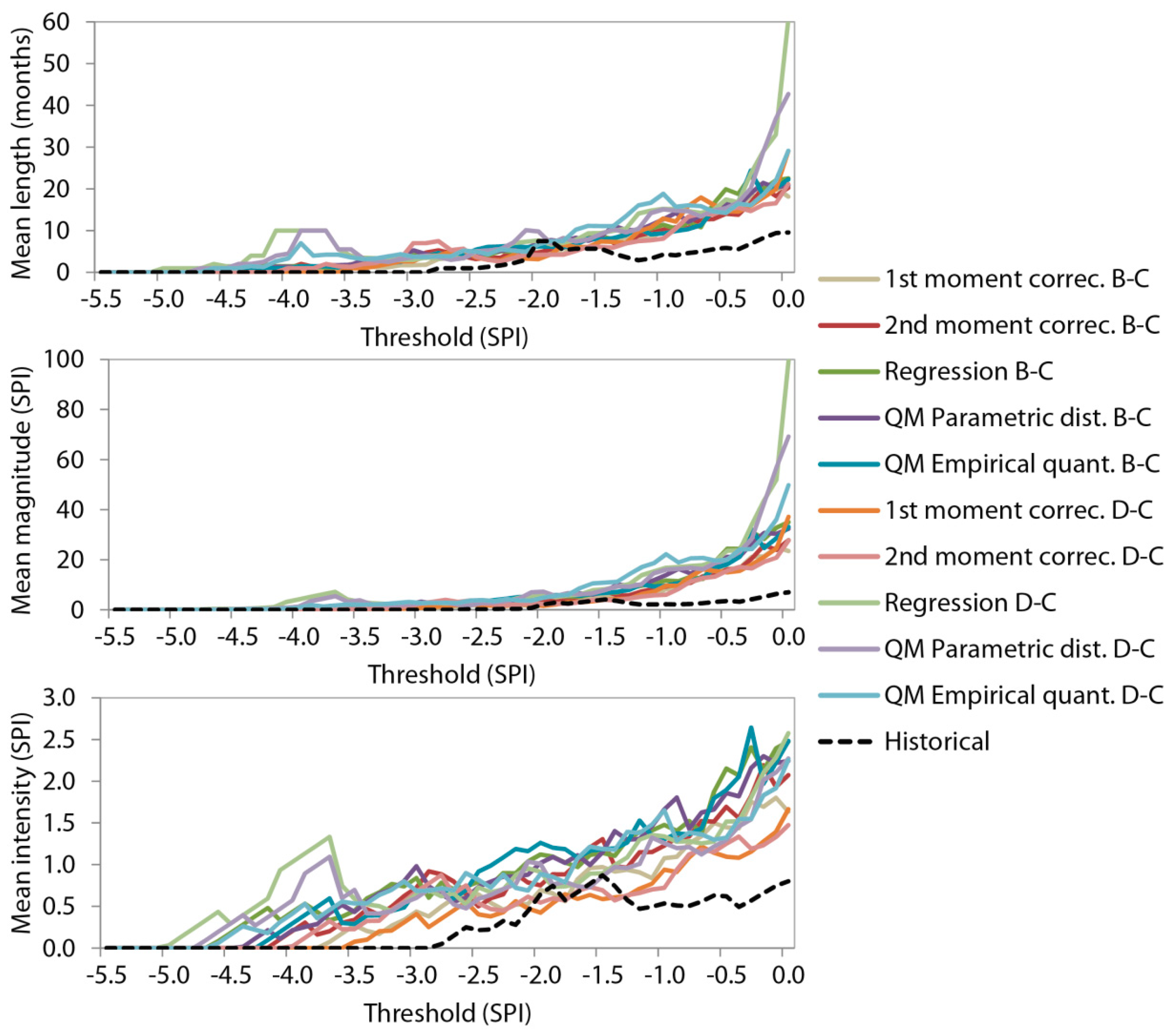
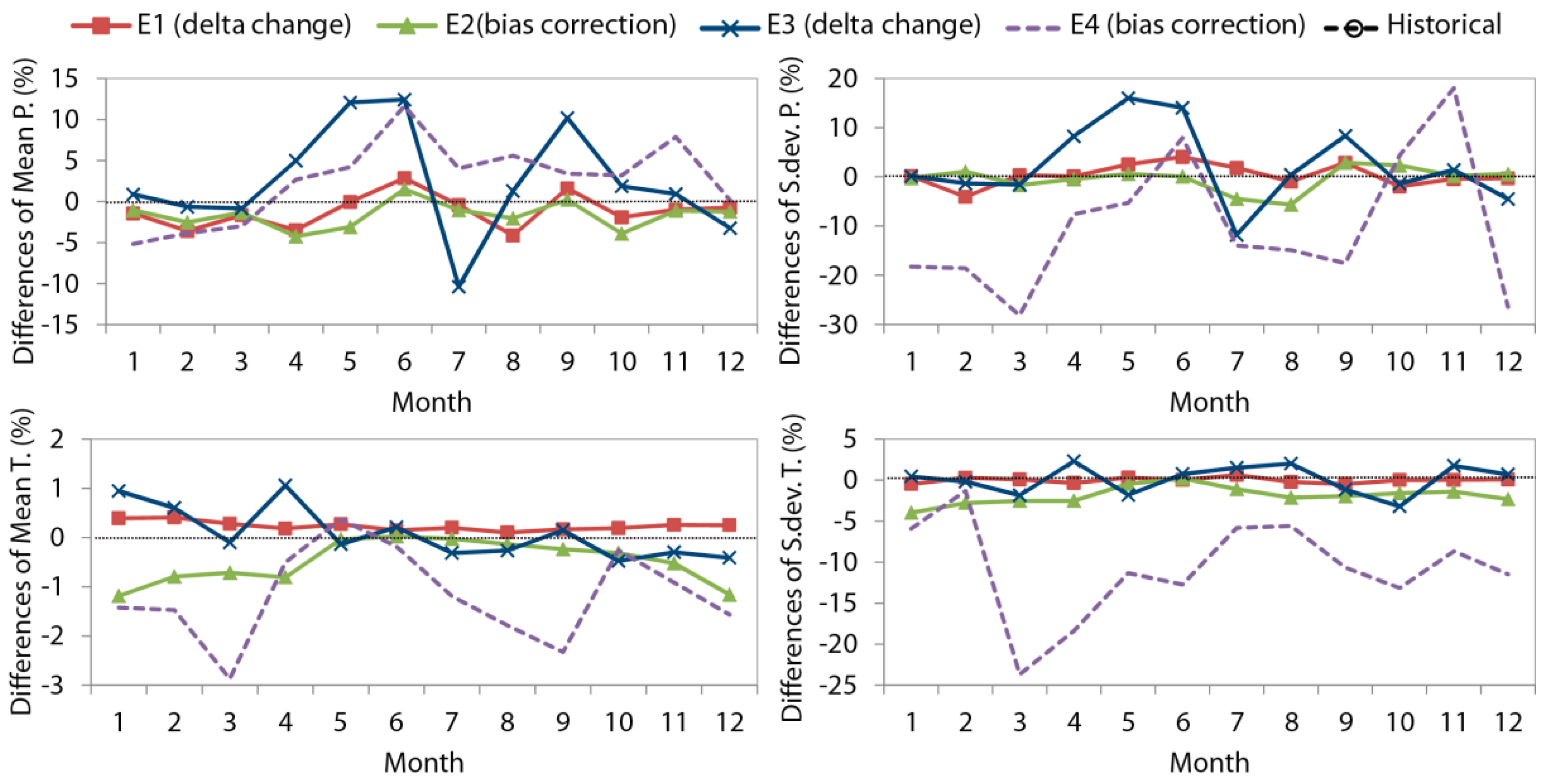
4.2. Multi-Objective Analysis of Basic and Drought Statistics
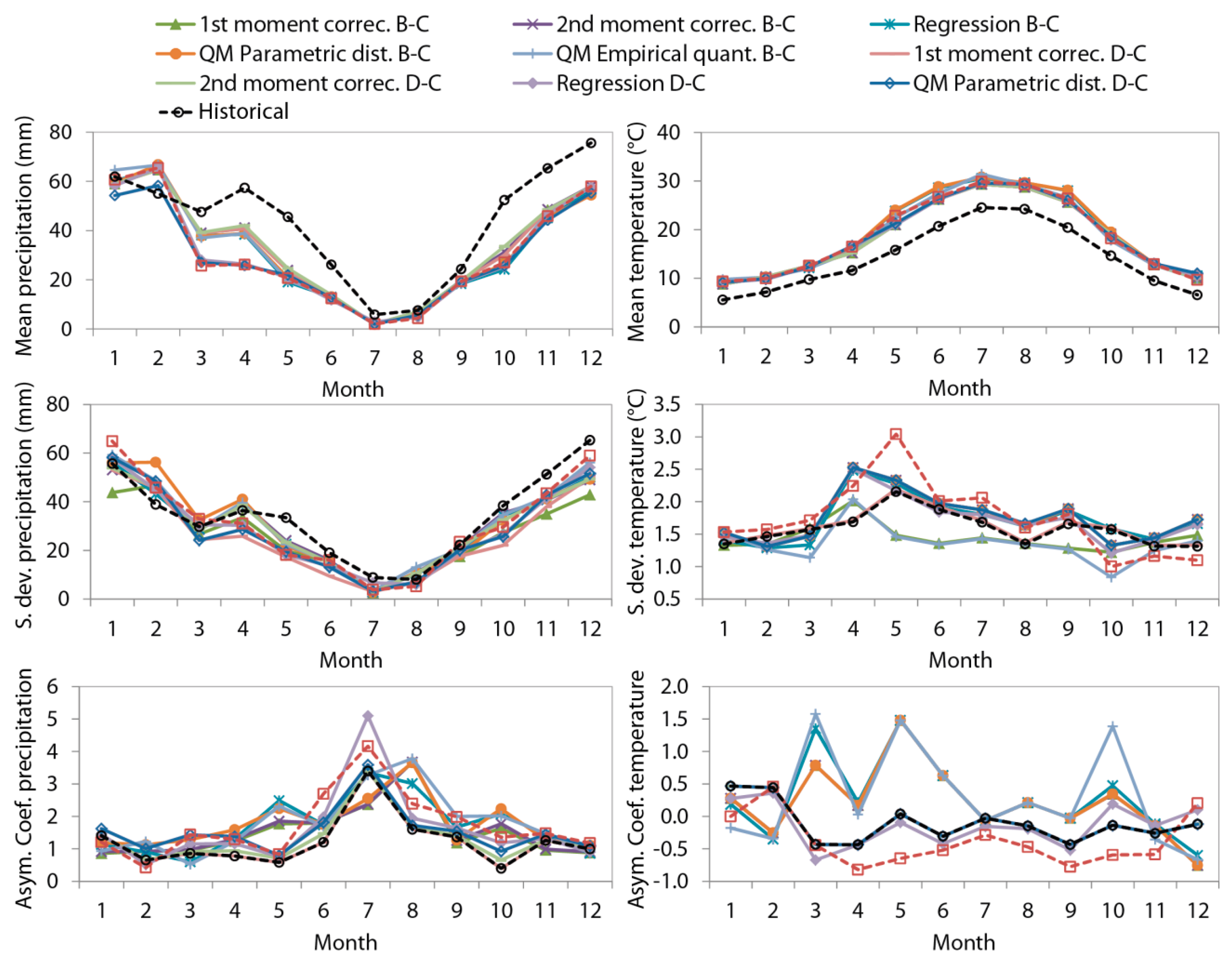
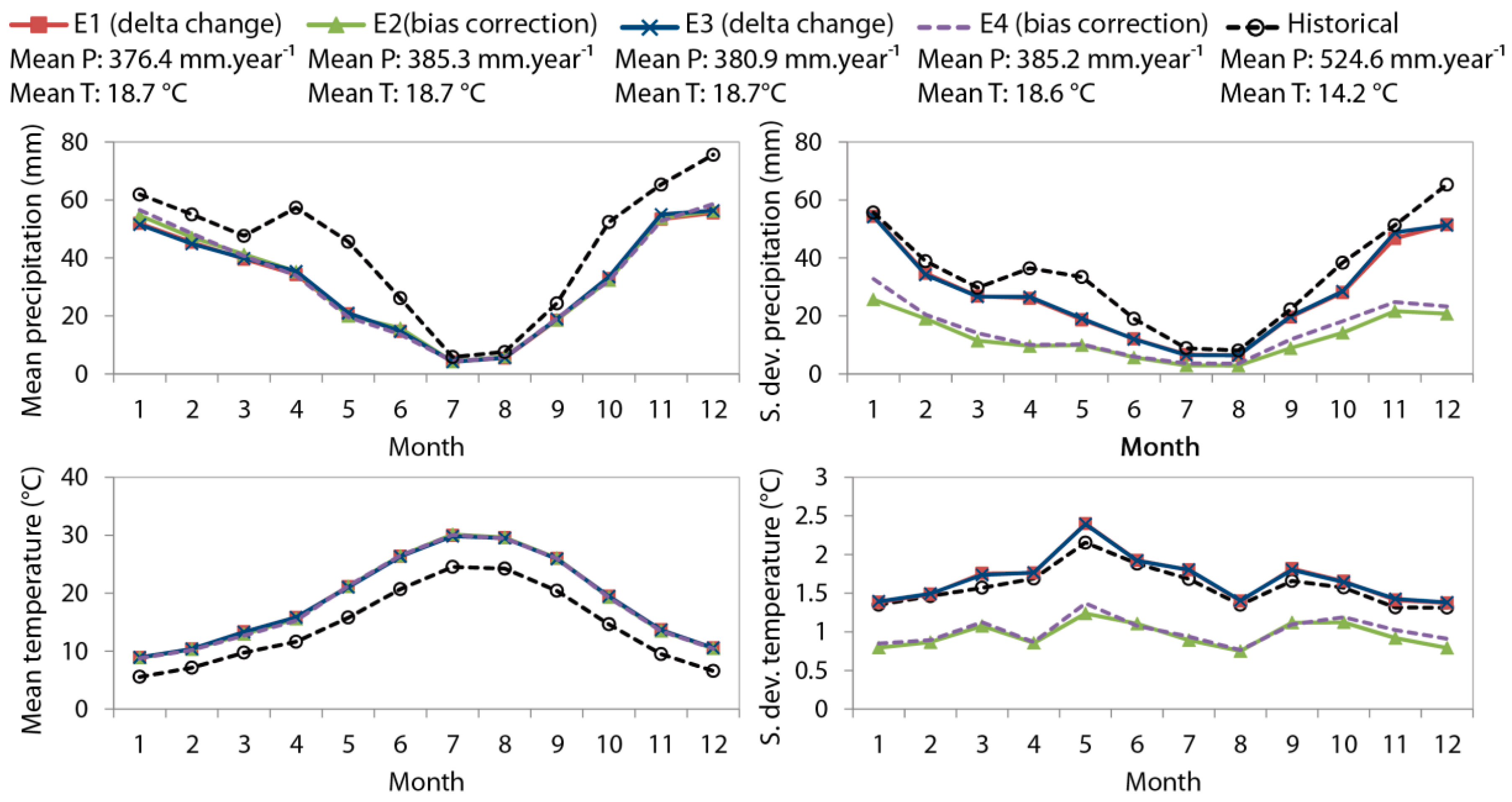
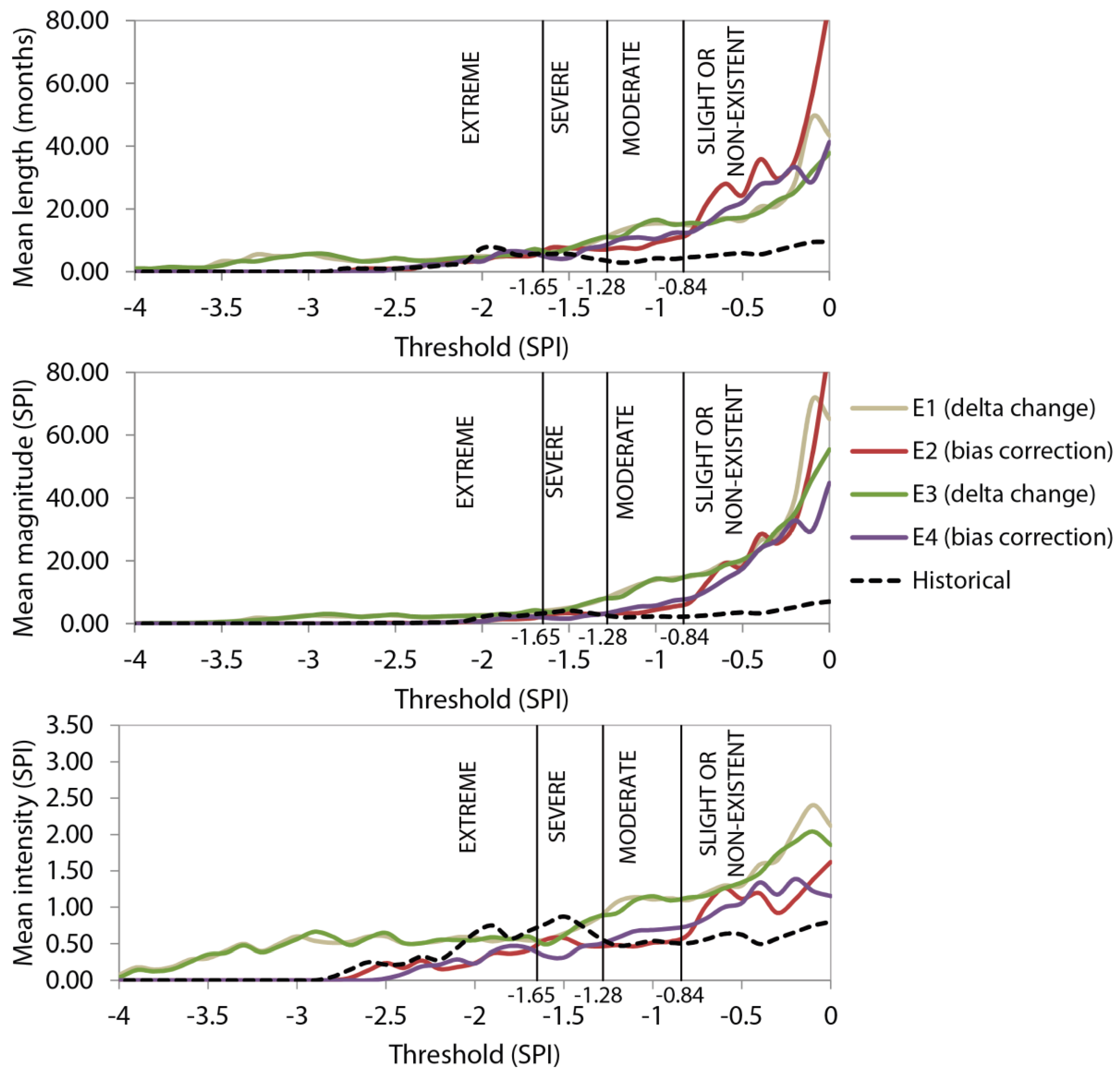
4.3. Ensembles of Predictions to Define More Representative Future Climate Scenarios
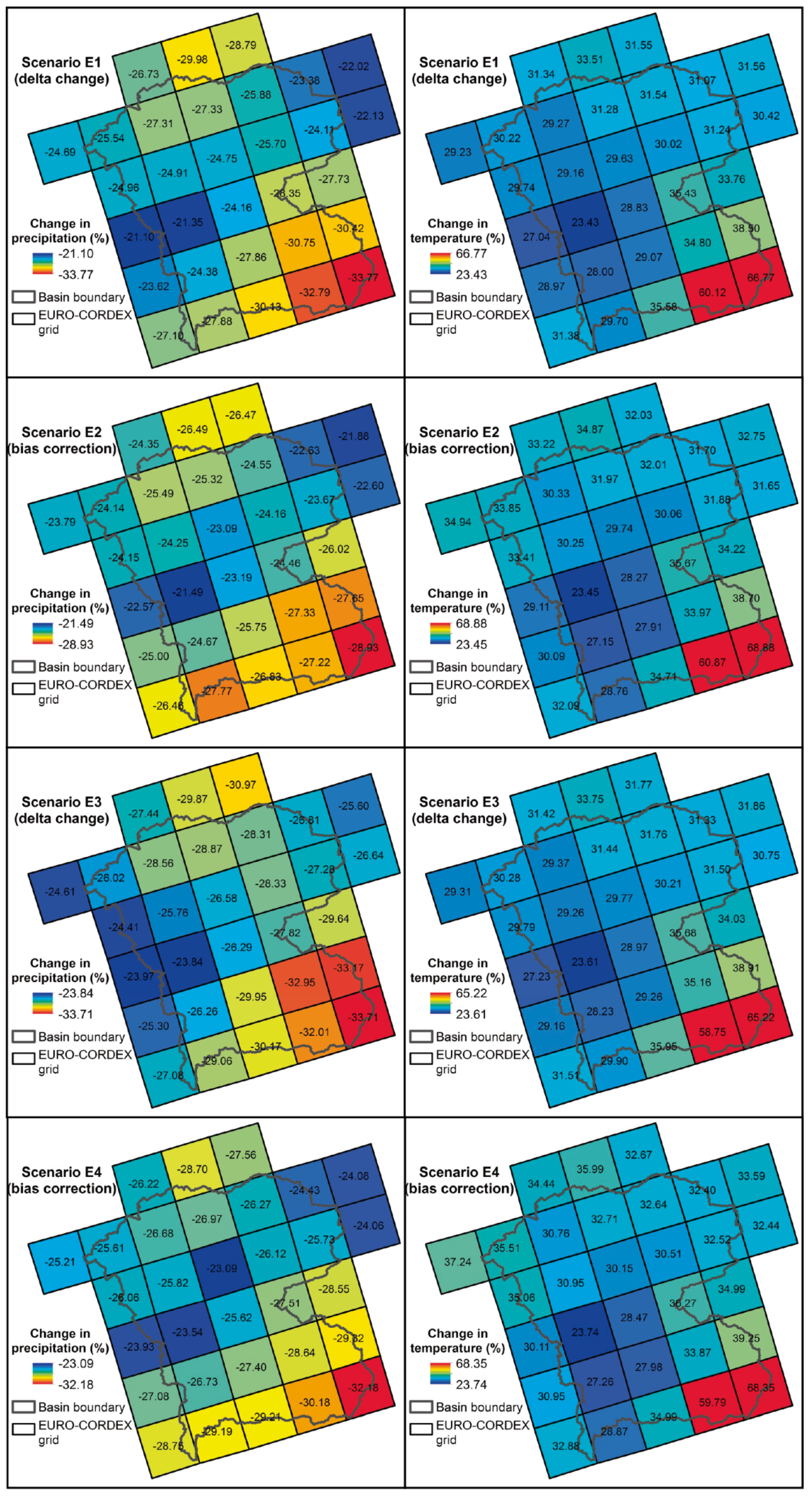
4.4. Sensitivity of Results to Spatial Scale
5. Limitations and Future Research Works
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feyen, L.; Dankers, R. Impact of global warming on streamflow drought in Europe. J. Geophys. Res. 2009, 114, D17116. [Google Scholar] [CrossRef]
- Iglesias, A.; Garrote, L.; Flores, F.; Moneo, M. Challenges to manage the risk of water scarcity and climate change in the Mediterranean. Water Resour. Manag. 2007, 21, 227–288. [Google Scholar] [CrossRef]
- Blenkinsop, S.; Fowler, H.J. Changes in drought characteristics for Europe projected by the PRUDENCE regional climate models. Int. J. Climatol. 2007, 27, 1595–1610. [Google Scholar] [CrossRef]
- Skaugen, T.; Astrup, M.; Roald, L.A.; Førland, E. Scenarios of extreme daily precipitation for Norway under climate change. Hydrol. Res. 2004, 35, 1–13. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Pedro-Monzonís, M.; Solera, A.; Ferrer, J.; Estrela, T.; Paredes-Arquiola, J. A review of water scarcity and drought indexes in water resources planning and management. J. Hydrol. 2015, 52, 482–493. [Google Scholar] [CrossRef]
- Lopez-Nicolas, A.; Pulido-Velazquez, M.; Macian-Sorribes, H. Economic risk assessment of drought impacts on irrigated agriculture. J. Hydrol. 2017, 550, 580–589. [Google Scholar] [CrossRef]
- Marcos-Garcia, P.; Lopez-Nicolas, A.; Pulido-Velazquez, M. Combined use of relative drought indices to analyze climate change impact on meteorological and hydrological droughts in a Mediterranean basin. J. Hydrol. 2017, 554, 292–305. [Google Scholar] [CrossRef]
- Herweijer, C.; Seager, R.; Cook, E. North American droughts of the mid to late nineteenth century: A history, simulation and implication for Mediaeval drought. Holocene 2006, 16, 159–171. [Google Scholar] [CrossRef]
- Seager, R.; Kushnir, Y.; Herweijer, C.; Naik, N.; Velez, J. Modeling of tropical forcing of persistent droughts and pluvials over western North America: 1856–2000. J. Clim. 2005, 18, 4065–4088. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.; Shaffrey, L.C.; Vidale, P.L.; Arnell, N.W. An evaluation of the spatiotemporal structure of large-scale European drought within the HiGEM climate model. Int. J. Climatol. 2013, 33, 2024–2035. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, Q.; Liu, X.; Leng, G.; Li, Z. Soil moisture drought monitoring and forecasting using satellite and climate model data over Southwest China. J. Hydrometeorol. 2017, 18, 5–23. [Google Scholar] [CrossRef]
- Cook, B.; Miller, R.; Seager, R. Dust and sea surface temperature forcing of the 1930s “Dust Bowl” drought. Geophys. Res. Lett. 2008, 35, L08710. [Google Scholar] [CrossRef]
- Seager, R.; Burgman, R.; Kushnir, Y.; Clement, A.; Cook, E.; Naik, N.; Miller, J. Tropical Pacific forcing of North American medieval megadroughts: Testing the concept with an atmosphere model forced by coral-reconstructed SSTs. J. Clim. 2008, 21, 6175–6190. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Performance and uncertainty evaluation of empirical downscaling methods in quantifying the climate change impacts on hydrology over two North American river basins. J. Hydrol. 2013, 479, 200–214. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Assessing regression-based statistical approaches for downscaling precipitation over North America. Hydrol. Process. 2014, 28, 3482–3504. [Google Scholar] [CrossRef]
- Räty, O.; Räisänen, J.; Ylhäisi, J. Evaluation of delta change and bias correction methods for future daily precipitation: Intermodal cross-validation using ENSEMBLES simulations. Clim. Dyn. 2014, 42, 2287–2303. [Google Scholar] [CrossRef]
- Sunyer, M.A.; Hundecha, Y.; Lawrence, D.; Madsen, H.; Willems, P.; Martinkova, M.; Vormoor, K.; Bürger, G.; Hanel, M.; Kriaučiuniene, J.; et al. Inter-comparison of statistical downscaling methods for projection of extreme precipitation in Europe. Hydrol. Earth Syst. Sci. 2015, 19, 1827–1847. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Clim. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Watanabe, S.; Kanae, S.; Seto, S.; Yeh, P.J.-F.; Hirabayashi, Y.; Oki, T. Intercomparison of bias-correction methods for monthly temperature and precipitation simulated by multiple climate models. J. Geophys. Res. 2012, 117, D23114. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Seaby, L.P.; Refsgaard, J.C.; Sonnenborg, T.O.; Højberg, A.L. Spatial uncertainty in bias corrected climate change projections and hydrogeological impacts. Hydrol. Process. 2015, 29, 4514–4532. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Garrote, L.; Andreu, J.; Martin-Carrasco, F.J.; Iglesias, A. A methodology to diagnose the effect of climate change and to identify adaptive strategies to reduce its impacts in conjunctive-use systems at basin scale. J. Hydrol. 2011, 405, 110–122. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; García-Aróstegui, J.L.; Molina, J.L.; Pulido-Velázquez, M. Assessment of future groundwater recharge in semi-arid regions under climate change scenarios (Serral-Salinas aquifer, SE Spain). Could increased rainfall variability increase the recharge rate? Hydrol. Process. 2015, 29, 828–844. [Google Scholar] [CrossRef]
- Räisänen, J.; Räty, O. Projections of daily mean temperature variability in the future: Cross-validation tests with ENSEMBLES regional climate simulations. Clim. Dyn. 2013, 41, 1553–1568. [Google Scholar] [CrossRef]
- Rupp, D.E.; Abatzoglou, J.T.; Hegewisch, K.C.; Mote, P.W. Evaluation of CMIP5 20th century climate simulations for the Pacific Northwest USA. J. Geophys. Res. Atmos. 2013, 118, 10884–10906. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Rana, A.; Moradkhani, H.; Sharma, A. Multi-criteria evaluation of CMIP5 GCMs for climate change impact analysis. Theor. Appl. Climatol. 2015, 128, 71–87. [Google Scholar] [CrossRef]
- Hashmi, M.Z.; Shamseldin, A.Y.; Melville, B.W. Statistically downscaled probabilistic multi-model ensemble projections of precipitation change in a watershed. Hydrol. Process. 2013, 27, 1021–1032. [Google Scholar] [CrossRef]
- AEMET (Spanish Meteorologial Agency). Generación de Escenarios Regionalizados de Cambio Climático Para España; Agencia Estatal de Meteorología (Ministerio de Medio Ambiente y Medio Rural y Marino): Madrid, Spain, 2009.
- Haerter, J.O.; Hagemann, S.; Moseley, C.; Piani, C. Climate model bias-correction and the role of timescales. Hydrol. Earth Syst. Sci. 2011, 15, 1065–1079. [Google Scholar] [CrossRef]
- Prudhomme, C.; Reynard, N.; Crooks, S. Downscaling of global climate models for flood frequency analysis: Where are we now? Hydrol. Process. 2002, 16, 1137–1150. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Hellström, C.; Chen, D.; Achberger, C.; Räisänen, J. Comparison of climate change scenarios for Sweden based on statistical and dynamical downscaling of monthly precipitation. Clim. Res. 2001, 19, 45–55. [Google Scholar] [CrossRef]
- Hessami, M.; Gachon, P.; Ouarda, T.; St-Hilaire, A. Automated regression-based statistical downscaling tool. Environ. Model. Softw. 2008, 23, 813–834. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models/Vérification, en conditions réelles, des modèles de simulation hydrologique. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Bennett, J.C.; Ling, F.L.N.; Graham, B.; Grose, M.R.; Corney, S.P.; White, C.J.; Holz, G.K.; Post, D.A.; Gaynor, S.M.; Bindoff, N.L. Climate Futures for Tasmania: Water and Catchments: Technical Report; Antarctic Climate & Ecosystems Cooperative Research Centre: Hobart, Tasmania, Australia, 2010. [Google Scholar]
- Terink, W.; Hurkmans, R.T.W.L.; Torfs, P.J.J.F.; Uijlenhoet, R. Evaluation of a bias correction method applied to downscaled precipitation and temperature reanalysis data for the Rhine basin. Hydrol. Earth Syst. Sci. 2010, 14, 687–703. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Is bias correction of regional climate model (RCM) simulations possible for non-stationary conditions? Hydrol. Earth Syst. Sci. 2013, 17, 5061–5077. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scale. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. Drought monitoring with multiple timescales. In Proceedings of the Ninth Conference on Applied Climatology, Dallas, TX, USA, 15–20 January 1995; Boston American Meteorological Society: Boston, MA, USA, 1995; pp. 233–236. [Google Scholar]
- Bonaccorso, B.; Bordi, I.; Cancelliere, A.; Rossi, G.; Sutera, A. Spatial Variability of Drought: An Analysis of the SPI in Sicily. Water Resour. Manag. 2003, 17, 273–296. [Google Scholar] [CrossRef]
- Livada, I.; Assimakopoulos, V.D. Spatial and temporal analysis of drought in Greece using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P.; Desai, V.R. Drought characterization: A probabilistic approach. Stoch. Environ. Res. Risk Assess. 2009, 23, 41–55. [Google Scholar] [CrossRef]
- González, J.; Valdés, J.B. New drought frequency index: Definition and comparative performance analysis. Water Resour. Res. 2006, 42, W11421. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Herrera, S.; Gutiérrez, J.M.; Ancell, R.; Pons, M.R.; Frías, M.D.; Fernández, J. Development and analysis of a 50-year high-resolution daily gridded precipitation dataset over Spain (Spain02). Int. J. Climatol. 2012, 32, 74–85. [Google Scholar] [CrossRef]
- Herrera, S.; Fernández, J.; Gutiérrez, J.M. Update of the Spain02 Gridded Observational Dataset for Euro-CORDEX evaluation: Assessing the Effect of the Interpolation Methodology. Int. J. Climatol. 2016, 36, 900–908. [Google Scholar] [CrossRef]
- Quintana-Seguí, P.; Turco, M.; Herrera, S.; Miguez-Macho, G. Validation of a new SAFRAN-based gridded precipitation product for Spain and comparisons to Spain02 and ERA-Interim. Hydrol. Earth Syst. Sci. 2017, 21, 2187–2201. [Google Scholar] [CrossRef]
- CORDEX PROJECT. The Coordinated Regional Climate Downscaling Experiment CORDEX. Program Sponsored by World Climate Research Program (WCRP). 2013. Available online: http://www.cordex.org/ (accessed on 8 September 2018).
- Escriva-Bou, A.; Pulido-Velazquez, M.; Pulido-Velazquez, D. The Economic Value of Adaptive Strategies to Global Change for Water Management in Spain’s Jucar Basin. J. Water Resour. Pl. Manag. 2016, 143, 04017005. [Google Scholar] [CrossRef]
- Fernandez-Montes, S.; Rodrigo, F.S. Trends in surface air temperatures, precipitation and combined indices in the southeastern Iberian Peninsula (1970–2007). Clim. Res. 2015, 63, 43–60. [Google Scholar] [CrossRef]
- Pepin, N.C.; Lundquist, J.D. Temperature trends at high elevations: Patterns across the globe. Geophys. Res. Lett. 2008, 35, L14701. [Google Scholar] [CrossRef]
- Ehret, U.; Zehe, E.; Wulfmeyer, V.; Warrach-Sagi, K.; Liebert, J. HESS Opinions “Should we apply bias correction to global and regional climate model data?”. Hydrol. Earth Syst. Sci. 2012, 16, 3391–3404. [Google Scholar] [CrossRef]
- Muerth, M.J.; Gauvin St-Denis, B.; Ricard, S.; Velázquez, J.A.; Schmid, J.; Minville, M.; Caya, D.; Chaumont, D.; Ludwig, R.; Turcotte, R. On the need for bias correction in regional climate scenarios to assess climate change impacts on river runoff. Hydrol. Earth. Syst. Sci. 2013, 17, 1189–1204. [Google Scholar] [CrossRef]

| Correction Technique | Pros | Cons |
|---|---|---|
| First-moment correction | - Does not generate negative values for P | - Only preserve the mean |
| Second-moment correction | - Preserve mean and standard deviation | - Generates some negative values for P |
| Regression | - Allow to use different regression models - Preserve mean and standard deviation | - Generates some negative values for P |
| Quantile mapping | - Preserve mean and standard deviation - No generates negative values of P - Variety of methods (theoretical distribution, parametric, non-parametric, empirical, splines) | - Required more complex transformations (application to the probability distribution of data) |
| GCM | CNRM-CM5 | EC-EARTH | MPI-ESM-LR | IPSL-CM5A-MR | |
| RCM | |||||
| CCLM4-8-17 | X | X | X | ||
| RCA4 | X | X | X | ||
| HIRHAM5 | X | ||||
| RACMO22E | X | ||||
| WRF331F | X | ||||
| RCM | GCM | Eliminated | |
|---|---|---|---|
| Lumped Cases | Distributed Case | ||
| CCLM4-8-17 | CNRM-CM5 | NO | NO |
| CCLM4-8-17 | EC-EARTH | NO | NO |
| CCLM4-8-17 | MPI-ESM-LR | NO | NO |
| HIRHAM5 | EC-EARTH | NO | YES |
| RACMO22E | EC-EARTH | NO | NO |
| RCA4 | CNRM-CM5 | NO | NO |
| RCA4 | EC-EARTH | NO | YES |
| RCA4 | MPI-ESM-LR | YES | NO |
| WRF331F | IPSL-CM5A-MR | NO | NO |
| CCLM4-8-17 | CNRM-CM5 | NO | NO |
| RCM | GCM | Technique | Lumped Case | Distributed Case |
|---|---|---|---|---|
| CCLM4-8-17 | CNRM-CM5 | 1st moment correc. | YES | YES |
| CCLM4-8-18 | CNRM-CM6 | 2nd moment correc. | NO | YES |
| CCLM4-8-19 | CNRM-CM7 | Regression | YES | YES |
| CCLM4-8-20 | CNRM-CM8 | QM Parametric dist. | NO | YES |
| CCLM4-8-21 | CNRM-CM9 | QM Empirical quant. | YES | NO |
| CCLM4-8-17 | EC-EARTH | 1st moment correc. | YES | YES |
| CCLM4-8-18 | EC-EARTH | 2nd moment correc. | YES | YES |
| CCLM4-8-19 | EC-EARTH | Regression | NO | YES |
| CCLM4-8-20 | EC-EARTH | QM Parametric dist. | YES | YES |
| CCLM4-8-21 | EC-EARTH | QM Empirical quant. | NO | NO |
| CCLM4-8-17 | MPI-ESM-LR | 1st moment correc. | YES | YES |
| CCLM4-8-17 | MPI-ESM-LR | 2nd moment correc. | NO | NO |
| CCLM4-8-17 | MPI-ESM-LR | Regression | NO | NO |
| CCLM4-8-17 | MPI-ESM-LR | QM Parametric dist. | NO | NO |
| CCLM4-8-17 | MPI-ESM-LR | QM Empirical quant. | NO | NO |
| HIRHAM5 | EC-EARTH | 1st moment correc. | YES | YES |
| HIRHAM5 | EC-EARTH | 2nd moment correc. | NO | NO |
| HIRHAM5 | EC-EARTH | Regression | NO | NO |
| HIRHAM5 | EC-EARTH | QM Parametric dist. | NO | YES |
| HIRHAM5 | EC-EARTH | QM Empirical quant. | NO | YES |
| RACMO22E | EC-EARTH | 1st moment correc. | YES | YES |
| RACMO22E | EC-EARTH | 2nd moment correc. | YES | YES |
| RACMO22E | EC-EARTH | Regression | NO | YES |
| RACMO22E | EC-EARTH | QM Parametric dist. | YES | YES |
| RACMO22E | EC-EARTH | QM Empirical quant. | YES | YES |
| RCA4 | CNRM-CM5 | 1st moment correc. | YES | YES |
| RCA4 | CNRM-CM5 | 2nd moment correc. | NO | YES |
| RCA4 | CNRM-CM5 | Regression | NO | YES |
| RCA4 | CNRM-CM5 | QM Parametric dist. | YES | YES |
| RCA4 | CNRM-CM5 | QM Empirical quant. | NO | NO |
| RCA4 | EC-EARTH | 1st moment correc. | YES | YES |
| RCA4 | EC-EARTH | 2nd moment correc. | YES | YES |
| RCA4 | EC-EARTH | Regression | YES | YES |
| RCA4 | EC-EARTH | QM Parametric dist. | YES | YES |
| RCA4 | EC-EARTH | QM Empirical quant. | YES | YES |
| RCA4 | MPI-ESM-LR | 1st moment correc. | YES | YES |
| RCA4 | MPI-ESM-LR | 2nd moment correc. | YES | YES |
| RCA4 | MPI-ESM-LR | Regression | YES | NO |
| RCA4 | MPI-ESM-LR | QM Parametric dist. | NO | NO |
| RCA4 | MPI-ESM-LR | QM Empirical quant. | YES | YES |
| WRF331F | IPSL-CM5A-MR | 1st moment correc. | YES | YES |
| WRF331F | IPSL-CM5A-MR | 2nd moment correc. | YES | YES |
| WRF331F | IPSL-CM5A-MR | Regression | YES | YES |
| WRF331F | IPSL-CM5A-MR | QM Parametric dist. | YES | YES |
| WRF331F | IPSL-CM5A-MR | QM Empirical quant. | NO | NO |
| Scenario | Lumped Case | Distributed Case | ||
|---|---|---|---|---|
| P | T | P | T | |
| Absolute Changes (mm or °C) | ||||
| E1 | −147.9 | 4.5 | −142.4 | 4.5 |
| E2 | −139.0 | 4.5 | −131.9 | 4.6 |
| E3 | −143.4 | 4.5 | −149.4 | 4.5 |
| E4 | −139.1 | 4.4 | −141.9 | 4.6 |
| Relative Changes (%) | ||||
| E1 | −28.21 | 31.94 | −27.16 | 31.66 |
| E2 | −26.51 | 31.59 | −25.16 | 32.05 |
| E3 | −27.35 | 31.74 | −28.50 | 31.79 |
| E4 | −26.53 | 30.99 | −27.06 | 32.49 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collados-Lara, A.-J.; Pulido-Velazquez, D.; Pardo-Igúzquiza, E. An Integrated Statistical Method to Generate Potential Future Climate Scenarios to Analyse Droughts. Water 2018, 10, 1224. https://doi.org/10.3390/w10091224
Collados-Lara A-J, Pulido-Velazquez D, Pardo-Igúzquiza E. An Integrated Statistical Method to Generate Potential Future Climate Scenarios to Analyse Droughts. Water. 2018; 10(9):1224. https://doi.org/10.3390/w10091224
Chicago/Turabian StyleCollados-Lara, Antonio-Juan, David Pulido-Velazquez, and Eulogio Pardo-Igúzquiza. 2018. "An Integrated Statistical Method to Generate Potential Future Climate Scenarios to Analyse Droughts" Water 10, no. 9: 1224. https://doi.org/10.3390/w10091224
APA StyleCollados-Lara, A.-J., Pulido-Velazquez, D., & Pardo-Igúzquiza, E. (2018). An Integrated Statistical Method to Generate Potential Future Climate Scenarios to Analyse Droughts. Water, 10(9), 1224. https://doi.org/10.3390/w10091224







