In-Situ and Numerical Investigation of Groundwater Inrush Hazard from Grouted Karst Collapse Pillar in Longwall Mining
Abstract
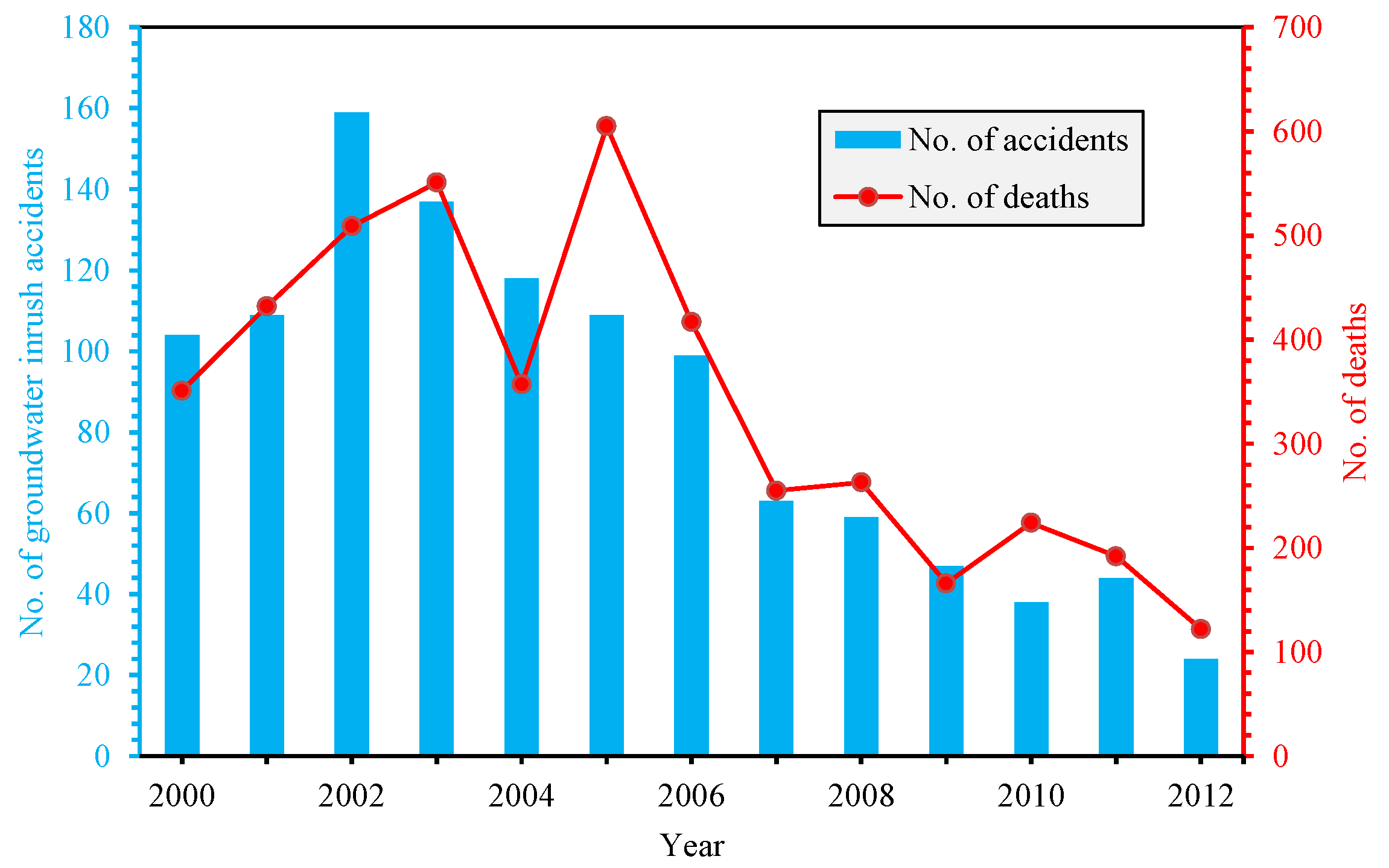
1. Introduction
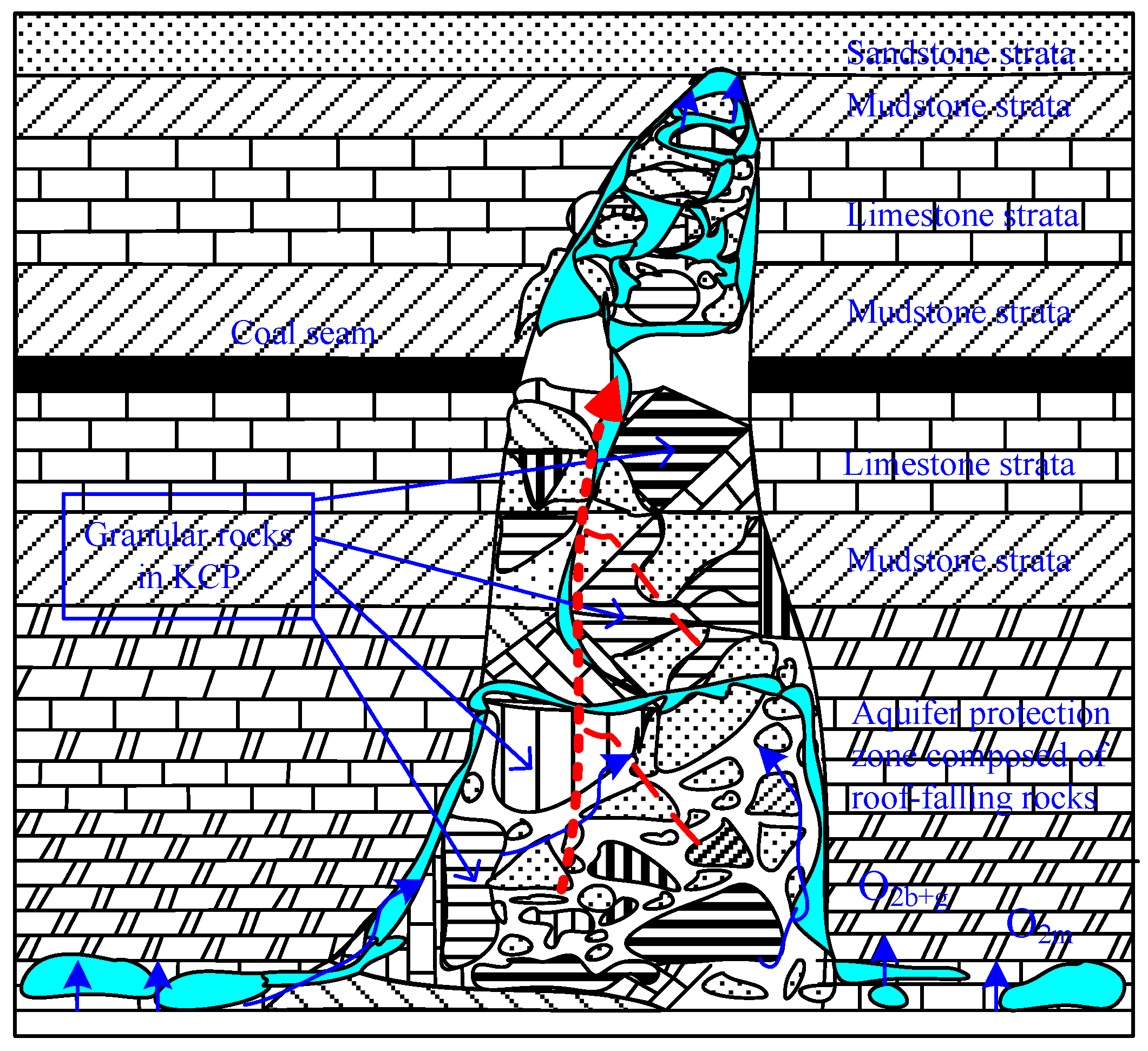
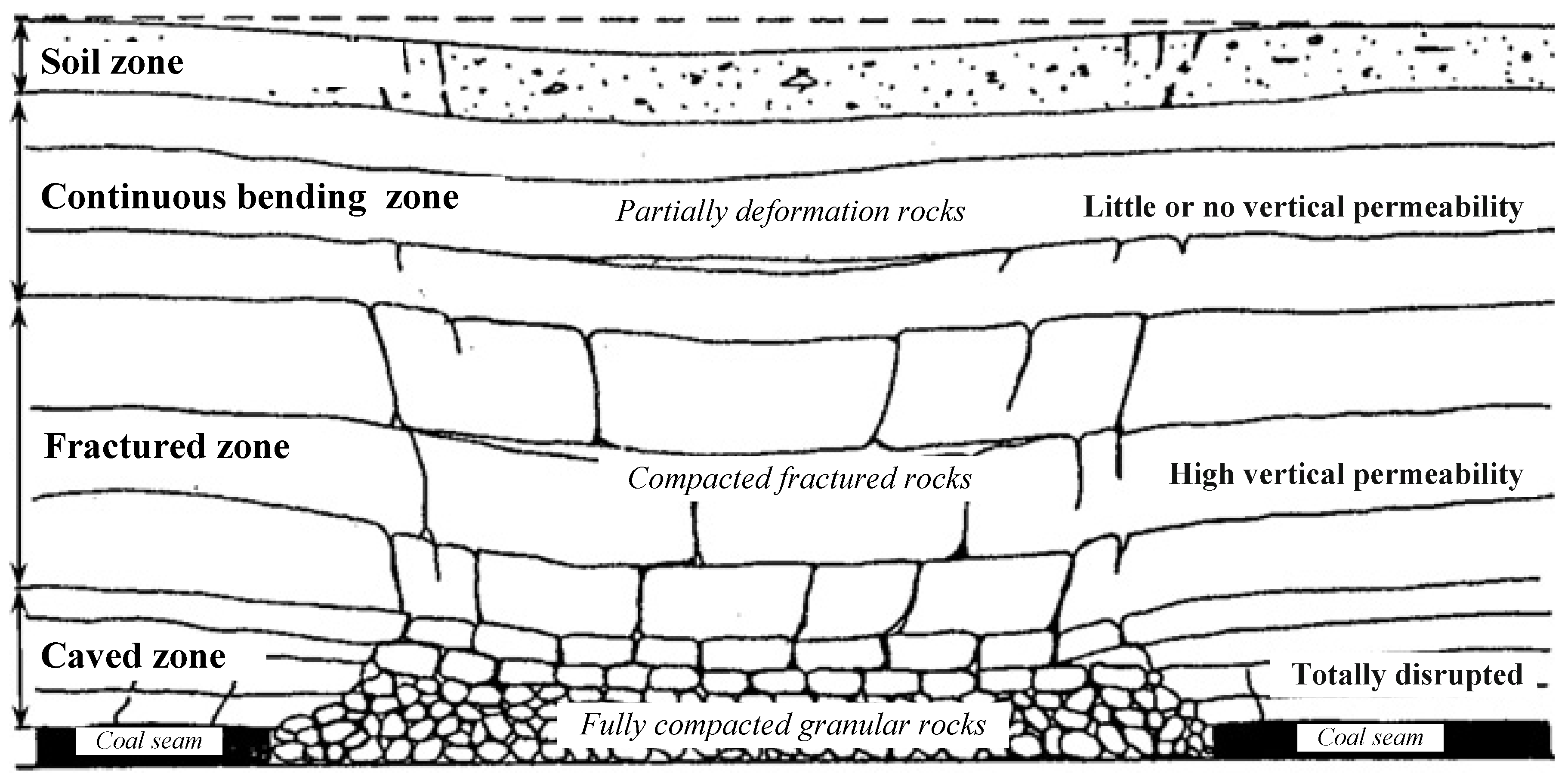
2. General Deformation and Groundwater Inrush Risk of Overlying Strata
2.1. Soil Zones
2.2. Continuous Deformation Zones
2.3. Fractured Zones
2.4. Caved Zones
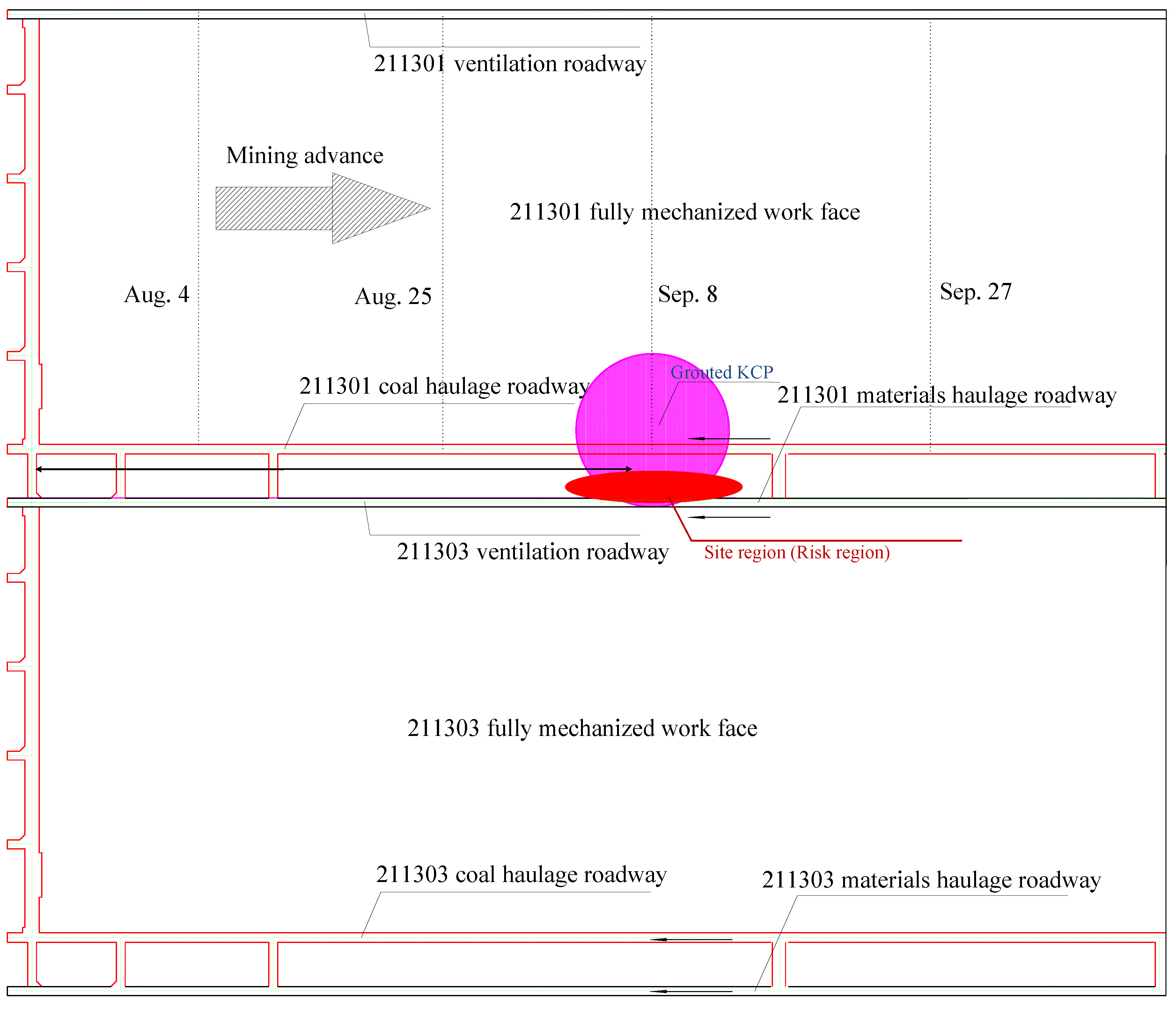
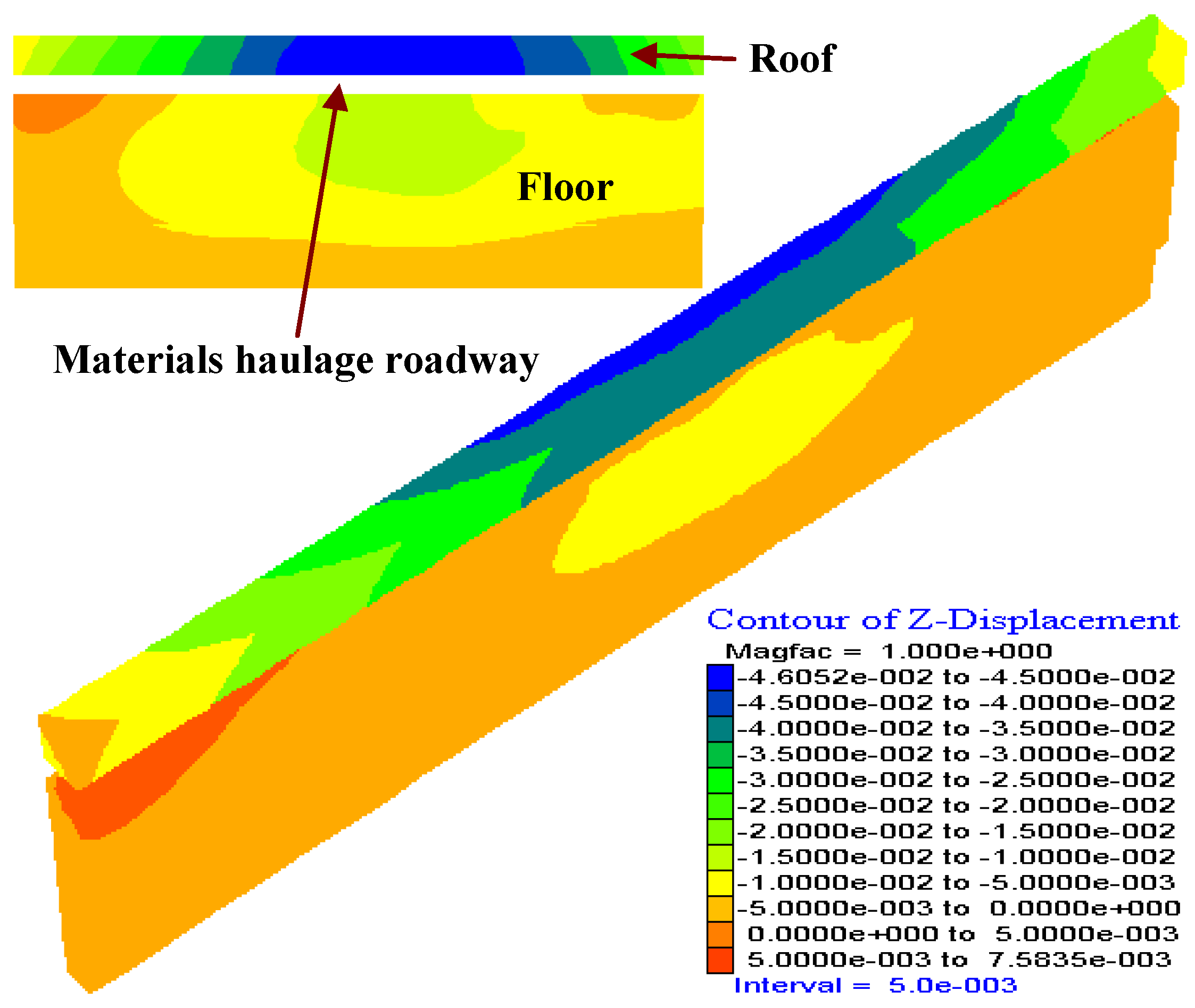
3. In-Situ investigation on the Deformation of Overlying Strata
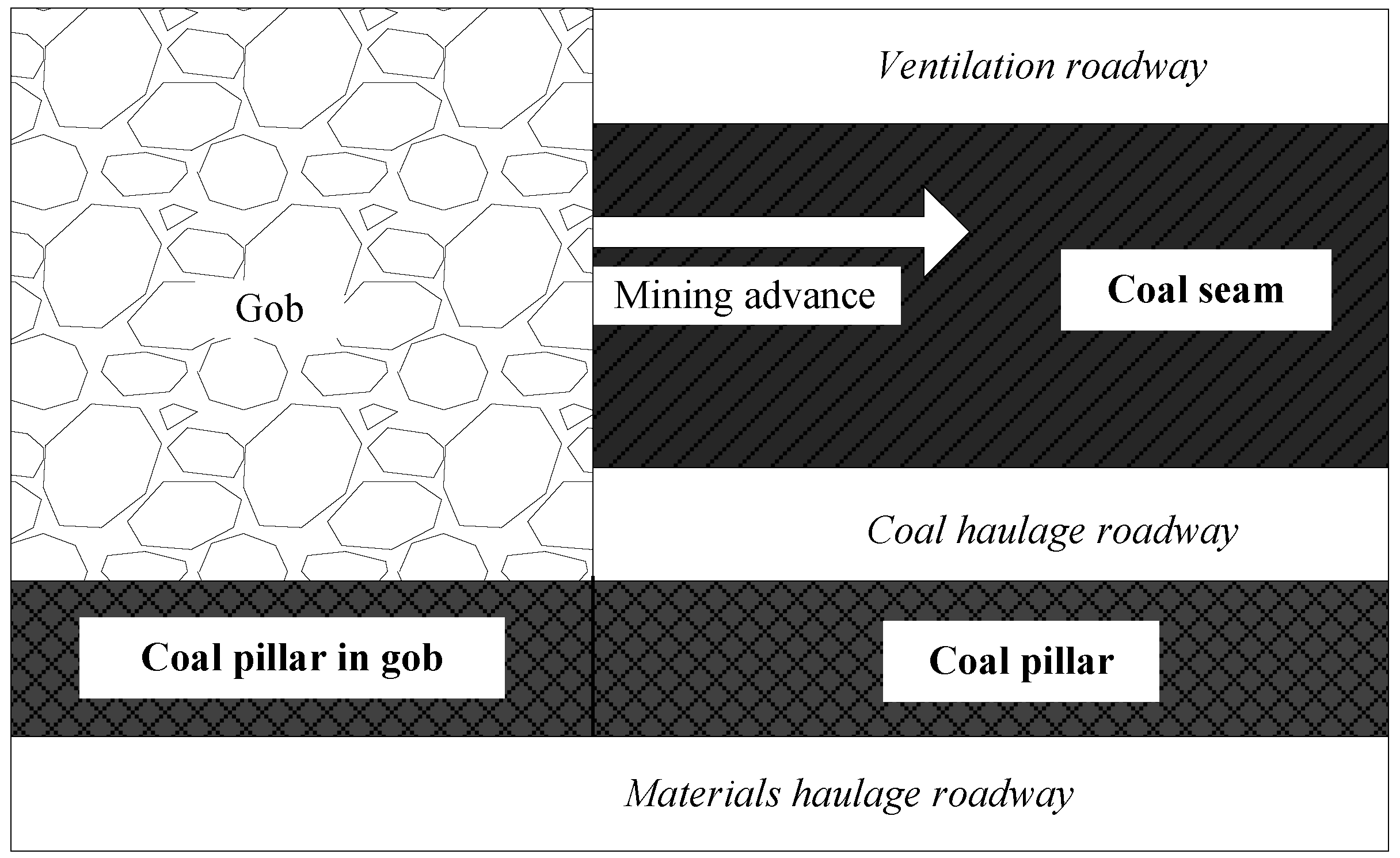
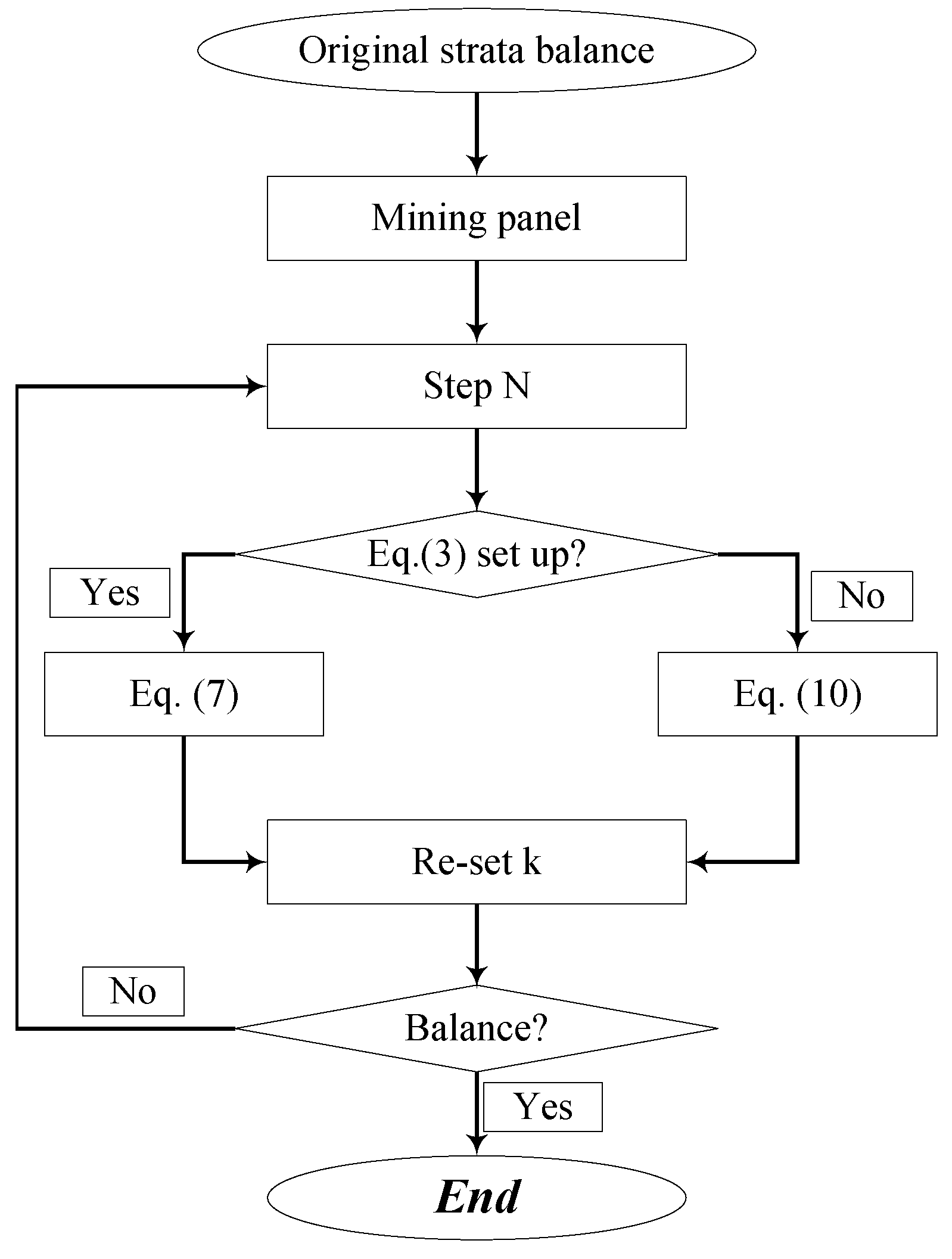
4. Modeling of the Coal Pillars Instability on the Strata Deformation
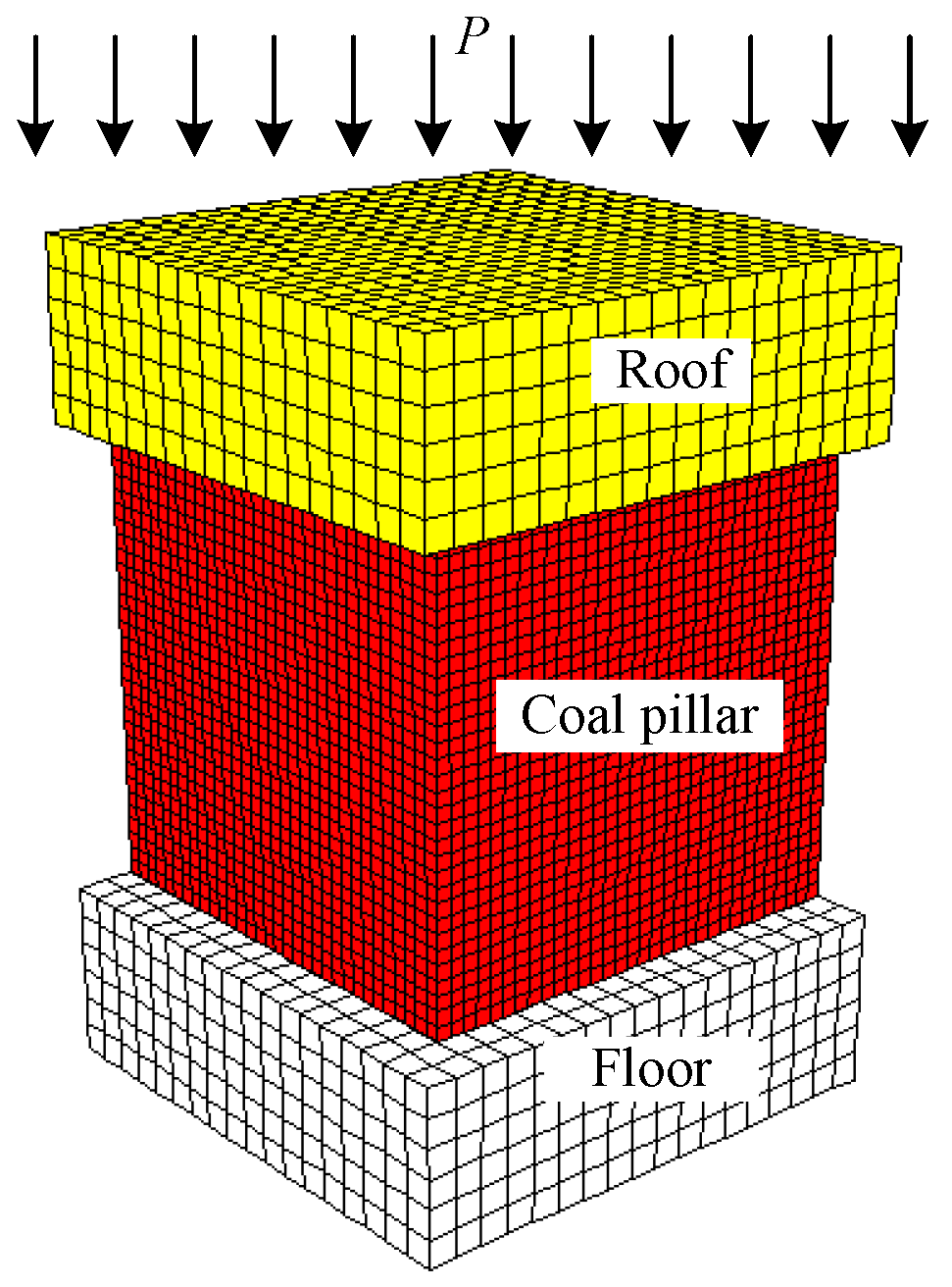
4.1. Instability Conditions of a Floor-Pillar-Roof System
4.2. Static and Dynamic Destruction of the System
4.2.1. Static Destruction
4.2.2. Dynamic Destruction of the System
5. Numerical Investigation of the Continuous Effect of Pillar Instability on Strata Deformation and Groundwater Inrush Risk from Aquifer
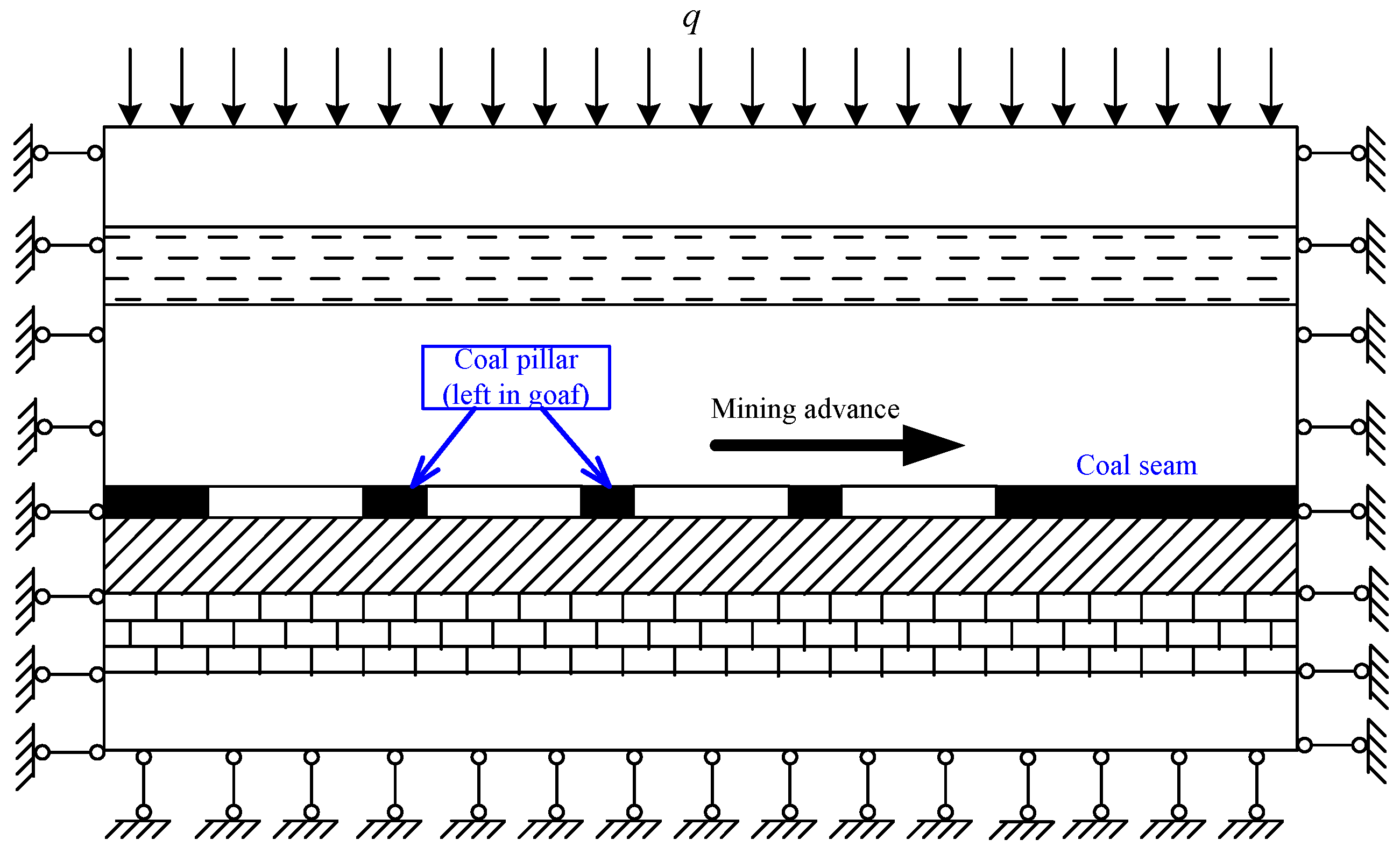
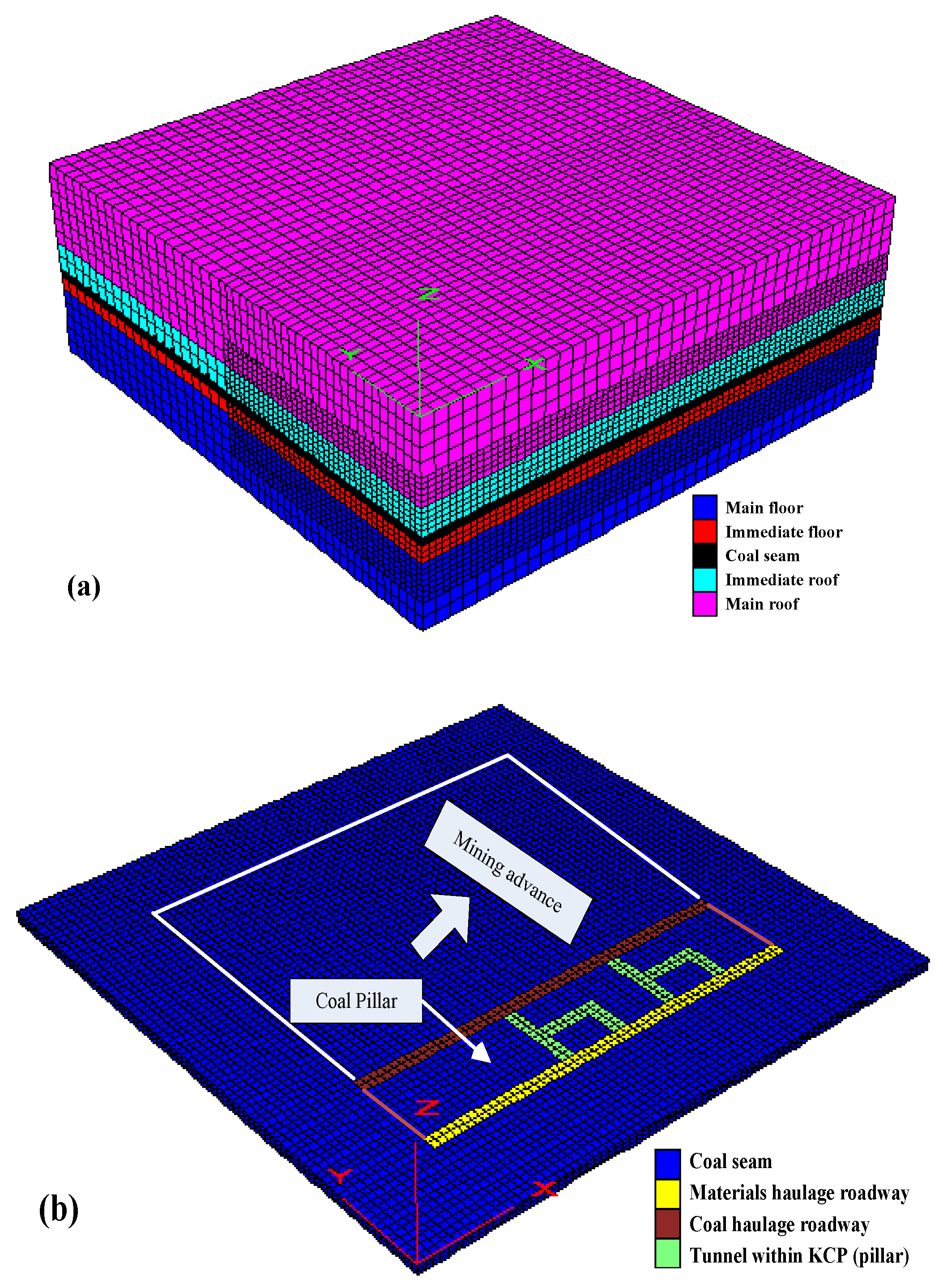
5.1. Numerical Modeling and Simulation Scheme
5.2. Modeling Results
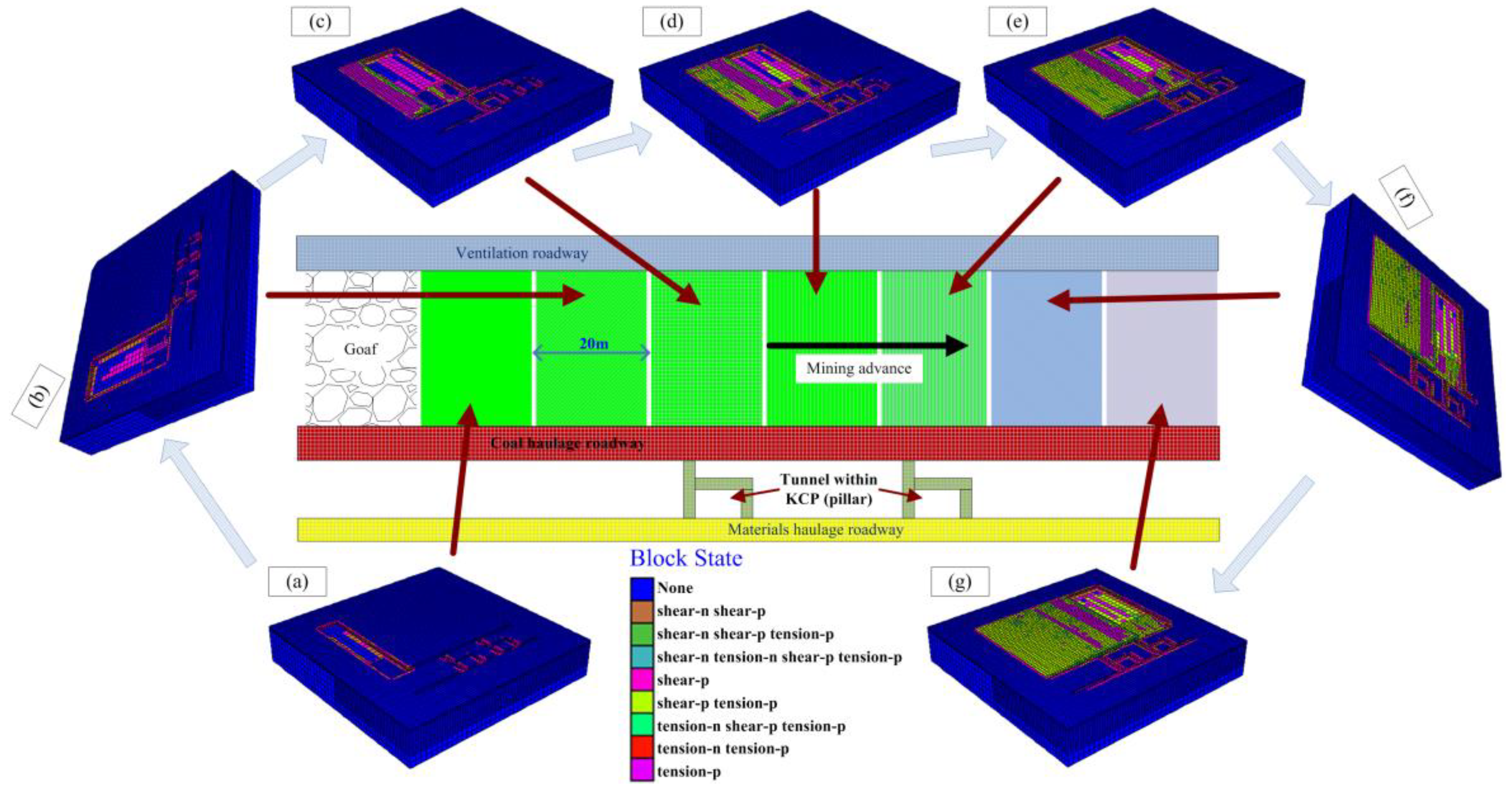
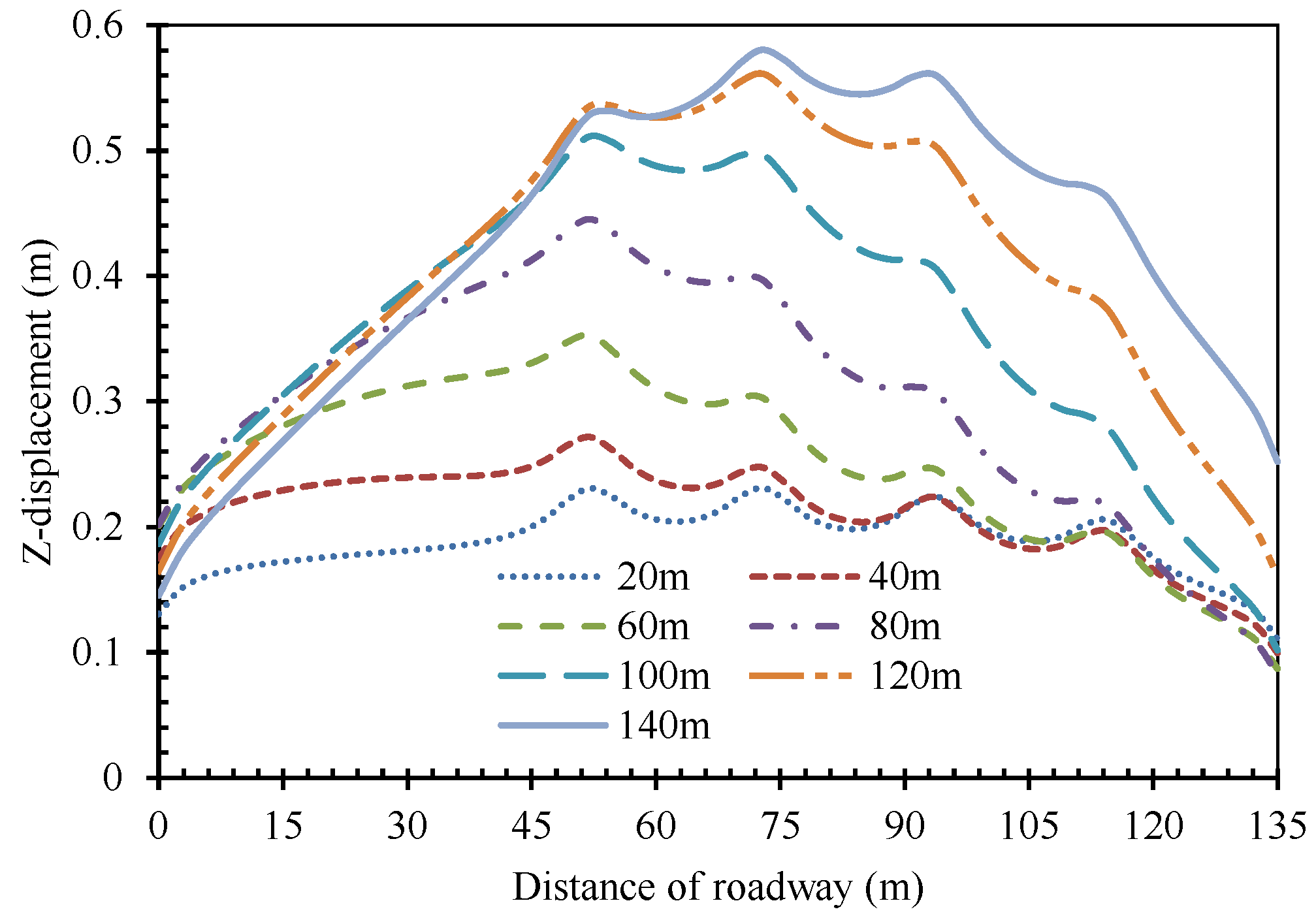
5.2.1. Plastic Zone Development during Longwall Mining
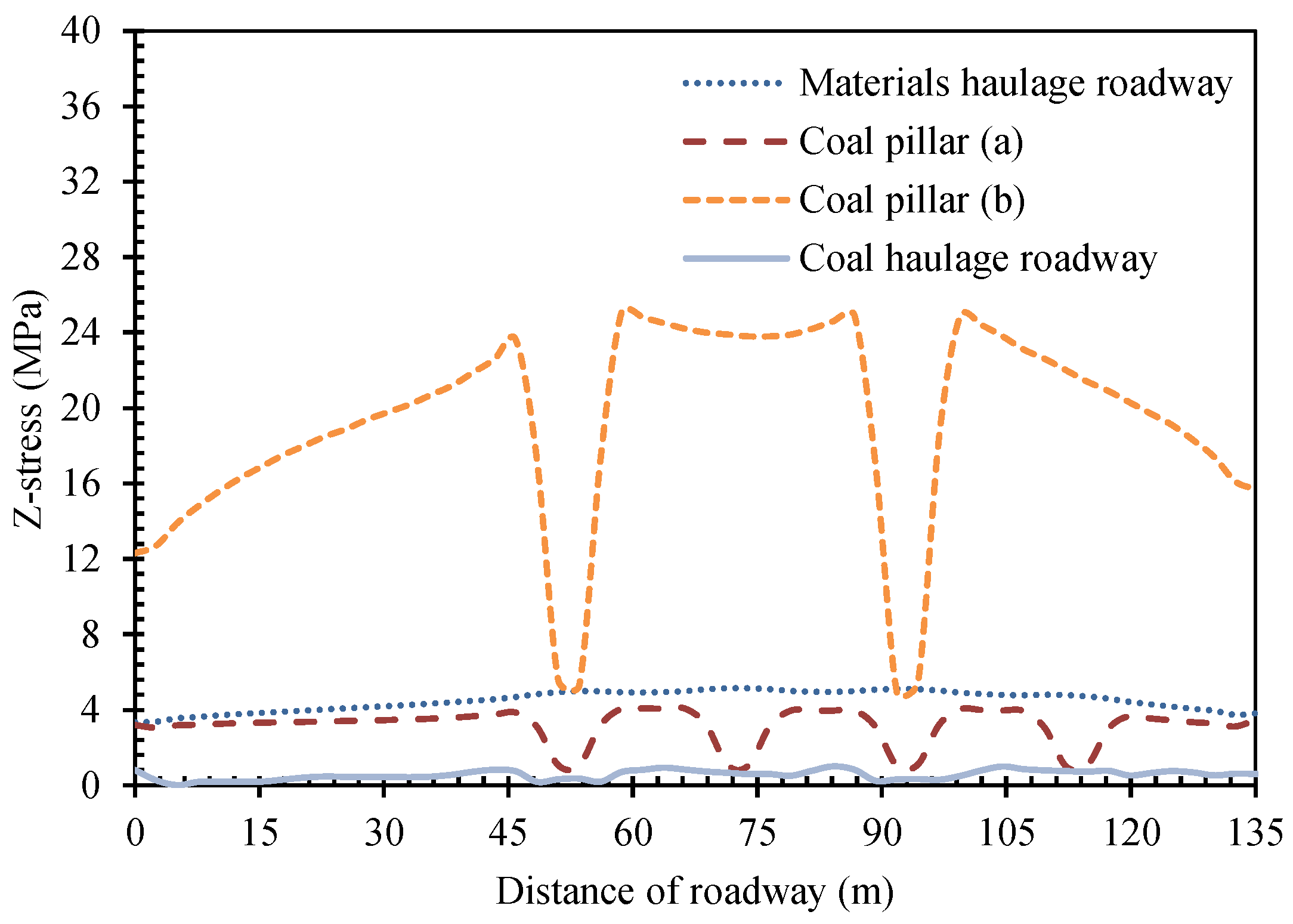
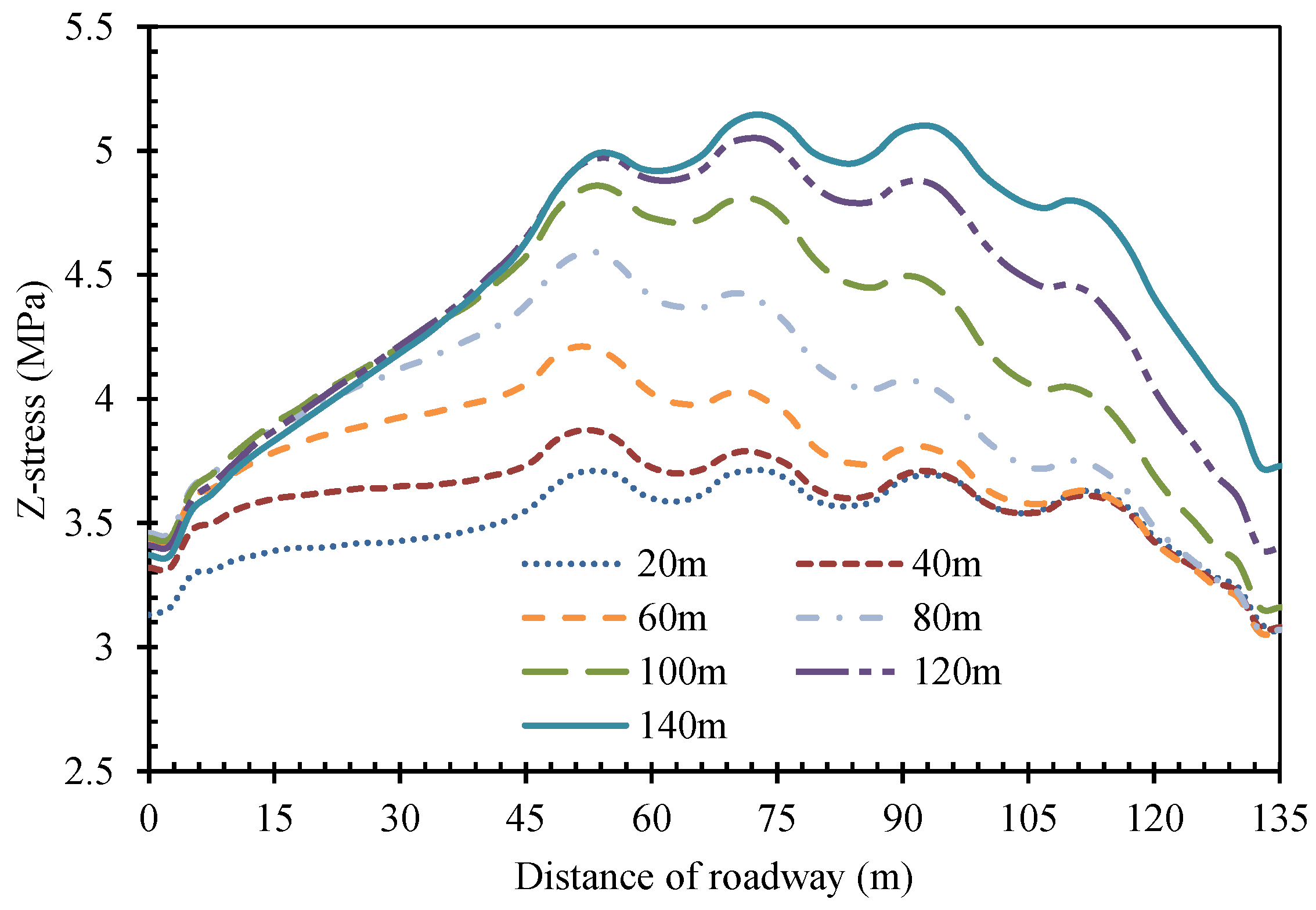
5.2.2. Vertical Stress Evolution
6. Conclusions
- (1)
- The collective energy in the “floor-pillar-roof” system is the first criterion for judging the stability of the system. Namely, the larger collective energy in coal pillar than that in floor-roof is the basic factor for the stability of “floor-pillar-roof” system.
- (2)
- The stiffness of the floor-roof and coal pillars is the second criterion for judging the instability of the system. Namely, if any of the stiffness of floor-roof or coal pillar meets a negative value, the system will lose its stability; the groundwater inrush pathway in the grouted KCP will be produced. However, when sum stiffness of “floor-pillar-roof” system meets a negative value, it means that the system structure is situated in a damage state.
- (3)
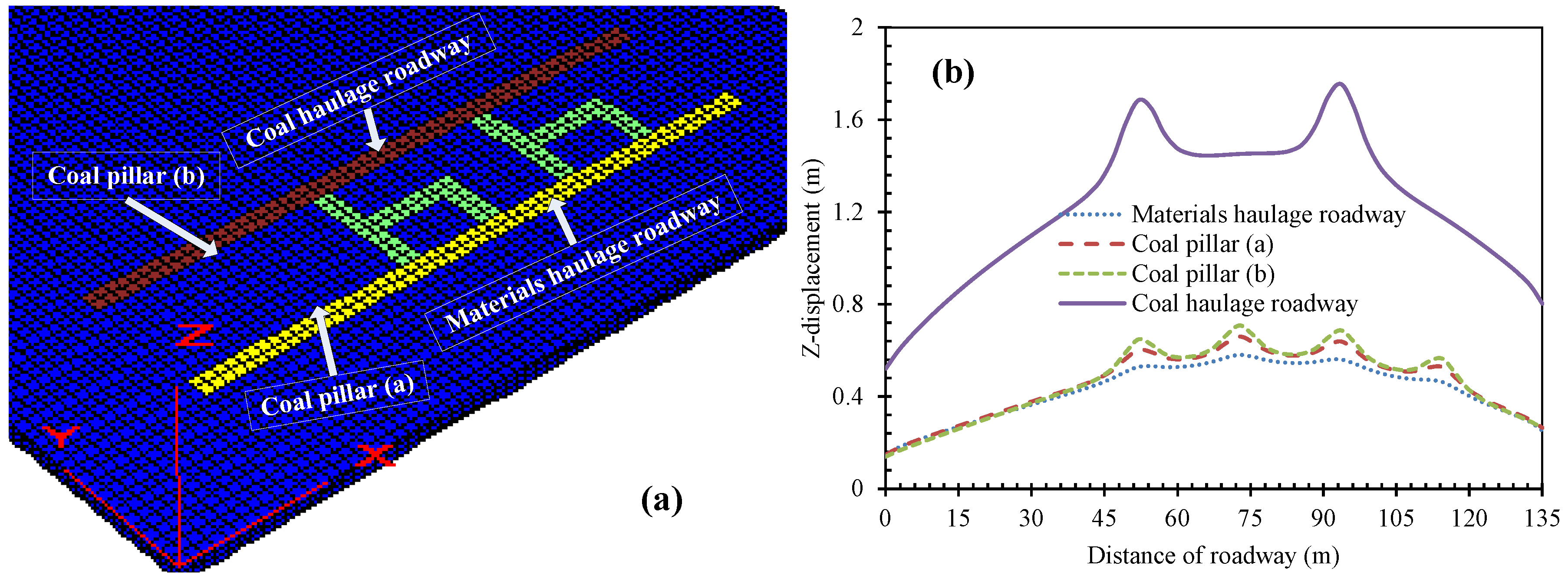
- A narrower coal pillar enlarges the risk of continuous instability of the system, resulting in the groundwater inrush pathway in the grouted KCP easily. Continuous coal pillars show a lower probability of instability. Conversely, the fractured coal pillars have a greater probability of failure.
- (4)
- The plastic zone and deformation of the roadway roof in the fractured coal pillar are larger than that of continuous coal pillar, indicating that the continuous coal pillar can mitigate the risk of groundwater inrush hazard from the grouted KCP effectively. The results that were obtained in this paper provide a scientific prevention for the groundwater inrush hazard from grouted KCP in practical engineering.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, G.Y.; Zhou, W.F. Impact of karst water on coal mining in North China. Environ. Geol. 2006, 49, 449–457. [Google Scholar] [CrossRef]
- Sun, W.J.; Zhou, W.F.; Jiao, J. Hydrogeological classification and water inrush accidents in China’s coal mines. Mine Water Environ. 2016, 35, 214–220. [Google Scholar] [CrossRef]
- Ma, D.; Rezania, M.; Yu, H.S.; Bai, H.B. Variations of hydraulic properties of granular sandstones during water inrush: Effect of small particle migration. Eng. Geol. 2017, 217, 61–70. [Google Scholar] [CrossRef]
- He, K.Q.; Yu, G.M.; Lu, Y.R. Palaeo-karst collapse pillars in Northern China and their damage to the geological environments. Environ. Geol. 2009, 58, 1029–1040. [Google Scholar]
- Ma, D.; Bai, H.B.; Miao, X.X.; Pu, H.; Jiang, B.Y.; Chen, Z.Q. Compaction and seepage properties of crushed limestone particle mixture: An experimental investigation for Ordovician karst collapse pillar groundwater inrush. Environ. Earth Sci. 2016, 75, 11. [Google Scholar] [CrossRef]
- Ma, D.; Miao, X.X.; Bai, H.B.; Huang, J.H.; Pu, H.; Wu, Y.; Zhang, G.M.; Li, J.W. Effect of mining on shear sidewall groundwater inrush hazard caused by seepage instability of the penetrated karst collapse pillar. Nat. Hazards 2016, 82, 73–93. [Google Scholar] [CrossRef]
- Zhang, J.C.; Zhang, Y.Z.; Liu, T.Q. Fluid Flow in Rock Mass and Water In-Rush through Coal Seam Floor; Geology Press: Beijing, China, 1997. (In Chinese) [Google Scholar]
- Zhang, J.C.; Shen, B.H. Coal mining under aquifers in China: A case study. Int. J. Rock Mech. Min. Sci. 2004, 41, 629–639. [Google Scholar] [CrossRef]
- Li, L.J.; Qian, M.G.; Li, S.G. Mechanism of water in-rush through fault. J. China Coal Soc. 1996, 21, 119–123. (In Chinese) [Google Scholar]
- Guo, W.J.; Liu, Y.X. The concept of water in-rush coefficient and its application. Hebei Coal 1989, 2, 56–60. (In Chinese) [Google Scholar]
- Miao, X.X.; Cui, X.M.; Wang, J.A.; Xu, J.L. The height of fractured water-conducting zone in undermined rock strata. Eng. Geol. 2011, 120, 32–39. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, H.; Pang, W. GIS and ANN coupling model: An innovative approach to evaluate vulnerability of karst water inrush in coalmines of North China. Environ. Geol. 2008, 54, 937–943. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, Y.Z.; Liu, D.H.; Zhou, W.F. Prediction of floor water inrush: The application of GIS-Based AHP vulnerable index method to Donghuantuo coalmine, China. Rock Mech. Rock Eng. 2011, 44, 591–600. [Google Scholar] [CrossRef]
- Bai, H.B.; Ma, D.; Chen, Z.Q. Mechanical behavior of groundwater seepage in karst collapse pillars. Eng. Geol. 2013, 164, 101–106. [Google Scholar] [CrossRef]
- Lu, Y.L.; Wang, L.G. Numerical simulation of mining-induced fracture evolution and water flow in coal seam floor above a confined aquifer. Comput. Geotech. 2015, 67, 157–171. [Google Scholar] [CrossRef]
- Wang, J.A.; Park, H.D. Coal mining above a confined aquifer. Int. J. Rock Mech. Min. Sci. 2003, 40, 537–551. [Google Scholar] [CrossRef]
- Zhang, R.; Jiang, Z.Q.; Sun, Q.; Zhu, S.Y. The relationship between the deformation mechanism and permeability on brittle rock. Nat. Hazards 2013, 66, 1179–1187. [Google Scholar] [CrossRef]
- Ma, D.; Zhou, Z.L.; Wu, J.Y.; Li, Q.; Bai, H.B. Grain size distribution effect on the hydraulic properties of disintegrated coal mixtures. Energies 2017, 10, 612. [Google Scholar] [CrossRef]
- Zhang, R.; Jiang, Z.Q.; Zhou, H.Y.; Yang, C.W.; Xiao, S.J. Groundwater outbursts from faults above a confined aquifer in the coal mining. Nat. Hazards 2014, 71, 1861–1872. [Google Scholar] [CrossRef]
- Yin, S.X.; Zhang, J.C.; Liu, D.M. A study of mine water inrushes by measurements of in situ stress and rock failures. Nat. Hazards 2015, 79, 1961–1979. [Google Scholar] [CrossRef]
- Zhang, D.S.; Fan, G.W.; Ma, L.Q.; Wang, X.F. Aquifer protection during longwall mining of shallow coal seams: A case study in the Shendong Coalfield of China. Int. J. Coal Geol. 2011, 86, 190–196. [Google Scholar] [CrossRef]
- Ma, D.; Bai, H.B.; Wang, Y.M. Mechanical behavior of a coal seam penetrated by a karst collapse pillar: Mining induced groundwater inrush risk. Nat. Hazards 2015, 75, 2137–2151. [Google Scholar] [CrossRef]
- Zhang, J.C. Investigations of water inrushes from aquifers under coal seams. Int. J. Rock Mech. Min. Sci. 2005, 42, 350–360. [Google Scholar] [CrossRef]
- Peng, S.S. Longwall Mining, 2nd ed.; West Virginia University: Morgantown, WV, USA, 2006; ISBN 0978938305. [Google Scholar]
- Ma, D.; Cai, X.; Zhou, Z.L.; Li, X.B. Experimental investigation on hydraulic properties of granular sandstone and mudstone mixtures. Geofluids 2018. [Google Scholar] [CrossRef]
- Fleck, N.A.; Hutchinson, J.W. A phenomenological theory for strain gradient effects in plasticity. J. Mech. Phys. Solids 1993, 41, 1825–1857. [Google Scholar] [CrossRef]
- Kaiser, P.K.; Tang, C.A. Numerical simulation of damage accumulation and seismic energy release during brittle rock failure—Part II: Rib pillar collapse. Int. J. Rock Mech. Min. Sci. 1998, 35, 123–134. [Google Scholar] [CrossRef]
- Qin, S.Q.; Wang, S.J.; Long, H.; Liu, J. A new approach to estimating geo-stresses from laboratory Kaiser effect measurements. Int. J. Rock Mech. Min. Sci. 1999, 36, 1073–1077. [Google Scholar] [CrossRef]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-brown failure criterion—2002 edition. In Proceedings of the 5th North American Rock Mechanics Symposium, Toronto, ON, Canada, 7–10 July 2002; pp. 267–273. [Google Scholar]
- Hoek, E.; Marinos, P.; Benissi, M. Applicability of the geological strength index (GSI) classification for very poor and sheared rock masses. The case of the Athens schist formation. Bull. Eng. Geol. Environ. 1998, 57, 151–160. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Cai, X.; Ma, D.; Cao, W.Z.; Chen, L.; Zhou, J. Effects of water content on fracture and mechanical behavior of sandstone with a low clay mineral content. Eng. Fract. Mech. 2018, 193, 47–65. [Google Scholar] [CrossRef]
- Fama, M.E.D.; Trueman, R.; Craig, M.S. Two- and three-dimensional elasto-plastic analysis for coal pillar design and its application to high wall mining. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 215–225. [Google Scholar] [CrossRef]
- Singh, R.; Sheorey, P.R.; Singh, D.P. Stability of the parting between coal pillar workings in level contiguous seams. Int. J. Rock Mech. Min. Sci. 2002, 39, 9–39. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Cai, X.; Ma, D.; Chen, L.; Wang, S.F.; Tan, L.H. Dynamic tensile properties of sandstone subjected to wetting and drying cycles. Constr. Build. Mater. 2018, 182, 215–232. [Google Scholar] [CrossRef]
- FLAC3D (Fast Lagrangian Analysis of Continua in 3 Dimensions), version 3.1; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2006.
- Ma, D.; Miao, X.X.; Wu, Y.; Bai, H.B.; Wang, J.G.; Rezania, M.; Huang, Y.H.; Qian, H.W. Seepage properties of crushed coal particles. J. Pet. Sci. Eng. 2016, 146, 297–307. [Google Scholar]
- Cheng, Y.M.; Wang, J.A.; Xie, G.X.; Wei, W.B. Three-dimensional analysis of coal barrier pillars in tailgate area adjacent to the fully mechanized top caving mining face. Int. J. Rock Mech. Min. Sci. 2010, 47, 1372–1383. [Google Scholar] [CrossRef]
- Jiang, Y.D.; Wang, H.W.; Xue, S.; Zhao, Y.X.; Zhu, J.; Pang, X.F. Assessment and mitigation of coal bump risk during extraction of an island longwall panel. Int. J. Coal Geol. 2012, 95, 20–33. [Google Scholar] [CrossRef]
- Ma, D.; Li, Q.; Hall, M.R.; Wu, Y. Experimental investigation of stress rate and grain size on gas seepage characteristics of granular coal. Energies 2017, 10, 527. [Google Scholar] [CrossRef]
- Wang, H.W.; Jiang, Y.D.; Zhao, Y.X.; Zhu, J.; Liu, S. Numerical investigation of the dynamic mechanical state of a coal pillar during longwall mining panel extraction. Rock Mech. Rock Eng. 2013, 46, 1211–1221. [Google Scholar] [CrossRef]

| Distance to Tunnel within Grouted KCP (m) | Width (m) | Height (m) | Actual Area (m2) | Deformation (%) | ||
|---|---|---|---|---|---|---|
| Actual | Deformation | Actual | Subsidence | |||
| 50 | 5.45 | 0.05 | 2.98 | 0.02 | 16.24 | 1.57 |
| 34 | 5.44 | 0.06 | 2.93 | 0.07 | 15.94 | 3.39 |
| 28 | 5.41 | 0.09 | 2.89 | 0.11 | 15.63 | 5.24 |
| 18 | 5.42 | 0.08 | 2.87 | 0.13 | 15.56 | 5.72 |
| 10 | 5.37 | 0.13 | 2.64 | 0.36 | 14.18 | 14.08 |
| −4 | 5.23 | 0.27 | 2.54 | 0.46 | 13.28 | 19.49 |
| −16 | 5.35 | 0.15 | 2.73 | 0.27 | 14.61 | 11.48 |
| −35 | 5.28 | 0.22 | 2.65 | 0.35 | 13.99 | 15.2 |
| −46 | 5.39 | 0.11 | 2.81 | 0.19 | 15.15 | 8.21 |
| Strata | Thickness (m) | Density (kg/m3) | Bulk Modulus (GPa) | Shear Modulus (GPa) | Cohesion (MPa) | Friction Angle (°) | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|---|
| Main roof | 30 | 2600 | 23.5 | 13.3 | 3.6 | 37 | 3.2 |
| Immediate roof | 10 | 2500 | 22.7 | 11.7 | 3.1 | 34 | 2.8 |
| Coal seam | 3 | 1500 | 7.1 | 2.5 | 2.5 | 28 | 1.2 |
| Immediate floor | 5 | 2600 | 22.2 | 12.7 | 3.8 | 34 | 3.8 |
| Main floor | 25 | 2500 | 20.1 | 10.9 | 3.5 | 36 | 3.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, D.; Cai, X.; Li, Q.; Duan, H. In-Situ and Numerical Investigation of Groundwater Inrush Hazard from Grouted Karst Collapse Pillar in Longwall Mining. Water 2018, 10, 1187. https://doi.org/10.3390/w10091187
Ma D, Cai X, Li Q, Duan H. In-Situ and Numerical Investigation of Groundwater Inrush Hazard from Grouted Karst Collapse Pillar in Longwall Mining. Water. 2018; 10(9):1187. https://doi.org/10.3390/w10091187
Chicago/Turabian StyleMa, Dan, Xin Cai, Qiang Li, and Hongyu Duan. 2018. "In-Situ and Numerical Investigation of Groundwater Inrush Hazard from Grouted Karst Collapse Pillar in Longwall Mining" Water 10, no. 9: 1187. https://doi.org/10.3390/w10091187
APA StyleMa, D., Cai, X., Li, Q., & Duan, H. (2018). In-Situ and Numerical Investigation of Groundwater Inrush Hazard from Grouted Karst Collapse Pillar in Longwall Mining. Water, 10(9), 1187. https://doi.org/10.3390/w10091187






