3.2. MLR Analysis
Four types of MLR models corresponding to Equations (3)–(6) were tested to identify the most suitable models (
Table 6). The
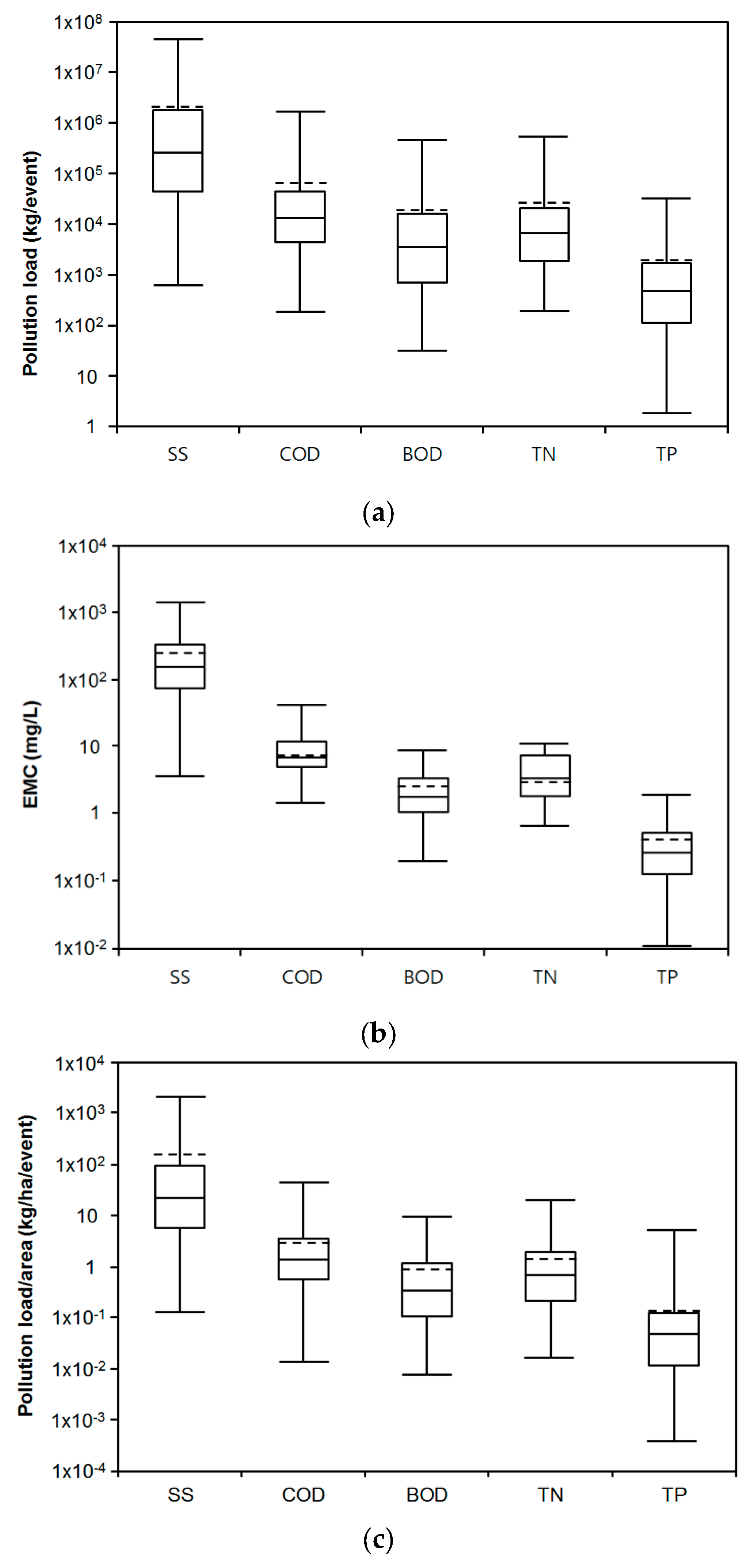
R2 values for SS, COD, BOD, TN, and TP in the type 1 MLR of pollutant load ranged from 0.275 to 0.447. The
R2 values for SS, COD, BOD, TN, and TP in the type 1 MLR of EMC and load/area were also low, indicating poor performance of the regression models. The
R2 values for SS, COD, BOD, TN, and TP in the type 2 MLR of pollutant load were 0.76, 0.67, 0.64, 0.65, and 0.80, respectively. The
R2 values of the type 2 MLR were quite high, but most of the VIF values were larger than 5, with a few values greater than 10. Thus, the VIF showed that multicollinearity was observed in the established models and that the type 2 MLR was not adapted. Although the
R2 values of the type 2 MLR for load/area were acceptable, the VIF values were high, indicating multicolinearity. VIF values and other statistics of MLRs were presented only for the selected model. The results of the MLR model employing the type 4 equation are listed in
Table 7,
Table 8 and
Table 9.
The R2 values for SS, COD, BOD, TN, and TP in the type 3 MLR of the pollutant load were also fairly high, but all VIF values were less than 5. Among the type 3 MLR models, the SS, TN, and TP in the MLR of EMC and the SS and TP in the MLR of load/area showed acceptable R2 values. The values of R2 for SS, COD, BOD, TN, and TP in the type 4 MLR of pollutant load were 0.74, 0.69, 0.69, 0.61, and 0.74 respectively. The R2 values of the type 4 MLR were a little better than those of the type 3 MLR, and all VIF values were less than 5. Thus, we selected the type 4 equation as the MLR model to predict the runoff pollutant discharge in the study area. However, the COD and BOD in the MLR of EMC and COD and TN in the MLR of load/area could not explain the variance in the pollutant discharge properly.
Using the stepwise variable selection method, two to five variables were retained in the pollutant load model, as shown in
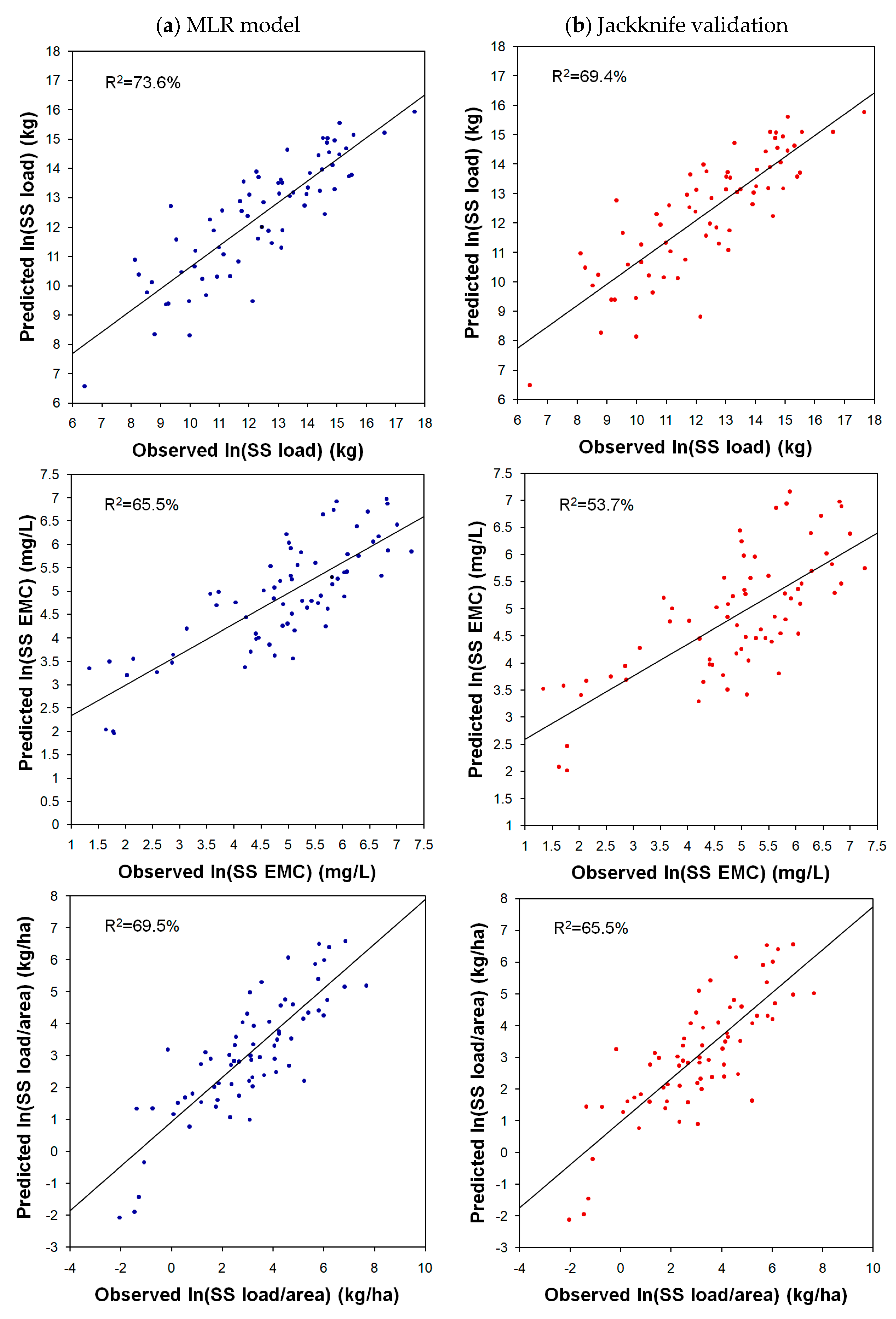
Table 7. In the case of the SS model, given the
R2 value, 73.6% of the variability of the dependent variable ln(SS load) is explained by the four explanatory variables. The MLR models indicated in
Table 7,
Table 8 and
Table 9 are statistically significant at
p < 0.0001 except for the ln(COD EMC) model (
p = 0.00019). The
R2 values for SS, COD, BOD, TN, and TP in the type 4 MLR of pollutant load were fairly high (0.614 <
R2 < 0.741), as indicated in
Table 7. The performance evaluation by CV(RMSE) [
35] shows that the SS model was the best and that the other models of the water quality variables were also acceptable. The range of RSR for SS, COD, BOD, and TP in the MLR models of pollutant load (
Table 7) was from 0.509 to 0.559, and the performance of the MLR for these variables was good [
34]. The RSR for TN was 0.622, and the performance of the TN model was satisfactory. The NSE values for the MLR models of pollutant load ranged from 0.61 to 0.74, and the MLR models of the pollutant load had good performance. As a special case, in linear regression forecasting models like this study, NSE is equal to the coefficient of determination,
R2 [
36]. Overall, all the MLR models of the pollutant load had good prediction performance.
All VIF values in
Table 7 are lower than 5, and the mean VIF values are not large. These results suggest that the coefficient of regression for the explanatory variables could be statistically acceptable and that multicollinearity was not present in the established models.
Standardized coefficients refer to how many standard deviations a dependent variable will change in response to an increase of one standard deviation in the predictor variable. This statistic allows us to compare the relative contribution of each independent variable in the prediction of the dependent variable. The higher the absolute value of a coefficient is, the more important the weight of the corresponding variable. Standardized coefficients are useful for comparing effects across different measures. The standardized regression coefficients of
Table 7 indicate that subbasin area (0.576 <
βi < 0.709) and rainfall depth (0.453 <
βi < 0.563) are important influential parameters for all the load predictions. In addition, % field has relatively small effects on the SS, BOD and TP models.
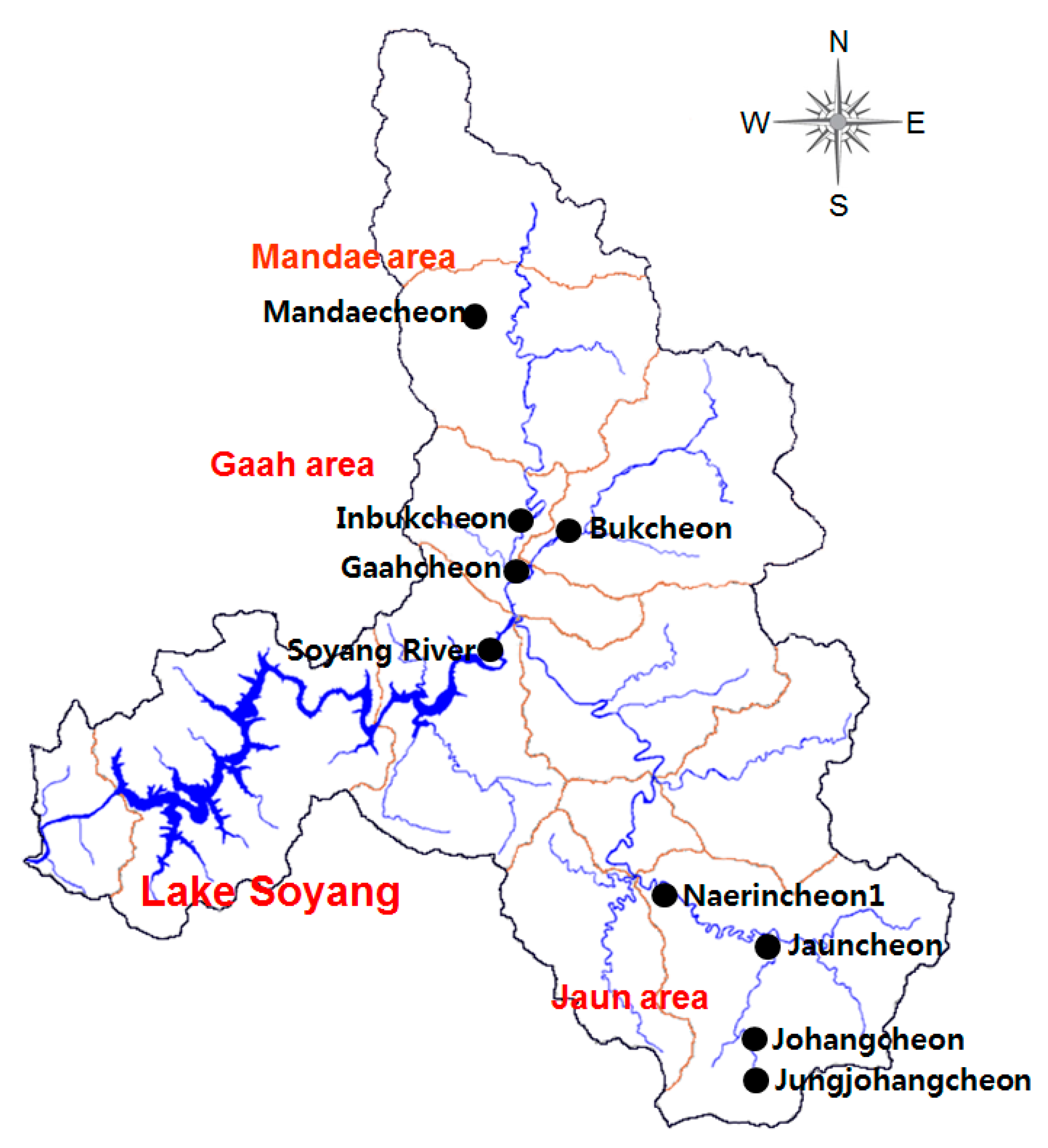
The area with the high density of highland fields in Lake Soyang basin has steeper slopes than the other areas. However, Lake Soyang basin also contains highly mountainous terrain; thus, the mean slopes of the dense highland field subbasins are lower than the average slope of the entire Lake Soyang basin. Therefore, the standardized regression coefficients of mean slope for the SS and TP load models have (−) signs, and the mean slope has a negative influence on the SS and TP loads.
The explanatory variables for the SS and TP models explained 65.5% and 66.2% of variation in the response variables of EMC. The
R2 values were fairly high, as indicated in
Table 8. The
R2 value for the TN model of EMC was 0.539, and the TN model was acceptable [
34]. The CV(RMSE) value of the BOD model was quite high, and the model was not acceptable. The RSR values for SS and TP in the MLR models of EMC (
Table 8) were 0.587 and 0.581, respectively, and the performances of these models were good. The RSR for the TN model was 0.679, and the performance of the TN model was satisfactory. However, the RSR values for the COD and BOD models were high, and these models were unsatisfactory. The NSE values for the MLR models of the EMC show that the SS, TP, and TN models were satisfactory but that the COD and BOD models were not satisfactory. The VIF values for the EMC models were lower than 5, and the mean VIF values were not large. Overall, the MLR models for SS and TP have good prediction performance, and the TN model has acceptable performance.
The standardized regression coefficients in
Table 8 indicate that rainfall intensity and rainfall depth are influential explanatory variables for the EMC response variables. Rainfall intensity (0.234 <
βi < 0.426) is an important factor for the TP, TN, and COD models, and rainfall depth is important for the SS and BOD models. In the pollutant load model, rainfall depth is a very important parameter, whereas rainfall intensity is not an important explanatory variable. However, rainfall intensity is an influential parameter for the EMC of a storm event. From the Pearson correlation matrix between natural log-transformed stormwater runoff discharge and subbasin characteristics in
Table 5, we also can see that EMCs are better correlated to rainfall intensity than rainfall depth, and pollutant loads are much better correlated to rainfall depth than rainfall intensity. In agricultural areas such as the study area, the larger the rainfall intensity, the more nutrients are released from fertilizer and vegetation roots. The standardized regression coefficients of the mean slope for the SS and TP load models have (−) sign, and the mean slope has a large negative influence on the SS and TP EMC. Additionally, % field also has a negative impact on the SS and TP EMC.
The explanatory variables for the SS and TP models explained 69.5% and 67.5% of the variation in the load/area response variables, and the
R2 values were fairly high, as indicated in
Table 9. The
R2 value for the BOD model of load/area was 0.51; thus, the BOD model was acceptable. The RSR values for SS and TP in the MLR models of load/area (
Table 9) were 0.55 and 0.57, respectively, and the performances of these models were good. The RSR for the BOD model was 0.70, and the performance of the TN model was satisfactory. The NSE values in the MLR models of the load/area show that the SS, TP, and BOD models were satisfactory. The VIF values for the load/area models were less than 5, and the mean VIF values were not large. Overall, the MLR models of load/area for SS and TP have good performance, and the BOD model has acceptable performance.
The standardized regression coefficients in
Table 9 indicate that rainfall depth (0.576 <
βi < 0.634) is a highly influential parameter for all response variables in the load/area prediction. The β coefficients of the mean slope for the SS and TP load/area models are −0.79 and −0.49, respectively, and the absolute values of the coefficients are comparable to the coefficients of rainfall depth, indicating that the mean slope is a remarkable negative parameter on the SS and TP load/area results.