1. Introduction
A number of studies have reported streamflow reduction in several rivers throughout the world [
1,
2,
3,
4,
5], putting enormous stress on ecological and socioeconomic systems. This is especially stressful for semiarid and semihumid regions, where the hydrological cycle and water yield will be more vulnerable to climate change and anthropogenic interference [
6]. Climatic changes include temperature changes and the redistribution of precipitation, which together affect streamflow discharge [
7]. Anthropogenic interference mainly consists of land use/cover change (LUCC), urbanized and industrialized extension, and hydropower development and irrigation intensification, which greatly alter the underlying surface and water resource reapportionment [
8]. Quantification of streamflow changes and identification of the various contributing factors are of considerable importance for a better understanding of the hydrologic mechanisms, which is beneficial for planning suitable adaptation strategies and water management.
There are various methods to separate the impacts of climate change and anthropogenic interference on streamflow, mainly including catchment experiments, hydrological models, and statistical methods [
9]. Catchment experiments are the most rigorous empirical research design for estimating the effects of land use on aquatic systems [
10], but they can be influenced by the variation in experimental conditions and the presentation of results [
11]. Most relevant studies indicate that catchment streamflow decreased significantly after afforestation and increased after deforestation [
10,
12,
13]. Hydrological models, both distributed and lumped, have been widely used [
7,
14,
15,
16]. Hu et al. applied the water and energy budget-based distributed hydrological model (WEB-DHM) to diagnose and quantify climate and human impacts on streamflow change [
17]. Hundecha et al. applied a conceptual rainfall–runoff model to 95 catchments in the Rhine basin to model the effect of land use change on runoff [
18]. Statistical methods such as streamflow elasticity have also been used in regions specifically with available long-term climate and hydrologic data [
9,
19,
20]. Tian et al. used regression analysis to illustrate runoff decline via comparison of precipitation–runoff correlation for the period prior to and after sharp runoff decline [
21].
The semiarid and arid Yellow River Basin (YRB) is the main source of surface water in the northwest and northern part of China. The annual streamflow is about 58 billion m
3, and the water resource per capita is 905 m
3—only a third of the national average, which poses a threat to the YRB’s water resources availability. The climbing industry, agriculture, and household demand for water induced by rapid economic development and expanding urbanization is also a challenge [
22]. In addition, some ecological programs launched by the Chinese government since 1999 have greatly altered the regional water cycle, including the Natural Forest Conservation Program (NFCP) and Grain for Green Project (GFGP) (
http://tghl.forestry.gov.cn/) [
6,
23], and therefore, the basin is very sensitive to climate change and anthropogenic interference. Attempts have been made to understand the long-term streamflow variation and the sensitivity of streamflow to climate change in the Yellow River Basin. Tang et al. used a distributed biosphere hydrological (DHB) model system to simulate hydroclimate connections in the Yellow River Basin and found that climate change dominated the predicted changes in the upper and middle reaches, but anthropogenic interference dominated the lower reaches [
24]. Liu et al. found that streamflow was more sensitive to precipitation in humid regions or wet years than in arid regions or dry years by means of streamflow elasticity [
25]. Li et al. investigated the changing properties and underlying causes for decreased streamflow by both the Budyko framework and hydrological modeling techniques [
26]. However, most of these previous studies focused on the entire basin or a local scale of catchments instead of comparing different subregions, let alone the comparison before and after the implementation of Natural Forest Conservation Program and Grain for Green Project. Moreover, few studies have paid attention to the contribution made by variations in the intra-annual distribution of precipitation, with only the annual precipitation considered.
The objectives of this paper are as follows: (1) to explore the spatial–temporal variation of annual precipitation, average temperature, the percentage of flood-season precipitation and natural streamflow in different subregions of YRB; (2) to quantitatively analyze the spatial–temporal characteristics of the contribution made by different meteorological factors and anthropogenic interference to streamflow changes in different subregions; (3) to analyze the spatial–temporal characteristics of the sensitivity of annual streamflow to various meteorological factors.
2. Study Area and Data
2.1. Study Area
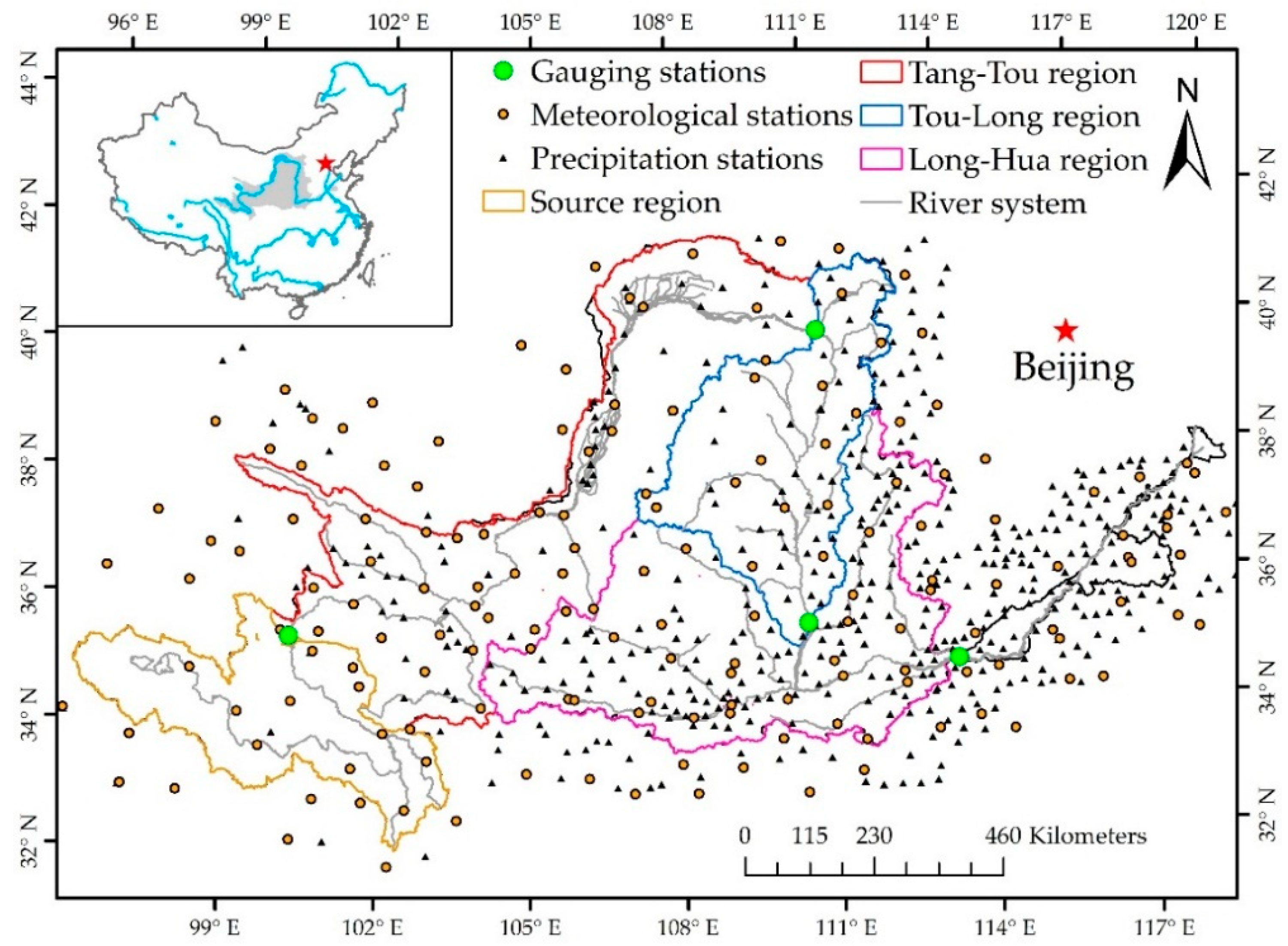
The Yellow River (
Figure 1) originates in the Qinghai Province of China and flows into Bohai Bay, forming the Yellow River Basin, which covers a total watershed area of 795,000 km
2 (including endoreic inter flow area). The main stream is 5464 km long with a slope of 4480 m. It can be divided into three parts. The upper reach travels 3472 km and drains 428,000 km
2 of land. The middle reach flows for 1206 km, with a drainage area of 344,000 km
2. When the middle reach flows through the Loess Plateau, the tributaries transport vast amounts of sediment, proclaiming the Yellow River as having the highest sediment content in the world. The remaining down reach has a length of 786 km and a drainage area of 23,000 km
2. The climatic and hydrologic conditions of the YRB are complex because of the large geographical extent and elevation difference. The precipitation exhibits high spatial and temporal variabilities: the ratio of rainfall between the North and South is greater than 5, 70% of precipitation falls between June and September, and the variation coefficient (C
v) is between 0.15 and 0.4. Temperature disparity is one of the major climate features in the YRB, with an annual mean temperature fluctuating from −4 °C to 14 °C. Considering the critical role played by the Yellow River in regional water supply and the tremendous challenges posed by water shortages, an analysis of the variation and sensitivity of annual streamflow is both important and imperative.
2.2. Data Collection and Preprocessing
The datasets used in this study include climate, streamflow, leaf area index (LAI), and Digital Elevation Model (DEM) data.
Climate data were obtained from the China Meteorological Administration (CMA), including daily precipitation from 582 rainfall gauges and the daily mean, maximum, and minimum temperatures from 97 meteorological stations inside and near the Yellow River basin from 1957 to 2010.
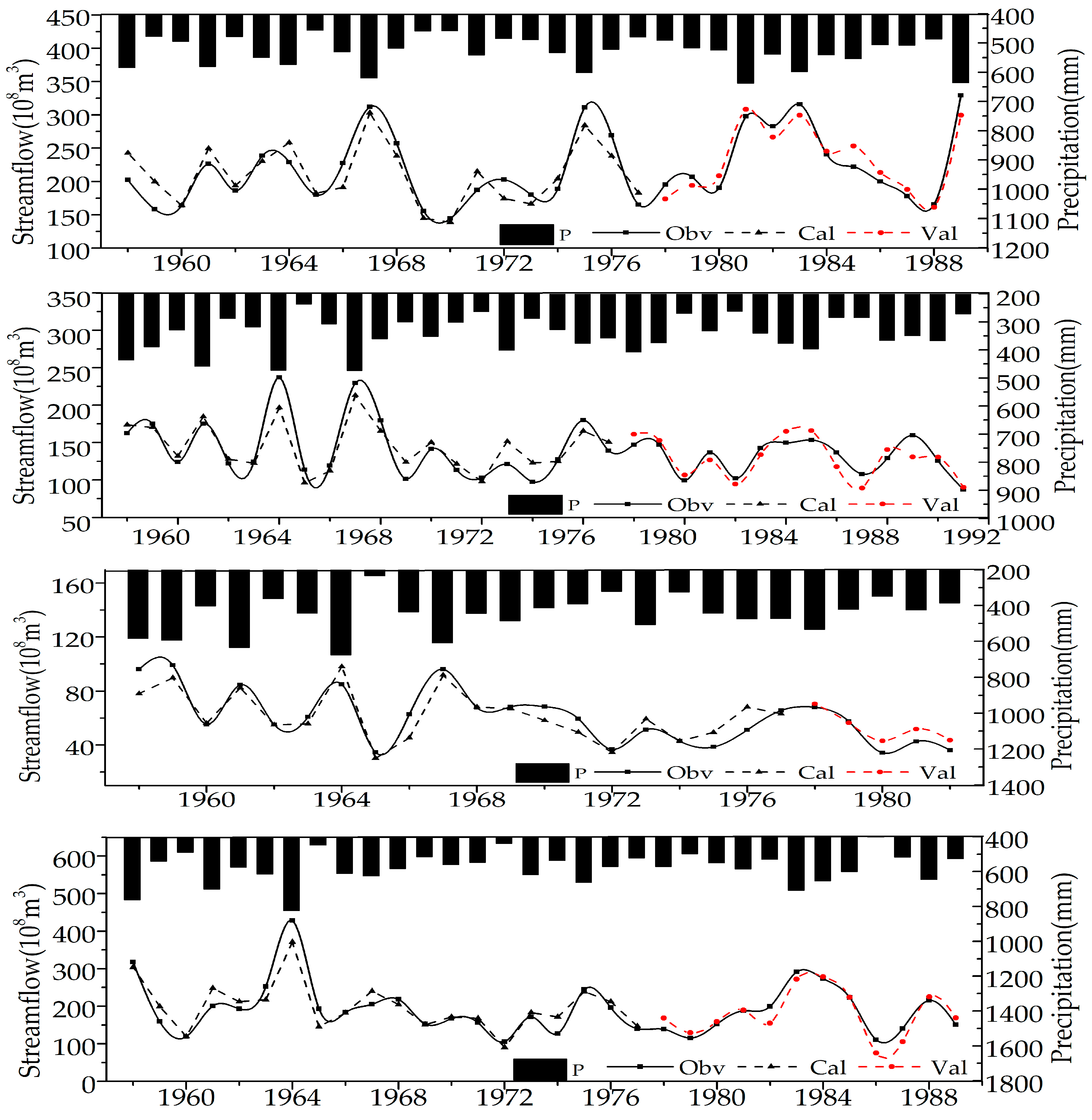
The monthly naturalized streamflow time-series for four hydrological stations (Tangnaihai, Toudaoguai, Longmen, and Huayuankou) between 1957 and 2010 were obtained from the Yellow River Hydrographic Bureau (YRHB). These four-gauge stations were selected with the intent of determining streamflow changes in four different subregions. Specifically, streamflow at Tangnaihai was considered the source region; the streamflow from the upper reach was the difference between Toudaoguai and Tangnaihai; the difference between Huayuankou and Toudaoguai was declared as the middle reach streamflow. Due to the complex hydrogeological conditions in middle reach (Loess Plateau), Longmen station was added to separate the middle reach into two detailed parts. Four regions were thus formed: the source region, Tang-Tou region, Tou-Long region, and Long-Hua region. Particularly, this dataset was the naturalized streamflow, having removed the variation caused by artificial water intake and reservoir storage and streamflow. That is to say, different from the broad sense, the anthropogenic interference defined in this study mainly included soil and water conservation measures.
GLASS LAI, one of the five typical global LAI products, was chosen for this study because it includes the longest duration (1982–2013) LAI product. Additionally, compared with those of the current MODIS and CYCLOPES LAI products, it provides temporally continuous LAI profiles with much better quality and accuracy [
27].
Furthermore, a 30 × 30 m digital elevation model (DEM) was used for the interpolation of climatic variables. ANUSPLIN, a well-performed spatial interpolation package based on thin-plate smooth-spline interpolation, was selected to interpolate climatic variables. Developed by Australian National University, it is a tool mainly used for the transparent analysis and interpolation of noisy multi-variants data [
28]. Using the longitude, latitude, and elevation of the meteorological stations as variables, daily precipitation and mean temperature datasets were aggregated to obtain mean monthly and annual values in four different subregions.
3. Methodology
3.1. Time-Series Analysis Method
3.1.1. Change-Point Detection and Trend Analysis of Hydrological and Climate Data
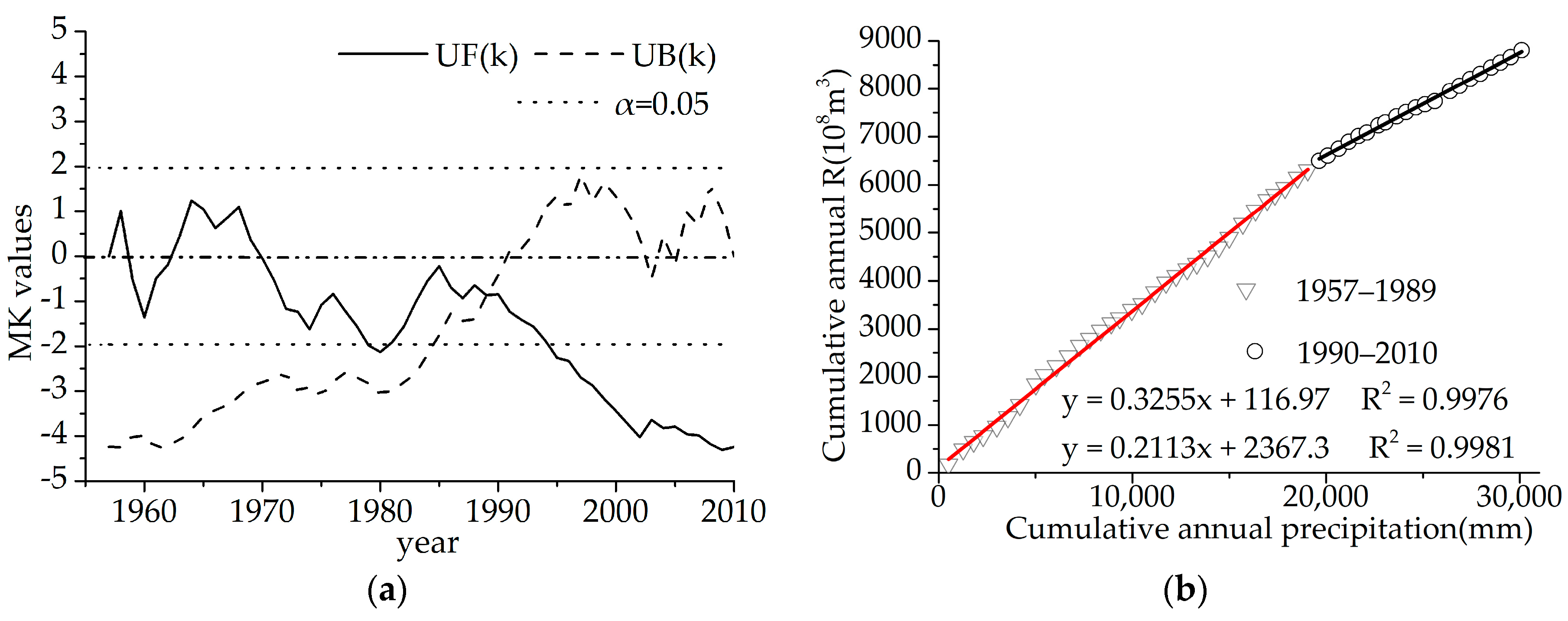
Both the change-point detection of annual streamflow data and trend analysis of hydrometeorological data were conducted by a Mann–Kendall (MK) test, which is widely used for its simplicity, robustness and the ability to deal with non-normal and missing data distributions [
29,
30]. After estimating the test statistics UF
i and UB
i, the curve of these two test statistics are plotted. If a match point of the two curves exists and the trend is statistically significant, the match point can be regarded as a change-point of the time series [
17]. In terms of trend analysis, the MK test statistic Z was calculated. A positive and negative Z value represent increasing and declining trends, respectively. The null hypothesis, H
0, states that there is no statistically significant trend in the series for a given significance level α. In this paper, α was set to be 0.05 and the 1−α/2 quantile of the standard normal distribution for α (Z
(1−α/2)) was 1.96. If |Z| > Z
(1−α/2), the null hypothesis is rejected, indicating the trend is significant. Otherwise, the H
0 hypothesis is accepted.
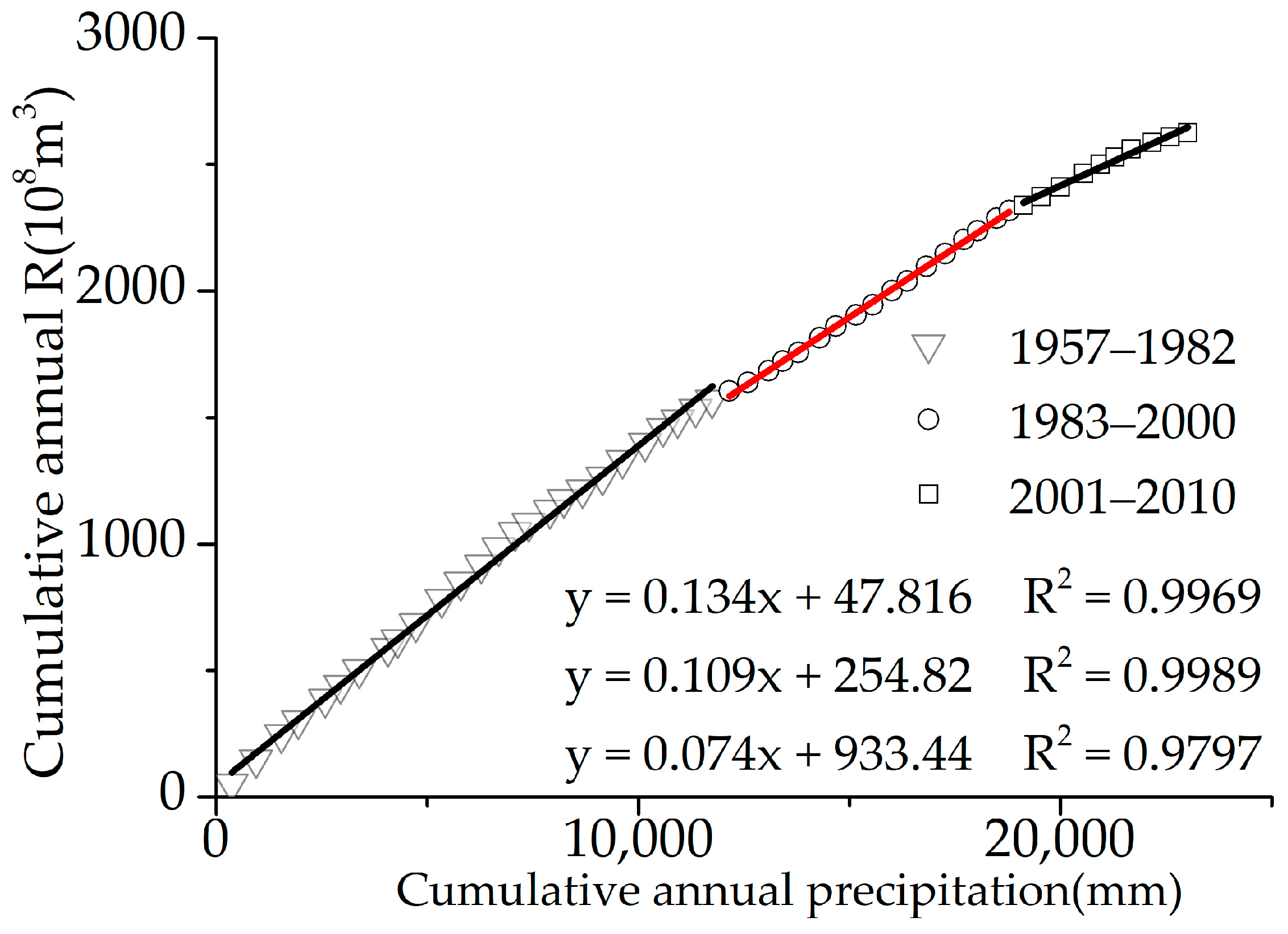
In addition, the precipitation–runoff double cumulative curve (DCC) was also used as an auxiliary confirmation of the change-points by providing a visual representation of the consistency of the precipitation and streamflow data [
31].
3.1.2. Trend Analysis of LAI
The temporal and spatial variation of the mean LAI were analyzed using a linear regression analysis method in this study. Using overall LAI trend computations to identify spatial patterns of directions and rates of change, a least squares regression was fit through the time series of each pixel and the slope coefficient that represent trends was calculated [
27]. The slope of the trend coefficient was defined as follows:
where
n is the cumulative number of years in the study periods,
i is the order of year, and
is the value of LAI in the
ith year. In general, if slope > 0, LAI will increase, suggesting better vegetation in this pixel.
3.2. Multitemproal-Scale Precipitation–Runoff Model
Since access to very limited information and data for basin geometry can hardly satisfy the minimal requirements of basin-scale models, statistical methods were employed to determine the relationship of streamflow and other climatic factors for the baseline period. Both an annual scale model and flood and nonflood season model were built.
At annual scale, the precipitation–runoff model was built using multiple linear regression analysis. At flood and nonflood season scale, given the fact that linear regression analysis method may not satisfy the requirement of model accuracy, a statistical model based on the Random Forest (RF) regression, which is one of the most effective machine learning models for predictive analytical approaches [
32,
33], was trained to reconstruct streamflow data in the human-affected period. RFs were developed as a method of improving the predictions of classification and regression trees by alleviating the overfitting concern of regression trees [
34]. It has proved to be more robust and accurate than traditional linear (e.g., multiple linear regression) or more complex methods [
35]. Two parameters need to be set in order to produce the forest trees: the number of decision trees to be generated (N
tree) and the number of variables to be selected and tested for the best split when growing the trees (M
try) [
36]. In this paper, N
tree was set as 200, and M
try was set as the default value in the R package for random forests.
In this study, the correlation of different climatic variables (annual precipitation, mean temperature, precipitation in the former years, flood-season precipitation and mean temperature, nonflood season precipitation and mean temperature, precipitation of the last month of the flood season) between annual streamflow, flood-season streamflow and nonflood season streamflow were analyzed using Pearson correlation coefficient analysis respectively, and those with a high correction coefficient between streamflow were chosen as the independent variable [
36] for developing annual, flood and nonflood seasonal precipitation–runoff models. Furthermore, variance analysis and an F-test were conducted to test the accountability of the statistical models.
3.3. Contribution Calculation of Climatic and Anthropogenic Factors on Annual Streamflow
Model simulation, along with the hypothesis that climate fluctuations and anthropogenic interference are independent, was employed to separate the impacts on streamflow variation. Several scenarios were designed to reconstruct natural streamflow and then separate the impact of climatic fluctuations and anthropogenic interference on natural streamflow:
S1: Conducting the control simulation based on the annual precipitation–runoff model with observed changes in precipitation and temperature over the human-affected period;
S2: Using the same forcing data as the control simulation S1, except the mean value of the temperature was fixed to the mean of the baseline period;
S3: Conducting the control simulation based on the flood and nonflood season precipitation–runoff model with observed changes in precipitation and temperature over the human-affected period;
S4: Using the same forcing data as the control simulation S3, except the mean of the percentage of flood-season precipitation was fixed at the level of the baseline period and the annual precipitation remained as the S3 observations.
The total streamflow change (
) can be obtained by the difference between the observed streamflow in baseline period (
Rob) and that in human-affected period (
Roh), which can be expressed as:
where
includes two main parts, the streamflow change caused by climate fluctuations
and anthropogenic interference
, and the former
is made up of precipitation-induced change
and temperature-induced variation
.
The difference between S1 and S2 (S1–S2) was used to estimate the change magnitude of the simulated annual streamflow caused by the temperature variation
:
where
is the mean of simulated annual natural streamflow in the scenario S1, and
is the mean of simulated annual natural streamflow for the scenario S2.
can be calculated by the following equation:
The streamflow change magnitudes caused by anthropogenic factor () and annual precipitation variation () are calculated using Equation (2).
The contribution rate of each factor, which is defined as
, is quantitatively estimated by:
where
k can be referred to as precipitation (P), temperature (T), and anthropogenic interference (H).
The difference between S3 and S4 (S3–S4) was used to estimate the change magnitude of the simulated annual streamflow caused by the variation of the percentage of flood-season precipitation:
where
is the mean of simulated annual natural streamflow in S3, and
is the mean of simulated annual natural streamflow for S4.
is the change magnitude of natural streamflow caused by the variation of the percentage of flood-season precipitation.
3.4. Sensitivity Calculation of Annual Streamflow to Climatic Factors
Contribution assessment alone cannot fully explain the response of streamflow to different variables. For example, certain variable contributions may be greater because of the larger change magnitude of this variable. Therefore, to better understand the streamflow response to climatic factor changes in different regions and periods, a modified sensitivity coefficient was defined that reflects sensitivity of streamflow to various climatic variables: The formula uses simulated streamflow data in different scenarios and observed meteorological factor data to calculate the sensitivity of streamflow to different meteorological factors. The specific calculation formulas are as follows:
where
,
,
,
are the means of annual natural streamflow, precipitation, temperature, and percentage of flood-season precipitation over the baseline period, respectively.
,
,
are the simulated natural streamflow in the ith year in S1, S3, and S4, respectively.
is the mean of simulated annual natural streamflow for S4.
,
,
are the observed annual precipitation, temperature, and percentage of flood-season precipitation over the human-affected period, respectively.
5. Discussion
5.1. Analysis of the Impact of Anthropogenic Interference on Natural Streamflow
Overall, the findings of this study agreed with the results of other research in the contribution assessment [
8,
29,
32,
39].
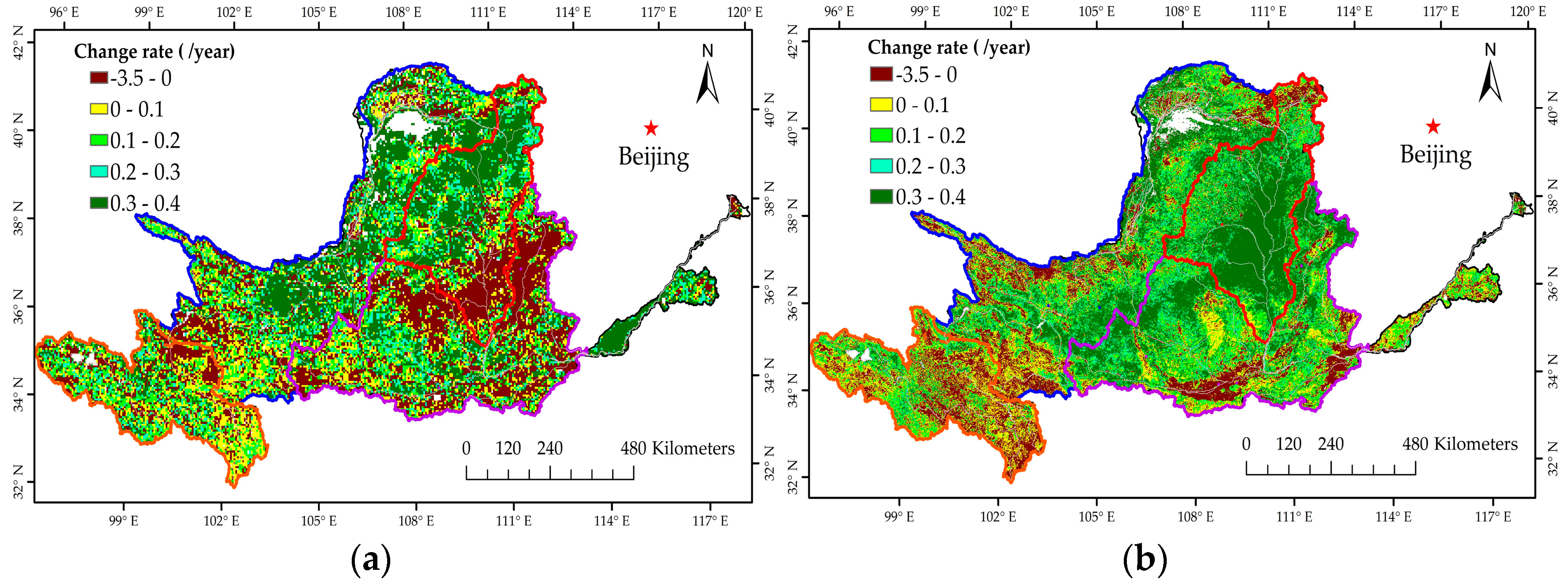
Table 5 shows that anthropogenic interference had a greater contribution in Tou-Long and Long-Hua regions after 2000, which was mainly due to the ecological program launched by the Chinese government in these two regions.
Table 8 displays the implementation of different soil and water conservation measures in the Tou-Long region (including 25 tributaries) in 1997, 2000, 2003, and 2006 [
40]. According to the table, the amount of all kinds of soil and water conservation had risen gradually. Among them, forestland and grassland increased more sharply. By 2006, 28,540 km
2 of terraced area, 1310.26 km
2 of dammed land, 58,613.53 km
2 of forest land, 14,072.64 km
2 of grassed land, and 8380.18 km
2 of closed hillside area had been constructed in the Tou-Long region. Moreover, according to the analysis of LAI data before and after 2000 in
Figure 8, the change intensity in forest and grass vegetation was largest in the Tou-Long region, followed by Long-Hua.
Studies have demonstrated that such large-scale land use and land-cover change, driven by soil and water conservation measures, were closely related to streamflow reduction [
41,
42]. For example, the terraced area can reduce the hillside slope and prolong streamflow retention, reducing surface streamflow [
17]. The increasing forests and grasslands play an important role in intercepting rainfall and alleviating streamflow [
43]. To conclude, all of these can explain why anthropogenic interference played a more critical role in streamflow reduction in the Tou-Long and Long-Hua regions, especially during Period II.
5.2. Analysis of the Sensitivity of Streamflow to Annual Precipitation and the Percentage of Flood-Season Precipitation
This study modified the traditional formula of the elasticity coefficient and used the calculated sensitivity coefficient to analyze the sensitivity of streamflow to meteorological factors. It should be pointed out that the advantage of this modified sensitivity coefficient calculation formula is that it can be combined with the runoff derived from scenario simulation. That is, the dynamic streamflow time series under the influence of the target factor (such as precipitation, mean temperature, the percentage of flood season precipitation, etc.) can be constructed by the scenario simulation method, and then the sensitivity of streamflow to the certain target factor can be directly calculated based on the sensitivity formula, and the underlying mechanics for calculating the sensitivity of streamflow to the specific factor is relatively easy to understand. In contrast, the traditional elastic coefficient model can only use the original observed streamflow, and the simulation accuracy of the elastic coefficient is affected by the type and number of factors selected in the construction of the elastic model, leading to the greater uncertainty in the sensitivity analysis of specific factors.
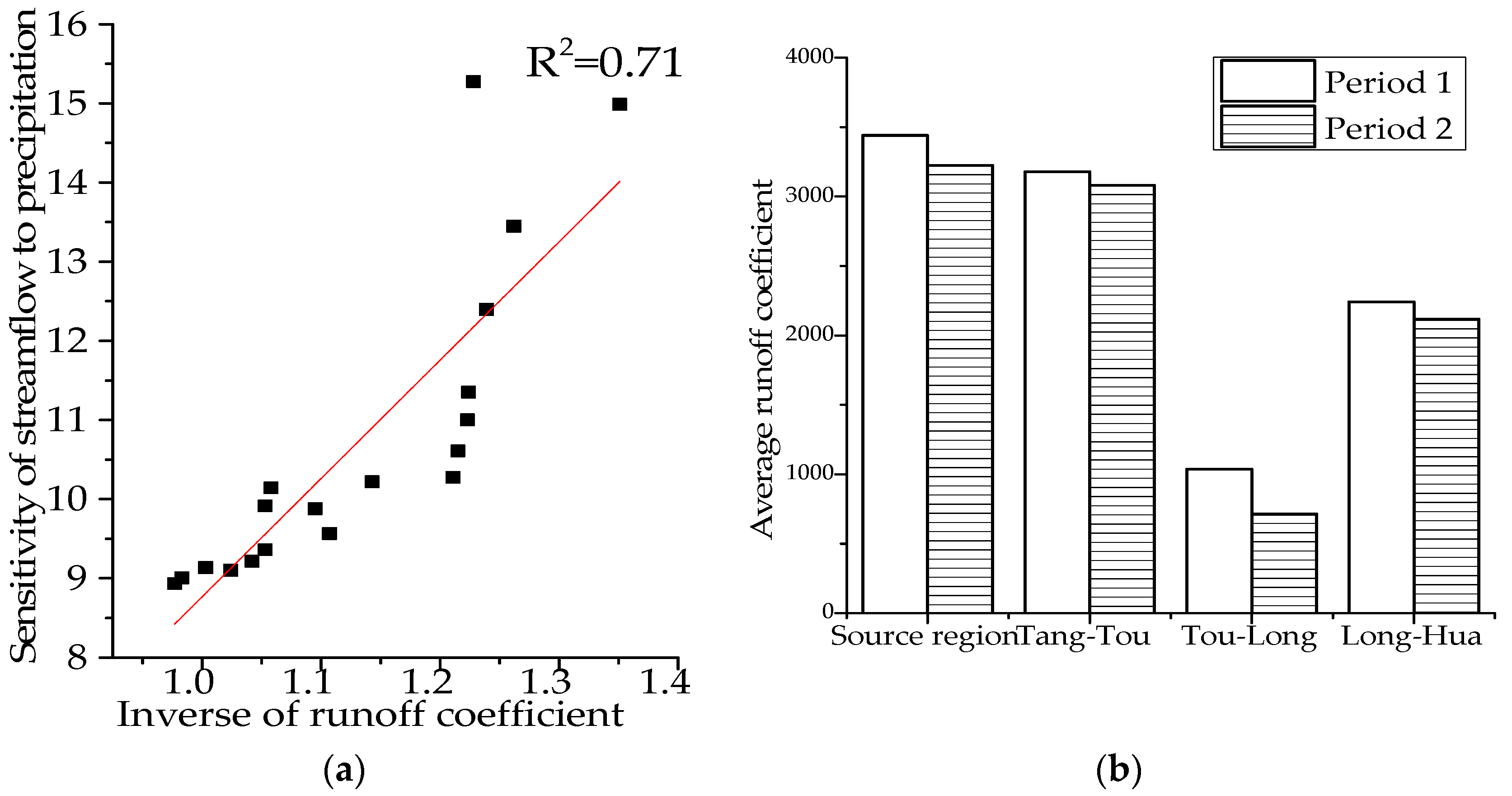
According to the results shown in
Table 7, the sensitivity to annual precipitation exhibited both temporal and spatial differences. The annual streamflow after 2000 became more sensitive to annual precipitation in the whole basin. Chiew [
44] reported a strong negative correlation between the elasticity coefficient to precipitation and streamflow coefficient (R
C) for 219 catchments in Australia. Inspired by Zheng et al. [
39], the relationship between the sensitivity to annual precipitation (
) and R
C, which were estimated within a moving window of 10 years, was analyzed in this study. The relationship in
Figure 9a shows that the sensitivity to annual precipitation (
) was positively related to the inverse of the runoff coefficient (1/R
c), indicating that streamflow was more sensitive to precipitation in catchments or periods with low streamflow coefficients. The declining trend of streamflow coefficients of four regions, illustrated in
Figure 8b, successfully explained the rise in sensitivity to annual precipitation from period I to period II. This also shows that the sensitivity coefficient calculated in this study has similar properties to the traditional elastic coefficient and can appropriately reflect the sensitivity of streamflow to meteorological elements. Furthermore, part of the reason for a streamflow coefficient decline may be that these regions experienced a significant rise in forest and grass vegetation, as demonstrated in previous studies [
42].
Table 7 also shows that streamflow in the source, Tou-Long, and Long-Hua regions was more sensitive to precipitation than that in the Tang-Tou region. This spatial difference partly accorded with their streamflow coefficient except for the source area, which was expected to have a similar sensitivity to that of Tang-Tou. In fact, the value of the sensitivity of streamflow depends on many factors, such as the stochastic nature of climate, vegetation conditions, field capacity of soils, soil moisture levels, length of soil water depletion, and saturated hydraulic conductivity [
24]. Compared with other regions, the source region has a relatively saturated soil condition ascribed to good vegetation cover (
Figure 8) and humid climate conditions (
Table 1), making it easy to form streamflow. Thus, streamflow in the source region is more sensitive to precipitation change than that in other dry regions, such as the arid Tang-Tou region.
As for the sensitivity to the percentage of flood-season precipitation, it increased more in the Tou-Long and Long-Hua regions than in the source and Tang-Tou regions. Given the same annual precipitation, streamflow yield would not be affected by the precipitation temporal pattern in the regions with less forest and grass vegetation. However, as illustrated in
Figure 8, forest and grass vegetation increased in the Tou-Long and Long-Hua regions, playing a crucial role in streamflow yield: streamflow would become more sensitive to flood-season precipitation, leading to greater sensitivity to the percentage of flood-season precipitation.
5.3. Uncertainties Analysis
There are some uncertainties associated with the contribution assessment and sensitivity analysis. First, combining two different-scaled models—namely, the annual model and flood and nonflood season model—generates some uncertainties. Another uncertainty in the results exists in the assumption that climate change is independent of anthropogenic interference. In fact, these two factors are interrelated. For example, land cover change and vegetation increase caused by afforestation would also lead to climatic changes.
Despite the uncertainties and limitations, this study provides a relatively easy way to analyze the contribution of climate variables and the sensitivity of streamflow to these factors, including the intra-annual distribution of precipitation. More detailed work, such as distributed models, should be introduced to improve the understanding of the monthly streamflow response mechanism.
6. Conclusions
With the intent of distinguishing the effect of climate fluctuations and anthropogenic interference on streamflow reduction and analyzing the sensitivity of streamflow, an improved three-parameter annual precipitation–streamflow model and flood and nonflood season models were built to simulate natural streamflow. The major findings from this study are summarized below.
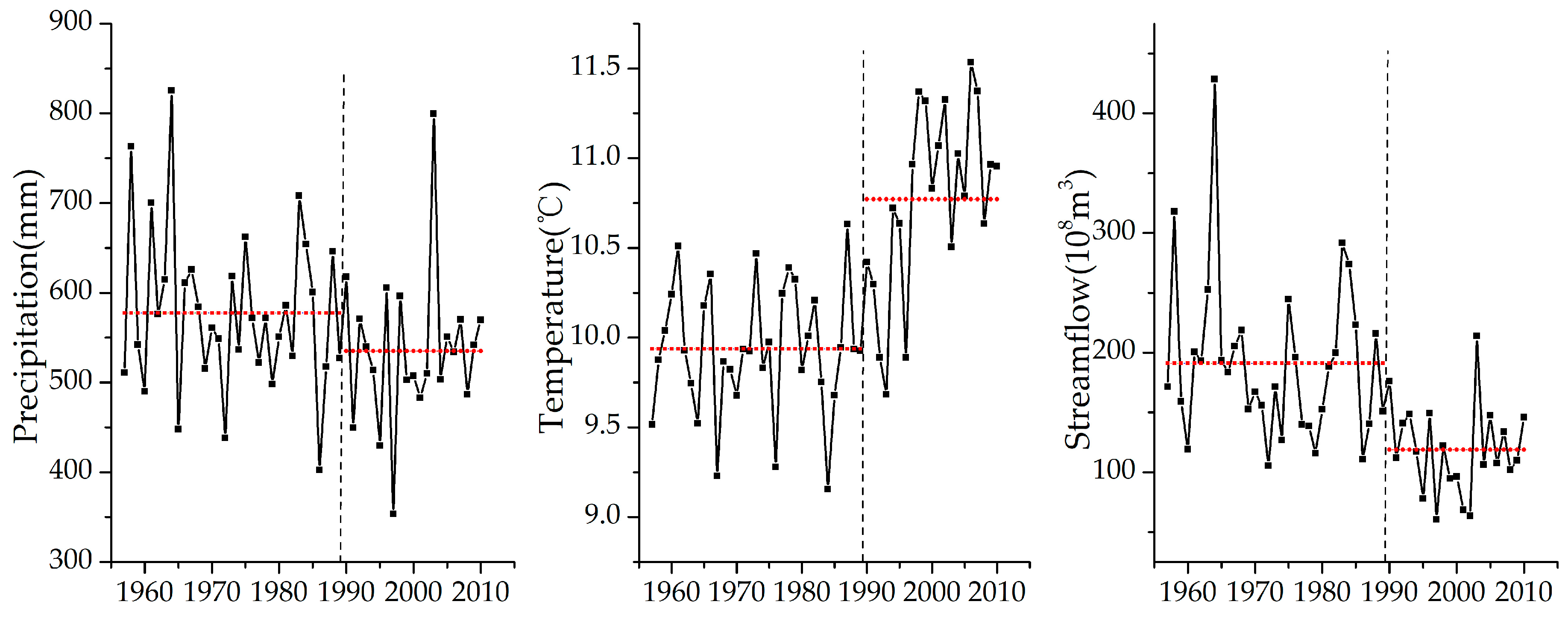
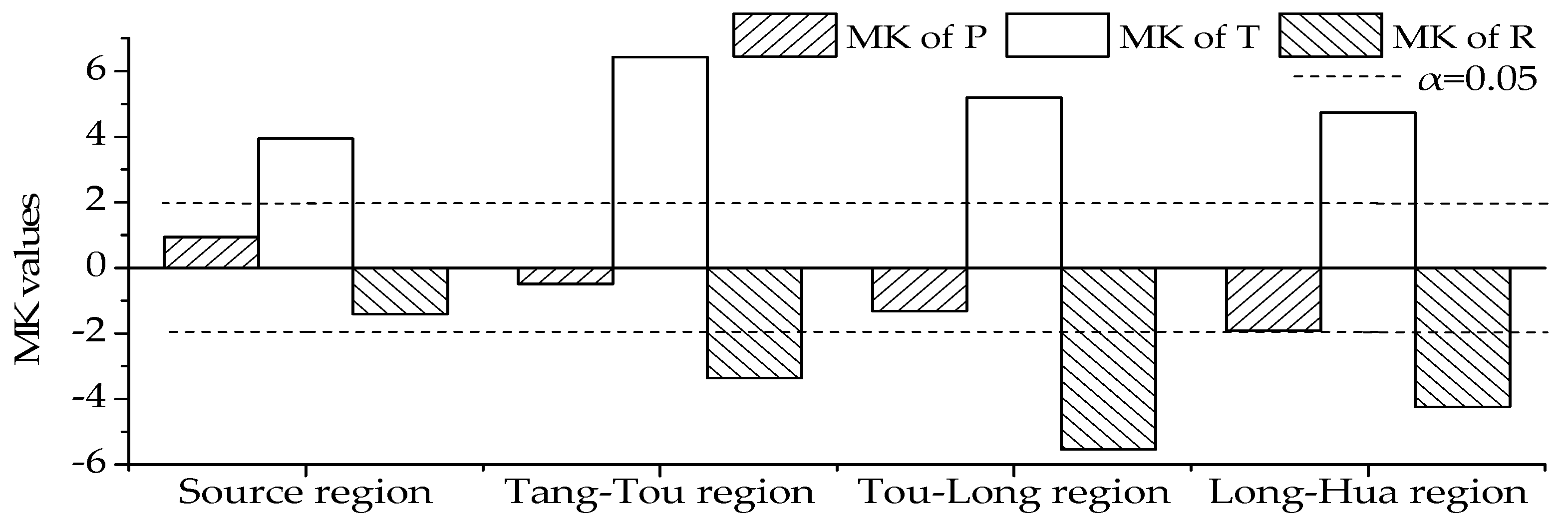
The MK results demonstrated a decreasing trend in annual precipitation, significant increasing trend in mean temperature, and decreasing trend in annual streamflow across the Yellow River, excluding the increasing annual precipitation in the source region during 1957–2010. Abrupt change did not take place simultaneously, with the earliest change-point detected in the Tou-Long region. On average, the percentage of flood-season precipitation exhibited a decreasing trend, with each of the four regions experiencing a different level of decline.
The intensity of streamflow reduction improved spatially from 19.00% in the source region to 37.82% in Long-Hua. The contribution made by the climatic fluctuations and anthropogenic interference varied spatially and temporally. From Tang-Tou to Long-Hua, the impacts of annual precipitation and anthropogenic interference increased, while the temperature effect decreased. Temporally, the dominant factor in the Tou-Long and Long-hua regions had shifted from precipitation to anthropogenic interference after 2000. Further, the variation in the percentage of flood-season precipitation was responsible for streamflow variation. The greater the percentage of flood-season precipitation, the greater the simulated streamflow will be.
The sensitivity of streamflow to various climatic factors are different for regions with different hydrothermal conditions in YRB: annual streamflow was more sensitive to annual precipitation than temperature in the humid regions, whereas an opposite situation was observed in the relatively arid regions. Sensitivity to precipitation and temperature both increased in the whole basin after 2000, indicating that substantial challenges and uncertainties might be introduced to regional water availability. The sensitivity of streamflow to the percentage of flood-season precipitation increased most significantly in the Tou-Long and Long-Hua regions, where the highest change intensity of forest and grass vegetation occurred after 2000. These research conclusions can provide a scientific reference for future Yellow River water resource management and ecological construction planning.