Abstract
Water pollution is a prominent and urgent environmental problem that represents a significant challenge in solving the water resource crisis. The ability to choose an optimal environmental policy can provide support for decision makers to effectively control water pollution. This study presents an agent-based model (ABM) approach involving two classes of agents, agricultural household agents and factory agents, to simulate pollutant discharge, and discusses the effectiveness of the whole system and subsystems under multiple policy scenarios involving a combination of environmental tax (ET) and payments for environmental services (PES). This idea is applied to the Shanmei Reservoir watershed, one of the important reservoirs watersheds in China. The results showed that: (1) the ABM represented well pollutant discharge scenarios where Nash coefficient (NSE) values were greater than 0.76; (2) though ET and PES policies were both effective in reducing water pollution, PES was more effective at reducing pollution from households, while ET was more effective at controlling industrial pollution emissions; (3) considering the environmental costs and general effect of the system, a medium degree of PES for agricultural household agents and a medium degree of ET for factory agents were found to be optimal for controlling water pollution in this watershed. A differential compensation mechanism and the introduction of market incentives were recommended to reduce the financial burden of the government. The results also demonstrated that ABM was helpful for choosing an effective policy to control pollution emissions and realizing environmental objectives and socio-economic co-benefits. The model structure and parameters should be optimized in specific cases because of the uncertainty of partial parameters and the neglect of the consumption process. These findings could be helpful for providing guidelines for water pollution control and sustainable water management in China.
1. Introduction
Water security has become a prominent and urgent global issue due to population growth, climate change, and anthropogenic activities. Water resources underlie the basic need of livelihoods as well as national welfare, and accordingly water resource crises are among the most severe environmental problems currently facing humankind [1]. Decreases in both the quantity and the quality of water contribute to water scarcity. During the Anthropocene Era, water pollution has increased in severity as the proliferation of modern agriculture and industry have driven socio-economic changes. Additionally, globalization has further accelerated the transfer of water pollutants in regions and countries [2]. Hence, it is crucial to ensure water security by controlling water pollution as well as promoting reasonable usage. Water resource issues in China have made notable progress, however, the problem of aggravated water pollution (e.g., eutrophication in lakes) has not been solved completely [3]. Unlike quantity-induced water scarcity, quality-induced water scarcity is usually easier to neglect. Water pollution therefore requires more focus as it is another challenge in solving water crises.
Water management policies became another approach in the attempt to resolve developing water conflicts after a series of massive water projects (e.g., Three Gorge Dam) were built. An environmental tax, like a water pollution tax, distributes environmental resources through market mechanisms that internalize the costs of environmental pollution and ecological destruction into production costs or market prices to control pollution. The water pollution tax system, which is favored by many countries including the members of Organization for Economic Co-operation and Development (OECD), has already produced remarkable achievements in practice [4,5]. Among OECD members, the Netherlands is the first country to levy a water pollution tax, which has remarkably reduced the levels of surface water pollution [5]. Payments for environmental services (PES) is a relatively new policy measure aimed at natural resource conservation that translates environmental values into financial incentives for local services. PES was initially applied to forest protection, but later gained wide implementation in ecological compensation for natural reserves and important ecological functional areas, mineral resource development and watershed water conservation. PES programs have been adopted nationally in Costa Rica, Mexico, China (the Sloping Land Conversion Program (SLCP)), in Europe and the USA via agri-environmental schemes [6,7,8,9,10,11,12].
The effect of PES and environmental tax has been compared in a wide variety of studies [13,14,15,16]. In some studies, PES is considered to be a secondary solution to environmental tax because of several sources of potential inefficiency [16]. However, other studies show that, in developed countries, PES has a greater impact on agricultural producers with strong political ties [17]. In China, the results of comparing the effect between a fertilizer tax and payments for environmental services show that it is proper to implement a fertilizer tax with a rate of 100% but now is not the best time [18]. However, the results of another study comparing the effect of a water pollution tax and PES in Taihu basin, China, indicated that a medium degree of environmental tax is optimal for controlling factory pollution emissions [19]. Since a single solution does not exist for all cases, when addressing water pollution caused by multiple factors, different environmental policies based on specific characteristics of industry and agriculture are required to control pollution effectively.
Given the complexities of managing water resources, agent-based modeling (ABM) can be an effective approach to develop an optimal plan. ABM can simulate the human decision-making process by delineating the behavior of agents [20]. This approach is now widely used in the simulation of complex water systems [21,22,23,24]. For example, Yang et al. studied the feasibility of the water market mechanism using ABM for water allocation management in the Yellow River Basin [25]. Nikolic et al. developed a management tool that captured the temporal and spatial dynamics of a physical–social–economic–biological system [26]. Yuan et al. used ABM to predict urban household water demand in Beijing by 2020 [27]. Akhbari and Grigg recommended using ABM to create a hydrologic–environmental–human interface to help manage water resource conflicts in the San Joaquin River watershed, California [28]. Shafiee et al. created an ABM framework for assessing the effect of water advisories on public health protection [29]. Other relevant applications of ABM include quantifying the economic importance of irrigation water reuse in a Chilean watershed [30]; simulating the dynamics of urban water supply [31]; and modeling for domestic water management in the Valladolid (Spain) metropolitan area [32]. ABM applications advance our understanding of interactions between agents in complex systems and can thus improve decision making.
In this study, we use ABM to simulate the effect of controlling water pollution in the Shaimei Reservoir watershed, Fujian, China. We select agricultural households and factories as agents in the model and characterize their behaviors in 49 environmental policy scenarios combining varying degrees of environmental tax and PES, before assessing their environmental and economic effects. This work demonstrates a new approach to control water pollution caused by agricultural and industrial emissions. The work is presented as follows: Section 2 describes the materials and methods, including a description of the case study area, and a description of the model used, including parameterization, scenarios design, policy effects analysis, and data source and processing; Section 3 presents the results; Section 4 provides the discussion; Section 5 outlines the conclusion and recommendations on how to further improve the approach.
2. Materials and Methods
2.1. Case Study Area
Figure 1 displays the ideal region for us to study the effects of optimal policies for controlling water pollution. The study area (Figure 1) is located in the middle reaches of East Creek in the Jin River basin in Fujian, China. The study area covers 1023 km2 and accounts for 53.4% of the East Creek catchment. The population of the study area is 598,537 and the area of crop land is 160.22 km2. The Shanmei Reservoir Project, operated in 1972, is a large-scale water conservation project involving irrigation, flood control and power generation in the region, and is also a main source of drinking water for the lower reaches zones of the Jin River basin, which annually supplies approximately one billion cubic meter serving four million people in eight cities. As the only large reservoir in the Jin River region, the Shanmei Reservoir is fundamental for guaranteeing water security in the lower reaches. Irrigation agriculture and industry are the main economic sectors in the region as well as the major sources of non-point pollution and point source pollution. Although the government has taken some measures to control pollution and improve water quality, water eutrophication and other water-related environmental problems remain issues in this region. Currently, the key problem is determining which policy or policies should be adopted to balance economic development and water resource protection from the perspective of management.
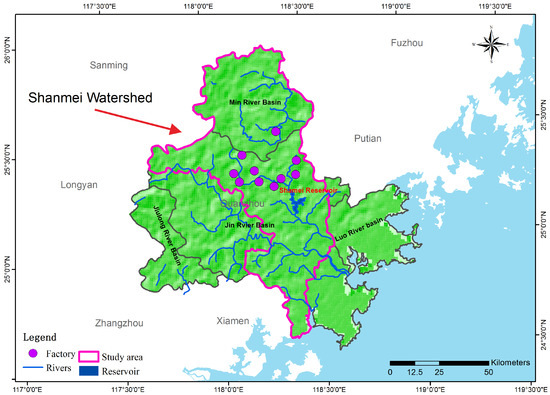
Figure 1.
Sketch map of the study area.
2.2. Model Description and Parameterization
ABM is a “bottom-up” approach that can simulate the interactions among agents with different goals and behaviors within an environment [20]. In particular, it emphasizes the processes and feedback of multi-agent systems (e.g., a human–natural system or water resource system) in different scenarios [33,34,35]. Agents of ABM, who have their own attributes and behavioral rules, can perceive their environment and interact with each other with a set of pre-defined goals [36,37]. In this study, we constructed an ABM to simulate the level of pollutant emissions by agents under different policy scenarios. There were four subsystem in this ABM model: a government design module, an agricultural household behavior module, a factory behavior module and an environment evaluation module, as shown in Figure 2. In the government design module, policy designers provide different policies depending on the feedback of environmental information and take some measures to control water pollution that do not require the involvement of agricultural household and factory agents. In the agricultural household behavior module, an agricultural household is the minimum unit, and has a specific attributes such as age, education level and number of family members. The decision-making behavior (decision of factor input and production) of agricultural household agents is involved in the agricultural production process. The behavioral rules for agricultural household agents are that the change of production factor investment depends on resource limitations and marginal revenue and production decisions depend on the production profit. Additionally, an agent’s decision will impact that of other agricultural household agents. The length of the behavior decision-making cycle of agents is one year and the goal of agents is to maximize profits. In the factory behavior module, a factory is the minimum unit, and has specific attributes such as type of equipment, number of members, etc. Factory agents’ decision-making behavior is also involved in the industrial production process and the behavioral rules are similar to those of agricultural household agents. The combined behavior of agricultural household agents and factory agents results in changes of the environment. The environmental change caused by agricultural households and factories are simulated using the following water pollutant discharge indicators: total nitrogen (TN), total phosphorus (TP) and chemical oxygen demand (COD). The model was realized with the aid of NetLogo [38]. More information about the model, including related critical equations and model parameters are given in Section 2.2.1, Section 2.2.2 and Section 2.2.3
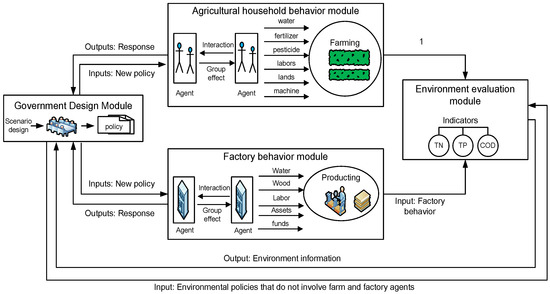
Figure 2.
Framework of the agent-based model at the watershed scale.
2.2.1. Agricultural Household Behavior Module
The design of the module aimed to determine the relationship between factor input and output in agricultural production in order to predict the consequences of production decision-making behaviors. The Cobb–Douglas production function was used to estimate the relationship between inputs and outputs in agricultural production. This function is given by Equation (1):
where is the Cobb–Douglas production function; represent the fertilizer, pesticides, land area, and agricultural machinery invested in farming, respectively; represents the labor force, , where N is the rural population in the region; is the technical efficiency; and β1, β2, β3, β4, θ1 represent the output elasticity coefficients of the corresponding production elements. The values of the parameters in Equation (1) can be defined by multiple linear regression analysis and time-series statistics.
The profit function used in this module is given by Equation (2) [39]:
where is the profit of agricultural products; is the price of agricultural products; is the price of the invested element; is the invested element, , where is the largest amount of the element that can be invested and represents other fixed costs or a subsidy given to farmers.
In farming, agricultural households generally seek to maximize profits. Whether or not the input of fertilizer, pesticide and other factors increases mainly depends on the household’s judgment of their marginal profit. When households estimate that their marginal output is higher than the cost, they tend to increase input; otherwise, they tend to reduce investment. According to the specific relationship of scale elasticity and output elasticity in the Cobb–Douglas production function (Equation (1)), the estimated value of the marginal revenue by agricultural households is given as follows, if there is increasing of the invested element:
where is the increased profit of agricultural products; is the price of agricultural products; is the Cobb–Douglas production function; is the output elasticity coefficient; is a random value in the range [0.8, 1.2], which represents a 20% error between the estimated value and the theoretical value of marginal revenue; is the price of the invested element; is the invested element, and is the increasing part of the invested element.
2.2.2. Factory Behavior Module
According to a survey of enterprises in the Shanmei Reservoir watershed, paper industries with high water demand and high waste water emissions are the main source of industrial pollution. As such, paper industries are included as another agent in the model shown in Figure 2. The goals of this agent include production profit and wastewater discharge, which are defined by the following three equations (Equations (4)–(6)):
where is the Cobb–Douglas production function for calculating yield; represent the input of water, assets, and wood, respectively; is the technical efficiency; and β5, β6, β7, θ2 represent the output elasticity coefficients of the corresponding production elements, respectively;
where is the profit of a factory; is the price of products; is the price of the invested element; is the invested element and is the depreciation of the equipment.
The relationship between water demanded and waste water discharged is given in Equation (6):
where represents waste water, is the rate of recycling of used water and is the input of water.
In the production process, factories generally seek to maximize profits. Whether or not the input of wood, water and other factors increases mainly depends on the judgment of their marginal profit. When factories estimate that the marginal output is higher than the cost, they tend to increase input; otherwise, they tend to reduce investment. The estimated value of marginal revenue by factories is similar to that given in Equation (3).
2.2.3. Environment Evaluation Module
In this study, we quantified the emitted pollutants to identify the resulting environmental change, especially that of water quality. Typical human-generated water pollutants were used to simulate the contribution to water pollution of households and factories. Nutrient indices, including TN, TP, and COD, were used as indicators for water quality. We modified a method used by the Intergovernmental Panel on Climate Change (IPCC) (2006) [40] to estimate nitrogen runoffs from leaching and runoff to estimate TN, TP and COD emissions. The formulas used to estimate TN emissions are as follows:
where is total nitrogen content discharged into water; and are total nitrogen content discharged by agricultural household agents and factory agents, respectively.
where , and are total nitrogen content discharged into the water by crop planting, livestock and poultry breeding and life, respectively; and , and are the nitrogen losses rates corresponding to the same process.
where is the amount of the fertilizer and is nitrogen content of the fertilizer.
where is the amount of the category poultry or livestock; is the nitrogen excretion of the category poultry or livestock; is the amount of poultry or livestock at the watershed and is the nitrogen emission factor during livestock breeding.
where is permanent resident population in the basin; is the annual protein consumption per capita; is the nitrogen content of the protein and is the non-consumed protein factor in wastewater.
where is the nitrogen content of wastewater discharged by factories.
The formulas used to estimate TP emissions are as follows:
where is the total phosphorus discharged into the water, and and are the total phosphorus contents discharged by agricultural household agents and factory agents, respectively.
where , and are the total phosphorus contents discharged into the water during crop planting, livestock and poultry breeding, and life respectively; , and are the phosphorus loss rates of the same processes.
where is the amount of the fertilizer and is phosphorus content of the fertilizer.
where is phosphorus content of the category poultry or livestock and is phosphorus emission factor during livestock breeding.
where is the emission factor of phosphorus during life per capita.
where is the phosphorus content in wastewater discharged by factories.
The formulas used to estimate COD emissions are given below:
where is the total COD discharged into the water; CODlivestock and CODlife are the content of total COD discharged into the water during livestock and poultry breeding and life, respectively; and CODfactories is the content of COD discharged by factory agents.
where is the content of COD in the category poultry or livestock; is the emission factor of COD during livestock breeding.
where is the emission factor of COD during the life of each person.
where is the COD content of wastewater discharged by factories.
2.3. Scenario Design
Based on a literature review and the programs of other countries, we designed different degrees of environmental tax and PES policy scenarios for agricultural households and factories [18,19,41]. A fertilizer tax collected from agricultural households was designed with three different tax rates: low (10% of fertilizer price); medium (50% of fertilizer price); and high (100% of fertilizer price). A water pollution tax collected from factories was also designed, also with three kinds of tax rate: low (1.5 RMB/m3 wastewater discharge); medium (3 RMB/m3 wastewater discharge); and high (100% of fertilizer price, 6 RMB/m3 wastewater discharge). One should note that the factory tax rate scheme is a direct charge for the discharge of sewage and the tax-increased cost is assumed to be entirely met by the factory. Additionally, low, medium, and high rates of PES were designed as an offset for agricultural households and factories that produce in an environmentally friendly manner. When agricultural households reduce fertilizer use and factories reduce wastewater discharge, they will gain 0.35 RMB/kg and 2 RMB/m3 offset, 1.75 RMB/kg and 4 RMB/m3 offset, and 3.5 RMB/kg and 6 RMB/m3 offset under the low, medium, and high PES scenarios, respectively. We additionally set up two control scenarios in which agricultural households and factories aim to maximize profits without any environmental policy. Overall, 49 different scenarios were designed, as depicted in Figure 3.
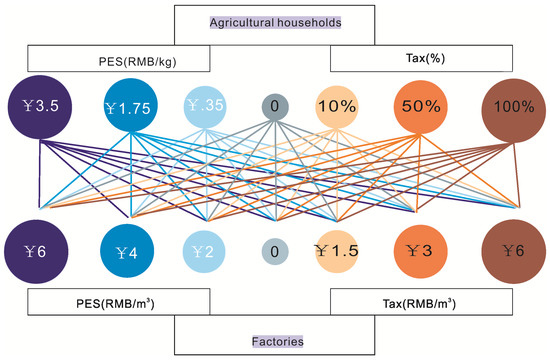
Figure 3.
The 49 scenarios used in this study. The upper part of the figure represents the different rates of payments for environmental services (PES) and fertilizer tax implemented for agricultural households and the lower part of the figure represents the different rates of PES and water pollution tax implemented for the factories.
2.4. Policy Effects Analysis
The effects analysis involved analyzing the general effect of the system, considering the cost of environmental governing and the change in pollutant emissions after adopting a specific policy. The cost of environmental governing increases with increasing pollutant emissions. Thus, when the government adopts an environmental tax, agricultural households’ profit should be presented as income minus the cost of fertilizer tax, and factory profits should show incomes minus the cost of the wastewater tax. When adopting a PES policy, the profits of agricultural households and factories should be given as income added to corresponding offsets. In this study, the general effect of each policy scenario was assessed using the following index consisting of agricultural households’ profit, factories’ profit and environmental cost:
where Esystem is the general effect of the whole system, prt′farming is the profit of agricultural households after adopting a specific policy; prt′factory is the profit of policy change by factories and is the environmental governing cost.
After implementing a policy, the profit of an agricultural household will change as follows:
where is the new profit of an agricultural household; is the price of agricultural products after policy change; is the Cobb–Douglas production function; and is the fertilizer tax or PES collected from an agricultural household.
where is the new profit of a factory; is the price of industrial products after the policy change; is the Cobb–Douglas production function; and is the water pollution tax or PES collected from a factory.
The methods of disability-adjusted life year (DALY) and energy analysis (EMA) were used to calculate the economic damage of the pollutants discharged by agricultural households and factories [42,43,44]. The environmental governing cost () was equivalent to the economic damage of the pollutant, which was estimated using the Equations (26)–(28):
where represents the damage to life caused by the pollutant, and represents the amount of the pollutant in the water; represents the annual energy consumption of the unit labor force (9.35 × 1013 kg/a); is the total value of energy in the pollutant; and Cg represents the ratio of energy to GDP of a country or region in per unit time.
2.5. Data Source and Processing
Statistical data were obtained from the “China Agricultural Development Report”, statistical yearbooks, the “National Agricultural Product Cost Income Data Compilation” and China paper industry yearbooks. The parameters in the Cobb–Douglas production function were obtained by using a fitting curve describing the relationship between yields and invested production elements (land area, labor, fertilizer, pesticide, mechanical, water, etc.) for 1991–2010. Other parameters were quantified from field survey results and from past literature. The quantified parameters are shown in Table 1. Statistical analysis were performed using the software package SPSS 20.0 for Windows (SPSS Inc., Armonk, NY, USA) and graphs were produced using the Origin 2017 (OriginLab, Northampton, MA, USA) software.

Table 1.
The values of the related parameters.
3. Results
3.1. Model Validation
The simulated values for TN, TP and COD discharged by agricultural household agents in 22 towns were 5.47 × 103 to 3.71 × 104 kg, 0.75 × 103 to 4.42 × 103 kg and 1.67 × 104 to 1.17 × 105 kg respectively (Figure 4(a1–a3)). Meanwhile, the simulated values of TN, TP and COD discharged by factory agents were 0.31 × 103 to 1.07 × 104 kg, 0.07 × 103 to 7.99 × 103 kg and 2.67 × 104 to 3.19 × 105 kg (Figure 4(b1–b3)). The simulated values of TN, TP, and COD were lower than the actual values, however, the difference was not statistically significant (p > 0.05). The slopes of the linear fitting lines were mostly greater than 0.85, and the coefficients of determination (R2) were greater than 0.9, indicating that the simulated values were close to the observed values (Figure 4). The Nash–Sutcliffe coefficient (NSE) is an indicator of evaluating model quality with the possible values of −∞ to 1.0 [53]. The value NSE was closer to 1.0, which represents that the simulated values are closer to the observed values, indicating a higher quality model. If the value is equal to 0.0, it means that the model is just as good as the mean value. If the value is far less than 0.0, the modeling result is not credible. In this study, the calculated NSE coefficient values for the simulation of pollutant emissions by agricultural households and factories were all greater than or equal to 0.76 (Figure 4), which indicates that the model represented the pollutant emissions relatively well.
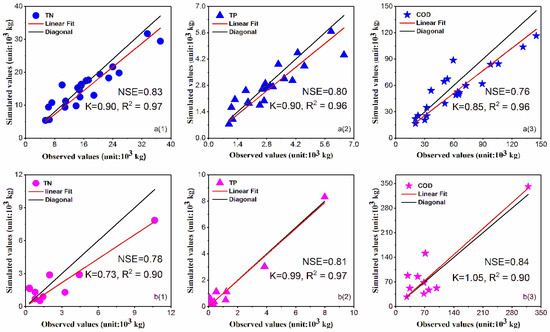
Figure 4.
Simulated and actual values of pollutant emissions by agricultural households and factories: (a1–a3) represent total nitrogen (TN), total phosphorus (TP), and chemical oxygen demand (COD) discharge by agricultural household agents, respectively, and (b1–b3) represent TN, TP, and COD discharge by factory agents, respectively.
3.2. Response Characteristics of Agricultural Household Agents and Factory Agents with Policy Change
The change in profits and pollutants (TN, TP, COD) discharged by agricultural household agents and factory agents under different policies are shown in Figure 5. The values of TN and TP discharged by the two classes of agents, as well as the value of COD discharged by factories, were significantly reduced by both environmental tax and PES. This indicates that these policies are effective for reducing water pollution in this particular case. With an increase of policy strength, the simulated pollutant content in the water discharged by agricultural households and factories decreased. Under the same policy strength, the simulated pollutant content discharged by agricultural household agents after implementing a PES was slightly lower than after implementing an environmental tax. Thus, PES was found to be more effective at reducing pollution from agricultural households. Environmental tax was found to be more effective at controlling industrial pollution emissions, as the content of pollutants discharged by factory agents after implementing an environmental tax was lower than after implementing a PES.
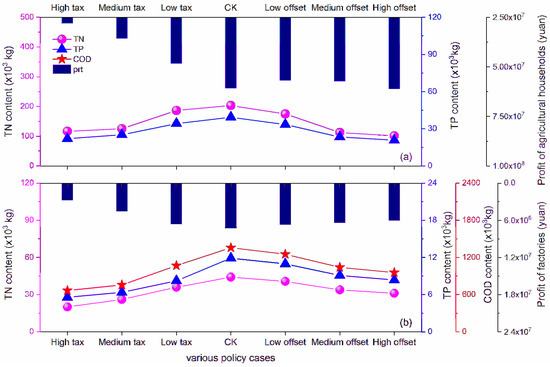
Figure 5.
Pollutant discharge and profits of agricultural households and factories in different scenarios: (a) represents TN and TP discharge into rivers and profit by agricultural household agents; and (b) represents TN, TP and COD discharge into rivers and profit by factory agents.
For agricultural household agents, profits were reduced (by 20.1%, 41.5% and 54%) after implementing an environmental tax under the low, medium, and high rates, respectively, and were reduced to a lesser degree (by up to 6.6%) after adopting a PES policy (Figure 5a). For factory agents, the profits were also reduced after adopting a specific policy and the range of reduced profits was wider after adopting an environmental tax (Figure 5b). We noticed that reducing the rate of agricultural household profits was higher than that of pollutant discharge after adopting an environmental tax. This might be due to the fact that agriculture in China is still mainly produced by small-scale agricultural households, and the tax has put an added strain on families. On the other side, agricultural households’ profits were increased during the implementation of the high offset, which might be the result of the government making up for the loss in profits caused by the reduction in fertilizer. Therefore, in order to protect the interests of agricultural households, the PES should be taken for agricultural household agents.
3.3. Scenario Analysis
3.3.1. Pollutant Emissions at the Whole Watershed Scale under Different Policies
Figure 6 shows that the simulated values of TN, TP and COD discharge by the agents across the whole basin. The values of TN, TP and COD were highest in the scenario where the government implemented no policies (CKCK), with values of 2.47 × 105 kg, 5.12 × 104 kg and 2.74 × 106 kg, respectively. When a high environmental tax was simulated for both agricultural households and factory agents (HTHT), the values of TN and TP were reduced by 51% and 48.7% compared with the CKCK scenario, respectively. When a high environmental tax was simulated for factory agents, the values of COD were reduced by 18.02% compared to those in the factory control scenarios. The values of COD were changed by the policies adopted by factories, rather than those adopted by agricultural households, because these policies only impact the content of COD in wastewater discharged by factory agents.
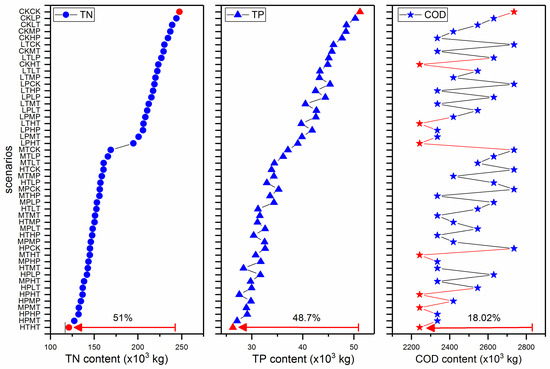
Figure 6.
Pollutant discharge and profit of agricultural households and factories in different scenarios. CK represents the control group; LT, MT and HT represent low tax, medium tax, and high tax, respectively; LP, MP and HP represent low offset, medium offset, and high offset, respectively. The first two letters of the scenario labels represent the policy of agricultural household agents, and the others represent the policy of factory agents.
3.3.2. General Effect on the System of Different Policy Scenarios
The general effect of the system and the effects of subsystems (agricultural household agents, factory agents and environment cost) are shown in Figure 7. The calculated values of the general effect of the system ranged from 1.91 × 107 RMB to 7.13 × 107 RMB. The LPCK scenario, in which agricultural household agents adopted a low degree of payment for environmental services, and factory agents adopted no policies, had the lowest general effect. The general effect of the MTHP and MPMT scenarios with values of 7.13 × 107 RMB and 7.07 × 107 RMB were relatively higher than the effect of other scenarios. The general effect values of 31 policy scenarios were lower than that of the control scenario (CKCK), and those of the remaining 17 groups (CKMP, MTLT, CKLT, LTHT, HPHT, CKMT, LTLT, LTMT, HTCK, HTMT, HTHP, CKHT, MTMT, HTLT, MPMT, MTHP and HTHT) were higher. In the different policy scenarios, the effects of agricultural household agents and factory agents ranged from 3.7 × 107 to 6.08 × 107 RMB and 5.28 × 107 to 7.28 × 107 RMB, respectively. The environmental cost was 4.74 × 107 to 8.69 × 107 RMB. Figure 7 also shows that there exists a high environmental cost either in taking a low degree of environmental tax or PES for agricultural household agents and factory agents, which suggests that a medium or high degree of taxation or that PES is more effective to balance environmental protection and regional economic development. The MPMT scenario was found to be the optimal policy to control pollutant discharge in the Shanmei River watershed, since it has a high general effect and a low environmental cost, the values of which were 7.07 × 107 and 4.99 × 107 RMB, respectively.
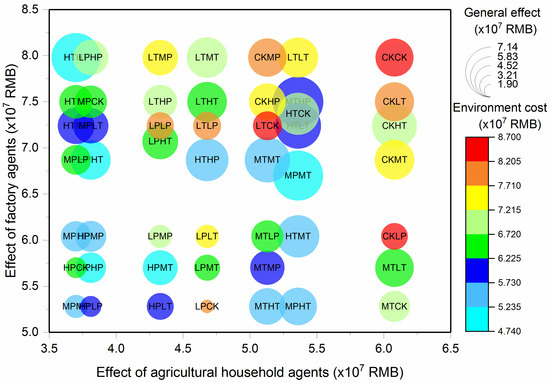
Figure 7.
The general effect and agents’ contributions in the system in different scenarios. CK represents the control group; LT, MT, HT represent low tax, medium tax, and high tax, respectively; LP, MP, HP represent low offset, medium offset, and high offset, respectively. The first two letters of the scenarios represent the policy of the agricultural household agents, and the others represent the policy of factory agents. Lighter colors represent lower environmental costs, and larger circles represent larger general effects.
4. Discussion
Water pollution has become a major environmental concern, and improving water quality has become one of the management goals of the Chinese government. It was previously shown that the economic cost of water pollution in the Minjiang River Basin was as large as 4.49 × 109 RMB to 15.11 × 109 RMB during 2004–2011 [54]. Indeed, agricultural nonpoint pollution and industrial point source pollution are two main forms for serious water quality deterioration in a region. Agricultural non-point pollution is mainly caused by the large-scale excessive use of fertilizers and pesticides and the disorderly discharge of livestock and poultry feces. The first national pollution survey bulletin showed that the levels of nitrogen and phosphorus loss from agricultural sources in China are 2.62 × 109 kg and 2.69 × 108 kg, respectively, which represent 55.5% and 63.6% of the total loss of these chemicals, respectively [55]. A previous study also showed that cropland nutrient losses and livestock and poultry emissions are the main non-point pollution sources in the middle and upper zones of the Min River Basin [49]. Thus, controlling fertilizer use is an effective way to mitigate agricultural non-point pollution by reducing the agricultural loss of nitrogen and phosphorus.
In recent years, some pollution control policies have been implemented in China, such as increasing fertilizer taxes collected from fertilizer production factories and allowing the increase of fertilizer prices [56]. In this study, we investigated the means of controlling fertilizer use to reduce agricultural nonpoint pollution by analyzing the pollution discharge changes after implementing different degrees of fertilizer taxes or PES (Figure 3 and Figure 5a). The results showed that implementing a high degree of tax results in the lowest pollution emissions but also in the lowest profit of agricultural households, so that it is preferable to adopt a PES policy rather than taxation policy considering the profit and the pollution discharge for agricultural household agents (Figure 5a). Among the countries that have actually implemented fertilizer taxes, such as Sweden, Finland and Austria, only low-tax schemes (25% tax rate) have been implemented. However, previous studies have shown that taxation is effective for controlling agricultural pollution only when implemented at no less than a rate of 100–200% [41]. Another similar study on comparing the effect of fertilizer tax and PES in China indicated that it proper to use a 100% fertilizer tax plan, but that this is not the best time to implement fertilizer taxes [18]. PES has been implemented to improve water quality in the Min River basin, Fuzhou, southern China [57]. Thus, these studies support our results to some extent.
To control industrial point source pollution, China has implemented some form of economic incentives, such as allowing the increase of the price of water and making a water pollution tax plan [3,57]. In this study, we also investigated ways to reduce industrial wastewater emissions to control water pollution from factories by analyzing the pollution discharge changes after implementing different degrees of water pollution taxes or PES (Figure 3 and Figure 5b). The results showed that tax was more effective at controlling pollutant discharge than PES for factory agents (Figure 5b). Water pollution tax, one of the four major categories of environmental taxes, has been successfully adopted in many developed countries, such as Denmark, Russia, France, Holland, and Germany [3]. However, the tax basis was different in these countries in that Denmark levies taxes based on pollution levels, while the Netherlands and Germany levy taxes based on pollution units. In our study, as a result of levying tax based on the pollution units shown, a high degree of water pollution tax (6 RMB per cubic meter of water) caused the largest reduction in pollutants. Jiao discussed the effect of different degrees of water pollution tax and PES in the Taihu basin, showing that adopting a medium degree of water pollution tax (1.6 RMB per pollutant equivalent) is superior to other policies in controlling pollution emissions by factories [19]. Water pollution taxes of 1.4–14 RMB per pollutant equivalent have been adopted in different zones of China since 1 January 2018, but the effect has not been reported. Thus, work determining the tax rate and tax basis is worth further study.
When only considering water pollution control across the whole region, the scenario of HTHT performed better than other policy scenarios (Figure 6). Regarding the balance of environmental protection and economic development at the watershed scale, the scenario of MPMT was the optimal policy. This paper investigated the effect of policy combinations on controlling water pollution and verified that they are useful for controlling water pollution at the watershed scale. Owing to the uncertainty of partial parameters, neglect of the consumption process and the fact that the policies have not been verified in practice, work optimizing the parameters and models, as well as introducing market mechanisms, should be conducted in the future.
5. Conclusions
This study used agent-based modeling (ABM) to simulate pollutant discharge in a reservoir basin district in Southern China under different policy scenarios combining environmental tax and payments for environment services (PES). We constructed multiple agent-based models that simulated well the pollutant discharge by agricultural households and factories. We then investigated the effect of different policy scenarios on controlling pollution emissions. The results suggest that environmental tax and PES policies were both effective in reducing water pollution. When balancing environmental protection and economic profits, PES appeared to be more effective at reducing pollution from agricultural households and taxation seemed to be more effective at controlling industrial pollution emissions. We additionally identified an optimal policy scenario to effectively reduce pollutant discharge in terms of maintaining economic development under the priority of environmental protection. The scenario implementing a medium degree of PES for agricultural household agents and a medium degree of environmental tax for factory agents was found to be the optimal choice to control the water pollution in this watershed. However, a completely government-led PES compensation mechanism may cause excessive financial burdens for the government. As such, we should likely set a differential compensation mechanism and introduce market incentives to reduce the financial burden on the government. In further studies, the rates of PES and environmental tax should be readjusted and the model structure and parameters should be optimized in specific cases. Overall, the present findings could be helpful in providing guidelines for water pollution control and sustainable water management in China.
Author Contributions
The article was mainly written by C.D., H.W. provided many valuable comments, W.Z. collected the data and made a preliminary analysis, and Z.J. reviewed the first draft manuscript. All authors read and approved the final version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number [51479003] and [51879010].
Acknowledgments
The authors thank the editors and anonymous reviewers for suggesting the constructive comments and corrections that substantially improved the quality of the paper.
Conflicts of Interest
The authors declare that they have no conflicts of interest to disclose.
References
- Harmancioglu, N.B. Overview of Water Policy Developments: Pre- and Post-2015 Development Agenda. Water Resour. Manag. 2017, 31, 3001–3021. [Google Scholar] [CrossRef]
- Wan, L.; Cai, W.; Jiang, Y.; Wang, C. Impacts on quality-induced water scarcity: Drivers of nitrogen-related water pollution transfer under globalization from 1995 to 2009. Environ. Res. Lett. 2016, 11, 074017. [Google Scholar] [CrossRef]
- Zhou, Y.; Khu, S.T.; Xi, B.; Su, J.; Hao, F.; Wu, J.; Huo, S. Status and challenges of water pollution problems in China: Learning from the European experience. Environ. Earth Sci. 2014, 72, 1243–1254. [Google Scholar] [CrossRef]
- Larsen, H. Environmental Taxes: Recent Developments in China and OECD Countries; OECD: Paris, France, 1999. [Google Scholar]
- Bongaerts, J.C.; Kraemer, A. Permits and effluent charges in the water pollution control policies of France, West Germany, and the Netherlands. Environ. Monit. Assess. 1989, 12, 127–147. [Google Scholar] [CrossRef] [PubMed]
- Baylis, K.; Peplow, S.; Rausser, G.; Simon, L. Agri-environmental policies in the EU and United States: A comparison. Ecol. Econ. 2008, 65, 753–764. [Google Scholar] [CrossRef]
- Claassen, R.; Cattaneo, A.; Johansson, R. Cost-effective design of agri-environmental payment programs: U.S. experience in theory and practice. Ecol. Econ. 2008, 65, 737–752. [Google Scholar] [CrossRef]
- Dobbs, T.L.; Pretty, J. Case study of agri-environmental payments: The United Kingdom. Ecol. Econ. 2008, 65, 765–775. [Google Scholar] [CrossRef]
- Hardner, J.; Rice, R. Rethinking green consumerism. Sci. Am. 2002, 286, 88–95. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Piña, C.; Guevara, A.; Torres, J.M.; Braña, J. Paying for the hydrological services of Mexico’s forests: Analysis, negotiations and results. Ecol. Econ. 2008, 65, 725–736. [Google Scholar] [CrossRef]
- Niesten, E.; Rice, R. Sustainable forest management and conservation incentive agreements. Int. For. Rev. 2004, 6, 56–60. [Google Scholar] [CrossRef]
- Pagiola, S. Payments for environmental services in Costa Rica. Ecol. Econ. 2008, 65, 712–724. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, J.; Zhang, C.; Zang, W.; Guo, W.; Qian, Z.; Liu, L.; Zhao, J.; Feng, J. Payments for Ecosystem Services for watershed water resource allocations. J. Hydrol. 2018, 556, 689–700. [Google Scholar] [CrossRef]
- Tobón Orozco, D.; Molina, C.; Vargas Cano, J.H. Pigouvian taxes and payments for environmental services in an economic model restricted by the resilience of a body of water. Water Resour. Econ. 2017, 19, 28–40. [Google Scholar] [CrossRef]
- Wunder, S.; Engel, S.; Pagiola, S. Taking stock: A comparative analysis of payments for environmental services programs in developed and developing countries. Ecol. Econ. 2008, 65, 834–852. [Google Scholar] [CrossRef]
- Engel, S.; Pagiola, S.; Wunder, S. Designing payments for environmental services in theory and practice: An overview of the issues. Ecol. Econ. 2008, 65, 663–674. [Google Scholar] [CrossRef]
- Pagiola, S.; Arcenas, A.; Platais, G. Can payments for environmental services help reduce poverty? An exploration of the issues and the evidence to date from Latin America. World Dev. 2005, 33, 237–253. [Google Scholar] [CrossRef]
- Yang, S.S.; Luan, S.J. Simulation on non-point pollution control from crop production based on a multi-agent model: Comparative research between fertilizer tax and payements for environmental services. Int. J. Ind. Eng. Theory 2014, 34, 777–786. (In Chinese) [Google Scholar]
- Jiao, Z.Q.; Zhang, W.G.; Wang, H.R.; Li, A.H. Somulating industrial water pollution control on a multi-agent model. J. Beijing Norm. Univ. 2017, 53, 486–494. (In Chinese) [Google Scholar]
- Terna, P. Simulation tools for social scientists: Building agent based models with swarm. J. Artif. Soc. Soc. Simul. 1998, 1, 1–12. [Google Scholar]
- Bandini, S.; Manzoni, S.; Vizzari, G. Agent Based Modeling and Simulation: An Informatics Perspective. J. Artif. Soc. Soc. Simul. 2009, 12, A51–A66. [Google Scholar]
- Berger, T.; Birner, R.; Diaz, J.; McCarthy, N.; Wittmer, H. Capturing the complexity of water uses and water users within a multi-agent framework. Water Resour. Manag. 2007, 21, 129–148. [Google Scholar] [CrossRef]
- Ng, T.L.; Eheart, J.W.; Cai, X.; Braden, J.B. An agent-based model of farmer decision-making and water quality impacts at the watershed scale under markets for carbon allowances and a second-generation biofuel crop. Water Resour. Res. 2011, 47, 113–120. [Google Scholar] [CrossRef]
- Zechman, E.M. Agent-Based Modeling to Simulate Contamination Events and Evaluate Threat Management Strategies in Water Distribution Systems. Risk Anal. 2011, 31, 758–772. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.C.E.; Zhao, J.S.; Cai, X.M. Decentralized Optimization Method for Water Allocation Management in the Yellow River Basin. J. Water Resour. Plan. Manag. 2012, 138, 313–325. [Google Scholar] [CrossRef]
- Nikolic, V.V.; Simonovic, S.P.; Milicevic, D.B. Analytical Support for Integrated Water Resources Management: A New Method for Addressing Spatial and Temporal Variability. Water Resour. Manag. 2013, 27, 401–417. [Google Scholar] [CrossRef]
- Yuan, X.C.; Wei, Y.M.; Pan, S.Y.; Jin, J.L. Urban Household Water Demand in Beijing by 2020: An Agent-Based Model. Water Resour. Manag. 2014, 28, 2967–2980. [Google Scholar] [CrossRef]
- Akhbari, M.; Grigg, N.S. Managing Water Resources Conflicts: Modelling Behavior in a Decision Tool. Water Resour. Manag. 2015, 29, 5201–5216. [Google Scholar] [CrossRef]
- Shafiee, M.E.; Berglund, E.Z.; Lindell, M.K. An agent-based modeling framework for assessing the public health protection of water advisories. Water Resour. Manag. 2018, 32, 2033–2059. [Google Scholar] [CrossRef]
- Arnold, R.T.; Troost, C.; Berger, T. Quantifying the economic importance of irrigation water reuse in a Chilean watershed using an integrated agent-based model. Water Resour. Res. 2015, 51, 648–668. [Google Scholar] [CrossRef]
- Mashhadi Ali, A.; Shafiee, M.E.; Berglund, E.Z. Agent-based modeling to simulate the dynamics of urban water supply: Climate, population growth, and water shortages. Sustain. Cities Soc. 2017, 28, 420–434. [Google Scholar] [CrossRef]
- Galán, J.M.; LópezParedes, A.; del Olmo, R. An agent-based model for domestic water management in valladolid metropolitan area. Water Resour. Res. 2009, 45, W05401. [Google Scholar] [CrossRef]
- Gilbert, G.N. Agent-Based Models; Sage Publications Inc.: Washington, DC, USA, 2007. [Google Scholar]
- Miller, J.H.; Page, S.E. Complex Adaptive Systems: An Introduction to Computational Models of Social Life; Princeton University Press: Princeton, NJ, USA, 2009; Volume 129, pp. 409–410. [Google Scholar]
- Wooldridge, M.; Jennings, N.R. Intelligent agents: Theory and practice. Knowl. Eng. Rev. 1995, 10, 115–152. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Macal, C.M.; North, M.J. Tutorial on agent-based modelling and simulation. J. Simul. 2010, 4, 151–162. [Google Scholar] [CrossRef]
- Wilensky, U. NetLogo; Center for Connected Learning and Computer-Based Modeling, Northwestern University: Evanston, IL, USA, 1999; Available online: http://ccl.northwestern.edu/netlogo/2017-9-19 (accessed on 9 August 2018).
- Schotter, A. Microeconomics: A Modern Approach, 2nd ed.; Addison-Wesley: Boston, MA, USA, 1997. [Google Scholar]
- Intergovernmental Panel on Climate Change. IPCC Guidelines for National Greenhouse Gas Inventories (Volume 4): Agriculture, Forestry and Other Land Use; IPCC: Geneva, Switzerland, 2006. [Google Scholar]
- Organisation for Economic Co-Operation and Development (OECD). Agricultural and Environmental Policies: Oppprtunities for Intergration; China Environemtal Science Press: Beijing, China, 1996. [Google Scholar]
- Goedkoop, M.; Spriensma, R. The Eco-indictor 99: A Damage Oriented Method for Life Cycle Impact Assessment—Methodology Annex, 3rd ed.; PRé Consultants BV: Amersfoort, The Netherlands, 2001. [Google Scholar]
- Odum, H.T. Environmental Accounting: Emergy and Environmental Decision Making; Wiley and Sons: New York, NY, USA, 1996. [Google Scholar]
- Lai, L.; Huang, X.J.; Wang, H.; Dong, Y.H.; Xiao, S.S. Estimation of environmental cost of chemical fertilizer utilization in China. Acta Pedol. Sin. 2009, 46, 64–69. (In Chinese) [Google Scholar]
- Ministry of Agriculture and Rural Affairs of the People’s Republic of China. 2012 China Agricultural Development Report. Available online: http://english.agri.gov.cn/service/ayb/201701/t20170105_246192.htm (accessed on 9 August 2018).
- CSYD. Almanac of China Paper Industry; China Light Industry Press: Beijing, China, 2009; Available online: http://tongji.cnki.net/overseas/engnavi/NaviDefault.aspx (accessed on 9 August 2018).
- Ma, B.Y.; Liu, Y.C.; Xue, J.J. Application of Chemical Fertilizer and the Loss of Nitrogen and Phosphorus in Rice and Wheat Rotation Soil in South Hebei. J. Irrig. Drain. Eng. 2007, 26, 72–74. (In Chinese) [Google Scholar]
- Xu, P.; Lin, Y.H.; Yang, S.S.; Luan, S.J. Input load to river and future projection for nitriogen and phpsphorous nutrient controlling of Pearl river basin. J. Lake Sci. 2017, 29, 1359–1371. [Google Scholar]
- Chen, C.; Huang, D.F.; Qiu, X.X.; Li, W.H. Survey and Evaluation of Agricultural Non-Point Source Pollution and Prevention-and-Cure Counter measures in Middle and Upriver of Minjiang Drainage Area. J. Agro-Environ. Sci. 2007, 26, 368–374. (In Chinese) [Google Scholar]
- National Bureau of Statistics of China. China Statistical Yearbook; China Statistics Press: Beijing, China, 2011. Available online: http://tongji.cnki.net/overseas/engnavi/HomePage.aspx?id=N2011090108&name=YINFN&floor=1 (accessed on 9 August 2018). (In Chinese)
- Mosier, A.; Kroeze, C.; Nevison, C.; Oenema, O.; Seitzinger, S.; Van Cleemput, O. Closing the global atmospheric N2O budget: Nitrous oxide emissions through the agricultural nitrogen cycle: OECD/IPCC/IEA phase II development of IPCC guidelines for national greenhouse gas inventory methodology. Nutr. Cycl. Agroecosyst. 1998, 52, 225–248. [Google Scholar] [CrossRef]
- Yang, Z.P. Estimation of Ammonia Emission from Livestock in China Based on Mass-Flow Method and Regional Comparison; Peking University: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Rao, Q.H.; Qiu, Y.; Xu, L.Z.; Wang, C.M.; Zhang, J.S. Estimating model of economic loss for Minjiang river basin casued by wayer pllution. Water Resour. Power 2014, 32, 47–50. [Google Scholar]
- MOA (Ministry of Agriculture of China); NBS (National Bureau of Statistics of China); MEP (Ministry of Environment Protection of China) (Eds.) The First National Pollution Census Report; MEP: Beijing, China, 2010.
- Qu, F.T.; Kuyvenhoven, A.; Shi, X.P.; Heerink, N. Sustainable natural resource use in rural China: Recent trends and policies. China Econ. Rev. 2011, 22, 444–460. [Google Scholar] [CrossRef]
- Jiang, Y.; Jin, L.S.; Lin, T. Higher water tariffs for less river pollution—Evidence from the Min River and Fuzhou City in China. China Econ. Rev. 2011, 22, 183–195. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).