Transient Analysis of Grout Penetration With Time-Dependent Viscosity Inside 3D Fractured Rock Mass by Unified Pipe-Network Method
Abstract
1. Introduction
- UPM uses pipes for capturing transport processes but ignores mechanical behaviors, while LEM uses trusses for capturing the mechanical behaviors;
- UPM introduces pipes parallel to the fracture planes to capture the transport processes in fractures. On the other hand, in LEM the breakages of trusses represent damage/fractures which originally intersect with the fracture planes, but are not parallel to;
- Unlike LEM, UPM cannot simulate fracture propagations and nucleations, which is suitable for simulating transport processes in naturally highly fractured rock mass.
2. Methodology
2.1. Rheological Models of Grout
2.2. Unified Pipe-Network Method (UPM) Discrete Model
2.3. Considering the Time-Dependent Viscosity in UPM
3. Model Verification
3.1. Verifying the Rheological Models
3.2. Transient Flow Considering the Time-Dependent Viscosity of Grout
4. Application in Simulating Grouting Process in Rock Mass with Fracture Networks
4.1. The Influence of Viscosity
4.2. The Influence of Fractures and Grout Operation Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| UPM | Unified Pipe-Network Method |
| LEM | Lattice Elements Method |
References
- Mohajerani, S.; Baghbanan, A.; Wang, G.; Forouhandeh, S. An efficient algorithm for simulating grout propagation in 2d discrete fracture networks. Int. J. Rock Mech. Min. Sci. 2017, 98, 67–77. [Google Scholar] [CrossRef]
- Jeannin, P.; Malard, A.; Rickerl, D.; Weber, E. Assessing karst-hydraulic hazards in tunneling: the brunnmühle spring system bernese jura, switzerland. Environ. Earth Sci. 2015, 74, 7655–7670. [Google Scholar] [CrossRef]
- Funehag, J.; Gustafson, G. Design of grouting with silica sol in hard rock–New methods for calculation of penetration length, Part I. Tunn. Undergr. Space Technol. 2008, 23, 1–8. [Google Scholar] [CrossRef]
- Bezuijen, A.; Grotenhuis, R.T.; van Tol, A.; Bosch, J.; Haasnoot, J. Analytical model for fracture grouting in sand. J. Geotech. Geoenviron. Eng. 2010, 137, 611–620. [Google Scholar] [CrossRef]
- Hernqvist, L.; Fransson, Å.; Gustafson, G.; Emmelin, A.; Eriksson, M.; Stille, H. Analyses of the grouting results for a section of the apse tunnel at äspö hard rock laboratory. Int. J. Rock Mech. Min. Sci. 2009, 46, 439–449. [Google Scholar] [CrossRef]
- Lisa, H.; Christian, B.; Åsa, F.; Gunnar, G.; Johan, F. A hard rock tunnel case study: Characterization of the water-bearing fracture system for tunnel grouting. Tunn. Undergr. Space Technol. 2012, 30, 132–144. [Google Scholar] [CrossRef]
- Seo, H.; Choi, H.; Lee, I. Numerical and experimental investigation of pillar reinforcement with pressurized grouting and pre-stress. Tunn. Undergr. Space Technol. 2016, 54, 135–144. [Google Scholar] [CrossRef]
- Gustafson, G.; Stille, H. Prediction of groutability from grout properties and hydrogeological data. Tunn. Undergr. Space Technol. 1996, 11, 325–332. [Google Scholar] [CrossRef]
- Amadei, B.; Savage, W. An analytical solution for transient flow of bingham viscoplastic materials in rock fractures. Int. J. Rock Mech. Min. Sci. 2001, 38, 285–296. [Google Scholar] [CrossRef]
- Xu, Y.; Peng, W.H. Research on multiple holes grouting of fractured rock Mass. Appl. Mech. Mater. 2013, 256, 547–551. [Google Scholar] [CrossRef]
- Foyo, A.; Sánchez, M.A.; Tomillo, C. A proposal for a secondary permeability index obtained from water pressure tests in dam foundations. Eng. Geol. 2005, 77, 69–82. [Google Scholar] [CrossRef]
- Stille, H.; Gustafson, G.; Hassler, L. Application of new theories and technology for grouting of dams and foundations on rock. Geotech. Geol. Eng. 2012, 30, 603–624. [Google Scholar] [CrossRef]
- Brantberger, M.; Stille, H.; Eriksson, M. Controlling grout spreading in tunnel grouting: Analyses and developments of the gin-method. Tunn. Undergr. Space Technol. 2000, 15, 343–352. [Google Scholar] [CrossRef]
- Axelsson, M.; Gustafson, G. A robust method to determine the shear strength of cement-based injection grouts in the field. Tunn. Undergr. Space Technol. 2006, 21, 499–503. [Google Scholar] [CrossRef]
- Draganović, A.; Stille, H. Filtration and penetrability of cement-based grout: Study performed with a short slot. Tunn. Undergr. Space Technol. 2011, 26, 548–559. [Google Scholar] [CrossRef]
- Lee, J.; Bang, C.; Mok, Y.; Joh, S. Numerical and experimental analysis of penetration grouting in jointed rock masses. Int. J. Rock Mech. Min. Sci. 2000, 37, 1027–1037. [Google Scholar] [CrossRef]
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- Moës, N.; Bolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef]
- Song, J.-H.; Areias, P.; Belytschko, T. A method for dynamic crack and shear band propagation with phantom nodes. Int. J. Numer. Methods Eng. 2006, 67, 868–893. [Google Scholar] [CrossRef]
- Areias, P.; Song, J.-H.; Belytschko, T. Analysis of fracture in thin shells by overlapping paired elements. Comput. Methods Appl. Mech. Eng. 2006, 195, 41–43. [Google Scholar] [CrossRef]
- Wu, J.-Y.; Li, F.-B. An improved stable XFEM (Is-XFEM) with a novel enrichment function for the computational modeling of cohesive cracks. Comput. Methods Appl. Mech. Eng. 2015, 295, 77–107. [Google Scholar] [CrossRef]
- Simo, J.; Oliver, J.; Armero, F. An analysis of strong discontinuities induced by strain-softening in rate-independent inelastic solids. Comput. Mech. 1993, 12, 277–296. [Google Scholar] [CrossRef]
- Saloustros, S.; Pelà, L.; Cervera, M.; Roca, P. Finite element modelling of internal and multiple localized cracks. Comput. Mech. 2017, 59, 299–316. [Google Scholar] [CrossRef]
- Saloustros, S.; Cervera, M.; Pelà, L. Tracking multi-directional intersecting cracks in numerical modelling of masonry shear walls under cyclic loading. Meccanica 2018, 53, 1757–1776. [Google Scholar] [CrossRef]
- Saloustros, S.; Cervera, M.; Pelà, L. Challenges, tools and applications of tracking algorithms in the numerical modelling of cracks in concrete and masonry structures. Arch. Comput. Methods Eng. 2018. [Google Scholar] [CrossRef]
- Nikolić, M.; Ibrahimbegovic, A.; Miscevic, P. Discrete element model for the analysis of fluid-saturated fractured poro-plastic medium based on sharp crack representation with embedded strong discontinuities. Comput. Methods Appl. Mech. Eng. 2016, 298, 407–427. [Google Scholar] [CrossRef]
- Nikolić, M.; Ibrahimbegovic, A.; Miscevic, P. Brittle and ductile failure of rocks: Embedded discontinuity approach for representing mode i and mode ii failure mechanisms. Int. J. Numer. Methods Eng. 2015, 102, 1507–1526. [Google Scholar] [CrossRef]
- Nikolić, M.; Ibrahimbegovic, A. Rock mechanics model capable of representing initial heterogeneities and full set of 3d failure mechanisms. Comput. Methods Appl. Mech. Eng. 2015, 290, 209–227. [Google Scholar] [CrossRef]
- Zhang, Y.; Lackner, R.; Zeiml, M.; Mang, H. Strong discontinuity embedded approach with standard SOS formulation: Element formulation, energy-based crack-tracking strategy, and validations. Comput. Methods Appl. Mech. Eng. 2015, 287, 335–366. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, X. Cracking elements: A self-propagating strong discontinuity embedded approach for quasi-brittle fracture. Finite Elem. Anal. Des. 2018, 144, 84–100. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, X. A softening-healing law for self-healing quasi-brittle materials: analyzing with strong discontinuity embedded approach. Eng. Fract. Mech. 2018, 192, 290–306. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X.; Zhu, H.; Rabczuk, T. Phase field modelling of crack propagation, branching and coalescence in rocks. Theor. Appl. Fract. Mech. 2018, 96, 174–192. [Google Scholar] [CrossRef]
- Wu, J.-Y.; Nguyen, V.-P. A length scale insensitive phase-field damage model for brittle fracture. J. Mech. Phys. Solids 2018, 119, 20–42. [Google Scholar] [CrossRef]
- Wu, J.-Y. Robust numerical implementation of non-standard phase-field damage models for failure in solids article. Comput. Methods Appl. Mech. Eng. 2018, 340, 767–797. [Google Scholar] [CrossRef]
- Zhou, S.; Rabczuk, T.; Zhuang, X. Phase field modeling of quasi-static and dynamic crack propagation: Comsol implementation and case studies. Adv. Eng. Softw. 2018, 122, 31–49. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X.; Rabczuk, T. A phase-field modeling approach of fracture propagation in poroelastic media. Eng. Geol. 2018, 240, 189–203. [Google Scholar] [CrossRef]
- Areias, P.; Reinoso, J.; Camanho, P.; César de Sá, J.; Rabczuk, T. Effective 2d and 3d crack propagation with local mesh refinement and the screened poisson equation. Eng. Fract. Mech. 2018, 189, 339–360. [Google Scholar] [CrossRef]
- Areias, P.; Msekh, M.; Rabczuk, T. Damage and fracture algorithm using the screened Poisson equation and local remeshing. Eng. Fract. Mech. 2016, 158, 116–143. [Google Scholar] [CrossRef]
- Areias, P.; Rabczuk, T.; Msekh, M. Phase-field analysis of finite-strain plates and shells including element subdivision. Comput. Methods Appl. Mech. Eng. 2016, 312, 322–350. [Google Scholar] [CrossRef]
- Areias, P.; Rabczuk, T.; Dias-da-Costa, D. Element-wise fracture algorithm based on rotation of edges. Eng. Fract. Mech. 2013, 110, 113–137. [Google Scholar] [CrossRef]
- Areias, P.; Rabczuk, T. Finite strain fracture of plates and shells with configurational forces and edge rotations. Int. J. Numer. Methods Eng. 2013, 94, 1099–1122. [Google Scholar] [CrossRef]
- Zhang, Y. Multi-slicing strategy for the three-dimensional discontinuity layout optimization (3D DLO). Int. J. Numer. Anal. Methods Geomech. 2017, 41, 488–507. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhuang, X. Stability analysis of shotcrete supported crown of NATM tunnels with discontinuity layout optimization. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 1199–1216. [Google Scholar] [CrossRef]
- Min, K.; Rutqvist, J.; Tsang, C.; Jing, L. Stress-dependent permeability of fractured rock masses: A numerical study. Int. J. Rock Mech. Min. Sci. 2004, 41, 1191–1210. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Stress effects on permeability in a fractured rock mass with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2008, 45, 1320–1334. [Google Scholar] [CrossRef]
- Saeidi, O.; Stille, H.; Torabi, S.R. Numerical and analytical analyses of the effects of different joint and grout properties on the rock mass groutability. Tunn. Undergr. Space Technol. 2013, 38, 11–25. [Google Scholar] [CrossRef]
- Huang, D.; Cen, D.; Ma, G.; Huang, R. Step-path failure of rock slopes with intermittent joints. Landslides 2015, 12, 911–926. [Google Scholar] [CrossRef]
- Huang, D.; Song, Y.; Cen, D.; Fu, G. Numerical modeling of earthquake-induced landslide using an improved discontinuous deformation analysis considering dynamic friction degradation of joints. Rock Mech. Rock Eng. 2016, 49, 4767–4786. [Google Scholar] [CrossRef]
- Ren, H.; Zhuang, X.; Rabczuk, T. Dual-horizon peridynamics: A stable solution to varying horizons. Comput. Meth. Appl. Mech. Eng. 2017, 318, 762–782. [Google Scholar] [CrossRef]
- Ren, H.; Zhuang, X.; Cai, Y.; Rabczuk, T. Dual-horizon peridynamics. Int. J. Numer. Methods Eng. 2016, 108, 1451–1476. [Google Scholar] [CrossRef]
- Rabczuk, T.; Zi, G.; Bordas, S.; Nguyen-Xuan, H. A simple and robust three-dimensional cracking-particle method without enrichment. Comput. Methods Appl. Mech. Eng. 2010, 199, 2437–2455. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Meth. Eng. 2004, 61, 2316–2343. [Google Scholar] [CrossRef]
- Han, F.; Lubineau, G.; Azdoud, Y. Adaptive coupling between damage mechanics and peridynamics: A route for objective simulation of material degradation up to complete failure. J. Mech. Phys. Solids 2016, 94, 453–472. [Google Scholar] [CrossRef]
- Han, F.; Lubineau, G.; Azdoud, Y.; Askari, A. A morphing approach to couple state-based peridynamics with classical continuum mechanics. Comput. Methods Appl. Mech. Eng. 2016, 301, 336–358. [Google Scholar] [CrossRef]
- Zhang, Y.; Pichler, C.; Yuan, Y.; Zeiml, M.; Lackner, R. Micromechanics-based multifield framework for early-age concrete. Eng. Struct. 2013, 47, 16–24. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeiml, M.; Pichler, C.; Lackner, R. Model-based risk assessment of concrete spalling in tunnel linings under fire loading. Eng. Struct. 2014, 77, 207–215. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeiml, M.; Maier, M.; Yuan, Y.; Lackner, R. Fast assessing spalling risk of tunnel linings under RABT fire: From a coupled thermo-hydro-chemo-mechanical model towards an estimation method. Eng. Struct. 2017, 142, 1–19. [Google Scholar] [CrossRef]
- Yang, M.; Yue, Z.; Lee, P.K.; Su, B.; Tham, L. Prediction of grout penetration in fractured rocks by numerical simulation. Can. Geotech. J. 2002, 39, 1384–1394. [Google Scholar] [CrossRef]
- Hässler, L.; Håkansson, U.; Stille, H. Computer-simulated flow of grouts in jointed rock. Tunn. Undergr. Space Technol. 1992, 7, 441–446. [Google Scholar] [CrossRef]
- Rahmani, H. Estimation of Grout Distribution in a Fractured Rock By Numerical Modeling. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2009. [Google Scholar]
- Fidelibus, C.; Lenti, V. The propagation of grout in pipe networks. Comput. Geosci. 2012, 45, 331–336. [Google Scholar] [CrossRef]
- Cacas, M.-C.; Ledoux, E.; Marsily, G.D.; Tillie, B.; Barbreau, A.; Durand, E.; Feuga, B.; Peaudecerf, P. Modeling fracture flow with a stochastic discrete fracture network: Calibration and validation: 1. the flow model. Water Resour. Res. 1990, 26, 479–489. [Google Scholar] [CrossRef]
- Dershowitz, W.; Einstein, H. Characterizing rock joint geometry with joint system models. Rock Mech. Rock Eng. 1988, 21, 21–51. [Google Scholar] [CrossRef]
- Ma, G.; Wang, H.; Fan, L.; Wang, B. Simulation of two-phase flow in horizontal fracture networks with numerical manifold method. Adv. Water Resour. 2017, 108, 293–309. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.; Fu, G.; Zhang, K. Investigation of the permeability anisotropy of 2d fractured rock masses. Eng. Geol. 2015, 196, 171–182. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.; Wang, Y.; Fan, L. Pipe network model for unconfined seepage analysis in fractured rock masses. Int. J. Rock Mech. Min. Sci. 2016, 88, 183–196. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.; Wang, Y.; Li, T.; Zhu, H. Unified pipe network method for simulation of water flow in fractured porous rock. J. Hydrol. 2017, 547, 80–96. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.; Wang, Y.; Fan, L.; Zhu, H. Two-phase flow pipe network method for simulation of CO2 sequestration in fractured saline aquifers. Int. J. Rock Mech. Min. Sci. 2017, 98, 39–53. [Google Scholar] [CrossRef]
- Nikolić, M.; Karavelić, E.; Ibrahimbegovic, A.; Miščević, P. Lattice element models and their peculiarities. Arch. Comput. Methods Eng. 2018, 25, 753–784. [Google Scholar] [CrossRef]
- Grassl, P. A lattice approach to model flow in cracked concrete. Cement Concr. Compos. 2009, 31, 454–460. [Google Scholar] [CrossRef]
- Nikolić, M.; Do, X.N.; Ibrahimbegovic, A.; Nikolić, Ż. Crack propagation in dynamics by embedded strong discontinuity approach: Enhanced solid versus discrete lattice model. Comput. Methods Appl. Mech. Eng. 2018, 340, 480–499. [Google Scholar]
- Kazemian, S.; Prasad, A.; Huat, B.; Bazaz, J.B.; Mohammed, T.; Aziz, F.A. Effect of aggressive ph media on peat treated by cement and sodium silicate grout. J. Central South Univ. Technol. 2011, 18, 840–847. [Google Scholar] [CrossRef]
- Kazemian, S.; Prasad, A.; Huat, B.B.; Ghiasi, V.; Ghareh, S. Effects of cement–sodium silicate system grout on tropical organic soils. Arab. J. Sci. Eng. 2012, 37, 2137–2148. [Google Scholar] [CrossRef]
- Porcino, D.; Marcianò, V.; Granata, R. Static and dynamic properties of a lightly cemented silicate-grouted sand. Can. Geotech. J. 2012, 49, 1117–1133. [Google Scholar] [CrossRef]
- Sun, Z.; Li, S.; Liu, R.; Zhang, Q.; Zhang, L.; Zheng, Z. Fracture defusing mechanism and pressure characteristic tests of rapid setting cement-based grouts. Yantu Lixue (Rock Soil Mech.) 2014, 35, 2219–2225. (In chinese) [Google Scholar]
- Zhang, Q.; Zhang, L.; Liu, R.; Li, S.; Zhang, Q. Grouting mechanism of quick setting slurry in rock fissure with consideration of viscosity variation with space. Tunnel. Underg. Space Technol. 2017, 70, 262–273. [Google Scholar] [CrossRef]
- Mohajerani, S.; Baghbanan, A.; Bagherpour, R.; Hashemolhosseini, H. Grout penetration in fractured rock mass using a new developed explicit algorithm. Int. J. Rock Mech. Mining Sci. 2015, 80, 412–417. [Google Scholar] [CrossRef]
- Ruan, W. Research on diffusion of grouting and basic properties of grouts. J. Geotech. Eng. 2005, 27, 69–73. (In Chinese) [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media (Dover Civil and Mechanical Engineering); Courier Corporation: ChelmsfordNorth Chelmsford, MA, USA, 1988; ISBN 978-0486656755. [Google Scholar]
- Bear, J. Hydraulics of Groundwater (Dover Books on Engineering); Courier Corporation: ChelmsfordNorth Chelmsford, MA, USA, 2007; ISBN 978-0486453552. [Google Scholar]
- Li, S.; Han, W.; Zhang, Q.; Liu, R.; Weng, X. Research on time-dependent behavior of viscosity of fast curing grouts in underground construction grouting. Chin. J. Rock Mech. Eng. 2013, 32, 1–7. [Google Scholar]
- Wang, Y.; Ma, G.; Ren, F.; Li, T. A constrained delaunay discretization method for adaptively meshing highly discontinuous geological media. Comput. Geosci. 2017, 109, 134–148. [Google Scholar] [CrossRef]
- Gustafson, G.; Stille, H. Stop criteria for cement grouting. Felsbau: Zeitschrift für Geomechanik und Ingenieurgeologie im Bauwesen und Bergbau 2005, 25, 62–68. [Google Scholar]
- Liu, R. Study on Diffusion and Plugging Mechanism of Quick Setting Cement Based Slurry in Underground Dynamic Water Grouting and Its Application; Shandong University: Jinan, China, 2012; pp. 84–86. [Google Scholar]
- Bandis, S.; Lumsden, A.; Barton, N. Fundamentals of rock joint deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 249–268. [Google Scholar] [CrossRef]
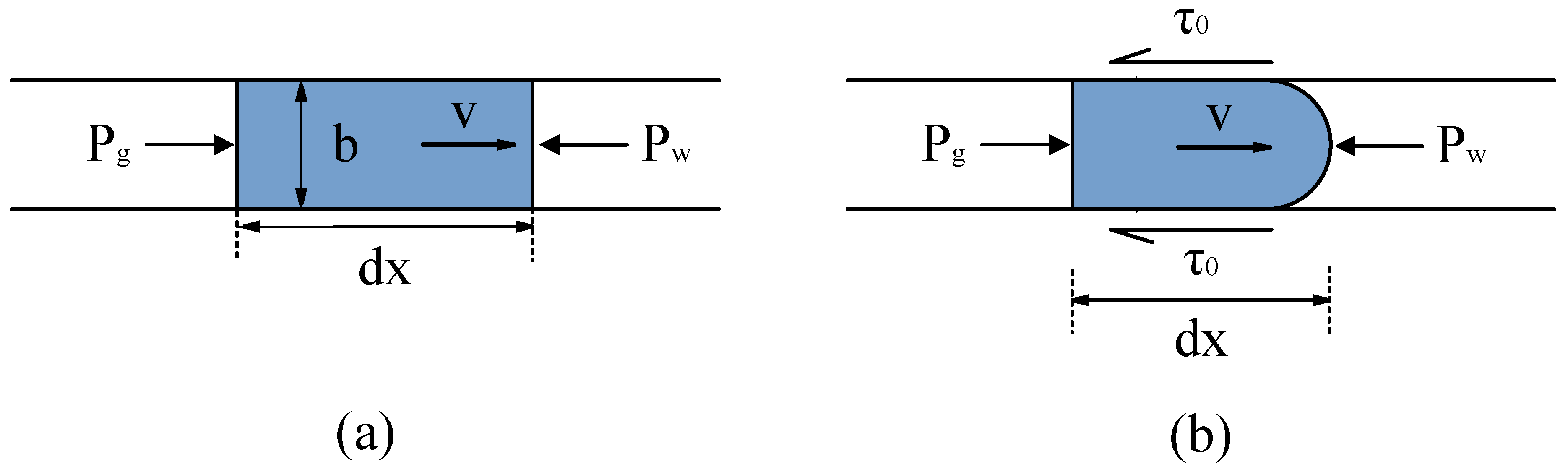
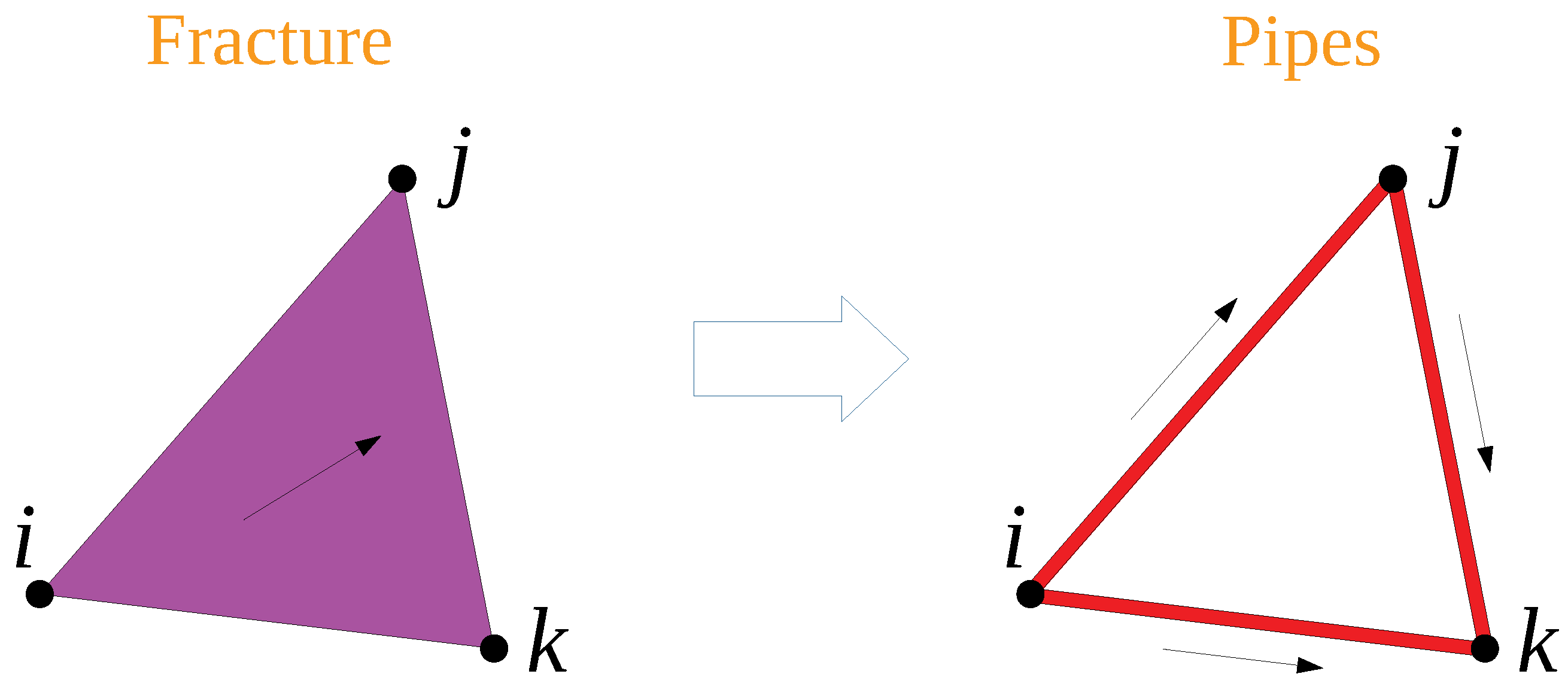
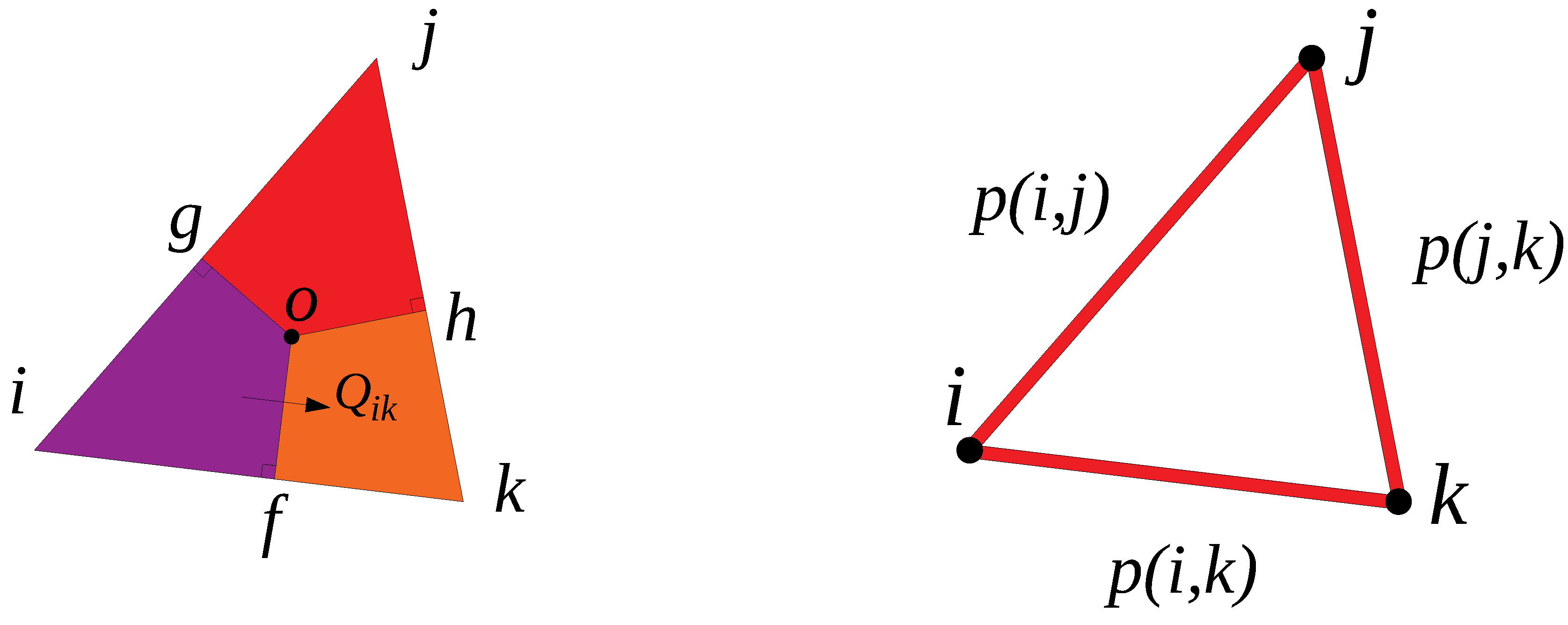
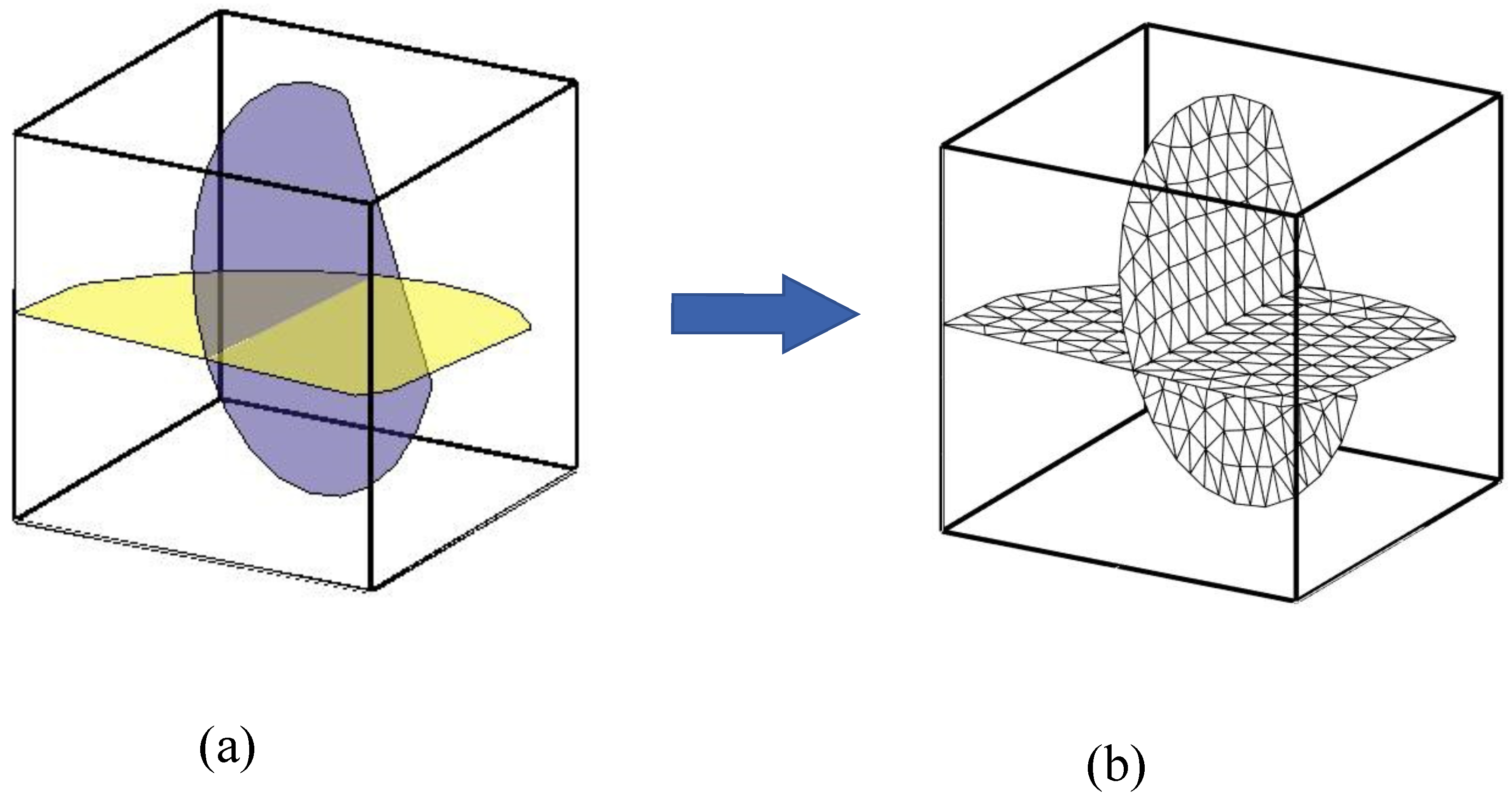
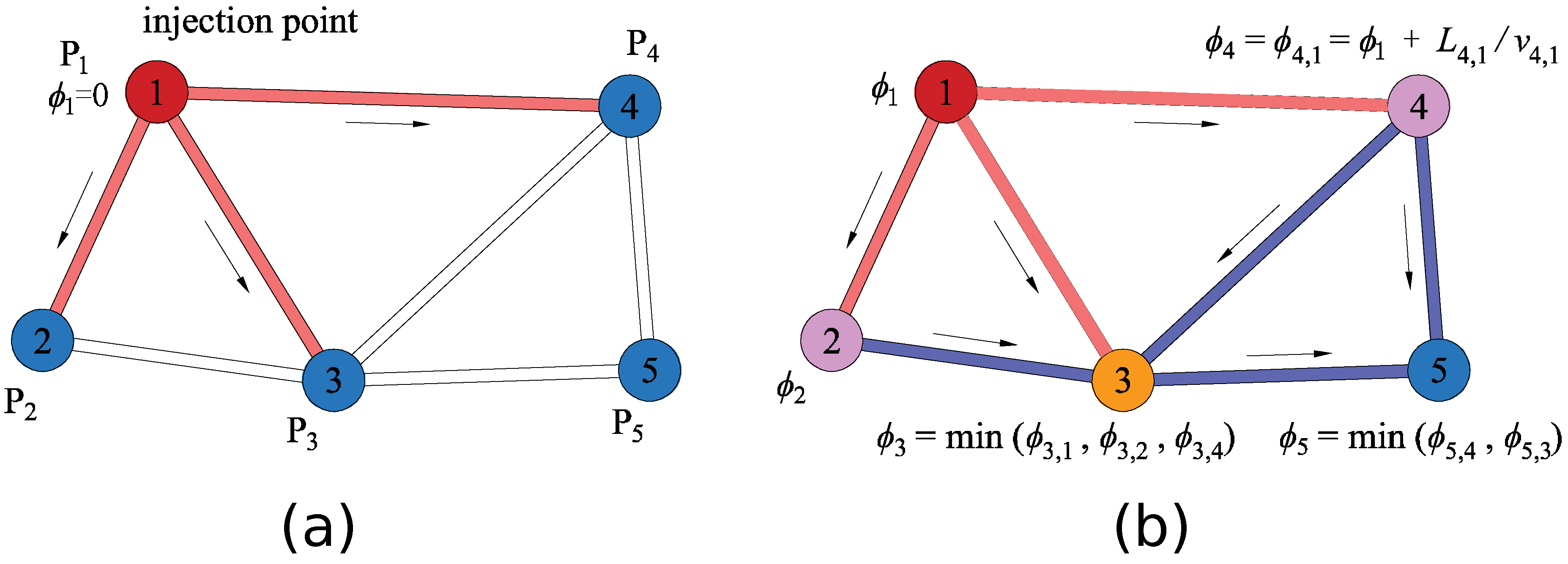
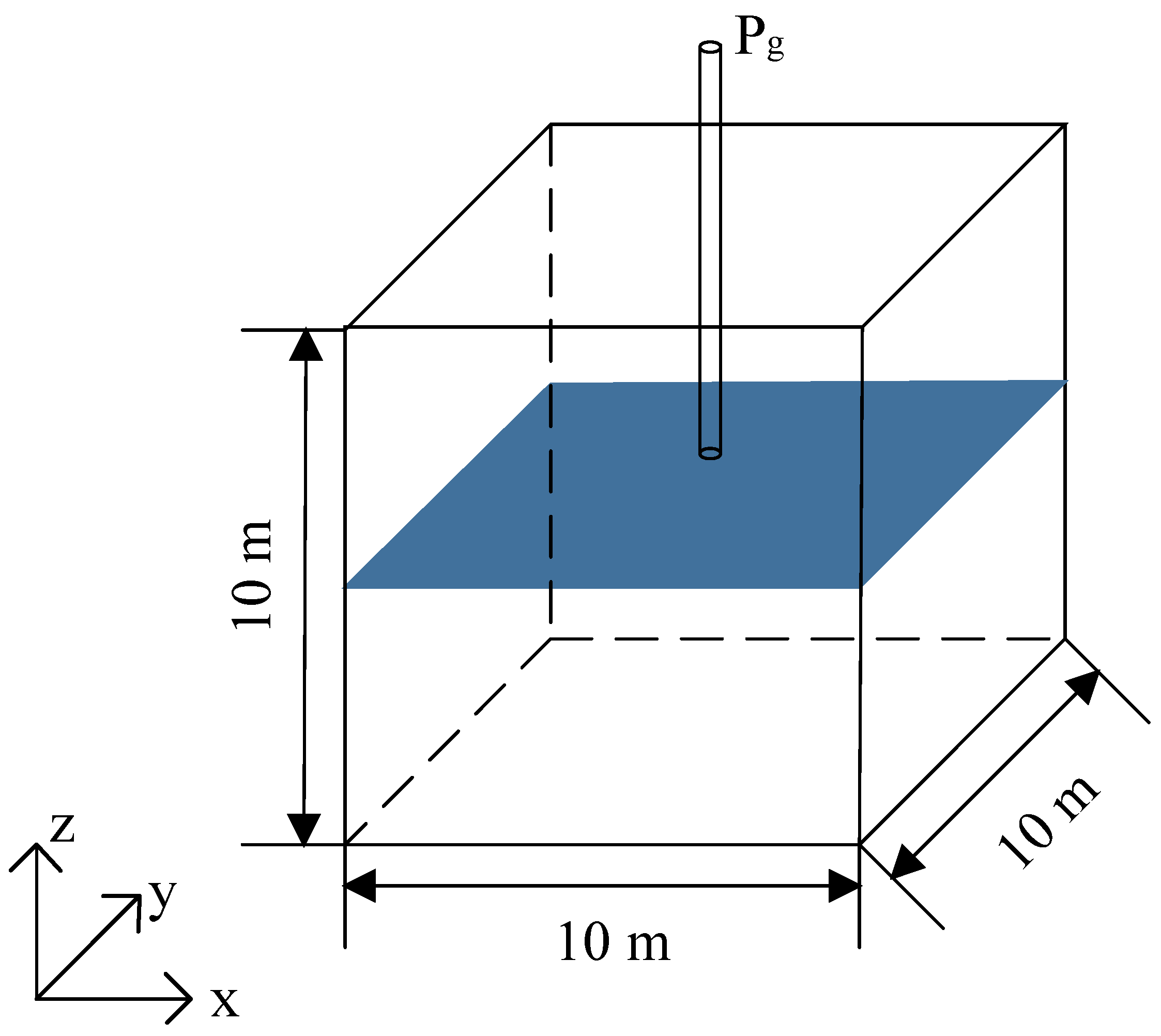
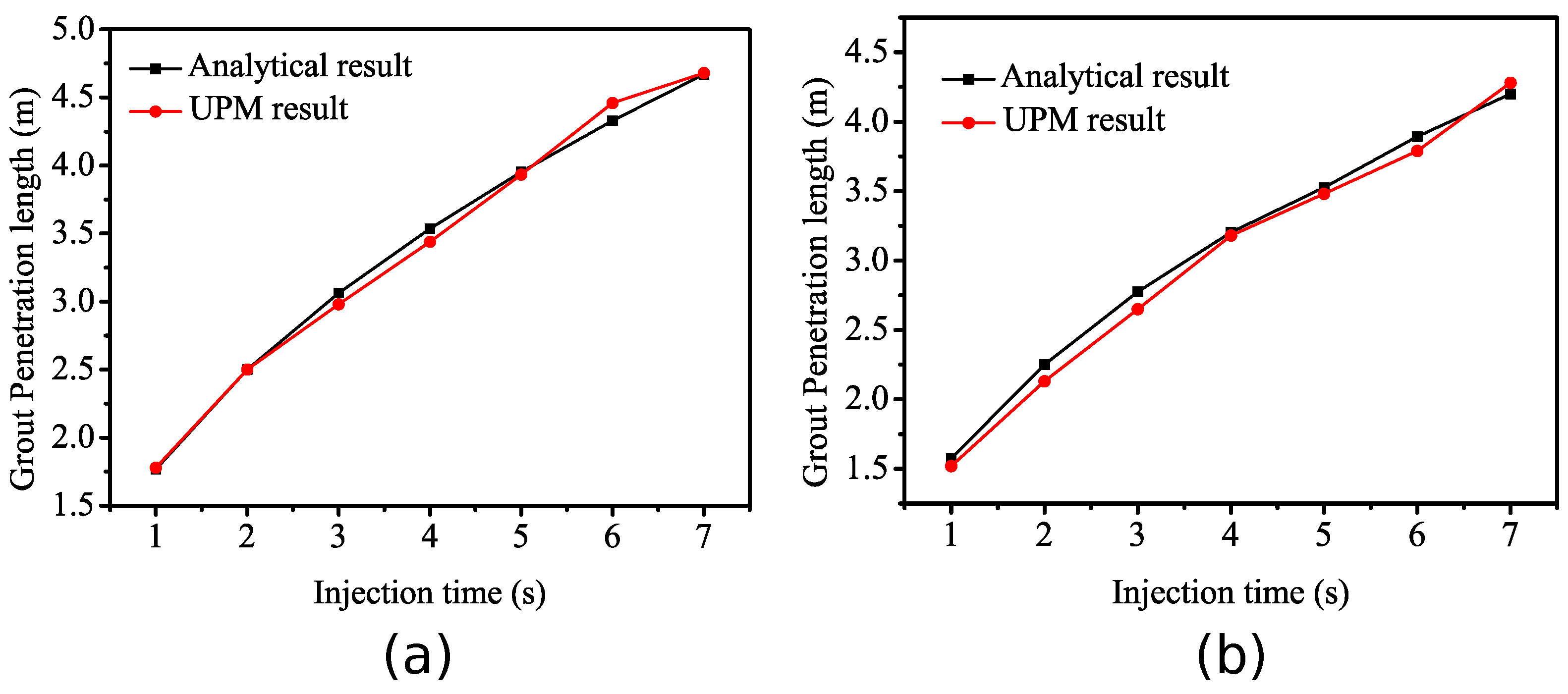
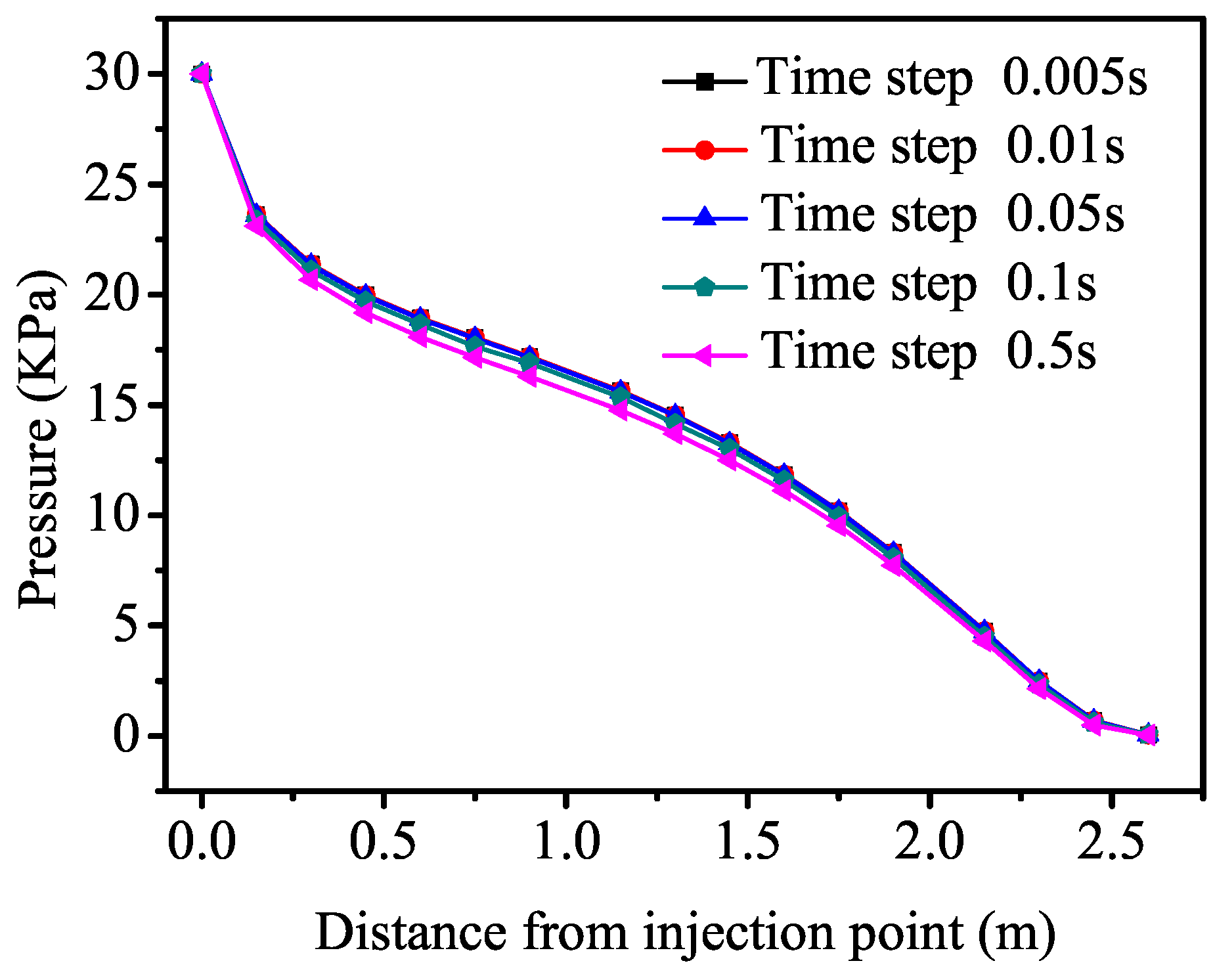
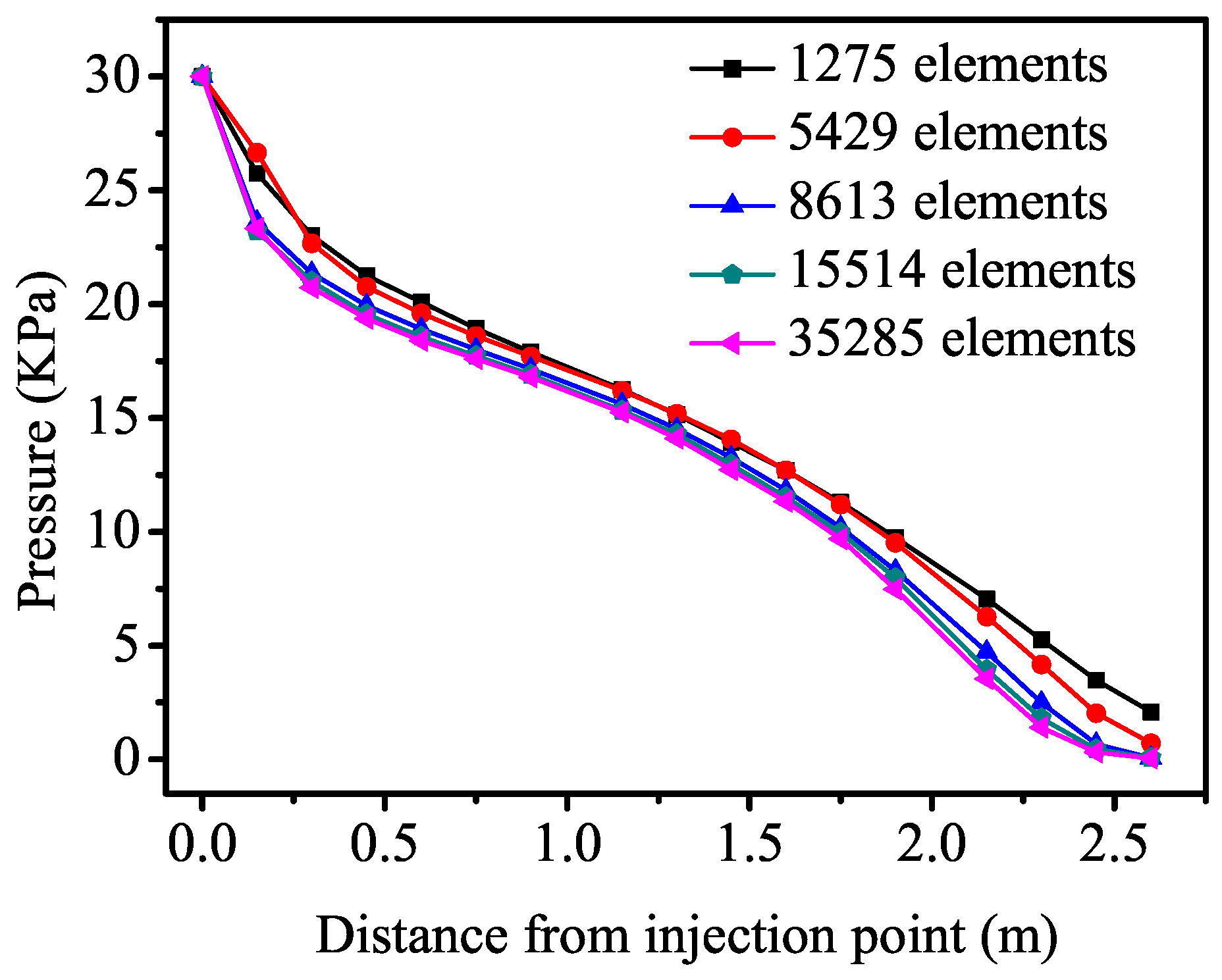
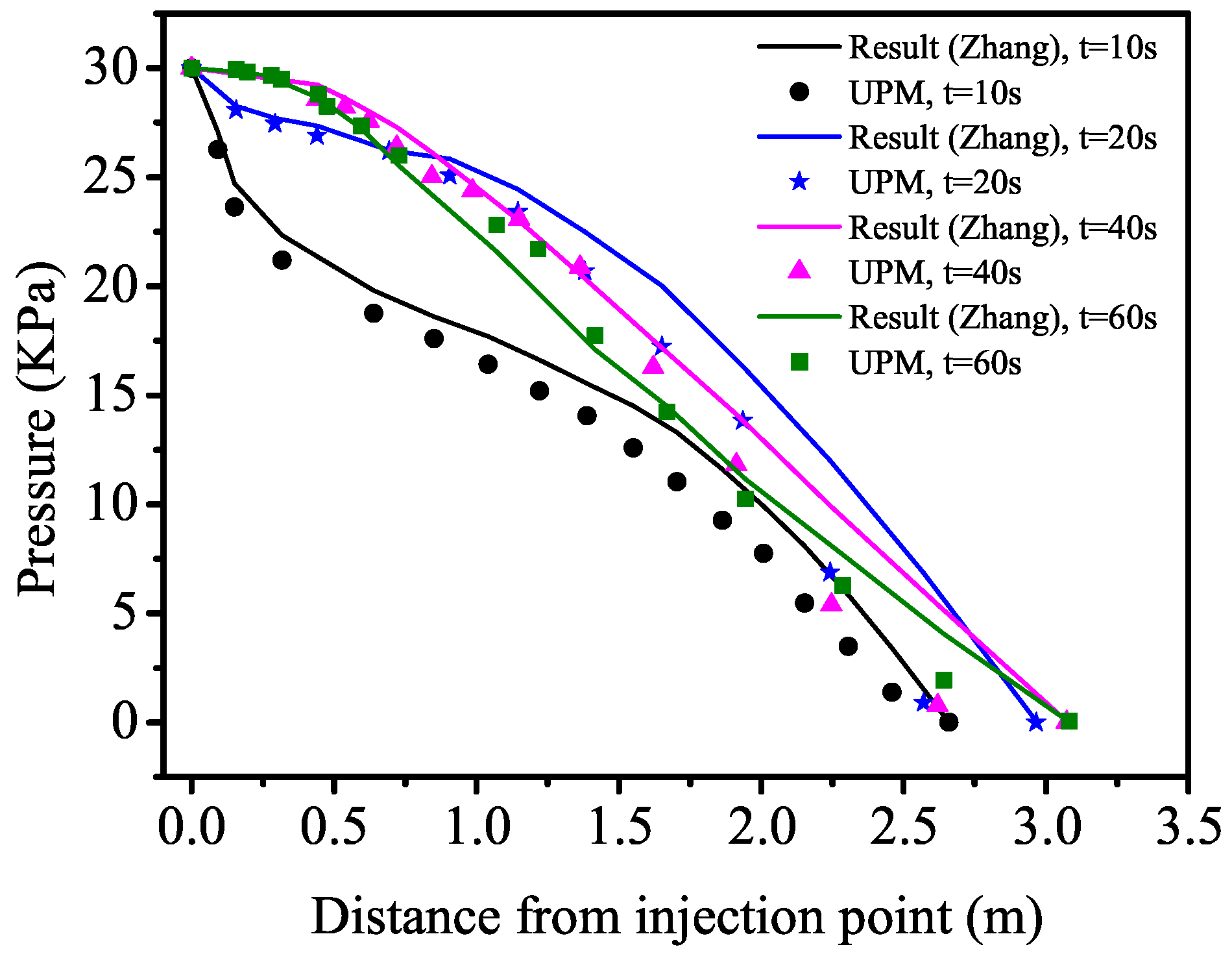
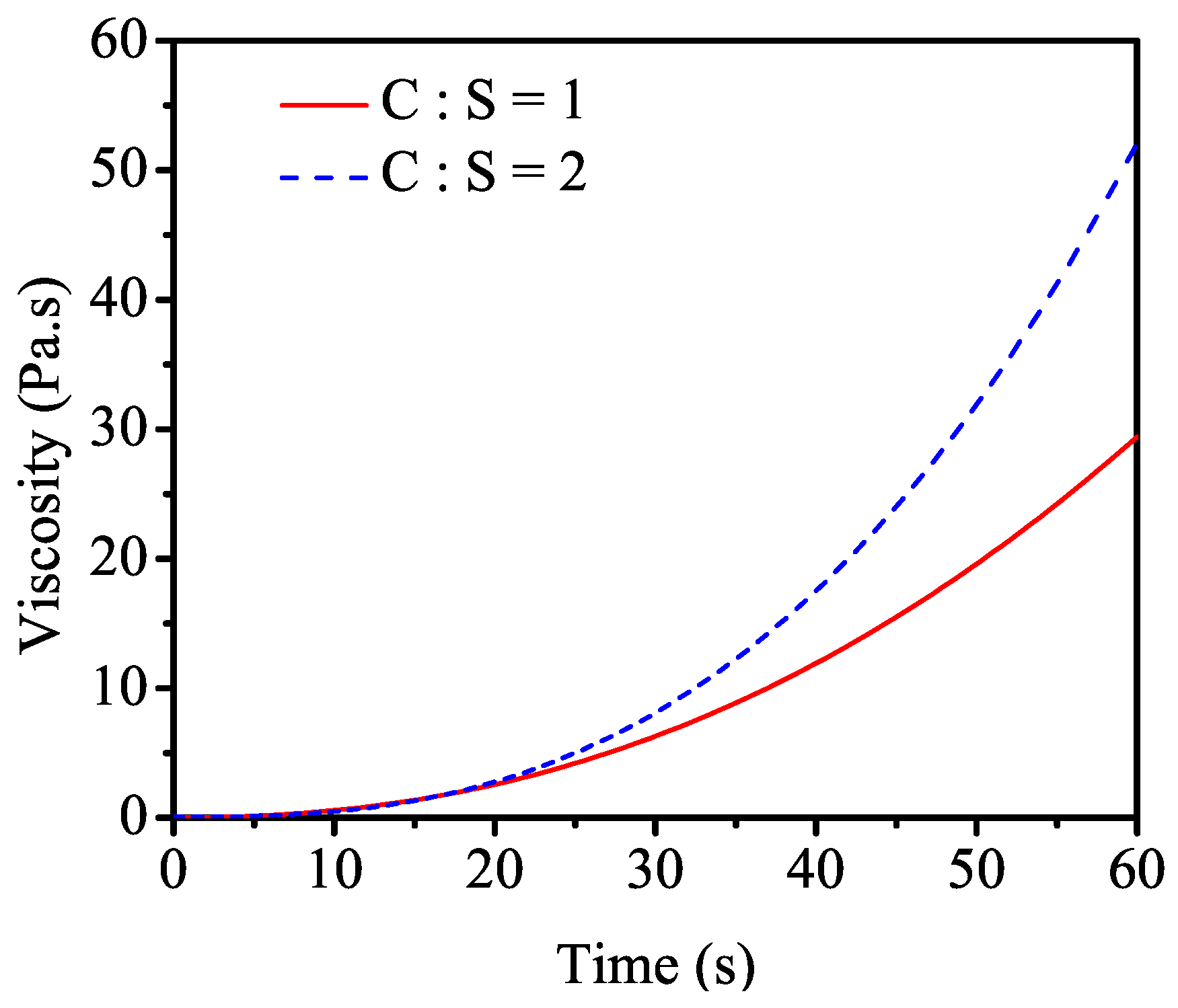
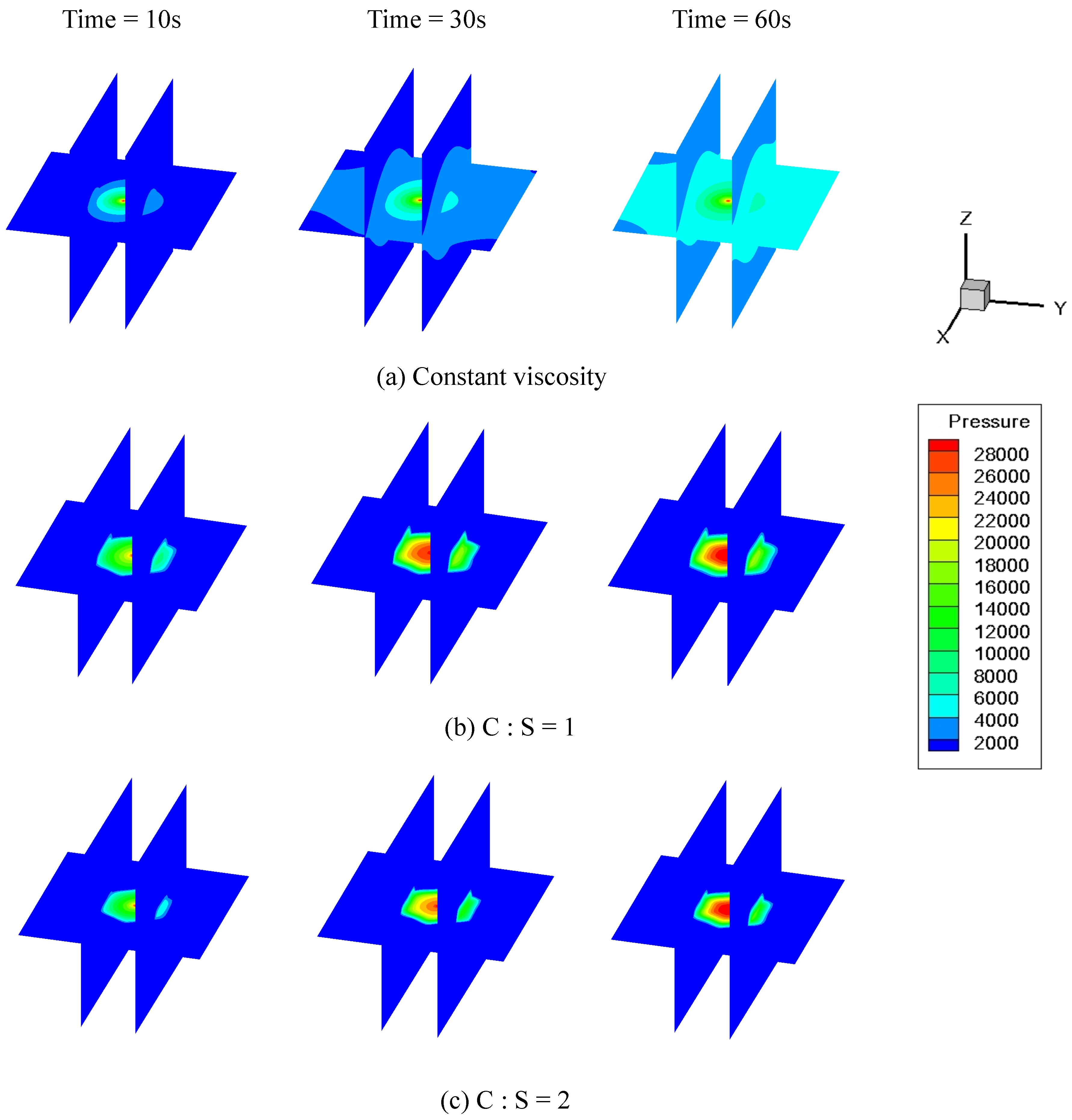
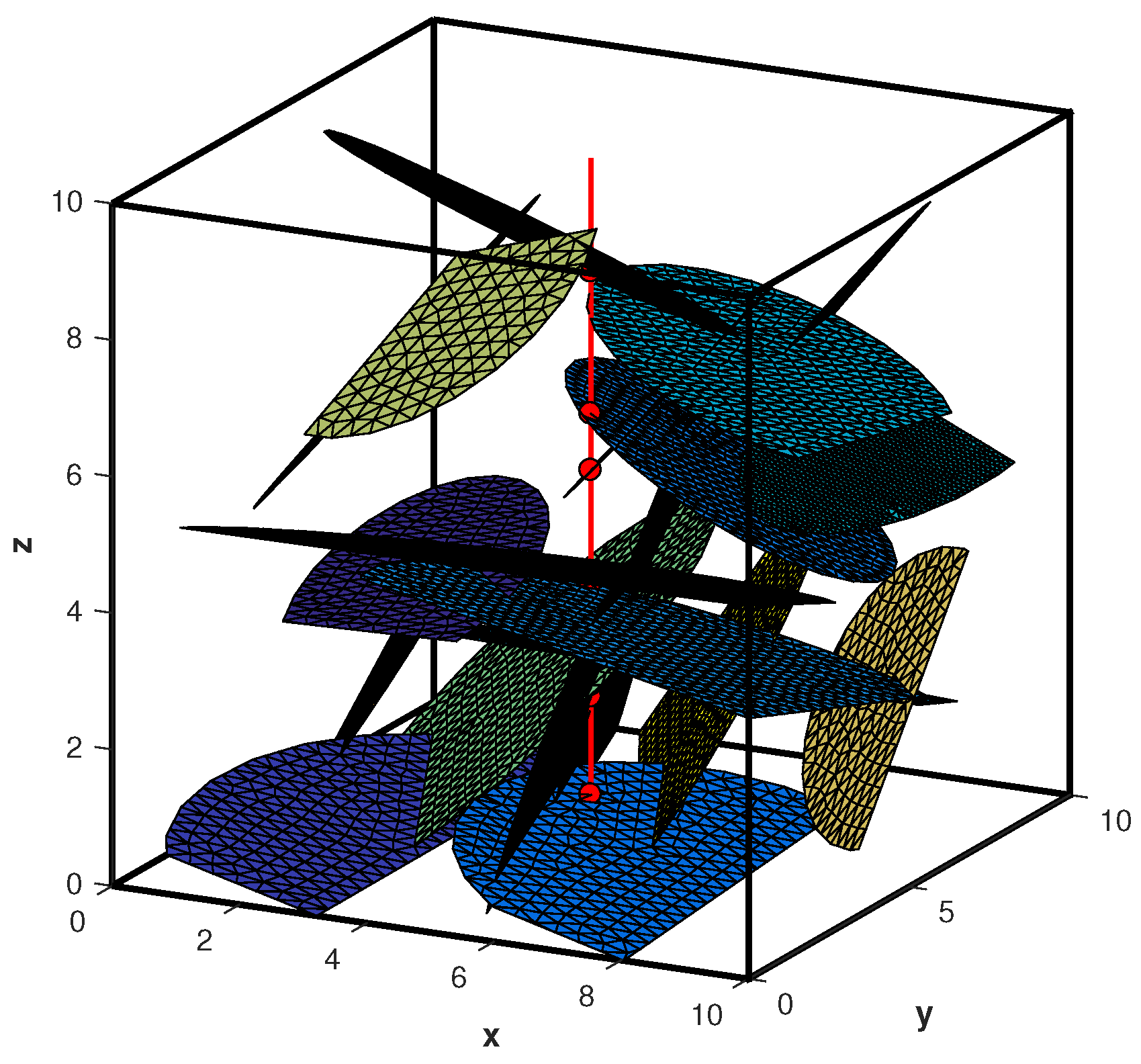
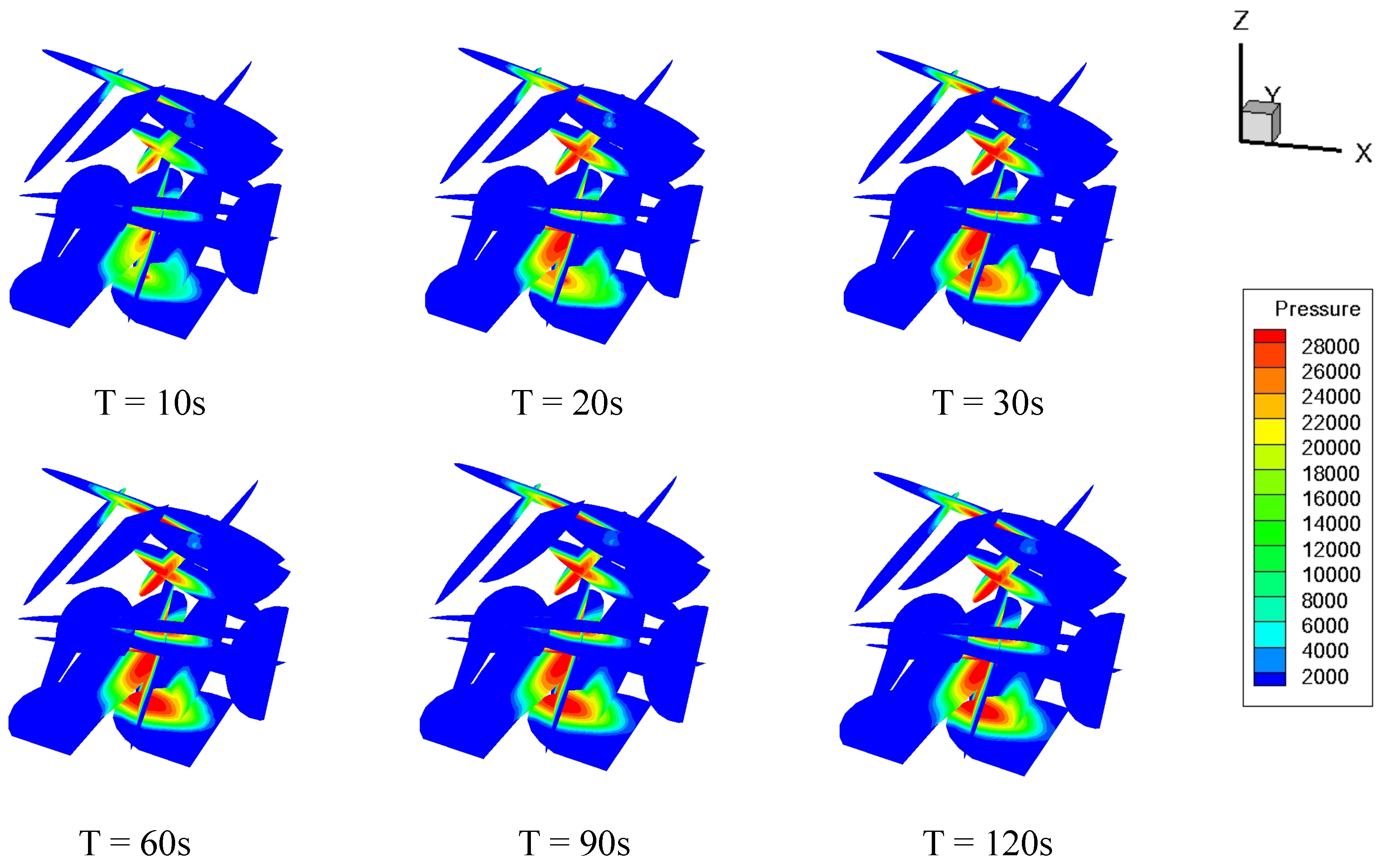
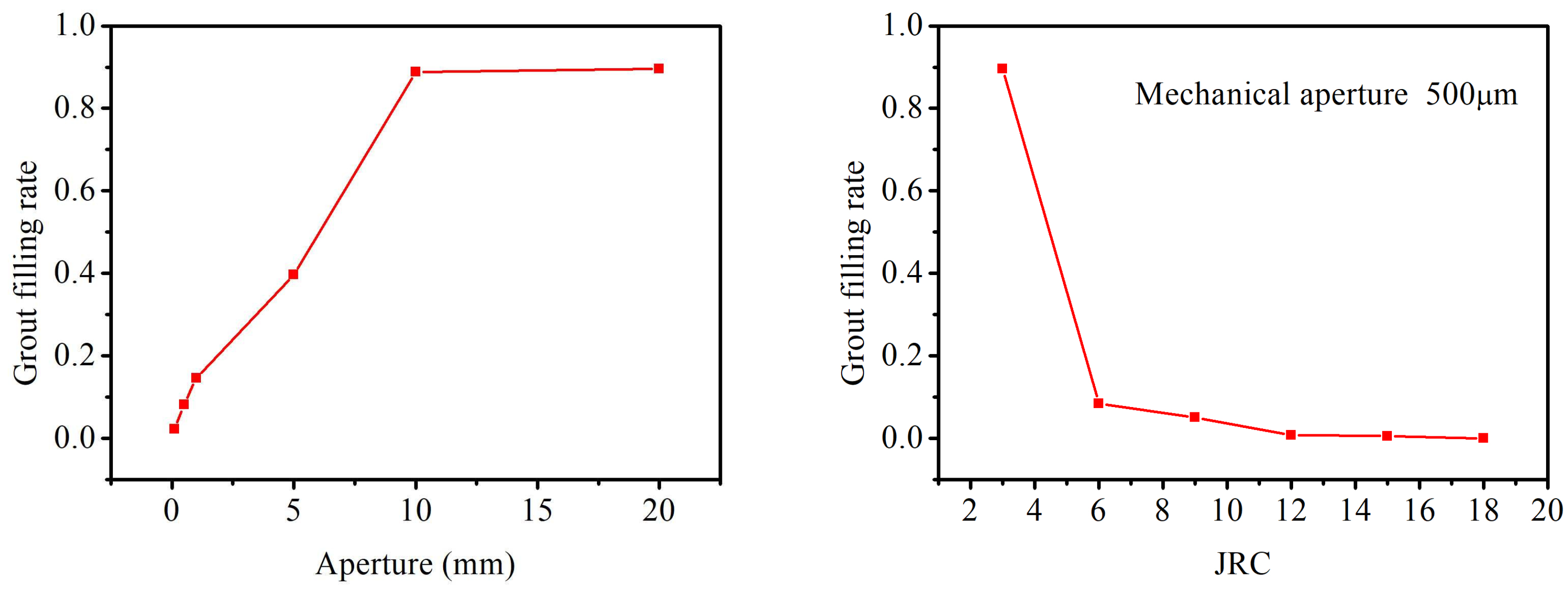
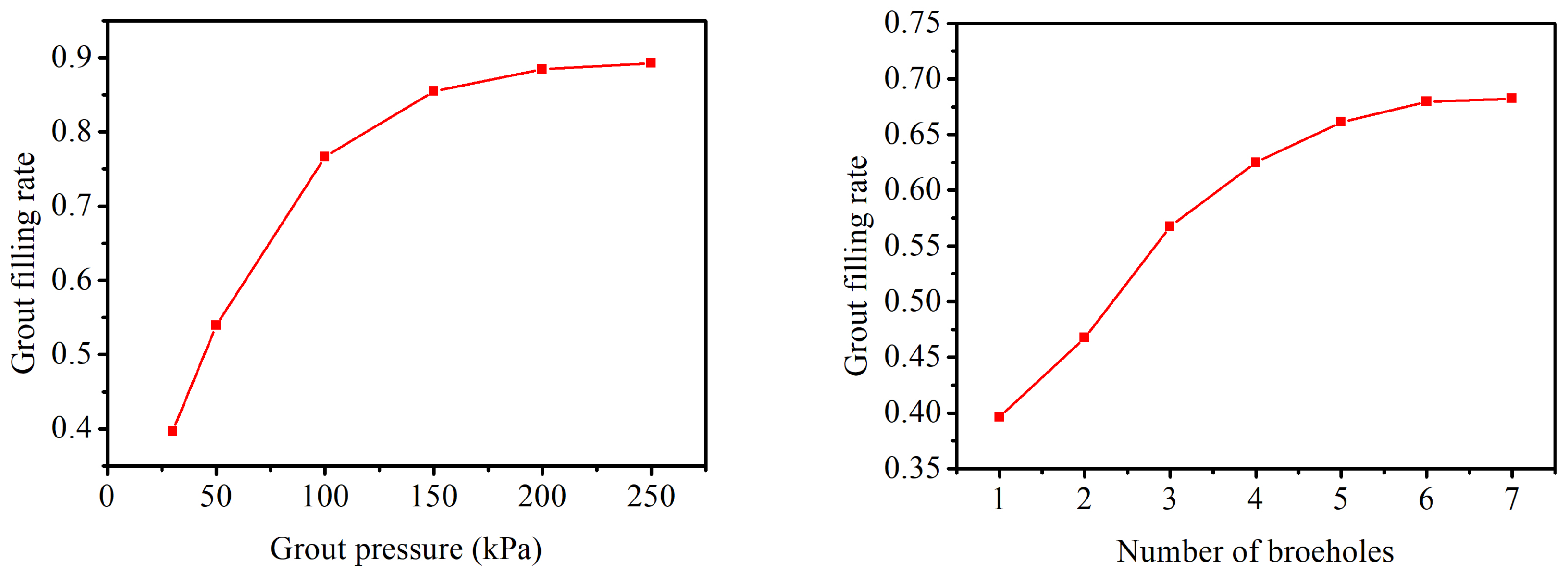
| Parameters | Symbol | Unit | Value |
|---|---|---|---|
| Grout injection pressure | p | 30,000 | |
| Pore pressure of fracture | 0 | ||
| Grout density | kg/m3 | 1400 | |
| Yield stress | 1.0 | ||
| Initial grout viscosity | 0.04 | ||
| Flow consistency index | k | 0.003182 | |
| Flow behavior index | n | − | 2.23 |
| Fracture aperture | b | m | 0.005 |
| Storage coefficient | S | [-] | 1.4 |
| Gravitational acceleration | g | m/s2 | 9.8 |
| Group | Fracture Number | Mean Length (m) | St Dev | Dip Angle (Degree) | Dip Direction (Degree) | |
|---|---|---|---|---|---|---|
| 1 | 10 | x-axis | 5 | 2 | 16 | 40 |
| y-axis | 3 | 2 | ||||
| 2 | 10 | x-axis | 3 | 2 | 56 | 256 |
| y-axis | 3 | 2 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Yan, X.; Liu, R.; Xu, Z.; Li, S.; Zhang, Y. Transient Analysis of Grout Penetration With Time-Dependent Viscosity Inside 3D Fractured Rock Mass by Unified Pipe-Network Method. Water 2018, 10, 1122. https://doi.org/10.3390/w10091122
Sun Z, Yan X, Liu R, Xu Z, Li S, Zhang Y. Transient Analysis of Grout Penetration With Time-Dependent Viscosity Inside 3D Fractured Rock Mass by Unified Pipe-Network Method. Water. 2018; 10(9):1122. https://doi.org/10.3390/w10091122
Chicago/Turabian StyleSun, Zizheng, Xiao Yan, Rentai Liu, Zhenhao Xu, Shucai Li, and Yiming Zhang. 2018. "Transient Analysis of Grout Penetration With Time-Dependent Viscosity Inside 3D Fractured Rock Mass by Unified Pipe-Network Method" Water 10, no. 9: 1122. https://doi.org/10.3390/w10091122
APA StyleSun, Z., Yan, X., Liu, R., Xu, Z., Li, S., & Zhang, Y. (2018). Transient Analysis of Grout Penetration With Time-Dependent Viscosity Inside 3D Fractured Rock Mass by Unified Pipe-Network Method. Water, 10(9), 1122. https://doi.org/10.3390/w10091122






