Variations of the Snow Water Equivalent in the Ourika Catchment (Morocco) over 2000–2018 Using Downscaled MERRA-2 Data

Abstract

The Ourika River is an important tributary of the Tensift River in the water-stressed region of Marrakesh (Morocco). The Ourika river flow is dominated by the snow melt contribution from the High Atlas mountains. Despite its importance in terms of water resources, the snow water equivalent (SWE) is poorly monitored in the Ourika catchment. Here, we used MERRA-2 data to run a distributed energy-balance snowpack model (SnowModel) over 2000–2018. MERRA-2 data were downscaled to 250-m spatial resolution using a digital elevation model. The model outputs were compared to in situ measurements of snow depth, precipitation, river flow and remote sensing observations of the snow cover area from MODIS. The results indicate that the model provides an overall acceptable representation of the snow cover dynamics given the coarse resolution of the MERRA-2 forcing. Then, we used the model output to analyze the spatio-temporal variations of the SWE in the Ourika catchment for the first time. We suggest that MERRA-2 data, which are routinely available with a delay of a few weeks, can provide valuable information to monitor the snow resource in high mountain areas without in situ measurements.

1. Introduction

The snowpack is an important resource in many semi-arid and Mediterranean catchments, mostly because it provides meltwater runoff for irrigation during the crop growing season. Snow melt is also important to replenish reservoirs before the dry summer season and contributes to the natural recharge of the groundwater in the lowlands [1,2].

The Tensift basin is a major basin in Morocco covering 20,450 km${}^2$ around the city of Marrakesh from the High Atlas mountains to the Atlantic coast. In this semi-arid region of Morocco, the precipitations are scarce, while the evaporative demand is high [3]. In the center of the basin, the Haouz plain (6000 km${}^2$) is extensively cultivated, and many farmers rely on irrigation to grow their crops. In Marrakesh, where the urban population is approximately one million inhabitants and rapidly growing (+2.5% per year) [4], the mean annual precipitation is only 250 mm and is concentrated between November and April [3]. By contrast, due to the orographic enhancement of the precipitation, the mean annual precipitation measured at Oukaimeden-club alpin francais (CAF) (2650 m.a.s.l.) in the High Atlas region of the Tensift basin ranged between 300 mm and 900 mm over 1989–2007 [5]. This precipitation pattern drives the hydrology of the Tensift basin: most of the streamflow in the Tensift River originates from five main tributaries, which have their headwaters in the northern slope of the High Atlas mountains [6]. These tributaries are (from east to west) the N’fis, Rheraya, Ourika, Zat and R’dat rivers (

Table 1. Characteristics of the five main tributaries of the Tensift River in the High Atlas. $z_0$: elevation of the river gauge station; $\overline{z}$: mean elevation of the catchment; Q: mean annual discharge; $Q_S$: mean annual specific discharge; $F_S$: mean annual fraction of snow melt in the discharge. The discharges are reported for the period 1970–2003 [8]. The fraction of snow melt was computed over 2002–2005 [6].

Catchment	Area (km${}^2$)	${\mathit{z}}_0$ (m)	$\overline{\mathit{z}}$ (m)	Q (Mm${}^3$)	${\mathit{Q}}_{\mathit{S}}$ (mm)	${\mathit{F}}_{\mathit{S}}$
N’fis (at Lalla Takerkoust)	1288	750	2069	175	136	19
R’dat (at Sidi Rahal)	557	645	2091	72	129	7
Zat (at Tafriat)	540	720	2293	104	193	22
Ourika (at Aghbalou)	507	974	2438	156	308	41
Rheraya (at Tahanaout)	225	1036	2577	48	213	36

, Figure 1). The estimated contribution of snow melt to streamflow in these catchments over the period 2002–2005 ranged between 2% for the R’dat catchment in 2004 to 51% in 2003 for the Ourika catchment [6]. Previous studies about the hydrological processes in the High Atlas have focused on the Rheraya catchment because this catchment was selected as a pilot site in the SUDMED program and Laboratoire Mixte Internationale de Télédétection et Ressources en Eau en Méditerranée semi-Aride (LMI-TREMA) [3]. These studies highlighted the importance of snow melt to the hydrological regime of the Rheraya River [6,7] and the large interannual variability of the snow accumulation over the last few decades [5]. In contrast, the snow regime in the Ourika catchment is largely undocumented, although this catchment arguably has a greater importance in terms of water resources due to its larger size. In addition, discharge measurements indicate that the Ourika catchment has the highest mean specific discharge among these five catchments (Table 1), which highlights its significance as a runoff production area.

Previous studies have analyzed the interannual variability of the snow cover area (SCA) in the Ourika catchment (among other catchments) using MODIS data [9], but the SCA is not a direct indicator of the water resources that are brought by the snowpack. The main variables of interest for water managers are the snow water equivalent (SWE) and snow melt.

There are different approaches to simulate SWE and snow melt in mountain catchments. Degree-day models are practical to implement since they require only the daily precipitation and temperature data [10]. On the other hand, physically-based distributed snowpack models solve the snowpack energy balance equation [11]. They offer a more realistic representation of the snow cover evolution especially in Mediterranean semi-arid areas where the solar radiation is a key forcing of the snowpack energy budget, and the sublimation can represent a significant part of the ablation [2,12,13]. Unlike degree-day models, energy balance models do not require the calibration of the model parameters, but they require more meteorological forcing data (precipitation, air temperature, air humidity, solar shortwave radiation, atmospheric longwave radiation, wind speed, air pressure). In many mountain regions like the High Atlas, these measurements are generally not available, and there is no direct way to measure the SWE in mountains by satellite remote sensing to this date [14]; therefore, a solution is to use atmospheric model outputs as forcing to run a snowpack model [15,16,17]. In particular, climate model reanalysis like NASA modern-era retrospective analysis for research and applications data (MERRA-2) provides an optimal reconstruction of the meteorological variables at the global scale by assimilation of available in situ and satellite observations into a climate model. Previous studies showed that MERRA-2 can provide a realistic representation of the precipitation for snow and hydrological studies [18]. In Africa, the MERRA-2 precipitation correction algorithm uses a specific configuration, which has been introduced to improve deficiencies in MERRA-Land [19]. This configuration has improved the simulation of the terrestrial water storage in Africa at coarse resolution as observed by GRACE, but MERRA-2 skills were not specifically evaluated in North Africa [18].

The objective of this study is to evaluate the combination of MERRA-2 data with a distributed snowpack model to simulate and analyze the spatio-temporal variability of the snow water equivalent (SWE) in the Ourika catchment from 1 November 2000–1 April 2018. The study period (2000–2018) was chosen because it corresponds to the observation period of the MODIS sensor, which we use as validation data to evaluate our SWE simulation.

We use SnowModel [20], a distributed energy-balance model to simulate the snowpack evolution. A key asset of SnowModel is its MicroMet (meteorological data interpolation) subroutine, which spatially interpolates the meteorological forcing over the domain using the digital elevation model. In addition, SnowModel accounts for the effect of the terrain slope and aspect on the incoming solar radiation, which can be significant in this semi-arid mountainous region. The MERRA-2 forcing was downscaled to 250-m using a digital elevation model to account for the effect of the topography on the temperature, humidity, wind, precipitation and solar radiation [16].

Finally, we take advantage of the availability of the MERRA-2 forcing in near real time until April 2018 to analyze the snow condition during the winter 2017–2018. According to a local newspaper, this winter was characterized by heavy snowfall events in the High Atlas above 1000 m in the middle of January and the beginning of February [21]. A rare snowfall event in the lower elevation areas also made the headlines in various media outlets [22].

2. Data and Method

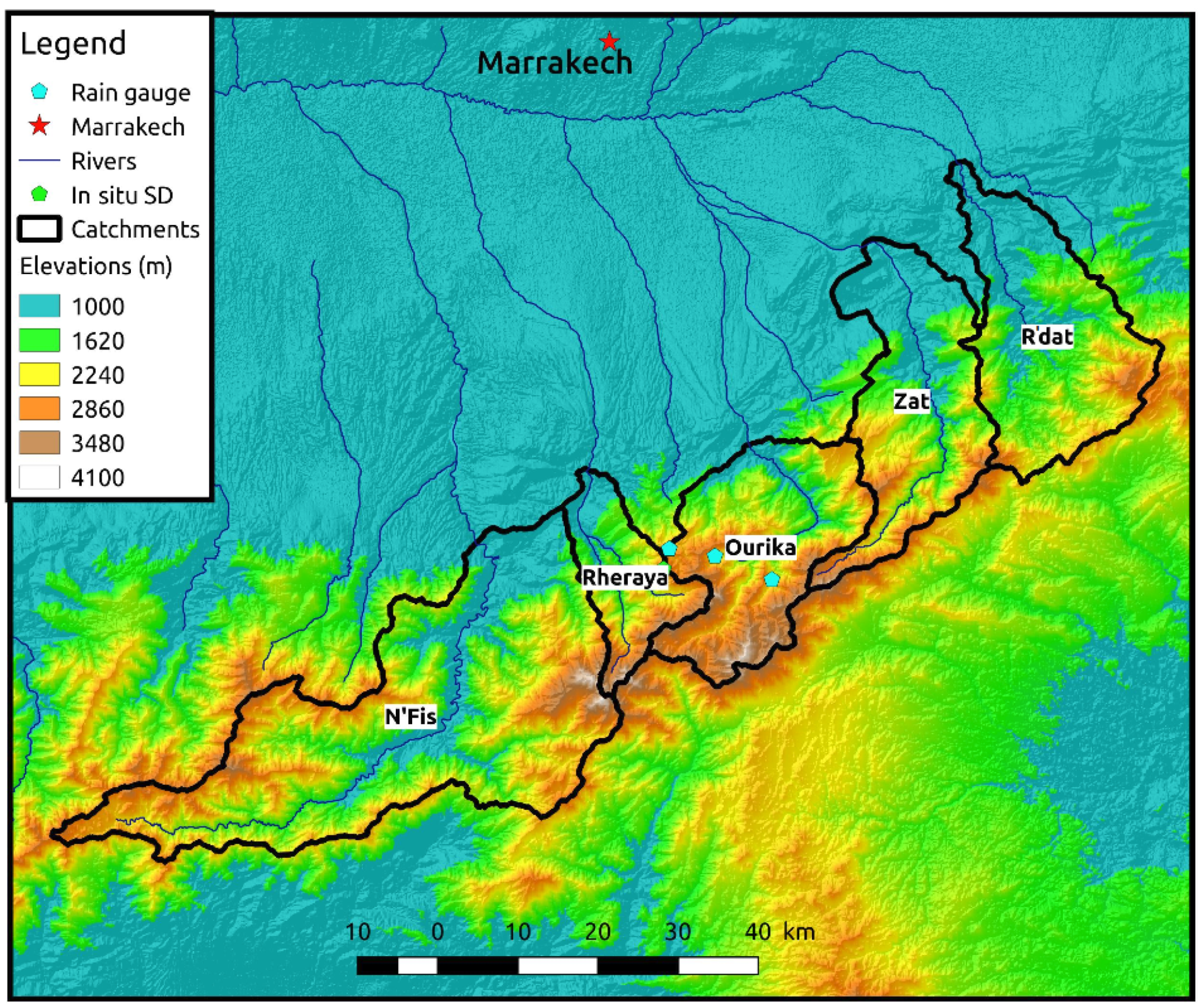
2.1. Study Area

The simulation domain covers the Ourika catchment at Aghbalou (982 m). The catchment is centered at 31°10 N, 7°40 W between the semi-arid Haouz plain and the northern slope of the High Atlas (Figure 1).

The Ourika river provides water resources to the rural communities living in the valleys of the High-Atlas (e.g., Setti-Fatma, Ourika). Meltwater is used to irrigate croplands and gardens (e.g., Paradise of saffron, Ourika Organic Aromatic Garden) and feeds many irrigation systems in the High-Atlas foothills and the Haouz plain until its confluence with the Tensift River near Marrakech.

The catchment elevation ranges between 974 m and 4001 m.a.s.l. (Jebel n’Tarourt). The fraction of the catchment area above 3000 m.a.s.l. is 25%. Winter precipitation mainly falls as snow in these high-elevation areas, but snow is also present above 2000 m more intermittently [9].

The catchment is sparsely vegetated, except for the valleys’ bottoms. The catchment geology favors the rapid runoff of snow melt and rainfall since two thirds of the catchment are occupied by Precambrian magmatic rocks characterized by a low infiltration rate [23].

The Ourika River regime at Aghbalou is dominated by the snow melt contribution with a maximum discharge in April (Figure 2). On average, 60% of the annual discharge occurs between March and May [8] (Figure 2). However, the hydrological regime is also influenced by the high annual variability in the snowfall amount and melt-out date [6,9,24].

2.2. Data

2.2.1. Meteorological Data

Despite the importance of the snow cover and its high interannual variability, there is only one automatic snow depth record at the western edge of the catchment at Oukaimeden (3200 m.a.s.l.) nearly on the water divide with the Rheraya catchment (Figure 1). The snow depth was measured by using an acoustic sensor every half-hour and aggregated to the daily time step for this study. There are many gaps in the measurements, but they still enable one to evaluate the model. The available data cover six snow seasons (2004–2005, 2005–2006, 2008–2009, 2010–2011, 2013–2014 and 2014–2015).

The meteorological forcings to run SnowModel were derived from the Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), available at 0.5° × 0.625° of spatial resolution. Each new month of MERRA-2 reanalysis is available approximately between the 15th and the 20th of the next month. The extracted variable are listed in

Table 2. MERRA-2 variables used in this study.

Variable Name	Description	Unit
PHIS	Geopotential height	m${}^2$/s${}^2$
LON	Longitude	°
LAT	Latitude	°
T2M	Temperature at 2 m	K
QV2M	2-m specific humidity	kg·kg${}^{-1}$
U2M	2-m eastward wind	m·s${}^{-1}$
V2M	2-m northward wind	m·s${}^{-1}$
PRECTOTCORR	Precipitation rate	kg·m${}^{-2}$·s${}^{-1}$

. Each MERRA-2 pixel is characterized by its latitude and longitude and surface geopotential height (named as PHIS in the data file), which were converted to (x, y, z) coordinates in the WGS-84 UTM-29N projection system (see Section 2.3).

2.2.2. DEM

A digital elevation model (DEM) is required to downscale the meteorological forcings and run the energy balance model (Section 2.3). Here, we used the Shuttle Radar Topography Mission Void Filled (SRTM-Void Filled Version 4.1) [25]. It was resampled with the bicubic method to 250-m spatial resolution to limit the computational cost of the simulation. This resolution was found to be a good trade-off between the computational cost and the accuracy of the simulation, because it allows capturing the main snow cover heterogeneities caused by the different radiative energy at the hillslope scale [26].

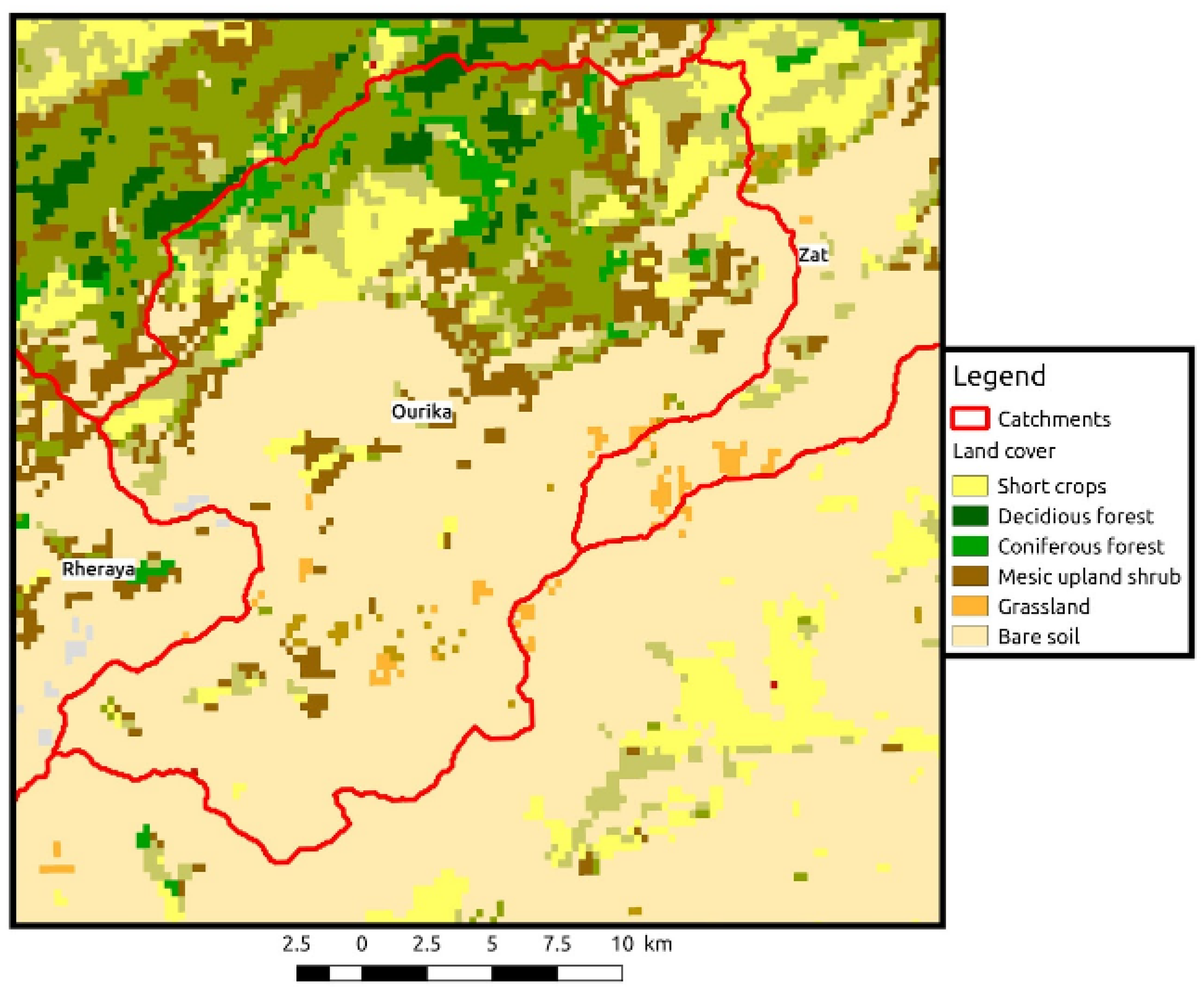
2.2.3. Land Cover

The catchment land cover was obtained from the European Space Agency Climate Change Initiative (ESA-CCI) classification map (Figure 3) [27]. The majority of the region (especially the high elevated areas) is classified as bare soil.

2.2.4. Snow Cover Area

We used 18 years of daily MODIS data at a 500-m spatial resolution to validate the simulation. These data provide the snow cover fraction (SCF) within each MODIS pixel. The cloud pixels were interpolated using the algorithm of Marchane et al. [9], which was specifically developed for the High Atlas. The accuracy of the algorithm was evaluated by comparison to snow depth measurements and a high-resolution snow mask derived from the Formosat-2 observations over the Rheraya catchment. The results showed that the algorithm allowed a reduction of the cloud coverage to less than 1% with an overall accuracy of 89% [9]. The MODIS data were produced from the Collection 5 MOD10A1 snow product. However, Collection 5 has been discontinued since 1 January 2017; therefore, the entire time series was reprocessed using Collection 6 MOD10A1. Since Collection 6 no longer provides the SCF, and only the normalized difference snow index (NDSI) of snow-covered pixels, we applied the same NDSI-SCF relationship that was used in collection 5 [9,28]:

$$\mathrm{SCF}=-0.01+1.45\times \mathrm{NDSI}$$

(1)

Then, we applied the cloud-removal algorithm to generate a continuous time series of the SCF from 1 September 2000–1 April 2018 in our study area, which is fully consistent with the data presented by [9].

2.2.5. Ourika River Discharge

We used monthly river discharge data at the Aghbalou River gauge (982 m, Figure 2) from the Tensift basin agency from 2000–2017 during the melt season (January–May). The daily discharge data were only available for seven years in this period. We used the daily data to compute the average discharge over a 10-day time step during the melt season.

2.2.6. In Situ Precipitation Gauge

We used daily precipitation measurements from three automatic weather stations (AWS) in the Ourika catchment (Figure 1) (Oukaimeden-CAF 2612 m.a.s.l., Agouns 2381 m.a.s.l. and Amenzal 2374 m.a.s.l.). These data are available from 2000–2009.

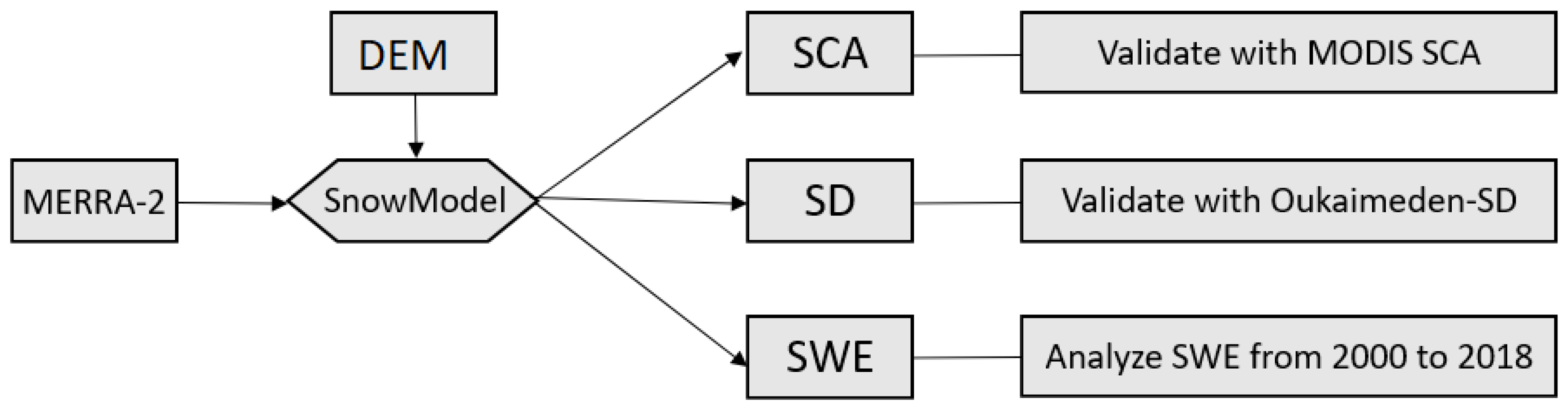
2.3. Methodology

2.3.1. Snow Energy and Mass Balance Model

To simulate the SWE, the melt and the discharge in the Ourika catchment, we fed SnowModel, a distributed energy balance snowpack evolution model [20], with MERRA-2 reanalysis. The SnowModel has previously been tested with success in the Arctic, Antarctic and high mountain regions, comparing simulated snow accumulation, distribution and ablation processes with observations [29,30,31,32,33,34,35,36,37,38]. SnowModel is composed of four sub-models: MicroMet (meteorological data interpolation), EnBal (energy balance computations) [20], SnowPack (snow depth evolution) and SnowTran-3D (wind transport) [39]. Given the lack of in situ meteorological observations, SnowTran-3D was not activated. We set all the SnowModel parameters to default values because we have a limited observations’ dataset in the study area. By using only default parameters, we can evaluate the accuracy of the model if it should be transposed to other catchments in the High Atlas without calibration.

MicroMet is the key interface between the MERRA-2 data and the snowpack model, since it enables distributing all meteorological data that are required to run the EnBal and SnowPack sub-models over the study area at the resolution of the DEM. These variables are precipitation, air temperature, relative humidity, wind speed, incoming solar radiation and incoming longwave radiation at the hourly time step. MicroMet was originally designed to interpolate station data onto a regular grid, but it can also be applied to downscale large-scale, surface-level forcing from climate model or reanalysis such as MERRA-2 [16]. In this case, each MERRA-2 grid cell intersecting the study domain is considered as a virtual station, which is located at the center of the cell.

To distribute the meteorological data from (virtual) station data, MicroMet performs a horizontal interpolation using the Barnes objective analysis scheme, which applies a Gaussian distance-dependent weighting function to interpolate the station data to the model grid resolution. Topography-dependent functions are applied to account for the effect of elevation, slope and aspect on the gridded meteorological forcing. In the case of air temperature, a linear lapse rate correction is used:

$$T_x=T_{stn}-\tau (Z_x-Z_{stn}),$$

(2)

where $T_{stn}$ (°C) is the air temperature at elevation $Z_{stn}$ (m), $T_x$ (°C) refers to the temperature at a given elevation $Z_x$ (m) and $\tau$ is default monthly lapse rate (°C·m${}^{-1}$) [40]. A non-linear function is used for the precipitation:

$$P_x=P_0\times \frac{[1+\chi (Z_x-Z_0)]}{[1-\chi (Z_x-Z_0)]},$$

(3)

where $P_x$ (mm) is the precipitation at $Z_x$, $P_0$ (mm) is the interpolated precipitation, $Z_0$ (m) is the interpolated station elevation and $\chi$ (km${}^{-1}$) is the monthly precipitation correction factor, which we set to default values [40]. The distributed relative humidity is derived from similar rules, while the distributed wind speed is generated by accounting for the deflection of the wind field by the terrain. The longwave and shortwave radiations are interpolated using the Barnes scheme, but the shortwave radiation is modified according to the slope and orientation. For further details, the reader can refer to [20].

2.3.2. Pre-Processing of MERRA-2 Variables

SnowModel takes as input the coordinates of the stations. However, a pre-processing of MERRA-2 variables was developed to make them compatible to SnowModel input. LON and LAT were projected to X, Y coordinates in the WGS-84 UTM 29N projection system. The elevation of the MERRA-2 grid cell was computed from the geopotential height (m${}^2$/s${}^2$) by dividing it by the Earth’s gravity (m/s${}^2$).

The relative humidity RH was retrieved from QV2M as follows:

$$\mathrm{RH}=\frac{\mathrm{QV}2\mathrm{M}}{0.62e_s\left(T\right)}$$

(4)

where $e_s\left(T\right)$ is the water vapor saturation pressure, which is a function of temperature and approximated by the Magnus–Tetens formula $e_s\left(T\right)=0.61exp\left(\frac{17.625T}{T+243.04}\right)$.

Eastward (u) and northward (v) wind components were converted to wind speed (WS) and wind direction (WD) using:

$$\mathrm{WS}=\sqrt[]{u^2+v^2}$$

(5)

$$\mathrm{WD}=\arctan (v/u)$$

(6)

2.3.3. Model Evaluation

The validation of the model outputs is challenging due to the lack of SWE measurements in Morocco and the difficulty of getting them otherwise (e.g., the cost of light detection and ranging (LIDAR) campaigns [41,42] is very high, and the use of unmanned aerial vehicles (UAV) to estimate the snow depth [43] is limited by its spatial coverage, on the one hand, and the complicated legal procedure to use it in Morocco, on the other). To deal with this, we have combined different hydrometeorological datasets and remote sensing observations. The simulated snow depth (SD) was extracted at the Oukaimeden station (3200 m.a.s.l.) to assess the model performance using the root mean square error (RMSE). We also evaluate the cumulative precipitation over the snow season (from 1 December–1 April from 2000–2009 by using in situ precipitation). The model was further evaluated at the catchment scale using the daily snow cover area of the Ourika catchment (SCA) from MODIS data (Figure 4). The simulated SCA was computed from the simulated SWE by computing, for every day of the simulation period, the number of grid cells where the simulated SWE exceeded a fixed threshold of 20 mm [44]. Then, the snow covered area of the catchment was computed and compared to the MODIS data using the coefficient of determination ($R^2$) for each hydrological year from 1 September–31 May. We excluded the period from 1 June–31 August, because the snow is absent during these months, which could artificially increase the $R^2$. We verified that varying an SWE-SCA threshold between 20 mm–50 mm did not significantly change the results. We also used the Ourika discharge to evaluate the simulated runoff. SnowModel does not have a soil reservoir and only computes for each grid cell a “runoff”, which is the total liquid water that leaves the snowpack or the rainfall if there is no snow cover. The liquid water in the snowpack comes from the snow melt or the rain-on-snow. It is released when the liquid water content exceeds the snowpack maximum storage capacity. Given the lack of hydrological routing in the model, we compared the modeled runoff with the observed discharge using monthly averages only.

3. Results

3.1. Validation

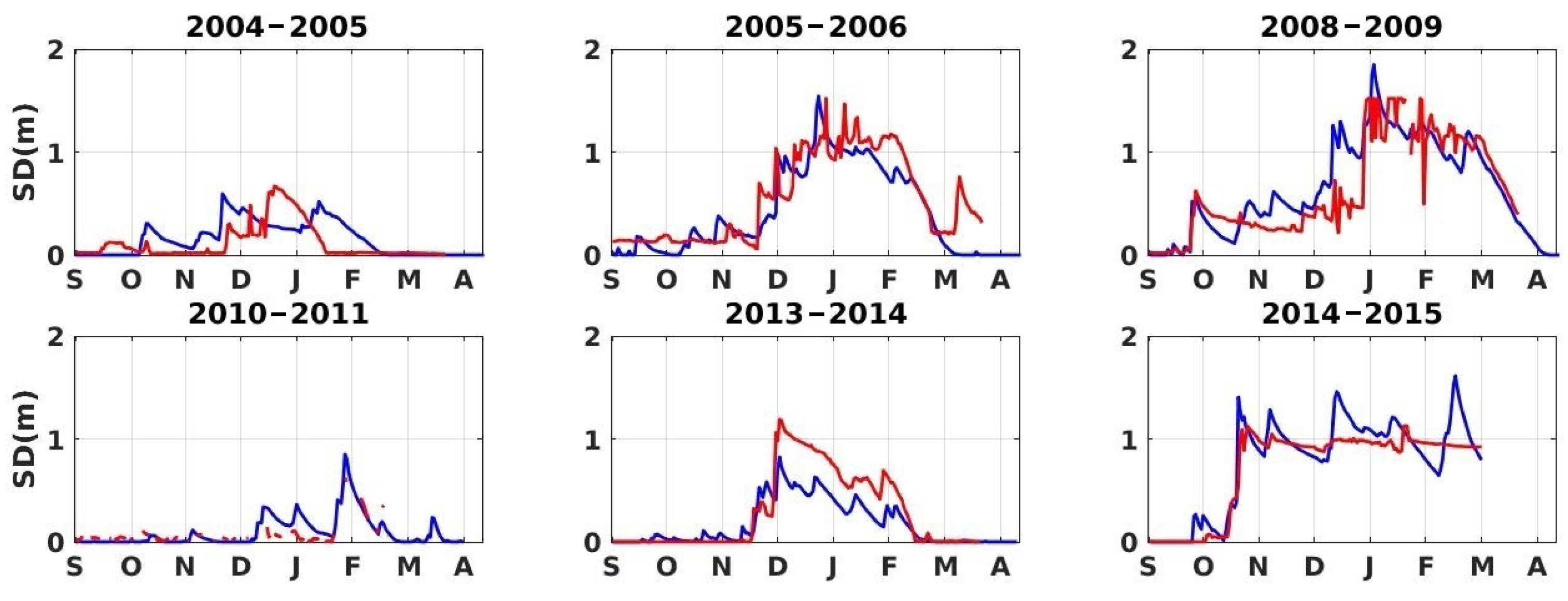
3.1.1. Snow Depth at Oukaimeden

In general, the model simulated reasonably well the snow depth at Oukaimeden station (Figure 5). The model failed to properly simulate the evolution of the snow depth in 2004–2005 because of inconsistent precipitation events. The accumulation was underestimated in 2013–2014, but otherwise, there is no clear tendency to overestimate or underestimate the snow depth at this point (

Table 3. RMSE, bias and correlation between simulated and observed snow depth at Oukaimeden (m).

Year	2004–2005	2005–2006	2008–2009	2010–2011	2013–2014	2014–2015
RMSE	0.21	0.19	0.22	0.15	0.33	0.17
Bias	0.06	−0.07	0.08	0.03	−0.11	0.01
$R^2$	0.37	0.88	0.82	0.49	0.66	0.92

). The melting rates were correctly reproduced in 2005–2006 and 2008–2009.

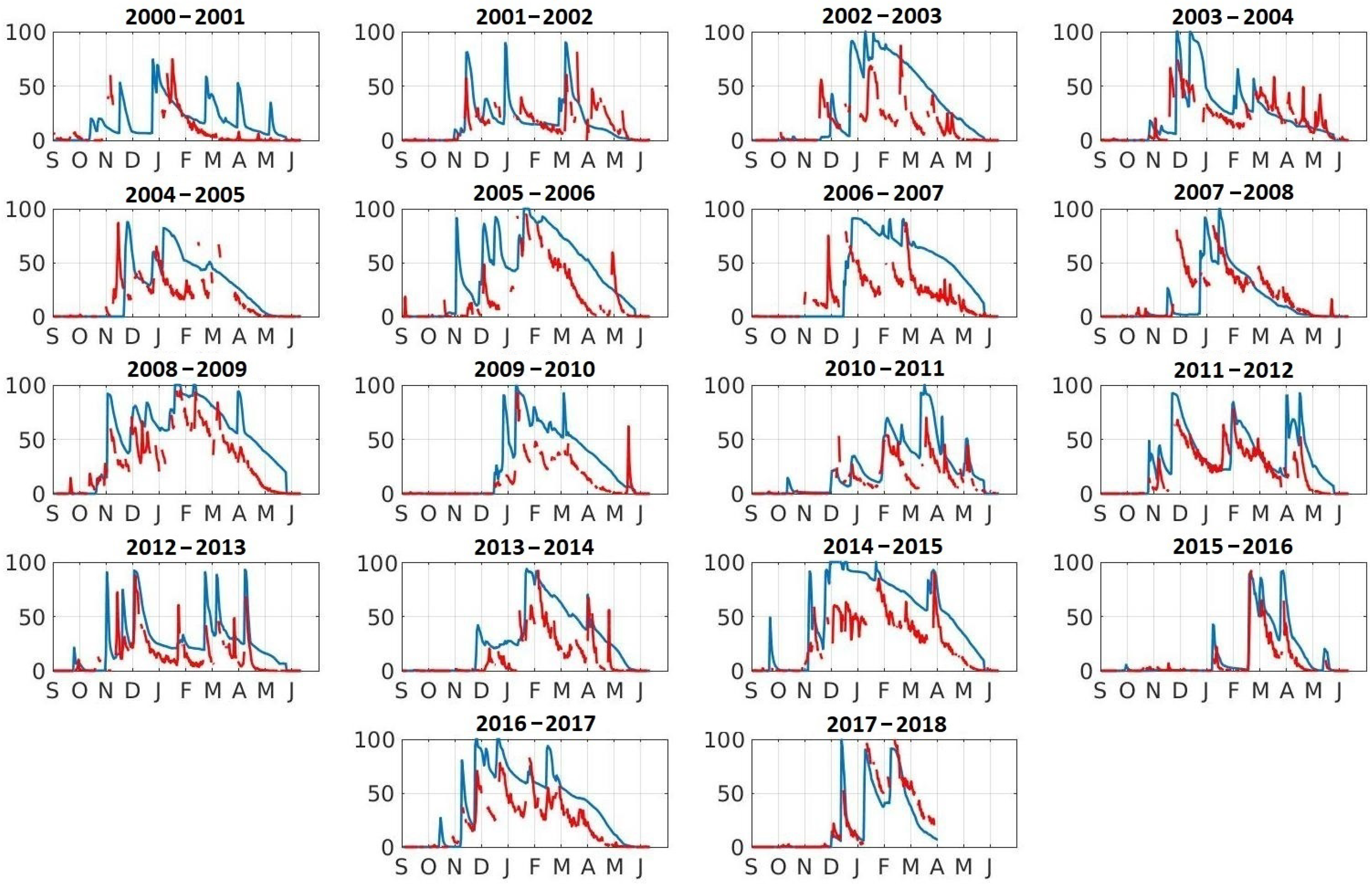
3.1.2. Snow Cover Area

The comparison with MODIS data shows that the model was able to produce a reasonable simulation of the snow cover area in the catchment (Figure 6). We found a $R^2$ greater than 0.70 for the majority of the hydrological years (

Table 4. $R^2$ between the simulated and observed snow cover area (SCA) and discharge (Q) in the Ourika catchment for every hydrological year of the study period. The $R^2$ was computed at the daily time step from 1 September–31 May for SCA and at the monthly time step from January–May for Q (NA: no measurements available for this year).

Years	2000–2001	2001–2002	2002–2003	2003–2004	2004–2005	2005–2006	2006–2007	2007–2008	2008–2009
SCA	0.32	0.52	0.68	0.62	0.57	0.71	0.73	0.61	0.89
Q	0.32	0.02	0.81	0.48	0.48	0.68	0.71	0.62	0.85
Years	2009–2010	2010–2011	2011–2012	2012–2013	2013–2014	2014–2015	2015–2016	2016–2017	2017–2018
SCA	0.87	0.87	0.81	0.80	0.77	0.90	0.88	0.90	0.73
Q	0.25	0.72	0.85	0.16	NA	0.78	0.39	0.01	NA

).

However, the SCA was poorly simulated in 2000–2001, 2002–2003, 2005–2006 and 2006–2007. We note that the model performance tends to increase over the study period. In particular, all $R^2$ are higher than 0.77 between 2009–2010 and 2016–2017. The $R^2$ is slightly lower in 2017–2018 ($R^2$ = 0.73), but the snow season was not completely over at the time of writing this study.

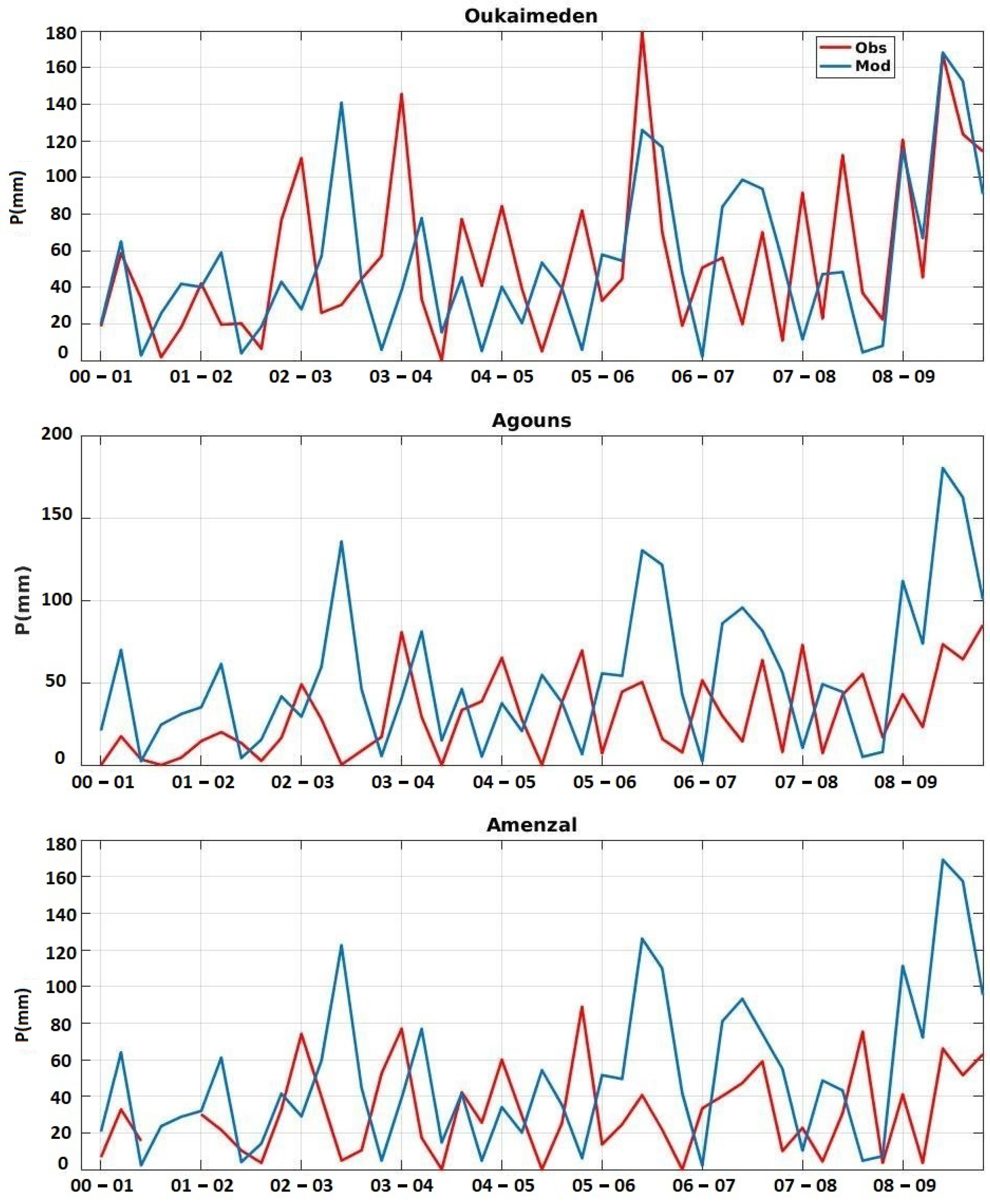
3.1.3. In Situ Precipitation

The simulated precipitation at Oukaimeden-CAF is poorly correlated with the observations ($R^2=0.22$), expect for the most recent months (Figure 7). At Amenzal and Agouns stations, the simulated precipitation does not agree with the observations, and contrary to Oukaimeden-CAF, the model largely overestimates the precipitation in the recent months (Figure 7). The model strongly overestimates the precipitation in 2002–2003 at the three stations. The model simulated a high precipitation total in 2005–2006, which was not recorded at Amenzal and Agouns stations, but it was recorded at Oukaimeden.

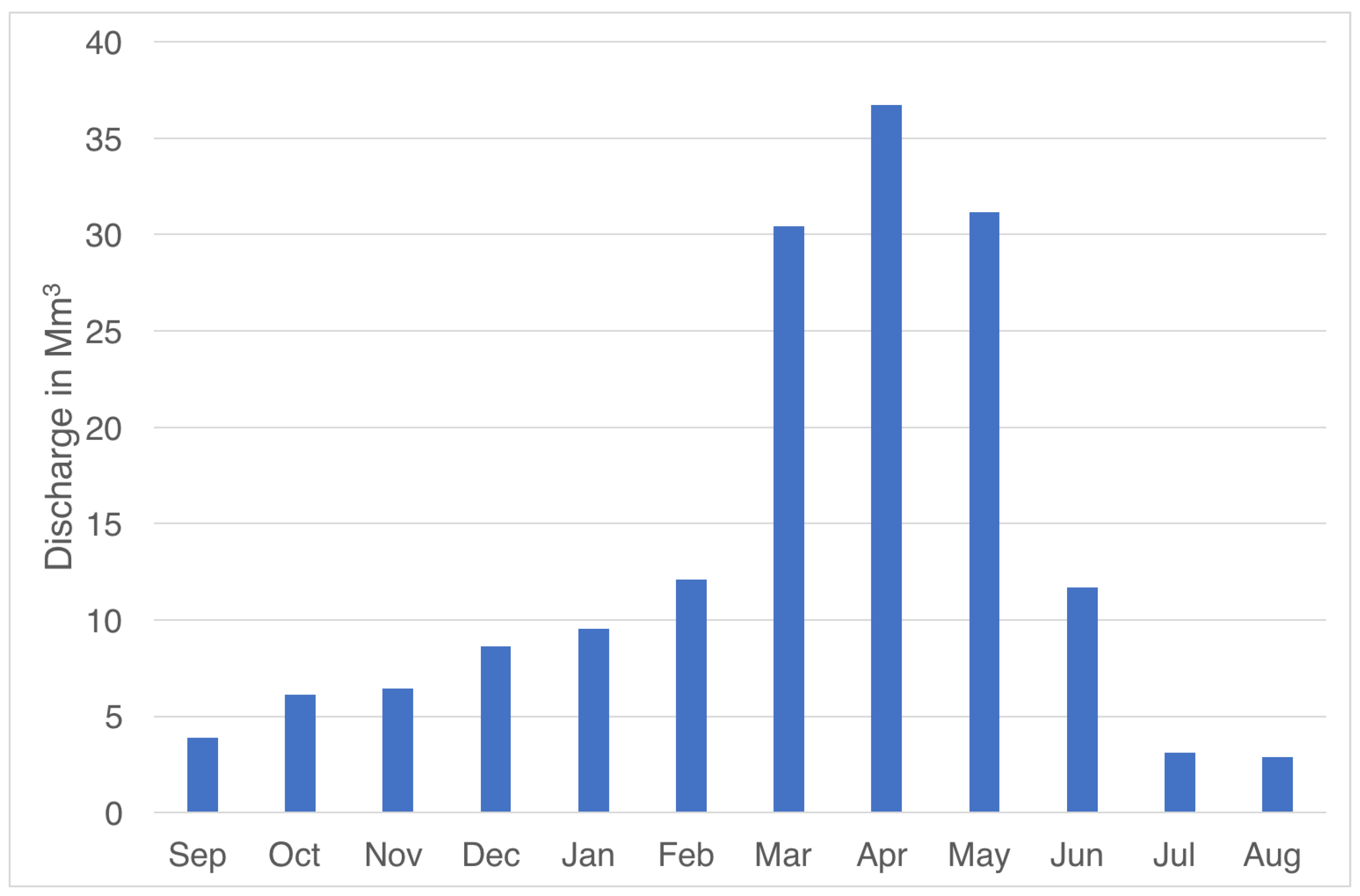
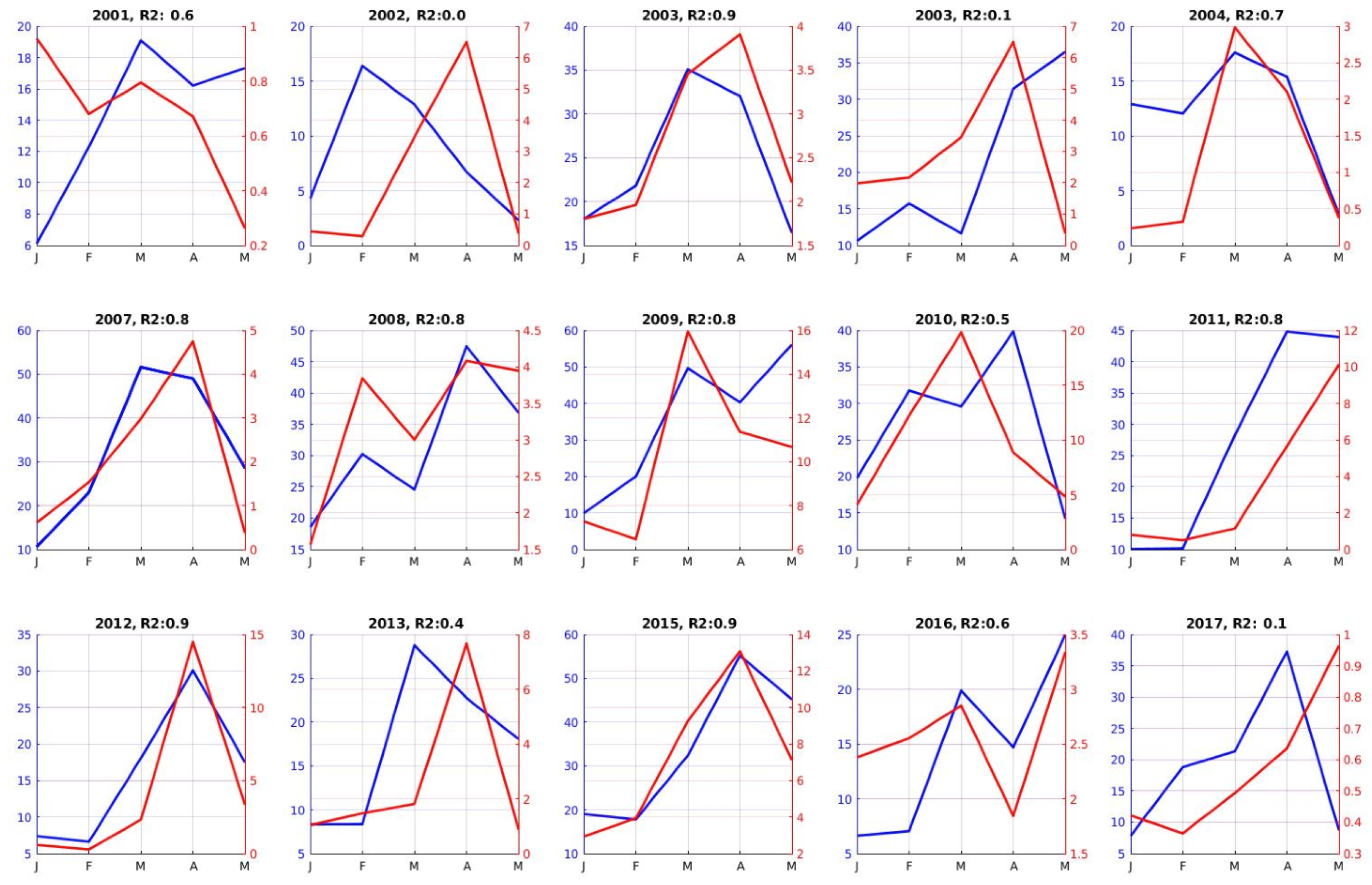
3.1.4. Ourika River Discharge

Figure 8 and Figure 9 show the comparison between the simulated runoff and the observed discharge at the outlet of the Ourika catchment. The mean $R^2$ between the modeled runoff and the observed discharge at the monthly time step from 2000–2017 is 0.55; 10 of 15 years have a $R^2$ value higher than 0.5 (Figure 8). However, there remain large discrepancies between both datasets, in particular the low $R^2$ in 2000–2001, 2001–2002, 2003–2004 and 2004–2005 are consistent with the lower $R^2$, which were obtained for this year for the SCA. However, this is not always the case, as for instance, a low $R^2$ in discharge was obtained in 2012–2013 despite the correct simulation of the SCA for this hydrological year (Figure 6). Figure 9 suggests that at the finer 10-day time step, the model can capture peak discharges; however, the discharge regime is generally poorly represented except in 2012 and 2015.

3.2. Variations of the Simulated SWE

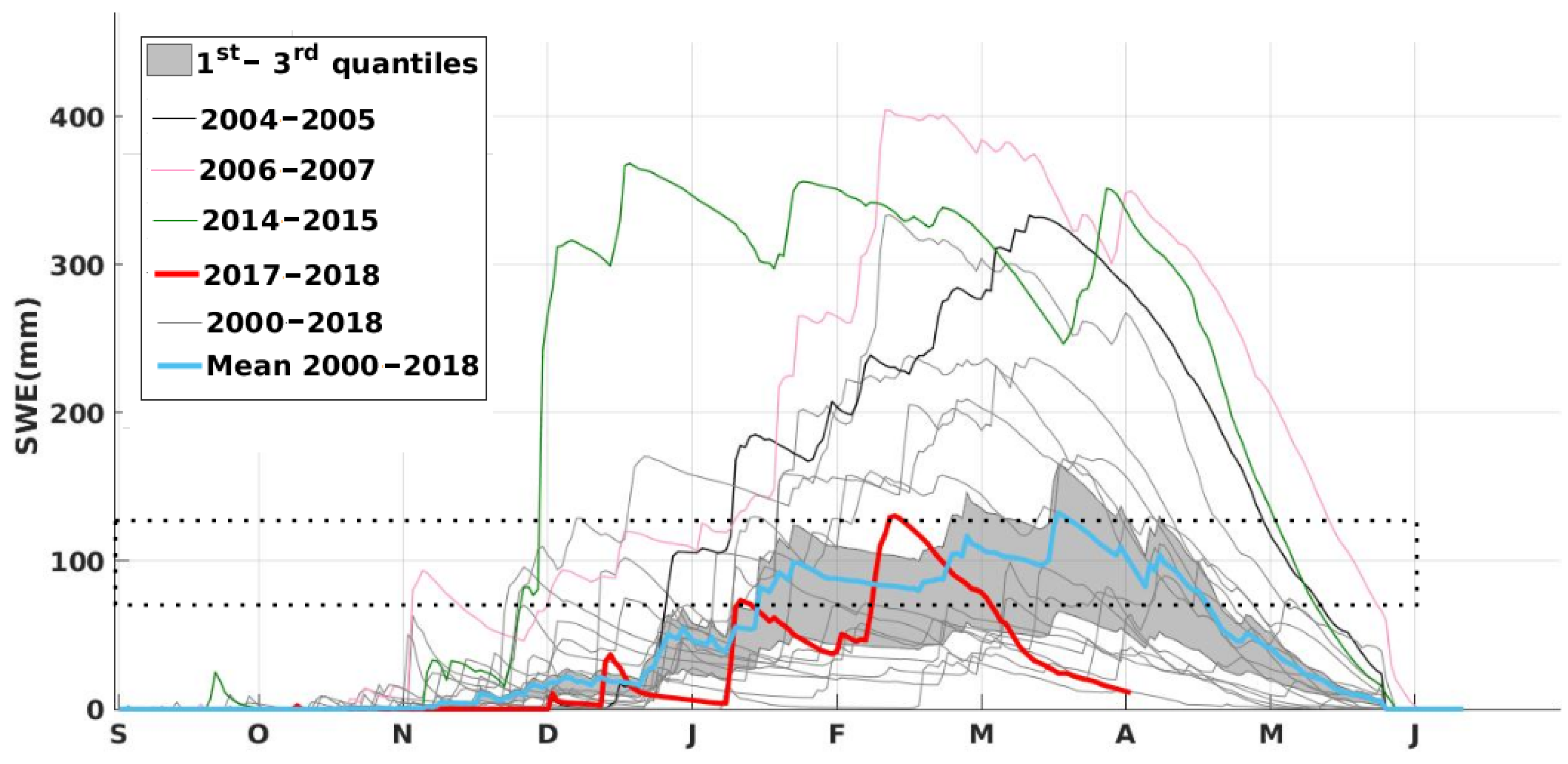
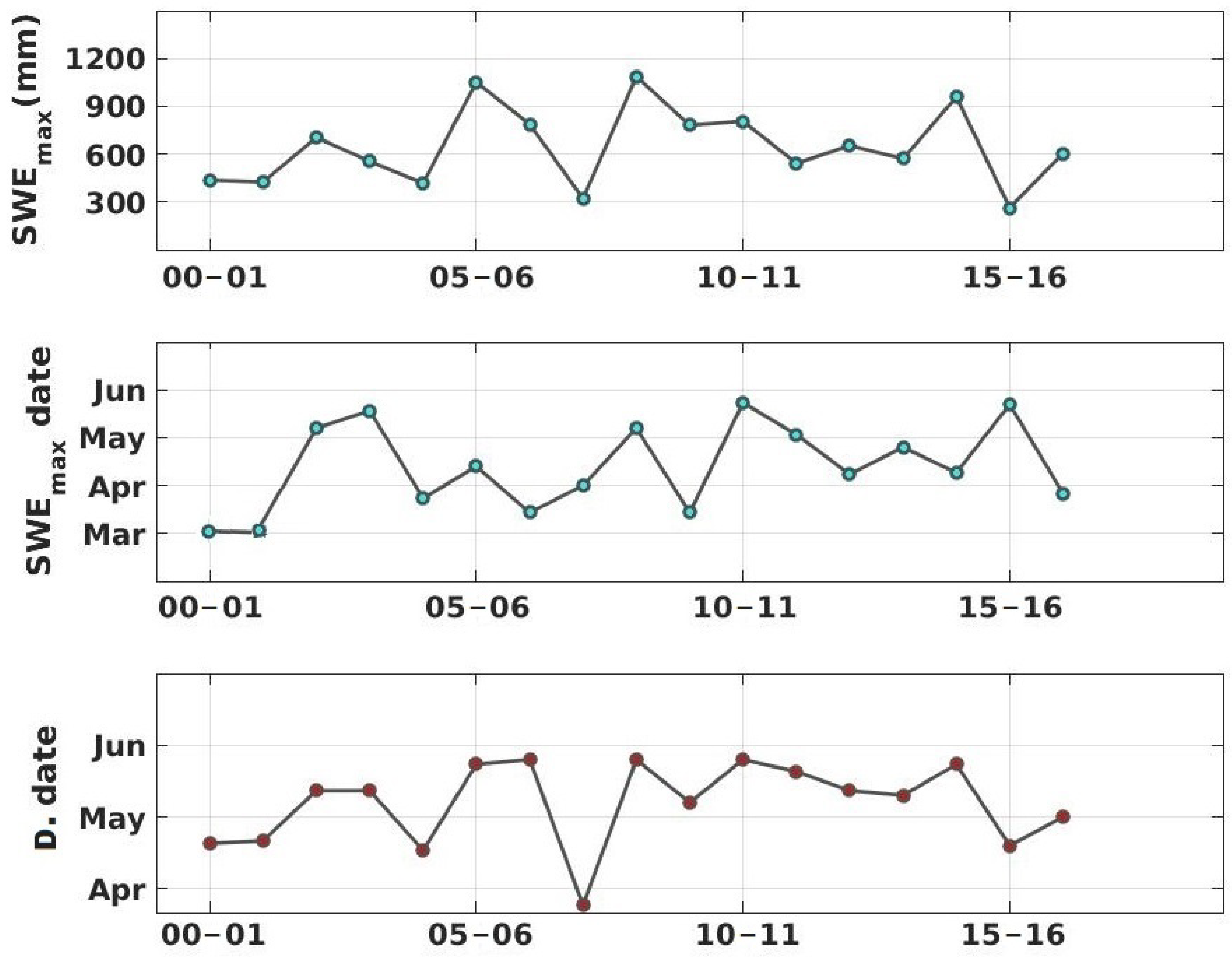
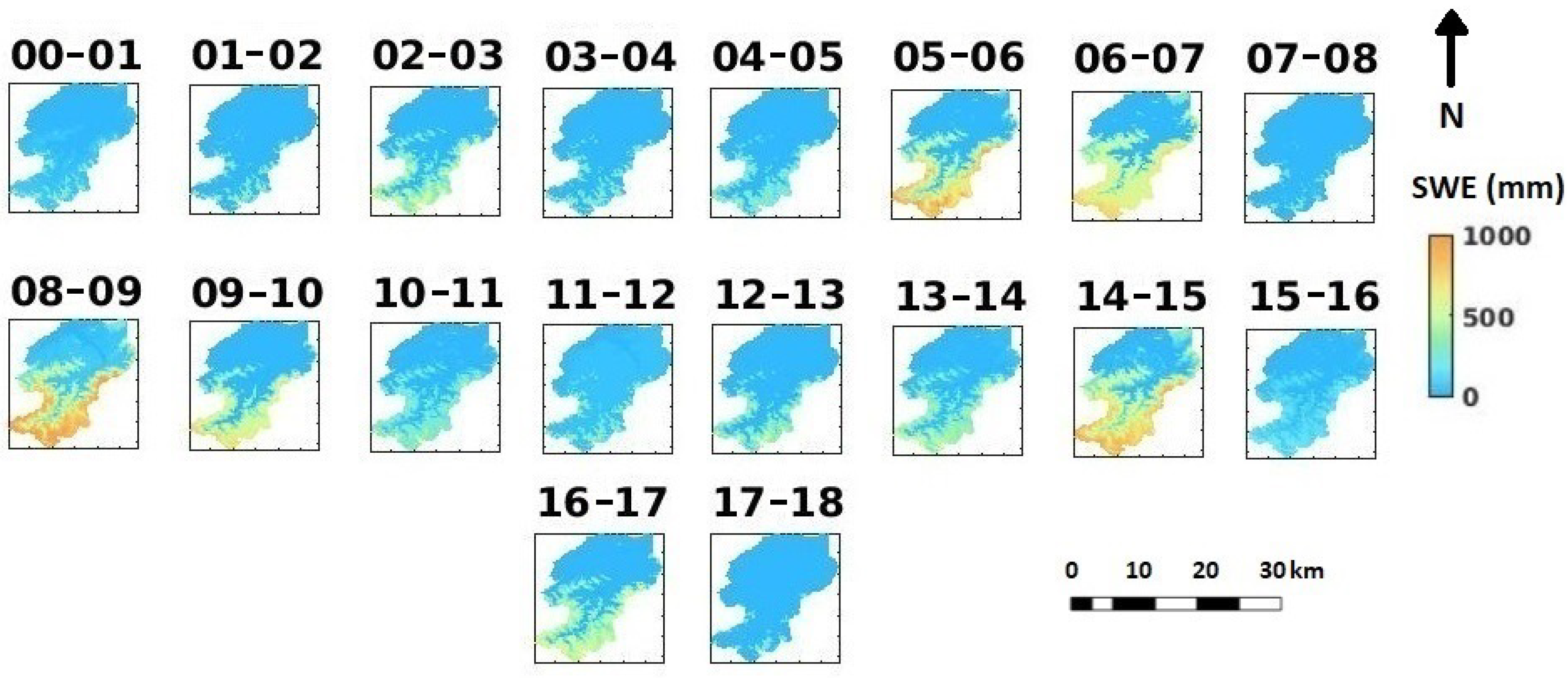
3.2.1. Variations of the Simulated SWE from 2000–2017

The simulated SWE was averaged over the catchment area and is plotted in Figure 10. The catchment SWE typically ranged between 80 and 120 mm we during the winter (Figure 10). However, this range was largely exceeded (e.g., in 2006–2007 and 2014–2015), with values reaching 300 mm and 400 mm. Figure 10 indicates that the melt season generally starts in March since the slopes of the SWE time series are generally negative after March. However, again, there is a large variability.

Indeed, Figure 11 (top panel) indicates that the annual maximum SWE, an indicator of the maximum water reserve in the catchment, varied between 290 mm we and 1100 mm we over the study period. The date of the peak SWE also exhibited a large variability, from early March-mid-May (Figure 11, middle panel). The date of the snowpack snow disappearance date has the same range of variability from mid-March–late May (Figure 11, lower panel). Using the Mann–Kendall test, we did not find any significant trend in these indicators at the 5% confidence level.

In order to visualize the spatial distribution of the simulated SWE within the catchment, we extracted the 1 April SWE for every year (Figure 12). The SWE on 1 April is commonly used as an indicator of the annual SWE before the melt season in the Northern Hemisphere [45]. In contrast with the large temporal variability of the SWE, there is a consistent pattern in the SWE spatial distribution at the scale of the catchment. Again, we did not find any significant trend at the resolution of the grid scale in the 1 April SWE. The model suggests that the SWE can reach 1000 mm we on 1 April in the highest part of the catchment during the wettest years (2005–2006, 2008–2009, 2014–2015). However, the SWE can be almost null in other years (Figure 12).

3.2.2. Variations of the Simulated SWE over the 2017–2018 Snow Season

In the beginning of the 2017–2018 snow season, the simulated SWE in the Ourika catchment was amongst the lowest values since 2000 (Figure 10). However, after the large snowfall events in January and February, the SWE exceeded the mean value of the previous 17 years. Despite this high SWE value in mid-February, the snowpack returned to a record low value on 1 April after one month of intense melt. The SWE was very low even at high elevation on 1 April (Figure 10).

4. Discussion

The evaluations of the simulation at the point-scale and at the catchment scale indicate that the model performs rather well given the coarse resolution of the MERRA-2 input data. The point-scale comparison with the observed snow depth at Oukaimeden gives correct results except for 2004–2005. A single station has a limited spatial representativeness at the scale of the catchment, but it is the only direct measurements of the snow depth in the area and provides a robust reference to evaluate the temporal variations of the simulated snow depth. The model outputs do not agree as well with the precipitations. The simulated precipitations are more consistent with observations at the high elevation station of Oukaimeden than with observations at Agouns and Amenzal stations. We think this is due to the fact that Agouns and Amenzal stations are located in valleys bottoms, while the Oukaimeden-CAF station is located in an open area. This station is probably less influenced by the local scale effects. Local atmospheric effects like orographic precipitation shadows are not resolved by a large-scale atmospheric model such as MERRA-2 and are not represented in MicroMet either, since it relies on a standard precipitation lapse rate to distribute the precipitation [40].

The validation of the simulated gridded precipitation with point-scale precipitation measurements remains challenging because the precipitation gauges are influenced by local wind turbulences, which can cause snow under-catch [46]. MODIS data suggest that the model performances at the catchment scale are better than what could be inferred from the precipitation measurements alone (Figure 6). The simulated runoff is also relatively consistent with the river discharge for the majority of years. This indicates that the mean SWE in the catchment is generally well simulated.

MODIS data enable one to better understand the causes of the model errors during those snow seasons, which exhibit the largest errors in the runoff simulation.

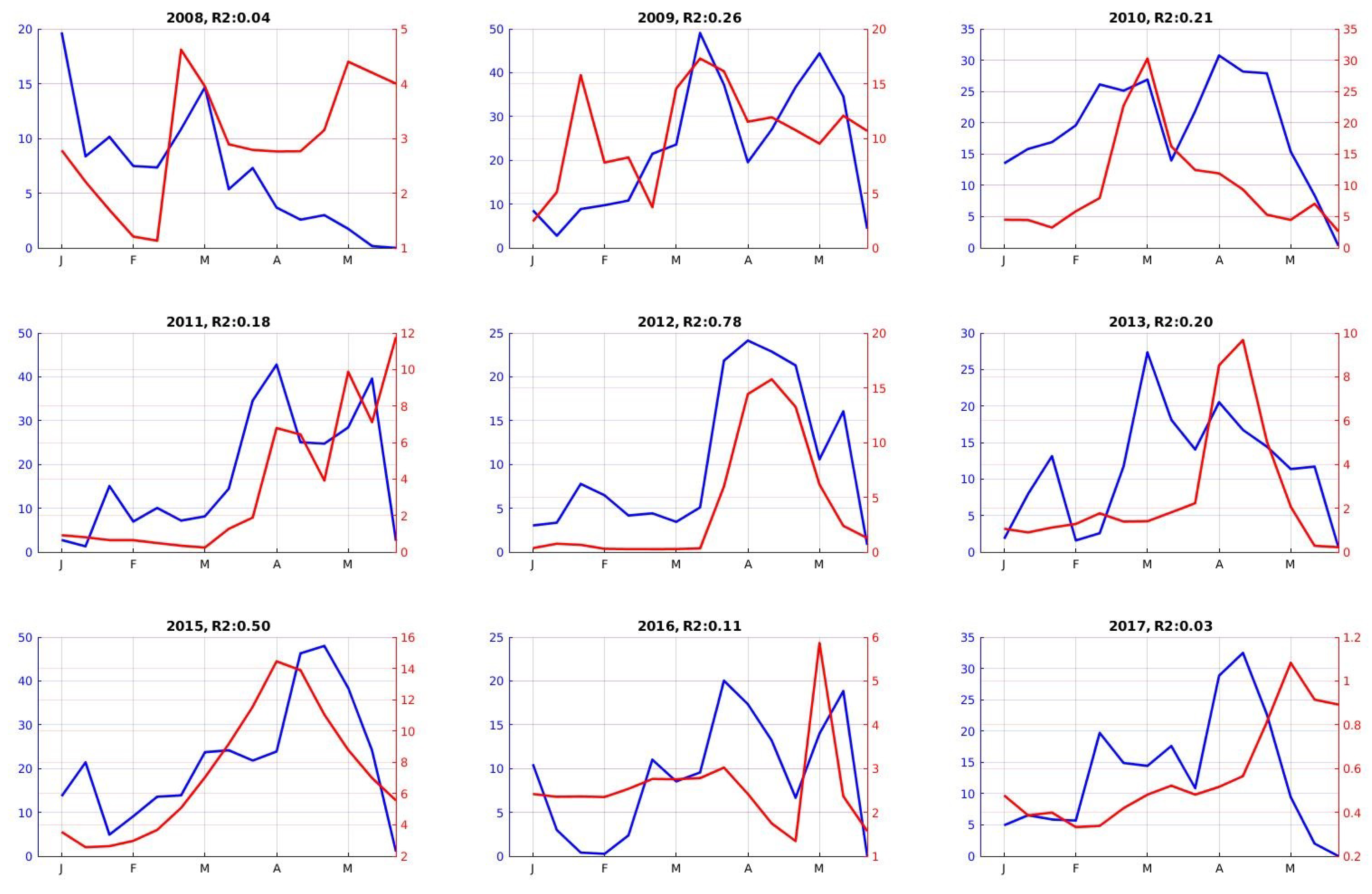
• In 2000–2001, the model produces high runoff values, while the discharge was low. In the same period, large variations in the SCA were simulated, while MODIS data indicate that the SCA was close to zero (Figure 6).
• In 2003–2004, the simulated SCA is well correlated to the MODIS SCA during the melt season, although the model overestimates the runoff from May–April. This suggests that there is an excess of liquid precipitation in the model forcing.
• In 2008–2009, the runoff simulation is completely anti-correlated with the discharge measurements. Given that the snow depth at Oukaimeden and the SCA over the catchment are properly simulated (Figure 5 and Figure 6), we conclude that the simulated rise in runoff in spring is due to erroneous rainfall events in MERRA-2.

We have used the runoff as an indicator of the discharge since the model does not simulate the water routing and storage in the river network, subsurface flow and evaporation. Additional work is needed to account for the hydrological routing of the snow melt and rain runoff within the catchment to explore the model performance more deeply. However, modest performances with a calibrated hydrological model were reported by [7] in the neighboring catchment of the Rheraya River, although the Rheraya catchment is better monitored with several weather stations. The validation of discharge in the High Atlas catchments is difficult, due to the frequent occurrence of flash floods, which modify the river bed and cast doubt on the rating curve accuracy.

The simulation yielded better results over the last decade, which suggests that the MERRA-2 reanalysis was improved over the Ourika region, by incorporating additional measurements in the recent years [47]. This confirms that this SWE simulation is not adapted for trend analysis, since the number of observations in the MERRA-2 assimilation scheme is not guaranteed to be constant. Therefore, we cannot firmly conclude that there is no trend in the snow cover in the Ourika catchment from our analyses. In addition, any trend might be extremely difficult to detect given the large interannual variability of the snow cover in the Ourika catchment.

The model outputs highlight the large interannual variability of the SWE in the Ourika catchment, in agreement with previous studies in the High Atlas [6,9,12,48]. This variability is typical of semi-arid catchments and is much higher than what is observed in other Mediterranean mountains like the Pyrenees [44] or Mount Lebanon [2].

Regarding the snow conditions in 2017–2018, the model indicates that this snow season was characterized by a series of extreme events. The winter started like a snow drought, with a long period without snow accumulation in November and December. The SWE rose drastically in January and February after two major snowfall events, but melted rapidly afterwards (Figure 10). The analysis of the air temperature over the Ourika catchment suggests that November 2017 was the hottest November since 2000, while February 2018 was the third coldest February since 2001. This low temperature in February 2018 explains the exceptional presence of snow in the low elevation areas. The rapid melt thereafter can be explained by a succession of hot days; for instance, in March 2018, the spatially-averaged maximum temperature was 8.5°, while the average for the period 2000–2018 was 8.0° with a standard deviation of 1.2°.

5. Summary and Conclusions

We showed the application of a distributed snowpack model in the snow-dominated Ourika catchment in the High Atlas. We focused on the Ourika catchment because there is a lack of knowledge regarding the snow dynamics in this catchment although snow melt is an essential water resource to sustain irrigation in the semi-arid Haouz plain. To our best knowledge, this study is the first to evaluate and analyze a spatially-distributed simulation of the SWE in the High Atlas mountains for a period covering almost the last two decades.

To cope with the lack of weather station measurements in the High Atlas, we used the MERRA-2 reanalysis and the MicroMet model to generate a distributed meteorological dataset, taking into account the main effects of topography on the meteorological variables. The model outputs were compared to a snow depth record and the time series of the catchment snow cover area from MODIS. The results suggest that the model gave a reasonable estimation of the snowpack evolution over the period 2000–2018, despite the coarse resolution of the MERRA-2 forcing. We have used SnowModel in its default configuration without calibration, which suggests that similar performances could be expected if the model were applied to other ungauged catchments in the High Atlas.

The simulated SWE exhibited a significant interannual variability, both in terms of amplitude (maximum amount of water stored in the snowpack) and duration of the snow season. The model also gave clues about the snow conditions during the hydrological year 2017–2018, which was characterized by different extreme meteorological events.

The model outputs, however, are still subject to large uncertainties. These results should be taken with caution since we could not use direct SWE measurements to validate the model, but only indirect observations of the snow cover dynamics. We suggest to conduct SWE measurement campaigns in the following years to better validate the SWE simulation over the catchment. Further work is required to evaluate the simulated SWE against discharge measurements at finer temporal timescales. The biases in the MERRA-2 forcing could also be reduced by assimilating snow cover maps retrieved from remote sensing data [49,50]. Satellite-derived snow cover maps are usually available with a shorter delay than MERRA-2 (less than a week). Therefore, it should be possible to develop a near-real-time data assimilation scheme to produce more accurate SWE maps. This is the focus of our ongoing work.

Yet, we think that the simple approach shown here could already be useful for water managers. The availability of the MERRA-2 forcing with a short delay (about one month) now enables producing interesting diagnostics regarding the state of the snowpack, over the course of the snow season, without ground measurements. These data could help assess the snow water resource in the Ourika catchment, and in other catchments in the High Atlas, to optimize the planning of the irrigation during the spring.