Horizontal and Vertical Variability of Soil Hydraulic Properties in Roadside Sustainable Drainage Systems (SuDS)—Nature and Implications for Hydrological Performance Evaluation
Abstract
1. Introduction
2. Material and Methods
2.1. Study Sites
2.2. Soil Hydraulic Properties
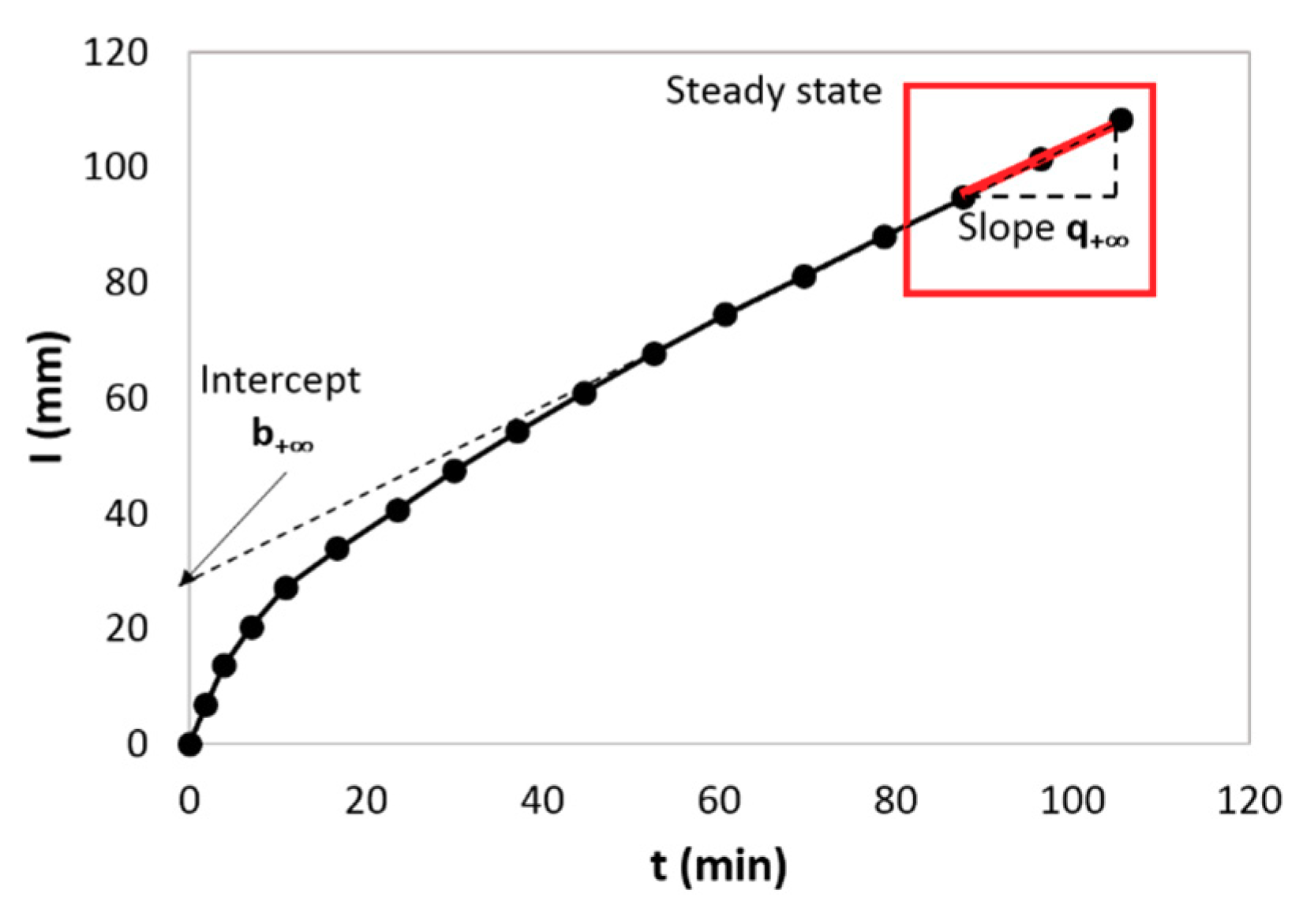
2.3. Infiltration Tests
2.3.1. Type and Number of Infiltration Measurements
2.3.2. Beerkan Infiltration Test and BEST Algorithm
“Beerkan” In-Situ Infiltration Test
“BEST” Algorithm
2.3.3. Guelph Permeameter
2.4. Data Analysis
2.5. Effect of Ks Variability on Hydrological Performance Modelling
3. Results and Discussion
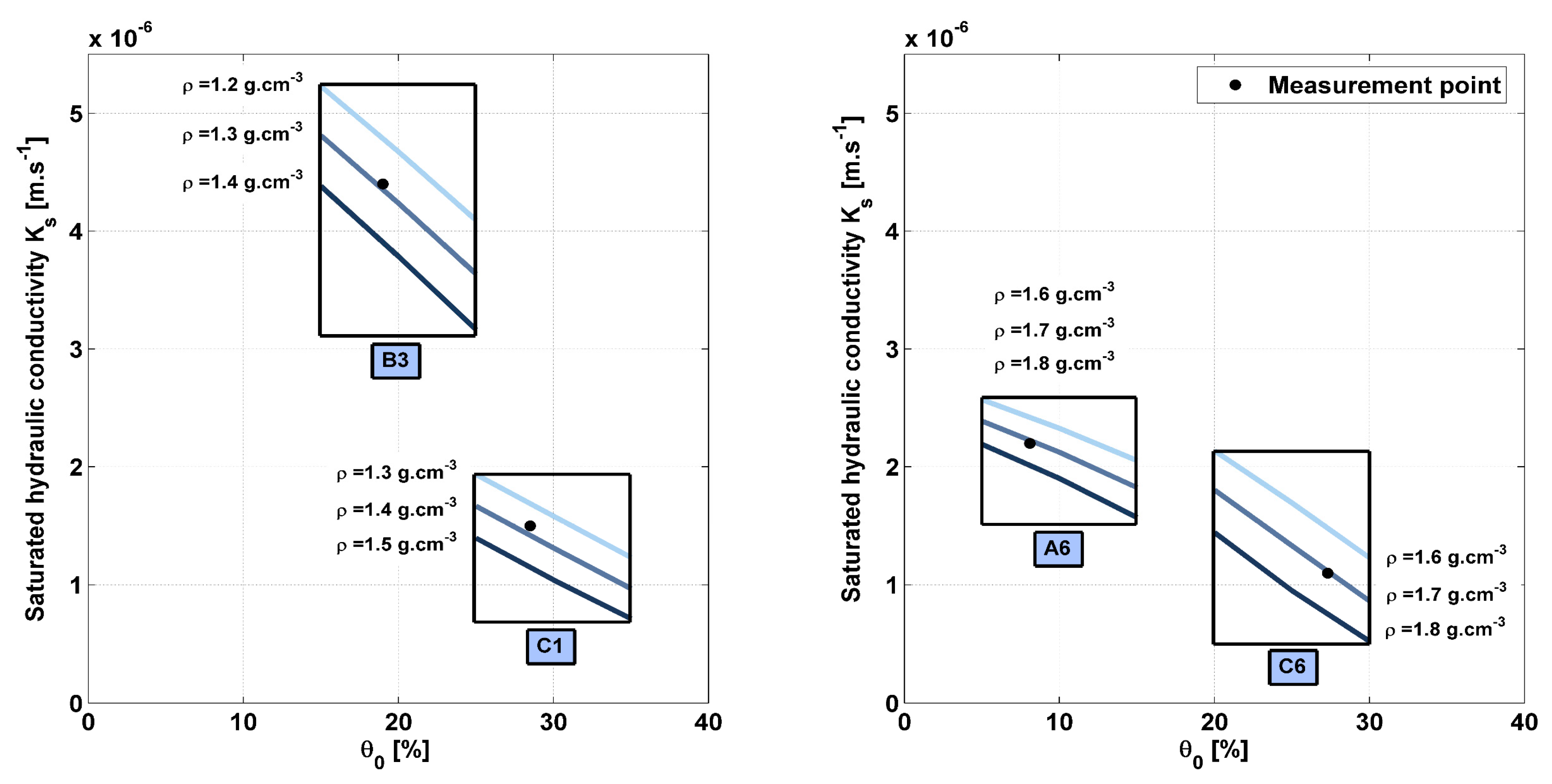
3.1. Horizontal and Vertical Variability of Soil Characteristics
3.2. Measurement Uncertainties
3.3. The Accuracy of the Pedotransfer Functions
3.4. Effect of Horizontal and Vertical Variability of Soil Hydraulic Properties on the Hydrological Performance
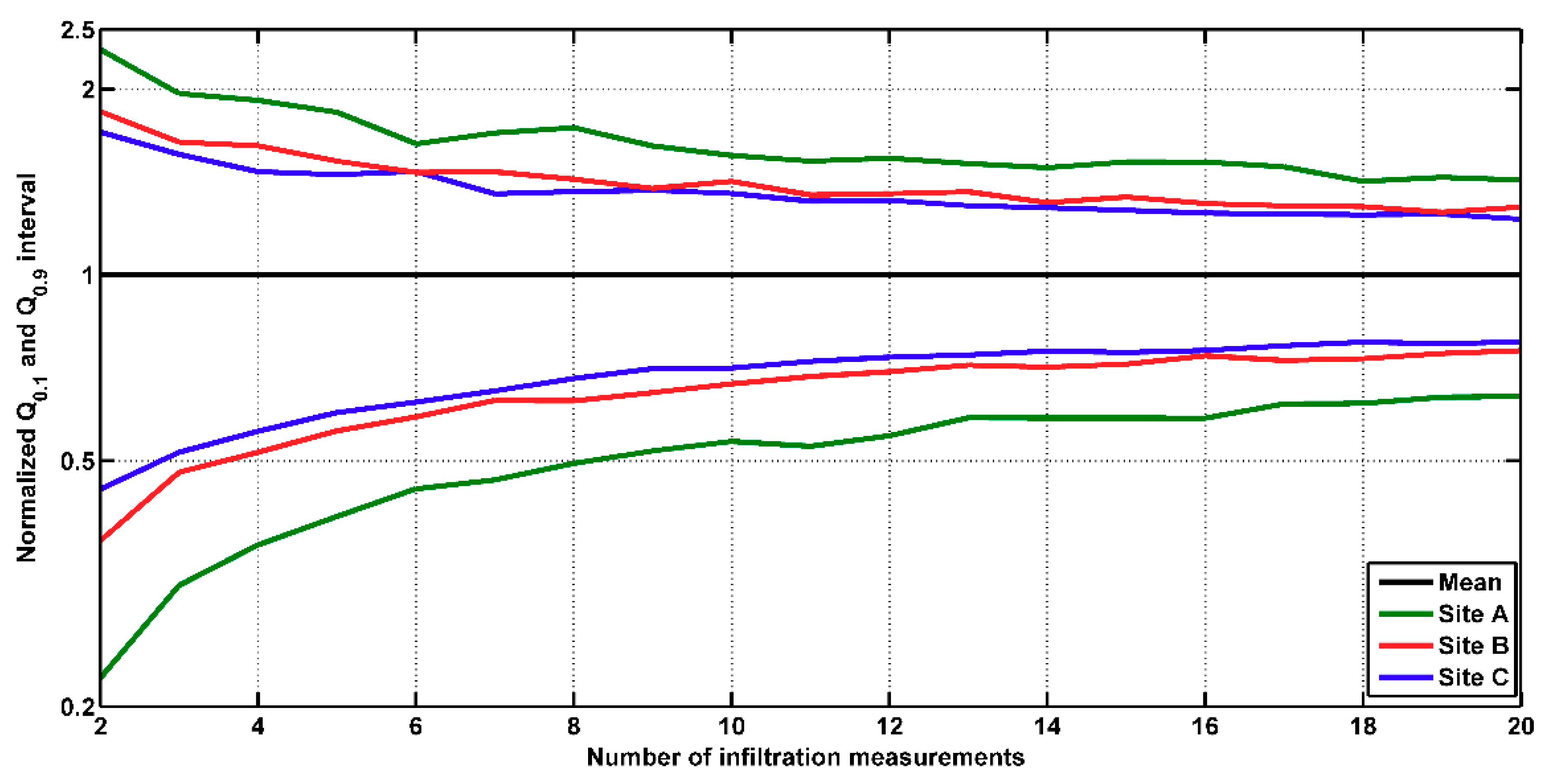
3.4.1. Number of Infiltration Measurements Needed for a Representative Value of Ks
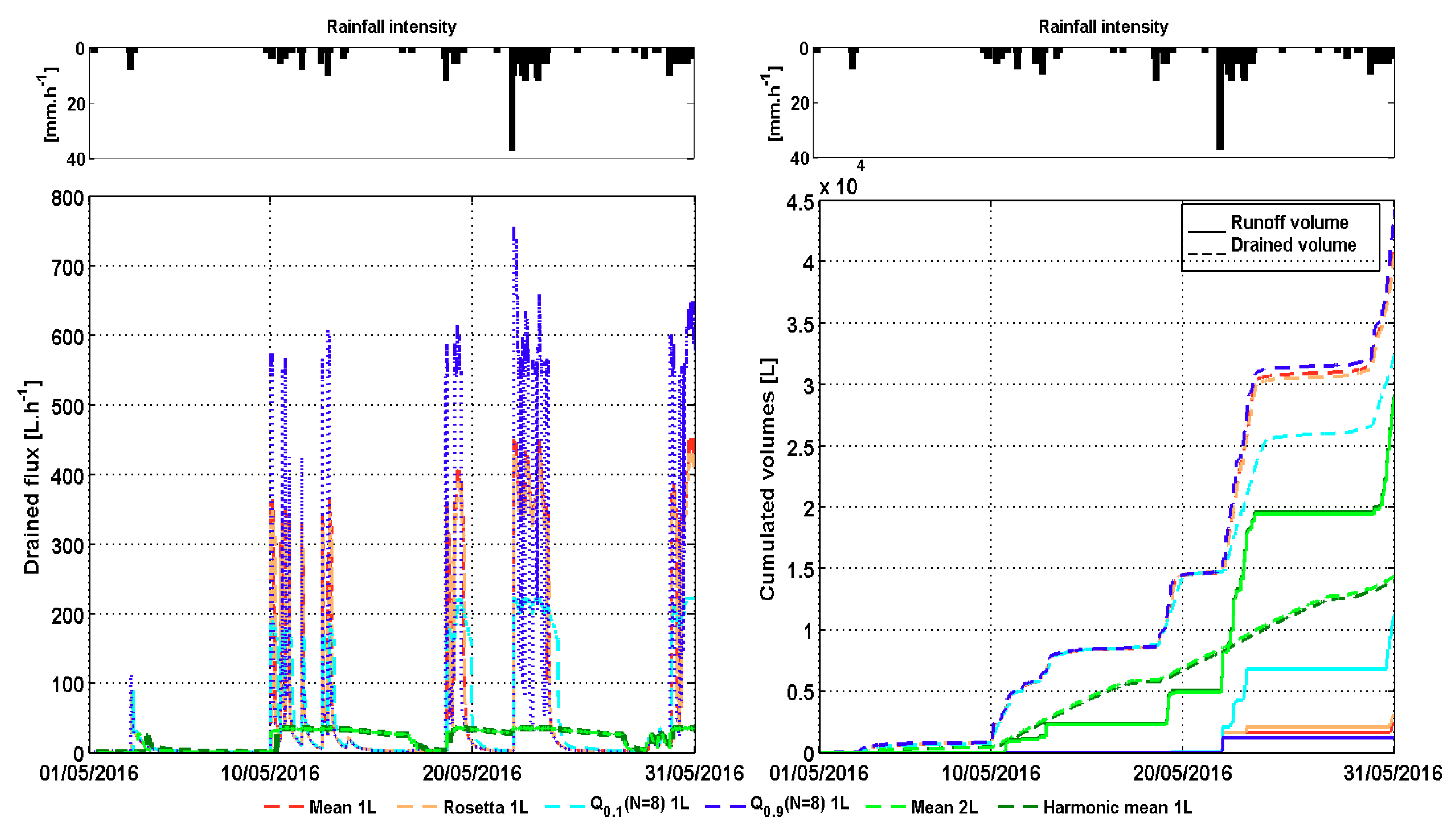
3.4.2. Effect of the Horizontal and Vertical Variability of Soil Hydraulic Properties on the Hydrological Modelling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Bulk Density ρ (g·cm3) | Initial Water Content θ0 (%) | Saturated Water Content θs Calculated (%) | Saturated Water Content θs Measured (%) | Saturated Hydraulic Conductivity Ks (m·s−1) | ||
|---|---|---|---|---|---|---|
| Site A (Surface) | A1 | 1.72 | 16.1 | 35.3 | 21.4 | 1.8 × 10−6 |
| A2 | 1.37 | 5.7 | 48.3 | 27.8 | 2.6 × 10−5 | |
| A3 | 1.83 | 13.2 | 30.9 | 26.6 | 7.7 × 10−6 | |
| A4 | 1.81 | 10.4 | 31.9 | 20.2 | 3.0 × 10−6 | |
| A5 | 1.72 | 11.6 | 35.3 | 20.7 | 2.9 × 10−6 | |
| A6 | 1.72 | 8.1 | 35.7 | 18.2 | 2.2 × 10−6 | |
| A7 | 1.75 | 12.4 | 34.2 | 27 | 6.7 × 10−6 | |
| A8 | 1.72 | 16.3 | 35.1 | 24.2 | 4.8 × 10−7 | |
| A9 | 1.77 | 8.7 | 33.2 | 26 | 1.8 × 10−6 | |
| Site A (20 cm depth) | A2–20 | - | - | - | - | 6.1 × 10−8 |
| A4–20 | 2 | - | - | - | 3.6 × 10−7 | |
| A5–20 | - | - | - | - | 4.5 × 10−8 | |
| A7–20 | 2.1 | - | - | - | 3.3 × 10−8 | |
| A8–20 | - | - | - | - | 1.5 × 10−8 | |
| A9–20 | 1.74 | - | - | - | 1.2 × 10−6 | |
| Site B | B1 | 1.21 | 39 | 54.3 | 46 | 4.0 × 10−5 |
| B2 | 1.04 | 14 | 60.8 | 50 | 3.2 × 10−5 | |
| B3 | 1.28 | 19 | 51.7 | 43 | 4.4 × 10−6 | |
| B4 | 1.24 | 23 | 53.2 | 45 | 4.9 × 10−5 | |
| B5 | 1.11 | 24 | 58.1 | 47 | 2.3 × 10−5 | |
| B6 | 1.16 | 30 | 56.2 | 48 | 1.0 × 10−5 | |
| B7 | 1.42 | 31 | 46.4 | 39 | 2.5 × 10−5 | |
| B8 | 1.33 | 29 | 49.8 | 39 | 1.4 × 10−5 | |
| B9 | 1.18 | 32 | 55.5 | 40 | 6.9 × 10−6 | |
| B10 | 1.19 | 26 | 55.1 | 39 | 1.0 × 10−5 | |
| Site C | C1 | 1.38 | 28.5 | 47.9 | 41.5 | 1.5 × 10−6 |
| C2 | 1.41 | 26.5 | 47.0 | 36.2 | 7.2 × 10−6 | |
| C3 | 1.72 | 21.8 | 35.3 | 41.4 | 4.9 × 10−6 | |
| C4 | 1.61 | 22.0 | 39.2 | 24.3 | 3.6 × 10−6 | |
| C5 | 1.57 | 16.8 | 40.8 | 31.5 | 3.8 × 10−6 | |
| C6 | 1.7 | 27.3 | 35.8 | 32.2 | 1.1 × 10−6 | |
| C7 | 1.71 | 18.4 | 35.5 | 28.2 | 3.8 × 10−6 | |
| C8 | 1.38 | 22.2 | 47.9 | 35.8 | 5.9 × 10−6 | |
| C9 | 1.41 | 27.4 | 46.8 | 50 | 1.1 × 10−5 |
Appendix B
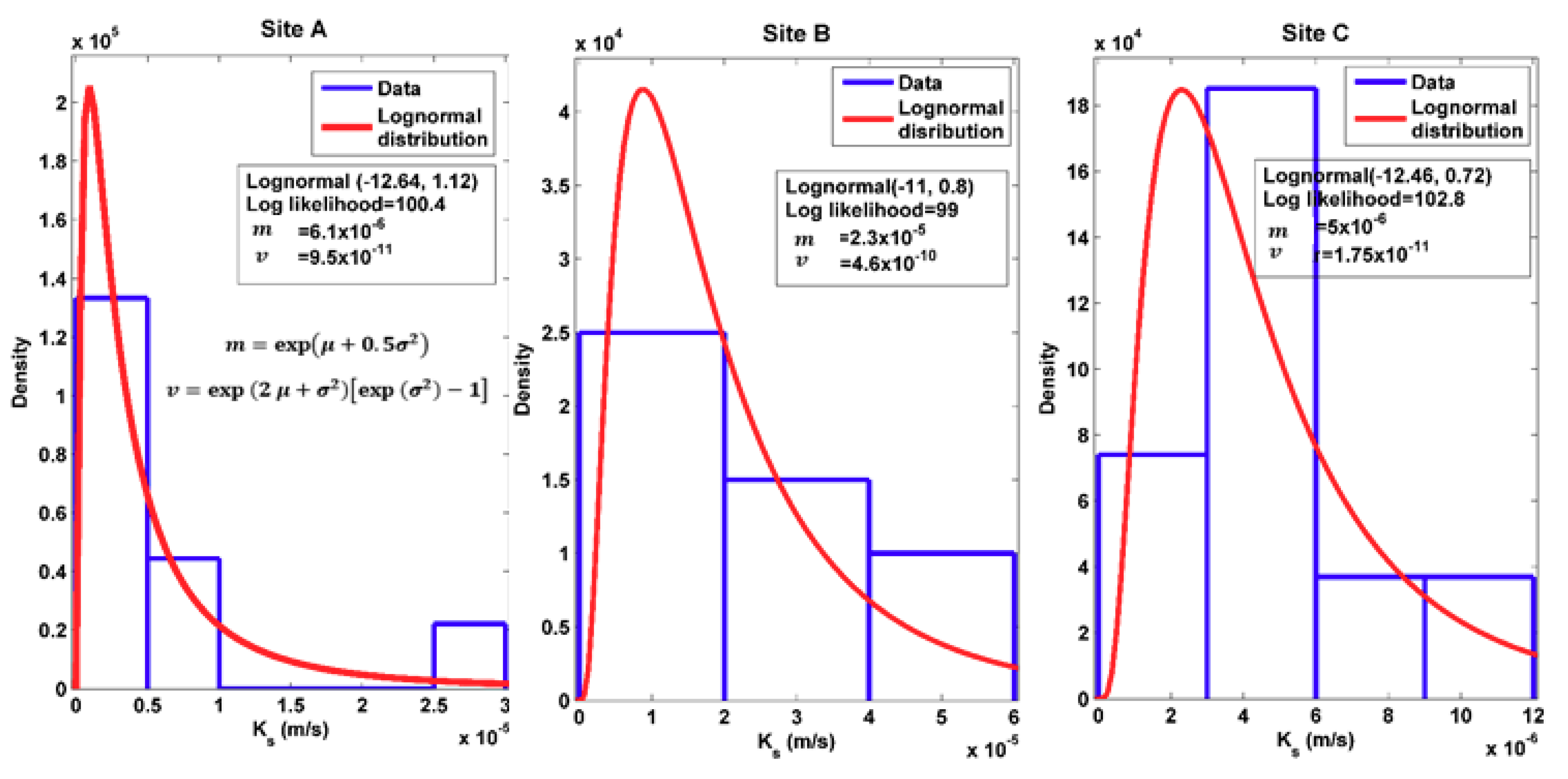
Appendix C
| Van Genuchten Parameters | θr (cm3·cm−3) | θs (cm3·cm−3) | 1/hg (cm−1) | n |
|---|---|---|---|---|
| At the surface | 0.0395 | 0.23 | 0.044 | 1.4128 |
| At 20 cm depth | 0.0354 | 0.275 | 0.0552 | 1.2775 |
References
- Coombes, P.J.; Kuczera, G.; Kalma, J.D.; Argue, J.R. An evaluation of the benefits of source control measures at the regional scale. Urban Water 2002, 4, 307–320. [Google Scholar] [CrossRef]
- Liu, A.; Goonetilleke, A.; Egodawatta, P. Taxonomy for rainfall events based on pollutant wash-off potential in urban areas. Ecol. Eng. 2012, 47, 110–114. [Google Scholar] [CrossRef]
- Davis, A.P. Green Engineering Promote Low-Impact Development. Environ. Sci. Technol. 2005, 39, 338A–344A. [Google Scholar] [CrossRef] [PubMed]
- Davis, A.P. Field Performance of Bioretention: Hydrology Impacts. J. Hydrol. Eng. 2008, 13, 90–95. [Google Scholar] [CrossRef]
- Bäckström, M.; Viklander, M.; Malmqvist, P.-A. Transport of stormwater pollutants through a roadside grassed swale. Urban Water J. 2006, 3, 55–67. [Google Scholar] [CrossRef]
- Barrett, M.E.; Walsh, P.M.; Malina, J.F., Jr.; Charbeneau, R.J. Performance of Vegetative Controls for Treating Highway Runoff. J. Environ. Eng. 1998, 124, 1121–1128. [Google Scholar] [CrossRef]
- Deletic, A.; Fletcher, T.D. Performance of grass filters used for stormwater treatment—A field and modelling study. J. Hydrol. 2006, 317, 261–275. [Google Scholar] [CrossRef]
- Rezaei, M.; Seuntjens, P.; Joris, I.; Boënne, W.; Van Hoey, S.; Campling, P.; Cornelis, W.M. Sensitivity of water stress in a two-layered sandy grassland soil to variations in groundwater depth and soil hydraulic parameters. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 6881–6920. [Google Scholar] [CrossRef]
- Clothier, B.E.; Smettem, K.R.J. Combining laboratory and field measurements to define the hydraulic properties of soil. Soil Sci. Soc. Am. J. 1990, 54, 299–304. [Google Scholar] [CrossRef]
- Jhorar, R.K.; Van Dam, J.C.; Bastiaanssen, W.G.M.; Feddes, R.A. Calibration of effective soil hydraulic parameters of heterogeneous soil profiles. J. Hydrol. 2004, 285, 233–247. [Google Scholar] [CrossRef]
- Angulo-Jaramillo, R.; Vandervaere, J.-P.; Roulier, S.; Thony, J.-L.; Gaudet, J.-P.; Vauclin, M. Field measurement of soil surface hydraulic properties by disc and ring infiltrometers: A review and recent developments. Soil Tillage Res. 2000, 55, 1–29. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, D.E.; Youngs, E.G.; Booltink, H.W.G.; Bouma, J.; Dane, J.H. Saturated and Field-Saturated Water Flow Parameters: Laboratory methods. In Methods of Soil Analysis; Soil Science Society of America: Madison, WI, USA, 2002; pp. 688–690. [Google Scholar]
- Ahmed, F.; Gulliver, J.S.; Nieber, J.L. Field infiltration measurements in grassed roadside drainage ditches: Spatial and temporal variability. J. Hydrol. 2015, 530, 604–611. [Google Scholar] [CrossRef]
- Weiss, P.T.; Gulliver, J.S. Effective saturated hydraulic conductivity of an infiltration-based stormwater control measure. J. Sustain. Water Built Environ. 2015, 1, 04015005. [Google Scholar] [CrossRef]
- Jabro, J.D.; Iversen, W.M.; Stevens, W.B.; Evans, R.G.; Mikha, M.M.; Allen, B.L. Physical and hydraulic properties of a sandy loam soil under zero, shallow and deep tillage practices. Soil Tillage Res. 2016, 159, 67–72. [Google Scholar] [CrossRef]
- Logsdon, S.D. CS616 Calibration: Field versus Laboratory. Soil Sci. Soc. Am. J. 2009, 73, 1. [Google Scholar] [CrossRef]
- Marín-Castro, B.E.; Geissert, D.; Negrete-Yankelevich, S.; Gómez-Tagle Chávez, A. Spatial distribution of hydraulic conductivity in soils of secondary tropical montane cloud forests and shade coffee agroecosystems. Geoderma 2016, 283, 57–67. [Google Scholar] [CrossRef]
- Sobieraj, J.A.; Elsenbeer, H.; Coelho, R.M.; Newton, B. Spatial variability of soil hydraulic conductivity along a tropical rainforest catena. Geoderma 2002, 108, 79–90. [Google Scholar] [CrossRef]
- Mubarak, I.; Angulo-Jaramillo, R.; Mailhol, J.C.; Ruelle, P.; Khaledian, M.; Vauclin, M. Spatial analysis of soil surface hydraulic properties: Is infiltration method dependent? Agric. Water Manag. 2010, 97, 1517–1526. [Google Scholar] [CrossRef]
- Rienzner, M.; Gandolfi, C. Investigation of spatial and temporal variability of saturated soil hydraulic conductivity at the field-scale. Soil Tillage Res. 2014, 135, 28–40. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, T. Hydraulic Properties of Porous Media; Hydrology Papers Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892. [Google Scholar] [CrossRef]
- Burdine, N. Relative permeability calculations from pore size distribution data. J. Pet. Technol. 1953, 5, 71–78. [Google Scholar] [CrossRef]
- Bouwer, H. Rapid field measurement of air entry value and hydraulic conductivity of soil as significant parameters in flow system analysis. Water Resour Res 1966, 2, 729–738. [Google Scholar] [CrossRef]
- McBratney, A.B.; Minasny, B.; Cattle, S.R.; Vervoort, R.W. From pedotransfer functions to soil inference systems. Geoderma 2002, 109, 41–73. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; Van Genuchten, M.T. ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Lin, H.S.; McInnes, K.J.; Wilding, L.P.; Hallmark, C.T. Effects of Soil Morphology on Hydraulic Properties. Soil Sci. Soc. Am. J. 1999, 63, 955. [Google Scholar] [CrossRef]
- Lassabatère, L.; Angulo-Jaramillo, R.; Winiarski, T.; Yilmaz, D. Advances in Unsaturated Soils. In BEST Method: Characterization of Soil Unsaturated Hydraulic Properties; CRC Press Taylor and Francis Group: London, UK, 2013. [Google Scholar]
- Reynolds, W.D.; Elrick, D.E. In situ measurement of field-saturated hydraulic conductivity, sorptivity, and the α-parameter using the Guelph permeameter. Soil Sci. 1985, 140, 292–302. [Google Scholar] [CrossRef]
- Cannavo, P.; Coulon, A.; Charpentier, S.; Béchet, B.; Vidal-Beaudet, L. Water balance prediction in stormwater infiltration basins using 2-D modeling: An application to evaluate the clogging process. Int. J. Sediment Res. 2018. [Google Scholar] [CrossRef]
- Lassabatère, L.; Angulo-Jaramillo, R.; Soria Ugalde, J.M.; Cuenca, R.; Braud, I.; Haverkamp, R. Beerkan Estimation of Soil Transfer Parameters through Infiltration Experiments—BEST. Soil Sci. Soc. Am. J. 2006, 70, 521. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, D.E. Ponded infiltration from a single ring: I. Analysis of steady flow. Soil Sci. Soc. Am. J. 1990. [Google Scholar] [CrossRef]
- Topp, G.C.; Ferré, P.A. 3.1 Water content. In Methods of Soil Analysis; Soil Science Society of America: Madison, WI, USA, 2002; pp. 417–545. [Google Scholar]
- Haverkamp, R.; Ross, P.J.; Smettem, K.R.J.; Parlange, J.Y. Three-dimensional analysis of infiltration from the disc infiltrometer: 2. Physically based infiltration equation. Water Resour. Res. 1994, 30, 2931–2935. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Prima, S.; Iovino, M. Comparing Alternative Algorithms to Analyze the Beerkan Infiltration Experiment. Soil Sci. Soc. Am. J. 2014, 78, 724. [Google Scholar] [CrossRef]
- Yilmaz, D.; Lassabatere, L.; Angulo-Jaramillo, R.; Deneele, D.; Legret, M. Hydrodynamic Characterization of Basic Oxygen Furnace Slag through an Adapted BEST Method. Vadose Zone J. 2010, 9, 107. [Google Scholar] [CrossRef]
- Philip, J.R. The theory of infiltration: 4. Sorptivity and algebraic infiltration equations. Soil Sci. 1957, 84, 257–264. [Google Scholar] [CrossRef]
- Di Prima, S.; Lassabatere, L.; Bagarello, V.; Iovino, M.; Angulo-Jaramillo, R. Testing a new automated single ring infiltrometer for Beerkan infiltration experiments. Geoderma 2016, 262, 20–34. [Google Scholar] [CrossRef]
- Eijkelkamp Guelph Permeameter—Operating Instructions; Eijkelkamp: Giesbeek, The Netherlands, 2011.
- Elrick, D.E.; Reynolds, W.D. Methods for Analyzing Constant-Head Well Permeameter Data. Soil Sci. Soc. Am. J. 1992, 56, 320. [Google Scholar] [CrossRef]
- Gardner, W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Bresler, E.; Dagan, G. Unsaturated flow in spatially variable fields: 2. Application of water flow models to various fields. Water Resour. Res. 1983, 19, 421–428. [Google Scholar] [CrossRef]
- Muñoz-Carpena, R.; Regalado, C.M.; Álvarez-Benedi, J.; Bartoli, F. Field evaluation of the new Philip-Dunne permeameter for measuring saturated hydraulic conductivity. Soil Sci. 2002, 167, 9–24. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979; p. 604. [Google Scholar]
- Simunek, J.; Sejna, M.; Saito, H.; Sakai, M.; Van Genuchten, M.T. The Hydrus-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2013; p. 342. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L.; Saxton, K.E. Estimation of soil water properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Archer, N.A.L.; Quinton, J.N.; Hess, T.M. Below-ground relationships of soil texture, roots and hydraulic conductivity in two-phase mosaic vegetation in South-east Spain. J. Arid Environ. 2002, 52, 535–553. [Google Scholar] [CrossRef]
- Nielsen, D.; Biggar, J.W.; Erh, K.T. Spatial variability of field-measured soil-water properties. Calif. Agric. 1973, 42, 215–259. [Google Scholar]
- Wang, C.; Zhao, C.; Xu, Z.; Wang, Y.; Peng, H. Effect of vegetation on soil water retention and storage in a semi-arid alpine forest catchment. J. Arid Land 2013, 5, 207–219. [Google Scholar] [CrossRef]
- Mulla, D.J.; McBratney, A.B.; Warrick, A.W. Soil spatial variability. In Soil Physics Companion; CRC Press: Boca Raton, FL, USA; 2002; pp. 343–373. [Google Scholar]
- Vauclin, M.; Vieira, S.R.; Bernard, R.; Hatfield, J.L. Spatial variability of surface temperature along two transects of a bare soil. Water Resour. Res. 1982, 18, 1677–1686. [Google Scholar] [CrossRef]
- Hillel, D. Spatial variability. In Environmental Soil Physics; Academic Press: San Diego, CA, USA, 1998; pp. 655–675. [Google Scholar]
- Mohanty, B.P.; Kanwar, R.S.; Everts, C.J. Comparison of saturated hydraulic conductivity measurement methods for a glacial-till soil. Soil Sci. Soc. Am. J. 1994, 58, 672–677. [Google Scholar] [CrossRef]
- Gupta, R.K.; Rudra, R.P.; Dickinson, W.T.; Patni, N.K.; Wall, G.J. Comparison of saturated hydraulic conductivity measured by various field methods. Trans. ASAE 1993, 36, 51–55. [Google Scholar] [CrossRef]
- Pitt, R.; Chen, S.-E.; Clark, S.E.; Swenson, J.; Ong, C.K. Compaction’s impacts on urban storm-water infiltration. J. Irrig. Drain. Eng. 2008, 134, 652–658. [Google Scholar] [CrossRef]
- Brown, R.A.; Hunt, W.F., III. Impacts of construction activity on bioretention performance. J. Hydrol. Eng. 2009, 15, 386–394. [Google Scholar] [CrossRef]
- Zamanian, K.; Pustovoytov, K.; Kuzyakov, Y. Pedogenic carbonates: Forms and formation processes. Earth-Sci. Rev. 2016, 157, 1–17. [Google Scholar] [CrossRef]
- Mermoud, A. Cours de Physique du Sol; Ecole Polytechnique Fédérale de Lausanne: Lausanne, Switzerland, 2001. [Google Scholar]
- Lewis, C.; Albertson, J.; Xu, X.; Kiely, G. Spatial variability of hydraulic conductivity and bulk density along a blanket peatland hillslope. Hydrol. Process. 2012, 26, 1527–1537. [Google Scholar] [CrossRef]
- Alvarez-Acosta, C.; Lascano, R.J.; Stroosnijder, L. Test of the Rosetta Pedotransfer Function for Saturated Hydraulic Conductivity. Open J. Soil Sci. 2012, 02, 203–212. [Google Scholar] [CrossRef]

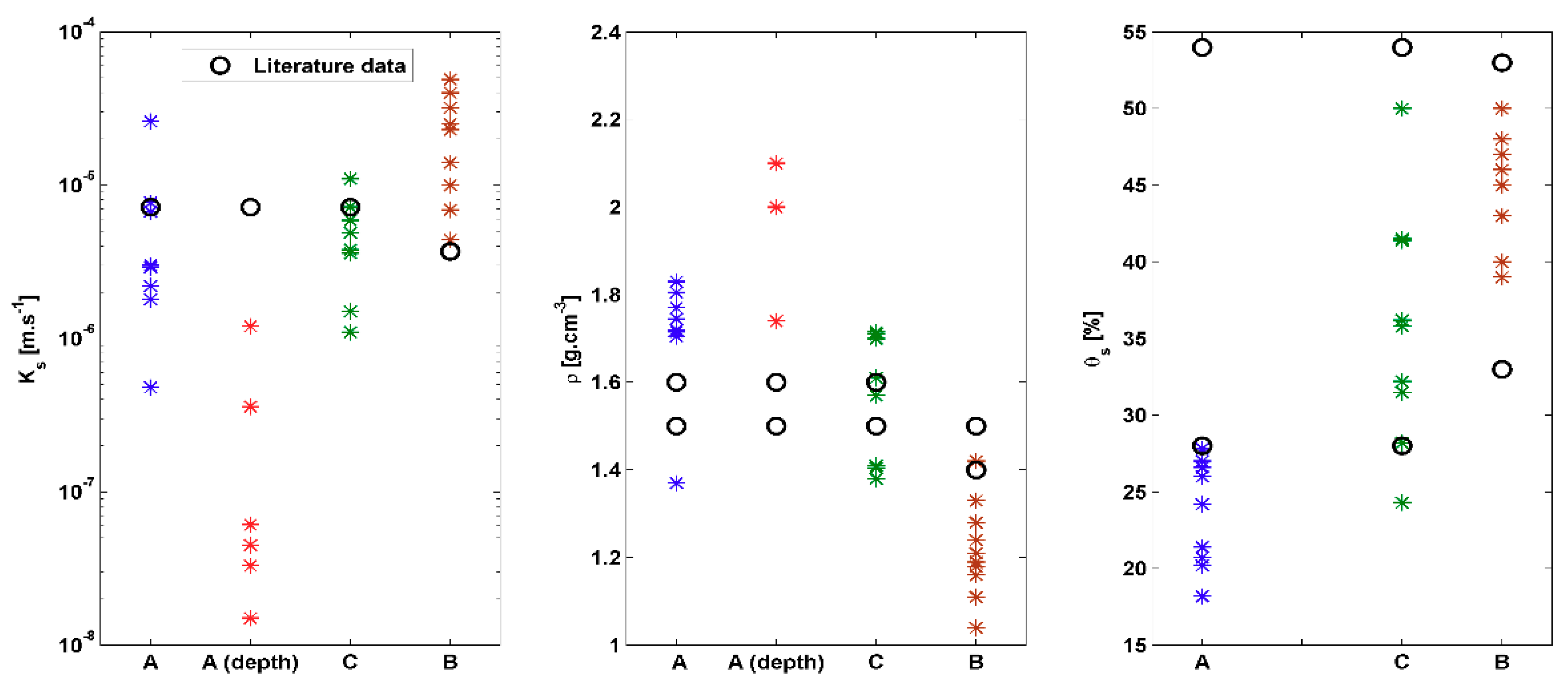
| Site A (Surface) | Site A (20 cm) | Site B | Site C | |
|---|---|---|---|---|
| Clay (<2 μm) | 9.7 | 10.5 | 14.8 | 11.1 |
| Fine silt (2–20 μm) | 9.0 | 8.8 | 18.2 | 9.6 |
| Coarse silt (20–50 μm) | 9.2 | 11.1 | 21.9 | 18.6 |
| Fine sand (50–200 μm) | 15.4 | 18.2 | 17.6 | 13.5 |
| Coarse sand (200–2000 μm) | 56.7 | 51.4 | 27.5 | 47.2 |
| Soil texture class (USDA) | Sandy Loam | Sandy Loam | Loam | Sandy Loam |
| n | Min | Max | Median | SD | CV [%] | Arithmetic Mean | ||
|---|---|---|---|---|---|---|---|---|
| Site A Surface | θs [%] | 9 | 18.2 | 27.8 | 24.2 | 3.5 | 15 | 23.6 |
| ρ [g·cm−3] | 9 | 1.37 | 1.83 | 1.72 | 0.13 | 8 | 1.70 | |
| Ks [m·s−1] | 9 | 4.8 × 10−7 | 2.6 × 10−5 | 2.9 × 10−6 | 7.9 × 10−6 | 134 | 5.8 × 10−6 | |
| Site A (20 cm) | ρ [g·cm−3] | 3 | 1.74 | 2.10 | 2.00 | 0.19 | 10 | 1.94 |
| Ks [m·s−1] | 6 | 1.5 × 10−8 | 1.2 × 10−6 | 5.3 × 10−8 | 4.7 × 10−7 | 163 | 2.9 × 10−7 | |
| Site B | θs [%] | 10 | 39 | 50 | 44 | 4.2 | 10 | 43.6 |
| ρ [g·cm−3] | 10 | 1.04 | 1.42 | 1.20 | 0.10 | 9 | 1.22 | |
| Ks [m·s−1] | 10 | 4.4 × 10−6 | 4.9 × 10−5 | 1.9 × 10−5 | 1.5 × 10−5 | 70 | 2.1 × 10−5 | |
| Site C | θs [%] | 9 | 24.3 | 50 | 35.8 | 7.8 | 22 | 35.7 |
| ρ [g·cm−3] | 9 | 1.38 | 1.72 | 1.57 | 0.15 | 10 | 1.54 | |
| Ks [m·s−1] | 9 | 1.1 × 10−6 | 1.1 × 10−5 | 3.8 × 10−6 | 3 × 10−6 | 64 | 4.8 × 10−6 |
| Permeability Curve K(h) (m·s−1) | Retention Curve θ(h) (%) | ||||||
|---|---|---|---|---|---|---|---|
| Ks | K (2.5 pF) | K (4 pF) | θs | θ (2.5 pF) θ/θs (%) | θ (4 pF) θ/θs (%) | ||
| Site A | Rosetta (Textural class) | 4.4 × 10−6 | 5.1 × 10−10 | 1.1 × 10−14 | 38.7 | 14.7 38 | 3.2 8 |
| Rosetta (%Sand, Silt, Clay) | 5.8 × 10−6 | 2.6 × 10−10 | 5.7 × 10−15 | 38.4 | 12.7 33 | 2.7 7 | |
| Rosetta (%Sand, Silt, Clay + ρ) | 2.9 × 10−6 | 8.0 × 10−11 | 2.5 × 10−15 | 33.0 | 11.2 34 | 2.8 8 | |
| Mean BEST values | 5.9 × 10−6 (7.9 × 10−6) | 3.4 × 10−10 (5.8 × 10−10) | 3.0 × 10−14 (5.1 × 10−14) | 23.5 (3.5) | 9.6 (1.9) 40 | 4.2 (0.9) 18 | |
| Site B | Rosetta (Textural class) | 1.4 × 10−6 | 2.1 × 10−9 | 4.4 × 10−14 | 39.9 | 21.0 53 | 4.3 10 |
| Rosetta (%Sand, Silt, Clay) | 1.7 × 10−6 | 3.0 × 10−9 | 5.3 × 10−14 | 39.6 | 20.7 52 | 4.0 10 | |
| Rosetta (%Sand, Silt, Clay + ρ) | 4.8 × 10−6 | 1.5 × 10−8 | 1.7 × 10−13 | 42.5 | 22.7 53 | 3.6 8 | |
| Mean BEST values | 2.1 × 10−5 (1.5 × 10−5) | 4.0 × 10−9 (7.1 × 10−9) | 4.6 × 10−13 (8.0 × 10−13) | 43.6 (4.2) | 20.4 (2.8) 47 | 9.9 (1.4) 23 | |
| Site C | Rosetta (Textural class) | 4.4 × 10−6 | 5.1 × 10−10 | 1.1 × 10−14 | 38.7 | 14.7 38 | 3.2 8 |
| Rosetta (%Sand, Silt, Clay) | 3.9 × 10−6 | 5.7 × 10−10 | 1.9 × 10−14 | 38.7 | 16.543 | 4.2 10 | |
| Rosetta (%Sand, Silt, Clay + ρ) | 3.3 × 10−6 | 3.7 × 10−10 | 1.1 × 10−14 | 36.6 | 14.8 40 | 3.6 10 | |
| Mean BEST values | 4.8 × 10−6 (3.0 × 10−6) | 5.9 × 10−10 (9.4 × 10−10) | 5.5 × 10−14 (8.8 × 10−14) | 35.7 (7.8) | 16.0 (4.4) 45 | 7.3 (2.0) 20 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanso, T.; Tedoldi, D.; Gromaire, M.-C.; Ramier, D.; Saad, M.; Chebbo, G. Horizontal and Vertical Variability of Soil Hydraulic Properties in Roadside Sustainable Drainage Systems (SuDS)—Nature and Implications for Hydrological Performance Evaluation. Water 2018, 10, 987. https://doi.org/10.3390/w10080987
Kanso T, Tedoldi D, Gromaire M-C, Ramier D, Saad M, Chebbo G. Horizontal and Vertical Variability of Soil Hydraulic Properties in Roadside Sustainable Drainage Systems (SuDS)—Nature and Implications for Hydrological Performance Evaluation. Water. 2018; 10(8):987. https://doi.org/10.3390/w10080987
Chicago/Turabian StyleKanso, Tala, Damien Tedoldi, Marie-Christine Gromaire, David Ramier, Mohamed Saad, and Ghassan Chebbo. 2018. "Horizontal and Vertical Variability of Soil Hydraulic Properties in Roadside Sustainable Drainage Systems (SuDS)—Nature and Implications for Hydrological Performance Evaluation" Water 10, no. 8: 987. https://doi.org/10.3390/w10080987
APA StyleKanso, T., Tedoldi, D., Gromaire, M.-C., Ramier, D., Saad, M., & Chebbo, G. (2018). Horizontal and Vertical Variability of Soil Hydraulic Properties in Roadside Sustainable Drainage Systems (SuDS)—Nature and Implications for Hydrological Performance Evaluation. Water, 10(8), 987. https://doi.org/10.3390/w10080987








