New Insights on Land Surface-Atmosphere Feedbacks over Tropical South America at Interannual Timescales
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Maximum Covariance Analysis
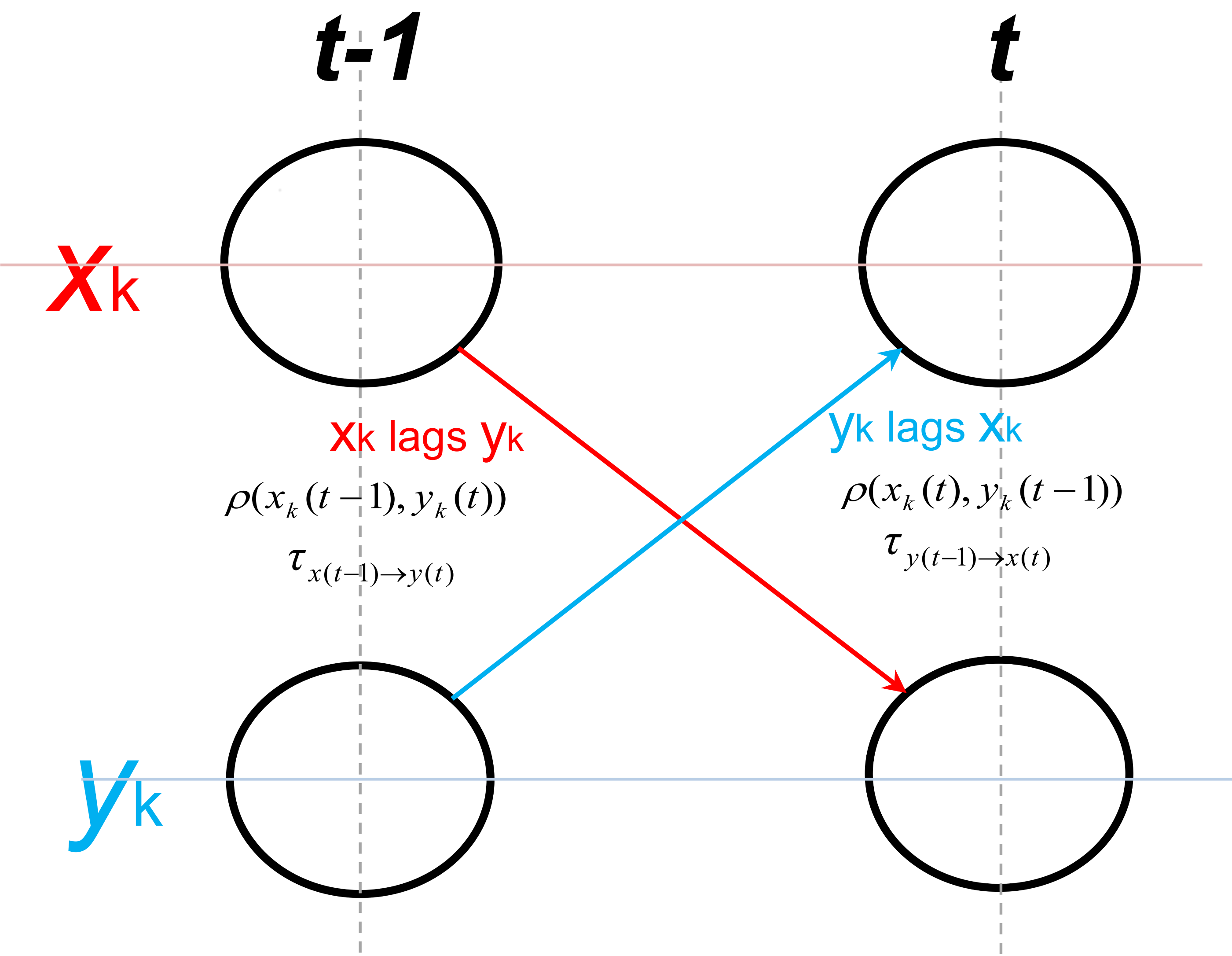
2.3. A Graph Model and Feedbacks at Interannual Timescales
3. Results
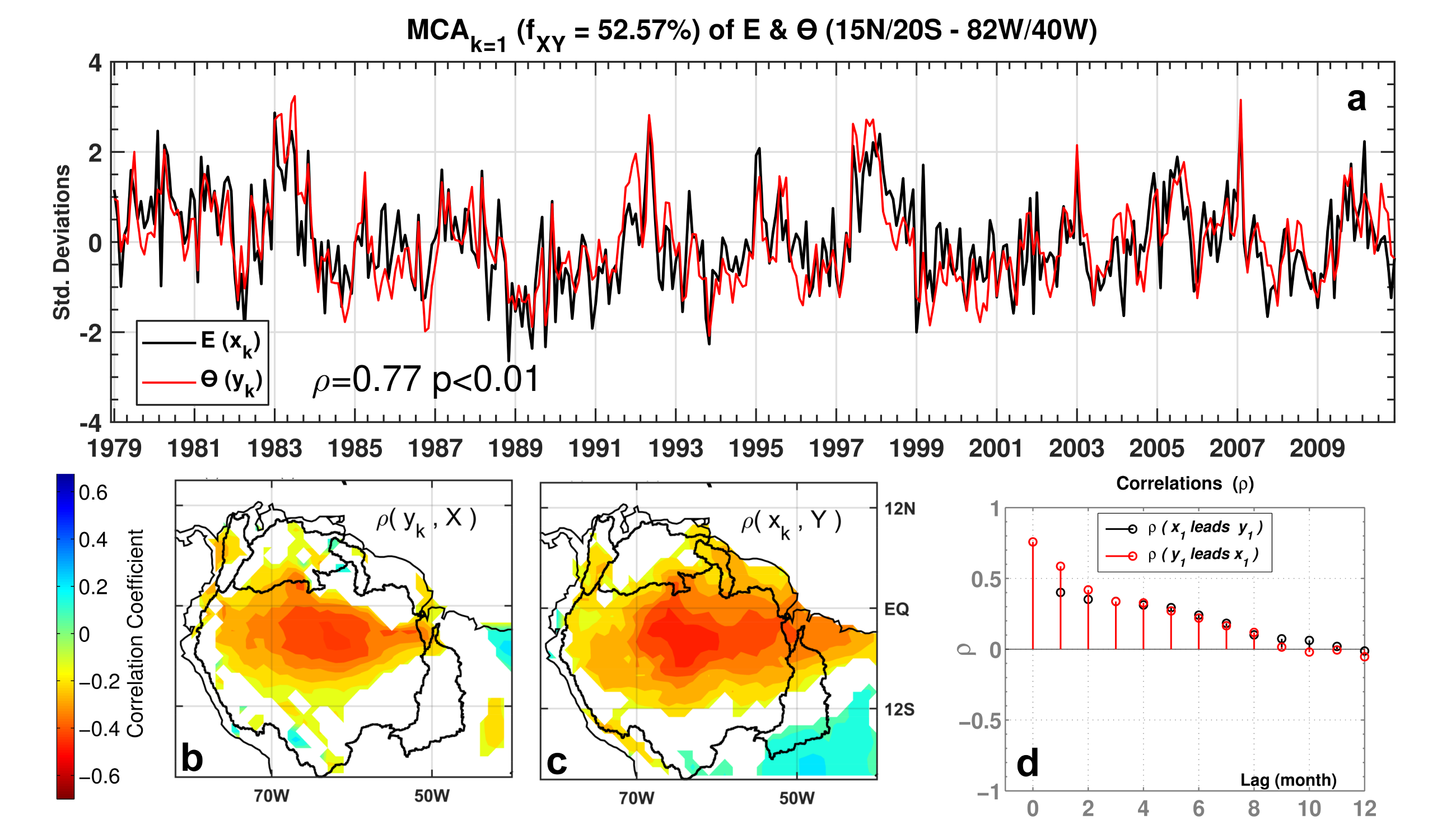
3.1. Maximum Covariance Analysis among Variables and Strength of ENSO Influence
3.2. Non-Linear Analysis of the MCA-Series and Feedbacks
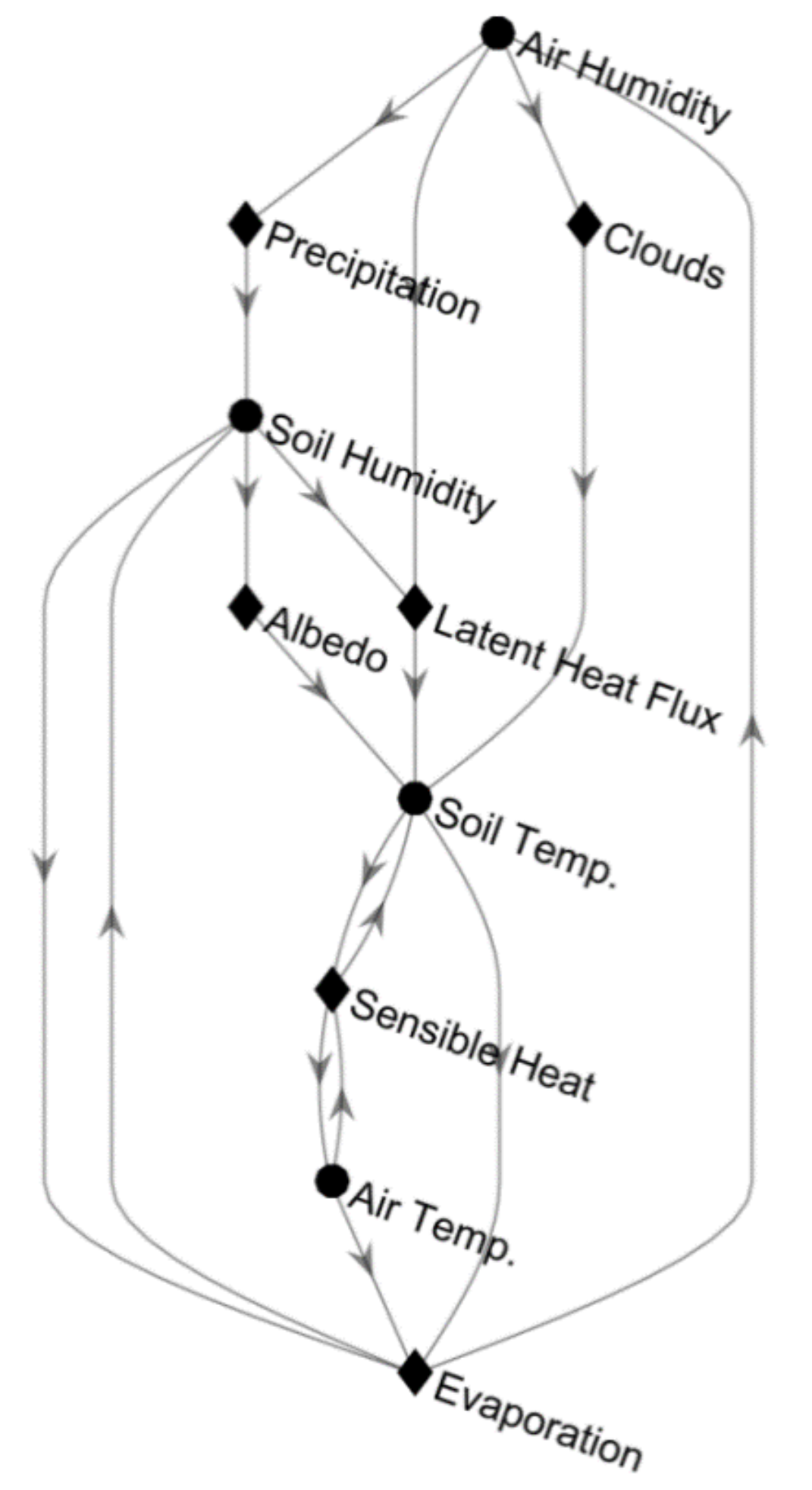
3.3. Visualizing Linear and Non-Linear Dependences Using Graph Theory
3.3.1. Linear Graphs
3.3.2. Non-Linear Graphs
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LAFs | Land-Atmosphere Feedbacks |
| ENSO | El Niño-Southern Oscillation |
| TropSA | Tropical South America |
| SAM | South American Monsoon |
| TNA | Tropical North America |
| SST | Sea Surface Temperature |
| T | Surface Temperature |
| q925 | Specific Humidity at 925 hPa |
| Θ | Volumetric Soil Water |
| P | Precipitation |
| E | Evaporation |
| GPCC | Global Precipitation Centre |
| SVD | Singular Value Decomposition |
| CXY | Covariance Matrix of Variables X and Y |
References
- Wohl, E.; Barros, A.; Brunsell, N.; Chappell, N.A.; Coe, M.; Giambelluca, T.; Goldsmith, S.; Harmon, R.; Hendrickx, J.M.; Juvik, J. The hydrology of the humid tropics. Nat. Clim. Chang. 2012, 2, 655–662. [Google Scholar] [CrossRef]
- Trenberth, K.E. Atmospheric moisture recycling: Role of advection and local evaporation. J. Clim. 1999, 12, 1368–1381. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Shea, D.J. Relationships between precipitation and surface temperature. Geophys. Res. Lett. 2005, 32, L14703. [Google Scholar] [CrossRef]
- Taylor, C.M.; De Jeu, R.A.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [PubMed]
- Seneviratne, S.I.; Stöckli, R. The role of land-atmosphere interactions for climate variability in Europe. In Climate Variability and Extremes during the Past 100 Years; Springer Science & Business Media: Heidelberg, Germany, 2008; pp. 179–193. [Google Scholar]
- Kolstad, E.W.; Barnes, E.A.; Sobolowski, S.P. Quantifying the role of land-atmosphere feedbacks in mediating near-surface temperature persistence. J. R. Meteorol. Soc. 2017, 143, 1620–1631. [Google Scholar] [CrossRef]
- Betts, A.K.; Ball, J.H.; Beljaars, A.; Miller, M.J.; Viterbo, P.A. The land surface-atmosphere interaction: A review based on observational and global modeling perspectives. J. Geophys. Res. 1996, 101, 7209–7225. [Google Scholar] [CrossRef]
- Schär, C.; Lüthi, D.; Beyerle, U.; Heise, E. The soil-precipitation feedback: A process study with a regional climate model. J. Clim. 1999, 12, 722–741. [Google Scholar] [CrossRef]
- Xue, Y.; De Sales, F.; Li, W.P.; Mechoso, C.R.; Nobre, C.A.; Juang, H.M. Role of land surface processes in South American monsoon development. J. Clim. 2006, 19, 741–762. [Google Scholar] [CrossRef]
- Berg, A.; Lintner, B.R.; Findell, K.; Seneviratne, S.I.; Van den Hurk, B.; Ducharne, A.; Chéruy, F.; Hagemann, S.; Lawrence, D.M.; Malyshev, S.; et al. Interannual coupling between summertime surface temperature and precipitation over land: Processes and implications for climate change. J. Clim. 2015, 28, 1308–1328. [Google Scholar] [CrossRef]
- Knist, S.; Goergen, K.; Buonomo, E.; Christensen, O.B.; Colette, A.; Cardoso, R.M.; Fealy, R.; Fernández, J.; García-Díez, M.; Jacob, D.; et al. Land-atmosphere coupling in EURO-CORDEX evaluation experiments. J. Geophys. Res. 2017, 122, 79–103. [Google Scholar] [CrossRef]
- Baisya, H.; Pattnaik, S.; Rajesh, P.V. Land surface-precipitation feedback analysis for a landfalling monsoon depression in the Indian region. J. Adv. Model. Earth Syst. 2017, 9, 712–726. [Google Scholar] [CrossRef]
- Zemp, D.C.; Schleussner, C.F.; Barbosa, H.M.; Hirota, M.; Montade, V.; Sampaio, G.; Staal, A.; Wang-Erlandsson, L.; Rammig, A. Self-amplified Amazon forest loss due to vegetation-atmosphere feedbacks. Nat. Commun. 2017, 8, 14681. [Google Scholar] [CrossRef] [PubMed]
- Koster, R.D.; Suarez, M.J. A simple framework for examining the interannual variability of land surface moisture fluxes. J. Clim. 1999, 12, 1911–1917. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Yamada, T. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Orlowsky, B.; Seneviratne, S.I. Statistical analyses of land–atmosphere feedbacks and their possible pitfalls. J. Clim. 2010, 23, 3918–3932. [Google Scholar] [CrossRef]
- Catalano, F.; Alessandri, A.; De Felice, M.; Zhu, Z.; Myneni, R.B. Observationally based analysis of land–atmosphere coupling. Earth Syst. Dyn. Discuss. 2015, 6, 1–39. [Google Scholar] [CrossRef]
- Wei, J.; Dirmeyer, P.A. Dissecting soil moisture-precipitation coupling. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Gimeno, L.; Stohl, A.; Trigo, R.M.; Dominguez, F.; Yoshimura, K.; Yu, L.; Drumond, A.; Durán-Quesada, A.M.; Nieto, R. Oceanic and terrestrial sources of continental precipitation. Rev. Geophys. 2012, 50, 4003. [Google Scholar] [CrossRef]
- Roy, S.B. Mesoscale vegetation-atmosphere feedbacks in Amazonia. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Konings, A.G.; Dekker, S.C.; Rietkerk, M.; Katul, G.G. Drought sensitivity of patterned vegetation determined by rainfall-land surface feedbacks. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Gentine, P.; Entekhabi, D.; Polcher, J. The diurnal behavior of evaporative fraction in the soil–vegetation–atmospheric boundary layer continuum. J. Hydrometeorol. 2011, 12, 1530–1546. [Google Scholar] [CrossRef]
- Bagley, J.E.; Desai, A.R.; Harding, K.J.; Snyder, P.K.; Foley, J.A. Drought and deforestation: Has land cover change influenced recent precipitation extremes in the Amazon? J. Clim. 2014, 27, 345–361. [Google Scholar] [CrossRef]
- Boers, N.; Marwan, N.; Barbosa, H.M.; Kurths, J. A deforestation-induced tipping point for the South American monsoon system. Sci. Rep. 2017, 7, 41489. [Google Scholar] [CrossRef] [PubMed]
- Yin, L.; Fu, R.; Zhang, Y.F.; Arias, P.A.; Fernando, D.N.; Li, W.; Fernandes, K.; Bowerman, A.R. What controls the interannual variation of the wet season onsets over the Amazon? J. Geophys. Res. Atmos. 2014, 119, 2314–2328. [Google Scholar] [CrossRef]
- Gentine, P.; Holtslag, A.A.; D’Andrea, F.; Ek, M. Surface and atmospheric controls on the onset of moist convection over land. J. Hydrometeorol. 2013, 14, 1443–1462. [Google Scholar] [CrossRef]
- Taylor, C.M. Detecting soil moisture impacts on convective initiation in Europe. Geophys. Res. Lett. 2015, 42, 4631–4638. [Google Scholar] [CrossRef]
- Salati, E.; Dall’Olio, A.; Matsui, E.; Gat, J.R. Recycling of water in the Amazon basin: An isotopic study. Water Resour. Res. 1979, 15, 1250–1258. [Google Scholar] [CrossRef]
- Lettau, H.; Lettau, K.; Molion, L.C.B. Amazonia’s hydrologic cycle and the role of atmospheric recycling in assessing deforestation effects. Mon. Weather Rev. 1979, 107, 227–238. [Google Scholar] [CrossRef]
- Eltahir, E.A.B.; Bras, R.L. Precipitation Recycling. Rev. Geophys. 1996, 34, 367–379. [Google Scholar] [CrossRef]
- Van der Ent, R.J.; Savenije, H.H.; Schaefli, B.; Steele-Dunne, S.C. Origin and fate of atmospheric moisture over continents. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Medvigy, D.; Walko, R.; Avissar, R. Effects of deforestation on spatio-temporal distributions of precipitation in South America. J. Clim. 2011, 24, 2147–2163. [Google Scholar] [CrossRef]
- Zemp, D.C.; Schleussner, C.F.; Barbosa, H.M.J.; Van der Ent, R.J.J.; Donges, F.; Heinke, J.; Sampaio, G.; Rammig, A. On the importance of cascading moisture recycling in South America. Atmos. Chem. Phys. 2014, 14, 13337–13359. [Google Scholar] [CrossRef]
- Zemp, D.C.; Schleussner, C.F.; Barbosa, H.M.; Rammig, A. Deforestation effects on Amazon forest resilience. Geophys. Res. Lett. 2017, 44, 6182–6190. [Google Scholar] [CrossRef]
- Rocha, V.M.; Correia, F.W.S.; Fonseca, P.A.M. Reciclagem de precipitação na Amazônia: Um estudo de revisão. Rev. Bras. Meteorol. 2015, 30, 59–70. [Google Scholar] [CrossRef]
- Sörensson, A.A.; Menéndez, C.G. Summer soil–precipitation coupling in South America. Tellus A 2011, 63, 56–68. [Google Scholar] [CrossRef]
- Barreiro, M.; Díaz, N.; Renom, M. Role of the global oceans and land–atmosphere interaction on summertime interdecadal variability over northern Argentina. Clim. Dyn. 2014, 42, 1733–1753. [Google Scholar] [CrossRef]
- Ruscica, R.C.; Sörensson, A.A.; Menéndez, C.G. Hydrological links in Southeastern South America: Soil moisture memory and coupling within a hot spot. Int. J. Climatol. 2014, 34, 3641–3653. [Google Scholar] [CrossRef]
- Ruscica, R.C.; Sörensson, A.A.; Menéndez, C.G. Pathways between soil moisture and precipitation in southeastern South America. Atmos. Sci. Lett. 2015, 16, 267–272. [Google Scholar] [CrossRef]
- Wang, H.; Fu, R. Influence of cross-Andes flow on the South American low-level jet. J. Clim. 2004, 17, 1247–1262. [Google Scholar] [CrossRef]
- Boers, N.; Bookhagen, B.; Marwan, N.; Kurths, J. Spatiotemporal characteristics and synchronization of extreme rainfall in South America with focus on the Andes Mountain range. Clim. Dyn. 2016, 46, 601–617. [Google Scholar] [CrossRef]
- Collini, E.A.; Berbery, E.H.; Barros, V.R.; Pyle, M.E. How does soil moisture influence the early stages of the South American monsoon? J. Clim. 2008, 21, 195–213. [Google Scholar] [CrossRef]
- Ma, H.-Y.; Mechoso, C.R.; Xue, Y.; Xiao, H.; Wu, C.-M.; Li, J.-L.; De Sales, F. Impact of land surface processes on the South American warm season climate. Clim. Dyn. 2011, 37, 187–203. [Google Scholar] [CrossRef]
- Poveda, G.; Mesa, O.J. Feedbacks between hydrological processes in tropical South America and large scale oceanic atmospheric phenomena. J. Clim. 1997, 10, 2690–2702. [Google Scholar] [CrossRef]
- Barreiro, M.; Diaz, N. Land-atmosphere coupling in El Niño influence over South America. Atmos. Sci. Lett. 2011, 12, 351–355. [Google Scholar] [CrossRef]
- Builes-Jaramillo, A.; Marwan, N.; Poveda, G.; Kurths, J. Nonlinear interactions between the Amazon River basin and the Tropical North Atlantic at interannual timescales. Clim. Dyn. 2018, 50, 2951–2969. [Google Scholar] [CrossRef]
- Builes-Jaramillo, A.; Ramos, A.; Poveda, G. Atmosphere-Land Bridge between the Pacific and Tropical North Atlantic SST’s Through the Amazon River Basin During the 2005 and 2010 Droughts; Universidad Nacional de Colombia: Medellín, Colombia, 2017. [Google Scholar]
- Brubaker, K.L.; Entekhabi, D. Analysis of feedback mechanisms in land-atmosphere interaction. Water Resour. Res. 1996, 32, 1343–1357. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Eltahir, E.A. A soil moisture–rainfall feedback mechanism: 1. Theory and observations. Water Resour. Res. 1998, 34, 765–776. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Lüthi, D.; Litschi, M.; Schär, C. Land–atmosphere coupling and climate change in Europe. Nature 2006, 443, 205–209. [Google Scholar] [CrossRef] [PubMed]
- Haghighi, E.; Kirchner, J.W. Near-surface turbulence as a missing link in modeling evapotranspiration-soil moisture relationships. Water Resour. Res. 2017, 53, 5320–5344. [Google Scholar] [CrossRef]
- Runge, J.; Petoukhov, V.; Kurths, J. Quantifying the strength and delay of climatic interactions: The ambiguities of cross correlation and a novel measure based on graphical models. J. Clim. 2014, 27, 720–739. [Google Scholar] [CrossRef]
- Donges, J.F.; Petrova, I.; Loew, A.; Marwan, N.; Kurths, J. How complex climate networks complement eigen-techniques for the statistical analysis of climatological data. Clim. Dyn. 2015, 45, 2407–2424. [Google Scholar] [CrossRef]
- Runge, J. Quantifying information transfer and mediation along causal pathways in complex systems. Phys. Rev. E 2015, 92, 062829. [Google Scholar] [CrossRef] [PubMed]
- Kretschmer, M.; Coumou, D.; Donges, J.F.; Runge, J. Using causal effect networks to analyze different Arctic drivers of midlatitude winter circulation. J. Clim. 2016, 29, 4069–4081. [Google Scholar] [CrossRef]
- Espinoza Villar, J.C.; Ronchail, J.; Guyot, J.L.; Cochonneau, G.; Naziano, F.; Lavado, W.; Vauchel, P. Spatio-temporal rainfall variability in the Amazon basin countries (Brazil, Peru, Bolivia, Colombia, and Ecuador). Int. J. Climatol. 2009, 29, 1574–1594. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, F.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land-surface precipitation climatology based on quality-controlled in-situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Albergel, C.; Dorigo, W.; Reichle, R.H.; Balsamo, G.; De Rosnay, P.; Muñoz-Sabater, J.; Isaksen, L.; De Jeu, R.; Wagner, W. Skill and global trend analysis of soil moisture from reanalyses and microwave remote sensing. J. Hydrometeorol. 2013, 14, 1259–1277. [Google Scholar] [CrossRef]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; De Rosnay, P. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]
- Nicolai-Shaw, N.; Gudmundsson, L.; Hirschi, M.; Seneviratne, S.I. Long-term predictability of soil moisture dynamics at the global scale: Persistence versus large-scale drivers. Geophys. Res. Lett. 2016, 43, 8554–8562. [Google Scholar] [CrossRef]
- Mayer, M.; Trenberth, K.E.; Haimberger, L.; Fasullo, J.T. The Response of Tropical Atmospheric Energy Budgets to ENSO. J. Clim. 2013, 26, 4710–4724. [Google Scholar] [CrossRef]
- Bjornsson, H.; Venegas, S.A. A Manual for EOF and SVD Analyses of Climatic Data; CCGCR Report No. 97-1; McGill University: Montréal, QC, Canada, 1997. [Google Scholar]
- Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Liang, X.-S. Unraveling the cause-effect relation between time series. Phys. Rev. E 2014, 90, 052150. [Google Scholar] [CrossRef] [PubMed]
- Kleinberg, J.M. Authoritative sources in a hyperlinked environment. J. ACM 1999, 46, 604–632. [Google Scholar] [CrossRef]
- Poveda, G.; Jaramillo, L.; Vallejo, L.F. Seasonal precipitation patterns along pathways of South American low-level jets and aerial rivers. Water Resour. Res. 2014, 50, 98–118. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2013, 84. [Google Scholar] [CrossRef]
- Marengo, J.A.; Nobre, C.A.; Tomasella, J.; Oyama, M.D.; Sampaio de Oliveira, G.; De Oliveira, R.; Brown, I.F. The drought of Amazonia in 2005. J. Clim. 2008, 21, 495–516. [Google Scholar] [CrossRef]
- Marengo, J.A.; Tomasella, J.; Alves, L.M.; Soares, W.R.; Rodriguez, D.A. The drought of 2010 in the context of historical droughts in the Amazon region. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Ronchail, J.; Frappart, F.; Lavado, W.; Santini, W.; Guyot, J.L. The major floods in the Amazonas River and Tributaries (western Amazon basin) during the 1970–2012 Period: A focus on the 2012 flood. J. Hydrometeorol. 2013, 14, 1000–1008. [Google Scholar] [CrossRef]
- Miralles, D.G.; Gentine, P.; Seneviratne, S.I.; Teuling, A.J. Land–atmospheric feedbacks during droughts and heatwaves: State of the science and current challenges. Ann. N. Y. Acad. Sci. 2018. [Google Scholar] [CrossRef] [PubMed]
- Mapes, B.E.; Warner, T.T.; Xu, M. Diurnal patterns of rainfall in northwestern South America. Part III: Diurnal gravity waves and nocturnal convection offshore. Mon. Weather Rev. 2003, 131, 830–844. [Google Scholar] [CrossRef]
- Vera, C.; Higgins, W.; Amador, J.; Ambrizzi, T.; Garreaud, R.; Gochis, D.; Nogues-Paegle, J. Toward a unified view of the American monsoon systems. J. Clim. 2006, 19, 4977–5000. [Google Scholar] [CrossRef]
- Grimm, A.M.; Tedeschi, R.G. ENSO and extreme rainfall events in South America. J. Clim. 2009, 22, 1589–1609. [Google Scholar] [CrossRef]
- Mo, K.C.; Berbery, E.H. Drought and persistent wet spells over South America based on observations and the US CLIVAR drought experiments. J. Clim. 2011, 24, 1801–1820. [Google Scholar] [CrossRef]
- Bracco, A.; Falasca, F.; Nenes, A.; Fountalis, I.; Dovrolis, C. Advancing climate science with knowledge-discovery through data mining. npj Clim. Atmos. Sci. 2018, 1. [Google Scholar] [CrossRef]
- Tsonis, A.A.; Roebber, P.J. The architecture of the climate network. Phys. A Stat. Mech. Appl. 2004, 333, 497–504. [Google Scholar] [CrossRef]
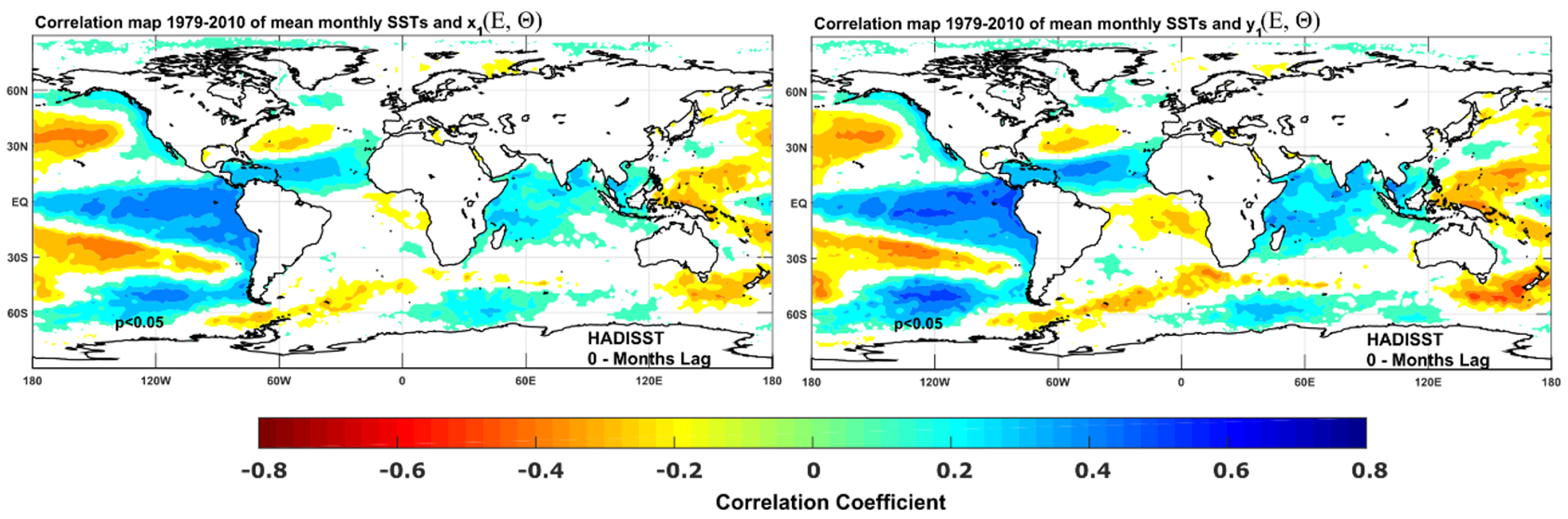
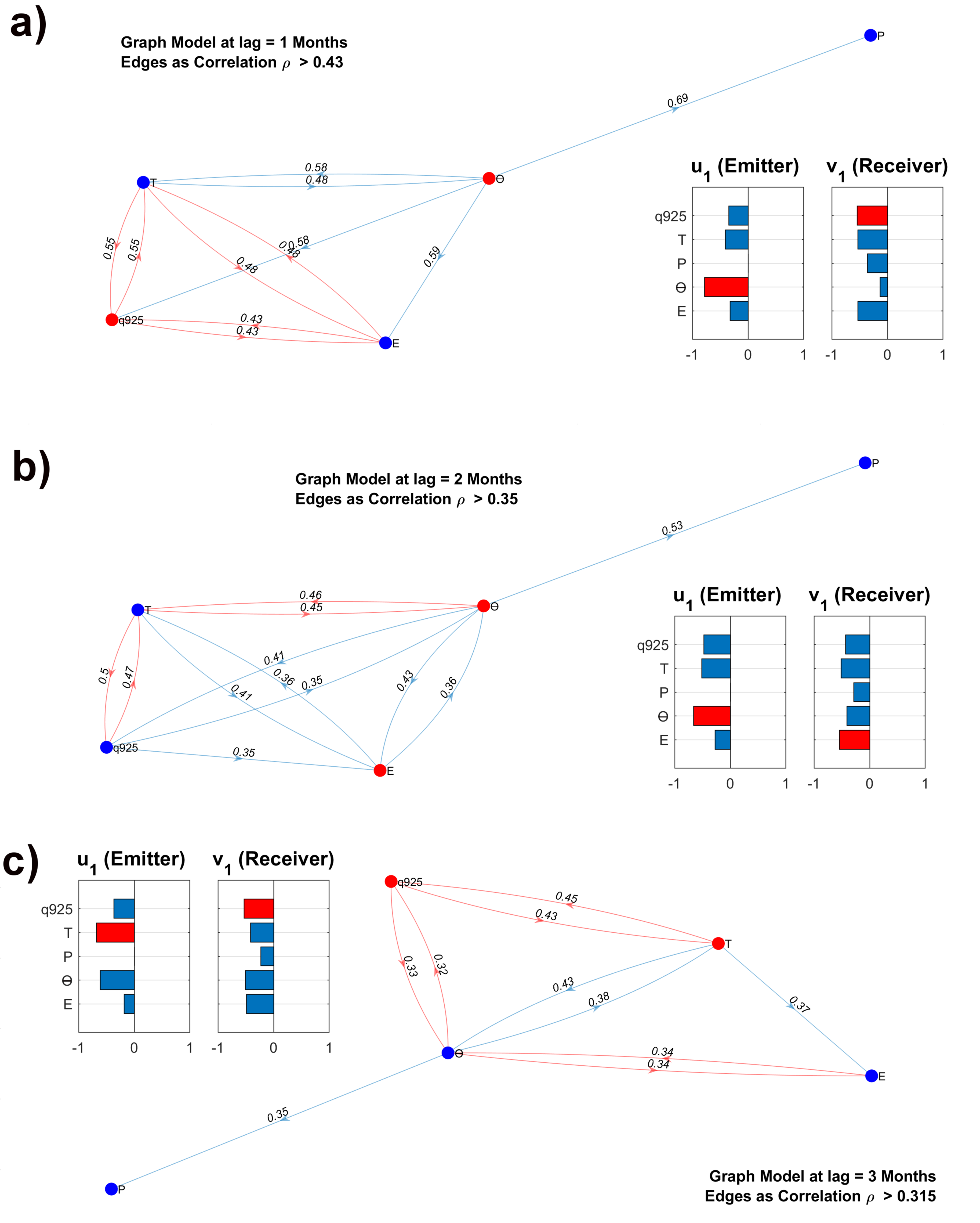
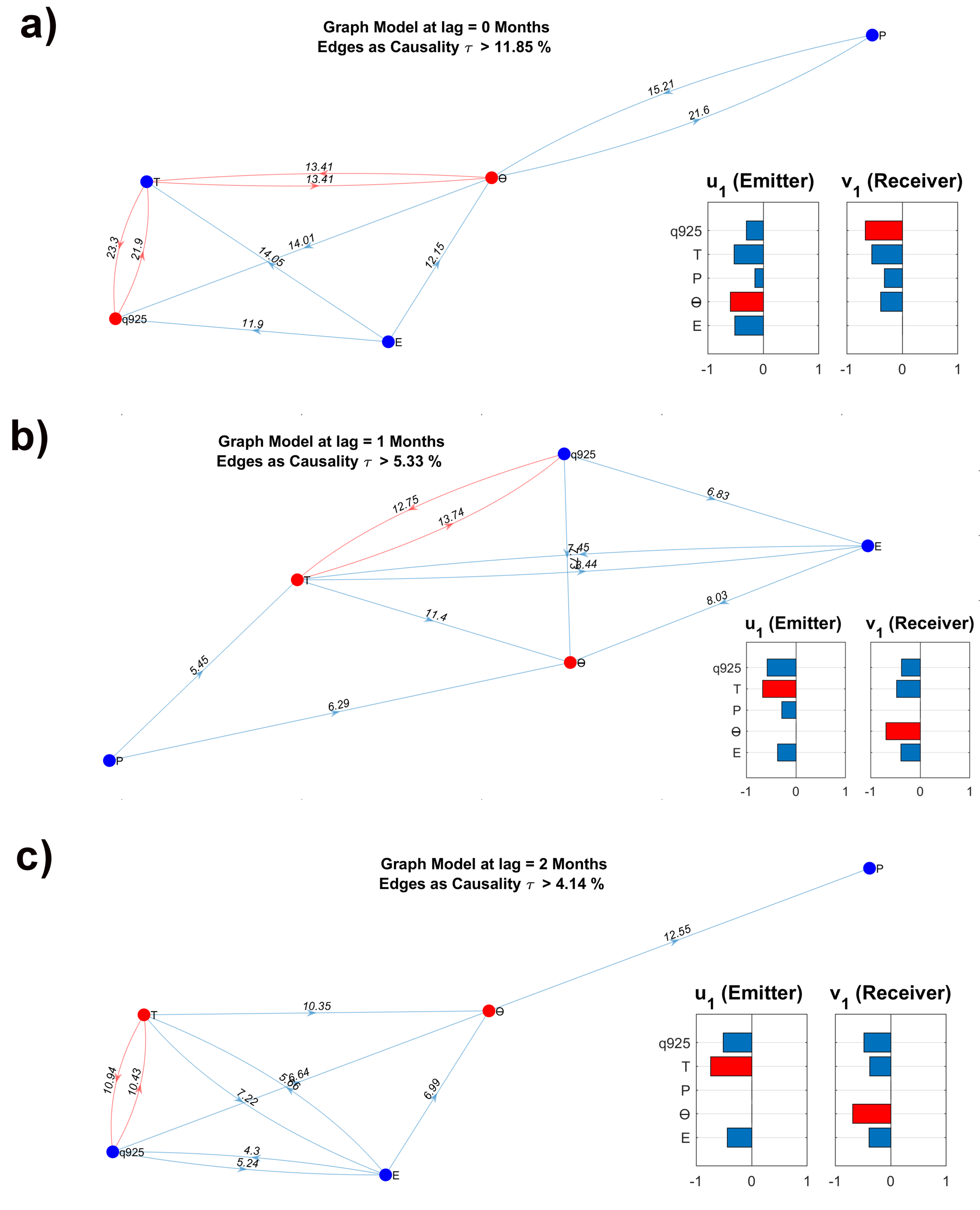
| CXY | Mode 1 | Mode 2 | Mode 3 | ||||
|---|---|---|---|---|---|---|---|
| X | Y | (%) | (%) | (%) | |||
| q925 | T | 73 (73) | 0.96 | 16 (88) | 0.97 | 5 (93) | 0.96 |
| E | Θ | 53 (53) | 0.77 | 17 (70) | 0.64 | 11 (81) | 0.64 |
| P | q925 | 51 (51) | 0.78 | 27 (78) | 0.6 | 9 (87) | 0.64 |
| P | T | 50 (50) | 0.72 | 29 (79) | 0.6 | 9 (86) | 0.64 |
| T | Θ | 50 (50) | 0.67 | 29 (78) | 0.66 | 7 (85) | 0.66 |
| E | T | 49 (49) | 0.58 | 18 (67) | 0.67 | 8 (76) | 0.64 |
| q925 | Θ | 48 (48) | 0.7 | 30 (78) | 0.57 | 8 (86) | 0.68 |
| E | q925 | 45 (45) | 0.58 | 23 (68) | 0.65 | 9 (76) | 0.65 |
| P | Θ | 39 (39) | 0.78 | 32 (71) | 0.78 | 12 (83) | 0.79 |
| E | P | 39 (39) | 0.71 | 32 (71) | 0.73 | 10 (81) | 0.71 |
| CXY | Mode 1 | Mode 2 | Mode 3 | ||||
|---|---|---|---|---|---|---|---|
| X | Y | ||||||
| q925 | T | −0.44 | −0.50 | 0.15 | 0.14 | 0.19 | −0.19 |
| E | Θ | 0.40 | 0.45 | 0.33 | 0.36 | 0.14 | 0.19 |
| P | q925 | 0.25 | 0.33 | −0.40 | −0.48 | −0.19 | −0.01 |
| P | T | −0.33 | −0.47 | −0.33 | −0.48 | −0.15 | −0.01 |
| T | Θ | 0.58 | −0.58 | −0.21 | −0.12 | −0.13 | −0.07 |
| E | T | −0.50 | −0.54 | −0.09 | −0.12 | −0.16 | −0.22 |
| q925 | Θ | 0.52 | 0.53 | −0.30 | −0.25 | −0.13 | −0.08 |
| E | q925 | −0.46 | −0.47 | −0.14 | −0.16 | −0.20 | 0.05 |
| P | Θ | 0.30 | 0.37 | 0.35 | 0.4 | −0.22 | −0.21 |
| E | P | 0.07 | 0.18 | −0.49 | −0.42 | −0.22 | 0.31 |
| X | Y | |||
|---|---|---|---|---|
| q925 | T | 21.9 | −23.3 | −1.06 |
| E | Θ | 12.1 | 9.4 | 0.78 |
| P | q925 | 7.7 | −2 | −0.26 |
| P | T | 10.4 | −6 | −0.58 |
| T | Θ | 13.4 | 13.4 | 1.00 |
| E | T | 14 | 11.8 | 0.84 |
| q925 | Θ | 11.4 | 14 | 1.22 |
| E | q925 | 11.9 | 9.6 | 0.81 |
| P | Θ | 15.2 | 21.6 | 1.43 |
| E | P | −6.1 | 5.8 | −0.95 |
| Metric Type | Lag | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| Correlation () | 0.68 | 0.43 | 0.35 | 0.315 | 0.3 | 0.265 | 0.22 |
| Relative Causality () | 11.85 | 5.33 | 4.14 | 4.54 | 3.53 | 1.75 | 1.89 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedoya-Soto, J.M.; Poveda, G.; Sauchyn, D. New Insights on Land Surface-Atmosphere Feedbacks over Tropical South America at Interannual Timescales. Water 2018, 10, 1095. https://doi.org/10.3390/w10081095
Bedoya-Soto JM, Poveda G, Sauchyn D. New Insights on Land Surface-Atmosphere Feedbacks over Tropical South America at Interannual Timescales. Water. 2018; 10(8):1095. https://doi.org/10.3390/w10081095
Chicago/Turabian StyleBedoya-Soto, Juan Mauricio, Germán Poveda, and David Sauchyn. 2018. "New Insights on Land Surface-Atmosphere Feedbacks over Tropical South America at Interannual Timescales" Water 10, no. 8: 1095. https://doi.org/10.3390/w10081095
APA StyleBedoya-Soto, J. M., Poveda, G., & Sauchyn, D. (2018). New Insights on Land Surface-Atmosphere Feedbacks over Tropical South America at Interannual Timescales. Water, 10(8), 1095. https://doi.org/10.3390/w10081095






