1. Introduction
The use of underdrain distribution pipes in the design of Stormwater Control Measure (SCM) is a common practice in bioretention and permeable pavement systems, particularly when the subsoils have lower infiltration properties [
1]. These underdrains are designed to evacuate water from a SCM to a defined outfall point. Most analyses for the clogging of such systems are limited to clogging of the filtering media [
2,
3,
4] or the permeable pavement surface [
5,
6], with a few studies focusing on the clogging of distribution pipes under permeable pavement systems [
7]. Since sediment is primarily captured by the surface layer [
8], clogging of distribution pipes are not considered by most studies, and distribution pipes are not considered as a restriction to water movement [
9].
In Philadelphia, the “Green City, Clean Waters” initiative was adopted in 2011 as part of the city’s Combined Sewer Overflow Long Term Control Plan. Over 1100 green infrastructures (GIs) have been built in Philadelphia since then [
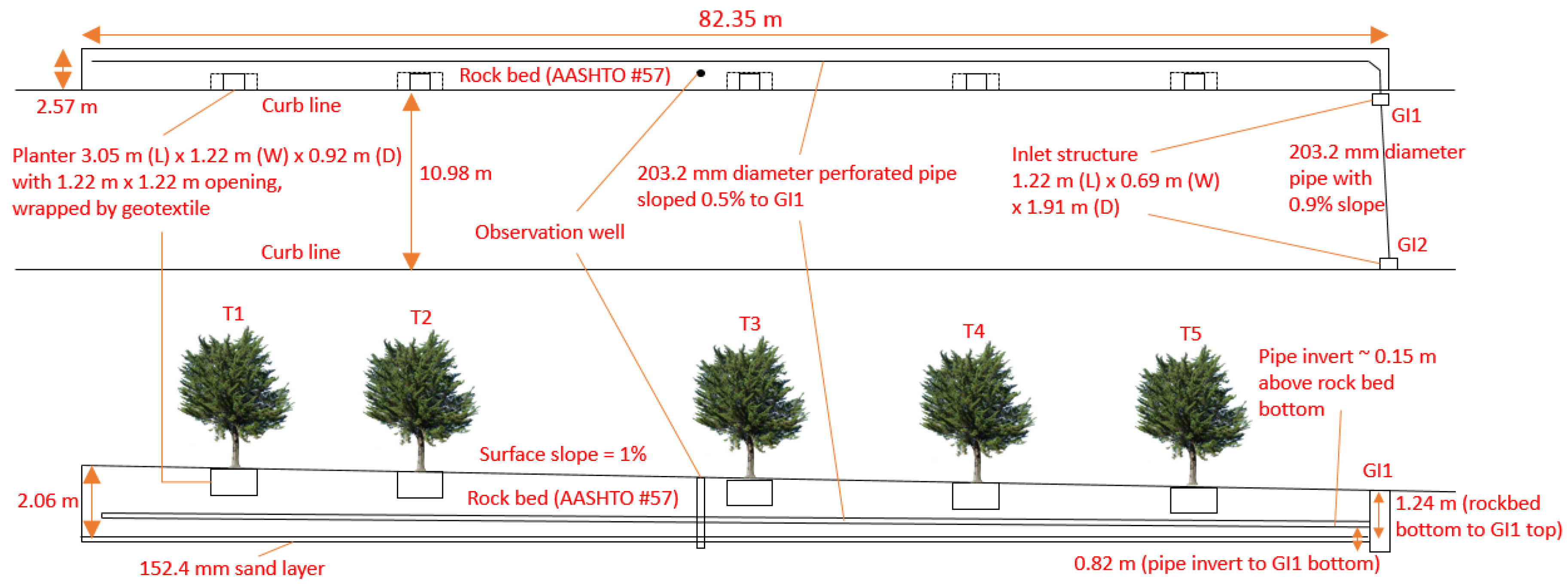
10]. Due to the limited building space in Philadelphia, many GIs have been built under sidewalks in the road right-of-way. For a typical tree trench GI built in Philadelphia, the runoff from the road surface enters an inlet structure, and a perforated distribution pipe transports and delivers water into the subsurface infiltration bed (i.e., a SCM), thus the flow direction is reversed from that of the application described earlier. Pretreatment is limited to a trash guard (a meshed filter bag) under the inlet grate or a sumped inlet due to space constraints.
Clogging analyses for similar systems are scarce. The hydraulic performance of similar systems has been investigated [
11,
12], but not the effects and characteristics of the clogging of an inflow distribution pipe as far as the authors could find. From the related field of drip irrigation, past studies have indicated that clogging is possible in similar systems [
13], but the differences in pipe specifications and sources of water preclude a direct comparison. In addition to sediment, trash and/or leaves, stormwater runoff from road surfaces can be products from vehicle waste, atmospheric deposition, and road materials [
14]. Since the characteristics of non-point pollution from stormwater runoff are complex [
15], studies dedicated to the clogging of distribution pipes from untreated stormwater runoff are required.
Urbanization is a global trend. By 2010, more than 50% of the world’s population had moved into urban areas and such a population shift was achieved in the United States in the early 20th century [
16]. As urban area expands, controlling non-point pollution from urban areas becomes more important as the impact to receiving water bodies from the complex human activities intensifies [
17,
18]. For such urban areas with limited building space, designs similar to the tree trench GI built in Philadelphia will play an important role in the future of urban stormwater management. Therefore, the purpose of this research is to understand the effects and characteristics of clogging and a cost-effective strategy in the maintenance of the distribution pipes of such systems.
3. Methods
Ongoing research determined that the flow rate sustained by the distribution pipe was limited by the orifices on the pipe wall, so the following analyses were based on the orifice flow equation. Assuming that the partial clogging blocked a portion of the orifice area, the orifice equation for a single orifice can be rewritten as Equation (1). In Equation (1),
q is the orifice flow rate,
is the portion (ranging from 0 to 1) of the orifice area that is functional,
C is the orifice discharge coefficient, a is the orifice area before partial clogging happens, g is the gravity constant (9.8 m/s
2), and
is the pressure head driving the orifice flow (called “driving head” hereafter).
Equation (1) can be rearranged for
in Equation (2).
In Equation (2),
C and
g can be considered constants, so
is linearly proportional to
. The authors decided to assume the discharge coefficient
C as a constant, based on the fact that the discharge coefficient
C for parallel flow (i.e., flow in the pipe is parallel to the plane of the orifice) was in a narrow range of 0.61–0.64 [
27].
For orifices uniformly distributed on a section of perforated pipe, Equation (2) can be rewritten as Equation (3), where
is the mean portion of clogging on the section of pipe,
Q is the sum of the orifice flow generated by the section of pipe,
A is the total orifice area on that section of pipe,
n is the number of orifices on the section of pipe,
represents the driving head at the
i-th orifice, and
represents the mean driving head among all orifices on the section of pipe. The approximation performed in Equation (3) delivered a low approximation error after being tested by actual examples of a numerical series. The goal of the derivation was only to provide a means to compare the relative magnitudes of partial clogging among different events.
Since the orifices are uniformly distributed on the perforated pipe, the total orifice area on the section of pipe is linearly proportional to the length of the pipe which allows orifice flow; therefore, performance index
(Equation (4)) can be derived to represent the performance of the perforated pipe based on Equation (3), with higher values representing less influence from partial clogging (i.e., higher performance).
where
is the effective length of distribution pipe that allows orifice flow, which is the equivalent length of water column with the same volume of water (
V) in the pipe and the cross-sectional area (
A) of the pipe, as explained by Equation (5).
Detailed definitions of parameters (for
and
) for the performance index under various scenarios are discussed below.
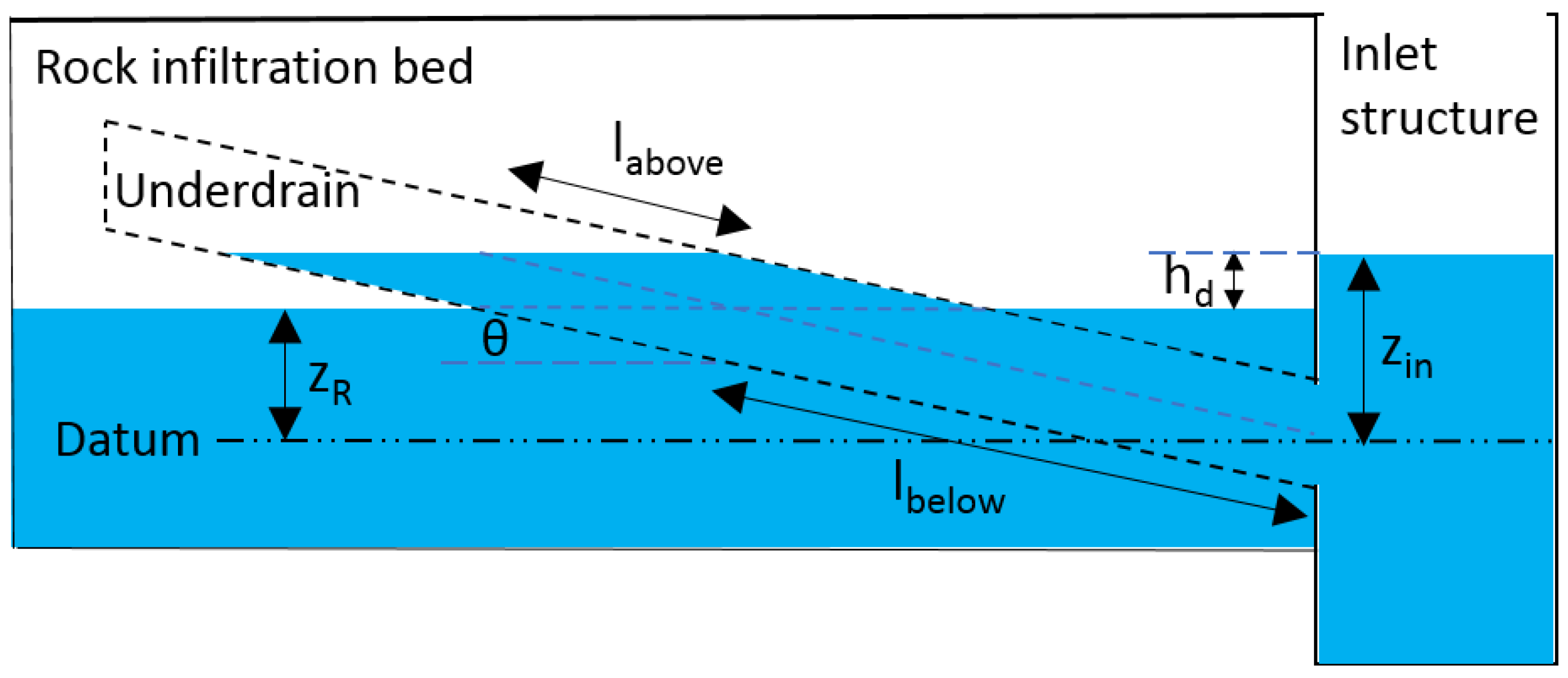
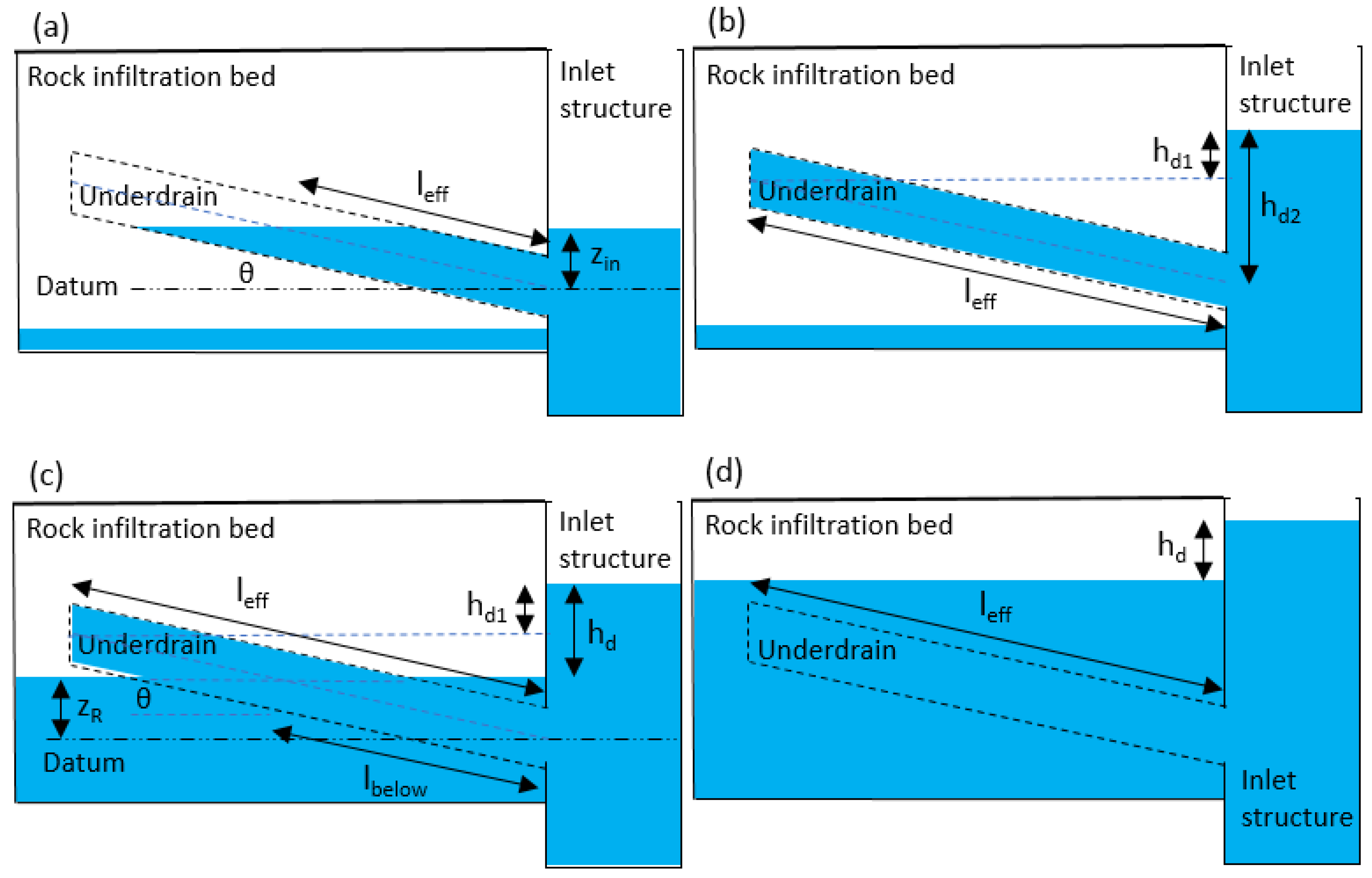
Figure 7 describes the operation of a typical distribution system. The datum was set at the elevation of the center of the distribution pipe at its inlet. Water elevation in the rock bed and in the inlet structure were
and
, respectively, with difference
. Along the centerline of the pipe (with inclination angle
), the length of water (along the pipe centerline) above and below the water in the rock bed (elevation
) was
(
) and
(
), respectively. For the condition considered by
Figure 7,
and
were both lower than the top of the distribution pipe. Other conditions were analyzed as provided below.
From the recorded data, the water surface inside the distribution pipe and that in the inlet structure were very close to each other in elevation as the difference of the velocity head was proven to be negligible. This implied that the driving head was the water surface elevation difference
. The driving head was constant anywhere below the rock bed water surface
. The driving head above
was simply the hydrostatic pressure of the water column above
, with zero at the top of the water column and linearly increasing to
at the elevation of
. The mean driving head (
) acting on the pipe can thus be derived in Equation (6) below.
The effective pipe length was simply provided by Equation (7):
Other than the condition depicted in
Figure 7, four other possible conditions were analyzed as illustrated in
Figure 8. All items in
Figure 8 were defined previously, except for
and
, which indicates the distance from the water surface in the inlet structure to the top and the inlet of the distribution pipe (along its centerline) in
Figure 8b, respectively. Note that conditions with either
or
below the top of the distribution pipe inlet were excluded from consideration as the effective length of water in the pipe of such conditions cannot be based on the pipe length with a fully wetted perimeter like that of the other considered conditions.
Analyses based on
Figure 8a were similar to those done for the water column above
in
Figure 7, with the mean driving head and the effective pipe length calculated by Equations (8) and (9) below:
Intense storms created conditions depicted by
Figure 8b–d, where the water elevation in the inlet structure builds up quickly. The distribution pipe was completely full, but water in the rock infiltration bed can still be relatively shallow. Similar to Equation (8), the mean driving head for
Figure 8b was provided by Equation (10) below, and the effective pipe length
is simply the length of the whole pipe.
Figure 8c has a form similar to that of
Figure 7 with the mean driving head for
Figure 8c provided by Equation (11) below, while the effective pipe length (
) is the length of the whole pipe (
).
where
is the length of pipe under
and is given by
.
The last condition (
Figure 8d) had a constant driving head throughout the distribution pipe because the whole pipe was submerged, thus
, and the effective pipe length
is the length of the whole pipe
.
4. Results
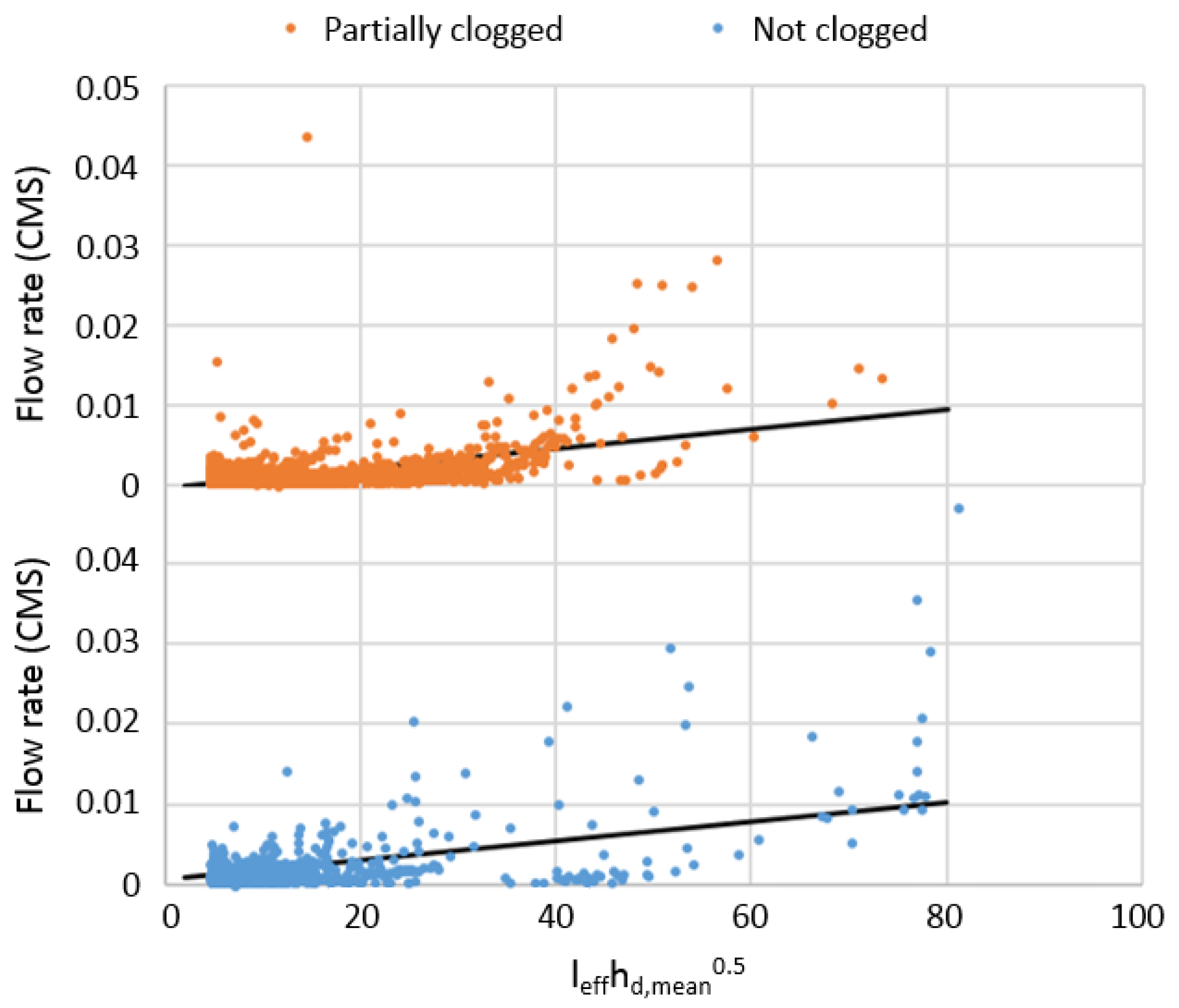
Variations of orifice performance can be examined by plotting the measured flow rate against
, as shown by
Figure 9 with the data with zero flow excluded. All data from November 2016 to April 2018 was utilized in
Figure 9. According to Equation (4), the flow rate Q divided by
in
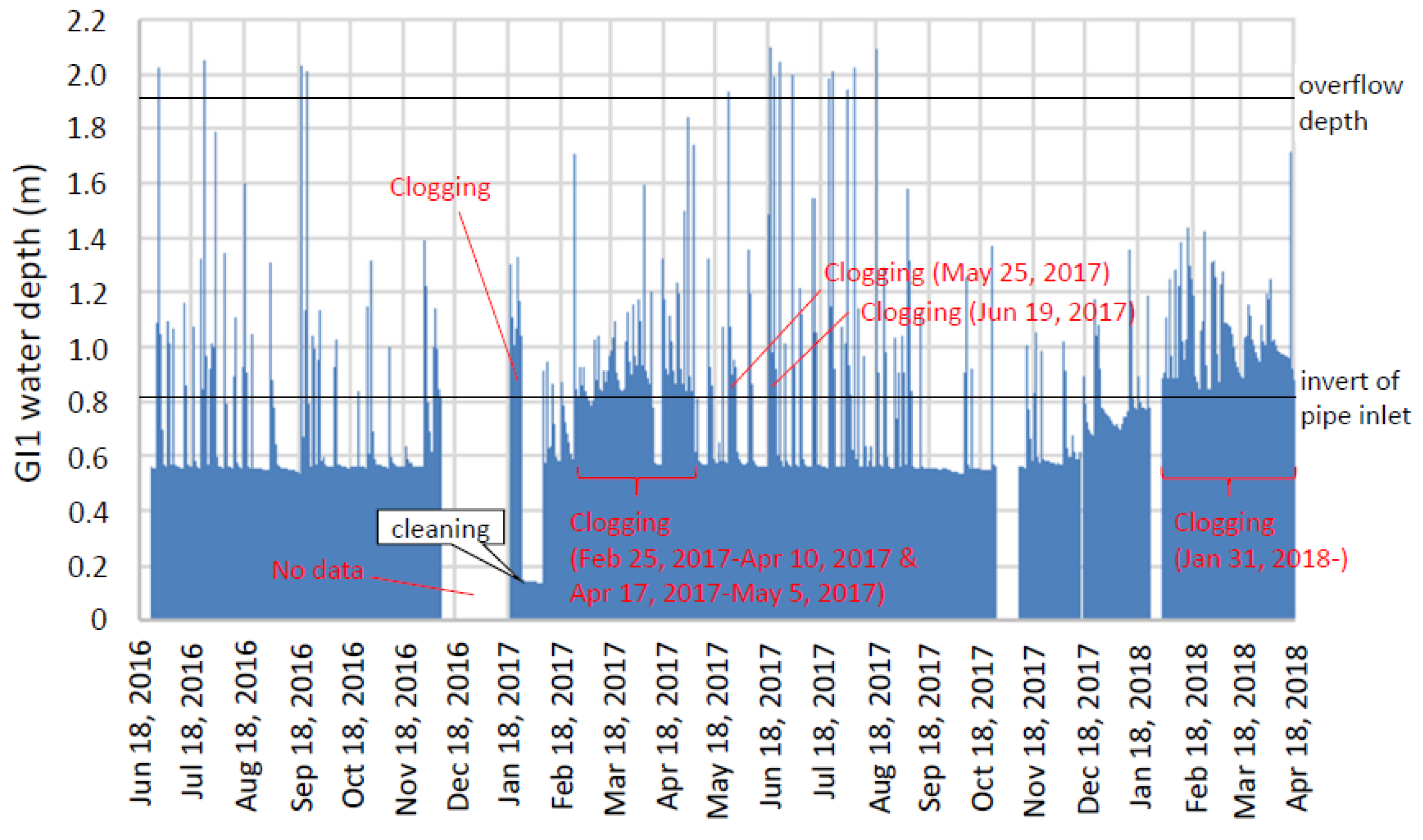
Figure 9 represents performance. The dates of partial clogging and no clogging were determined from
Figure 4. Thick black lines in
Figure 9 represent the linear regression lines generated through ANCOVA, as discussed below.
appeared to be a strong predictor for flow rate with
p < 0.0001 for both the non-clogging and partial clogging data. ANCOVA (ANalysis of COVAriance) was utilized to examine the effect of partial clogging on the distribution of the pipe performance. Similar to the popular ANOVA (ANalysis Of VAriance), ANCOVA tests the null hypothesis that two population means are equal, but ANCOVA considers the effect of a “covariate”, which is likely to be correlated with the dependent variable [
28]. Such a covariate was coded as one dummy variable of either 0 (represents no clogging) or 1 (represents partial clogging) in the linear regressions in this research. The shift of linear regression lines due to the covariate in
Figure 9 between periods with and without clogging appeared to be small through visual inspections, but statistical analyses by ANCOVA showed strong evidence (
p < 0.0001) that partial clogging, on average, had an impact on performance.
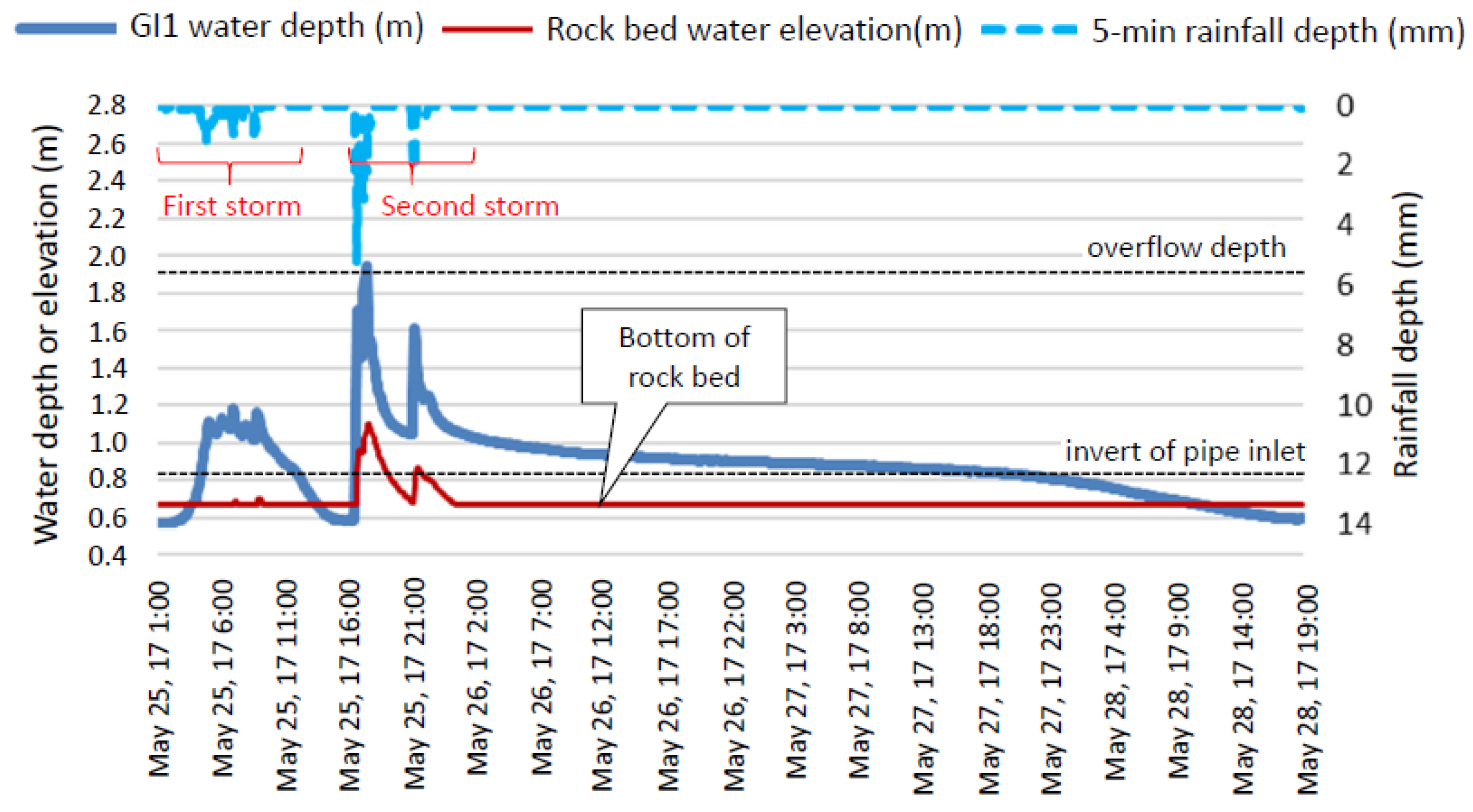
The above ANCOVA result was based on all data, with a large portion of the data from periods with very slow drawdown of water level in the inlet structure after the storms ended, as illustrated in
Figure 5. As the focus of this research was on how partial clogging can affect orifice performance during larger storm events (when overflow occurs), the results from periods with slow drawdown and lower rainfall intensities were of less interest.
Table 1 provides the ANCOVA results with the different rainfall intensity criteria below which shows which data entries were excluded. The
p-value showing no difference in performance between no clogging and partial clogging were in bold.
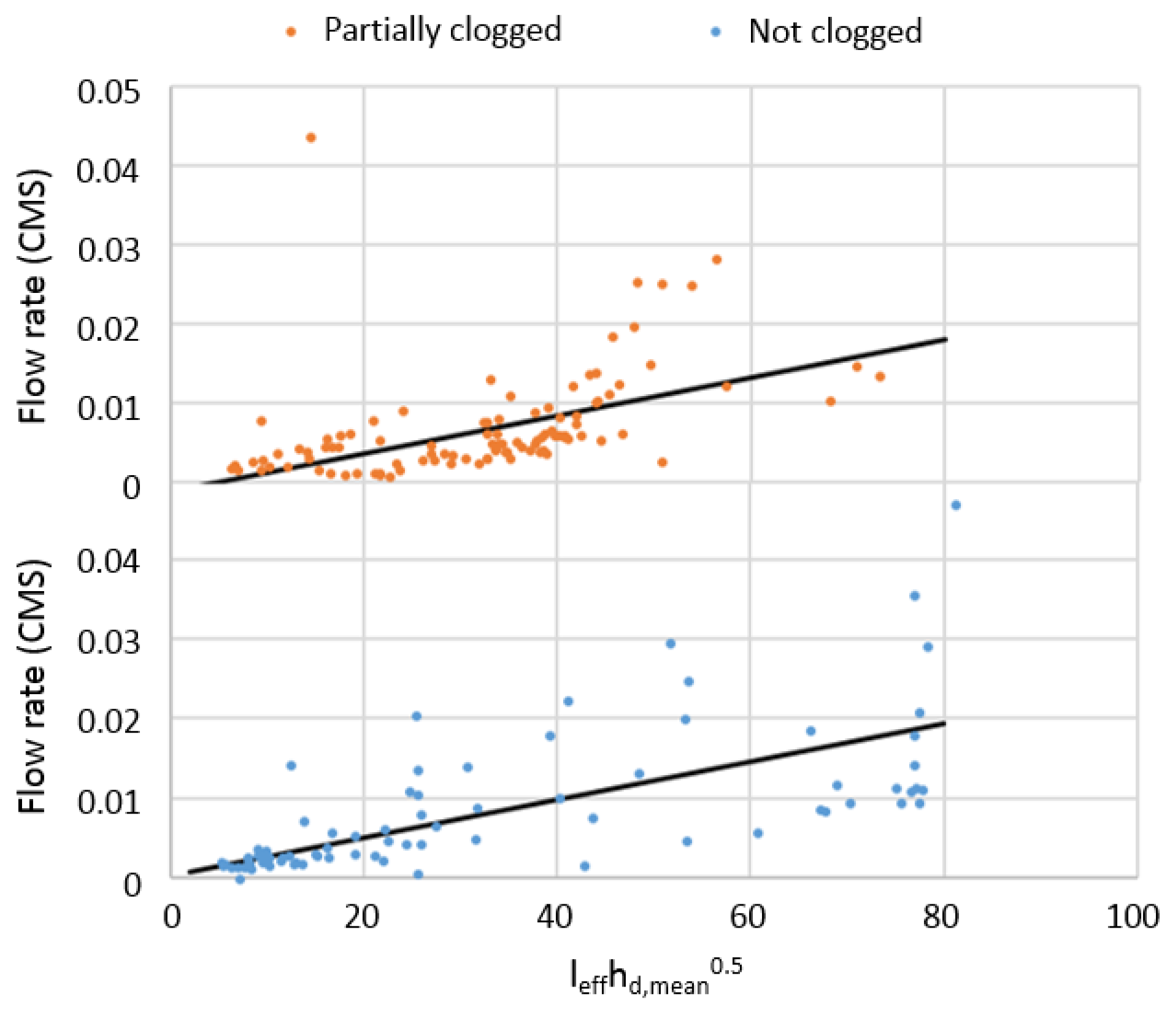
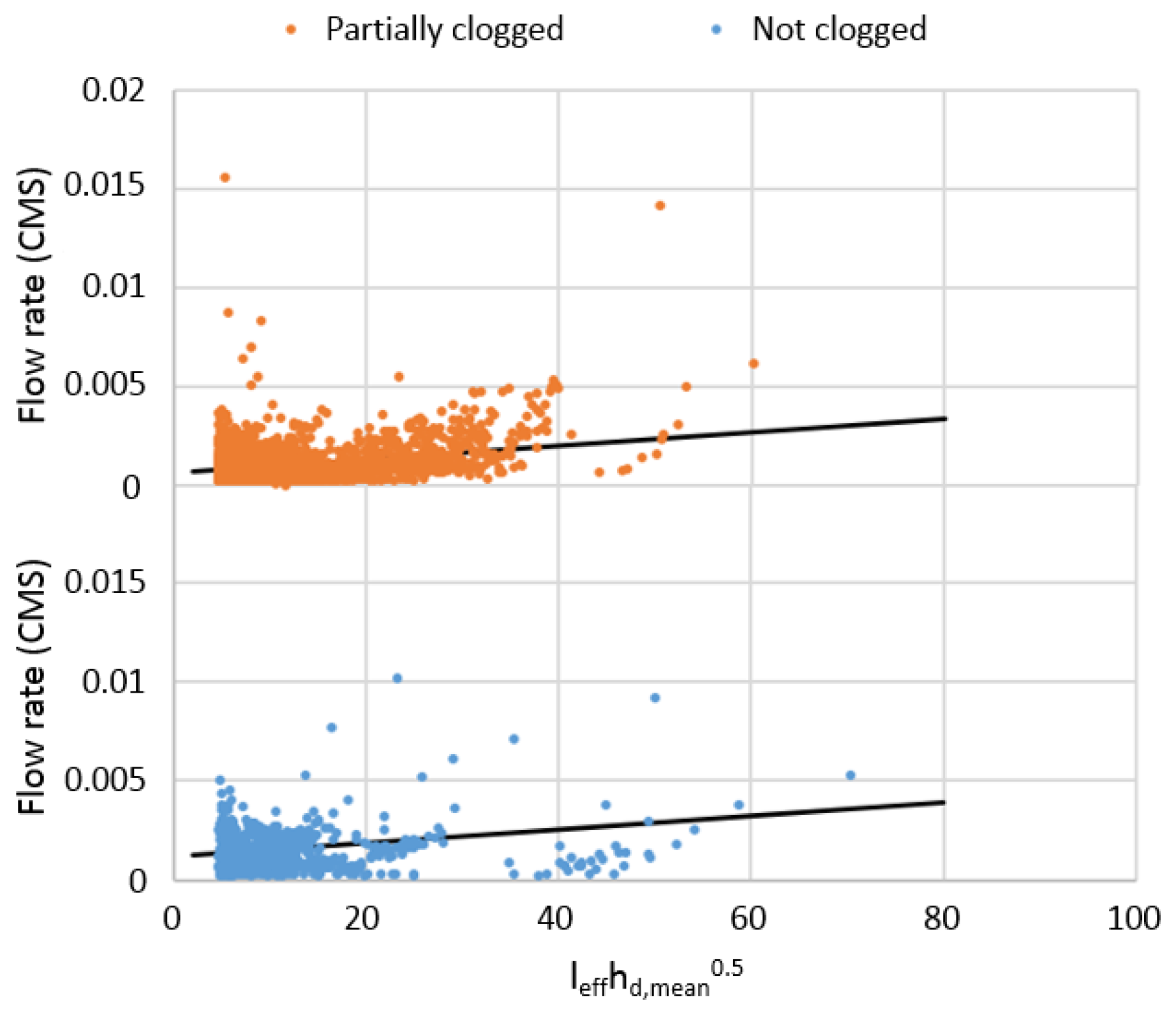
Table 1 shows that even though partial clogging had a significant effect during dry periods or low-intensity storms, its effect declines as the storm intensity increases. When rainfall intensity was higher than approximately 0.65 mm/5 min, the effect of partial clogging was not statistically distinguishable, and thus did not impact system performance. The distribution of data with a rainfall intensity criterion of 0.65 mm/5 min is provided in
Figure 10, while the distribution of data with a rainfall intensity lower than the criterion was provided in
Figure 11 for comparison. Thick black lines represent the linear regression lines generated through ANCOVA. Please note that the scale on the
y-axis in
Figure 11 is different from that of
Figure 9 or
Figure 11. Again, the shift of linear regression lines due to the covariate of clogging appeared to be small in both figures through visual inspection; however, statistical analyses by ANCOVA provided clear evidence that the effects of clogging could not be distinguished (
p = 0.152,
Table 1) in
Figure 10 but were significant (
p < 0.0001) in
Figure 11.
5. Discussion
First, the drawdown data of the infiltration bed were examined. The relation between water depth and drawdown rate exhibited little variation throughout the observation period, thus showing no clogging of the infiltration bed. Therefore, the infiltration bed had no influence in explaining the results from the above analyses.
Second, the Froude number was examined. It was determined that 99.89% of non-zero flow during storms was in the subcritical state; therefore, the effect from switching between subcritical and supercritical states could be ignored.
The records of subsurface maintenance done in the past were then examined to explain the results from the analyses. The archived video observation (20 June 2016) showed a significant quantity of debris deposited close to the 90-degree turn of the pipe near the entrance, as shown in
Figure 12a. After passing the debris pile, the distribution pipe was generally clean, as
Figure 12b shows. Another subsurface maintenance performed on 25 January 2017 found more debris, and the debris was piled mostly in the lower (i.e., close to the inlet) 30 m of the pipe. The spatially uneven distribution of debris might be explained by the reversed slope of the distribution pipe that would bring most debris back to the entrance.
Since most debris was accumulated near the lowest point of the distribution pipe, it appeared to cause partial clogging as water lower than the elevation of the debris cannot enter the rock infiltration bed through the orifices at the bottom section of the pipe. However, during storm events, the incoming water either moved the debris block, thus exposing the orifices, or overtopped the debris block thus accessing the remaining distribution pipe. Such moving of debris can cause the partial clogging to break temporarily (e.g., 10 April 2017–17 April 2017) as observed in
Figure 4.
In
Figure 12a, it was visible that a significant portion of debris appeared to be leaves and paper with only a small portion being plastic, even though a trash guard had been installed in the inlet structure to minimize the amount of leaves entering the inlet structure with runoff. Due to the ample supply of fallen leaves in late autumn in Philadelphia, the debris pile would potentially continue to grow in winter if the leaves can get past the trash guard.
As the supply of leaves is ample in winter and most winter storms are low in both depth and intensity, the clogging effect was significant in winter. As larger storms appeared in summer, the leaves and debris could be pushed into the higher end of the pipe, thus exposing the orifices. No subsurface cleaning was performed after January 2017 in the observation period; therefore, such mechanisms can sustain the pipe performance (during larger storms) for at least a full year. In any event, scheduled cleaning of the distribution pipe is recommended to reduce the amount of accumulated debris as the debris does not disappear completely and could still cause short episodes of partial clogging during the summer. If left unchecked, the accumulated debris may block the distribution pipe and cause a significant drop in system performance.
6. Conclusions
Partial clogging of a distribution pipe system was found by both visual observations and data analyses as evidenced by continuous ponding in the inlet structure, partially submerging the entrance of the distribution pipe. The impact on orifice performance of the distribution pipe from such partial clogging was examined by plotting the flow rate vs. where is the mean driving head and the effective pipe length. ANCOVA was used to determine the impact of partial clogging on orifice performance of the distribution pipe. Although partial clogging was found to exhibit a statistically significant effect on pipe performance, its effect declined with higher rainfall intensity, and was eventually not distinguishable when rainfall intensity was higher than approximately 0.65 mm/5 min. From ongoing research, the system overflowed only when the rainfall intensity was higher than approximately 3.3 mm/5 min. Therefore, partial clogging did not have any detrimental effect on the overflow generating characteristics of this system.
The subsurface maintenance records showed that most debris was piled up near the lower portion of the distribution pipe, which caused the observed partial clogging. However, the incoming water during larger storms (rainfall intensity higher than approximately 0.65 mm/5 min) either moved the debris block thus exposing the orifices, or overtopped the debris block thus accessing the remaining distribution pipe, so the performance of the distribution system during larger storms was not affected. It was hypothesized that most debris was composed of leaves, which are in abundant supply during late fall and early winter in Philadelphia. This explained why the occurrence of partial clogging was most frequent in winter.
Partial clogging was difficult to completely eliminate even with the installation of a trash guard and cleaning of the distribution pipe (the first clogging happened only one month after cleaning in January 2017). For drainage systems with space limitations such as the system under examination by this research, effective pretreatment is often not an option. Therefore, it poses a question to maintenance staff and practitioners—do we need to multiply the maintenance cost to eliminate all observed partial clogging? The result of this research implied that it is not necessary to increase the cleaning frequency to eliminate all partial clogging. In Philadelphia or locations with similar climate and flora, a typical trash guard and regular (once to twice per year) pipe cleaning was sufficient to keep the distribution pipe system at a satisfactory performance. Typical partial clogging does not harm the system performance during storms, when sufficient pipe delivery performance is needed the most.
However, such guidelines are qualitative, and more specific quantitative directives are required. For future research, two directions are suggested on this topic:
Find the minimal maintenance schedule needed to maintain the performance, and
Find the relations between the distribution pipe specification, pipe diameter, orifice size, orifice density), and the minimal needed maintenance schedule, so that a balance between construction cost and maintenance cost can be found.