Drought Analysis in Europe and in the Mediterranean Basin Using the Standardized Precipitation Index
Abstract
1. Introduction
2. Methodology
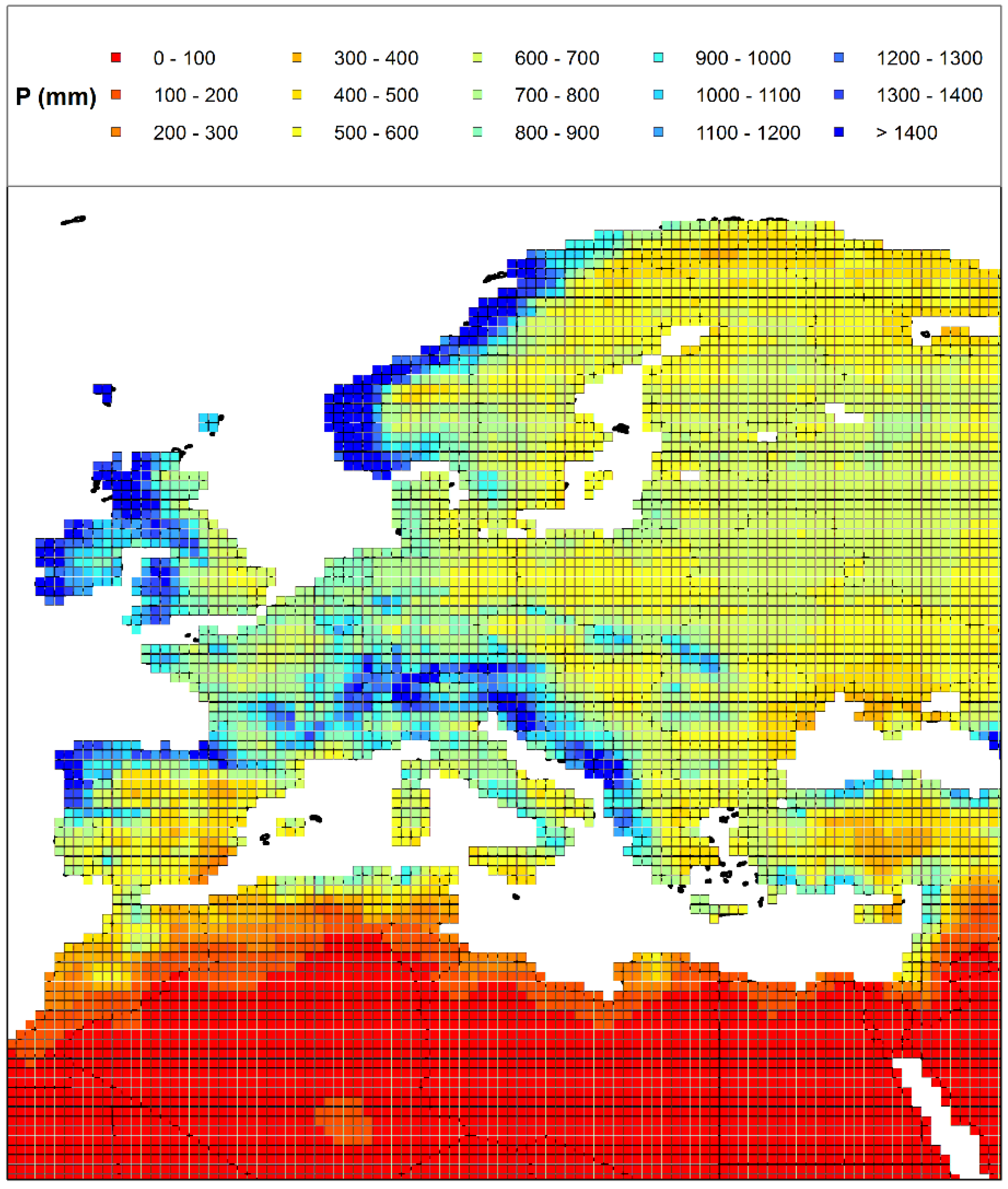
3. Study Area and Data
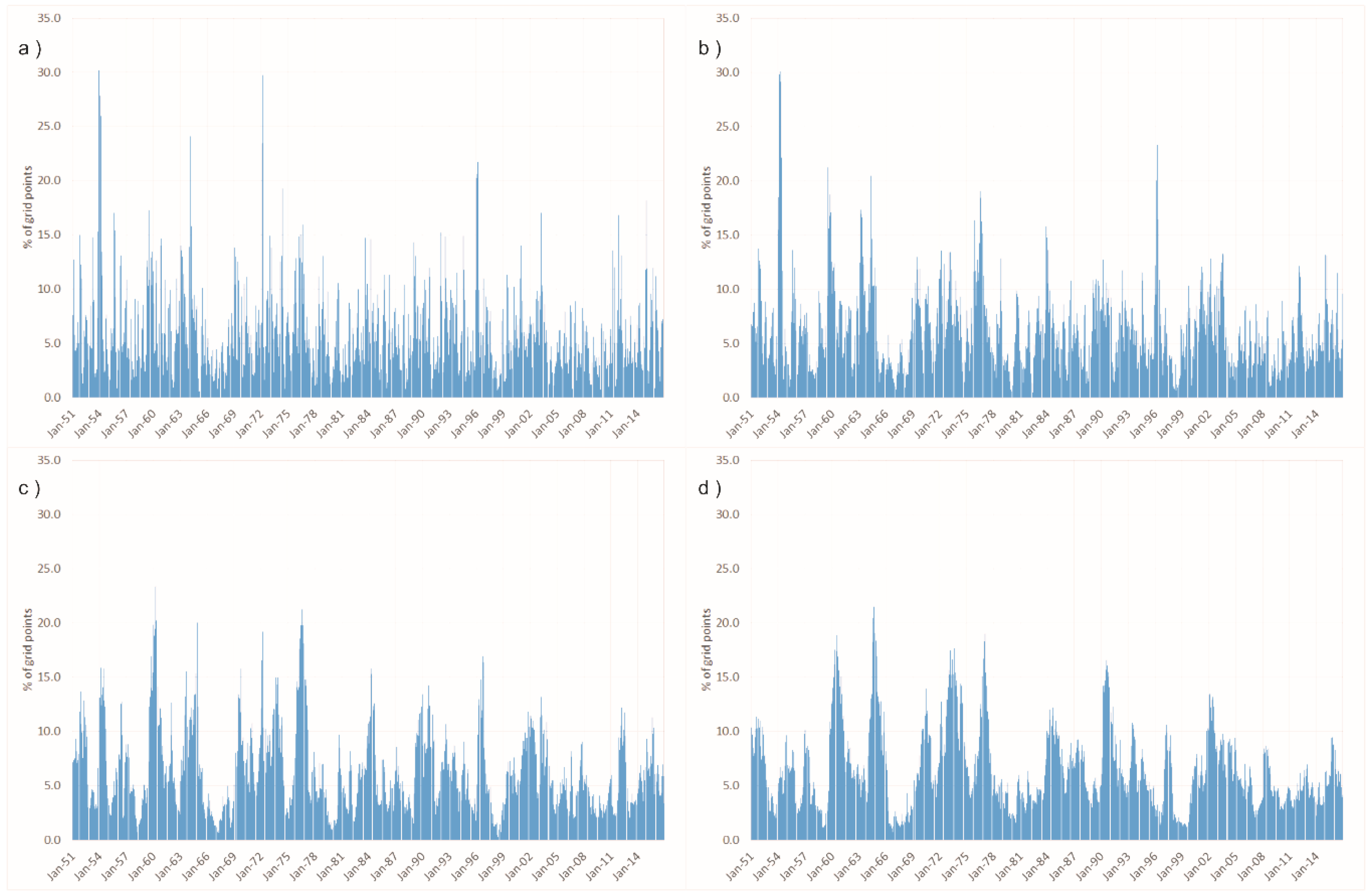
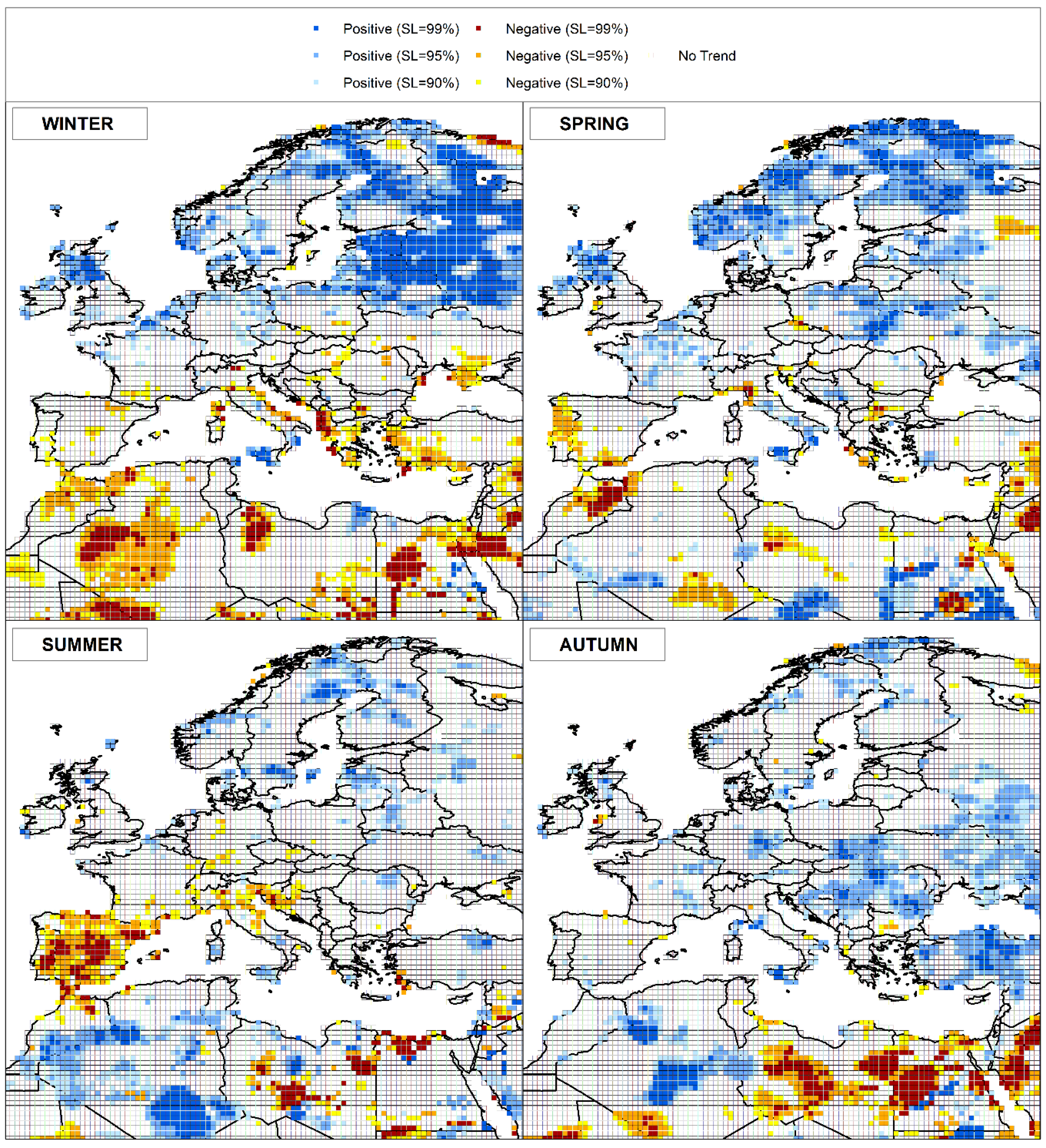
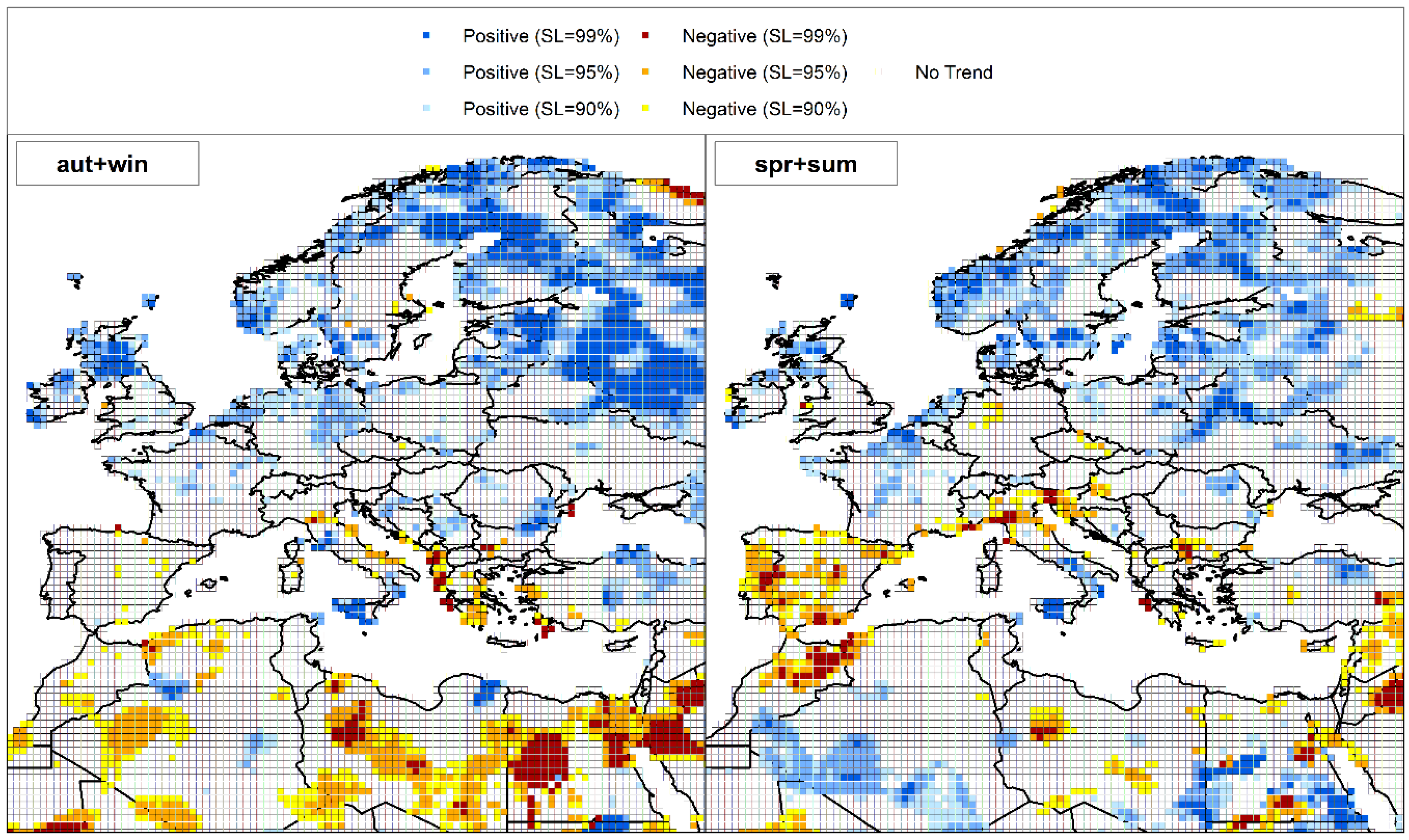
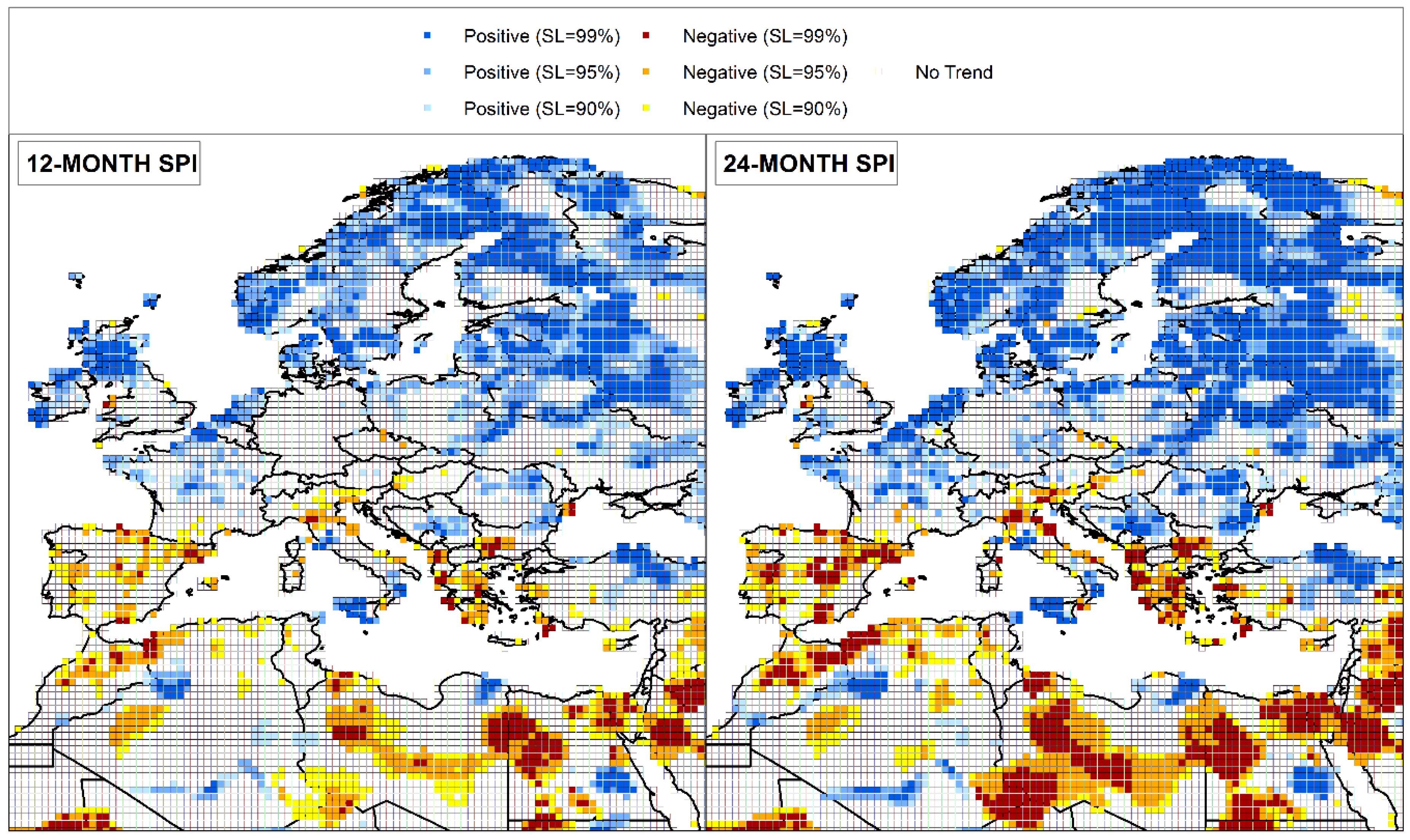
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IPCC. Summary for Policymakers. In Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Estrela, T.; Vargas, E. Drought management plans in the European Union. Water Resour. Manag. 2010, 26, 1537–1553. [Google Scholar] [CrossRef]
- Kreibich, H.; Di Baldassarre, G.; Vorogushyn, S.; Aerts, J.C.J.H.; Apel, H.; Aronica, G.T.; Arnbjerg-Nielsen, K.; Bouwer, L.M.; Bubeck, P.; Caloiero, T.; et al. Adaptation to flood risk: Results of international paired flood event studies. Earth’s Future 2017, 5, 953–965. [Google Scholar] [CrossRef]
- Fang, K.; Gou, X.; Chen, F.; Davi, N.; Liu, C. Spatiotemporal drought variability for central and eastern Asia over the past seven centuries derived from tree-ring based reconstructions. Q. Int. 2013, 283, 107–116. [Google Scholar] [CrossRef]
- Hua, T.; Wang, X.M.; Zhang, C.X.; Lang, L.L. Temporal and spatial variations in the Palmer Drought Severity Index over the past four centuries in arid, semiarid, and semihumid East Asia. Chin. Sci. Bull. 2013, 58, 4143–4152. [Google Scholar] [CrossRef]
- Minetti, J.L.; Vargas, W.M.; Poblete, A.G.; de la Zerda, L.R.; Acuña, L.R. Regional droughts in southern South America. Theor. Appl. Climatol. 2010, 102, 403–415. [Google Scholar] [CrossRef]
- Feng, S.; Hu, Q.; Oglesby, R.J. Influence of Atlantic sea surface temperatures on persistent drought in North America. Clim. Dyn. 2011, 37, 569–586. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Kohn, I.; Stahl, K.; van Loon, A.F. A European Drought Reference (EDR) Database: Design and Online Implementation; DROUGHT-R&SPI Deliverable D1.1; Technical Report No. 12. European Drought Centre, 2013. Available online: http://www.eu-drought.org/media/default.aspx/emma/org/10832306/DROUGHT-RSPI+Techincal+Report+No++12+European+Drought+Reference+Database+Stagge+et+al++30Sept2013.pdf (accessed on 4 July 2018).
- Lloyd-Huhes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Łabędzki, L. Estimation of local drought frequency in central Poland using the standardized precipitation index SPI. Irrig. Drain. 2007, 56, 67–77. [Google Scholar] [CrossRef]
- Szalai, S.; Szinell, C. Comparison of two drought indices for drought monitoring in Hungary—A case study. In Drought and Drought Mitigation in Europe; Kluwer: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Buttafuoco, G.; Caloiero, T.; Ricca, N.; Guagliardi, I. Assessment of drought and its uncertainty in a southern Italy area (Calabria region). Measurement 2018, 113, 205–210. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. Analysis of Dry Spells in Southern Italy (Calabria). Water 2015, 7, 3009–3023. [Google Scholar] [CrossRef]
- Sirangelo, B.; Caloiero, T.; Coscarelli, R.; Ferrari, E. Stochastic analysis of long dry spells in Calabria (Southern Italy). Theor. Appl. Climatol. 2017, 127, 711–724. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorlogical drought. US Weather Bur. 1965, 45, 1–58. [Google Scholar]
- Tsakiris, G.; Pangalounad, D.; Vangelis, H. A regional drought assessment based on the reconnaissance drought index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. Drought monitoring with multiple time scales. In Proceedings of the 9th Conference on Applied Climatology, Dallas, TX, USA, 15–20 January 1995; pp. 233–236. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multi-scalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index—SPEI. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Shafer, B.A.; Dezman, L.E. Development of a surface water supply index (SWSI) to assess the severity of drought conditions in snow pack runoff areas. In Proceedings of the 50th Annual Western Snow Conference, Reno, NV, USA, 19–23 April 1982; pp. 164–175. [Google Scholar]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Van Rooy, M.P. A rainfall anomaly index independent of time and space. Notos 1965, 14, 43–48. [Google Scholar]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef]
- Tabari, H.; Abghari, H.; Hosseinzadeh Talaee, P. Temporal trends and spatial characteristics of drought and rainfall in arid and semi-arid regions of Iran. Hydrol. Process. 2012, 26, 3351–3361. [Google Scholar] [CrossRef]
- Bayissa, Y.A.; Moges, S.A.; Xuan, Y.; Van Andel, S.J.; Maskey, S.; Solomatine, D.P.; Griensven, A.; Van Tadesse, T. Spatio-temporal assessment of meteorological drought under the influence of varying record length: The case of Upper Blue Nile Basin, Ethiopia. Hydrol. Sci. J. 2015, 60, 1927–1942. [Google Scholar] [CrossRef]
- Capra, A.; Scicolone, B. Spatiotemporal variability of drought on a short–medium time scale in the Calabria Region (Southern Italy). Theor. Appl. Climatol. 2012, 3, 471–488. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Differences in spatial patterns of drought on different time sales: An analysis of the Iberian Peninsula. Water Resour. Manag. 2006, 20, 37–60. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Wilhite, D.A.; Svoboda, M.D. The effect of the length of record on the standardized precipitation index calculation. Int. J. Climatol. 2005, 25, 505–520. [Google Scholar] [CrossRef]
- Guttman, N.B. Comparing the Palmer drought severity index and the standardized precipitation Index. J. Am. Water Res. Assoc. 1998, 34, 113–121. [Google Scholar] [CrossRef]
- Hayes, M.J.; Svoboda, M.; Wilhite, D.A.; Vanyarkho, O. Monitoring the 1996 drought using the SPI. Bull. Am. Meteorol. Soc. 1999, 80, 429–438. [Google Scholar] [CrossRef]
- Guttman, N.B. Accepting the standardized precipitation index: A calculating algorithm. J. Am. Water Resour. Assoc. 1999, 35, 311–323. [Google Scholar] [CrossRef]
- Cancelliere, A.; Di Mauro, G.; Bonaccorso, B.; Rossi, G. Drought forecasting using the Standardised Precipitation Index. Water Resour. Manag. 2007, 21, 801–819. [Google Scholar] [CrossRef]
- Khan, S.; Gabriel, H.F.; Rana, T. Standard precipitation index to track drought and assess impact of rainfall on watertables in irrigation areas. Irrig. Drain. Syst. 2008, 22, 159–177. [Google Scholar] [CrossRef]
- Manatsa, D.; Mukwada, G.; Siziba, E.; Chinyanganya, T. Analysis of multidimensional aspects of agricultural droughts in Zimbabwe using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2010, 102, 287–305. [Google Scholar] [CrossRef]
- Golian, S.; Mazdiyasni, O.; AghaKouchak, A. Trends in meteorological and agricultural droughts in Iran. Theor. Appl. Climatol. 2015, 119, 679–688. [Google Scholar] [CrossRef]
- Zhai, J.; Su, B.; Krysanova, V.; Vetter, T.; Gao, C.; Jiang, T. Spatial variation and trends in pdsi and spi indices and their relation to streamflow in 10 large regions of china. J. Clim. 2010, 23, 649–663. [Google Scholar] [CrossRef]
- Zhai, L.; Feng, Q. Spatial and temporal pattern of precipitation and drought in Gansu Province Northwest China. Nat. Hazards 2009, 49, 1–24. [Google Scholar] [CrossRef]
- Caloiero, T. Drought analysis in New Zealand using the standardized precipitation index. Environ. Earth Sci. 2017, 76, 569. [Google Scholar] [CrossRef]
- Caloiero, T. SPI Trend Analysis of New Zealand Applying the ITA Technique. Geosciences 2018, 8, 101. [Google Scholar] [CrossRef]
- Bordi, I.; Fraedrich, K.; Sutera, A. Observed drought and wetness trends in Europe: An update. Hydrol. Earth Syst. Sci. 2009, 13, 1519–1530. [Google Scholar] [CrossRef]
- Trnka, M.; Balek, J.; Štěpánek, P.; Zahradníček, P.; Možný, M.; Eitzinger, J.; Žalud, Z.; Formayer, H.; Turňa, M.; Nejedlík, P.; et al. Drought trends over part of Central Europe between 1961 and 2014. Clim. Res. 2016, 70, 143–160. [Google Scholar] [CrossRef]
- Spinoni, J.; Vogt, J.V.; Naumann, G.; Barbosa, P.; Dosio, A. Will drought events become more frequent and severe in Europe? Int. J. Climatol. 2018, 38, 1718–1736. [Google Scholar] [CrossRef]
- Livada, I.; Assimakopoulos, V.D. Spatial and temporal analysis of drought in Greece using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
- Sönmez, F.K.; Kömüscü, A.Ü.; Erkan, A.; Turgu, E. An analysis of spatial and temporal dimension of drought vulnerability in Turkey using the Standardized Precipitation Index. Nat. Hazards 2005, 35, 243–264. [Google Scholar] [CrossRef]
- Mendicino, G.; Senatore, A.; Versace, P. A Groundwater Resource Index (GRI) for drought monitoring and forecasting in a Mediterranean climate. J. Hydrol. 2008, 357, 282–302. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Caloiero, T. Drought events at different timescales in southern Italy (Calabria). J. Maps 2014, 10, 529–537. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Analyses of Drought Events in Calabria (Southern Italy) Using Standardized Precipitation Index. Water Resour. Manag. 2015, 29, 557–573. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. An Analysis of the Occurrence Probabilities of Wet and Dry Periods through a Stochastic Monthly Rainfall Model. Water 2016, 8, 39. [Google Scholar] [CrossRef]
- Caloiero, T.; Sirangelo, B.; Ferrari, E.; Coscarelli, R. Occurrence Probabilities of Wet and Dry Periods in Southern Italy through the SPI Evaluated on Synthetic Monthly Precipitation Series. Water 2018, 10, 336. [Google Scholar] [CrossRef]
- Edwards, D.; McKee, T. Characteristics of 20th Century Drought in the United States at Multiple Scale; Atmospheric Science Paper 634; Department of Atmospheric Science Colorado State University: Fort Collins, CO, USA, 1997. [Google Scholar]
- Bonaccorso, B.; Bordi, I.; Cancelliere, A.; Rossi, G.; Sutera, A. Spatial variability of drought: An analysis of SPI in Sicily. Water Resour. Manag. 2003, 17, 273–296. [Google Scholar] [CrossRef]
- Angelidis, P.; Maris, F.; Kotsovinos, N.; Hrissanthou, V. Computation of drought index SPI with Alternative Distribution Functions. Water Resour. Manag. 2012, 26, 2453–2473. [Google Scholar] [CrossRef]
- Thom, H.C.S. A note on the gamma distribution. Mon. Weather Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications, INC.: New York, NY, USA, 1970. [Google Scholar]
- National Drought Mitigation Center (NDMC) University of Nebraska. Available online: http://drought.unl.edu (accessed on 4 July 2018).
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin & Company Limited: London, UK, 1962. [Google Scholar]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M. GPCC Full Data Monthly Product Version 2018 at 0.5°: Monthly Land-Surface Precipitation from Rain-Gauges Built on GTS-Based and Historical Data; Deutscher Wetterdienst: Offenbach am Main, Germany, 2018. [Google Scholar] [CrossRef]
- Beck, C.; Grieser, J.; Rudolf, B. A New Monthly Precipitation Climatology for the Global Land Areas for the Period 1951 to 2000. In Klimastatusbericht 2004; Deutscher Wetterdienst: Offenbach, Germany, 2005; pp. 181–190. [Google Scholar]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global landsurface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth Syst. Sci. Data 2013, 5, 921–998. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land-surface precipitation climatology based on quality-controlled in-situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Caloiero, T.; Caloiero, P.; Frustaci, F. Long-term precipitation trend analysis in Europe and in the Mediterranean basin. Water Environ. J. 2018. [Google Scholar] [CrossRef]
- Herweijer, C.; Seager, R. The global footprint of persistent extra-tropical drought in the instrumental era. Int. J. Climatol. 2008, 28, 1761–1774. [Google Scholar] [CrossRef]
- Briffa, K.R.; Jones, P.D.; Hulme, M. Summer moisture variability across Europe, 1892–1991: An analysis based on the Palmer drought severity index. Int. J. Climatol. 1994, 14, 475–506. [Google Scholar] [CrossRef]
- Van der Schrier, G.; Briffa, K.R.; Jones, P.D.; Osborn, T.J. Summer moisture variability across Europe. J. Clim. 2006, 19, 2818–2834. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Lorenzo-Lacruz, J.; El Kenawy, A.; Azorin-Molina, C.; Morán-Tejeda, E.; Pasho, E.; Zabalza, J.; Begueria, S.; Angulo-Martinez, M. The NAO impact on droughts in the Mediterranean region. In Hydro-Logical, Socioeconomic and Ecological Impacts of the North Atlantic Oscillation in the Mediterranean Region Advances in Global Change Research; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Hoerling, M.; Eischeid, J.; Perlwitz, J.; Quan, X.; Zhang, T.; Pegion, P. On the increased frequency of Mediterranean drought. J. Clim. 2012, 25, 2146–2161. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Vogt, J.V.; Barbosa, P. The biggest drought events in Europe from 1950 to 2012. J. Hydrol. Reg. Stud. 2015, 3, 509–524. [Google Scholar] [CrossRef]
- Labudová, L.; Labuda, M.; Takáč, J. Comparison of SPI and SPEI applicability for drought impact assessment on crop production in the Danubian Lowland and the East Slovakian Lowland. Theor. Appl. Clim. 2017, 128, 491–506. [Google Scholar] [CrossRef]
- Woollings, T.; Hannachi, A.; Hoskins, B. Atlantic eddy-driven jet stream. Q. J. R. Meteorol. Soc. 2010, 136, 856–868. [Google Scholar] [CrossRef]
- Bader, J.; Mesquita, M.D.S.; Hodges, K.I.; Keenlyside, N.; Østerhus, S.; Miles, M. A review on Northern Hemisphere seaice, storminess and the North Atlantic Oscillation: Observations and projected changes. Atmos. Res. 2011, 101, 809–834. [Google Scholar] [CrossRef]
- Trigo, I.F.; Davies, T.D.; Bigg, G.R. Decline in Mediterranean rainfall caused by weakening of mediterranean cyclones. Geophys. Res. Lett. 2000, 27, 2913–2916. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Mancini, M. Precipitation change in Southern Italy linked to global scale oscillation indexes. Nat. Hazards Earth Syst. Sci. 2011, 11, 1683–1694. [Google Scholar] [CrossRef]
- Ferrari, E.; Caloiero, T.; Coscarelli, R. Influence of the North Atlantic Oscillation on winter rainfall in Calabria (southern Italy). Theor. Appl. Climatol. 2013, 114, 479–494. [Google Scholar] [CrossRef]
- Quadrelli, R.; Pavan, V.; Molteni, F. Wintertime variability of Mediterranean precipitation and its links with large-scale circulation anomalies. Clim. Dyn. 2001, 17, 457–466. [Google Scholar] [CrossRef]
- Mariotti, A.; Struglia, M.V.; Zeng, N.; Lau, K.M. The hydrological cycle in the Mediterranean region and implications for the water budget of the Mediterranean Sea. J. Clim. 2002, 15, 1674–1690. [Google Scholar] [CrossRef]
- Paredes, D.; Trigo, R.M.; Garcia-Herrera, R.; Trigo, I.F. Understanding precipitation changes in Iberia in early Spring: Weather typing and storm-tracking approaches. J. Hydrometeorol. 2005, 7, 101–113. [Google Scholar] [CrossRef]
- Jung, T.; Hilmer, M. The link between the North Atlantic Oscillation and Arctic sea ice export through Fram Strait. J. Clim. 2001, 14, 3932–3943. [Google Scholar] [CrossRef]
- Giannini, A.; Saravanan, R.; Chang, P. Oceanic forcing of Sahel rainfall on interannual to interdecadal time scales. Science 2003, 302, 1027–1030. [Google Scholar] [CrossRef] [PubMed]
| SPI Value | Class | Probability (%) |
|---|---|---|
| SPI ≥ 2.00 | Extremely wet | 2.3 |
| 1.50 ≤ SPI < 2.00 | Severely wet | 4.4 |
| 1.00 ≤ SPI < 1.50 | Moderately wet | 9.2 |
| 0.00 ≤ SPI < 1.00 | Mildly wet | 34.1 |
| −1.00 ≤ SPI < 0.00 | Mild drought | 34.1 |
| −1.50 ≤ SPI < −1.00 | Moderate drought | 9.2 |
| −2.00 ≤ SPI < −1.50 | Severe drought | 4.4 |
| SPI < −2.00 | Extreme drought | 2.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caloiero, T.; Veltri, S.; Caloiero, P.; Frustaci, F. Drought Analysis in Europe and in the Mediterranean Basin Using the Standardized Precipitation Index. Water 2018, 10, 1043. https://doi.org/10.3390/w10081043
Caloiero T, Veltri S, Caloiero P, Frustaci F. Drought Analysis in Europe and in the Mediterranean Basin Using the Standardized Precipitation Index. Water. 2018; 10(8):1043. https://doi.org/10.3390/w10081043
Chicago/Turabian StyleCaloiero, Tommaso, Simone Veltri, Paola Caloiero, and Francesco Frustaci. 2018. "Drought Analysis in Europe and in the Mediterranean Basin Using the Standardized Precipitation Index" Water 10, no. 8: 1043. https://doi.org/10.3390/w10081043
APA StyleCaloiero, T., Veltri, S., Caloiero, P., & Frustaci, F. (2018). Drought Analysis in Europe and in the Mediterranean Basin Using the Standardized Precipitation Index. Water, 10(8), 1043. https://doi.org/10.3390/w10081043





