1. Introduction
According to the Intergovernmental Panel on Climate Change (IPCC) Fifth assessment report [
1], global warming will be a considerable issue in the future, resulting in subtle changes in the global water cycle and even the global distribution of water. Furthermore, high intensity human activities have resulted in substantial changes in the land surface conditions of many river basins [
2], thus affecting the mechanism of runoff generation and convergence in basins. Under the joint influence of the above aspects, the observed hydrological time series have changed substantially, which makes the assumption of “stationarity” questionable in traditional hydrological frequency analysis [
3].
Liang et al. [
4] grouped non-stationarity flood frequency methods into two types: indirect and direct methods. The indirect methods are mainly based on the rainfall-runoff relation of the basin as well as the decomposition and composition of time series or the hydrological model to revise the hydrological series to eliminate the influence of climate change and human activities and to finally construct stationary time series. A large amount of literature has carried out studies with the indirect methods [
5,
6,
7,
8]. However, because the direct methods do not need to restore the hydrological time series, they have been widely used. The direct methods can be divided into three methods: the mixed distribution method, time variant moment method [
9,
10,
11] and conditional probability distribution method [
12].
The mixed distribution (MD) method was employed by Singh and Sinclair for the first time [
13]. Although this method was widely used in non-stationary flood frequency analysis, parameter estimation is a substantial limit in this method. Alila and Mtiraoui found that the MD model provided a more satisfactory fitting than a traditional single distribution model in the Gila River Basin [
14]. Meanwhile, the authors noted that the key to ensuring the accuracy of the MD model lies in two aspects. One aspect is to analyze the formation mechanism of floods in detail and to rationally divide the series of hydrological extremes. In some cases, the sub-distributions were divided by the different causes of floods, such as seasonality [
15,
16,
17], or the change point of the hydrological series [
18]. The other aspect is to keep the number of sub-distributions to a minimum, mainly because the increase in sub-distributions will increase the number of parameters and affect the accuracy of the model parameter estimation. Thus, the determination of the estimated parameter is key to the MD model. Various parameter estimation methods were used to address this problem, such as the maximum likelihood method [
19], principle of maximum entropy (POME) [
20], EM/ECM algorithm [
21] and simulated annealing algorithm (SAA) [
22]. These examples illustrate that the application of an intelligent optimization algorithm is more and more widely used in parameter estimation and the accuracy of estimation is improved.
Recently, Yan et al. [
22] considered the time variability of the parameters in the mixed distribution. The authors proposed the time-varying two-component mixed distributions (TTMD), which considers the time variant in both the weighting coefficients of MD and the parameters of individual component distributions. However, the conventional mixed distributions method often uses the continuous gauged flood sequence as the study sample, without considering historical extraordinary flood data. The historical extraordinary floods refer to the rare extraordinary floods that have occurred in history but were not observed by hydrological stations. The peak discharge of historical extraordinary floods can be attained through historical flood investigation generally. Schendal et al. [
23] and Strupczewski et al. [
24] showed that the historical extraordinary flood event has a large influence on the calculation accuracy of flood frequency analysis. Taking historical extraordinary flood events into consideration not only increases the information of the flood samples [
25,
26] but also effectively reduces the uncertainty of flood frequency analysis [
27,
28]. This idea provides an important reference for the design, operation and management of water conservancy projects. However, due to the addition of historical extraordinary floods, the hydrological series has become a discontinuous series. Many scientists have exploited the employment of historical extraordinary flood data in flood frequency analysis for the last few decades [
29,
30]. However, the study of considering both historical extraordinary flood events and non-stationarity of flood series is limited. Machado et al. [
31] used the time-varying model based on Generalized Additive Models for Location, Scale and Shape (GAMLSS) modelling and incorporated the external covariates to analyze the flood frequency of a 400-year flood record from the Tagus River in Spain, which obtained a better fitting Zeng et al. [
18] used the mixed distribution model to handle non-stationarity. The authors divided the series by the change point and added the historical extraordinary flood data into the sub-series before the change point but not in the post-sub-series. In other words, the authors did not consider the influence of historical extraordinary flood events for the sub-series after the change point. However, historical extraordinary flood events are likely to occur at any time, regardless of whether the environment is changing or not.
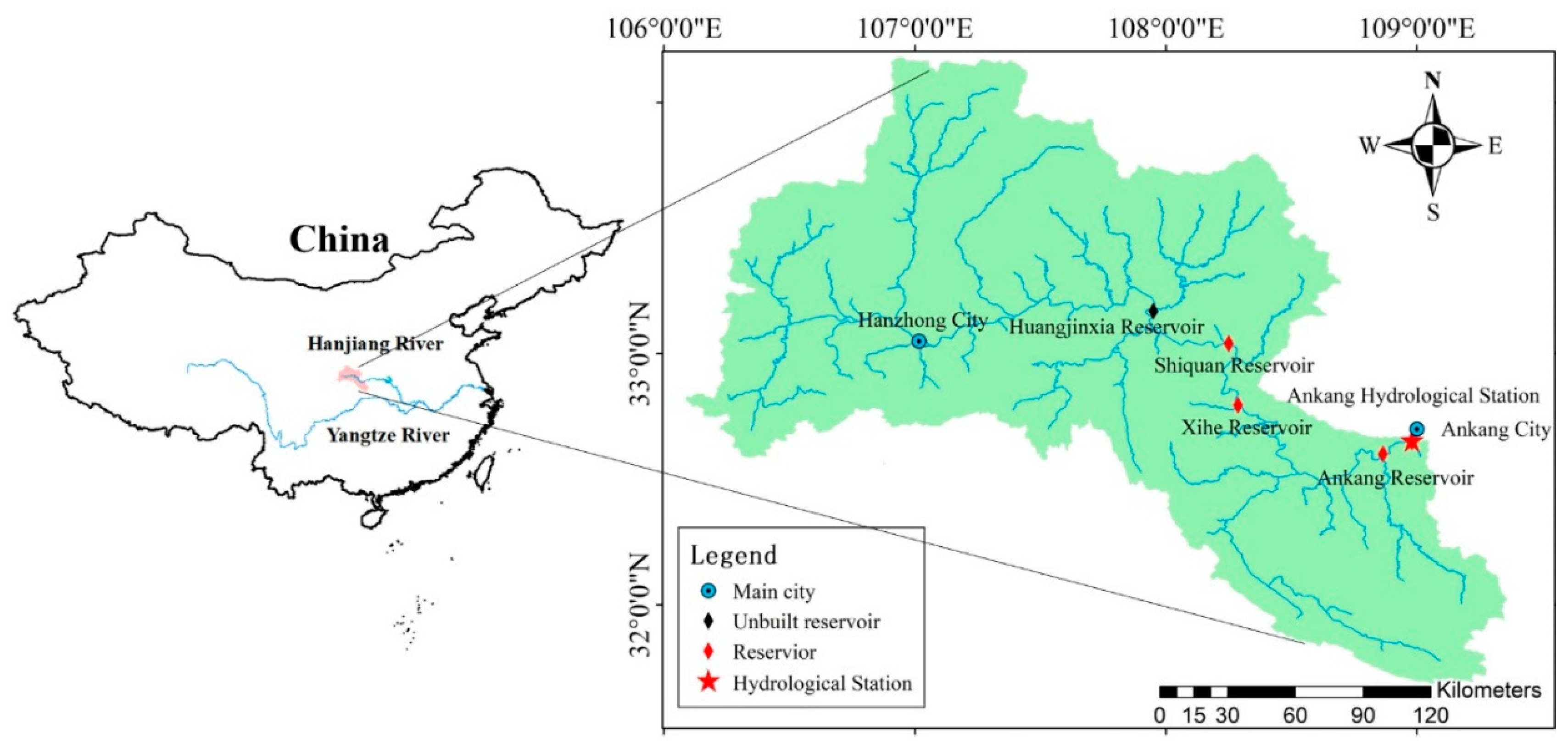
Therefore, the results of design floods will first be compared in this paper in a variety of cases, such as with or without historical extraordinary floods. The novelty of this paper is to propose an improved mixed distribution (IMD) method, which adds historical extraordinary flood events in both sub-series divided by a change point. As case studies, the proposed IMD method will be applied to the Ankang hydrological station in the upper stream of the Hanjiang River Basin, China, where many extraordinary floods have occurred in history. A genetic algorithm will be employed to estimate the optimal parameters. The change in the design flood under different return periods will be compared and analyzed, which will provide a new method for non-stationarity flood frequency analysis considering historical extraordinary flood events.
4. Results and Discussion
4.1. Results of the Variation Diagnosis System
4.1.1. Primary Diagnosis
The Hurst exponent
h values of the flood characteristics series of the Ankang hydrological station for 1968~2013 were calculated and the variation degree was determined according to the classification of variation degree shown in
Table 1. The results are shown in
Table 3. AMPDS, 24-h AMFVS and 72-h AMFVS all exhibit medium variation, which requires further detailed diagnosis.
4.1.2. Detailed Diagnosis
First, we used the Spearman and Kendall rank correlation coefficient methods to investigate the trends in the three flood characteristics series and then adopted the Lee-Heghinian method, Sequential clustering method, Pettitt test, Mann-Kendall test and R/S analysis method to identify the change points in the series. With a 5% significance level, the critical values of the Spearman and Kendall rank correlation statistics were 2.015 and 1.96, respectively. If the absolute value of the statistics exceeds the critical value, it illustrates that the trend component is significant. The positive and negative values of the statistics show that the trends of the series are increasing or decreasing. From the results, as shown in
Table 4, we can learn that the statistics of the two trend analysis methods were negative and the three flood characteristic series have a significant downward trend at the 0.05 significant level. Furthermore, the change points in the flood characteristic series occur between the end of the 1980s and the early 1990s.
4.1.3. Comprehensive Diagnosis
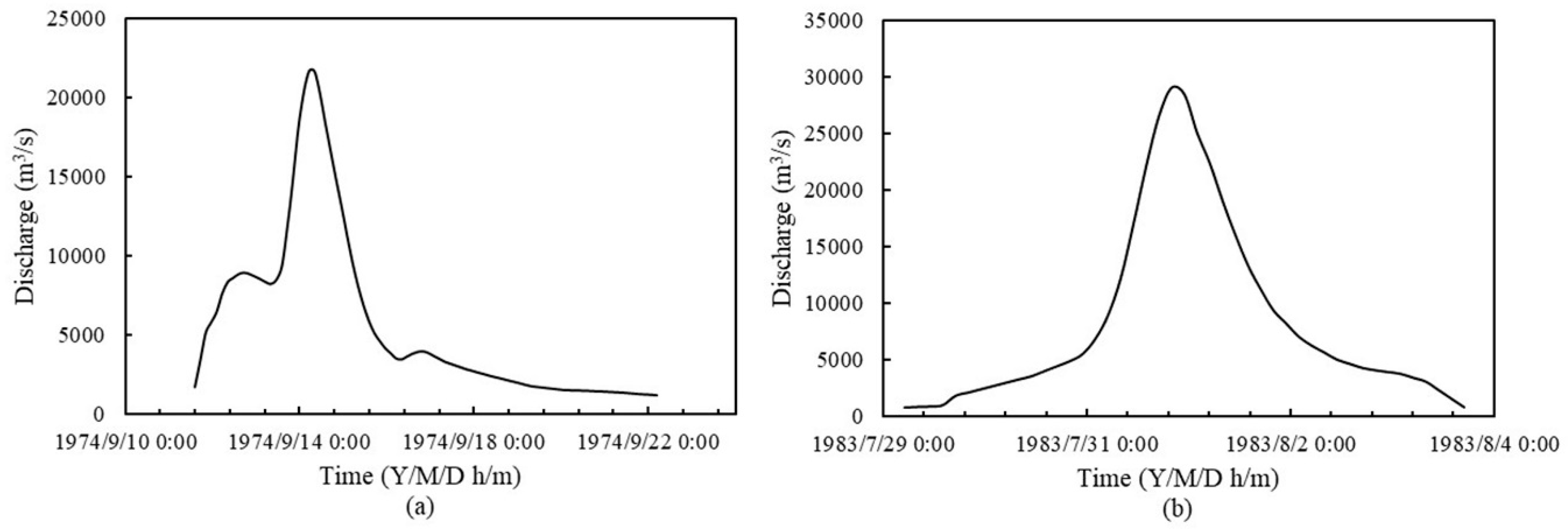
Table 4 illustrates that the possible change point of AMPDS and 24-h AMFVS are in 1987 but the possible change point of 72-h AMFVS appears in 1985 and 1987, which is in accordance with the results of Xiong et al. [
53]. Ankang reservoir construction was started in 1978. It began to store water in 1989 and was finished in 1992. These authors considered that the change point was closely linked with the construction of the Ankang reservoir. Zhang et al. [
2] compared the catchment runoff change during 2001–2010 with the previous 40 years (1960–2000) and noted that the decrease in runoff in the Hanjiang River Basin was mainly due to the significant change in the land surface conditions. In addition, since there are many dam-break floods that inundated the urban areas of Ankang City, water conservancy projects such as reservoirs and dams began to be built to control floods in the 1980s. Especially after the extraordinary floods that occurred in July of 1983, causing serious economic losses, a ten-mile-long dyke began thorough renovation and was completed in 1987. Therefore, the fact that the change points of the three flood characteristic series, AMPDS, 24-h AMFVS and 72-h AMFVS, are all in 1987 is reasonable.
We also used the Kendall rank correlation coefficient method to investigate the trend for the flood series before the change point (1968–1986) and after the change point (1987–2013). The results are shown in
Table 5. From the results, we can see that both trend component of the flood series before and after the change point is not significant. In addition, the trend of flood series before the change point is increasing and the trend of flood series after the change point is decreasing. Thus, the results also verified that the change point is 1987.
Due to the fact that the trends and change point of each flood characteristic series are all significant, the final variation form is determined by calculating the efficiency coefficient, which is given by
where
is the observed hydrological series.
denotes the mean value of the observed hydrological series. For the trend component,
is the fitted value of each point on the trend line.
denotes the change point of the flood characteristic series and the formula of
is expressed by
As
Table 6 shows, the efficiency coefficients of the change points of the flood characteristic series are all larger than those of the trend variation; thus, the final variation forms of all flood characteristic series are change points and the possible change point is 1987.
4.2. Results of Monte Carlo Simulation and Uncertainty Analysis
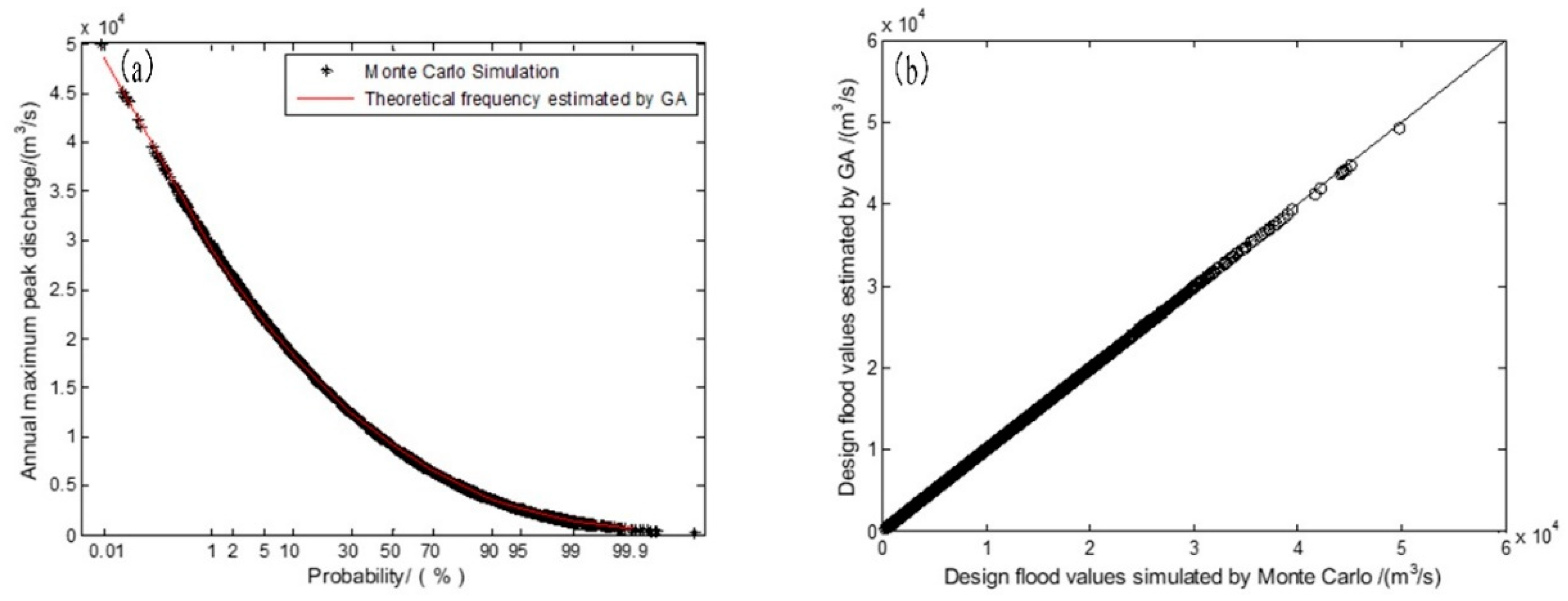
Taking the observed 1968–2013 flood characteristic series with four historical extraordinary flood events as an example, we compared the variation between the design flood value results simulated by Monte Carlo method and estimated by GA. Values of NMB and RRMSE statistical parameters are shown in
Table 7.
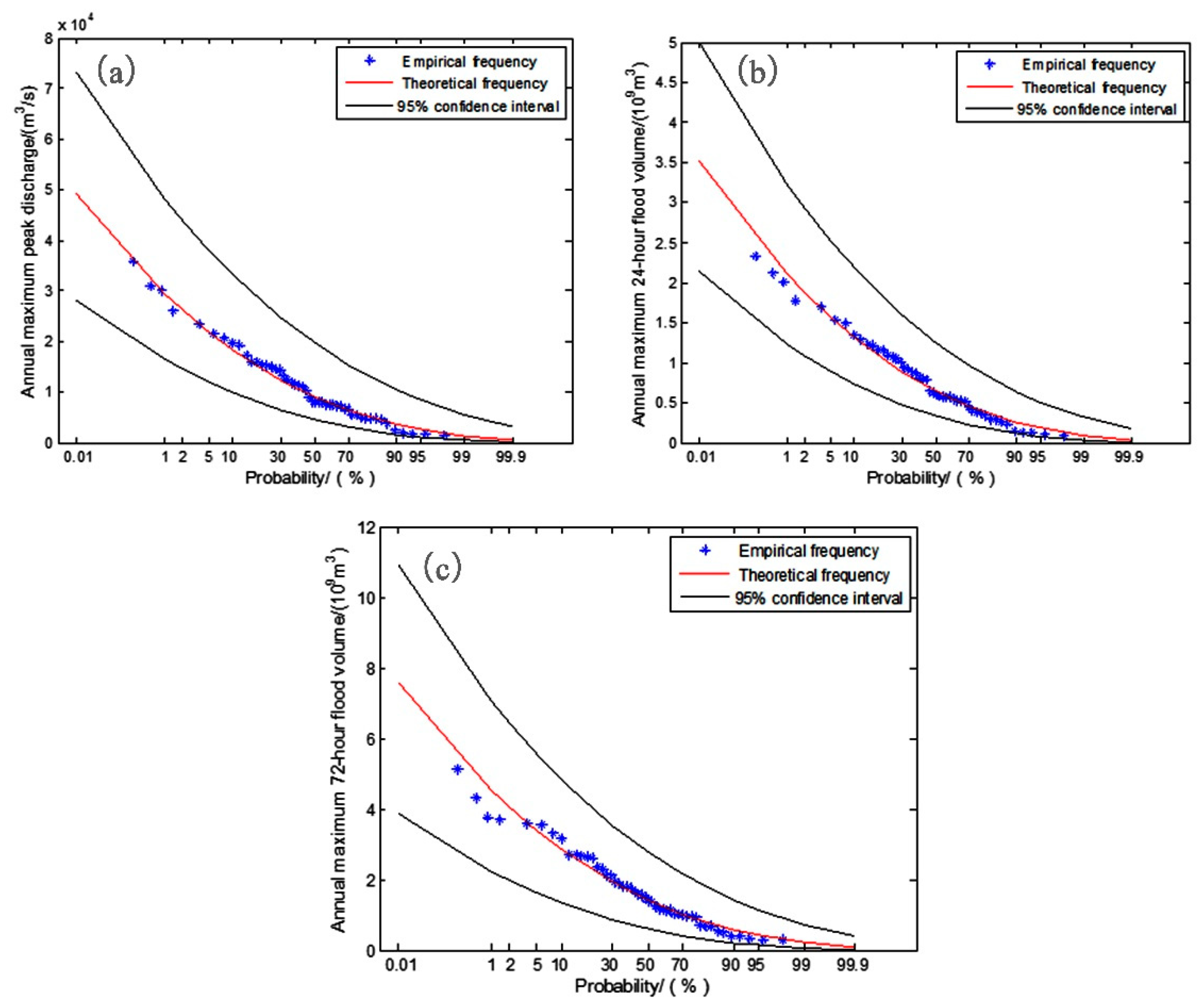
Figure 4 shows the variation between the design flood values of AMPDS. It illustrates that there is little deviation between the Monte Carlo simulated design flood values and the estimated design flood values by observed flood series. The Monte Carlo simulation of AMPDS exhibited the best results. The statistical parameters of 24-h AMFVS and 72-h AMFVS are slightly larger than AMPDS. It is mainly because the peak discharge of historical extraordinary floods is obtained through historical flood investigation. The historical flood volume data were obtained according to the peak volume relationship of flood, which adds some deviations. However, the statistical parameters are still within the acceptable range. This indicates that we can use 50-year-long datasets including historical extraordinary floods to estimate the design flood values at high return periods.
To estimate the uncertainties for flood characteristic series, nonparametric bootstrap method was used to calculate the 95% confidence interval for flood frequency curve. We obtained a bootstrapped sample from the original flood data with the length of 2000.
Figure 5 shows the 95% confidence interval for flood characteristic series.
4.3. Analysis of the Design Flood Results under Changing Environments
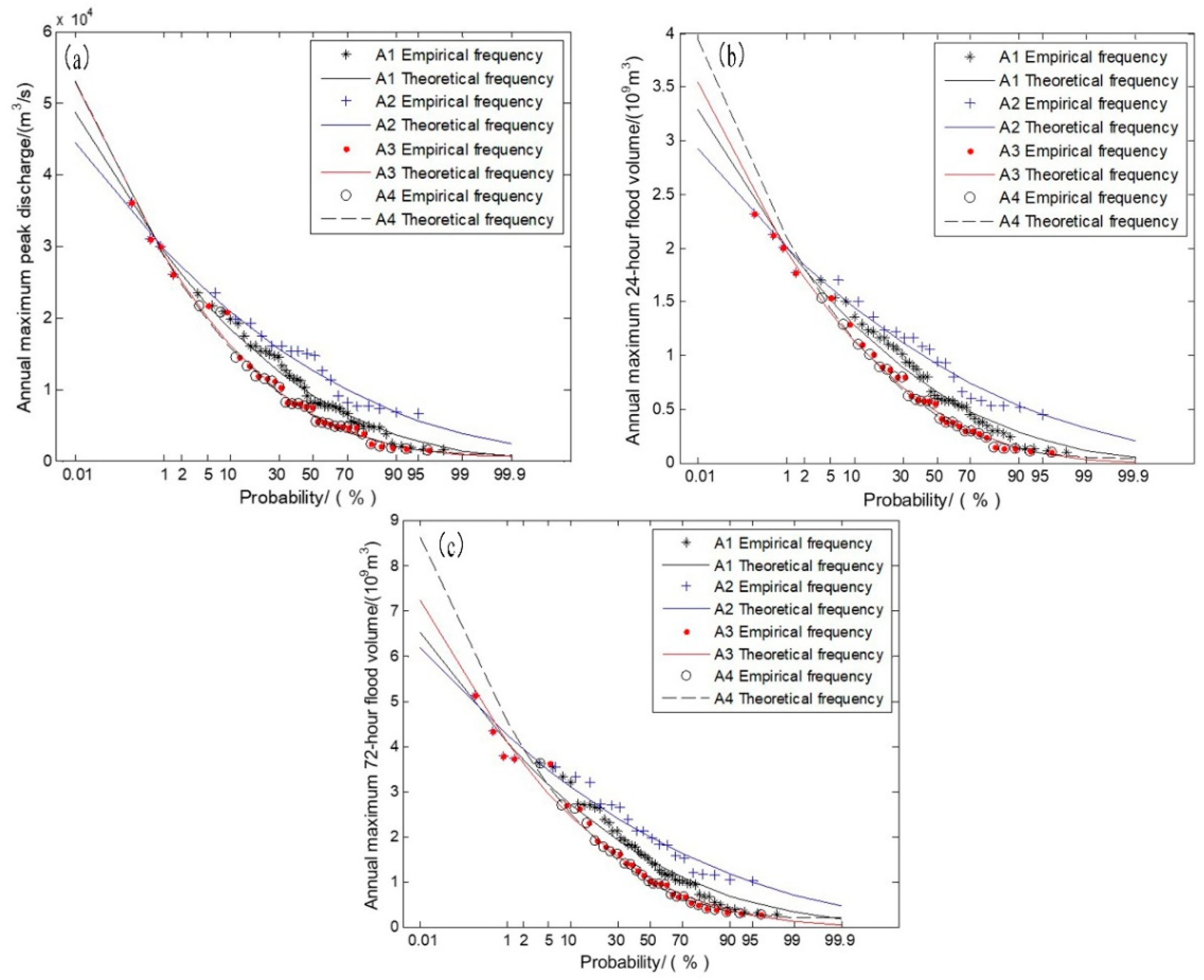
Combined with the results of the change point diagnosis, the flood characteristic series can be divided into two sub-series: the observed series before the change point and the observed series after the change point. Taking historical extraordinary flood data into consideration, we designed four cases fitting the P3 distribution to analyze the difference in the design flood under changing environmental conditions, which are as follows.
Case 1: original flood characteristic series (1968–2013) that do not consider the variation but add the historical extraordinary flood data, denoted as series .
Case 2: observed flood characteristic series before the change point (1968–1987) with the addition of the historical extraordinary flood data, denoted as series .
Case 3: observed flood characteristic series after the change point (1987–2013) with the addition of the historical extraordinary flood data, denoted as series .
Case 4: only the observed flood characteristic series after the change point (1987–2013), denoted as series .
Where represents the AMPDS, 24-h AMFVS and 72-h AMFVS, respectively.
The design floods at different return periods of each flood characteristic series are calculated separately for the four different cases. The genetic algorithm is also used to estimate the parameters of the P3 distribution for the flood series.
Table 8 shows the results of the estimated parameters for all flood series.
Table 9 illustrates that the results all pass the goodness-of-fit test and the fitting results are shown in
Figure 6. According to the optimized parameters obtained, the design values of each flood characteristic series are calculated as shown in
Table 10.
As shown in
Table 10, we learn that the design flood results of
, which considered historical extraordinary flood data but not non-stationary data, are larger than the 1999 design flood results of the Ankang hydrological station at 10,000-year and 5000-year return periods. However, the
design flood results are smaller at other return periods and the difference is between −8.9% and 1.1%. Compared with the design AMPDS results of the 1999 design report, the design flood of
, which does not consider the non-stationarity of the series, tends to be larger at a high return period and smaller at a low return period, which may be caused by the increase of the sample size. Mainly because of the decreasing trend of the mean value for the flood characteristic series, the addition of data increases the
of the computed series, resulting in the increase in the upper tail of the frequency curve and the decrease in the lower tail.
In the same way, it can be clearly seen that the design values after the change point of the three flood characteristic series , considering the historical extraordinary flood data, are smaller than the design values of at 100-year, 20-year and 5-year return periods. For the other return periods, the design values are larger. The difference range of AMPDS is −31.5% to 19.0%, the difference of 24-h AMFVS ranges from −31.0% to 18.2% and the difference of 72-h AMFVS is 29.9% to 17.0%. It can be seen from Fig. 6 that the design flood value, without considering the variation of flood series, is almost between the design values before and after the variation series.
Comparing the design flood results between case 3 and case 4 shows that the design values of 24-h AMFVS and 72-h AMFVS are larger than the designed flood values, except the 5-year return level. The ranges of difference are −1.7%~12.2% and −1.7%~19.2%. For AMPDS, the design values are larger than the design values at 10,000-year and 5000-year return periods and are smaller for the rest of the return periods. The range of difference is −2.8%~0.1%.
The design flood of compared with results in the same trends, with an increase in the upper tail of the frequency curve and a decrease in the lower tail. Although the mean value decreases after the environment changes, the increase in for the flood characteristic series illustrated the change in land surface of the Ankang hydrology station, which reflects the necessity of considering non-stationarity. The results indicate that the current regulation of reservoirs in the upper stream of the Hanjiang River may not satisfy the requirements of flood control. Furthermore, the comparison between and exhibits the importance of adding historical extraordinary flood data. Taking historical extraordinary flood data into consideration revised the design flood value and improved the accuracy of flood frequency analysis.
4.4. Analysis of the Design Flood Results Based on IMD in Consideration of Historical Extraordinary Floods
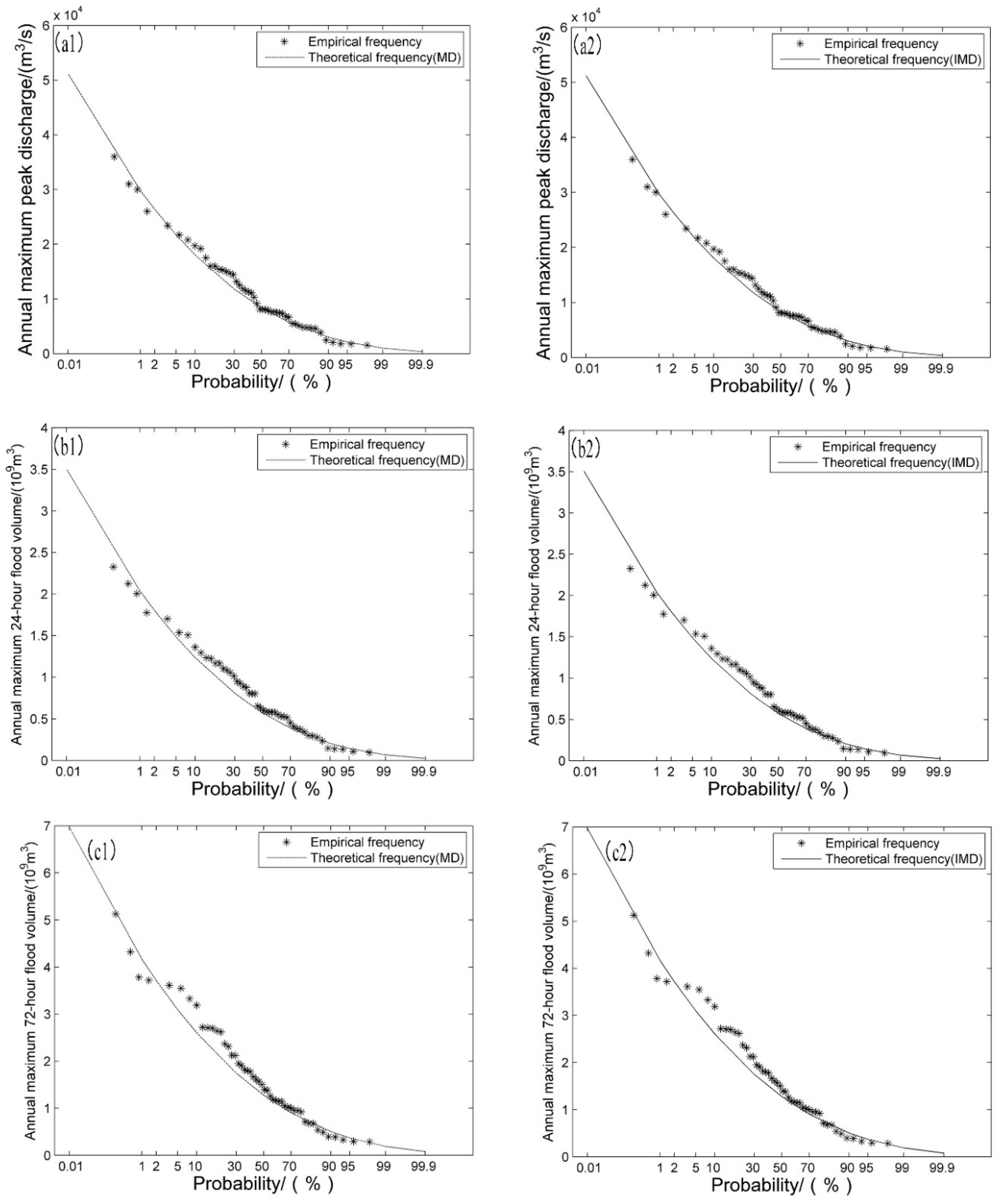
The flood characteristic series from the Ankang hydrological station are investigated to illustrate the superiority of the improved mixed distribution (IMD) method proposed in
Section 2.3 compared with conventional mixed distribution (MD) methods. According to
Section 2.2.2, parameter estimations for the two mixed distribution methods by GA are given in
Table 11. We also use P3 to calculate design floods for different return periods for each flood characteristic series. The goodness-of-fit values of these three methods are shown in
Table 12.
The D values for AMPDS, 24-h AMFVS and 72-h AMFVS are all less than the critical value
, which is equal to 0.194 at the 5% significance level. This result means that the P3, MD and IMD methods provide a satisfactory fit. The results show that P3 provides the best fit of the three methods. However, regarding the mechanism, the use of P3 distribution fitting is based on satisfying the stationarity hypothesis; in fact, the observed data of the Ankang hydrological station are consistent with the non-stationarity phenomenon. Thus, it is not reasonable to use the P3 distribution after environmental change. Meanwhile, it can also be seen that the
AIC criterion values of the IMD method for the three flood characteristic series are all less than the corresponding criterion values of the MD method, which indicates that the IMD method is better. This result proved that our method improved the mechanism of mixed distribution and that our work is meaningful. The fitting results of the MD and IMD methods are given in
Figure 7.
As is shown in
Table 13, for AMPDS, the differences in the design flood values between the best fitness MD methods and the 1999 design flood results are larger at high return periods and smaller at low return periods, with a difference of −11.88%~6.39%. The design flood value between the best fitness MD methods and the P3 results, without considering the non-stationarity data, has the same changing trends. The differences of AMPDS, 24-h AMFVS and 72-h AMFVS are −3.24%~5.21%, −6.67%~6.29% and −6.34%~7.19%, respectively. From
Table 13, we can also see that the design value calculated by the IMD method of the flood series is slightly increased compared with the MD method. However, the IMD method may cause larger changes in the design flood values in other basins.
Tang et al. [
54] developed the historical extraordinary flood-concerned mixed-distribution method (HFCMM) to overcome the shortcomings of the traditional methods without considering historical extraordinary flood events. However, their study focused on comparing the modelling results of different probability distribution function tail types rather than the difference in the design flood values.
Zeng et al. [
18] used MD to estimate the design flood values of the Xidayang reservoir, which is located in the Daqinghe River Basin, in the northern part of China. All the design values decreased by 0.03%–20.24% with different return periods compared with the P3 distribution. However, both design flood values estimated by MD or IMD in our study increased for high return periods but decreased for small return periods. The cause of this phenomenon may be that our study area and the study area of Zeng are located in different river basins and different parts of China. Different factors such as different changes in land use cause different mechanisms of runoff generation and convergence in different basins. Thus, the design flood results we obtained are also reasonable. Yan et al. [
22] noted that the time-varying two-component mixture distribution (TTMD) models exhibited better fitting results than and outperformed the stationary models in both the Huanxian and Xianyang stations of the Weihe River Basin. We can also develop the time-varying improved mixed distribution to consider the time variations of the parameters in future work.