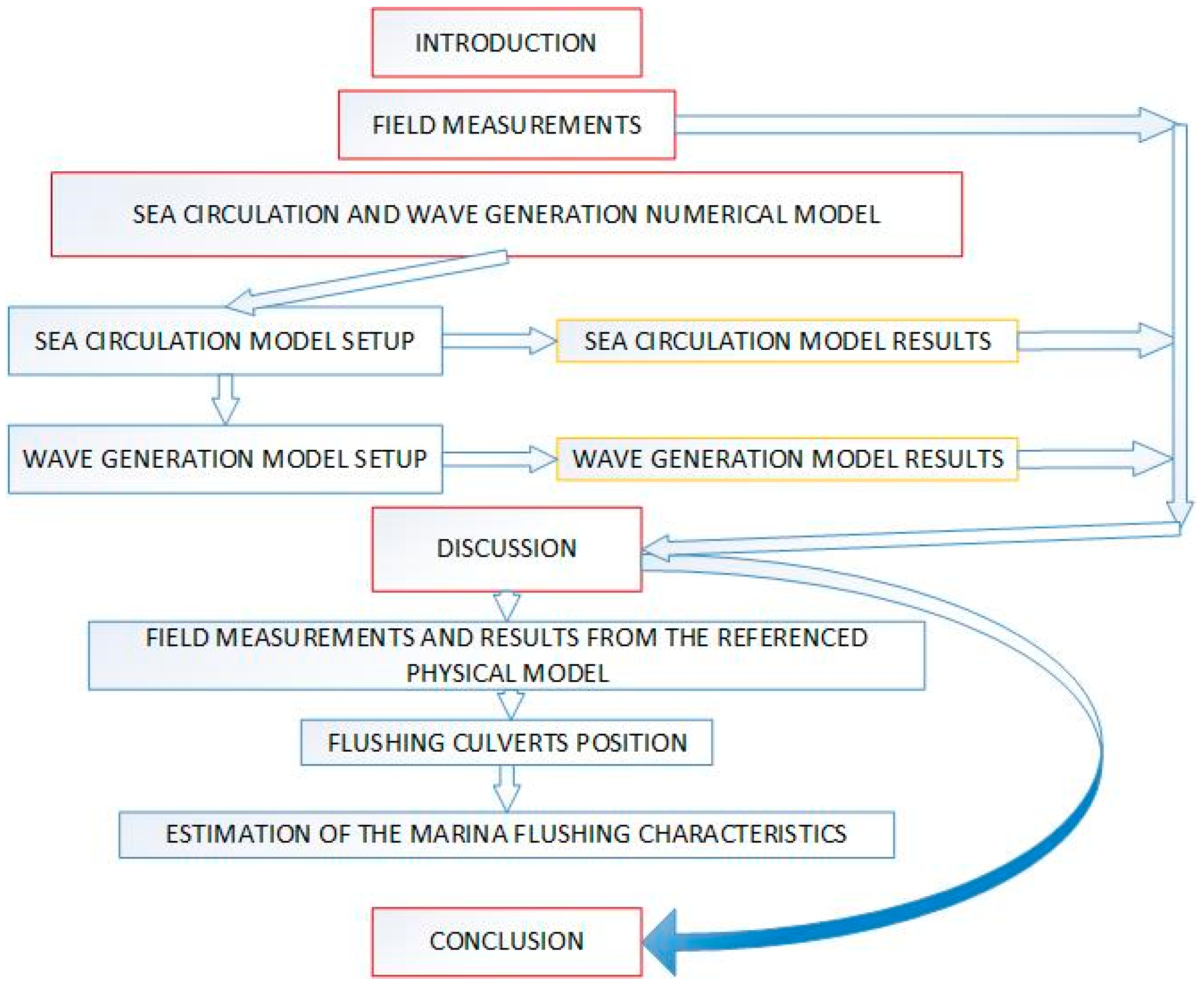
The Flow Generator Relations for Water Renewal through the Flushing Culverts in Marinas
Abstract
1. Introduction
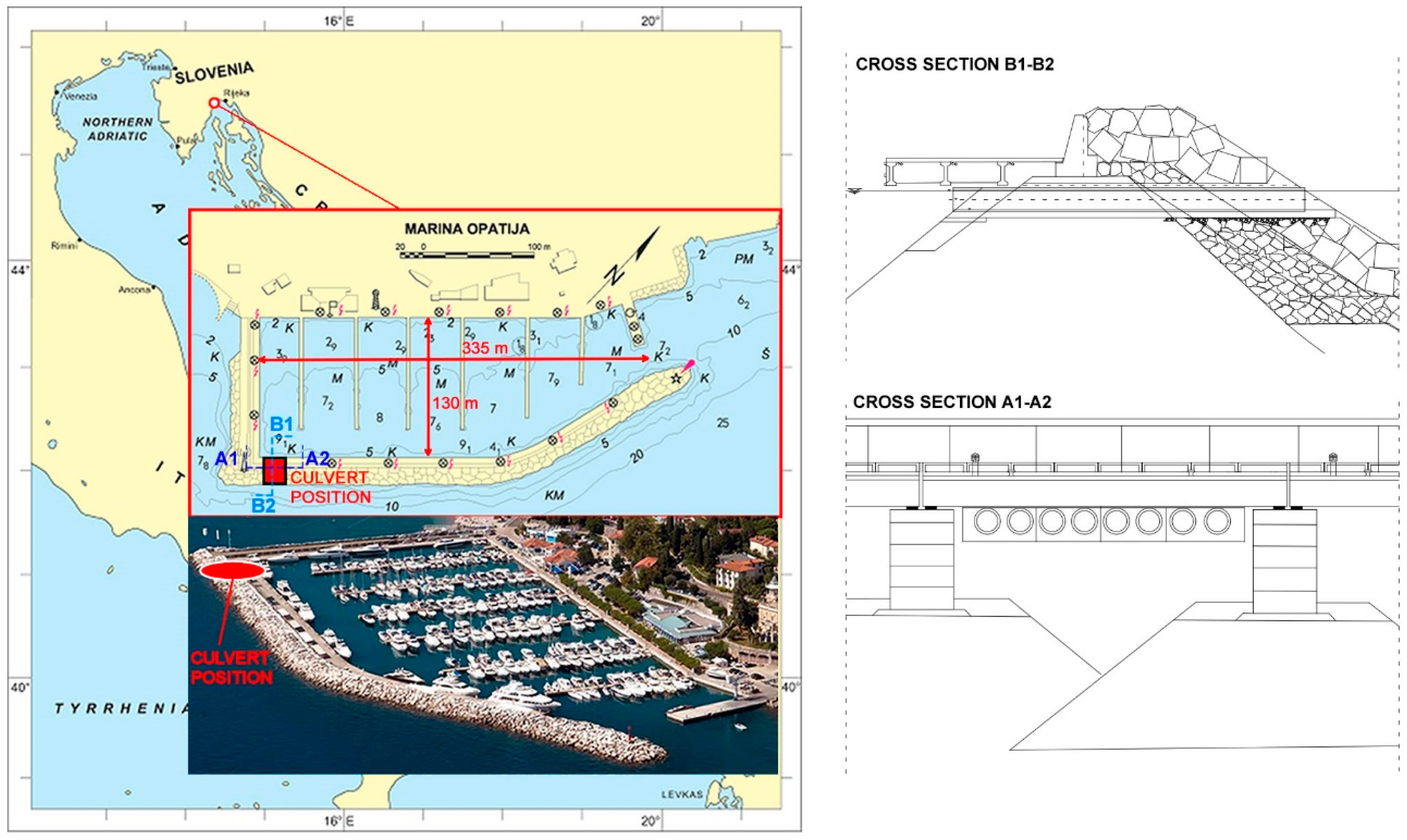
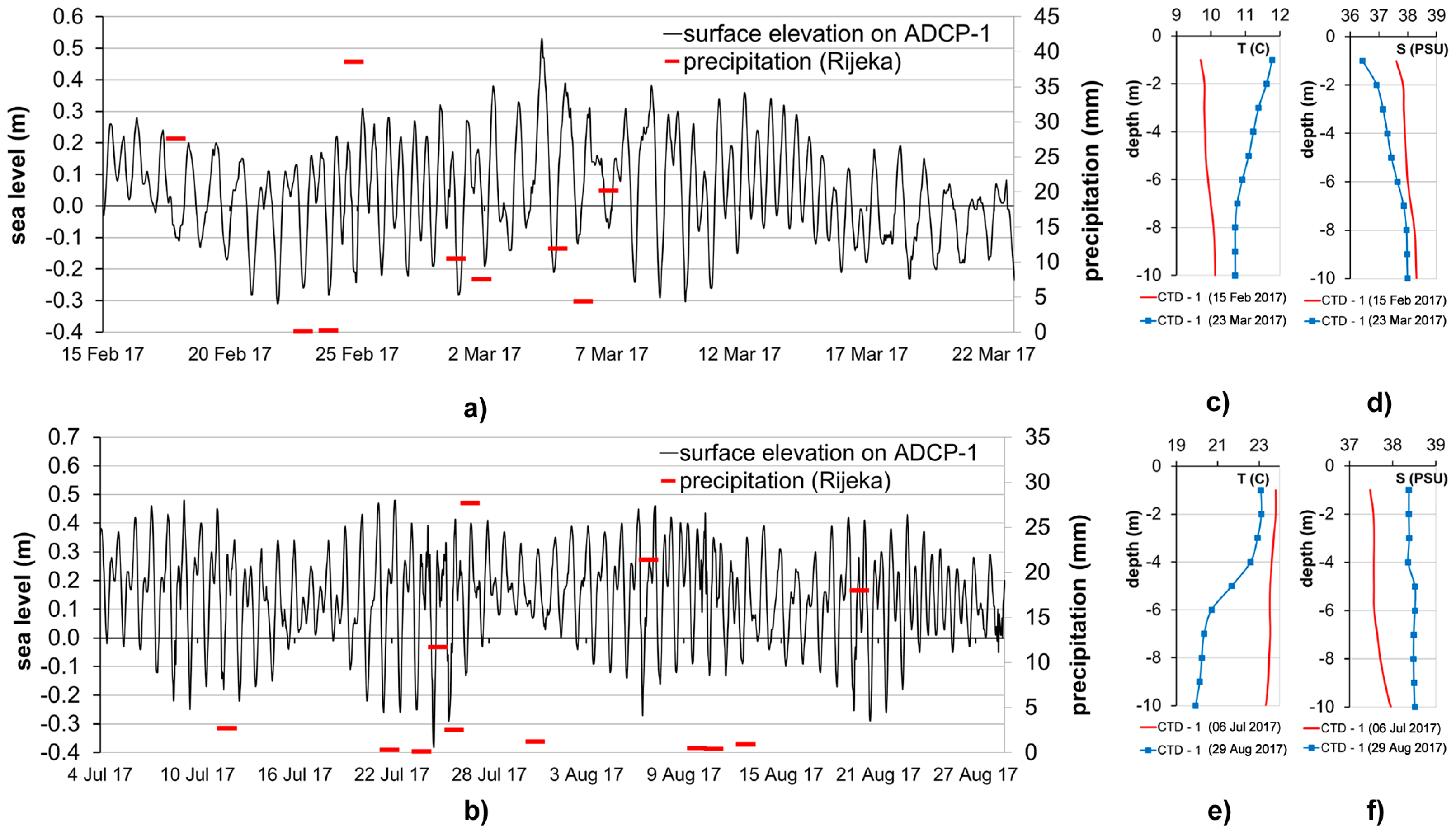
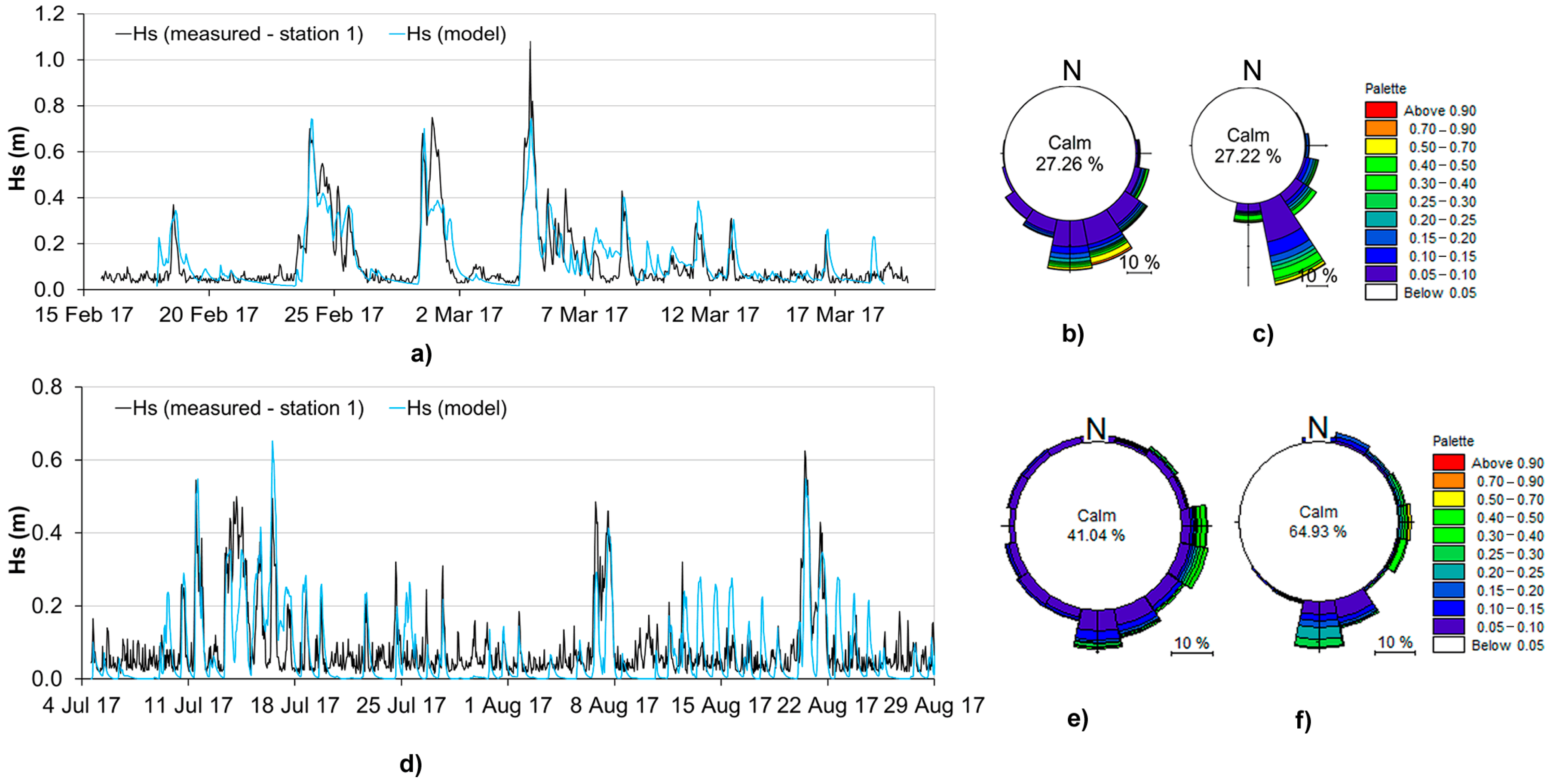
2. Field Measurements
3. Sea Circulation and Wave Generation Numerical Model
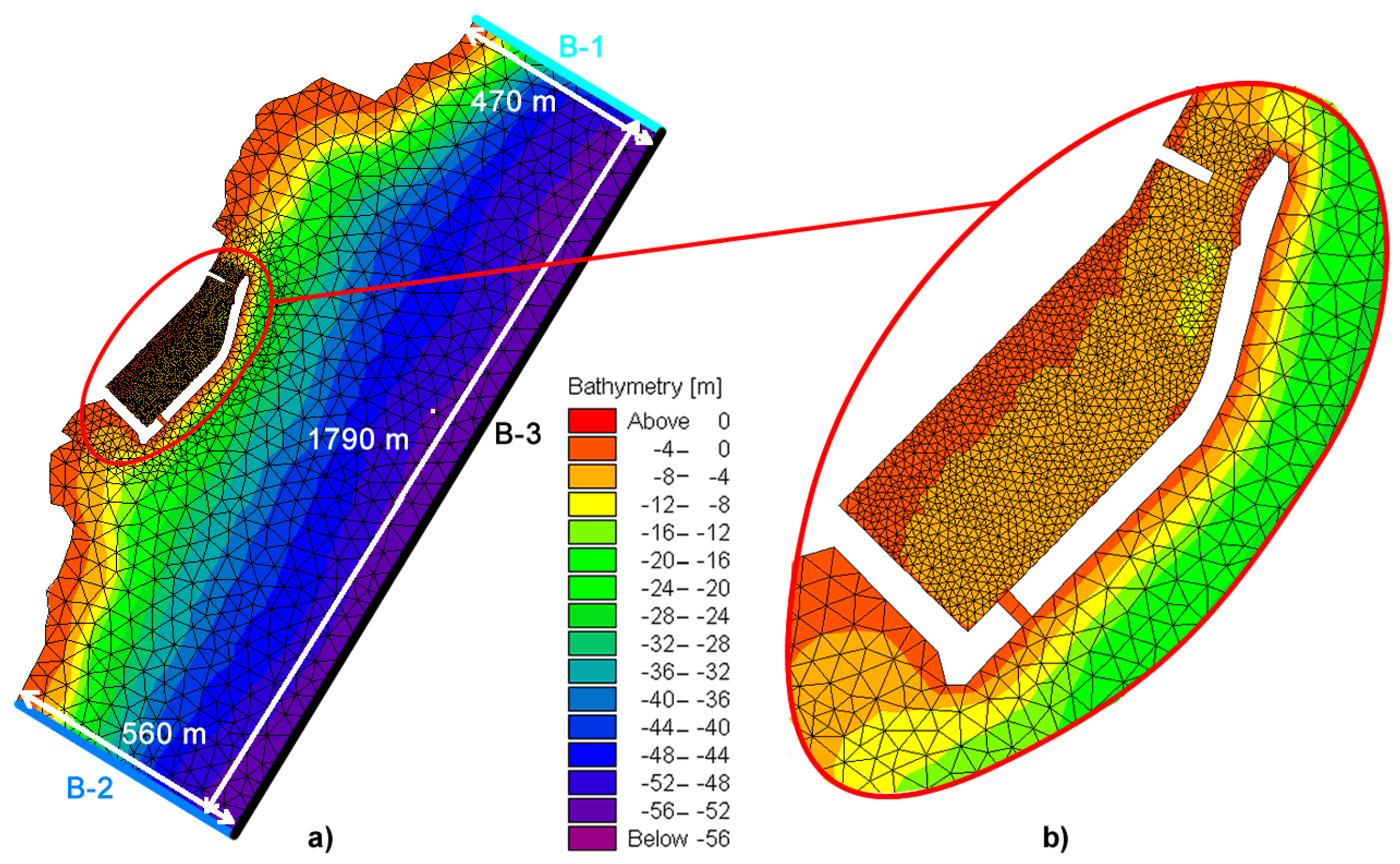
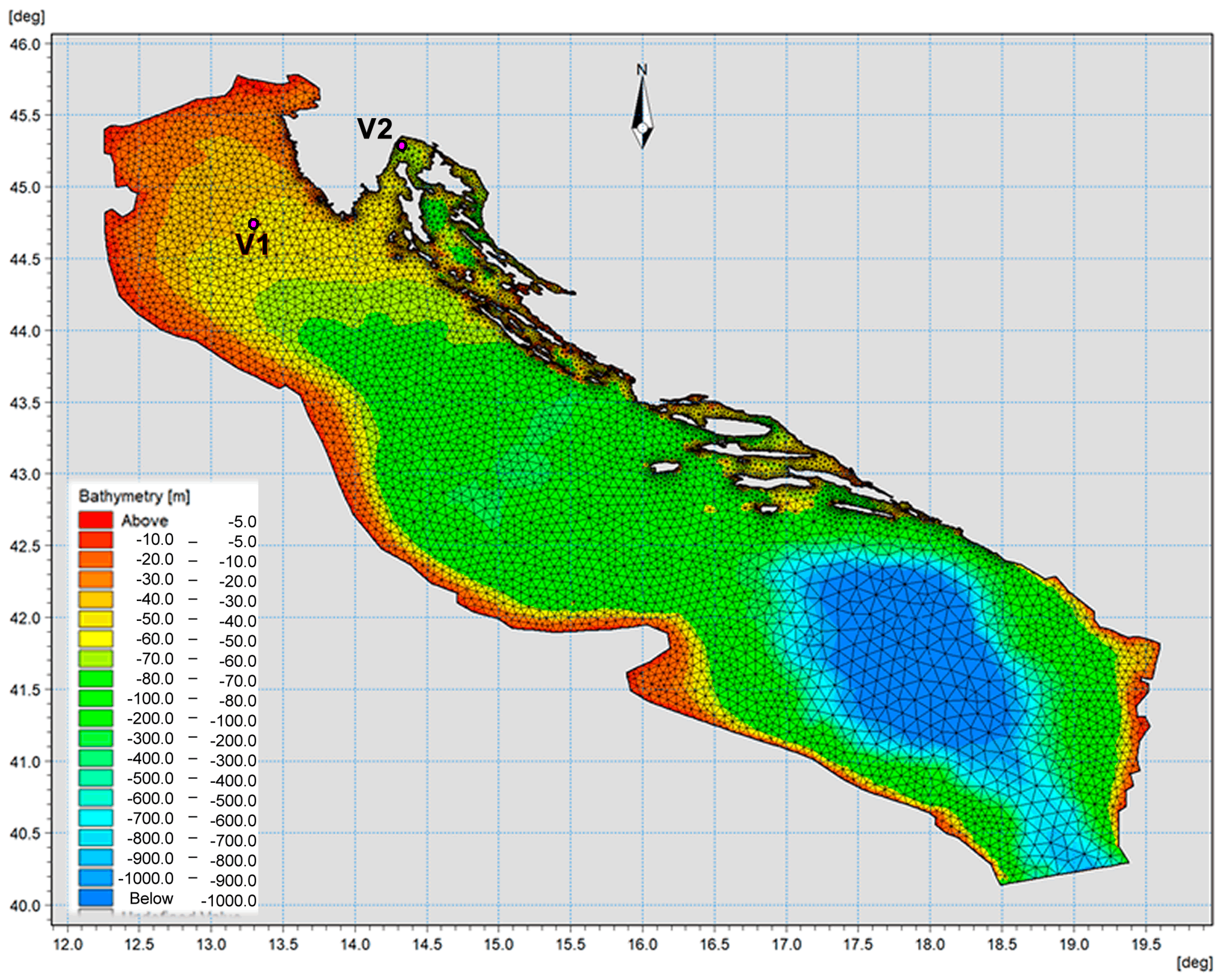
3.1. Sea Circulation Model Setup
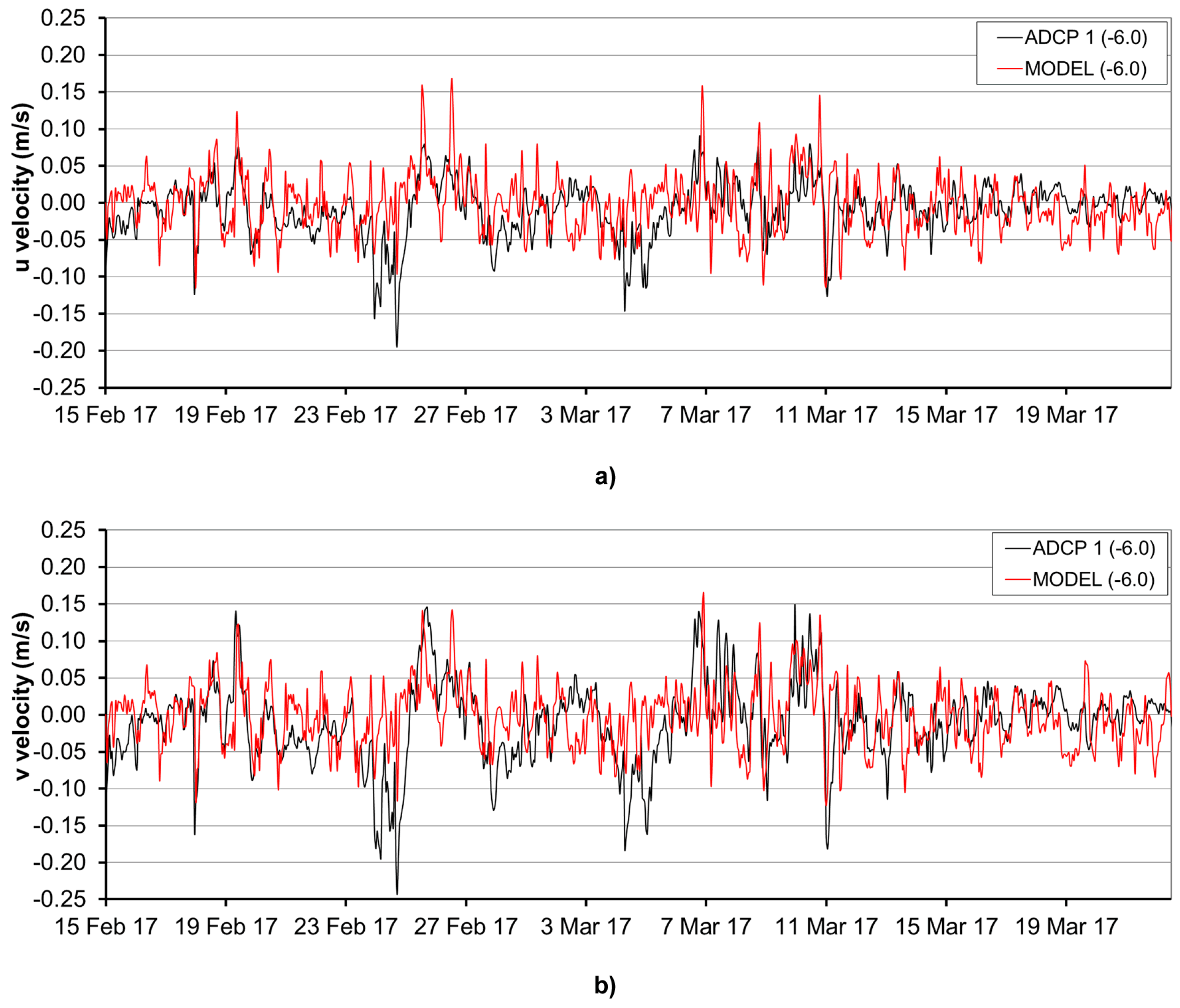
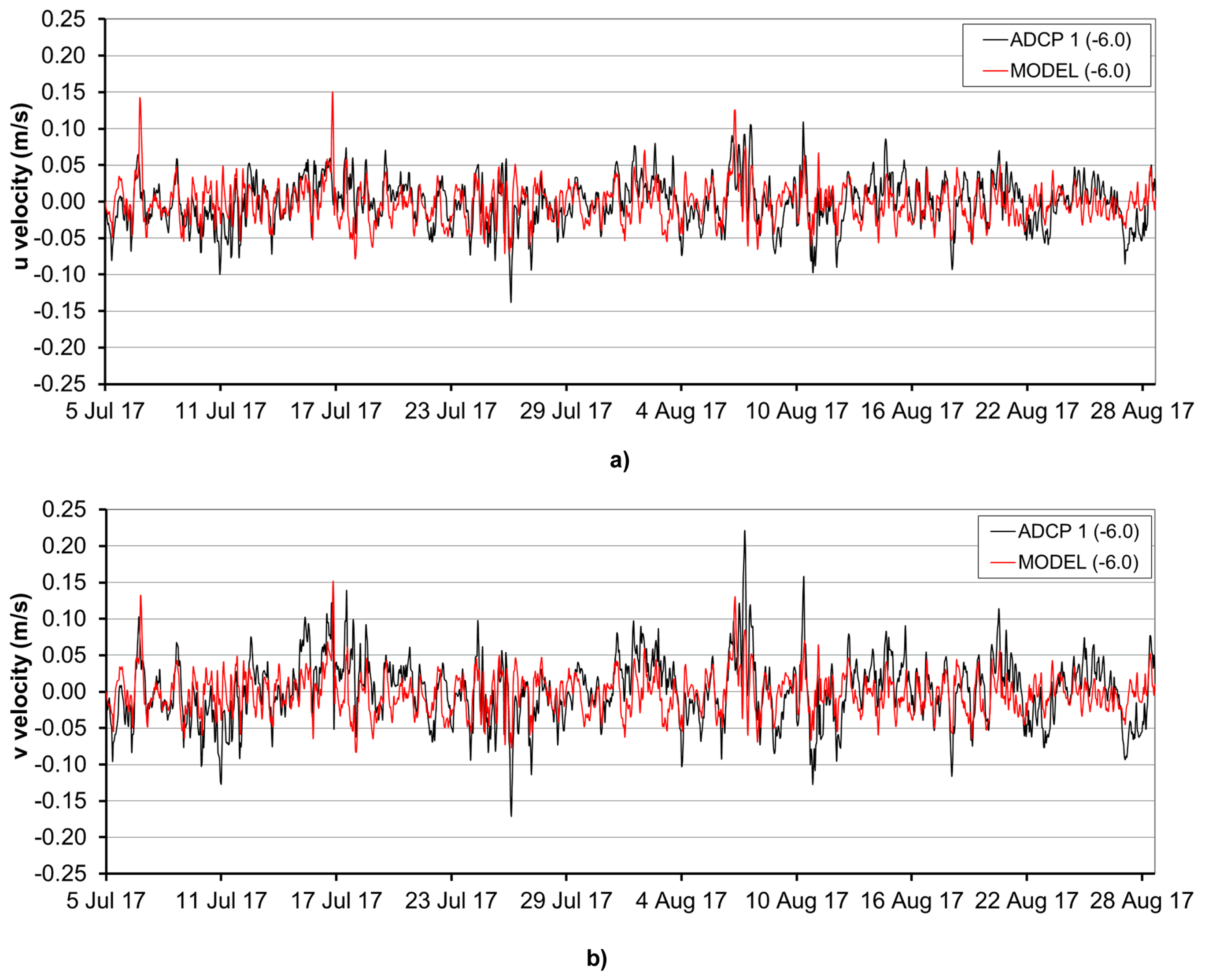
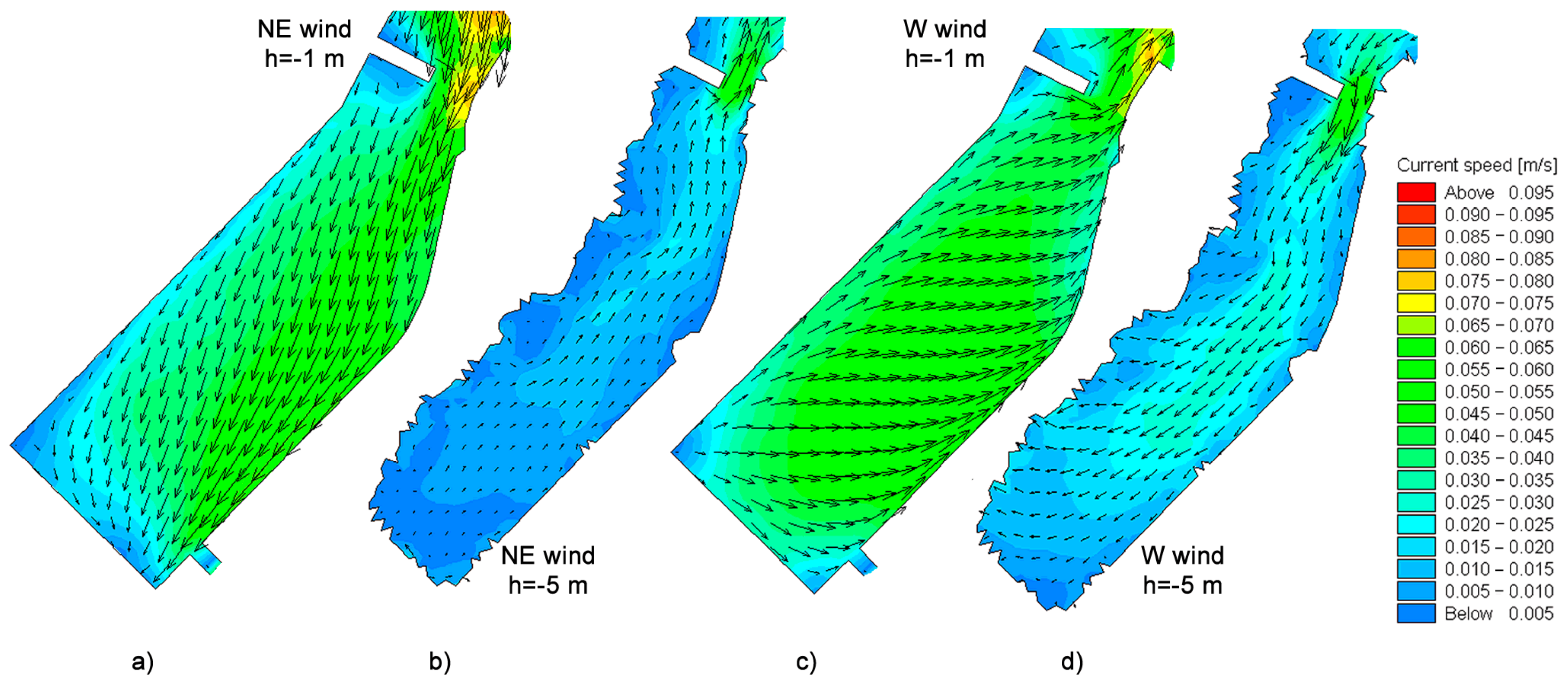
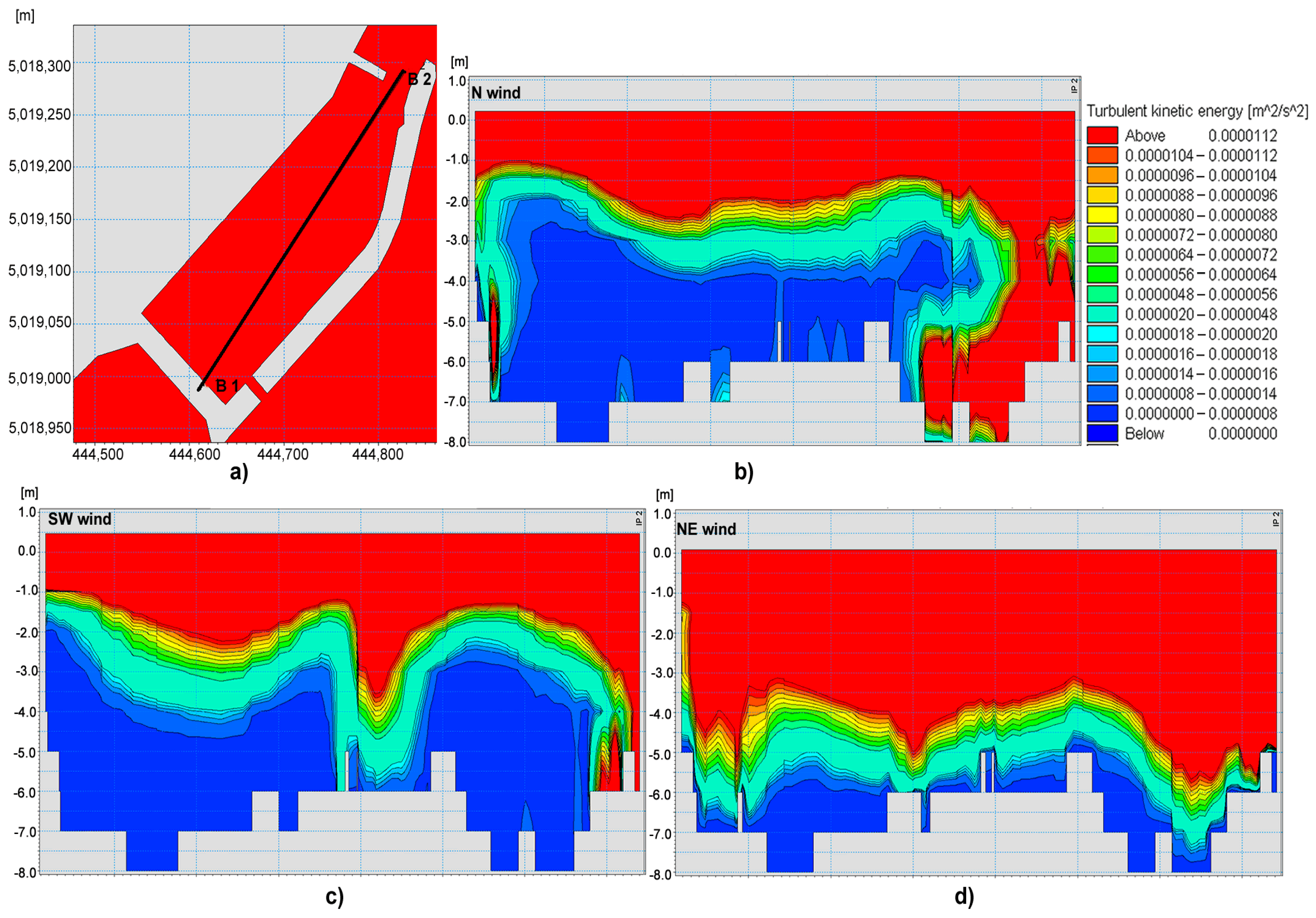
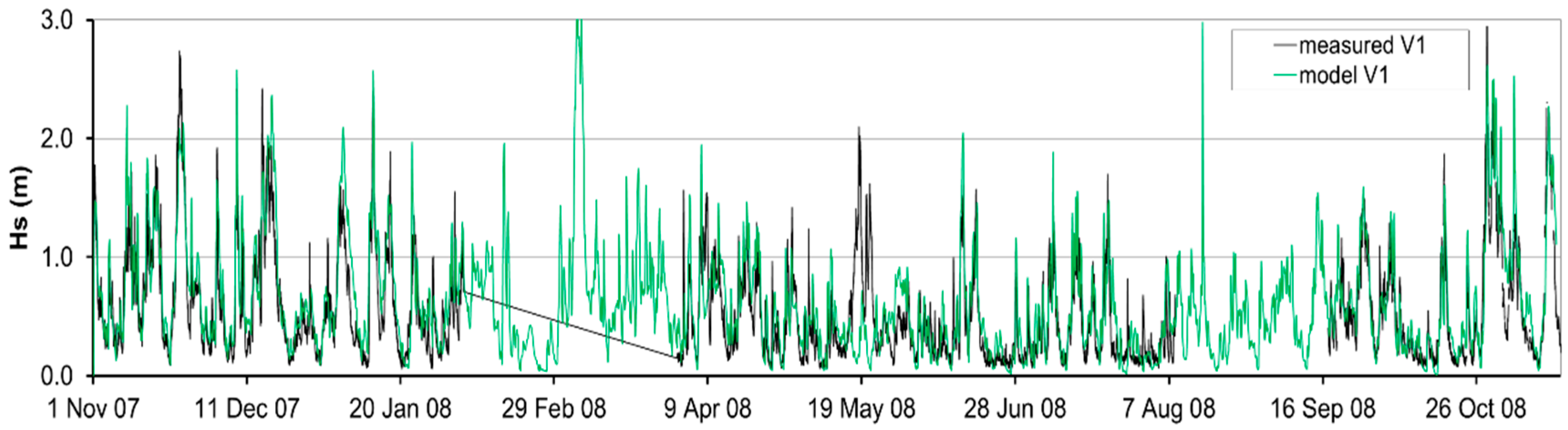
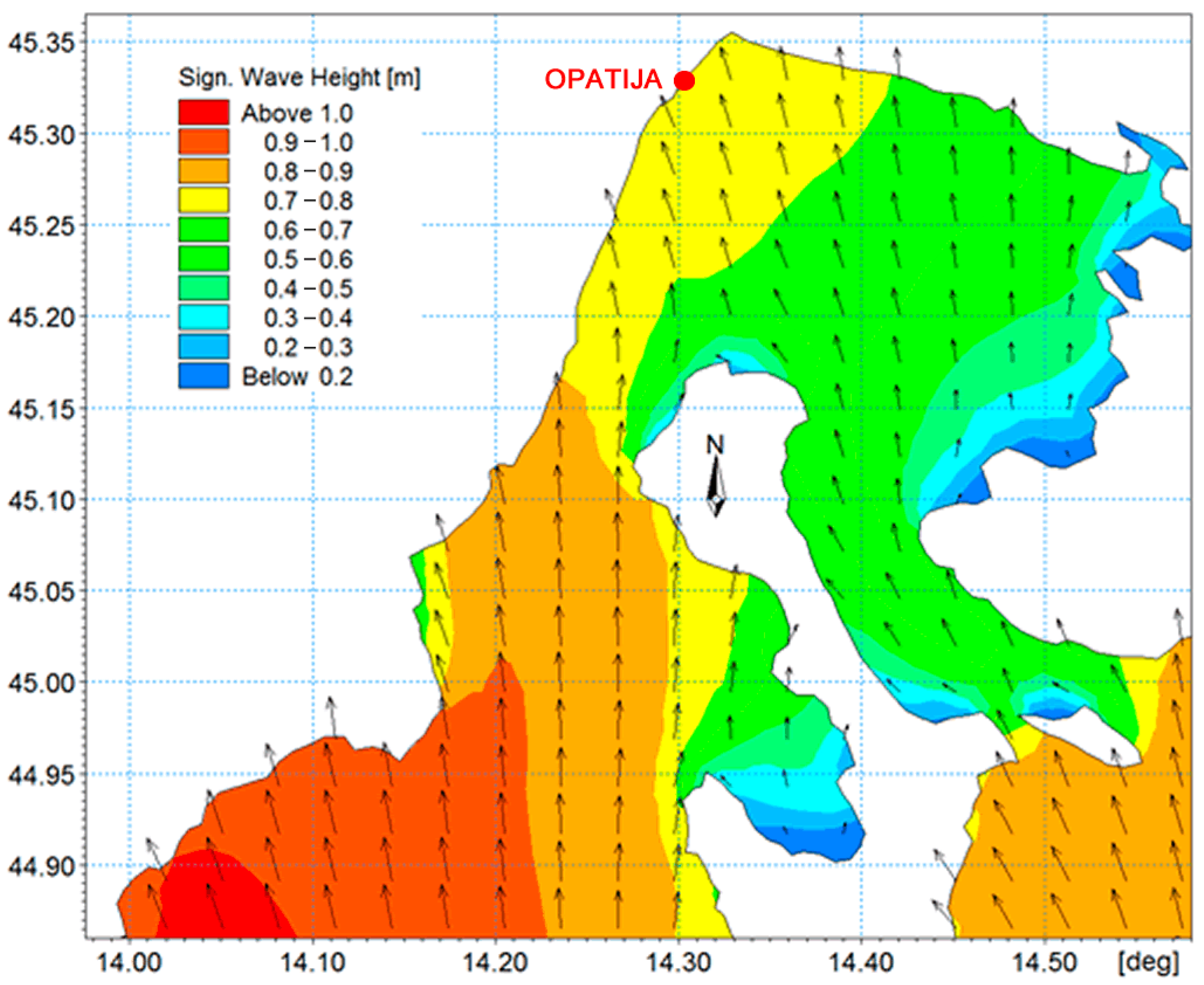
3.2. Sea Circulation Model Results
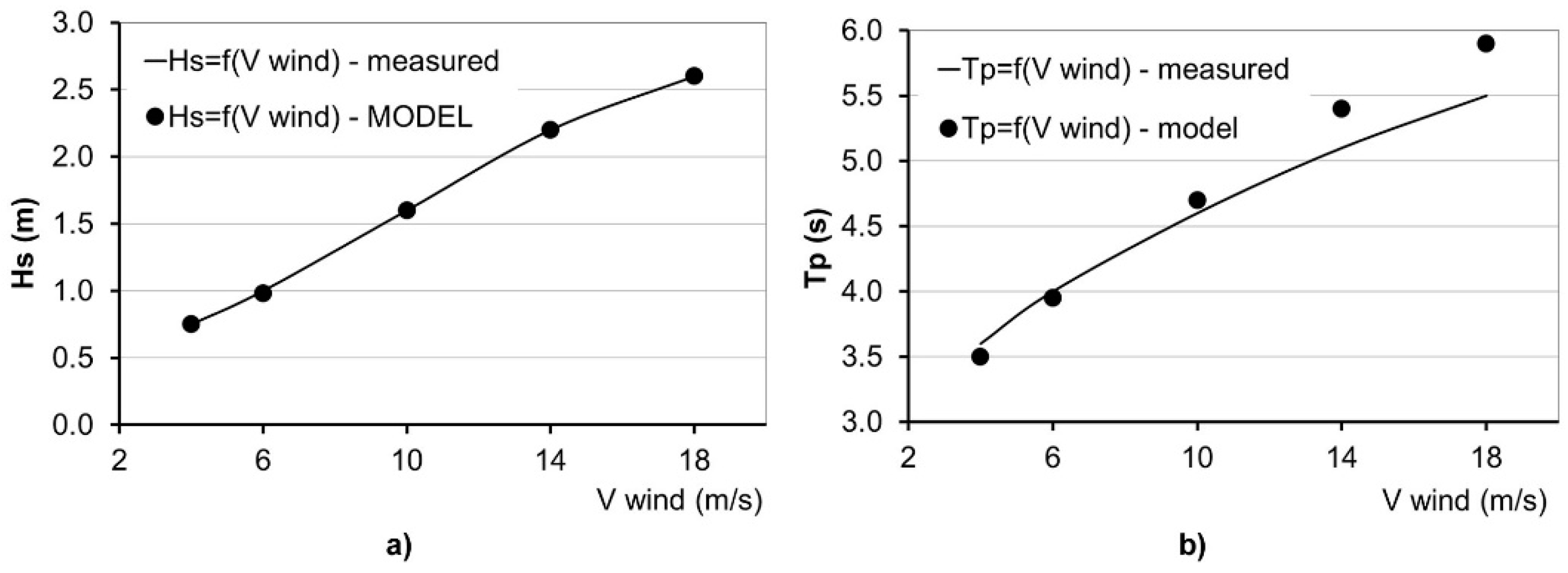
3.3. Wave Generation Model Setup
3.4. Wave Generation Model Results
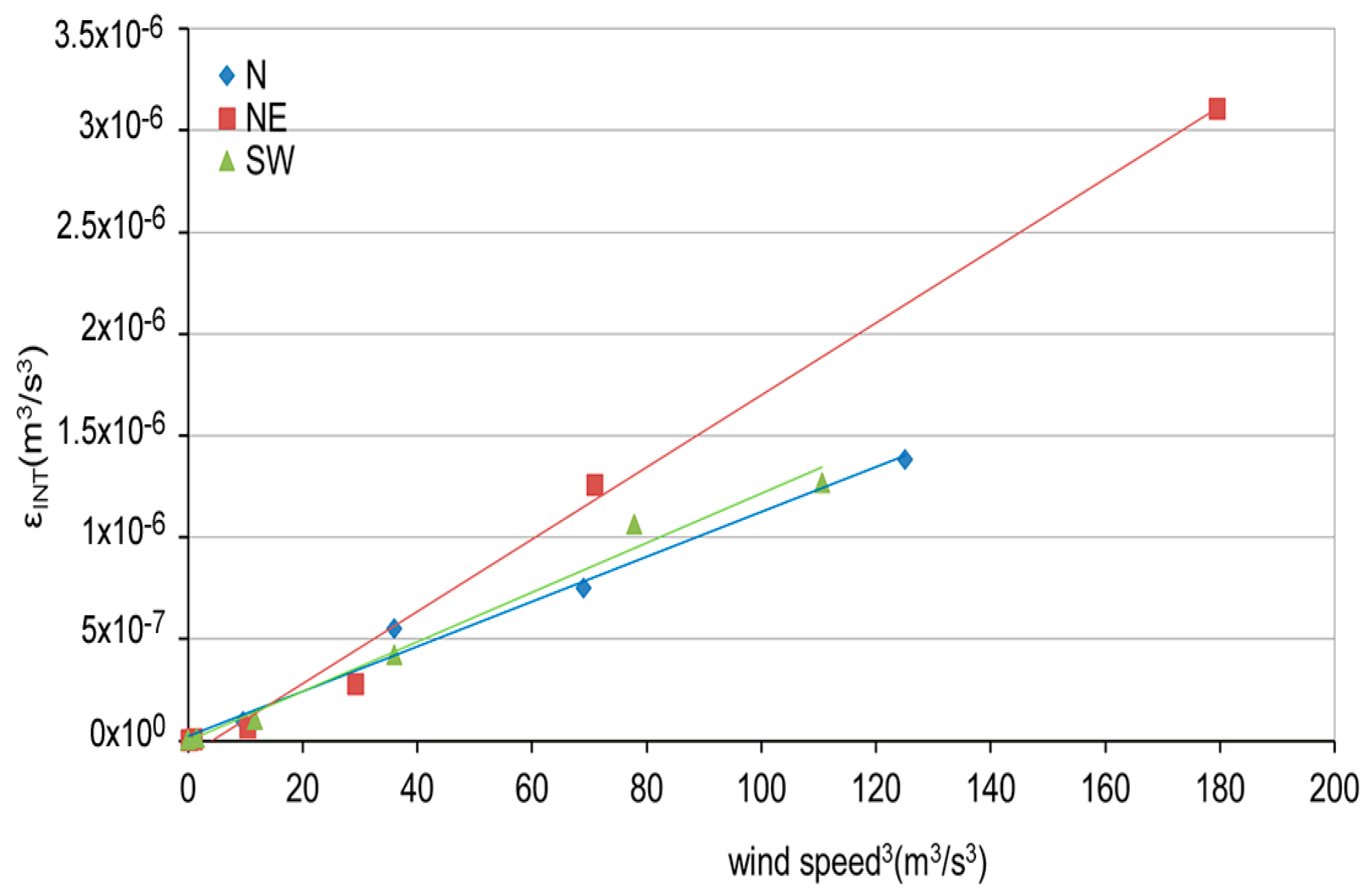
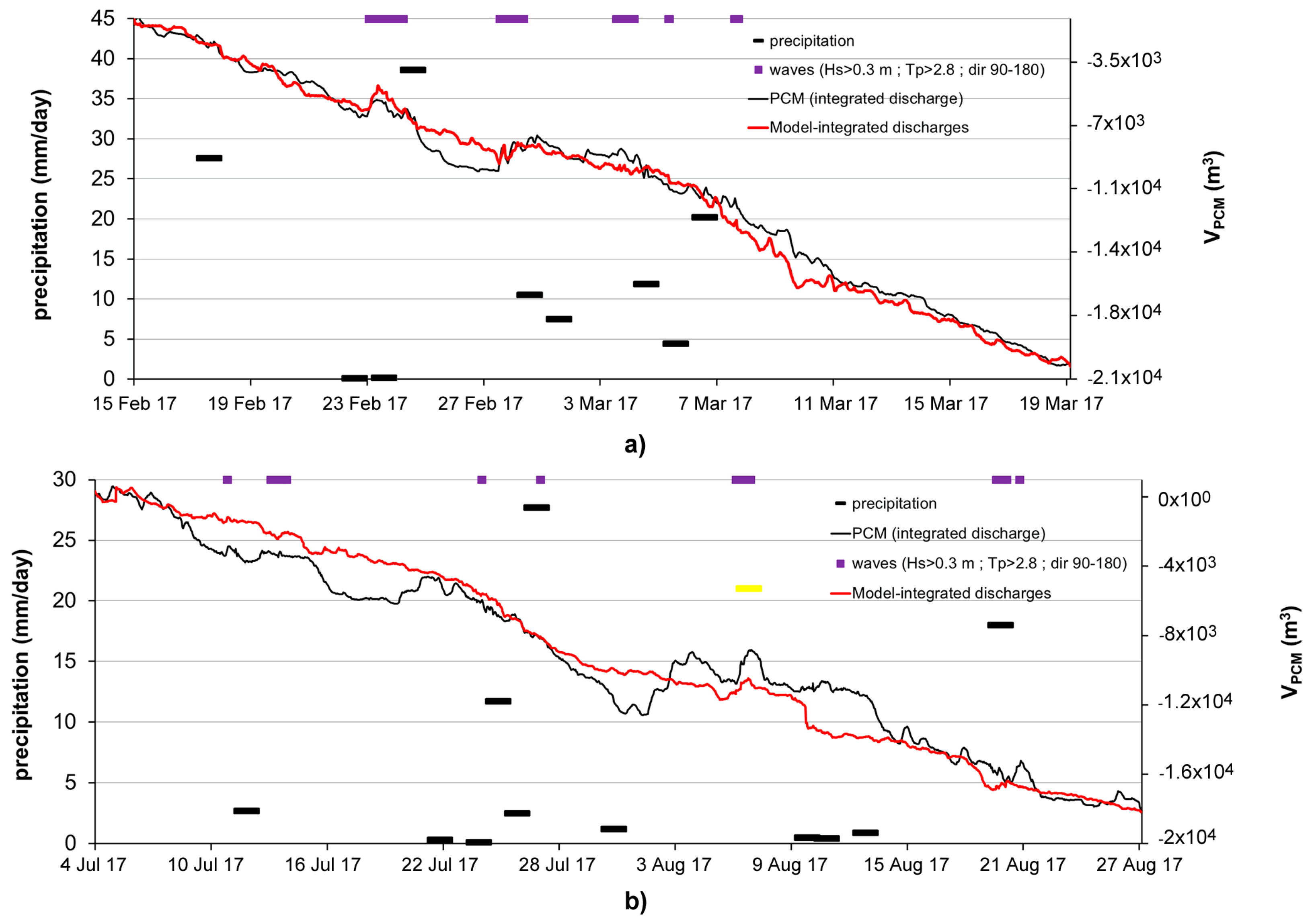
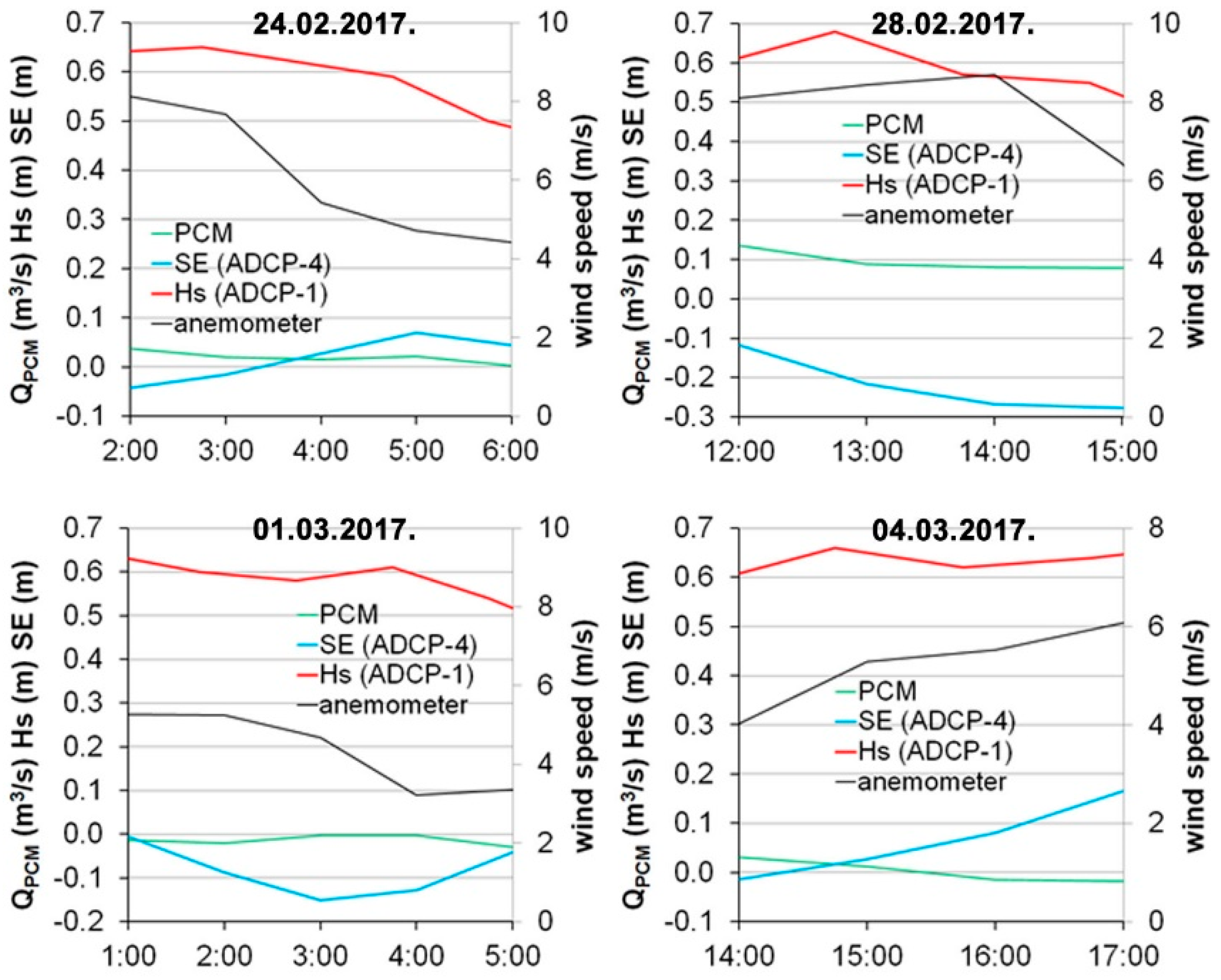
4. Discussion
4.1. Field Measurements and Results from the Referenced Physical Model
4.2. Flushing Culverts Position
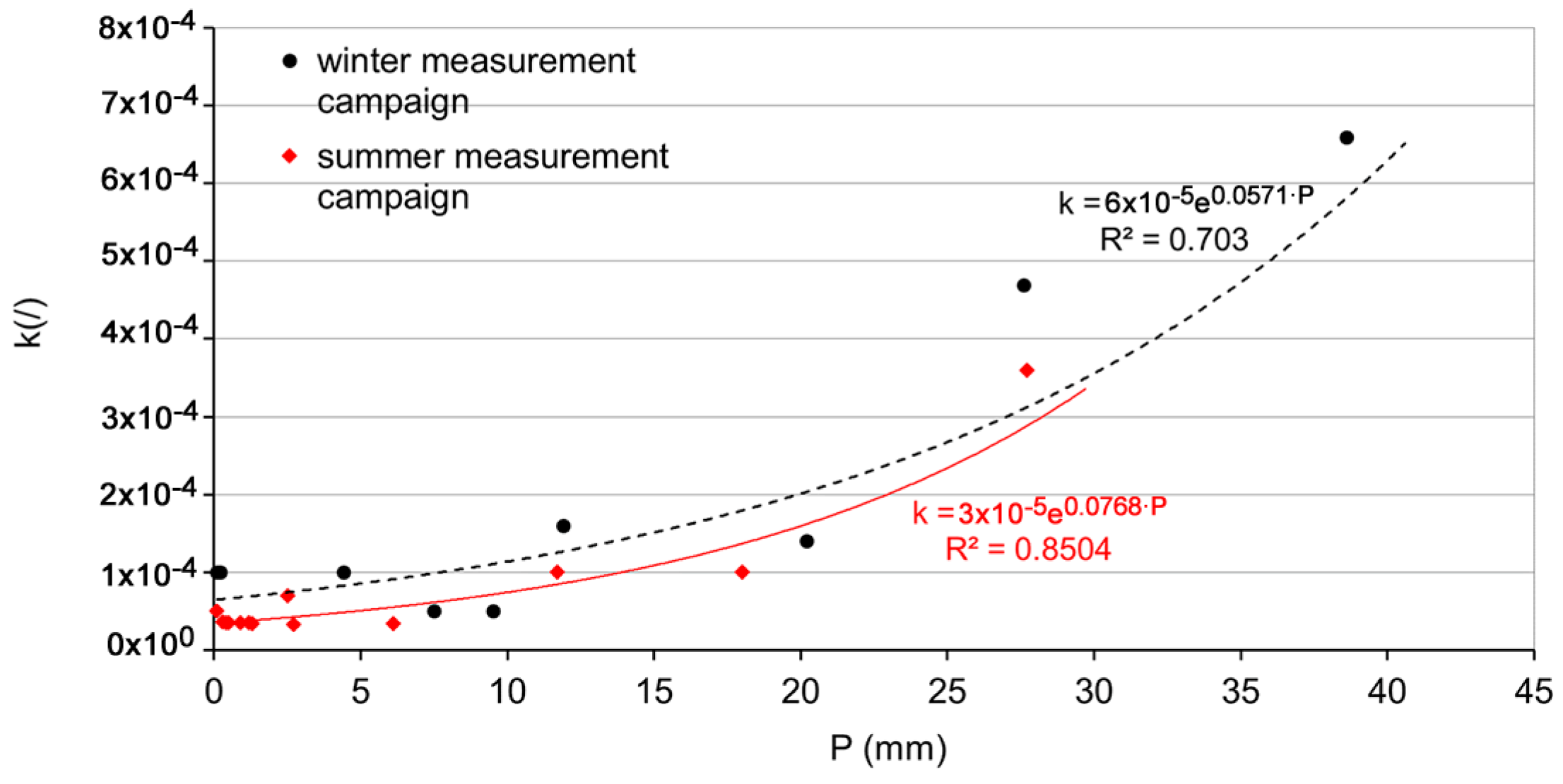
4.3. Estimation of the Marina Flushing Characteristics
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Airoldi, L.; Beck, M.W. Loss, Status and Trends Forcoastal Marine Habitats of Europe. Oceanogr. Mar. Biol. 2007, 45, 345–405. [Google Scholar]
- United Nations, Department of Economic and Social Affairs, Population Division. World Population Prospects the 2017 Revision Key Findings and Advance Tables; United Nations: New York, NY, USA, 2017; Volume 2017, pp. 1–46. [Google Scholar]
- Di Franco, A.; Graziano, M.; Franzitta, G.; Felline, S.; Chemello, R.; Milazzo, M. Do Small Marinas Drive Habitat Specific Impacts? A Case Study from Mediterranean Sea. Mar. Pollut. Bull. 2011, 62, 926–933. [Google Scholar] [CrossRef] [PubMed]
- Valdor, P.F.; Gómez, A.G.; Puente, A. Environmental Risk Analysis of Oil Handling Facilities in Port Areas. Application to Tarragona Harbor (NE Spain). Mar. Pollut. Bull. 2015, 90, 78–87. [Google Scholar] [CrossRef] [PubMed]
- Bedri, Z.; Corkery, A.; O’Sullivan, J.J.; Deering, L.A.; Demeter, K.; Meijer, W.G.; O’Hare, G.; Masterson, B. Evaluating a Microbial Water Quality Prediction Model for Beach Management under the Revised EU Bathing Water Directive. J. Environ. Manag. 2016, 167, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Pinto, M.I.; Burrows, H.D.; Sontag, G.; Vale, C.; Noronha, J.P. Priority Pesticides in Sediments of European Coastal Lagoons: A Review. Mar. Pollut. Bull. 2016, 112, 6–16. [Google Scholar] [CrossRef] [PubMed]
- Tavakoly Sany, S.B.; Hashim, R.; Rezayi, M.; Salleh, A.; Safari, O. A Review of Strategies to Monitor Water and Sediment Quality for a Sustainability Assessment of Marine Environment. Environ. Sci. Pollut. Res. 2014, 21, 813–833. [Google Scholar] [CrossRef] [PubMed]
- Mujal-Colilles, A.; Gironella, X.; Sanchez-Arcilla, A.; Puig Polo, C.; Garcia-Leon, M. Erosion Caused by Propeller Jets in a Low Energy Harbour Basin. J. Hydraul. Res. 2017, 55, 121–128. [Google Scholar] [CrossRef]
- Tsoukala, V.K.; Gaitanis, C.K.; Stamou, A.I.; Moutzouris, C.I. Wave and Dissolved Oxygen Transmission Analysis in Harbors Using Flushing Culverts: An Experimental Approach. Glob. Nest J. 2010, 12, 152–160. [Google Scholar]
- Gaitanis, C.K.; Douka, E.; Tsoukala, V.K.; Stamou, A.I.; Moutzouris, C.I. Dissolved Oxygen Transmission in Harbor Basins Through Flushing Culverts. In Proceedings of the 11th International Conference on Environmental Science and Technology, Chania, Greece, 3–5 September 2009; pp. 285–292. [Google Scholar]
- Schwartz, R.A.; Imberger, J. Flushing Behaviour of a Coastal Marina. Coast. Eng. Proc. 1988, 1, 2626–2640. [Google Scholar]
- Grifoll, M.; Jorda, G.; Borja, A.; Espino, M. A New Risk Assessment Method for Water Quality Degradation in Harbour Domains, Using Hydrodynamic Models. Mar. Pollut. Bull. 2010, 60, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters. J. Fluid Mech. 1979, 114, 315–316. [Google Scholar]
- DiLorenzo, J.L.; Ram, R.V.; Huang, P.; Najarian, T.O. Pollution Susceptibility of Well-Mixed Tidal Basins. J. Waterw. Port Coast. Ocean Eng. 1994, 120, 404–422. [Google Scholar] [CrossRef]
- Nece, B.R.E.; Asce, F.; Nece, R.E.; Asce, F. Planform Effects on Tidal Flushing of Marinas. J. Waterw. Port Coast. Ocean Eng. 1984, 110, 251–269. [Google Scholar] [CrossRef]
- Sanford, L.P.; Boicourt, W.C.; Rives, S.R. Model For Estimating Tidal Flushing of Small Embayments. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 635–654. [Google Scholar] [CrossRef]
- Falconer, R.A.; Yu, G. Effects of Depth, Bed Slope and Scaling on Tidal Currents and Exchange in a Laboratory Model Harbour. Proc. Inst. Civ. Eng. Part 2 1991, 91, 561–576. [Google Scholar]
- US Army Corps of Engineers. Coastal Engineering Manual; US Army Corps of Engineers: Washington, DC, USA, 2002.
- Lončar, G.; Carević, D.; Bujak, D.; Bartolić, I.; Beg Paklar, G. Analiza Utjecaja Vjetra, Plimnih Oscilacija i Razdiobe Gustoće Na Izmjenu Mora Kroz Propuste u Marinama: Primjer Marine Ičići. Hrvat. Vode 2017, 25, 139–148. [Google Scholar]
- Tsoukala, V.K.; Moutzouris, C.I. Wave Transmission in Harbors through Flushing Culverts. Ocean Eng. 2009, 36, 434–445. [Google Scholar] [CrossRef]
- Fountoulis, G.; Memos, C. Optimization of Openings for Water Renewal in a Harbour Basin. J. Mar. Environ. Eng. 2005, 7, 297–305. [Google Scholar]
- Umgiesser, G.; Ferrarin, C.; Cucco, A.; De Pascalis, F.; Bellafiore, D.; Ghezzo, M.; Bajo, M. Comparative Hydrodynamics of 10 Mediterranean Lagoons by Means of Numerical Modeling. J. Geophys. Res. Oceans 2014, 119, 2212–2226. [Google Scholar] [CrossRef]
- Cucco, A.; Umgiesser, G. Modeling the Venice Lagoon Residence Time. Ecol. Model. 2006, 193, 34–51. [Google Scholar] [CrossRef]
- Canu, D.M.; Solidoro, C.; Umgiesser, G.; Cucco, A.; Ferrarin, C. Assessing Confinement in Coastal Lagoons. Mar. Pollut. Bull. 2012, 64, 2391–2398. [Google Scholar] [CrossRef] [PubMed]
- Bujak, D.; Carević, D.; Mostečak, H. Velocities inside Flushing Culverts Induced by Waves. Proc. Inst. Civ. Eng. Marit. Eng. 2017, 170, 112–121. [Google Scholar] [CrossRef]
- Carevic, D.; Mostecak, H.; Bujak, D.; Loncar, G. Influence of Water Level Variations on Wave Transmission through Flushing Culverts Positioned in Breakwater Body. J. Waterw. Port Coast. Ocean Eng. ASCE 2018, 144, 04018012. [Google Scholar] [CrossRef]
- Rubinić, J.; Horvat, B.; Kuhta, M.; Stroj, A. Analiza Izdašnosti Priobalnih Izvora Na Području Opatije Korištenjem Termalnih Infracrvenih Satelitskih Snimaka. In Hrvatska Konferencija o Vodama, Hrvatske Vode i Europska Unija—Izazovi i Mogućnosti; CROSBI: Opatija, Hrvatska, 2007; pp. 211–216. [Google Scholar]
- Mike 3 Flow Model. Available online: www.mikepoweredbydhi.com (accessed on 20 January 2018).
- Song, Y.; Haidvogel, D. A Semi-Implicit Ocean Circulation Model Using a Generalised Topography-Following Coordinate System. J. Comp. Phys. 1994, 115, 228–244. [Google Scholar] [CrossRef]
- Sleigh, D.H.; Gaskel, P.H. An Unstructured Finite Volume Algorithm for Predicting Flow in Rivers and Estuaries. Comput. Fluids 1998, 27, 479–508. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann Solvers, Parameters Vectors and Difference Schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Smagorinsky, J. Some Historical Remarks on the Use of Nonlinear Viscosities. In Large Eddy Simulations of Complex Engineering and Geophysical Flows; Galperin, B., Orszag, S., Eds.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Rodi, W. Examples of Calculation Methods for Flow and Mixing in Stratified Fluids. J. Geophys. Res. 1987, 92, 5305–5328. [Google Scholar] [CrossRef]
- Wu, J. An Estimation of Wind Effects on Dispersion in Wide Channels. Water Resour. Res. 1969, 5, 1097–1104. [Google Scholar] [CrossRef]
- Richter, K.; Hank, T.B.; Atzberger, C.; Mauser, W. Goodness-of-Fit Measures: What Do They Tell about Vegetation Variable Retrieval Performance from Earth Observation Data. Remote Sens. Agric. Ecosyst. Hydrol. XIII 2011. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Imberger, J. The Diurnal Mixed Layer. Limnol. Ocean. 1985, 30, 737–770. [Google Scholar] [CrossRef]
- Oakey, N.S.; Elliott, J.A. Dissipation Within the Surface Mixed Layer. J. Phys. Oceanogr. 1982, 12, 171–185. [Google Scholar] [CrossRef]
- Mike 21/SW. Available online: www.dhigroup.com (accessed on 23 January 2018).
- Komen, G.J.; Cavaleri, M.; Donelan, K.; Hasselman, S.; Hasselman, K.; Janssen, P.A.E.M. Modelling of Dynamic of Ocean Surface Waves; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Samaras, A.G.; Gaeta, M.G.; Miquel, A.M.; Archetti, R. High-Resolution Wave and Hydrodynamics Modelling in Coastal Areas: Operational Applications for Coastal Planning, Decision Support and Assessment. Nat. Hazards Earth Syst. Sci. 2016, 16, 1499–1518. [Google Scholar] [CrossRef]
- Sánchez-Arcilla, A.; García-León, M.; Gracia, V. Hydro-Morphodynamic Modelling in Mediterranean Storms—Errors and Uncertainties under Sharp Gradients. Nat. Hazards Earth Syst. Sci. 2014, 14, 2993–3004. [Google Scholar] [CrossRef]
- Brzović, N.; Strelec-Mahović, N. Modelling of Induced Circulation. WSEAS Trans. Fluid Mech. 1999, 5, 653–657. [Google Scholar]
- Ivatek-Sahdan, S.; Tudor, M. Use of High-Resolution Dynamical Adaptation in Operational Suite and Research Impact Studies. Meteorol. Z. 2004, 13, 99–108. [Google Scholar] [CrossRef]
- Monsen, N.E.; Cloern, J.E.; Lucas, L.V.; Monismith, S.G. A Comment on the Use of Flushing Time, Residence Time, and Age as Transport Time Scales. Limnol. Oceanogr. 2002, 47, 1545–1553. [Google Scholar] [CrossRef]
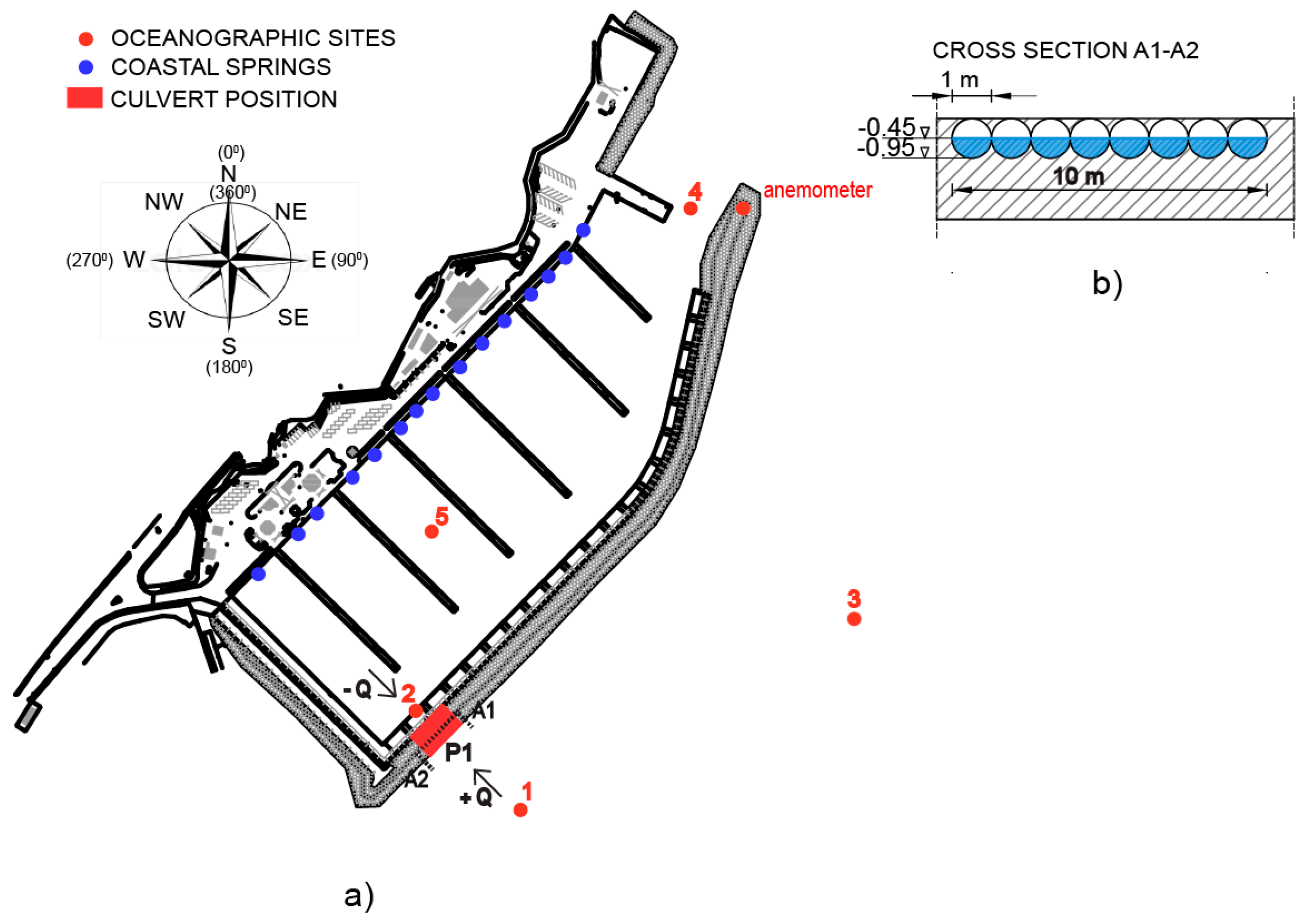
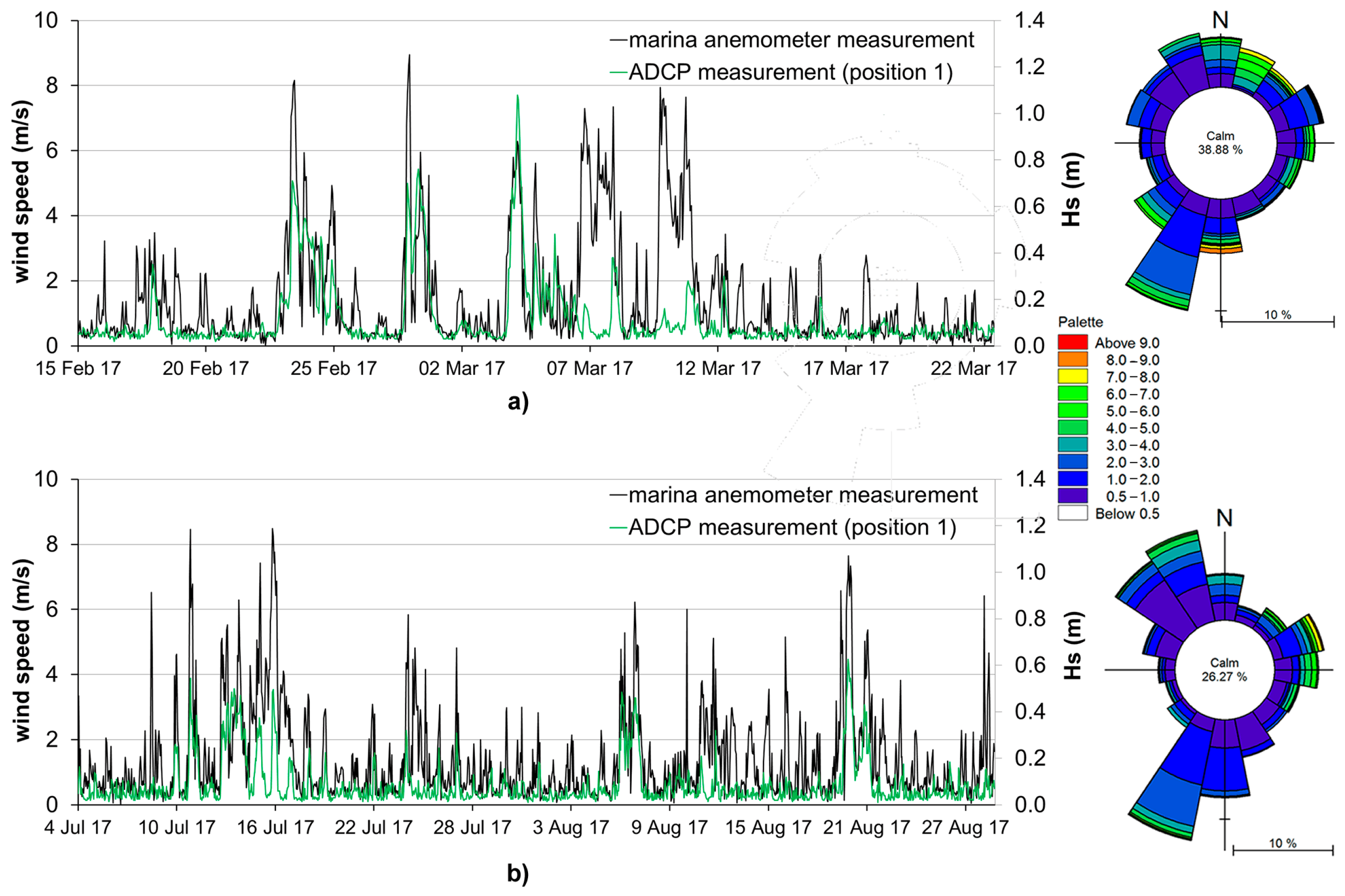
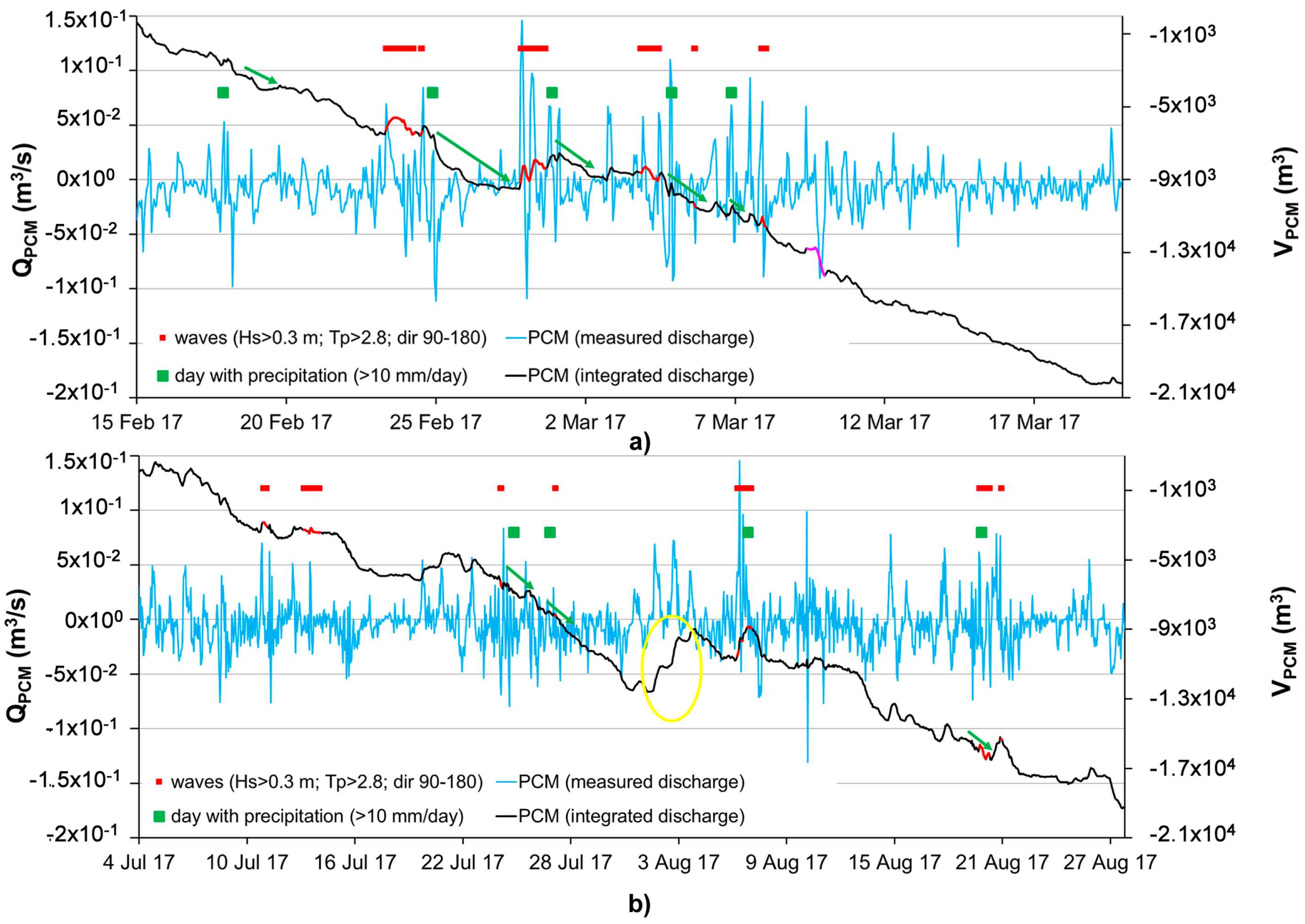

| Instrument | Sampling Rate | Output (Averaging) |
|---|---|---|
| ADCP 1, 2 | 1 s | Wave—15 min Currents—10 min |
| ADCP 3, 4, 5 | 1 s | Currents—10 min |
| CTD | 1 s | 10 min |
| Anemometer | 1 s | 10 min |
| PCM | Varies with hydraulic and physical conditions | 2 min |
| Winter Measurement Campaign | Deepwater Conditions | |||||
|---|---|---|---|---|---|---|
| Duration | HS-AV | TP-AV | HS-MAX | dirAV | ||
| Situation Onset | (h) | (m) | (s) | (m) | (°) | |
| 1 | 23 February 2017 23:00 | 23 | 0.51 | 3.60 | 0.71 | 165 |
| 2 | 25 February 2017 3:00 | 2 | 0.45 | 3.50 | 0.47 | 100 |
| 3 | 28 February 2.2017 11:00 | 21 | 0.55 | 3.64 | 0.76 | 159 |
| 4 | 4 March 2017 11:00 | 16 | 0.65 | 4.41 | 1.08 | 161 |
| 5 | 6 March 2017 6:00 | 2 | 0.42 | 5.40 | 0.48 | 174 |
| 6 | 8 March 2017 12:00 | 5 | 0.35 | 2.90 | 0.38 | 105 |
| 7 | 12 March 2017 20:00 | 2 | 0.30 | 2.85 | 0.30 | 103 |
| Summer Measurement Campaign | Deepwater Conditions | |||||
|---|---|---|---|---|---|---|
| Duration | HS-AV | TP-AV | HS-MAX | dirAV | ||
| Situation Onset | (h) | (m) | (s) | (m) | (°) | |
| 1 | 11 July 2017 11:00 | 2 | 0.45 | 2.91 | 0.55 | 169 |
| 2 | 13 July 2017 17:00 | 4 | 0.40 | 2.83 | 0.44 | 97 |
| 3 | 13 July 2017 23:00 | 16 | 0.42 | 3.07 | 0.46 | 104 |
| 4 | 24 July 2017 15:00 | 2 | 0.30 | 2.88 | 0.32 | 181 |
| 5 | 27 July 2017 16:00 | 2 | 0.30 | 2.68 | 0.31 | 175 |
| 6 | 6 August 2017 19:00 | 3 | 0.30 | 3.31 | 0.34 | 108 |
| 7 | 7 August 2017 1:00 | 2 | 0.30 | 3.3 | 0.34 | 108 |
| 8 | 7 August 2017 10:00 | 5 | 0.43 | 2.74 | 0.43 | 111 |
| 9 | 20 August 2017 6:00 | 15 | 0.44 | 3.11 | 0.48 | 105 |
| 10 | 21 August 2017 11:00 | 2 | 0.38 | 2.93 | 0.43 | 104 |
| ADCP-1 (−6 m) | ||||
|---|---|---|---|---|
| Winter | Summer | |||
| u | v | u | v | |
| NRMSE | 1.10 | 0.98 | 0.94 | 0.86 |
| NSE | −0.36 | −0.01 | 0.12 | 0.25 |
| HS > 0.3 m, TP > 2.8 s, dir 90–180° | Winter (November–April) | Summer (May–October) | |
|---|---|---|---|
| Year | Total Duration (h) | (h) | (h) |
| 1992 | 820 | 450 | 370 |
| 1993 | 752 | 263 | 489 |
| 1994 | 820 | 475 | 345 |
| 1995 | 765 | 380 | 385 |
| 1996 | 760 | 476 | 284 |
| 1997 | 695 | 311 | 384 |
| 1998 | 675 | 411 | 264 |
| 1999 | 760 | 476 | 284 |
| 2000 | 838 | 411 | 427 |
| 2001 | 1128 | 712 | 416 |
| average | 801 | 437 | 365 |
| Date | HS-M [m] | TP-M [s] | LP-M [m] | HS-P [m] | TP-P [s] | LP-P [m] | SE [m] | QP [m3/s] | QP-PCM [m3/s] |
|---|---|---|---|---|---|---|---|---|---|
| 28 February 2017 | 0.06 | 0.98 | 1.50 | 0.60 | 3.10 | 15.0 | −0.15 | 0.04 | 0.08 |
| 4 March 2017 | 0.06 | 0.98 | 1.50 | 0.60 | 3.10 | 15.0 | 0.17 | −0.07 | −0.02 |
| Measurement Duration T (h) | 1 Culvert Absolute Sum |V1-culvert| (m3) | 1 Culvert Mean abs. Discharge |V1-culvert|/T (m3/h) | Wave sit. Duration Tw (h) | Wave sit. Absolute Sum |V1-waves| (m3) | Wave sit. Mean abs. Discharge |V1-waves|/Tw (m3/h) | |
|---|---|---|---|---|---|---|
| Winter | 786 | 50,213 | 64 | 71 | 7406 | 104 |
| Summer | 1340 | 76,966 | 57 | 53 | 3166 | 60 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartolić, I.; Lončar, G.; Bujak, D.; Carević, D. The Flow Generator Relations for Water Renewal through the Flushing Culverts in Marinas. Water 2018, 10, 936. https://doi.org/10.3390/w10070936
Bartolić I, Lončar G, Bujak D, Carević D. The Flow Generator Relations for Water Renewal through the Flushing Culverts in Marinas. Water. 2018; 10(7):936. https://doi.org/10.3390/w10070936
Chicago/Turabian StyleBartolić, Ivana, Goran Lončar, Damjan Bujak, and Dalibor Carević. 2018. "The Flow Generator Relations for Water Renewal through the Flushing Culverts in Marinas" Water 10, no. 7: 936. https://doi.org/10.3390/w10070936
APA StyleBartolić, I., Lončar, G., Bujak, D., & Carević, D. (2018). The Flow Generator Relations for Water Renewal through the Flushing Culverts in Marinas. Water, 10(7), 936. https://doi.org/10.3390/w10070936





