Three Geostatistical Methods for Hydrofacies Simulation Ranked Using a Large Borehole Lithology Dataset from the Venice Hinterland (NE Italy)
Abstract
1. Introduction
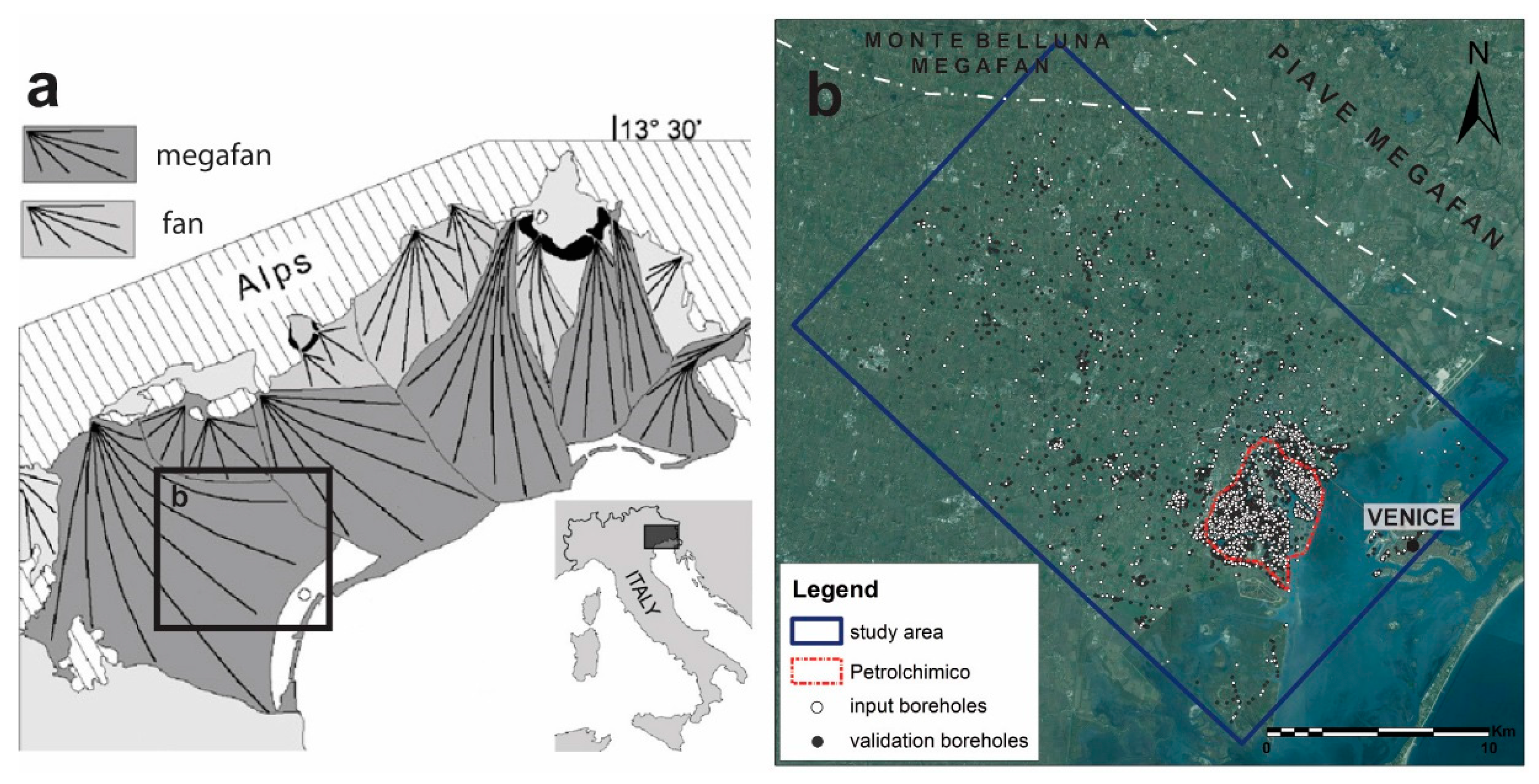
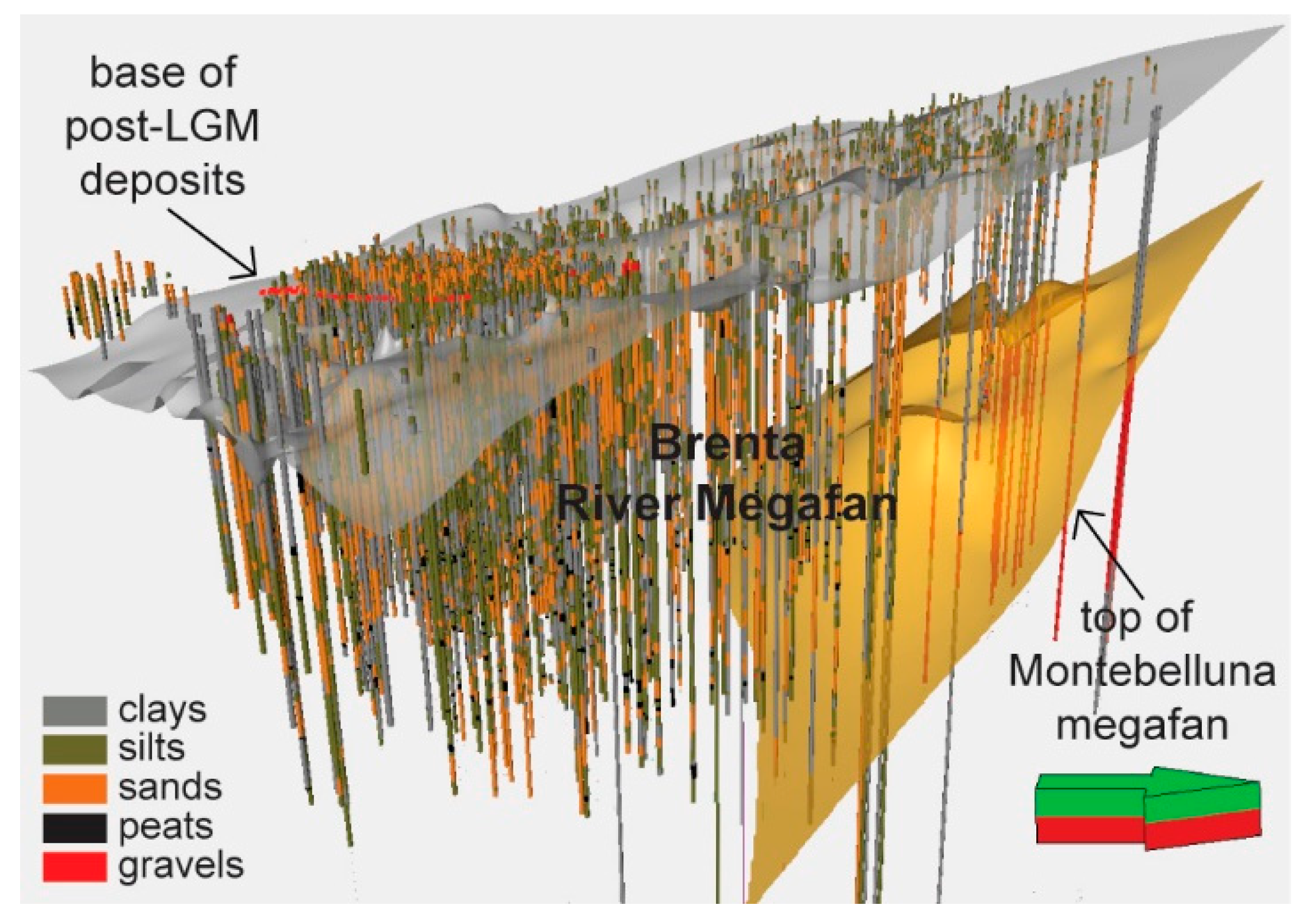
2. Geological and Hydrogeological Framework
3. Materials and Methods
4. Results
4.1. Facies Models
4.1.1. Object-Based Simulation
4.1.2. Truncated Gaussian Simulation
4.1.3. Sequential Indicator Simulation
4.2. Conditioning to Input Data and Facies Prediction at Validation Boreholes
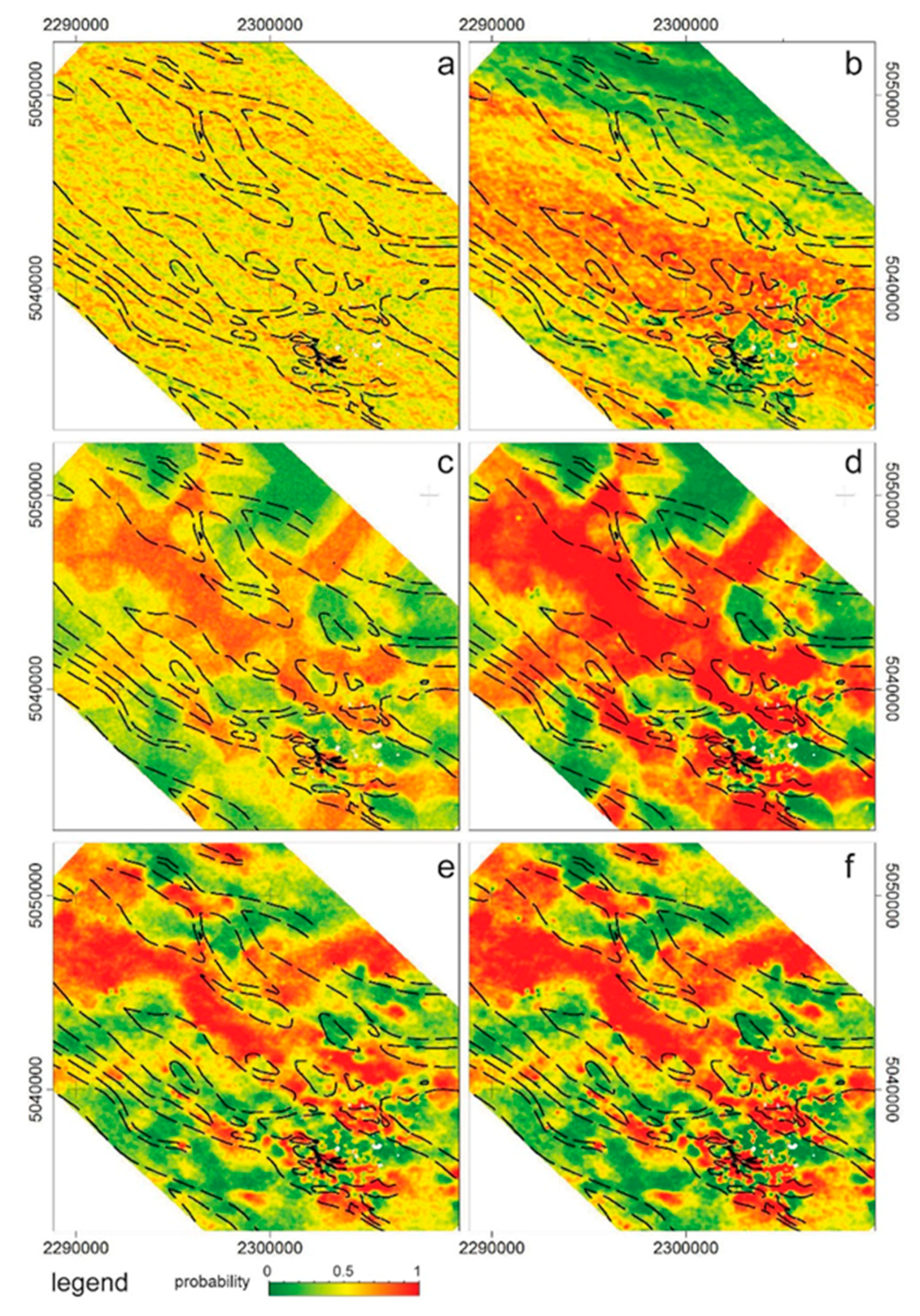
4.3. Sand Probability Models
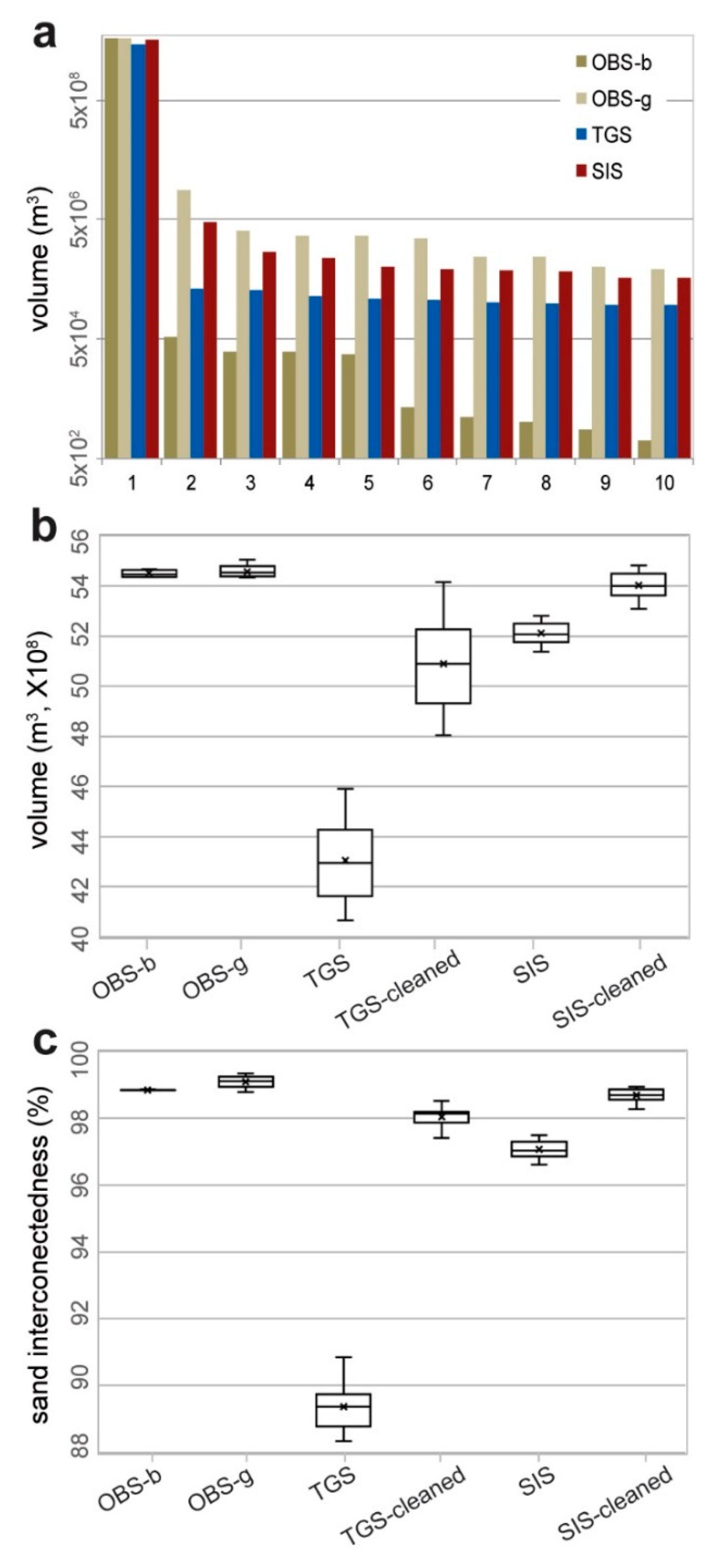
4.4. Connectivity of Modelled Sands
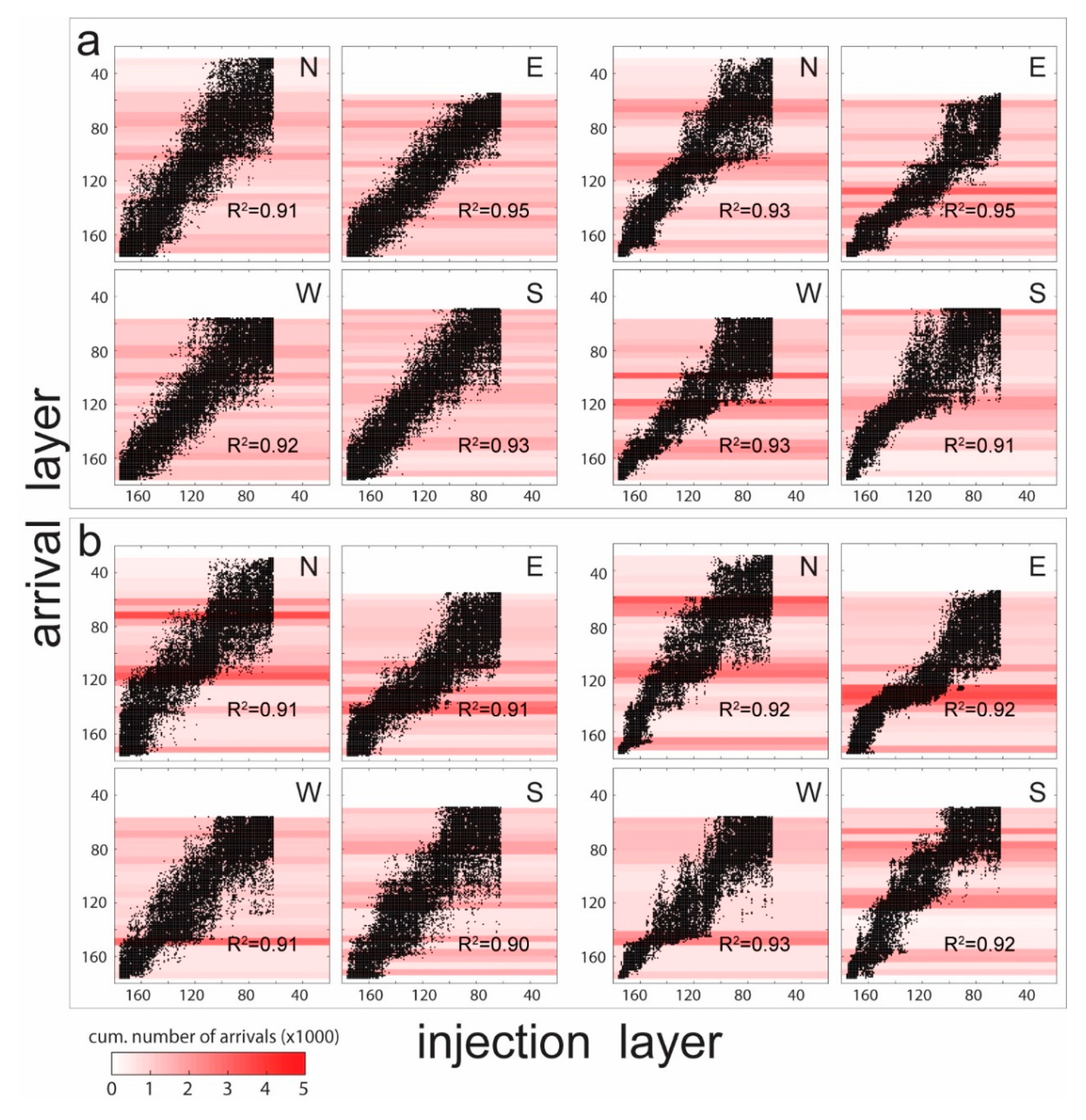
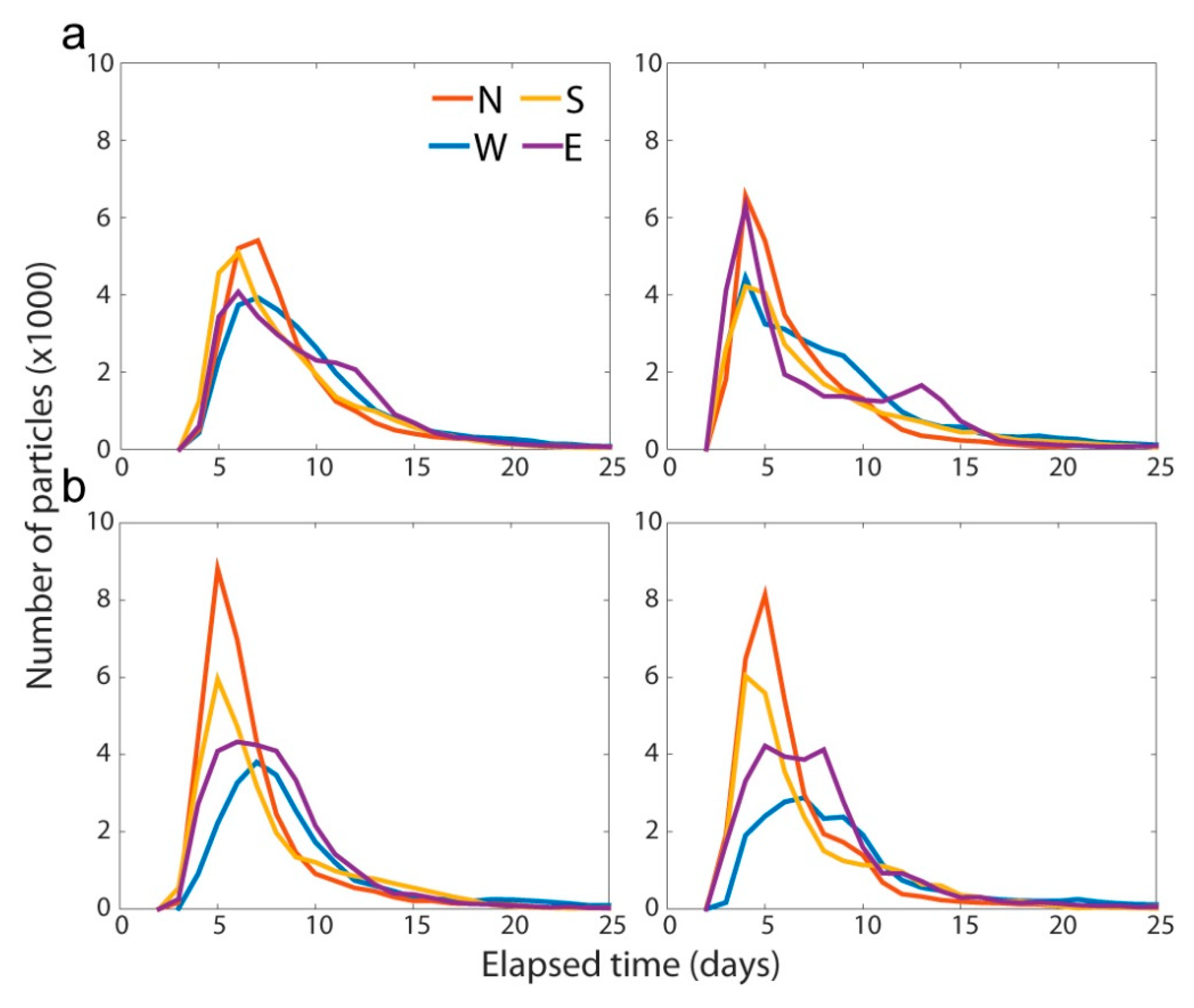
4.5. Particle Tracking Results
5. Discussion
5.1. Which Modelling Algorithm Does Better with Lithology from Dense Borehole Data?
5.2. Likely Implications for Aquifer and Groundwater Flow Assessment
6. Conclusions
- Though compromising with geological realism of facies clusters shapes, TGS and SIS are better suited in place of OBS for their ease of conditioning to closely spaced boreholes.
- Pixel-based facies models of this study, especially those from TGS, suffer for ‘noise’ in form of unwanted isolated cells taking outlier hydrofacies values, which require cleaning for better assessment of aquifer facies distribution.
- SIS provides better facies prediction and renders a less noisy picture of subsurface geology than TGS, without requiring assumptions about spatial relationship among operative facies, which makes it the best suited for use with large borehole lithology datasets lacking detail and quality consistency.
- Statistics of connected sands and results of the particle tracking simulation indicate TGS and SIS hydrofacies models are associated with significantly different aquifer connectivity scenarios, e.g., a relatively poorly connected aquifer (TGS) typified by diffuse, nearly isotropic flow as opposed to a better-connected aquifer (SIS) featuring preferential flow paths hosted within the sandy channel-fills of BRM.
- Differences between the two alternative pixel-based aquifer models are due to widespread noise in TGS realizations, suggesting that noise cleaning should be considered and implemented with care before simulating groundwater flow.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dell’arciprete, D.; Felletti, F.; Bersezio, R. Simulation of fine-scale heterogeneity of meandering river aquifer analogues: Comparing different approaches. In geoENV VII—Geostatistics for Environmental Applications, Quantitative Geology and Geostatistics; Atkinson, P., Lloyd, C., Eds.; Springer: Dordrecht, The Netherlands, 2010; Volume 16, pp. 127–137. [Google Scholar] [CrossRef]
- Dell’arciprete, D.; Bersezio, R.; Felletti, F.; Giudici, M.; Comunian, A.; Renard, P. Comparison of three geostatistical methods for hydrofacies simulation: A test on alluvial sediments. Hydrogeol. J. 2012, 20, 299–311. [Google Scholar] [CrossRef]
- Colombera, L.; Felletti, F.; Mountney, N.P.; McCaffrey, W.D. A database approach for constraining stochastic simulations of the sedimentary heterogeneity of fluvial reservoirs. Am. Assoc. Pet. Geol. Bull. 2012, 96, 2143–2166. [Google Scholar] [CrossRef]
- Colombera, L.; Mountney, N.P.; Felletti, F.; McCaffrey, W.D. Models for guiding and ranking well-to-well correlations of channel bodies in fluvial reservoirs. Am. Assoc. Pet. Geol. Bull. 2014, 98, 1943–1965. [Google Scholar] [CrossRef]
- Comunian, A.; De Micheli, L.; Lazzati, C.; Felletti, F.; Giacobbo, F.; Giudici, M.; Bersezio, R. Hierarchical simulation of aquifer heterogeneity: Implications of different simulation settings on solute-transport modelling. Hydrogeol. J. 2016, 24, 319–334. [Google Scholar] [CrossRef]
- Fogg, G.E.; Noyes, C.D.; Carle, S.F. Geologically based model of heterogeneous hydraulic conductivity in an alluvial setting. Hydrogeol. J. 1998, 6, 131–143. [Google Scholar] [CrossRef]
- Anderson, M.P.; Aiken, J.S.; Webb, E.K.; Mickelson, D.M. Sedimentology and hydrogeology of two braided stream deposits. Sediment. Geol. 1999, 129, 187–199. [Google Scholar] [CrossRef]
- De Marsily, G.; Delay, F.; Gonçalvès, J.; Renard, P.; Teles, V.; Violette, S. Dealing with spatial heterogeneity. Hydrogeol. J. 2005, 13, 161–183. [Google Scholar] [CrossRef]
- Bianchi, M.; Zheng, C. A lithofacies approach for modelling non-Fickian solute transport in a heterogeneous alluvial aquifer. Water Resour. Res. 2016, 52, 552–565. [Google Scholar] [CrossRef]
- Matheron, G. Random Functions and their Application in Geology. In Geostatistics Computer Applications in the Earth Sciences; Merriam, D.F., Ed.; Springer: Boston, MA, USA, 1970; pp. 79–87. [Google Scholar]
- Pyrcz, M.J.; Deutsch, C.V. Geostatistical Reservoir Modelling, 2nd ed.; Oxford University Press: Oxford, UK, 2014; p. 348. ISBN 9780199731442. [Google Scholar]
- Seifert, D.; Jensen, J.L. Object and pixel-based reservoir modelling of a braided fluvial reservoir. Math. Geol. 2000, 32, 581–603. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Tran, T.T. FLUVSIM: A program for object-based stochastic modelling of fluvial depositional systems. Comput. Geosci. 2002, 28, 525–535. [Google Scholar] [CrossRef]
- Keogh, K.J.; Martinius, A.W.; Osland, R. The development of fluvial stochastic modelling in the Norwegian oil industry: A historical review, subsurface implementation and future directions. Sediment. Geol. 2007, 202, 249–268. [Google Scholar] [CrossRef]
- Pyrcz, M.J.; Boisvert, J.B.; Deutsch, C.V. A library of training images for fluvial and deepwater reservoirs and associated code. Comput. Geosci. 2008, 34, 542–560. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User's Guide, 2nd ed.; Oxford University Press: New York, NY, USA, 1998; p. 369. [Google Scholar]
- Beucher, H.; Renard, D. Truncated Gaussian and derived methods. C. R. Geosci. 2016, 348, 510–519. [Google Scholar] [CrossRef]
- Dethlefsen, F.; Ebert, M.; Dahmke, A. A geological database for parameterization in numerical modelling of subsurface storage in northern Germany. Environ. Earth Sci. 2014, 71, 2227–2244. [Google Scholar] [CrossRef]
- Vázquez-Suñé, E.; Marazuela, M.Á.; Velasco, V.; Diviu, M.; Pérez-Estaún, A.; Álvarez-Marrón, J. A geological model for the management of subsurface data in the urban environment of Barcelona and surrounding area. Solid Earth 2017, 7, 1317. [Google Scholar] [CrossRef]
- Pham, H.V.; Tsai, F.T.C. Modelling complex aquifer systems: A case study in Baton Rouge, Louisiana (USA). Hydrogeol. J. 2017, 25, 601–615. [Google Scholar] [CrossRef]
- Deutsch, C.V. Cleaning categorical variable (lithofacies) realizations with maximum a-posteriori selection. Comput. Geosci. 1998, 24, 551–562. [Google Scholar] [CrossRef]
- Hong, S.; Deutsch, C.V. Another Look at Realization Cleaning; Centre for Computational Geostatistics Report 12; University of Alberta: Edmonton, AB, Canada, 2010; p. 118. [Google Scholar]
- Vitturi, A.; Bondesan, A.; Fontana, A.; Mozzi, P.; Primon, S.; Bassan, V. Geologia. In Atlante Geologico Della Provincia di Venezia—Note Illustrative, Quarto d’Altino (Venezia); Vitturi, A., Bassan, V., Mazzuccato, A., Primon, S., Bondesan, A., Ronchese, F., Zangheri, P., Eds.; Arti Grafiche Venete: Venezia, Italia, 2011; pp. 333–357. ISBN 9788890720703. [Google Scholar]
- Bondesan, A.; Primon, S.; Bassan, V.; Vitturi, A. (Eds.) Le Unità Geologiche Della Provincia di Venezia; Provincia di Venezia, Servizio Geologico e Difesa del Suolo: Venezia, Italia, 2008. [Google Scholar]
- Fontana, A.; Mozzi, P.; Marchetti, M. Alluvial fans and megafans along the southern side of the Alps. Sediment. Geol. 2014, 301, 150–171. [Google Scholar] [CrossRef]
- Donnici, S.; Serandrei-Barbero, R.; Bini, C.; Bonardi, M.; Lezziero, A. The caranto paleosol and its role in the early urbanization of Venice. Geoarchaeology 2011, 26, 514–543. [Google Scholar] [CrossRef]
- Fabri, P.; Zàngheri, P.; Bassan, V.; Fagarazzi, E.; Mazzuccato, A.; Primon, S.; Zogno, C. Sistemi Idrogeologici Della Provincia di Venezia: Acquiferi Superficiali; Provincia di Venezia, Servizio Geologico, Difesa del Suolo e Tutela del Territorio: Venezia, Italia, 2013. [Google Scholar]
- Carbognin, L.; Rizzetto, F.; Tosi, L.; Teatini, P.; Gasparetto-Stori, G. The salt intrusion in the Venetian lagoon area: II. The southern basin. Geol. Appl. 2005, 2, 124–229. [Google Scholar]
- Da Lio, C.; Tosi, L.; Zambon, G.; Vianello, A.; Baldin, G.; Lorenzetti, G.; Manfè, G.; Teatini, P. Long-term groundwater dynamics in the coastal confined aquifers of Venice (Italy). Estuar. Coast. Shelf Sci. 2013, 135, 248–259. [Google Scholar] [CrossRef]
- Beretta, G.P.; Terrenghi, J. Groundwater flow in the Venice lagoon and remediation of the Porto Marghera industrial area (Italy). Hydrogeol. J. 2017, 25, 847–861. [Google Scholar] [CrossRef]
- Associazione Geotecnica Italiana. Raccomandazioni Sulla Programmazione ed Esecuzione Delle Indagini Geotecniche; AGI; SGE: Padova, Italy, 1977. [Google Scholar]
- Folk, R.L. Petrology of Sedimentary Rocks; Hemphill Publishing Company: Austin, TX, USA, 1980. [Google Scholar]
- Daly, C.; Quental, S.; Novak, D. A faster, more accurate Gaussian simulation. In Proceedings of the GeoCanada Conference, Calgary, AB, Canada, 10–14 May 2010. [Google Scholar]
- Deutsch, C.V. A Short Note on Cross Validation of Facies Simulation Methods; Centre for Computational Geostatistics Annual Report, Report 1; University of Alberta: Edmonton, AB, Canada, 1998; p. 109. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the US Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; Department of the Interior, US Geological Survey: Reston, VA, USA, 2005.
- Pollock, D.W. Semianalytical Computation of Path Lines for Finite-Difference Models. Groundwater 1998, 26, 743–750. [Google Scholar] [CrossRef]
- Pollock, D.W. User Guide for MODPATH Version 6—A Particle-Tracking Model for MODFLOW. US Geological Survey Techniques and Methods 6-A41; Department of the Interior, US Geological Survey: Reston, VA, USA, 2012.
- Jha, S.K.; Mariethoz, G.; Mathews, G.; Vial, J.; Kelly, B.F. Influence of Alluvial Morphology on Upscaled Hydraulic Conductivity. Groundwater 2016, 54, 384–393. [Google Scholar] [CrossRef] [PubMed]
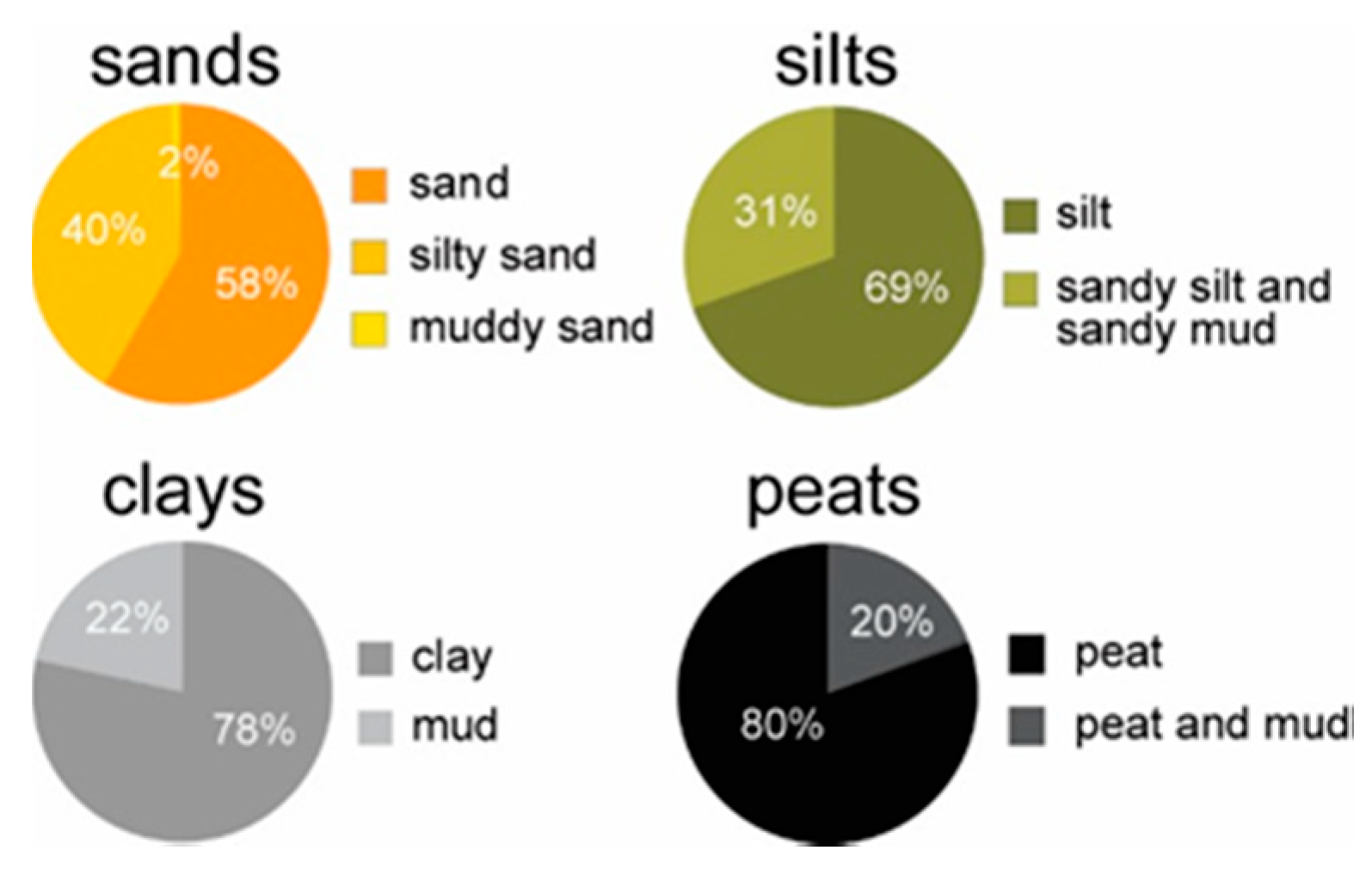
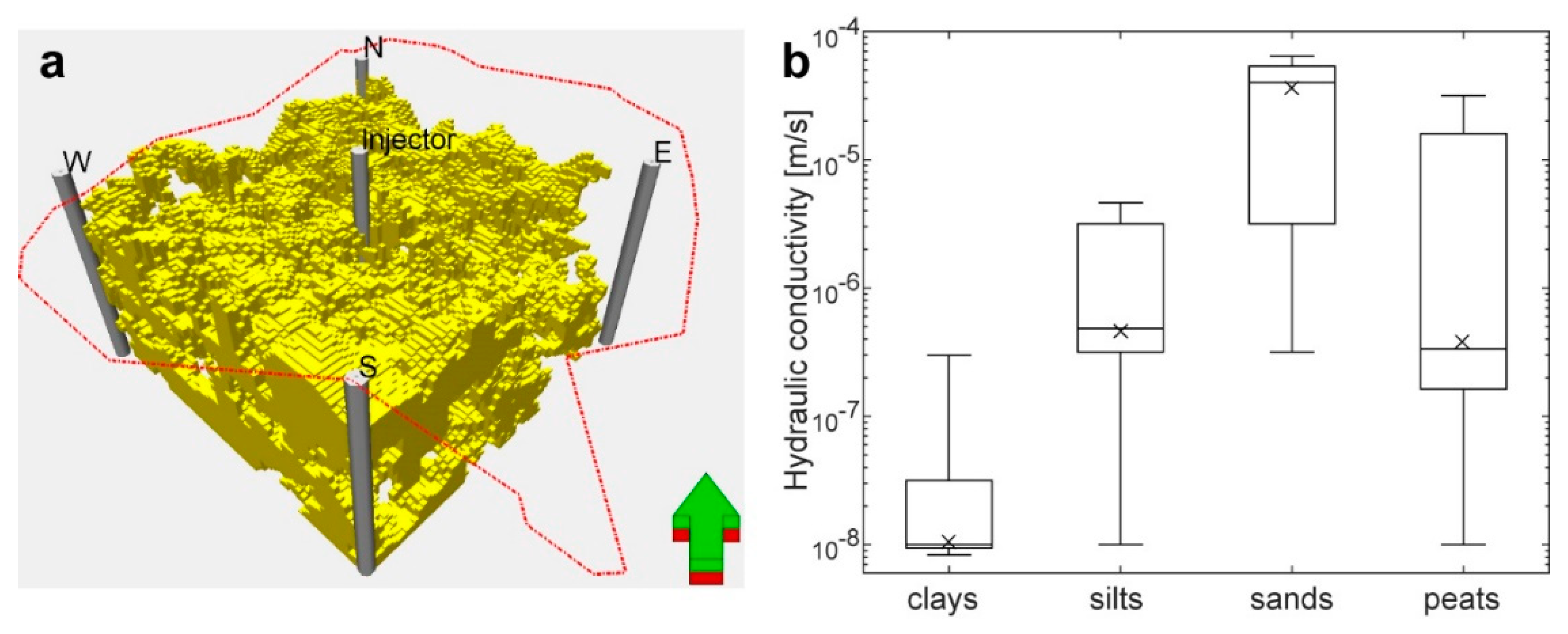
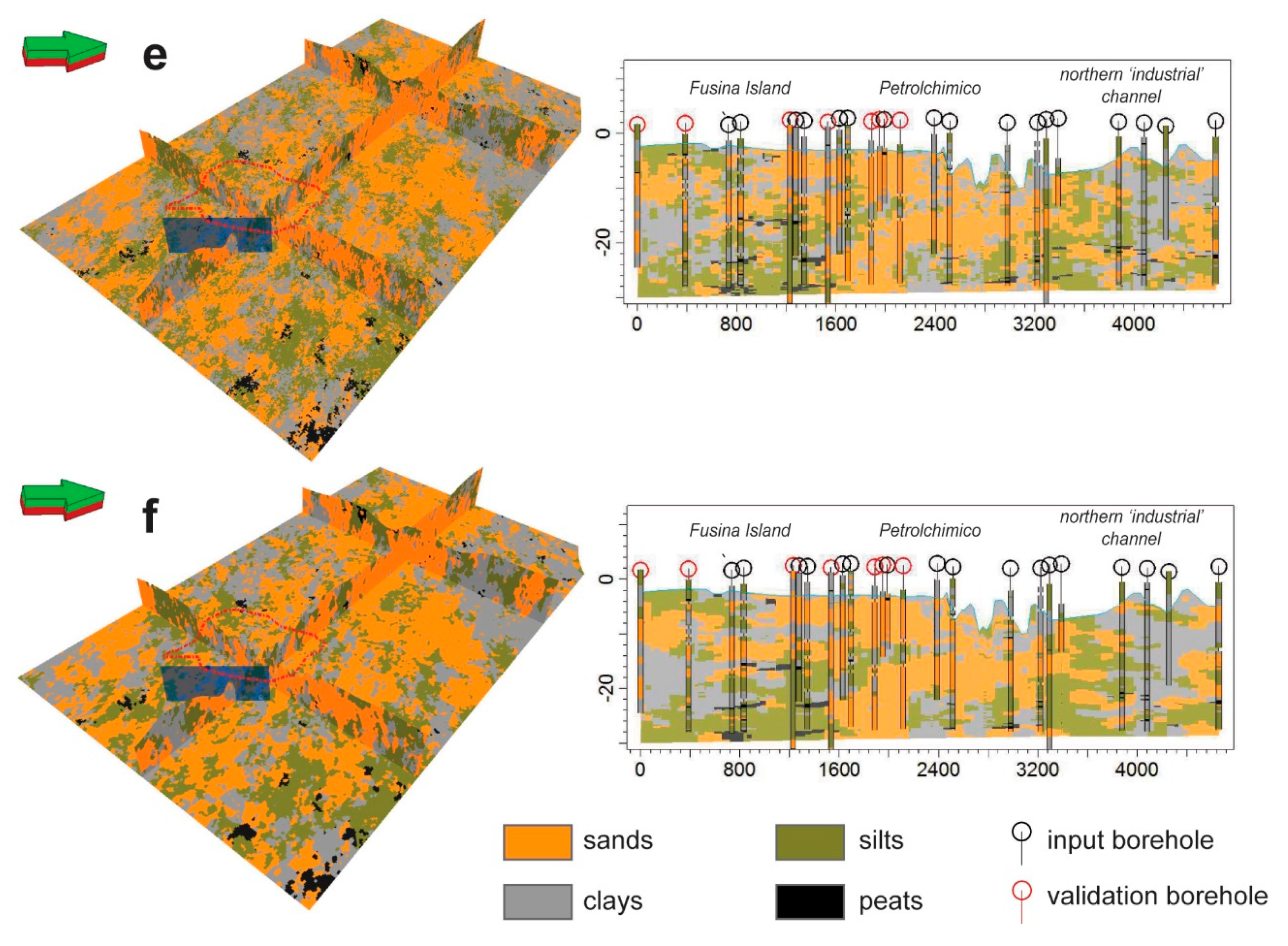
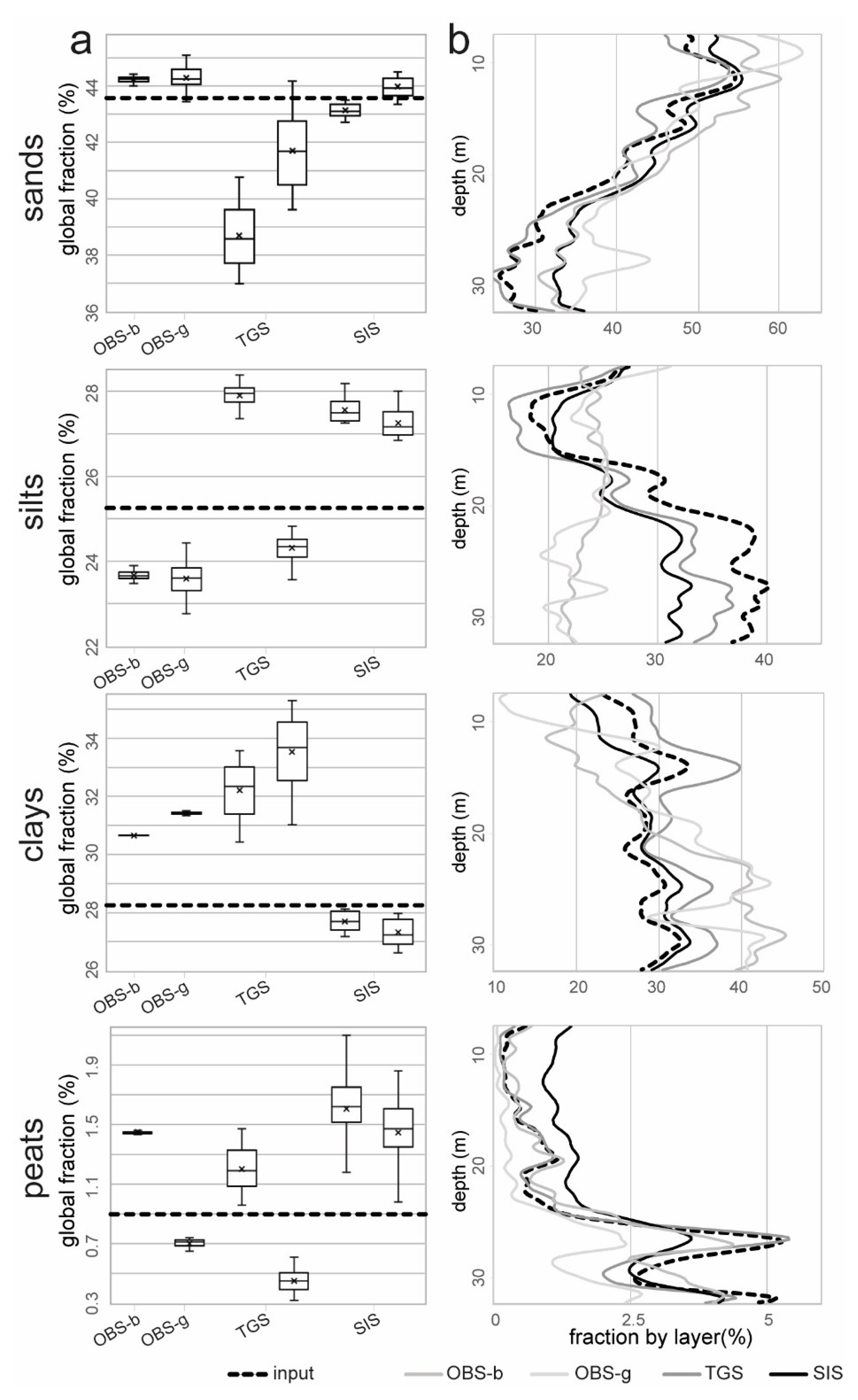

| Facies | Depositional Environment | Depositional Process | Abundance (%) | Mean K (m/s) |
|---|---|---|---|---|
| sands | fluvial channel | point bar migration | 43.2 | 2.00 × 10−5 |
| silts | levee | overbanking | 27.5 | 5.00 × 10−7 |
| clays | floodplain | overbanking | 28.4 | 1.00 × 10−8 |
| peats | peatland | plant debris accumulation | 0.9 | 3.50 × 10−7 |
| Object Type | Facies | Insertion Order/Replacement Rules | Shape | Size, Layout and Orientation | |||||
|---|---|---|---|---|---|---|---|---|---|
| Cross-Sectional | Plan-View | Min | Mean | Max | Drift 1 | ||||
| (m) | (%) | ||||||||
| fluvial channel | sands | after peats; can replace peats | half-pipe | string-like, sinuous | width | - | 300 | - | 1 |
| length | infinite | ||||||||
| thickness | 1 | 2.5 | 5 | 0.3 | |||||
| orientation (°) | - | 110 | - | 0.1 | |||||
| sinuosity amplitude | - | 500 | - | 0.3 | |||||
| wave-length | - | 2500 | - | 0.5 | |||||
| levee | silts | in tandem with/on both sides of channels; can replace peats | wedge | string-like, sinuous | width | 0.63 × channel width | 0.5 | ||
| length | infinite | ||||||||
| thickness | 0.63 × channel thick. | 0.5 | |||||||
| orientation/sinuosity | same as channels | ||||||||
| background | clays | last, fills in gaps between previously inserted objects | n/a | ||||||
| peat accumulation | peats | first to be inserted | elliptical | elliptical | width | 100 | 250 | 2000 | - |
| length | 100 | 625 | 5000 | - | |||||
| thickness | 0.2 | 0.5 | 1 | - | |||||
| orientation (°) | - | 110 | - | 0.1 | |||||
| Operative Facies | Major Direction (°) | Function Type 1 | Sill | Ranges (m) | ||
|---|---|---|---|---|---|---|
| Major | Minor | Vertical | ||||
| sands | 105 | exp (exp) | 0.7 (0.3) | 215 (4500) | 210 (1500) | 3.7 (16.4) |
| silts | 180 | exp (exp) | 0.7 (0.3) | 70 (3100) | 35 (3000) | 2.6 (17.8) |
| clays | 110 | exp (exp) | 0.7 (0.3) | 50 (3100) | 50 (1300) | 2.7 (25) |
| peats | n/a | exp | 1.0 | 500 | 500 | 1.1 |
| continuous variable 2 | 110 | exp (sph) | 0.6 (0.4) | 90 (10,700) | 30 (10500) | 1.3 (9.5) |
| Object Type | OBS-b | OBS-g | |
|---|---|---|---|
| fluvial channels | honored cells (%) | 50 | 45 |
| number of inserted items | 2525 | 1002 | |
| width | 125 (5) | 300 (0) | |
| thickness | 1.15 (0.3) | 2.83 (0.81) | |
| levees | honored cells (%) | 35 | 33 |
| number of inserted items | 2525 | 1002 | |
| width | 75 (3.23) | 189 (0) | |
| thickness | 0.72 (0.04) | 1.15 (0) | |
| peats | honored cells (%) | 100 | 99 |
| number of inserted items | 957 | 931 | |
| maximum length | 967 (401) | 906 (423) | |
| minimum length | 645 (399) | 608 (411) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marini, M.; Felletti, F.; Beretta, G.P.; Terrenghi, J. Three Geostatistical Methods for Hydrofacies Simulation Ranked Using a Large Borehole Lithology Dataset from the Venice Hinterland (NE Italy). Water 2018, 10, 844. https://doi.org/10.3390/w10070844
Marini M, Felletti F, Beretta GP, Terrenghi J. Three Geostatistical Methods for Hydrofacies Simulation Ranked Using a Large Borehole Lithology Dataset from the Venice Hinterland (NE Italy). Water. 2018; 10(7):844. https://doi.org/10.3390/w10070844
Chicago/Turabian StyleMarini, Mattia, Fabrizio Felletti, Giovanni Pietro Beretta, and Jacopo Terrenghi. 2018. "Three Geostatistical Methods for Hydrofacies Simulation Ranked Using a Large Borehole Lithology Dataset from the Venice Hinterland (NE Italy)" Water 10, no. 7: 844. https://doi.org/10.3390/w10070844
APA StyleMarini, M., Felletti, F., Beretta, G. P., & Terrenghi, J. (2018). Three Geostatistical Methods for Hydrofacies Simulation Ranked Using a Large Borehole Lithology Dataset from the Venice Hinterland (NE Italy). Water, 10(7), 844. https://doi.org/10.3390/w10070844





