Derivation of Soil Moisture Recovery Relation Using Soil Conservation Service (SCS) Curve Number Method
Abstract
1. Introduction
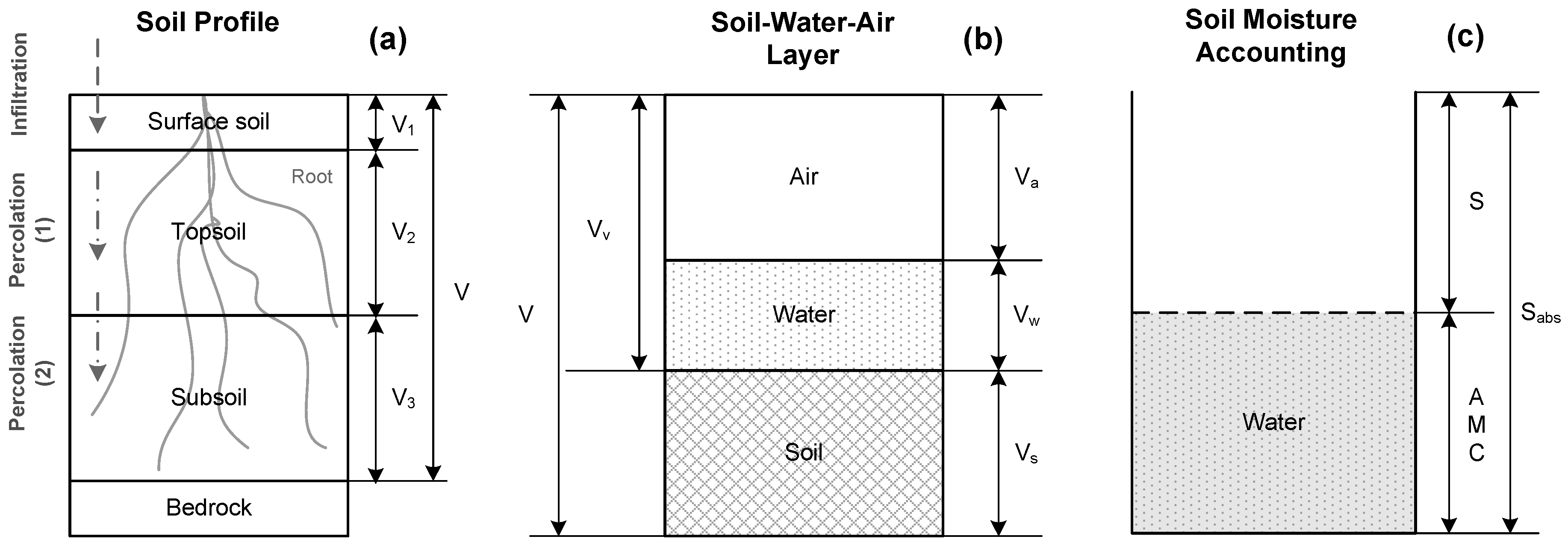
2. Curve Number Method and Soil Moisture Retention
3. Methodology to Derive R-Curve
4. Data
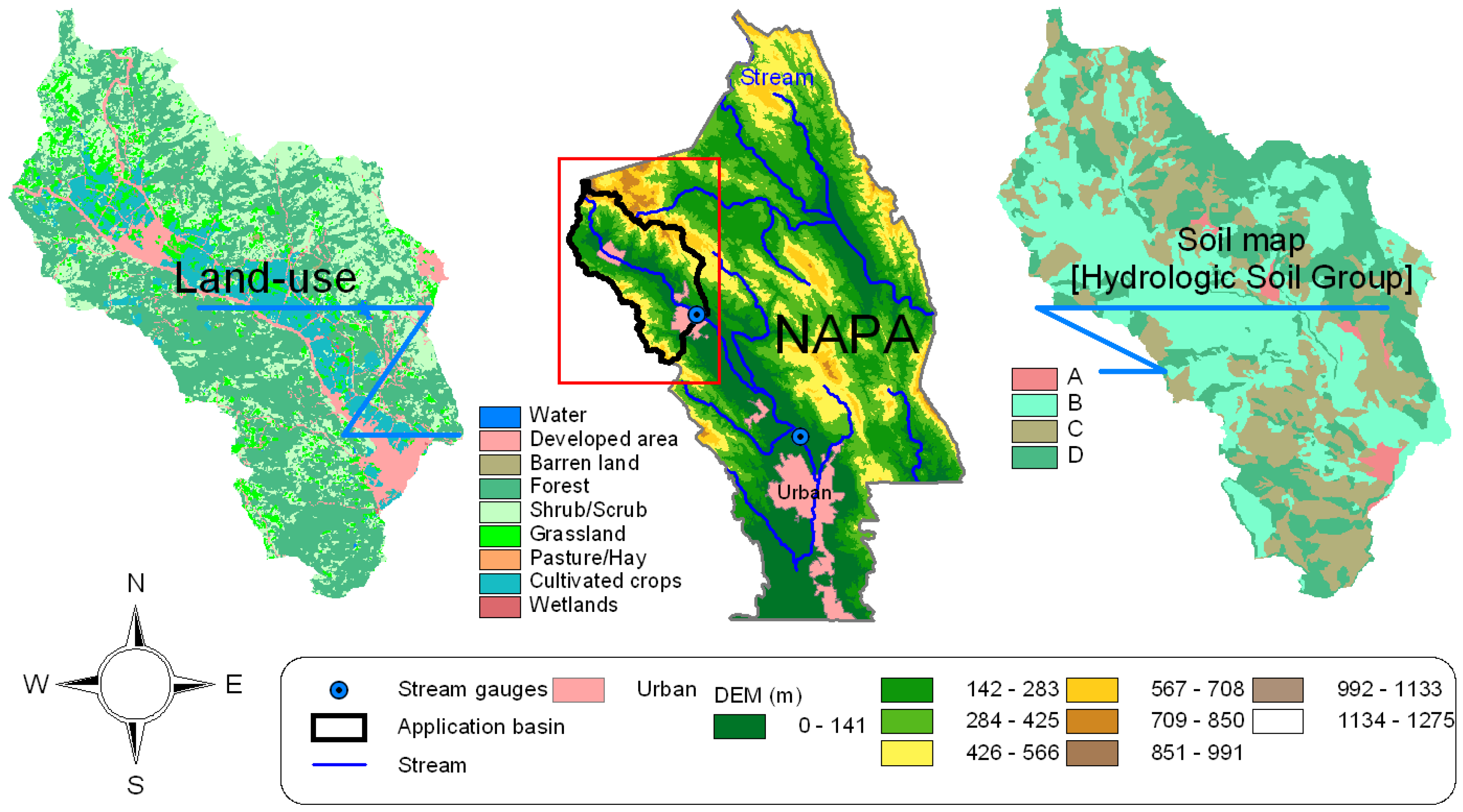
4.1. Watershed
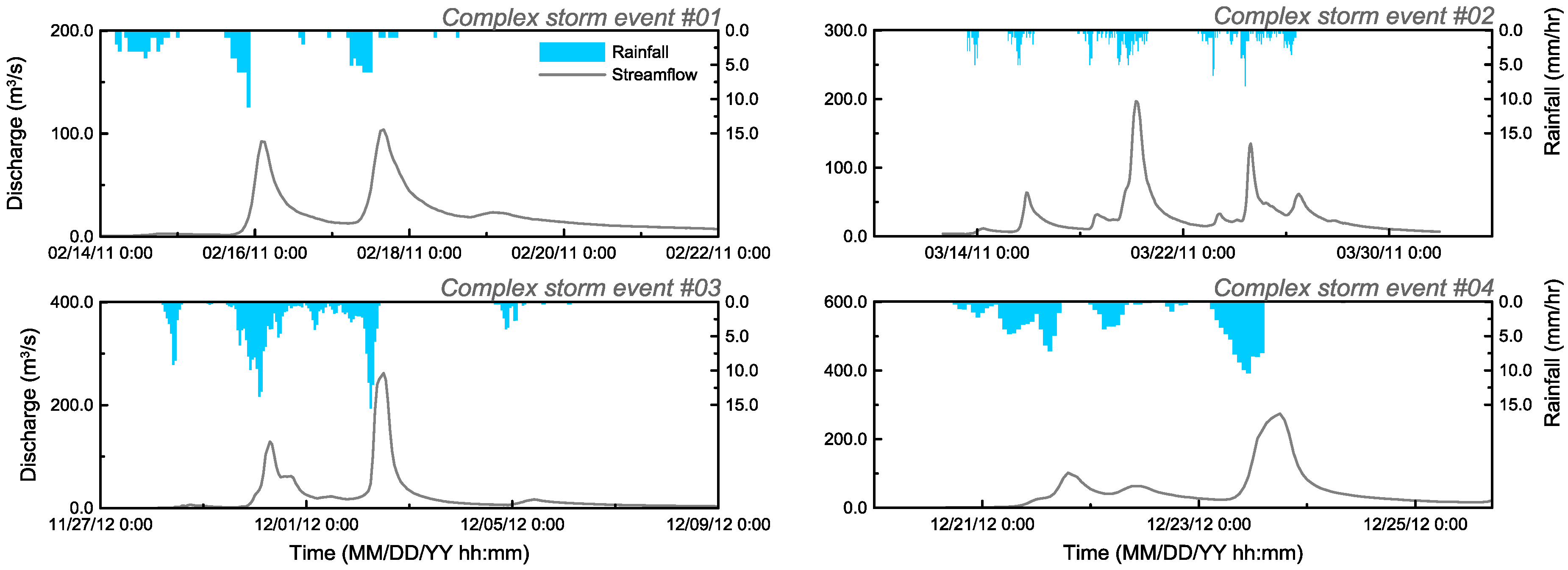
4.2. Complex Storm Event
4.3. Radar-Based Rainfall Data
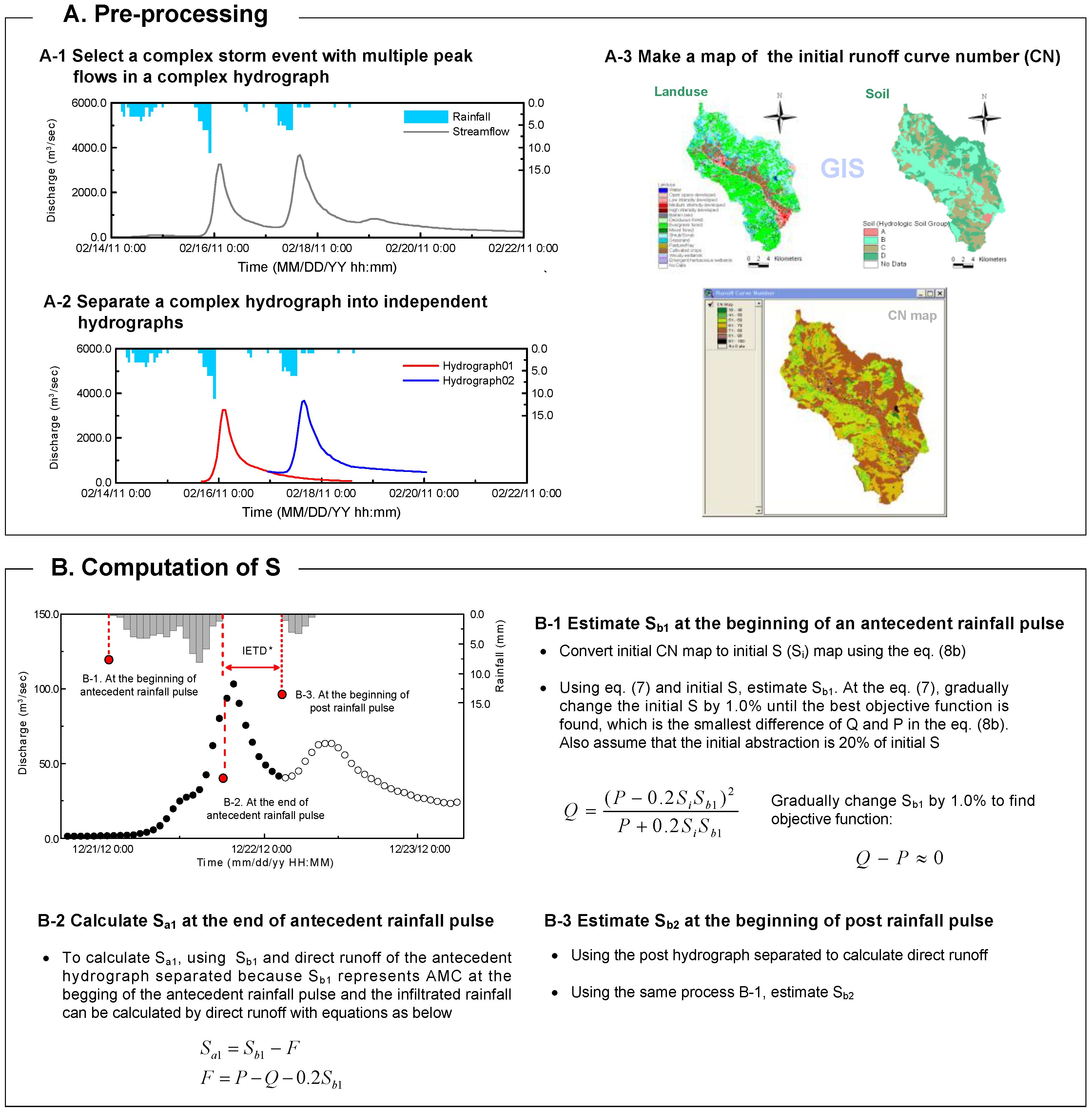
5. Pre-Processing
5.1. Complex Hydrograph Separation
5.2. Estimation of Soil Moisture Retention
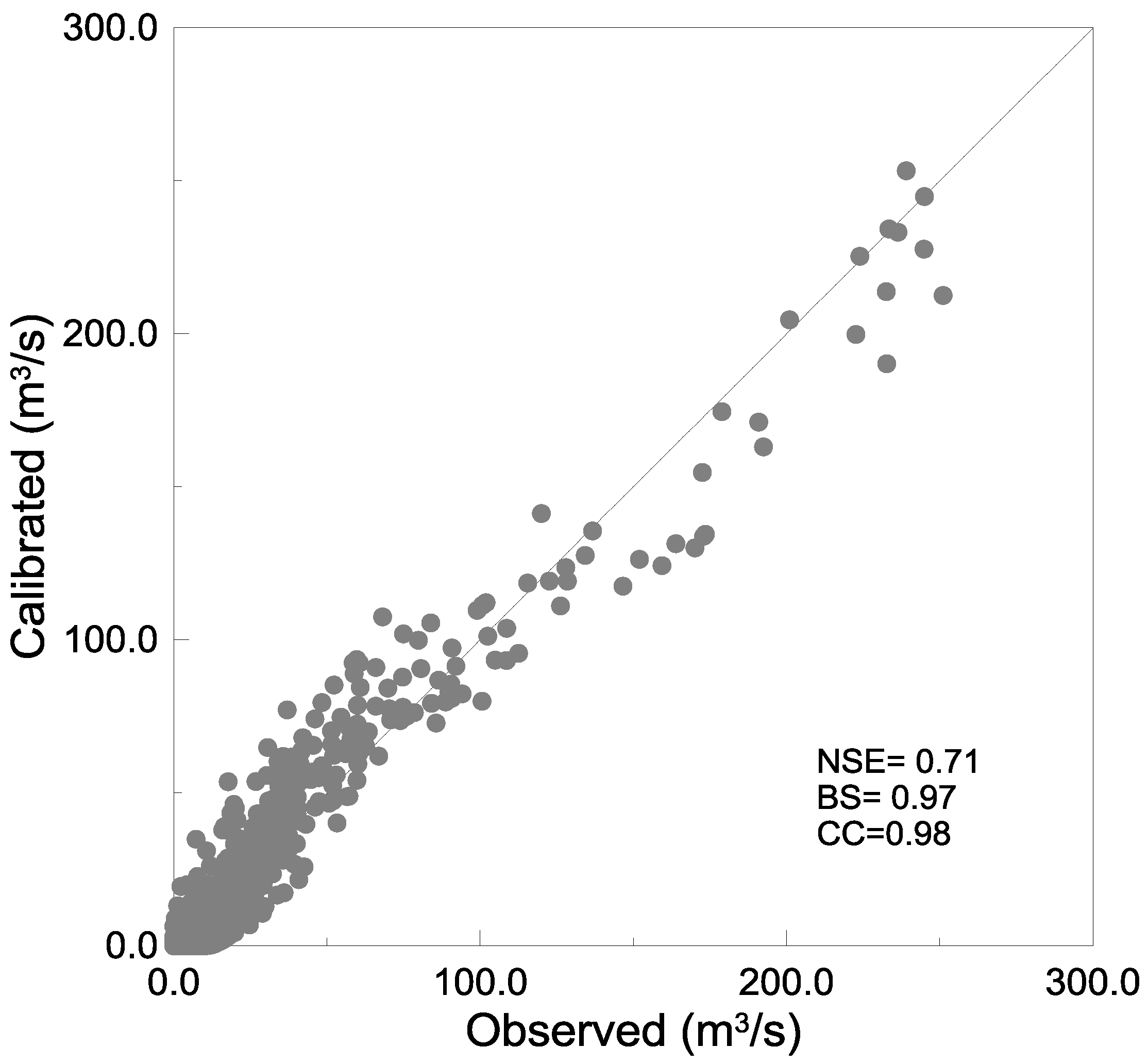
6. Results
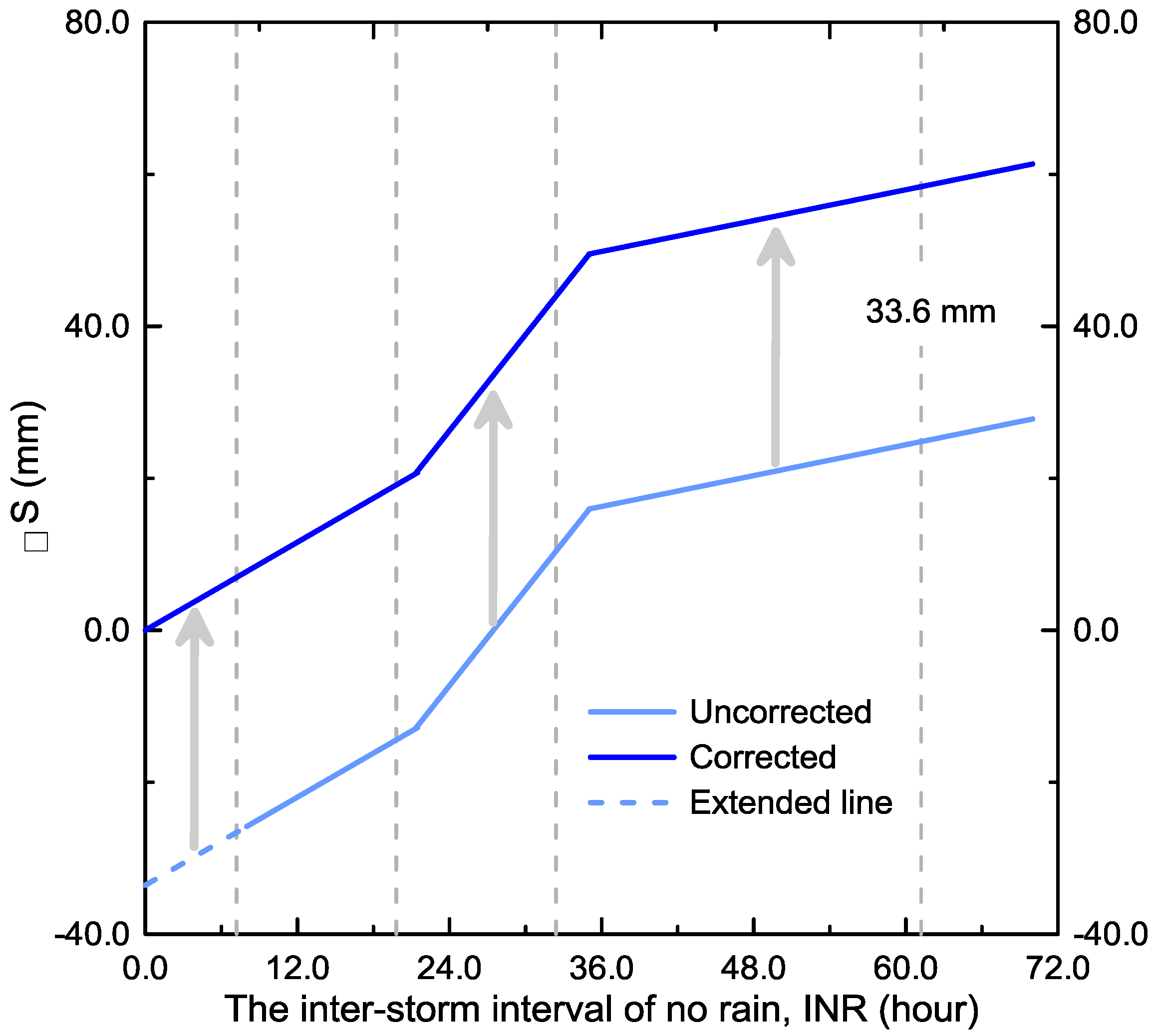
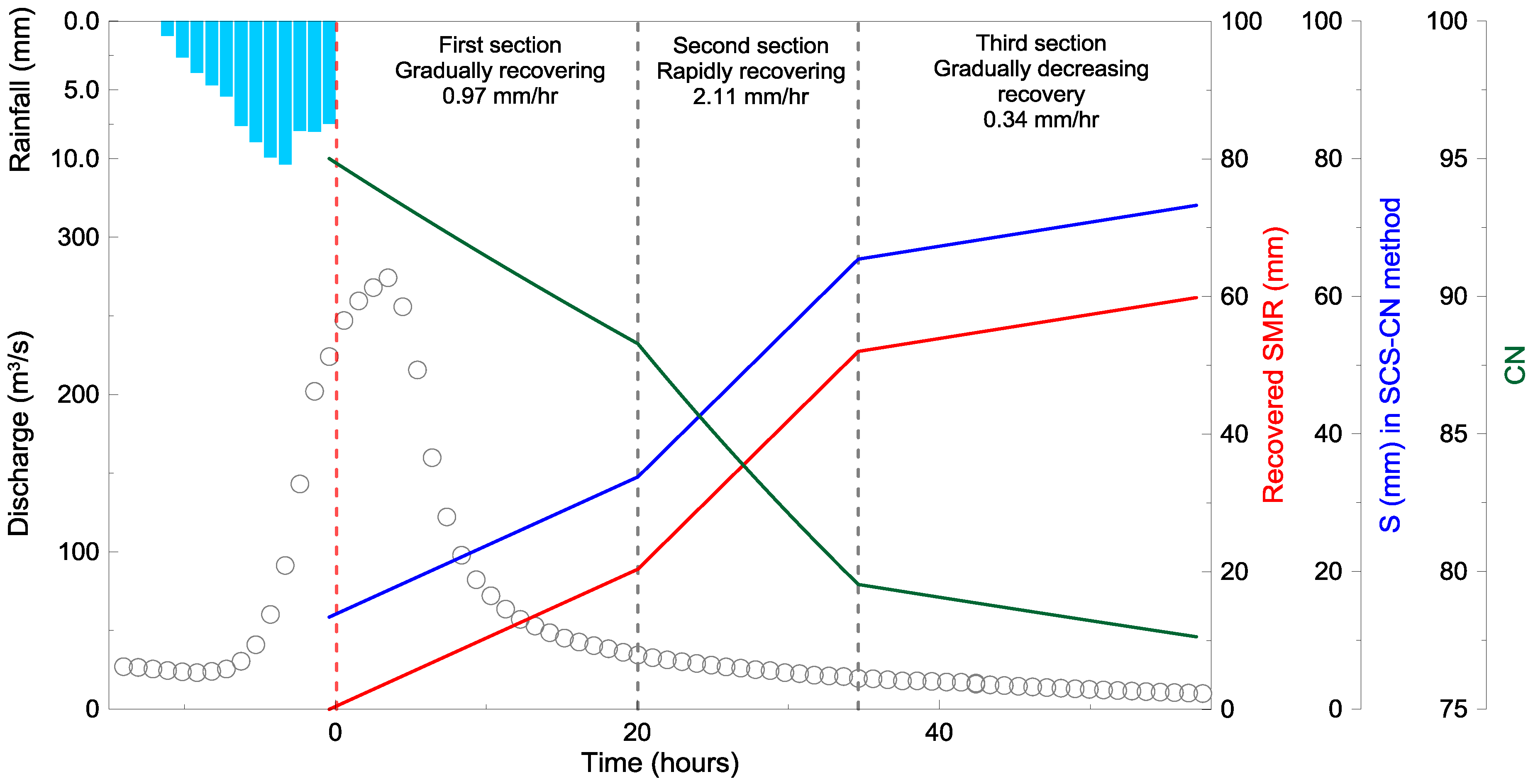
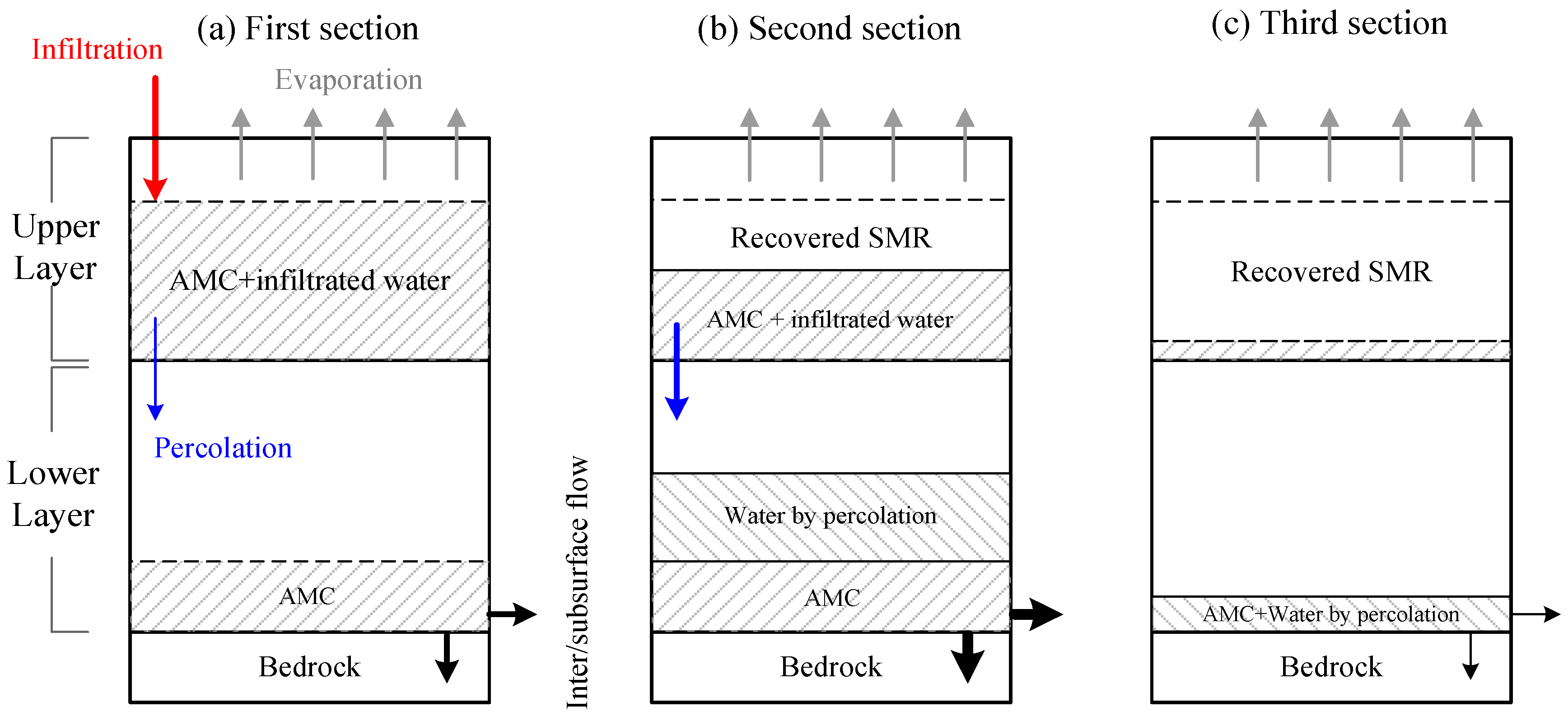
6.1. Derivation of the Recovery Curve
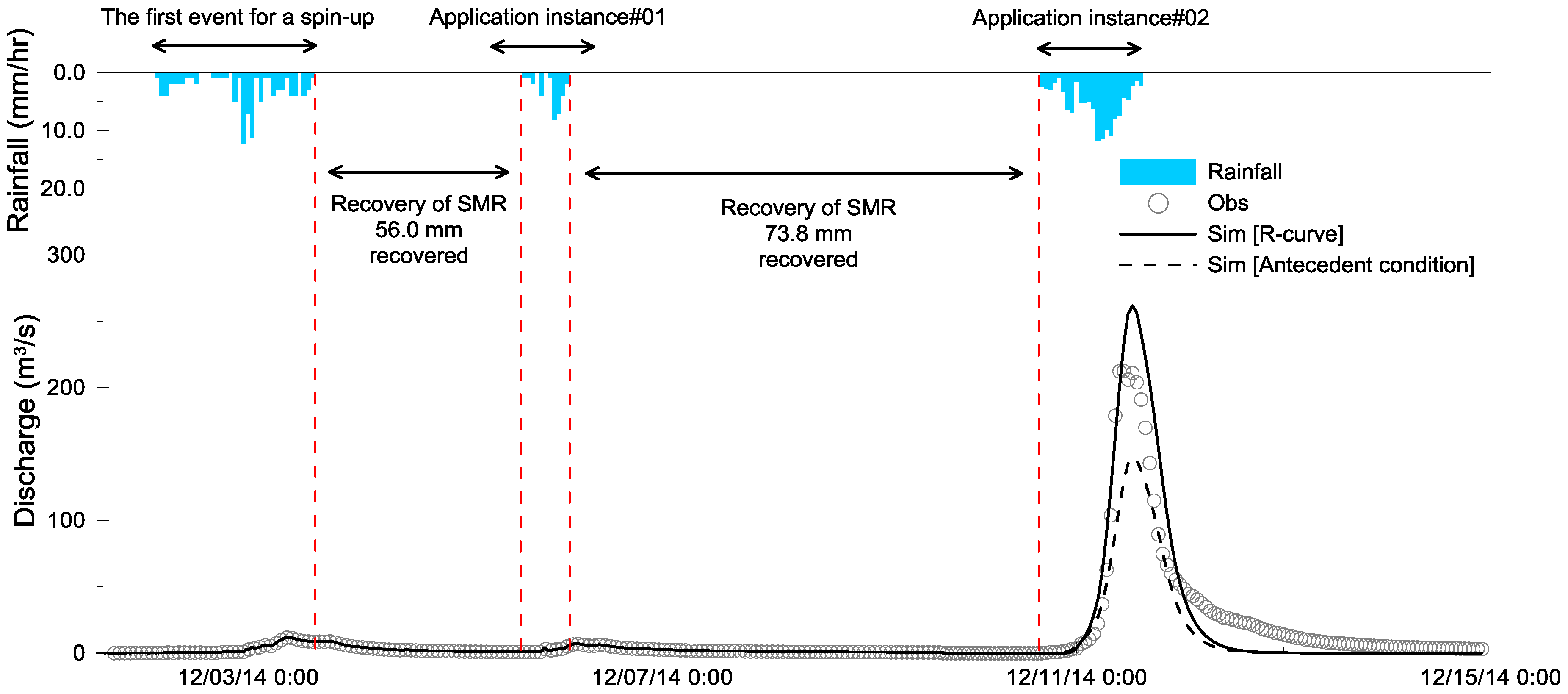
6.2. Application Instance
7. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agnese, C.; Bagarello, V.; Corrao, C.; D’Agostino, L.; D’Asaro, F. Influence of the rainfall measurement interval on the erosivity determinations in the Mediterranean area. J. Hydrol. 2006, 329, 39–48. [Google Scholar] [CrossRef]
- Anderson, E. Calibration of Conceptual Hydrologic Models for Use in River Forecasting; National Weather Service, Hydrology Laboratory: Silver Spring, MD, USA, August 2002.
- Hawkins, R.H. Effect of rainfall intensity on runoff curve numbers. In Hydrology and Water Resources in Arizona and the Southwest; Arizona-Nevada Academy of Science: Glendale, AZ, USA, 1978; Volume 8, pp. 53–64. [Google Scholar]
- Hawkins, R.H. Runoff curve numbers with varying site moisture. J. Irrig. Drain. Div. 1978, 104, 389–398. [Google Scholar]
- Michel, C.; Andreassian, V.; Perrin, C. Soil conservation service curve number method: How to mend a wrong soil moisture accounting procedure? Water Resour. Res. 2005, 41, 1–6. [Google Scholar] [CrossRef]
- Mishra, S.K.; Singh, V.P. Soil Conservation Service curve Number (CN) Methodology; Water Science and Technology Library: New York, NY, USA, 2003. [Google Scholar]
- Bauer, S.W. A modified Horton equation for infiltration during intermittent rainfall. Hydrol. Sci. Bull. 1974, 19, 219–225. [Google Scholar] [CrossRef]
- Pitt, R.; Lantrip, J.; Harrison, R.; Henry, C.H.; Xue, D. Infiltration through Disturbed Urban Soils and Compost-Amended Soil Effects on Runoff Quality and Quantity; Research Report; United States Environmental Protection Agency (EPA): Washington, DC, USA, 1999.
- Aron, G. Adaptation of Horton and SCS infiltration equation to complex storm. J. Irrig. Drain. Eng. 1992, 118, 275–284. [Google Scholar] [CrossRef]
- Gupta, V.K.; Sorooshian, S. Uniqueness and observability of conceptual rainfall-runoff model parameters: The percolation process examined. Water Resour. Res. 1983, 19, 269–276. [Google Scholar] [CrossRef]
- Armstrong, B.L. Derivation of initial soil moisture accounting parameters from soil properties for the National Weather Service River Forecast System. In NOAA Technical Memorandum NWS HYDRO 37; National Weather Service Office of Hydrology: Silver Spring, MD, USA, March 1978. [Google Scholar]
- Burnash, R.J.C.; Ferral, R.L.; McGuire, R.A. A Generalized Streamflow Simulation System: Conceptual Modeling for Digital Computers; U.S. Department of Commerce; National Weather Service; State of California, Department of Water Resources: Sacramento, CA, USA, March 1973.
- Mishara, S.K.; Singh, V.P. Long-term hydrological simulation based on the soil conservation service curve number. Hydrol. Process. 2004, 18, 1291–1313. [Google Scholar] [CrossRef]
- Williams, J.R.; LaSeur, V. Water yield model using SCS curve numbers. J. Hydraul. Eng. 1976, 102, 1241–1253. [Google Scholar]
- Soil Conservation Department (SCD). Handbook of Hydrology; Ministry of New Delhi: New Delhi, India, 1972.
- Soil Conservation Service (SCS). National Engineering Handbook; Section 4; US 444 Department of Agriculture, US Government Printing Office: Washington, DC, USA, 1985.
- Wischmeier, W.H. A rainfall erosion index for a universal soil-loss equation. Soil Sci. Soc. Am. J. 1959, 23, 246–249. [Google Scholar] [CrossRef]
- Baltas, E.A.; Dervos, V.A.; Mimikou, M.A. Technical note: Determination of the SCS initial abstraction ratio in an experimental watershed in Greece. Hydrol. Earth Syst. Sci. 2007, 11, 1825–1829. [Google Scholar] [CrossRef]
- Ponce, V.M.; Hawkins, R.H. Runoff curve number: Has it reached maturity? J. Hydrol. Eng. 1996, 1, 11–19. [Google Scholar] [CrossRef]
- Sahu, R.K.; Mishra, S.K.; Eldho, T.I.; Jain, M.K. An advanced soil moisture accounting procedure for SCS curve number method. Hydrol. Process. 2007, 21, 2872–2881. [Google Scholar] [CrossRef]
- Kim, N.W.; Lee, J. Temporally weighted average curve number method for daily runoff simulation. Hydrol. Process. 2008, 22, 4936–4948. [Google Scholar] [CrossRef]
- Yoo, C.; Kim, J.; Yoon, J. Uncertainty of areal average rainfall and its effect on runoff simulation: A case study for the Chungju Dam basin, Korea. KSCE J. Civ. Eng. 2012, 16, 1085–1092. [Google Scholar] [CrossRef]
- Verma, S.; Verma, R.K.; Mishra, S.K.; Singh, A.; Jayaraj, G.K. A revisit of NRCS-CN inspired models coupled with RS and GIS for runoff estimation. Hydrol. Sci. J. 2017, 62, 1891–1930. [Google Scholar] [CrossRef]
- Moglen, G.E.; McCuen, R.H.; Moglen, R.L. Consequences of changes to the NRCS rainfall-runoff relations on hydrologic design. J. Hydrol. Eng. 2018, 23. [Google Scholar] [CrossRef]
- Singh, V.P. Elementary Hydrology; Prentice Hall: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Wangemann, S.; Kohl, R.; Molumeli, P. Infiltration and percolation influenced by antecedent soil water content and air entrapment. Trans. Am. Soc. Agric. Eng. 2000, 43, 1517–1523. [Google Scholar] [CrossRef]
- Bouma, J. Evaluation of the field percolation test and an alternative procedure to test soil potential for disposal of septic tank effluent. Soil Sci. Soc. Am. Proc. 1971, 35, 871–875. [Google Scholar] [CrossRef]
- Sammis, T.W.; Evans, D.D.; Warrick, A.W. Comparison of methods to estimate deep percolation rates. JAWRA J. Am. Water Resour. Assoc. 1982, 18, 465–470. [Google Scholar] [CrossRef]
- Jansson, P.E.; Thoms-Hjärpe, C. Stimulated and measured soil water dynamics of unfertilized and fertilzedbarley. Acta Agric. Scand. 1986, 36, 162–172. [Google Scholar] [CrossRef]
- Johnsson, H.; Lundin, L.C. Surface runoff and soil water percolation as affected by snow and soil frost. J. Hydrol. 1991, 122, 141–159. [Google Scholar] [CrossRef]
- Sonu, J. Vertical infiltration into stratified soil for ground water accretion, Conjunctive Water Use. IAHS 1986, 156, 365–374. [Google Scholar]
- Sorooshian, S.; Duan, Q.; Gupta, V.K. Calibration of rainfall-runoff models: Application of global optimization to the Sacramento soil moisture accounting model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Dunkerley, D. Identifying individual rain events from pluviograph records: A review with analysis of data from an Australian dryland site. Hydrol. Process. 2008, 22, 5024–5036. [Google Scholar] [CrossRef]
- Restrepo-Posada, P.J.; Eagleson, P.S. Identification of independent events. J. Hydrol. 1982, 55, 303–319. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Madsen, H.; Clausen, B. On the definition and modeling of streamflow drought duration and deficit volume. Hydrol. Sci. J. 1997, 42, 15–33. [Google Scholar] [CrossRef]
- Loukas, A.; Quick, M.C. Spatial and temporal distribution of storm precipitation in southwestern British Columbia. J. Hydrol. 1996, 174, 37–56. [Google Scholar] [CrossRef]
- Manfroi, O.J.; Koichiro, K.; Nobuaki, T.; Masakazu, S.; Nakagawa, M.; Nakashizuka, T.; Chong, L. The stremflow of trees in a Bornean lowland tropical forest. Hydrol. Process. 2004, 18, 2455–2474. [Google Scholar] [CrossRef]
- Murakami, S. A proposal for a new forest canopy interception mechanism: Splash droplet evaporation. J. Hydrol. 2006, 319, 72–82. [Google Scholar] [CrossRef]
- Tobón Marin, C.; Bouten, W.; Sevink, J. Gross rainfall and its partitioning into throughfall, stemflow and evaporation of intercepted water in four forest ecosystems in western Amazonia. J. Hydrol. 2000, 237, 40–57. [Google Scholar] [CrossRef]
- Holtan, H.N.; Overton, D.E. Analyses and application of simple hydrographs. J. Hydrol. 1963, 1, 250–264. [Google Scholar] [CrossRef]
- Linsley, R.K.; Kohler, M.A.; Paulhus, J.L.H. Hydrology for Engineers; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Baltas, E.A.; Dervos, N.A.; Mimikou, M.A. Technical Note: Determination of the SCS initial abstraction ratio in an experimental watershed in Greece. In Hydrology and Earth System Sciences Discussions; European Geosciences Union: Vienna, Austria, 2007; Volume 11, pp. 1825–1829. [Google Scholar]
- Yuan, Y.; Nie, W.; McCutcheon, S.C.; Taguas, E.V. Initial abstraction and curve numbers for semiarid watersheds in Southeastern Arizona. Hydrol. Process. 2014, 28, 774–783. [Google Scholar] [CrossRef]
- Zhang, J.; Howard, K.; Langston, C.; Kaney, B.; Qi, Y.; Tang, L.; Grams, H.; Wang, Y.; Cocks, S.; Martinaitis, S.; et al. Multi-Radar Multi-Sensor (MRMS) quantitative precipitation estimation: Initial operating capabilities. Bull. Am. Meteorol. Soc. 2016, 97, 621–638. [Google Scholar] [CrossRef]
- Willie, D.; Chen, H.; Chandrasekar, V.; Cifelli, R.; Campbell, C.; David, R.; Sergey, M.; Zhang, Y. Evaluation of multisensory quantitative precipitation estimation in Russian River basin. J. Hydrol. Eng. 2016, 22, E5016002. [Google Scholar] [CrossRef]
- Kim, J.; Yoo, C. Use of a dual Kalman filter for real-time correction of mean field bias of radar rain rate. J. Hydrol. 2014, 519, 2785–2796. [Google Scholar] [CrossRef]
- Kim, J.; Yoo, C.; Lim, S.; Choi, J. Usefulness of relay-information-transfer for radar QPE. J. Hydrol. 2015, 531, 308–319. [Google Scholar] [CrossRef]
- Mei, Y.; Anagnostou, E.N. A hydrograph separation method based on information from rainfall and runoff records. J. Hydrol. 2015, 523, 636–649. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on soil physics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Thomas, C.L.; Stewart, A.E.; Constantz, J. Determination of Infiltration and Percolation Rates Along a Reach of the Santa Fe River Near La Bajada, New Mexico; Water-Resources Investigations Report 00-4141; U.S. Geological Survey: Reston, VA, USA, 2000.
- Veihmeyer, F.J.; Hendrickson, A.H. Does transpiration decrease as the soil moisture decreases? Trans. Am Geophys Union 1955, 36, 425–448. [Google Scholar] [CrossRef]
- Roberts, J. Forest transpiration: A conservative hydrological process? J. Hydrol. 1983, 66, 133–141. [Google Scholar] [CrossRef]
- Tromp-van Meerveld, H.J.; McDonnell, J.J. On the interrelations between topography, soil depth, soil moisture, transpiration rates and species distribution at the hillslope scale. Adv. Water Resour. 2006, 29, 293–310. [Google Scholar] [CrossRef]
- Clark, C.O. Storage and the unit hydrograph. Trans. Am. Soc. Civ. Eng. 1945, 110, 1419–1446. [Google Scholar]
- Peters, J.C.; Easton, D.J. Runoff Simulation Using Radar Rainfall Data; Technical Paper No. 155; U.S. Army Corps of Engineers: Davis, CA, USA, 1996; pp. 187–236.
- Kull, D.W.; Feldman, A.D. Evolution of Clark’s unit graph method to spatially distributed runoff. J. Hydrol. Eng. 1998, 3, 9–19. [Google Scholar] [CrossRef]
- Hydrologic Engineering Center (HEC). A Pilot Application of Weather Radar-Based Runoff Forecasting, Salt River Basin, MO; U.S. Army Corps of Engineers: Davis, CA, USA, 1996.
- Ahrens, S.R.; Maidment, D.R. Flood forecasting for the Buffalo Bayou using CRWR-PrePro and HEC-HMS, CRWR Report 99-6. In Center for Research in Water Resources; University of Texas at Austin: Austin, TX, USA, 1999; pp. 1–139. [Google Scholar]
- Daly, S.F.; Davis, T.P.; Ochs, E.; Rosenthal, W.; Affleck, R.; Baldwin, T.; Bryabt, E.; Hardy, J.; Taylor, S.; Dotson, H.; et al. Spatially distributed snow modeling for a comprehensive study of the Sacramento and San Joaquin basins, California. In Proceedings of the 57th Eastern Snow Conference, Syracuse, NY, USA, 17–19 May 2000. [Google Scholar]
- Emerson, C.H.; Welty, C.; Traver, R.G. Watershed-scale evaluation of a system of storm water detention basins. J. Hydrol. Eng. 2005, 10, 237–242. [Google Scholar] [CrossRef]
- Hu, H.H.; Kreymborg, L.R.; Doeing, B.J.; Baron, K.S.; Jutila, S.A. Gridded snowmelt and rainfall-runoff CWMS hydrologic modeling of the Red River of the North basin. J. Hydrol. Eng. 2006, 11, 91–100. [Google Scholar] [CrossRef]
- Clarke, B.; Barrere, C.; Luna, M.; Yates, D. Using multiple-sensor quantitative precipitation estimation for flood forecasting in the lower Colorado River basin. In Proceedings of the Climate Aspects of Hydrometeorology 21st Conference on Hydrology, San Antonio, TX, USA, 15–18 Jan 2007. [Google Scholar]
- Harris, A.; Rahman, S.; Hossain, F.; Yarborough, L.; Bagtzoglou, A.C.; Easson, G. Satellite-based flood modeling using TRMM-based rainfall products. Sensors 2007, 12, 3416–3427. [Google Scholar] [CrossRef] [PubMed]
- Gabriele, S.; Chiaravalloti, F. Merging MSG infrared images and raingauge data to estimate the rainfall field on small catchments for hydrological applications: A case study of Vibo Valentia, Italy. In Proceedings of the BALWOIS 2008, Ohrid, Republic of Macedonia, 27–31 May 2008. [Google Scholar]
- Hydrologic Engineering Center (HEC). HEC-HMS: Hydrologic Modeling System, Technical Reference Manual; U.S. Army Corps of Engineers: Davis, CA, USA, 2000.
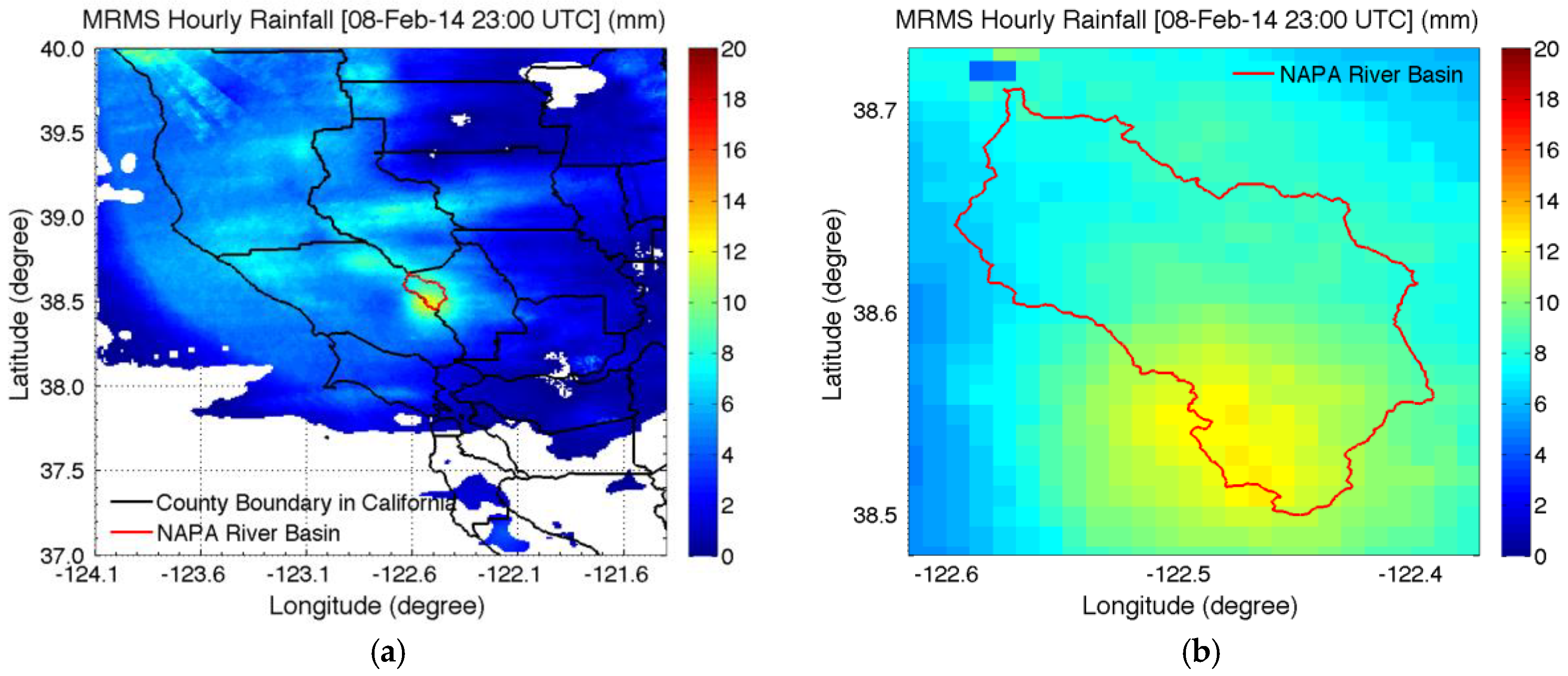
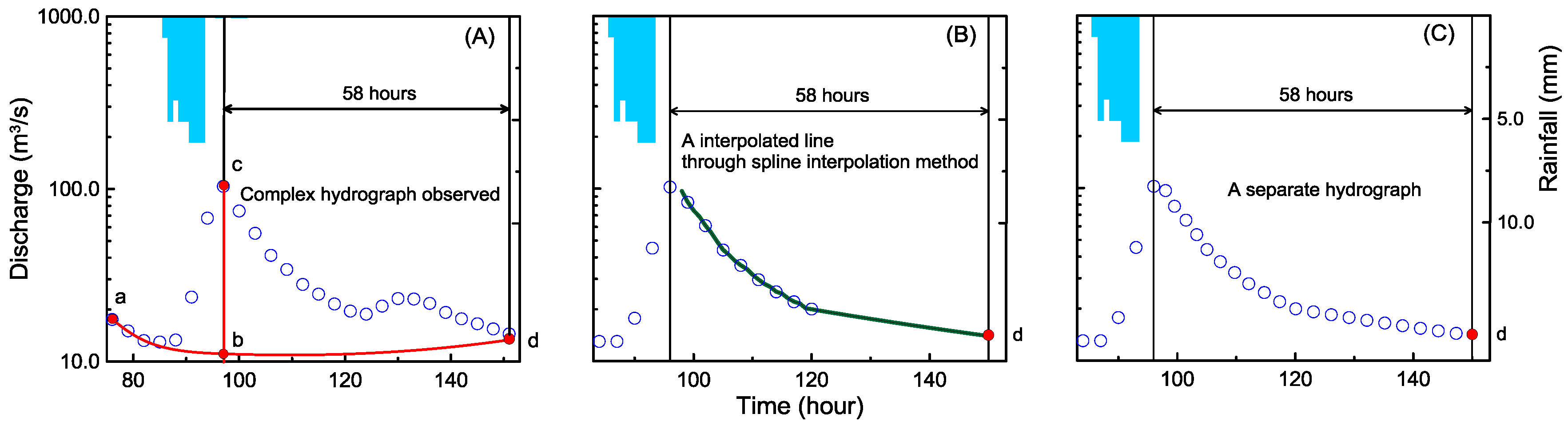
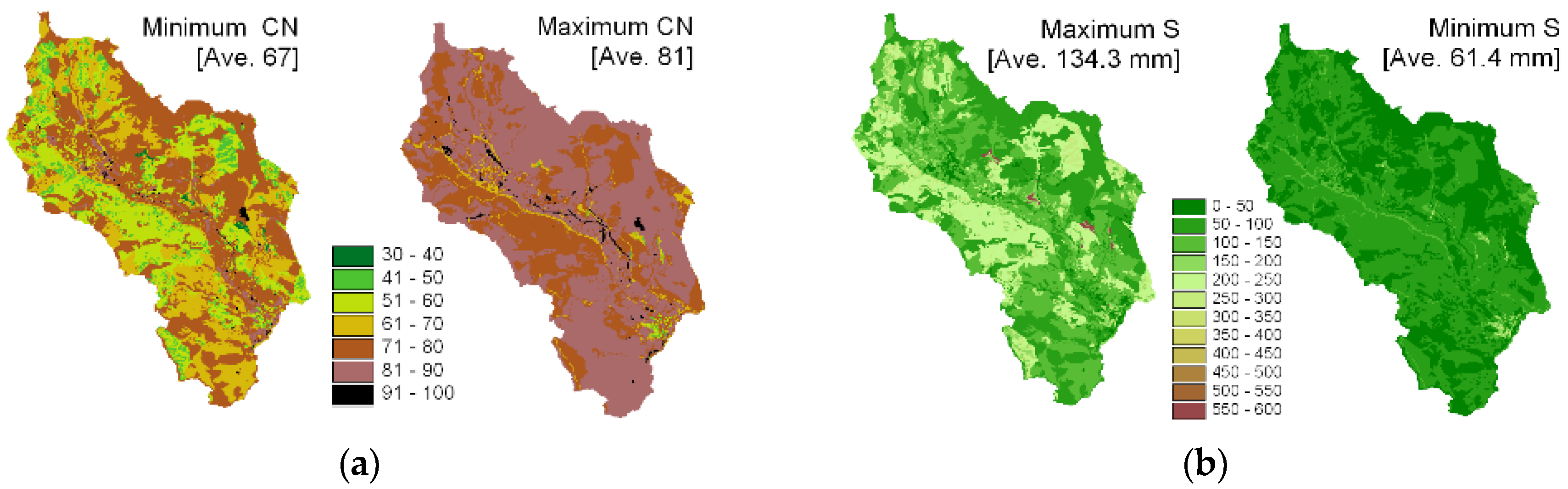

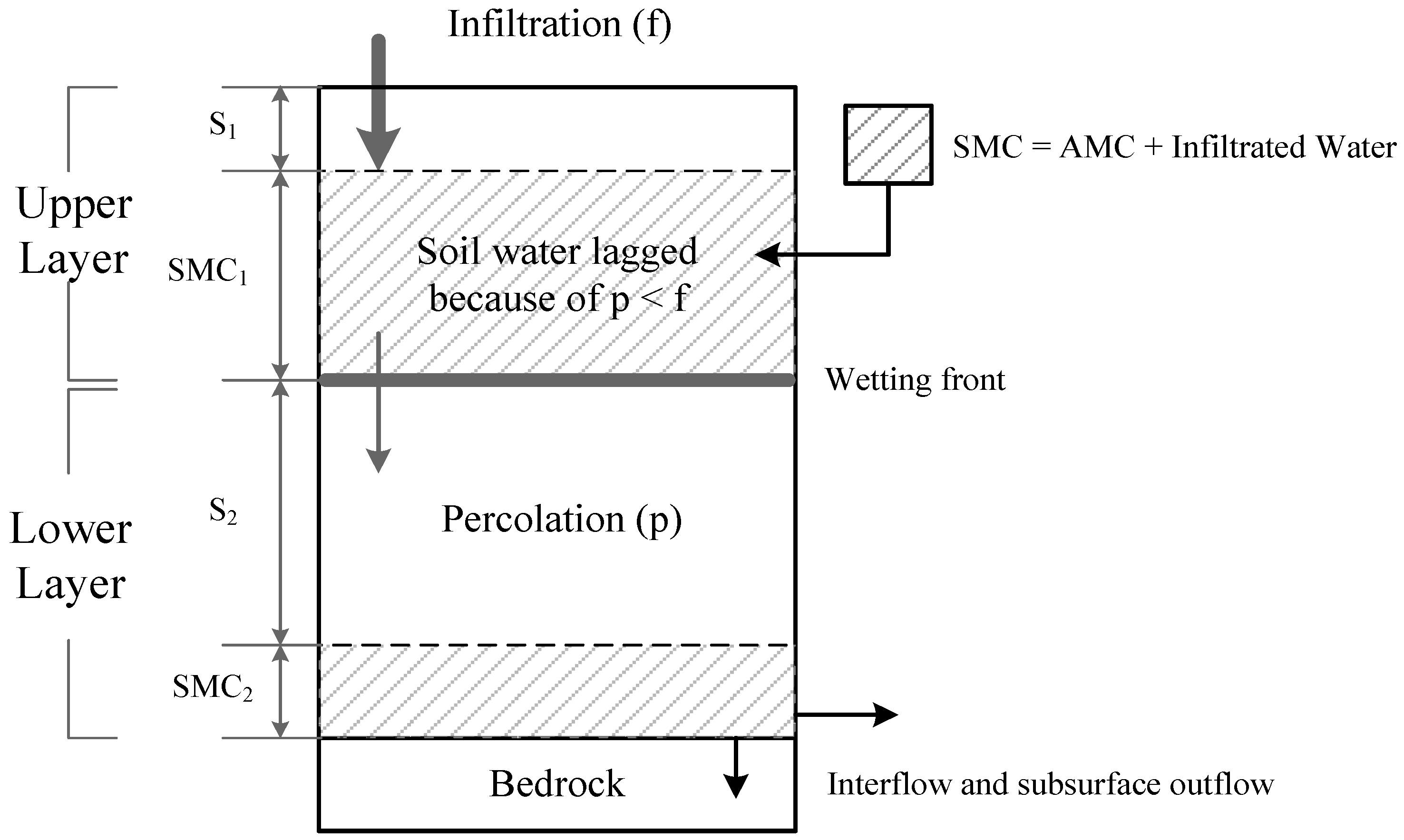
| Primary Landuse | Fraction(%) | NRCS Cover Type Description (Cover Type and Hydrologic Condition) | Max./Min. | CN Values in Hydrologic Soil Group (fraction) | |||
|---|---|---|---|---|---|---|---|
| A (1.5%) | B (40.4%) | C (28.6%) | D (29.5%) | ||||
| Forest | 39.6 | Wood-Good | Min. | 30 | 55 | 70 | 77 |
| Wood-grass combination-Poor | Max. | 57 | 73 | 82 | 86 | ||
| Grassland/herbaceous | 25.7 | Meadow-continuous grass, protected from grazing and generally mowed for hay-Good | Min. | 30 | 58 | 71 | 78 |
| Pasture, grassland, or range continuous forage for grazing-Poor | Max | 68 | 79 | 86 | 89 | ||
| Cultivated crops | 9.9 | Row crops: Contoured & terraced-Good | Min. | 62 | 71 | 78 | 81 |
| Row crops: Straight row-Poor | Max | 72 | 81 | 88 | 91 | ||
| Pasture/hay | 8.4 | Meadow-continuous grass, protected from grazing and generally mowed for hay-Good | Min. | 30 | 58 | 71 | 78 |
| Pasture, grassland, or range continuous forage for grazing-Poor | Max | 68 | 79 | 86 | 89 | ||
| Shrub/scrub | 7.1 | Brush-brush-forbs-grass mixture with brush the major element-Good | Min. | 30 | 48 | 65 | 73 |
| Desert shrub-major plants (salt brush, grease wood, creosote bush, black brush, etc.) | Max | 63 | 77 | 85 | 88 | ||
| Complex Storm Event No. | Independent Rainfall No. | Period (Pacific Standard Time, PST) | Total Rainfall (mm) | Interval with No Rain (h) | Runoff Coefficient |
|---|---|---|---|---|---|
| 1 | 1 | 14 February 2011 03:00–15 February 2011 00:00 | 19.2 | over 72 | 0.05 |
| 2 | 15 February 2011 05:00–16 February 2011 01:00 | 46.3 | 21 | 0.43 | |
| 3 | 17 February 2011 02:00–18 February 2011 15:00 | 34.4 | 29 | 0.60 | |
| 2 | 4 | 13 March 2011 10:00–14 March 2011 00:00 | 21.4 | over 72 | 0.17 |
| 5 | 15 March 2011 02:00–16 March 2011 15:00 | 36.3 | 28 | 0.51 | |
| 6 | 18 March 2011 01:00–19 March 2011 04:00 | 23.8 | 59 | 0.37 | |
| 7 | 19 March 2011 05:00–20 March 2011 19:00 | 61.0 | 14 | 0.82 | |
| 8 | 22 March 2011 22:00–23 March 2011 10:00 | 21.9 | 66 | 0.27 | |
| 9 | 24 March 2011 05:00–24 March 2011 14:00 | 26.1 | 23 | 0.99 | |
| 10 | 25 March 2011 18:00–26 March 2011 15:00 | 22.0 | 36 | 0.28 | |
| 3 | 11 | 29 November 2012 08:00–01 December 2012 10:00 | 164.8 | 17 | 0.23 |
| 12 | 01 December 2012 16:00–02 December 2012 12:00 | 80.8 | 10 | 0.50 | |
| 13 | 04 December 2012 15:00–06 December 2012 05:00 | 21.7 | 56 | 0.17 | |
| 4 | 14 | 20 December 2012 18:00–21 December 2012 19:00 | 61.7 | over 72 | 0.38 |
| 15 | 22 December 2012 00:00–22 December 2012 13:00 | 25.3 | 11 | 0.10 | |
| 16 | 23 December 2012 03:00–23 December 2012 14:00 | 77.8 | 21 | 0.61 |
| Independent Rainfall Event No. | CNb1 | INR (h) | Soil Moisture Retentions (mm) | (3)–(2) Recovery (mm) | ||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | ||||
| Sb1 | Sa1 | Sb2 | ||||
| 1 | 78.2 | - | 70.9 | 49.9 | 40.2 | - |
| 21 | −9.7 | |||||
| 2 | 86.3 | 40.2 | 14.0 | 22.0 | ||
| 29 | 8.0 | |||||
| 3 | 92.0 | 22.0 | 9.1 | - | ||
| Over 72 | - | |||||
| 4 | 84.7 | 45.7 | 28.7 | 27.3 | ||
| 28 | −1.3 | |||||
| 5 | 90.3 | 27.3 | 11.3 | 32.2 | ||
| 59 | 20.8 | |||||
| 6 | 88.7 | 32.2 | 17.1 | 3.9 | ||
| 14 | −13.2 | |||||
| 7 | 94.8 | 3.9 | 0.1 | 27.9 | ||
| 66 | 27.8 | |||||
| 8 | 90.1 | 27.8 | 17.2 | 8.6 | ||
| 23 | −8.5 | |||||
| 9 | 96.7 | 8.6 | 3.7 | 37.3 | ||
| 36 | 16.5 | |||||
| 10 | 87.2 | 37.3 | 22.1 | - | ||
| 17 | - | |||||
| 11 | 65.9 | 131.0 | 51.8 | 25.4 | ||
| 10 | −26.3 | |||||
| 12 | 90.9 | 25.4 | 6.6 | 31.3 | ||
| 56 | 24.6 | |||||
| 13 | 89.0 | 31.3 | 20.6 | - | ||
| Over 72 | - | |||||
| 14 | 79.6 | 64.8 | 25.4 | 45.0 | ||
| 11 | −25.3 | |||||
| 15 | 84.9 | 45.0 | 30.5 | 11.3 | ||
| 21 | −19.1 | |||||
| 16 | 95.7 | 11.3 | 2.5 | - | ||
| Event | Parameter | Error Indices | ||||||
|---|---|---|---|---|---|---|---|---|
| Tc (hr) | K (hr) | Peak Flow (%) | Total Runoff Flow(%) | Time to Peak (h) | CC | BS | NSE | |
| 1 | 8.3 | 9.2 | 105.6 | 39.1 | 0.0 | 0.95 | 1.39 | −0.56 |
| 2 | 6.5 | 8.4 | −10.8 | −0.9 | 0.0 | 0.98 | 0.99 | 0.95 |
| 3 | 8.2 | 4.9 | −8.7 | 1.7 | −1.0 | 0.98 | 1.02 | 0.96 |
| 4 | 9.5 | 8.0 | 86.1 | −2.3 | −1.0 | 0.92 | 0.98 | −0.14 |
| 5 | 7.9 | 8.5 | −14.4 | −7.4 | 0.0 | 0.96 | 0.93 | 0.89 |
| 6 | 7.6 | 9.3 | 8.9 | 9.8 | 7.0 | 0.96 | 1.10 | 0.79 |
| 7 | 9.9 | 6.1 | −22.5 | 8.4 | 0.0 | 0.95 | 1.08 | 0.90 |
| 8 | 7.4 | 9.7 | 19.4 | −3.3 | 0.0 | 0.96 | 0.97 | 0.72 |
| 9 | 7.8 | 5.7 | −15.0 | −23.1 | 0.0 | 0.95 | 0.77 | 0.86 |
| 10 | 9.3 | 6.0 | −5.8 | 9.8 | 0.0 | 0.99 | 1.10 | 0.98 |
| 11 | 7.7 | 2.5 | −3.4 | 2.7 | 0.0 | 0.95 | 1.05 | 0.81 |
| 12 | 9.5 | 2.3 | 3.4 | −5.6 | −1.0 | 0.99 | 0.94 | 0.97 |
| 13 | 9.0 | 9.7 | −9.5 | −23.1 | −4.0 | 0.96 | 0.77 | 0.86 |
| 14 | 8.9 | 5.7 | −18.1 | −15.1 | 1.0 | 0.97 | 0.85 | 0.92 |
| 15 | 8.1 | 3.0 | −5.8 | 4.3 | −1.0 | 0.95 | 1.04 | 0.90 |
| 16 | 9.7 | 4.5 | −7.1 | 2.0 | −2.0 | 0.98 | 1.02 | 0.96 |
| Min | 6.5 | 2.3 | −22.5 | −23.1 | −4.0 | 0.92 | 0.77 | −0.56 |
| Max | 9.9 | 9.7 | 105.6 | 39.1 | 7.0 | 0.99 | 1.39 | 0.98 |
| Mean | 8.4 | 6.5 | 6.4 | −0.2 | −0.1 | 0.96 | 1.00 | 0.74 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Johnson, L.E.; Cifelli, R.; Choi, J.; Chandrasekar, V. Derivation of Soil Moisture Recovery Relation Using Soil Conservation Service (SCS) Curve Number Method. Water 2018, 10, 833. https://doi.org/10.3390/w10070833
Kim J, Johnson LE, Cifelli R, Choi J, Chandrasekar V. Derivation of Soil Moisture Recovery Relation Using Soil Conservation Service (SCS) Curve Number Method. Water. 2018; 10(7):833. https://doi.org/10.3390/w10070833
Chicago/Turabian StyleKim, Jungho, Lynn E. Johnson, Rob Cifelli, Jeongho Choi, and V. Chandrasekar. 2018. "Derivation of Soil Moisture Recovery Relation Using Soil Conservation Service (SCS) Curve Number Method" Water 10, no. 7: 833. https://doi.org/10.3390/w10070833
APA StyleKim, J., Johnson, L. E., Cifelli, R., Choi, J., & Chandrasekar, V. (2018). Derivation of Soil Moisture Recovery Relation Using Soil Conservation Service (SCS) Curve Number Method. Water, 10(7), 833. https://doi.org/10.3390/w10070833






