Nonstationary Flood Frequency Analysis Using Univariate and Bivariate Time-Varying Models Based on GAMLSS
Abstract
1. Introduction
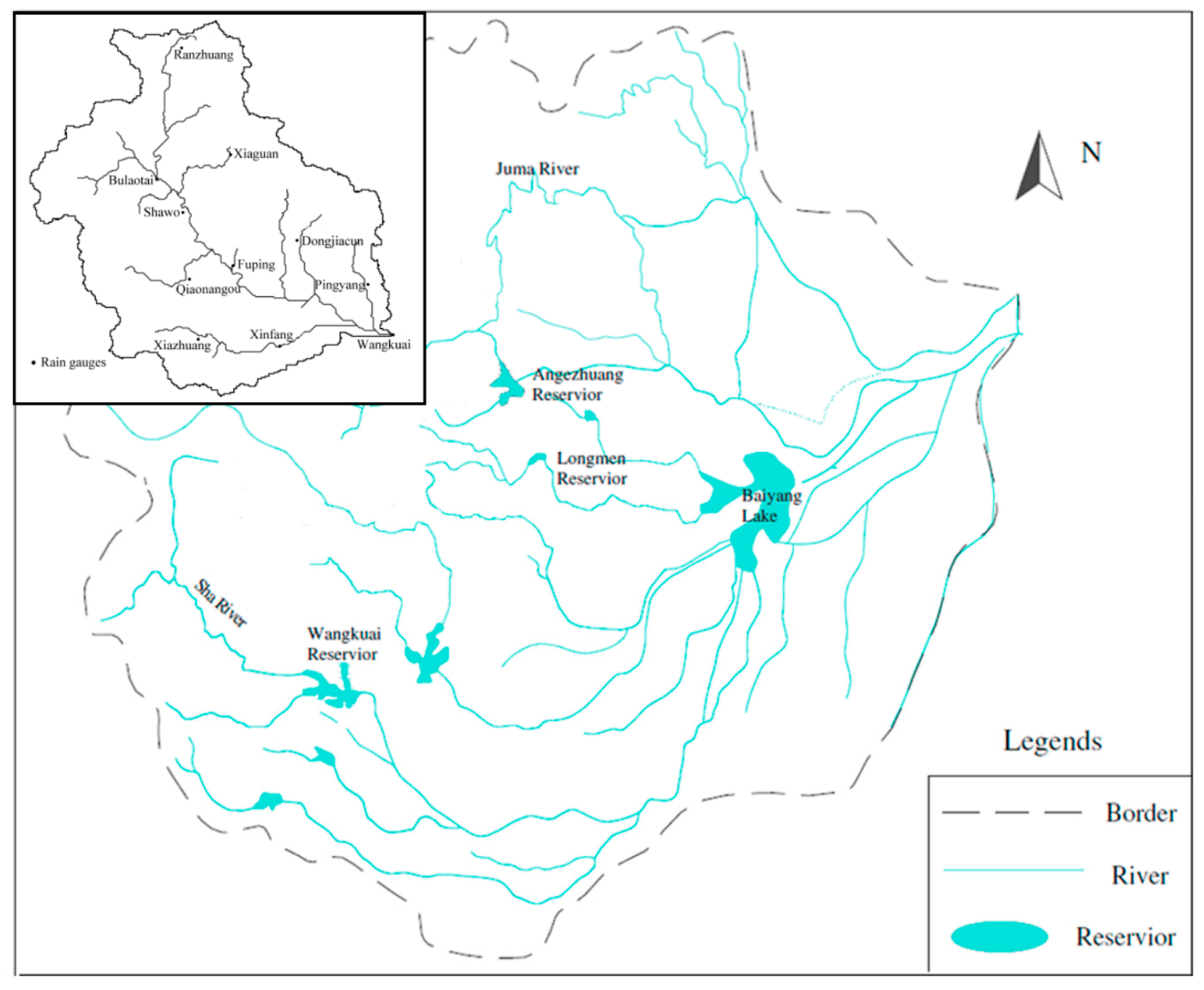
2. Study Region and Data
3. Methods
3.1. Generalized Additive Models in Location, Scale, and Shape (GAMLSS)
3.2. Univariate Time Varying Model Based on GAMLSS Theory
3.3. Bivariate-Joint Time Varying Model Based on Copulas
4. Results
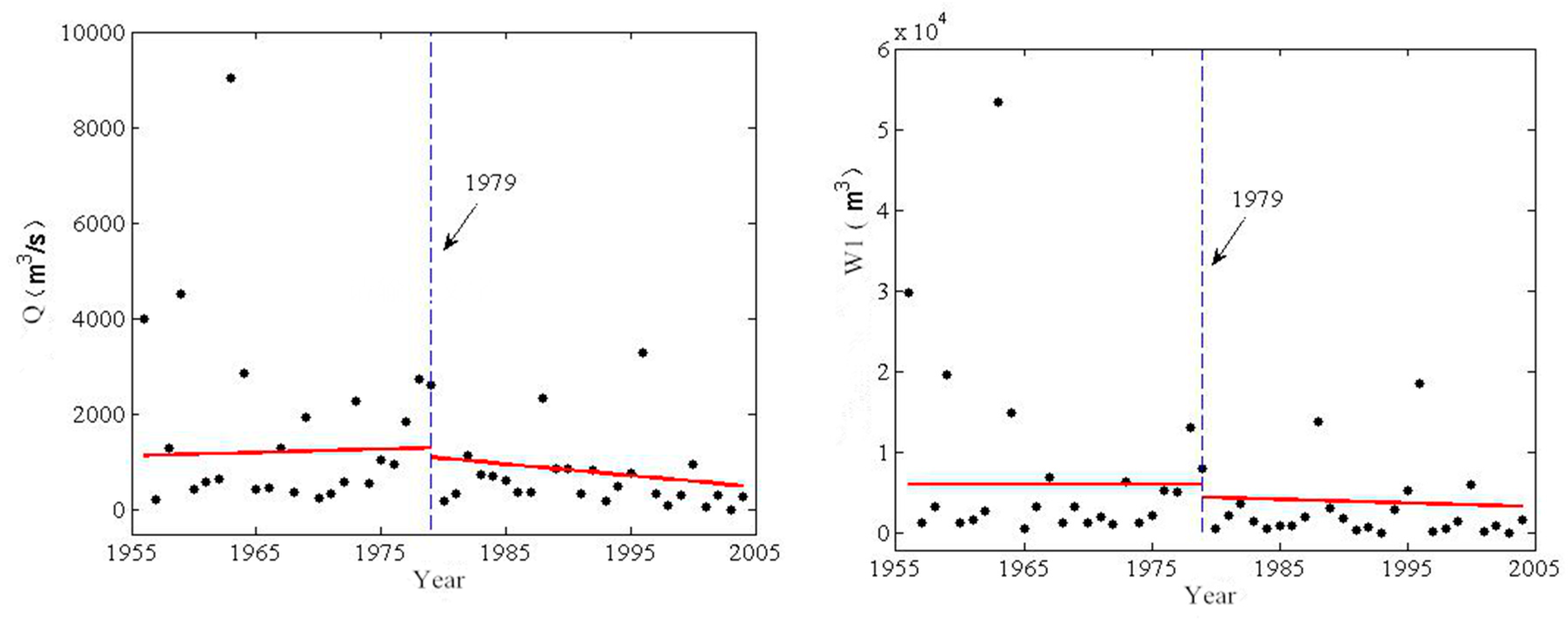
4.1. Identification of Nonstationarity for Flood Sequences
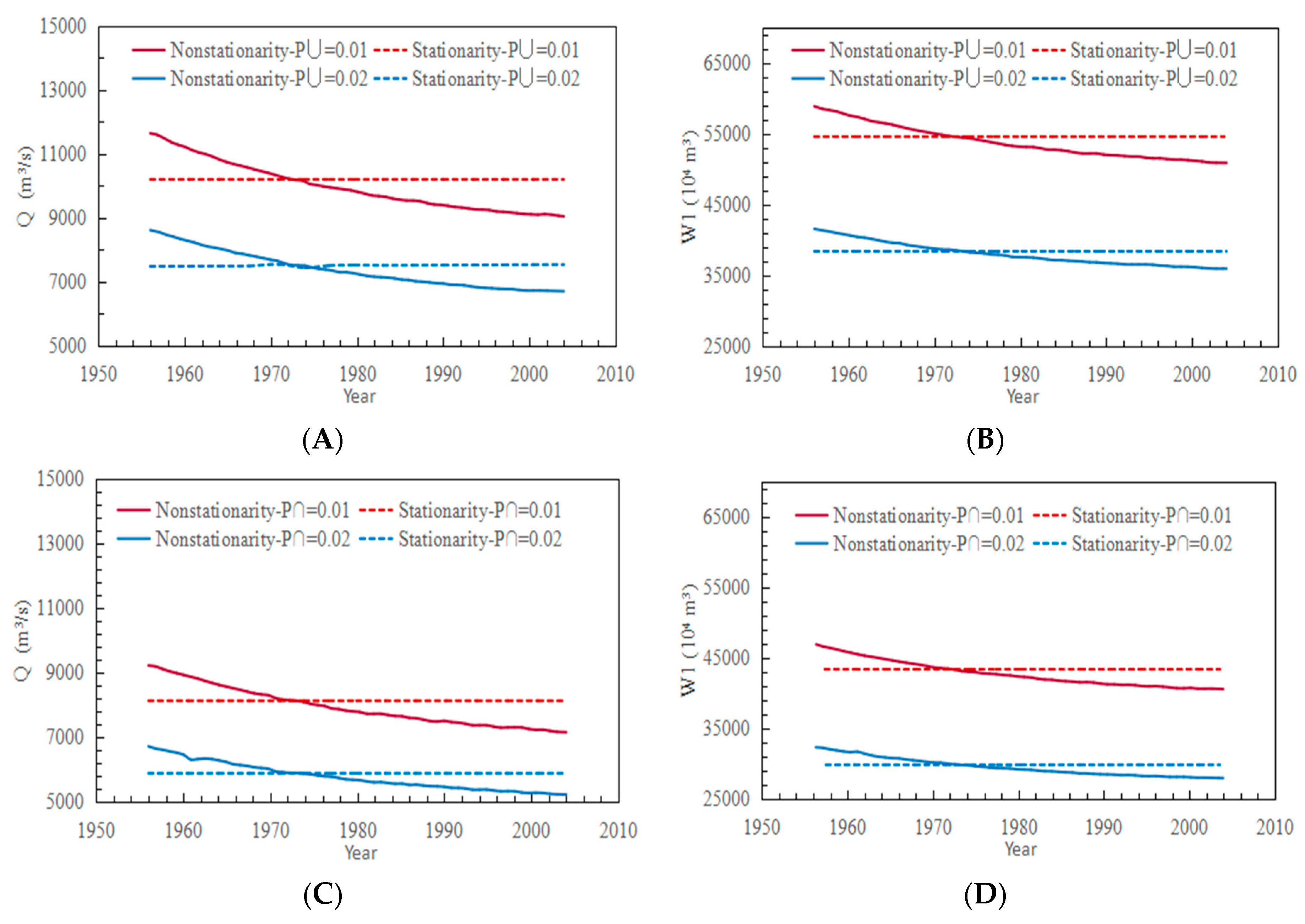
4.2. Nonstationary Model of Univariate Flood Frequency Analysis with Time as Covariate
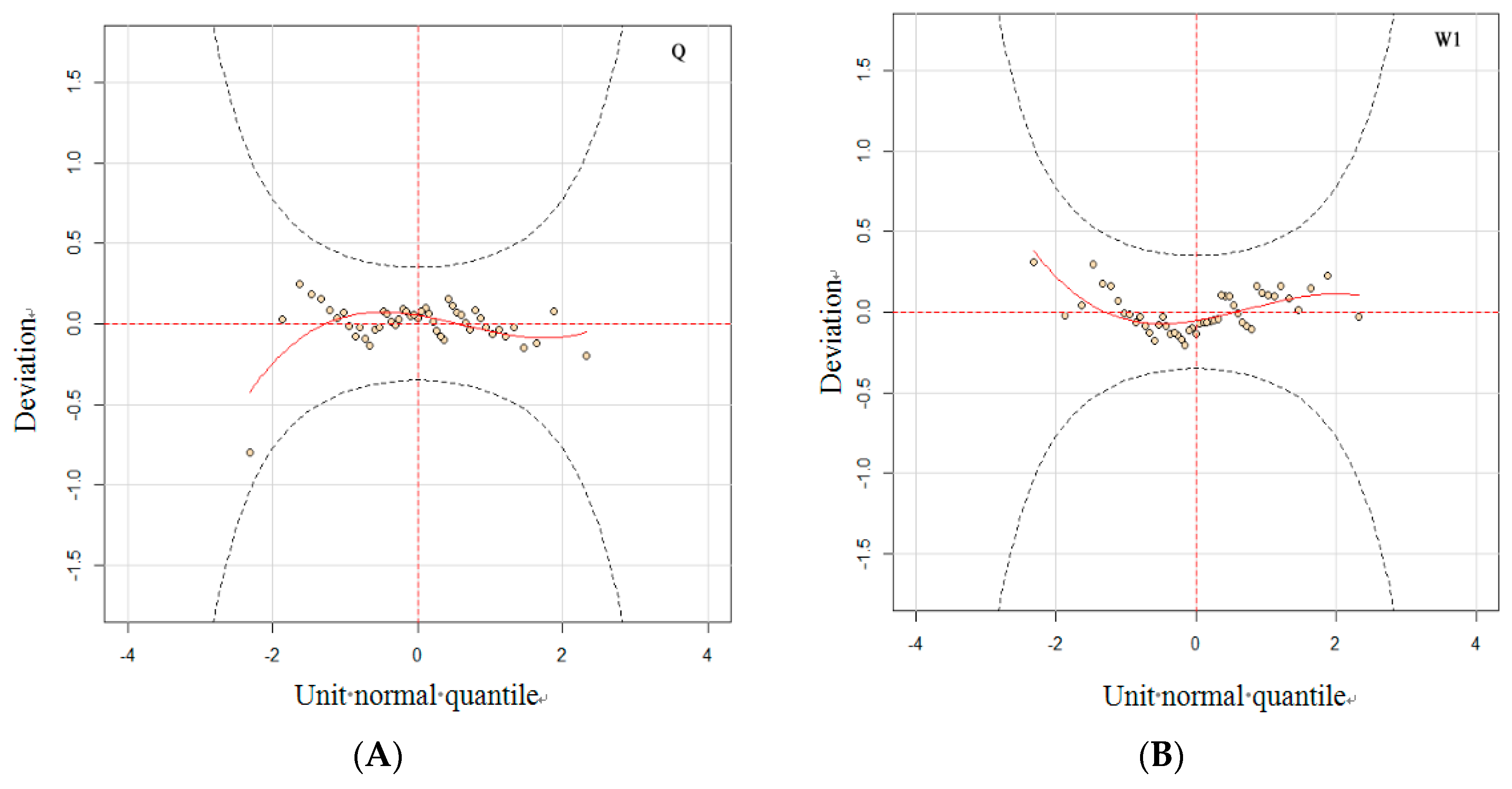
4.2.1. Model Fitting Evaluation
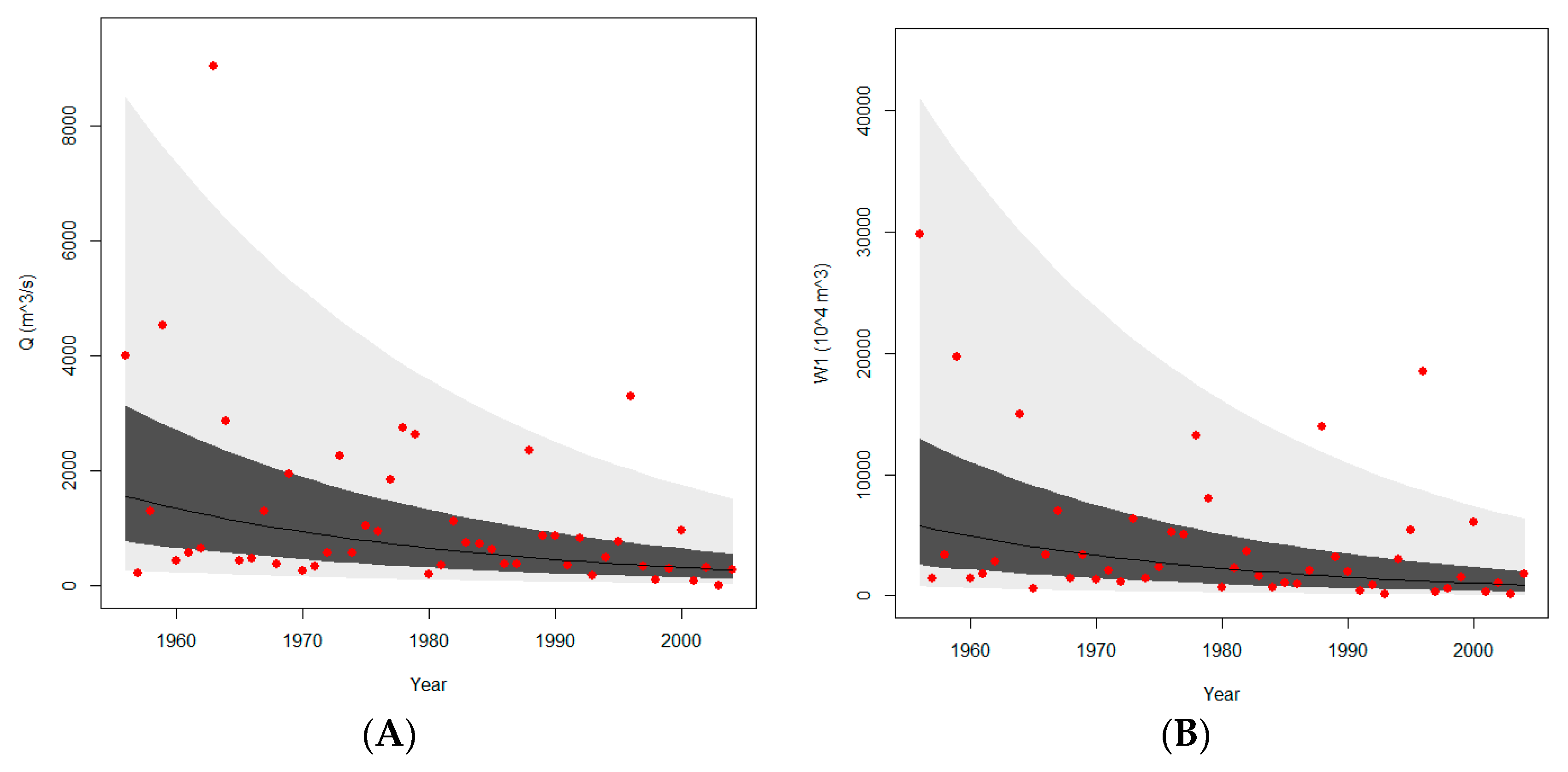
4.2.2. Model Results Analysis
4.3. Nonstationary Model of Bivariate-Joint Flood Frequency Analysis with Time as Covariate
4.3.1. Parameters Calculation, Fitting Test, and Result Optimization of Joint Probability Distribution
4.3.2. Most Likely Combination of the Flood Peak and Volume
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zheng, F.; Westra, S.; Leonard, M.; Sisson, S.A. Modeling dependence between extreme rainfall and storm surge to estimate coastal flooding risk. Water Resour. Res. 2014, 50, 205–2071. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M. Stationarity is dead: Whither water management. Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Ishak, E.H.; Rahman, A.; Westra, S.; Sharma, A.; Kuczera, G. Evaluating the non-stationarity of Australian annual maximum flood. J. Hydrol. 2013, 494, 134–145. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Waylen, P.; Woo, M.K. Prediction of annual floods generated by mixed processes. Water Resour. Res. 1982, 18, 1283–1286. [Google Scholar] [CrossRef]
- Singh, V.P.; Wang, S.X.; Zhang, L. Frequency analysis of nonidentically distributed hydrologic flood data. J. Hydrol. 2005, 307, 175–195. [Google Scholar] [CrossRef]
- Cunderlik, J.M.; Burn, D.H. Non-stationary pooled flood frequency analysis. J. Hydrol. 2003, 276, 210–223. [Google Scholar] [CrossRef]
- Vasiliades, L.; Galiatsatou, P.; Loukas, A. Nonstationary frequency analysis of annual maximum rainfall using climate covariates. Water Resour. Manag. 2015, 29, 339–358. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Stasinopoulos, D.M.; Rigby, R.A. Generalized additive models for location scale and shape (GAMLSS) in R. J. Stat. Softw. 2007, 23, 1–46. [Google Scholar] [CrossRef]
- Boutselis, P.; Ringrose, T.J. GAMLSS and networks in combat simulation metamodelling: A case study. Expert Syst. Appl. 2013, 40, 6087–6093. [Google Scholar] [CrossRef]
- Luo, J.W.; Chen, L.N.; Liu, H. Distribution characteristics of stock market liquidity. Phys. A Stat. Mech. Appl. 2013, 382, 6004–6014. [Google Scholar] [CrossRef]
- Wahl, S.; Fenske, N.; Zeilinger, S.; Suhre, K.; Gieger, C.; Waldenberger, M.; Grallert, H.; Schmid, M. On the potential of models for location and scale for genome-wide DNA methylation data. BMC Bioinform. 2014, 15, 1471–2105. [Google Scholar] [CrossRef] [PubMed]
- Serinaldi, F.; Kilsby, C.G. A modular class of multisite monthly rainfall generators for water resource management and impact studies. J. Hydrol. 2012, 464–465, 528–540. [Google Scholar] [CrossRef]
- López, J.; Francés, F. Non-stationary flood frequency analysis in continental Spanish rivers, using climate and reservoir indices as external covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef]
- Hawkes, P.J. Joint probability analysis for estimation of extremes. J. Hydraul. Res. 2008, 46, 246–256. [Google Scholar] [CrossRef]
- Fiorentino, M.; Gioia, A.; Iacobellis, V.; Manfreda, S. Regional analysis of runoff thresholds behaviour in Southern Italy based on theoretically derived distributions. Adv. Geosci. 2011, 26, 139–144. [Google Scholar] [CrossRef]
- Zheng, F.; Westra, S.; Sisson, S.A. Quantifying the dependence between extreme rainfall and storm surge in the coastal zone. J. Hydrol. 2013, 505, 172–187. [Google Scholar] [CrossRef]
- Mirabbasi, R.; Fakheri-Fard, A.; Dinpashoh, Y. Bivariate drought frequency analysis using the copula method. Theor. Appl. Climatol. 2012, 108, 191–206. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate rainfall frequency distributions using Archimedean copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Fu, G.; Butler, D. Copula-based frequency analysis of overflow and flooding in urban drainage systems. J. Hydrol. 2014, 510, 49–58. [Google Scholar] [CrossRef]
- Li, J.; Liu, X.; Chen, F. Evaluation of Nonstationarity in Annual Maximum Flood Series and the Associations with Large-scale Climate Patterns and Human Activities. Water Resour. Manag. 2015, 29, 1653–1668. [Google Scholar] [CrossRef]
- Li, J.; Tan, S. Nonstationary Flood Frequency Analysis for Annual Flood Peak Series, Adopting Climate Indices and Check Dam Index as Covariates. Water Resour. Manag. 2015, 29, 5533–5550. [Google Scholar] [CrossRef]
- Zeng, H.; Feng, P.; Li, X. Reservoir flood routing considering the non-stationarity of flood series in north China. Water Resour. Manag. 2014, 28, 4273–4287. [Google Scholar] [CrossRef]
- Cole, T.J.; Green, P.J. Smoothing reference centile curves: The lms method and penalized likelihood. Stat. Med. 2010, 11, 1305–1319. [Google Scholar] [CrossRef]
- Filliben, J.J. The Probability Plot Correlation Coefficient Test for Normality. Technometrics 1975, 17, 111–117. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Répartition À N Dimensions Et Leurs Marges; Institut de Statistique Université de Paris: Paris, France, 1959; pp. 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Olsen, J.R.; Stedinger, J.R.; Matalas, N.C.; Stakhiv, E.Z. Climate variability and flood frequency estimation for the Upper Mississippi and Lower Missouri Rivers. J. Am. Water Resour. Assoc. 1999, 35, 1509–1524. [Google Scholar] [CrossRef]
- Gräler, B.; van den Berg, M.J.; Vandenberghe, S.; Petroselli, A.; Grimaldi, S.; De Baets, B.; Verhoest, N.E.C. Multivariate return periods in hydrology: A critical and practical review focusing on synthetic design hydrograph estimation. Hydrol. Earth Syst. Sci. 2013, 17, 1281–1296. [Google Scholar] [CrossRef]
- Li, X.; Zeng, H.; Feng, P. Flood frequency analysis considering variation in flood time series. J. Hydroelectr. Eng. 2014, 33, 11–19. [Google Scholar]
- Wang, Y.; Li, J.; Feng, P.; Chen, F. Effects of large-scale climate patterns and human activities on hydrological drought: a case study in the luanhe river basin, China. Nat. Hazards 2015, 76, 1687–1710. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Zhou, S.; Chen, F. Quantifying the Effects of Land Surface Change on Annual Runoff Considering Precipitation Variability by SWAT. Water Resour. Manag. 2016, 30, 1071–1084. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Chen, X.; Jiang, T. Nonstationary flood frequency analysis considering the combined effects of climate change and human activities in the East River Basin. Trop. Geogr. 2014, 34, 746–757. [Google Scholar]
| Distributions | Q | W1 | ||||
|---|---|---|---|---|---|---|
| AIC | θ1 | θ2 | AIC | θ1 | θ2 | |
| Gumbel | 895.80 | t | - | 1074.23 | t | - |
| Weibull | 786.60 | t | - | 928.57 | t | - |
| Gamma | 785.99 | t | - | 930.55 | t | - |
| Log-Normal | 783.92 | t | - | 919.26 | t | - |
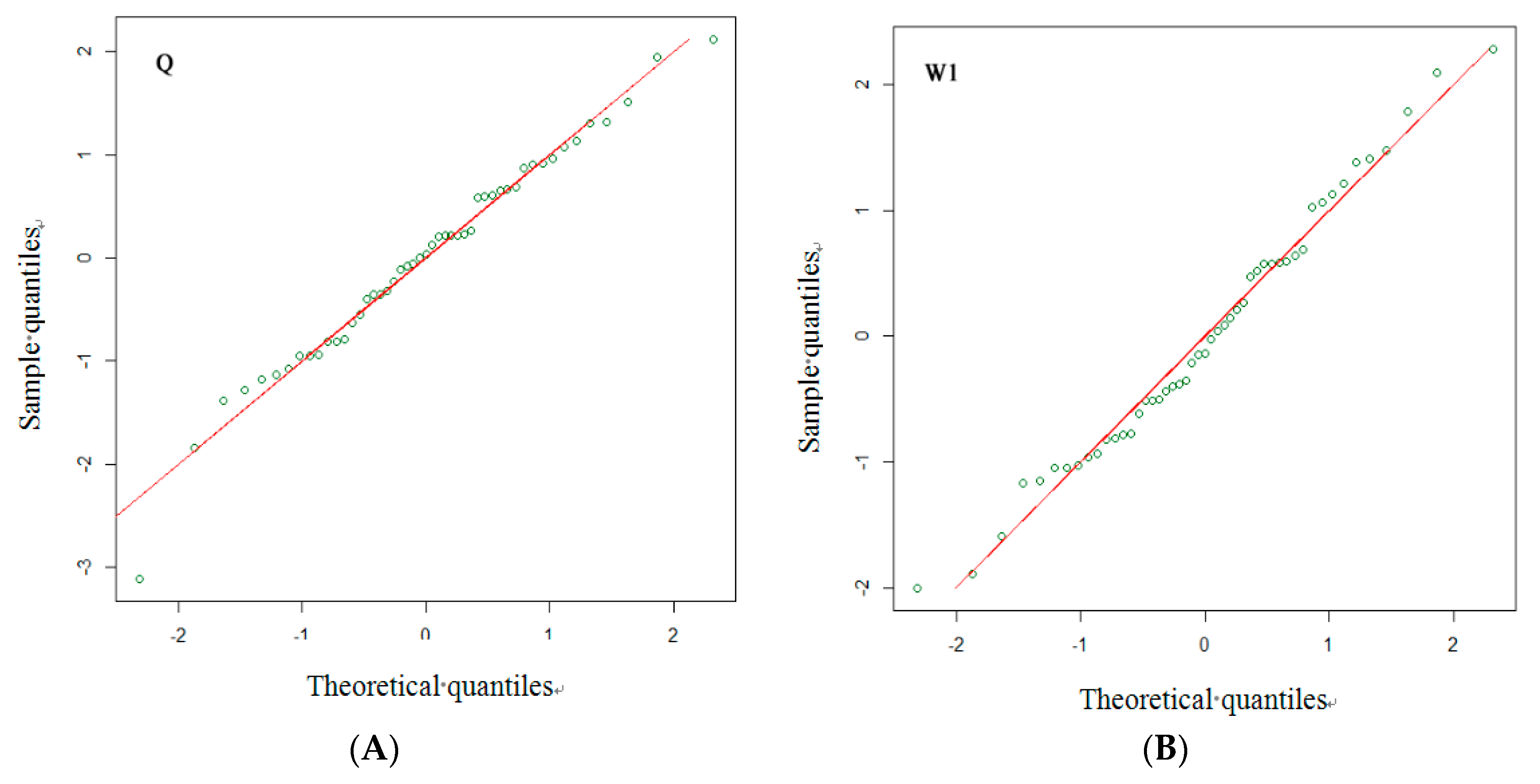
| Flood Series | Optimal Distribution | Mean | Variance | Coefficient of Skewness | Coefficient of Kurtosis | Filliben Coefficient |
|---|---|---|---|---|---|---|
| Q | Log-Normal | 0 | 1.021 | −0.357 | 3.408 | 0.9895 |
| W1 | Log-Normal | 0 | 1.021 | 0.249 | 2.402 | 0.9925 |
| Copulas | Copula Parameter (θ) | Indices of Fitting Test and Model Selection | ||
|---|---|---|---|---|
| D (K-S) | OLS | AIC | ||
| Gumbel-Hougaard Copula | 2.9224 | 0.1648 | 0.0404 | −312.3751 |
| Clayton Copula | 1.6444 | 0.1940 | 0.0470 | −297.7266 |
| Frank Copula | 9.1480 | 0.2537 | 0.0469 | −297.7374 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Wang, Y.; Wang, B.; Tan, S.; Feng, P. Nonstationary Flood Frequency Analysis Using Univariate and Bivariate Time-Varying Models Based on GAMLSS. Water 2018, 10, 819. https://doi.org/10.3390/w10070819
Zhang T, Wang Y, Wang B, Tan S, Feng P. Nonstationary Flood Frequency Analysis Using Univariate and Bivariate Time-Varying Models Based on GAMLSS. Water. 2018; 10(7):819. https://doi.org/10.3390/w10070819
Chicago/Turabian StyleZhang, Ting, Yixuan Wang, Bing Wang, Senming Tan, and Ping Feng. 2018. "Nonstationary Flood Frequency Analysis Using Univariate and Bivariate Time-Varying Models Based on GAMLSS" Water 10, no. 7: 819. https://doi.org/10.3390/w10070819
APA StyleZhang, T., Wang, Y., Wang, B., Tan, S., & Feng, P. (2018). Nonstationary Flood Frequency Analysis Using Univariate and Bivariate Time-Varying Models Based on GAMLSS. Water, 10(7), 819. https://doi.org/10.3390/w10070819





