Parameter Estimation for Soil Water Retention Curve Using the Salp Swarm Algorithm
Abstract
1. Introduction
2. The Van Genuchten Model
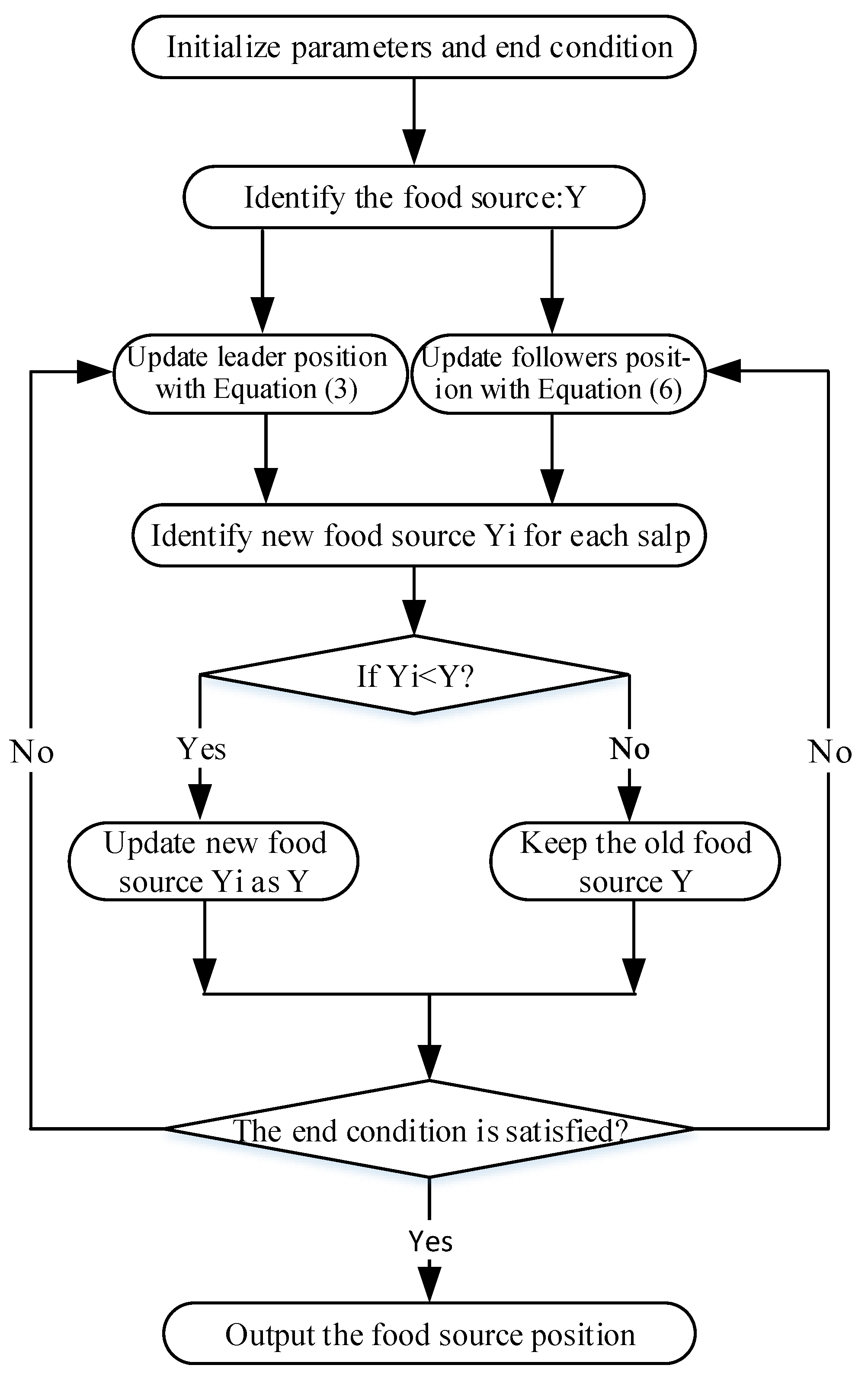
3. Salp Swarm Algorithm
| Algorithm 1 The Procedure of the Salp Swarm Algorithm (SSA) Algorithm. |
Require: Initialize the salp population consider and . while (End condition is not satisfied) Calculate the fitness of each search salp F=the best search solution Update by Equation (4) for each salp () if () Update the position of the leading salp by Equation (3) esle Update the position of the followers salp by Equation (6) end end Verify the position of salps based on the upper and lower bounds end returnF |
Benchmarking Algorithms
4. Estimation Algorithms and Dataset
Data Description
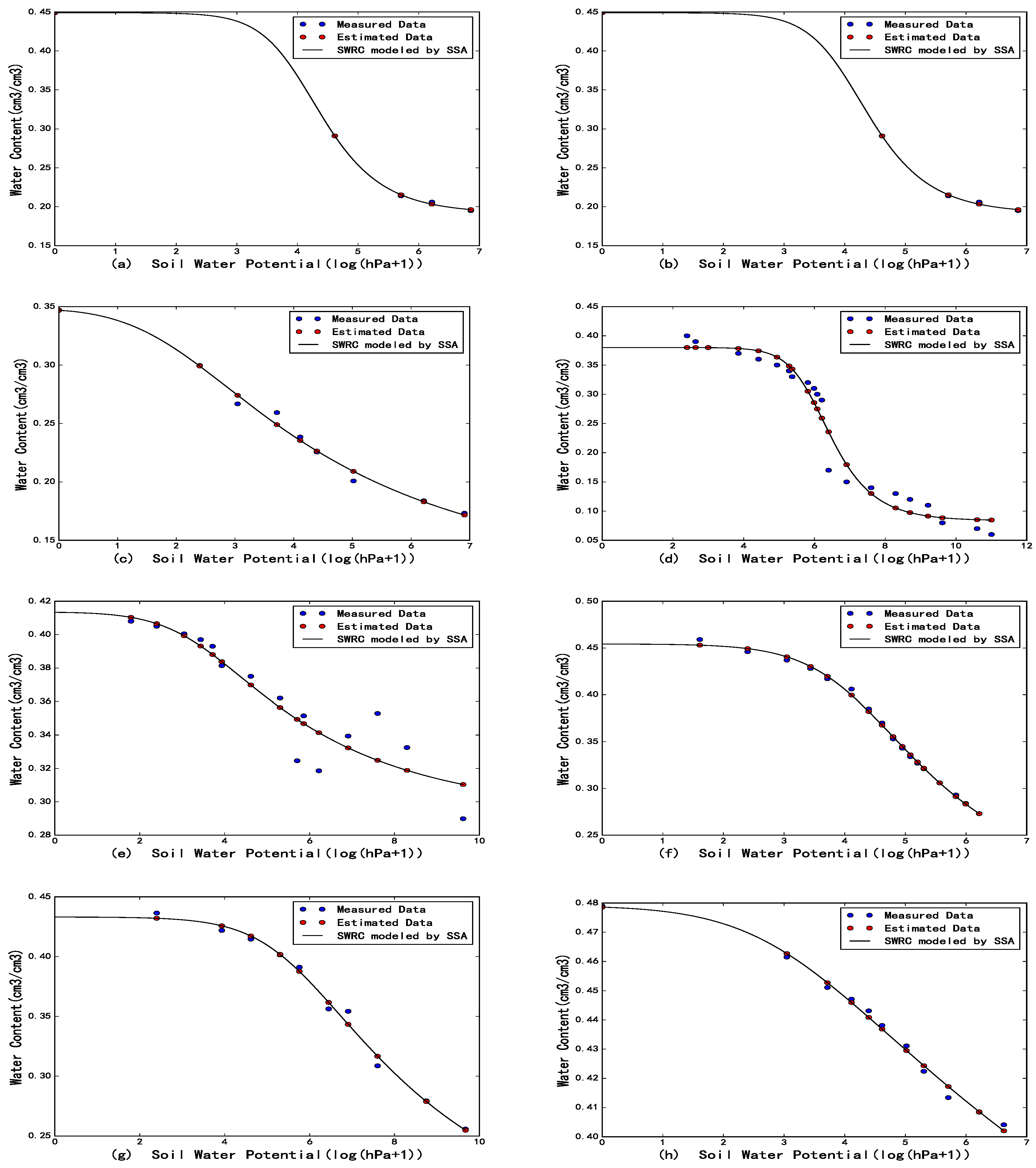
5. Estimation Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Leong, E.; Rahardjo, H. Review of Soil-Water Characteristic Curve Equations. J. Geotech. Geoenviron. Eng. 1997, 123. [Google Scholar] [CrossRef]
- Hosseini, S.M.M.M.; Ganjian, N.; Pisheh, Y.P. Estimation of the water retention curve for unsaturated clay. Can. J. Soil Sci. 2011, 91, 543–549. [Google Scholar] [CrossRef]
- Too, V.K.; Omuto, C.T.; Biamah, E.K.; Obiero, J.P. Review of Soil Water Retention Characteristic (SWRC) Models between Saturation and Oven Dryness. Open J. Mod. Hydrol. 2014, 4, 173–182. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media and their relation to drainage design. Trans. ASAE 1964, 7, 26–0028. [Google Scholar] [CrossRef]
- Gardner, W.R.; Hillel, D.; Benyamini, Y. Post-Irrigation Movement of Soil Water 2. Simultaneous Redistribution and Evaporation. Water Resour. Res. 1970, 6, 1148–1153. [Google Scholar] [CrossRef]
- Van Genuchten, M. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892. [Google Scholar] [CrossRef]
- Campbell, G. A Simple Method for Determining Unsaturated Conductivity From Moisture Retention Data. Soil Sci. 1974, 117, 311–314. [Google Scholar] [CrossRef]
- Omuto, C. Biexponential model for water retention characteristics. Geoderma 2009, 149, 235–242. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the Soil–Water Characteristic Curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Guangzhou Chen, L.J.; Li, X. Sensitivity Analysis and Identification of Parameters to the Van Genuchten Equation. J. Chem. 2016, 2016. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, D.; Yang, L.T.; Liu, J.; Chang, X.; Ning, H. A kernel machine-based secure data sensing and fusion scheme in wireless sensor networks for the cyber-physical systems. Future Gener. Comput. Syst. 2016, 61, 85–96. [Google Scholar] [CrossRef]
- Luo, X.; Deng, J.; Wang, W.; Wang, J.H.; Zhao, W. A Quantized Kernel Learning Algorithm Using a Minimum Kernel Risk-Sensitive Loss Criterion and Bilateral Gradient Technique. Entropy 2017, 19. [Google Scholar] [CrossRef]
- Van Genuchten, M.V.; Leij, F.J.; Yates, S.R. The RETC Code for Quantifying Hydraulic Functions of Unsaturated Soils; EPA/600/2-91/065, R.S.; U.S. Environmental Protection Agency: Ada, OK, USA, 1991; Volume 83.
- Luo, X.; Cao, L.; Wang, L.; Zhao, Z.; Huang, C. Parameter Identification of the Photovoltaic Cell Model with a Hybrid Jaya-NM Algorithm. Optik 2018. [Google Scholar] [CrossRef]
- Li, Y.B.; Liu, Y.; Nie, W.B.; Ma, X.Y. Inverse Modeling of Soil Hydraulic Parameters Based on a Hybrid of Vector-Evaluated Genetic Algorithm and Particle Swarm Optimization. Water 2018, 10, 84. [Google Scholar] [CrossRef]
- Xing, X.; Wang, H.; Ma, X. Brooks–Corey Modeling by One-Dimensional Vertical Infiltration Method. Water 2018, 10, 593. [Google Scholar] [CrossRef]
- Oh, S.; Kim, Y.K.; Kim, J.W. A Modified van Genuchten-Mualem Model of Hydraulic Conductivity in Korean Residual Soils. Water 2015, 7, 5487–5502. [Google Scholar] [CrossRef]
- Wang, L.; Huang, C.; Huang, L. Parameter Estimation of the Soil Water Retention Curve Model with Jaya Algorithm. Comput. Electron. Agric. 2018, 151, 349–353. [Google Scholar] [CrossRef]
- Matula, S.; Miháliková, M.; Batkova, K. Estimation of the Soil Water Retention Curve (SWRC) Using Pedotransfer Functions (PTFs). Soil Water Res. 2007, 2, 113–122. [Google Scholar] [CrossRef]
- Maggi, S. Estimating water retention characteristic parameters using differential evolution. Comput. Geotech. 2017, 86, 163–172. [Google Scholar] [CrossRef]
- Bayat, H.; Zadeh, G.E. Estimation of the soil water retention curve using penetration resistance curve models. Comput. Electron. Agric. 2018, 144, 329–343. [Google Scholar] [CrossRef]
- Do Nascimento, Í.V.; de Assis Júnior, R.N.; de Araújo, J.C.; de Alencar, T.L.; Freire, A.G.; Lobato, M.G.R.; da Silva, C.P.; Mota, J.C.A.; do Nascimento, C.D.V. Estimation of van Genuchten Equation Parameters in Laboratory and through Inverse Modeling with Hydrus-1D. J. Agric. Sci. 2018, 10, 102. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 16–191. [Google Scholar] [CrossRef]
- Sayed, G.I.; Khoriba, G.; Haggag, M.H. A novel chaotic salp swarm algorithm for global optimization and feature selection. Appl. Intell. 2018. [Google Scholar] [CrossRef]
- Luo, X.; Deng, J.; Liu, J.; Wang, W.; Ban, X.; Wang, J.H. A quantized kernel least mean square scheme with entropy-guided learning for intelligent data analysis. China Commun. 2017, 14, 127–136. [Google Scholar] [CrossRef]
- Luo, X.; Jiang, C.; Wang, W.; Xu, Y.; Wang, J.H.; Zhao, W. User behavior prediction in social networks using weighted extreme learning machine with distribution optimization. Future Gener. Comput. Syst. 2018. [Google Scholar] [CrossRef]
- Luo, X.; Xu, Y.; Wang, W.; Yuan, M.; Ban, X.; Zhu, Y.; Zhao, W. Towards enhancing stacked extreme learning machine with sparse autoencoder by correntropy. J. Frankl. Inst. 2018, 355, 1945–1966. [Google Scholar] [CrossRef]
- Luo, X.; Yang, X.; Jiang, C.; Ban, X. Timeliness online regularized extreme learning machine. Int. J. Mach. Learn. Cybern. 2018, 9, 465–476. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Huang, C.; Tsui, K.L. A GPU-accelerated parallel Jaya algorithm for efficiently estimating Li-ion battery model parameters. Appl. Soft Comput. 2018, 65, 12–20. [Google Scholar] [CrossRef]
| Soil Sample ID | Location | Bulk Density | Data Number | Soil Type |
|---|---|---|---|---|
| 3020 | Moscow, Russia | 1.21 | 5 | Sand |
| 1120 | Rome, AL, USA | 1.63 | 10 | Sandy Loam |
| 3154 | Dickey Co., ND, USA | 1.53 | 10 | Sand |
| 1330 | Hannover, Germany | 1.37 | 21 | Silt |
| 1173 | Clemson, SC, USA | 1.38 | 11 | Clay Loam |
| 1102 | Blackville, SC, USA | 1.71 | 9 | Sandy Clay |
| 1162 | Watkinsville, GA, USA | 1.54 | 15 | Clay |
| 1361 | Reinhausen (Goettingen), Germany | 1.49 | 11 | Silty Clay |
| 2400 | Cass County, ND, USA | 1.08 | 17 | Loam |
| Parameter | n | |||
|---|---|---|---|---|
| Lower Bound | 0 | 0 | 0 | 1 |
| Upper Bound | 1 | 1 | 100 | 100 |
| Soil Sample ID | Algorithm | (cmcm) | (cmcm) | (cm) | n | |
|---|---|---|---|---|---|---|
| 3020 | SSA | 0.19166 | 0.44901 | 0.06244 | 2.40869 | 0.011171 |
| DE | 0.19166 | 0.44901 | 0.01796 | 2.40869 | 0.011724 | |
| RETC | 0.19166 | 0.44901 | 0.01796 | 2.40885 | 0.011718 | |
| PSO | 0.19220 | 0.44900 | 0.01780 | 2.43342 | 0.011732 | |
| 1120 | SSA | 0.07951 | 0.28940 | 0.02583 | 1.88130 | 0.261462 |
| DE | 0.07951 | 0.28940 | 0.01238 | 1.88130 | 0.261464 | |
| RETC | 0.07951 | 0.28940 | 0.01239 | 1.88119 | 0.261465 | |
| PSO | 0.07951 | 0.28940 | 0.01238 | 1.88131 | 0.261463 | |
| 3154 | SSA | 0.06941 | 0.41611 | 0.06706 | 2.69126 | 0.214173 |
| DE | 0.06941 | 0.41611 | 0.02813 | 2.69128 | 0.214174 | |
| RETC | 0.06942 | 0.41609 | 0.02813 | 2.69178 | 0.214175 | |
| PSO | 0.06941 | 0.41611 | 0.02813 | 2.69131 | 0.214174 | |
| 1330 | SSA | 0.08362 | 0.38004 | 0.00337 | 2.11588 | 11.25378 |
| DE | 0.08362 | 0.38004 | 0.00259 | 2.11588 | 11.25378 | |
| RETC | 0.08373 | 0.37998 | 0.00259 | 2.11992 | 11.25386 | |
| PSO | 0.08344 | 0.38021 | 0.00260 | 2.10977 | 11.25391 | |
| 1173 | SSA | 0.29087 | 0.47857 | 0.03335 | 1.14316 | 0.037139 |
| DE | 0.30479 | 0.47850 | 0.03022 | 1.16004 | 0.037951 | |
| RETC | 0.30130 | 0.47850 | 0.04960 | 1.15530 | 0.499869 | |
| PSO | 0.03266 | 0.47909 | 0.05867 | 1.04872 | 0.041419 | |
| 1102 | SSA | 0.12175 | 0.34674 | 0.09208 | 1.29730 | 0.240458 |
| DE | 0.12198 | 0.34673 | 0.09168 | 1.29806 | 0.240460 | |
| RETC | 0.12170 | 0.34670 | 0.15910 | 1.29720 | 1.402827 | |
| PSO | 0.12183 | 0.34677 | 0.09208 | 1.29753 | 0.240460 | |
| 1162 | SSA | 0.29374 | 0.41333 | 0.01369 | 1.31096 | 2.711846 |
| DE | 0.29372 | 0.41334 | 0.01371 | 1.31075 | 2.711846 | |
| RETC | 0.29400 | 0.41330 | 0.03770 | 1.31270 | 4.622924 | |
| PSO | 0.29311 | 0.41346 | 0.01424 | 1.30620 | 2.711884 | |
| 1361 | SSA | 0.16454 | 0.43307 | 0.00105 | 1.25767 | 0.266938 |
| DE | 0.16448 | 0.43308 | 0.00106 | 1.25746 | 0.266939 | |
| RETC | 0.16450 | 0.43319 | 0.00430 | 1.25760 | 10.92369 | |
| PSO | 0.16128 | 0.43329 | 0.00112 | 1.25138 | 0.267039 | |
| 2400 | SSA | 0.19672 | 0.45414 | 0.00139 | 1.58303 | 0.144518 |
| DE | 0.19633 | 0.45419 | 0.00139 | 1.58259 | 0.144576 | |
| RETC | 0.19670 | 0.45410 | 0.00157 | 1.58310 | 0.418468 | |
| PSO | 0.19455 | 0.45444 | 0.00147 | 1.57232 | 0.144657 |
| Soil Sample Id | SSE on Raspberry Pi 3 | SSE on Windows 10 System |
|---|---|---|
| 2400 | 0.144518 | 0.144518 |
| 3020 | 0.011171 | 0.011171 |
| 1361 | 0.266938 | 0.266938 |
| 1102 | 0.240458 | 0.240458 |
| 1330 | 11.25378 | 11.25378 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, Z.; Luo, X. Parameter Estimation for Soil Water Retention Curve Using the Salp Swarm Algorithm. Water 2018, 10, 815. https://doi.org/10.3390/w10060815
Zhang J, Wang Z, Luo X. Parameter Estimation for Soil Water Retention Curve Using the Salp Swarm Algorithm. Water. 2018; 10(6):815. https://doi.org/10.3390/w10060815
Chicago/Turabian StyleZhang, Jing, Zhenhua Wang, and Xiong Luo. 2018. "Parameter Estimation for Soil Water Retention Curve Using the Salp Swarm Algorithm" Water 10, no. 6: 815. https://doi.org/10.3390/w10060815
APA StyleZhang, J., Wang, Z., & Luo, X. (2018). Parameter Estimation for Soil Water Retention Curve Using the Salp Swarm Algorithm. Water, 10(6), 815. https://doi.org/10.3390/w10060815







