Simulation of Fluid and Complex Obstacle Coupling Based on Narrow Band FLIP Method
Abstract
1. Introduction
2. Related Research
3. Proposed Method
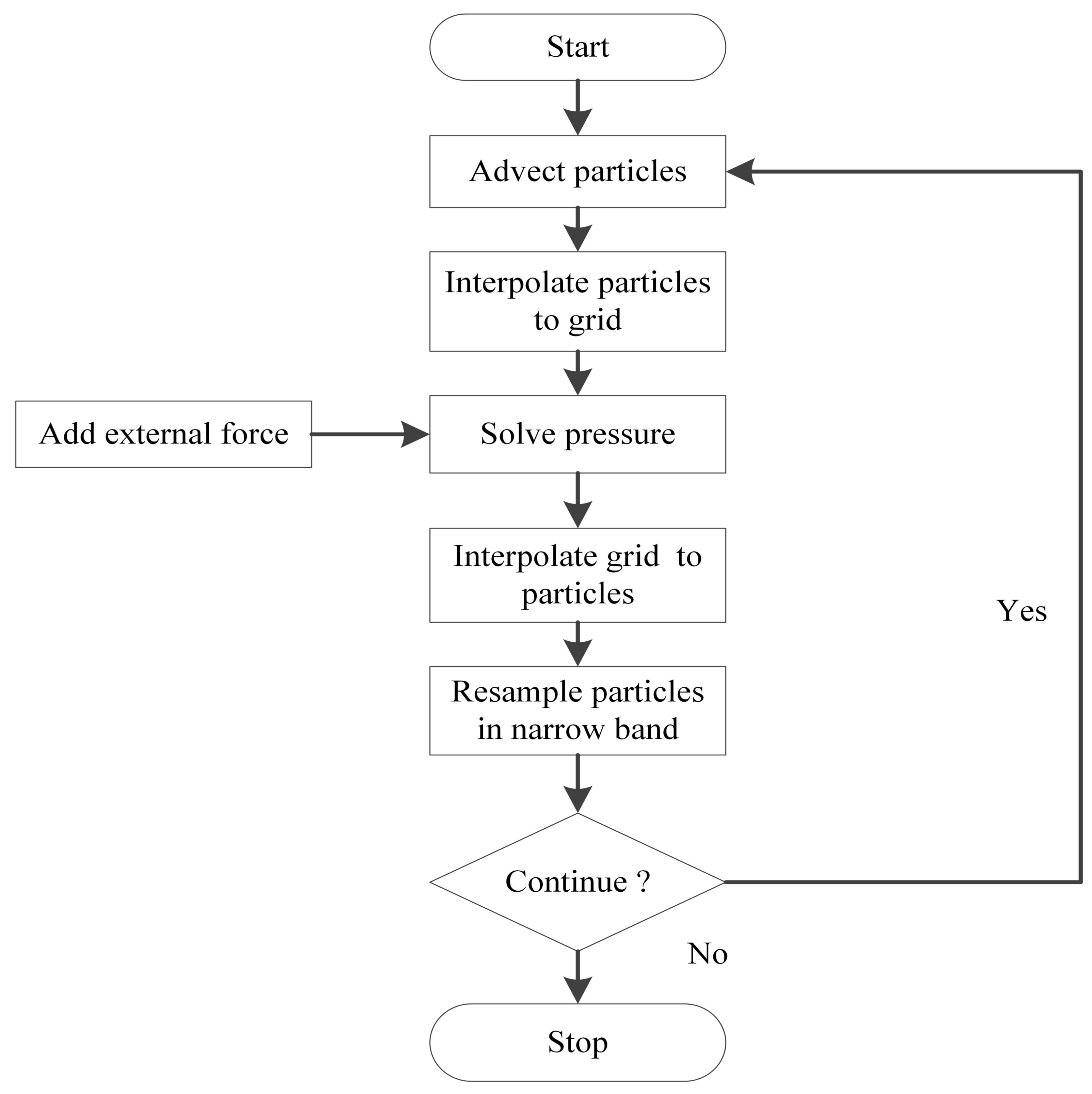
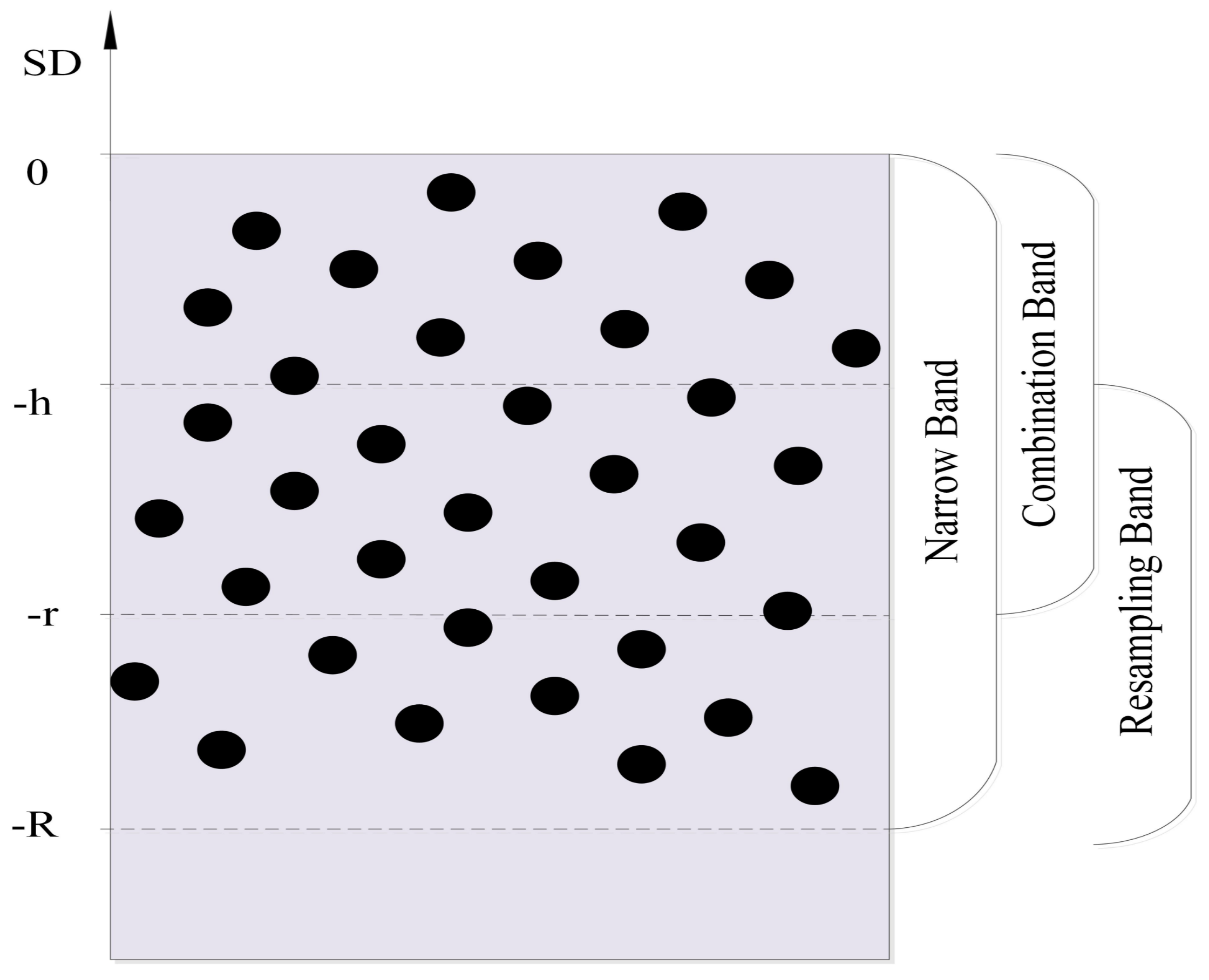
3.1. NBFLIP Method
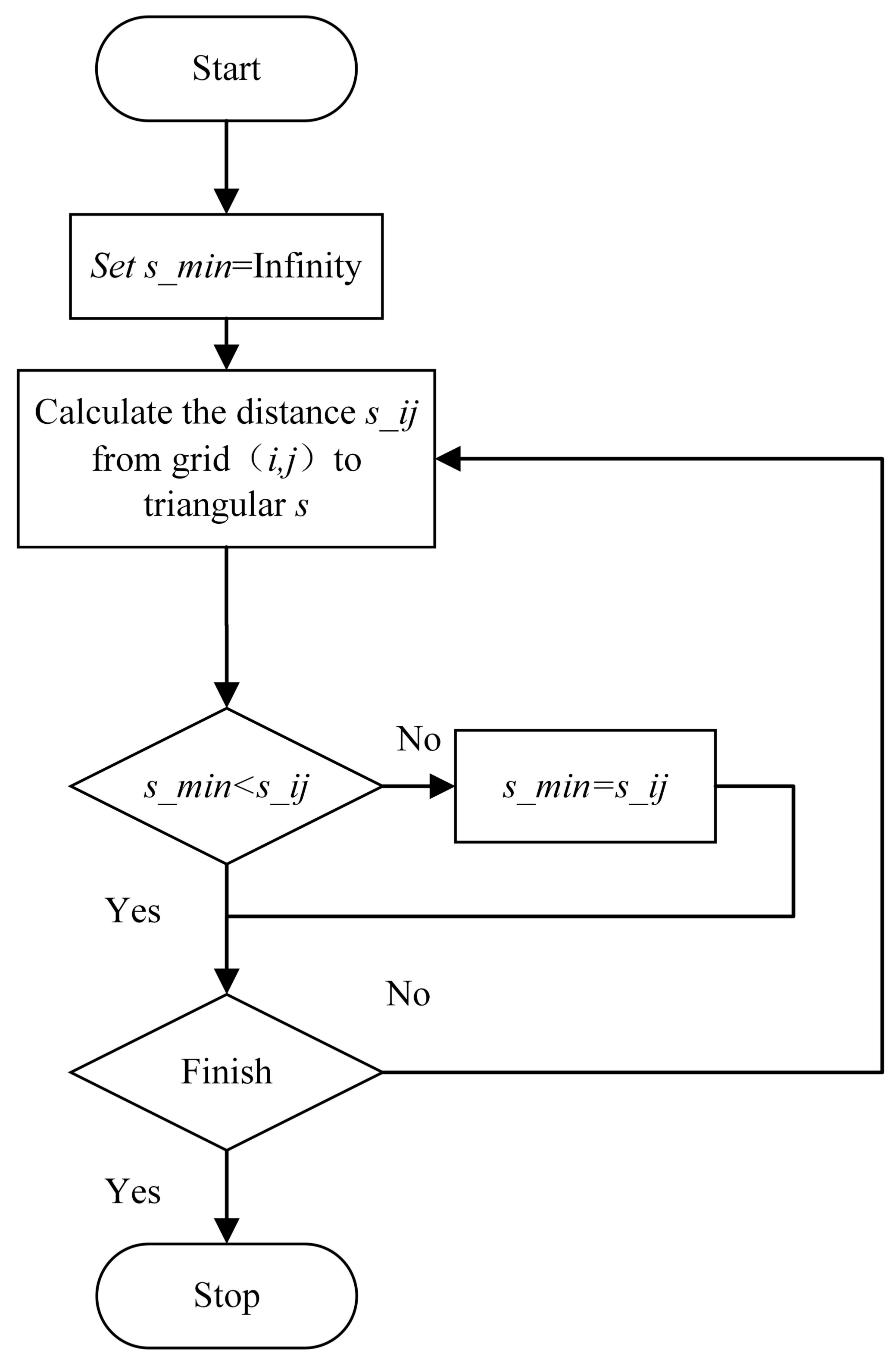
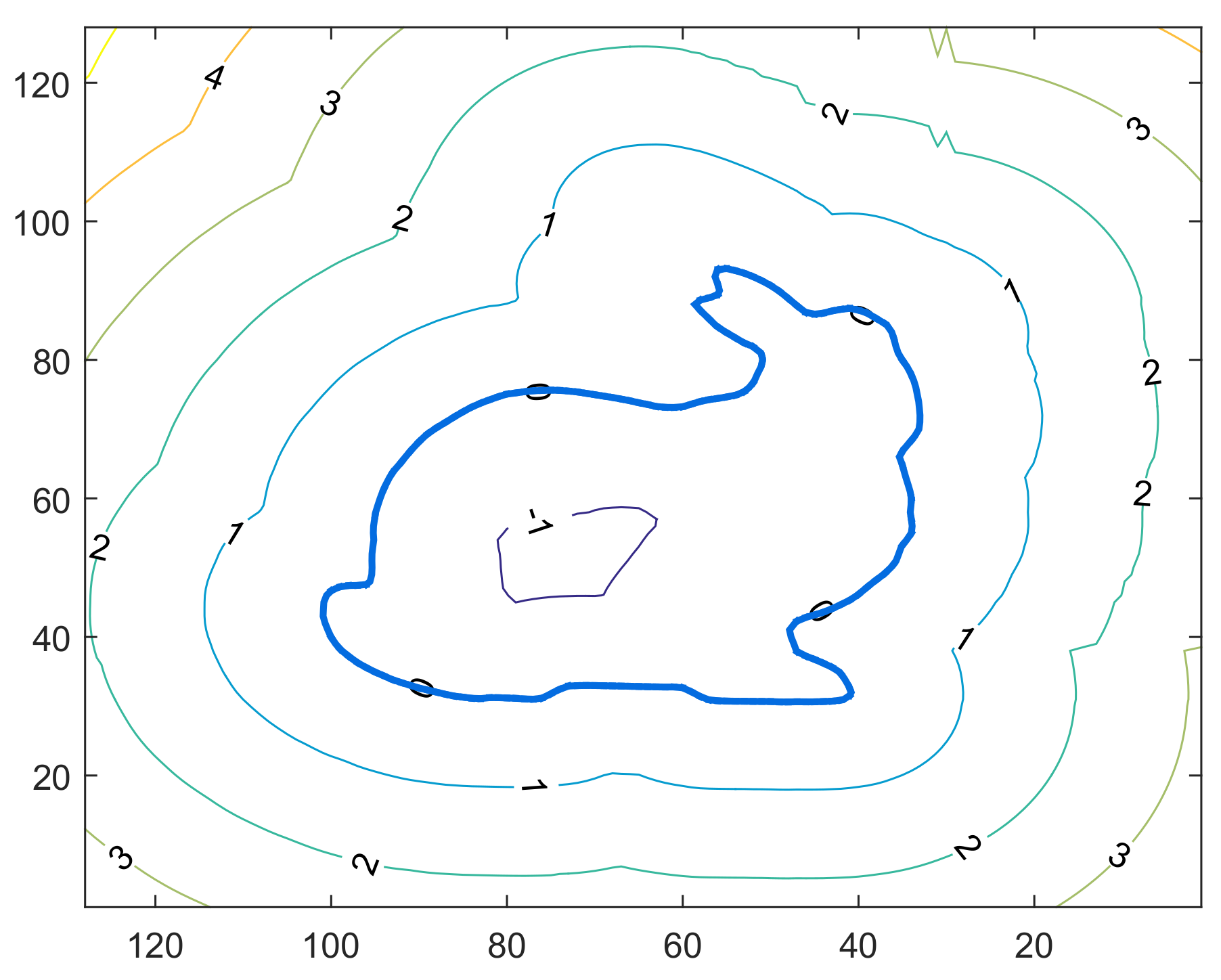
3.2. Complex Obstacle Representation Based on SDF
| Algorithm 1: SDF Calculation Procedure. |
| Step1. Initial Smin=Inf. Inf is a big value used to initialize the Smin which will be replaced by the real distance in the next. Step2. Calculate the distance from grid (i,j) center to triangular S, the distance is set as s1. Step2.1 Compare Smin and s1, if Smins1, set Smin=s1. Step2.2 Else if Smin<s1, Smin remains the same. Step3. Repeat Step2, go through all the grids until finished |
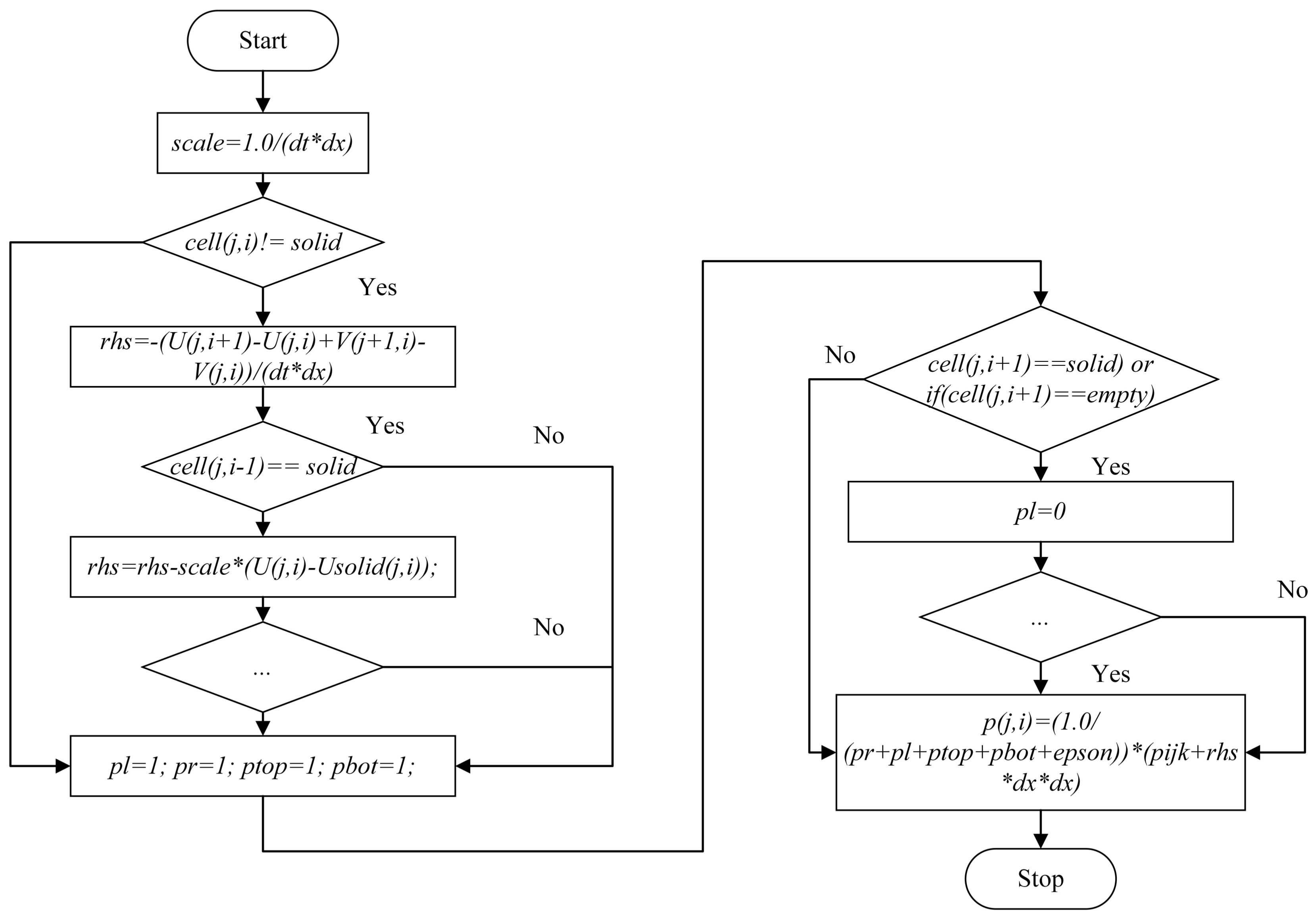
3.3. Free Surface and Complex Obstacle Interaction
| Algorithm 2: Free surface and solid obstacle boundary treatment in projection. |
| scale=1.0/(dt*dx); if(cell(j,i) solid) rhs=-(U(j,i+1)-U(j,i)+V(j+1,i)-V(j,i))/(dt*dx); if(cell(j,i-1)==solid) rhs=rhs-scale*(U(j,i)-Usolid(j,i)); end if(cell(j,i+1)==solid) rhs=rhs+scale*(U(j,i+1)-Usolid(j,i+1)); end if(cell(j-1,i)==solid) rhs=rhs-scale*(V(j,i)-Vsolid(j,i)); end if(cell(j+1,i)==solid) rhs=rhs+scale*(V(j+1,i)-Vsolid(j+1,i)); end pl=1; pr=1; ptop=1; pbot=1; if(cell(j,i+1)==solid) or if(cell(j,i+1)==empty) pr=0; end if(cell(j,i-1)==solid) or if(cell(j,i-1)==empty) pl=0; end if(cell(j+1,i)==solid) or if(cell(j+1,i)==empty) ptop=0; end if(cell(j-1,i)==solid)or if(cell(j-1,i)==empty) pbot=0; end |
4. Interactions Simulation of Fluid with Complex Obstacle
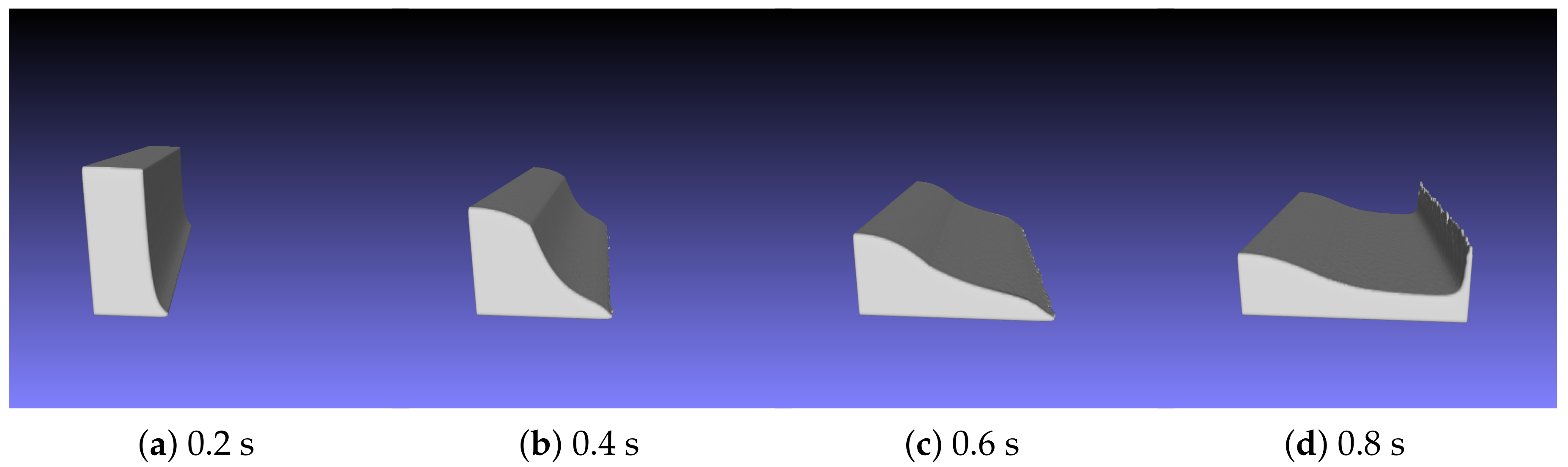
4.1. Dam Break Simulation Results
4.2. Free Surface Simulation Results
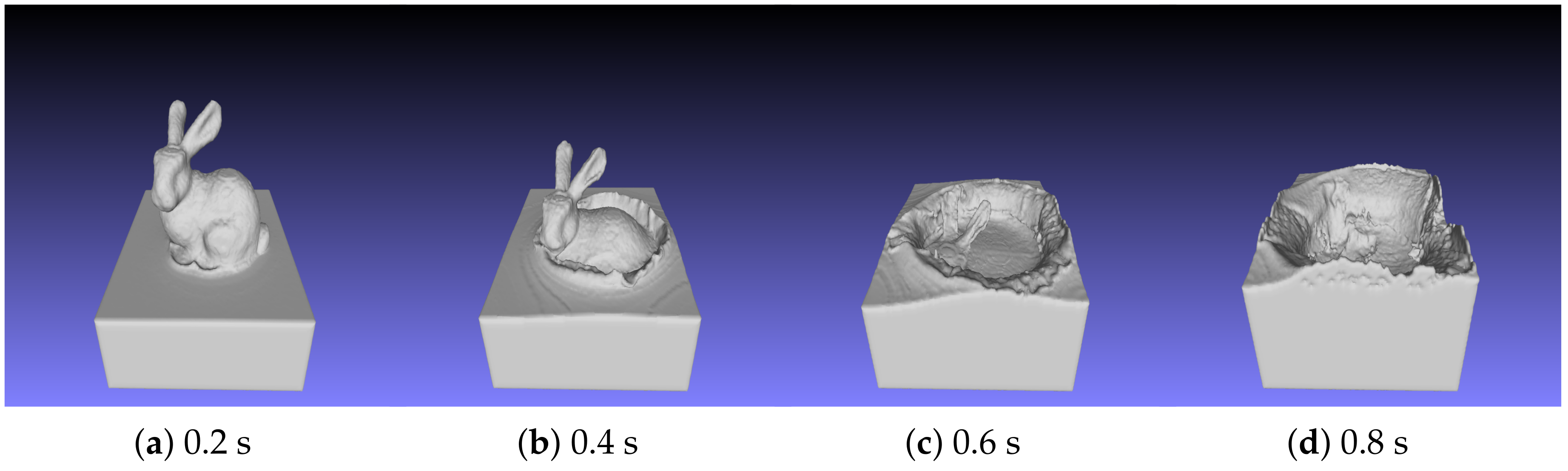
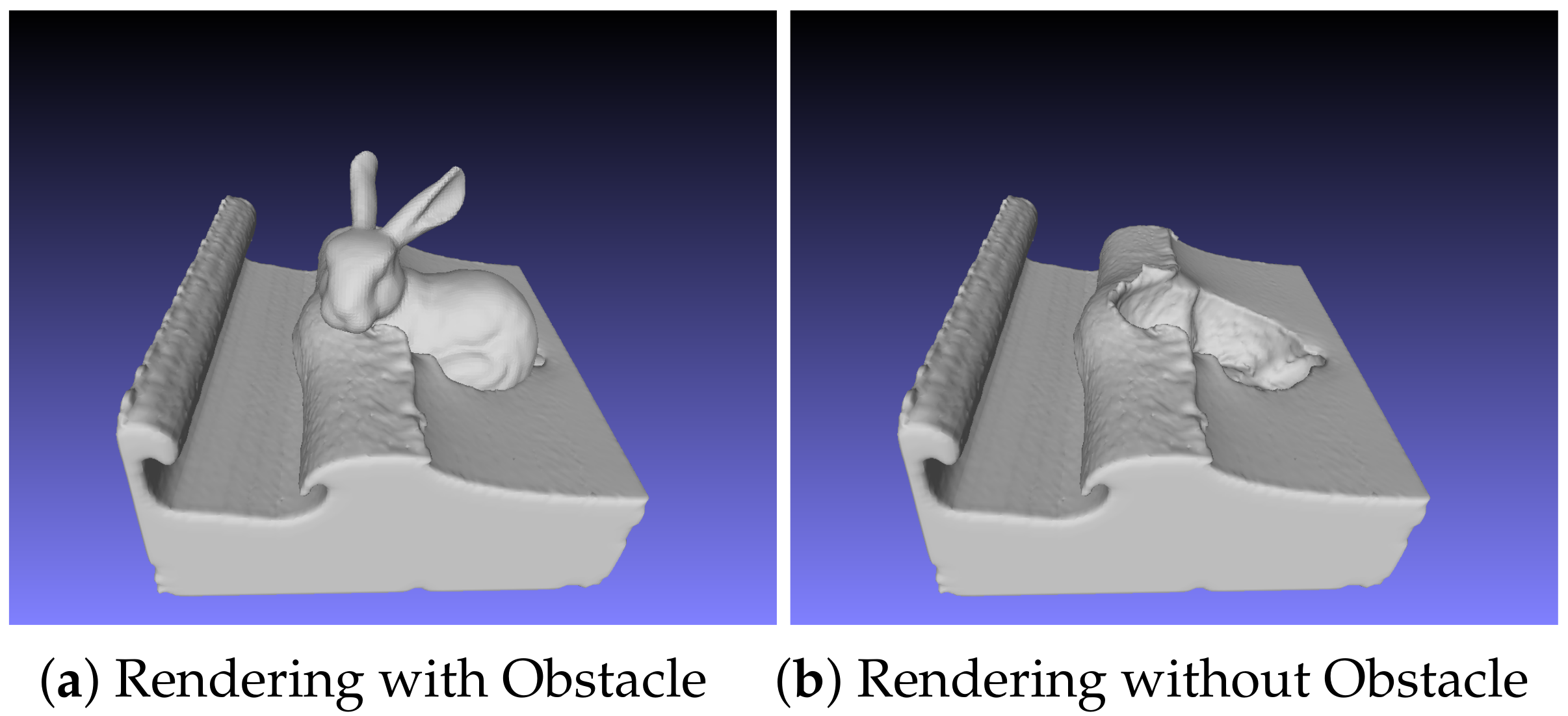
4.3. Simulation of Fluid Interactions with Complex Obstacle
4.4. Interaction with Moving Obstacle
5. Result Analysis
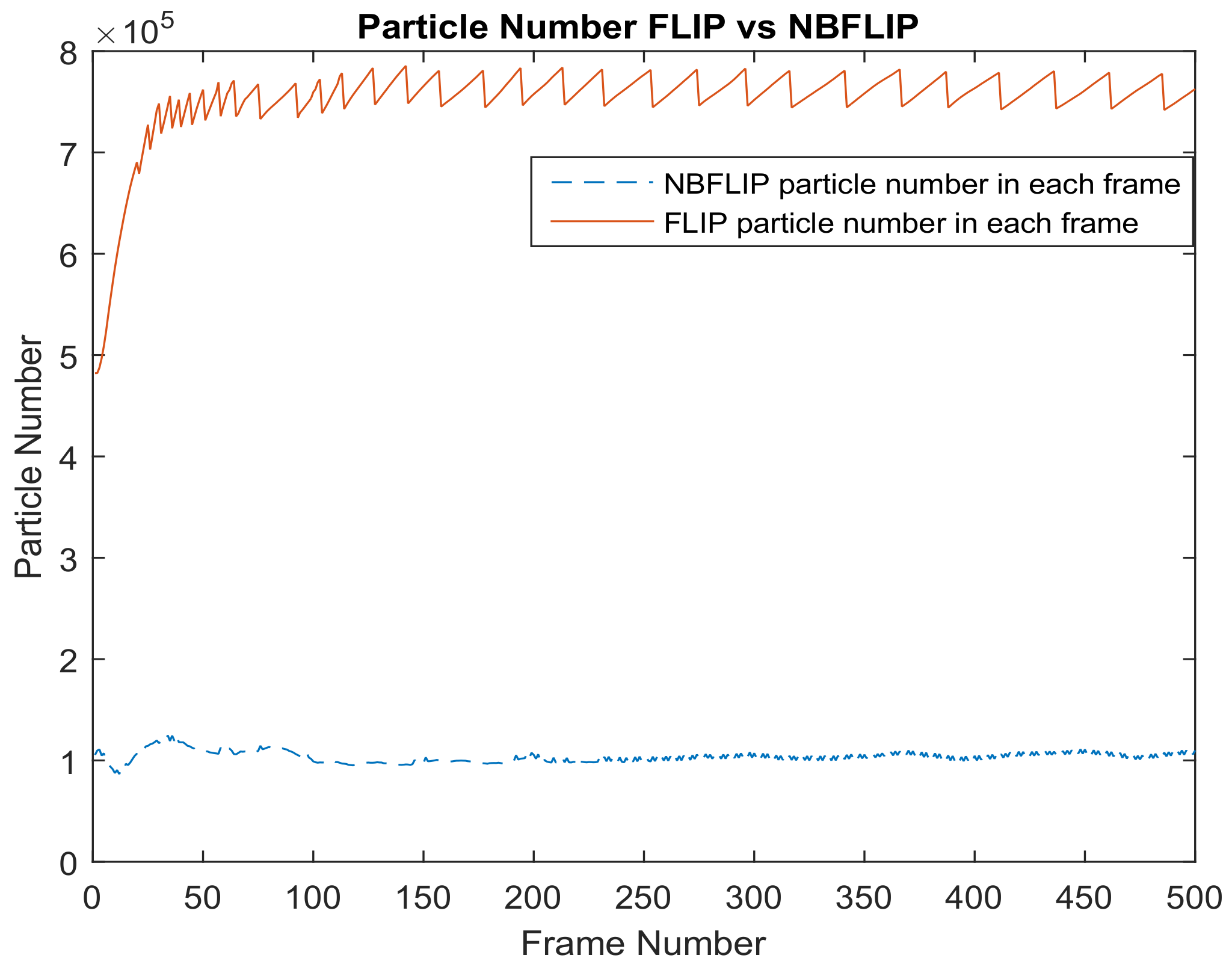
5.1. Particle Number Comparison
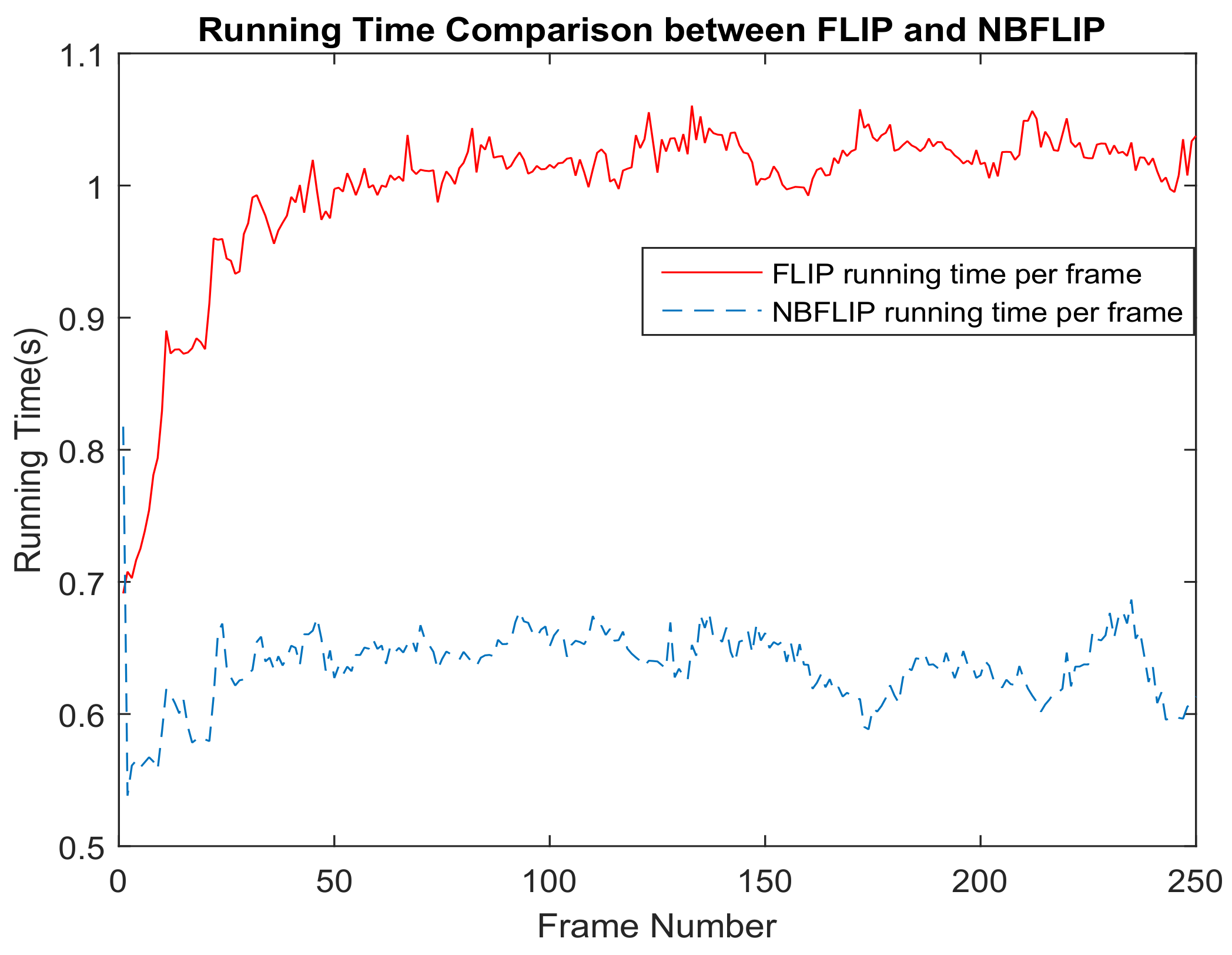
5.2. Runtime Comparison
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NSE | Navier-Stokes Equation |
| FLIP | Fluid Implicit Particle |
| NBFLIP | Narrow Band FLIP |
| KE | Kinetic Energy |
| SDF | Signed Distance Function |
| SD | Signed Distance |
| CPM | Closest Point Method |
References
- Brackbill, J.U.; Kothe, D.B.; Ruppel, H.M. Flip (fluid-implicit-particle): A low-dissipation, particle-in-cell method for fluid flow. In Proceedings of the Workshop on Particle Methods in Fluid Dynamics and Plasma Physics, Los Alamos, NM, USA, 13 April 1987; pp. 25–38. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Ruppel, H.M. Flip: A low-dissipation, particle-in-cell method for fluid flow. Comput. Phys. Commun. 1988, 48, 25–38. [Google Scholar] [CrossRef]
- Ferstl, F.; Ando, R.; Wojtan, C.; Westermann, R.; Thuerey, N. Narrow band flip for liquid simulations. Comput. Graphics Forum 2016, 35, 225–232. [Google Scholar] [CrossRef]
- Zhu, Y.; Bridson, R. Animating sand as a fluid. ACM Trans. Graph. 2005, 24, 965–972. [Google Scholar] [CrossRef]
- Batty, C.; Bertails, F.; Bridson, R. A fast variational framework for accurate solid-fluid coupling. ACM Trans. Graph. 2007, 26, 100. [Google Scholar] [CrossRef]
- Cornelis, J.; Ihmsen, M.; Peer, A.; Teschner, M. Iisph-flip for incompressible fluids. Comput. Graphics Forum 2014, 33, 255–262. [Google Scholar] [CrossRef]
- Zhu, B.; Yang, X.; Fan, Y. Creating and preserving vortical details in sph fluid. Comput. Graphics Forum 2010, 29, 2207–2214. [Google Scholar] [CrossRef]
- Boyd, L.; Bridson, R. Multiflip for energetic two-phase fluid simulation. ACM Trans. Graph. 2012, 31, 1–12. [Google Scholar] [CrossRef]
- Nan, C. Research on Enhancing Details of Fluid Simulation. Master’s Thesis, Changan University, Xi’an, China, 2015; pp. 1–67. (In Chinese). [Google Scholar]
- Stam, J. Stable fluids. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 8–13 August 1999; pp. 121–128. [Google Scholar]
- Foster, N.; Metaxas, D. Controlling fluid animation. In Proceedings of the Conference on Computer Graphics International, Diepenbeek, Belgium, 23–27 June 1997; pp. 178–188. [Google Scholar]
- Monaghan, J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Charypar, D.; Gross, M. Particle-based fluid simulation for interactive applications. In Proceedings of the ACM Siggraph/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 26–27 July 2003; Eurographics Association: Geneva, Switzerland, 2003; pp. 154–159. [Google Scholar]
- Müller, M.; Solenthaler, B.; Keiser, R.; Gross, M. Particle-based fluid-fluid interaction. In Proceedings of the ACM Siggraph/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 29–31 July 2005; pp. 237–244. [Google Scholar]
- Calakli, F.; Taubin, G. SSD: Smooth signed distance surface reconstruction. Comput. Graphics Forum 2011, 30, 1993–2002. [Google Scholar] [CrossRef]
- Macdonald, C.B.; Ruuth, S.J. Levelset equations on surfaces via the closest point method. J. Sci. Comput. 2008, 35, 219–240. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Dominguez, J.M.; Gesteira, M.; Barreiro, A.; Rogers, B.D. User Guide for the DualSPHysics Code v1.0. Available online: http://www.dual.sphysics.org (accessed on 1 May 2018).
- Ando, R.; Wojtan, C. Highly adaptive liquid simulations on tetrahedral meshes. ACM Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Sethian, J.A. Levelset methods and fast marching methods. J. Comput. Inf. Technol. 1999, 11, 400–410. [Google Scholar]












| Symbols | Meaning |
|---|---|
| V | Velocity vector |
| ∇ | Nabla Operator |
| Fluid density | |
| Fluid viscosity | |
| f | External force |
| t | Time |
| p | Pressure |
| r | Radius |
| Grid width | |
| Position | |
| Grid position index |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, C.; Yin, Y. Simulation of Fluid and Complex Obstacle Coupling Based on Narrow Band FLIP Method. Water 2018, 10, 811. https://doi.org/10.3390/w10060811
Zou C, Yin Y. Simulation of Fluid and Complex Obstacle Coupling Based on Narrow Band FLIP Method. Water. 2018; 10(6):811. https://doi.org/10.3390/w10060811
Chicago/Turabian StyleZou, Changjun, and Yong Yin. 2018. "Simulation of Fluid and Complex Obstacle Coupling Based on Narrow Band FLIP Method" Water 10, no. 6: 811. https://doi.org/10.3390/w10060811
APA StyleZou, C., & Yin, Y. (2018). Simulation of Fluid and Complex Obstacle Coupling Based on Narrow Band FLIP Method. Water, 10(6), 811. https://doi.org/10.3390/w10060811




