1. Introduction
A negatively buoyant jet (NBJ) is the phenomenon that develops when a fluid is discharged, with a non-negligible momentum, in a less dense fluid. As the jet tends to fall downwards, it is typically released upwards, with a certain angle to the horizontal, in order to increase the path length and, consequently, the final dilution. Due to the several practical applications of inclined NBJs (see Ferrari and Querzoli, 2010 [
1], for a list), many researches during the last few years focused on this topic.
In particular, many experimental investigations on NBJs released into a stationary receiving body can be found in recent years. Qiao et al. (2017, [
2]) carried out an experimental and theoretical study on the internal hydraulics of NBJs from diffusers for sewage disinfection. Bashitialshaaer et al. (2012, [
3] and 2015, [
4]), measured in a laboratory model the geometrical features and the dilution of inclined NBJs. Seo and Song (2015, [
5]) tested the influence of different diffuser types on the dispersion of NBJs for the particular application of the discharge of cooled water. Christodoulou et al. (2015, [
6]) focused on the achieved dilution at the impact point and on its dependence on the NBJ inclination and on the densimentric Froude number. Oliver et al. (2013, [
7]) removed the bottom boundary to find dilutions not affected by the stratification of dense effluent at the bottom. Geyer et al. (2012, [
8]) experimentally obtained a chart of the dependence of flow types on Richardson, Reynolds and Weber numbers. Papakonstantis et al. (2011-a [
9] and 2011-b [
10]) experimentally studied the geometrical characteristics (via image analysis techniques) and the concentration (via probes) of inclined NBJs. In other experiments, velocity measurements were performed (e.g., Crowe et al., 2012 [
11] and 2016 [
12], Besalduch et al., 2013 [
13] and 2014 [
14]), highlighting, among the other results, the different turbulent quantities in the upper and lower boundaries of NBJs.
The number of experimental investigations on the discharge of NBJs into a non-stationary receiving body are much less. Malcangio et al., 2016 [
15], studied in the laboratory the turbulent features of vertical buoyant jets discharged into a transversal current. Hajikandi and Barjastehmaleki (2015, [
16]) and Lai and Lee (2014, [
17]) experimentally studied the mixing of inclined NBJs discharged into, respectively, a co-flow and a perpendicular cross-flow. Yang et al. (2005, [
18]) experimentally investigated NBjs with a different angle discharged in a cross flow. Davies et al. (2001, [
19]) and Davies and Ahmed (1996, [
20]) studied, with both laboratory and numerical simulations, the peculiar case of an NBJ discharged horizontally into a rotating homogeneous fluid. Moreover, Stancanelli et al. (2018, [
21]), experimentally investigated a buoyancy current in the presence of regular waves.
Regarding the jets released into a wave environment, some experimental researches on horizontal NBJs, on positively buoyant jets and on simple jets can be found in the literature. Bas et al. (2012, [
22]) focused their experiments on the effect of the wave direction (discharge in the wave direction or in the opposite direction) on the dilution of horizontal NBJ. They found a higher dilution for the discharge in the opposite direction to the wave propagation, compared to both the dilution obtained in a stagnant receiving environment and the dilution of the co-flow discharge. Lin et al. (2011, [
23]), investigated experimentally the turbulent properties of horizontal NBJs and non-buoyant jets under regular progressive waves via Particle Image Velocimetry (PIV). They found that dilution is increased by the wave motion. The same authors (Lin et al. 2013, [
24]) measured, via PIV, the mean velocity and turbulence properties in a horizontal (positively, neutrally and negatively) buoyant jet discharged in the opposite direction to the wave propagation. They found that the width and the dilution of the positively and negatively buoyant jets increased in the wave receiving environment. Also Chin (1987, [
25]) and Sharp (1986, [
26]) observed experimentally that the dilution of a buoyant jet in a wave environment is significantly higher than in a stagnant one.
Many other Authors found similar results about the increased dilution due to the larger spreading caused by waves also on simple jets (e.g., Xu et al., 2016-a [
27] and 2016-b [
28], Hsiao et al., 2011 [
29], Chang et al., 2009 [
30], Ryu et al., 2005 [
31], Mossa, 2004 [
32], Chyan and Hwung, 1993 [
33], Chyan et al., 1991 [
34]). In this context, the classification formulated by Chyan and Hwung (1993, [
33]) for the regions of a jet interacting with waves is particularly relevant: They identified three regions, namely the jet deflection region, the transition region and the developed jet region. In the jet deflection region, the jet still has most of its initial momentum and so it tends to preserve its shape; the influence of the wave on the jet deflection region is consequently an oscillation of the jet around its stationary position. This behavior has been confirmed by the experiments of Mossa (2004, [
32]), Chyan et al. (1991, [
34]) and Sharp (1986, [
24]): They have shown that this oscillation has a considerable effect on the jet dilution. In the developed jet region, a periodic deflection, observed by Chyan and Hwung (1993, [
31]) and Chin (1987, [
26]), was found to be one of the main reasons for the higher dilution reached by a jet released in the presence of waves.
Although the increase of the dilution of a jet has been measured in many experimental investigations, to the best of the authors’ knowledge the effects of regular waves on inclined (not horizontal or vertical) NBJs were never investigated before. For this reason, Ferrari and Querzoli, 2015 [
35], performed a preliminary series of experiments that highlighted significant differences among the behavior of simple or positively buoyant jets and the case of the inclined negatively buoyant jets. As a consequence, a new set of carefully designed experiments were performed, with the main aim of better characterizing the peculiar behavior of negatively buoyant jets in a wavy environment and, in particular, of measuring the changes in the most important parameter for the design of environmentally friendly sea outfalls, i.e., the achieved dilution. In the present paper we present the results arising from this new set of experiments.
This paper is structured as follows: In
Section 2, the experimental set-up, the run parameters and the data elaboration are briefly described; in
Section 3, the results are shown and discussed; in
Section 4, the conclusions are drawn.
2. Materials and Methods
The experimental set-up simulates a typical configuration of a submarine outfall, i.e., the discharge from an orifice in the lateral wall of a pipe laid down on the sea bottom. A solution of water, sodium-sulphate and fluorescein was released, through a sharp-edged orifice outlet with a diameter D = 4.0 mm and an angle to the horizontal θ = 67°, into a flume with glass walls. The solution came from a constant head tank to a cylindrical pipe with a 25.0 mm diameter. The sodium-sulphate was employed to increase the density of the solution, the fluorescein to allow concentration measurements via a Light Induced Fluorescence (LIF) technique (a non-intrusive and full-field image analysis technique). The flume is 21.00 m long and 0.30 m wide and it is equipped with a piston-type wavemaker, on one side, and an absorbing beach, on the opposite side, to minimize the reflections. The wavemaker can produce monochromatic or random waves. The water depth d was kept constant at 0.40 m.
The key parameter controlling the behavior of negatively buoyant jets is the densimetric Froude number
Fr:
where
U is the outlet mean velocity,
g the gravitational acceleration,
ρD the discharged fluid density and
ρR the receiving fluid density. The Reynolds number is defined here as
Re =
UD/
υ, where
υ is the kinematic viscosity of the discharged fluid. Two sets of experiments were performed, with
Fr equal to 18.0 and 28.0, and a
Re of 10
3 (higher than the critical value of around 500 for the present set-up, as shown by Ferrari and Querzoli, 2010 [
1]) and five monochromatic waves, with wave periods
T of 0.50 s, 1.00 s and 1.50 s (corresponding to wave lengths
L of 0.39 m, 1.56 m and 3.51 m) and wave amplitudes
A of 5.00 mm and 12.50 mm (see
Table 1). A reference run with a NBJ released in a stagnant environment was performed for each
Fr. The ratio of the water depth
d to the wave length
L was in the deep-water regime (
d/L = 1.02) or in the intermediate-depth water regime (
d/L = 0.26 and 0.11); the ratio between the wave height
H = 2
A and
L was between 0.003 and 0.026, typical values of a long wave. The experimental set-up dimensions and wave parameters were chosen in order to simulate a typical submerged discharge in the Mediterranean Sea, with respect to the geometrical similarity (scale model
KL =
LM/LP = 1/40; the subscript
M stands for Model and the subscript
P for Prototype), to the kinematic similarity and to the dynamic (Froude) similarity, achieved through the respect of the following equations (see e.g., Von Ellenrieder and Dhanak, 2016 [
36]):
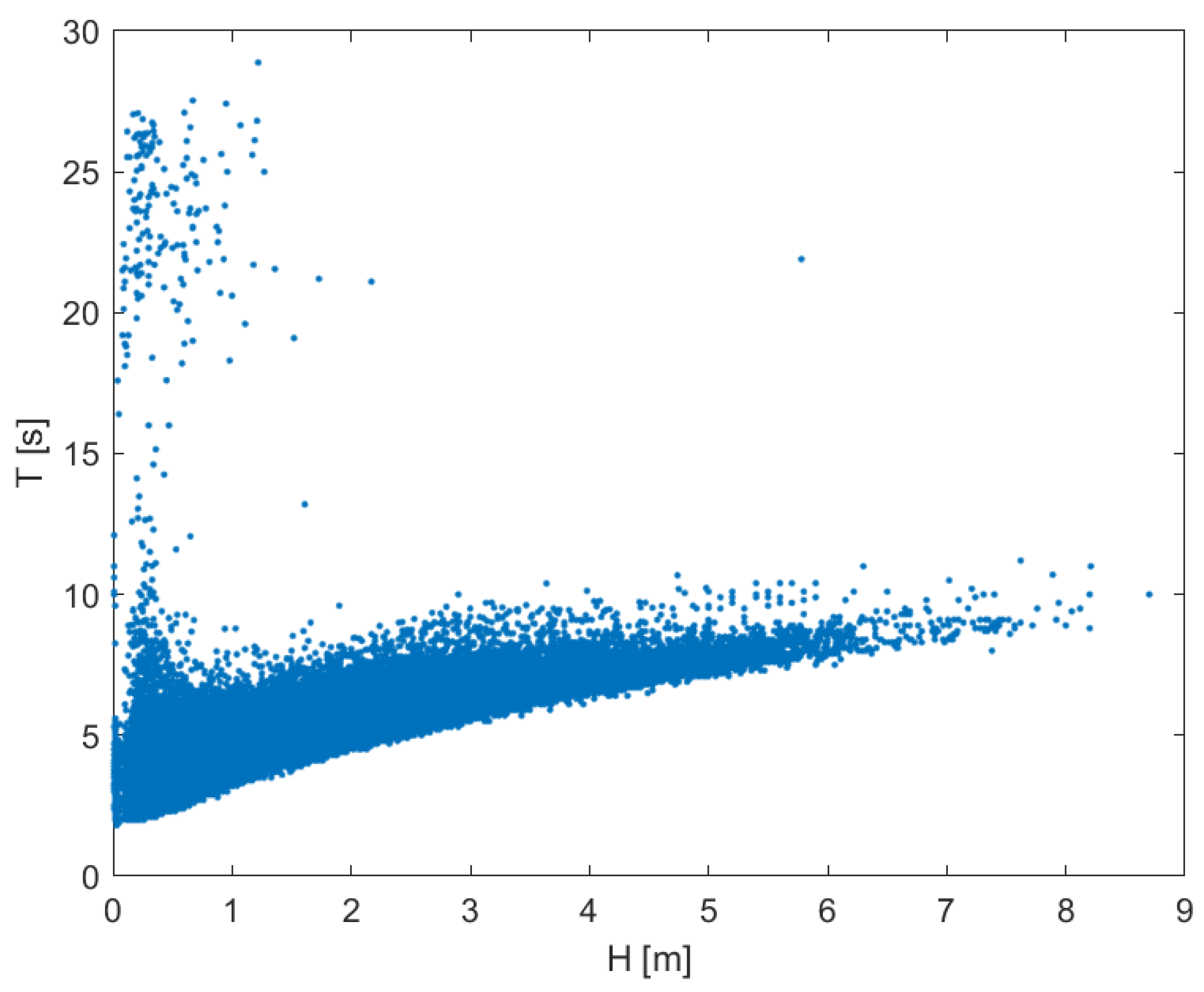
In
Figure 1, the data of the wave period,
T, versus the wave height
H recorded by the Alghero wave buoy (in the north-western sea of Sardinia) of the RON—Rete Ondametrica Nazionale (Italian national wavemetric system [
37]) from 2002 to 2014 are shown. These data were employed to define the wave parameters of the present experiments. As a matter of fact, by using Equations (2) and (3), the simulated prototype waves have
H = 2
A = 0.40 − 1.00 m and
T = 3.16 − 6.32 − 9.49 s, hence their values are within the range of those registered by the Alghero wave buoy.
The jet is discharged rightwards, in the opposite direction to the wave propagation and the flume is long enough to avoid an accumulation of dense fluid on the bottom during the duration of the experiment.
The axial vertical jet section was illuminated by a light sheet and a 3-CCD video-camera placed orthogonal to the light sheet. The experiments were recorded with a frame rate of 25 fps, a resolution of 720 × 576 pixels and a bit depth of 8 bit per color. As a consequence, the recorded images showed a bright jet on a dark background and, as the fluorescein concentration was very low, a linear relationship between the light intensity and the salt concentration holds true (Troy and Kosseff, 2005 [
38], Sutton et al., 2008 [
39]), so we used light intensity as a proxy for the salt concentration.
The free surface levels were measured via the image analysis technique developed by Ferrari et al., 2016 [
40]; the framed zone for the wave height measurement had a spatial resolution of around 11.62 px/mm, so the 10 mm height wave was measured with a resolution of around ±0.86% and the 25 mm height wave with a resolution of around ±0.34%. The resolution in the concentration measurements is around 0.4%. The resolution on the measured distances (
X/D and
Y/D) depends on the spatial resolution of the investigation area, which is not the same for every experiment and varies from a minimum of 14.26 px/cm (run 7) to 20.89 px/cm (run 6). In addition, following Bendat and Piersol, 2010 [
41], the uncertainty of the statistics presented in this paper was estimated from their standard deviation and was then computed over all the recorded images for each experiment (5000 for
T = 0.5 s, 10000 for
T = 1.0 s, 15,000 for
T = 1.5 s); the maximum uncertainty varies from a minimum of 3.35% (run 3) to a maximum of 4.52% (run 8).
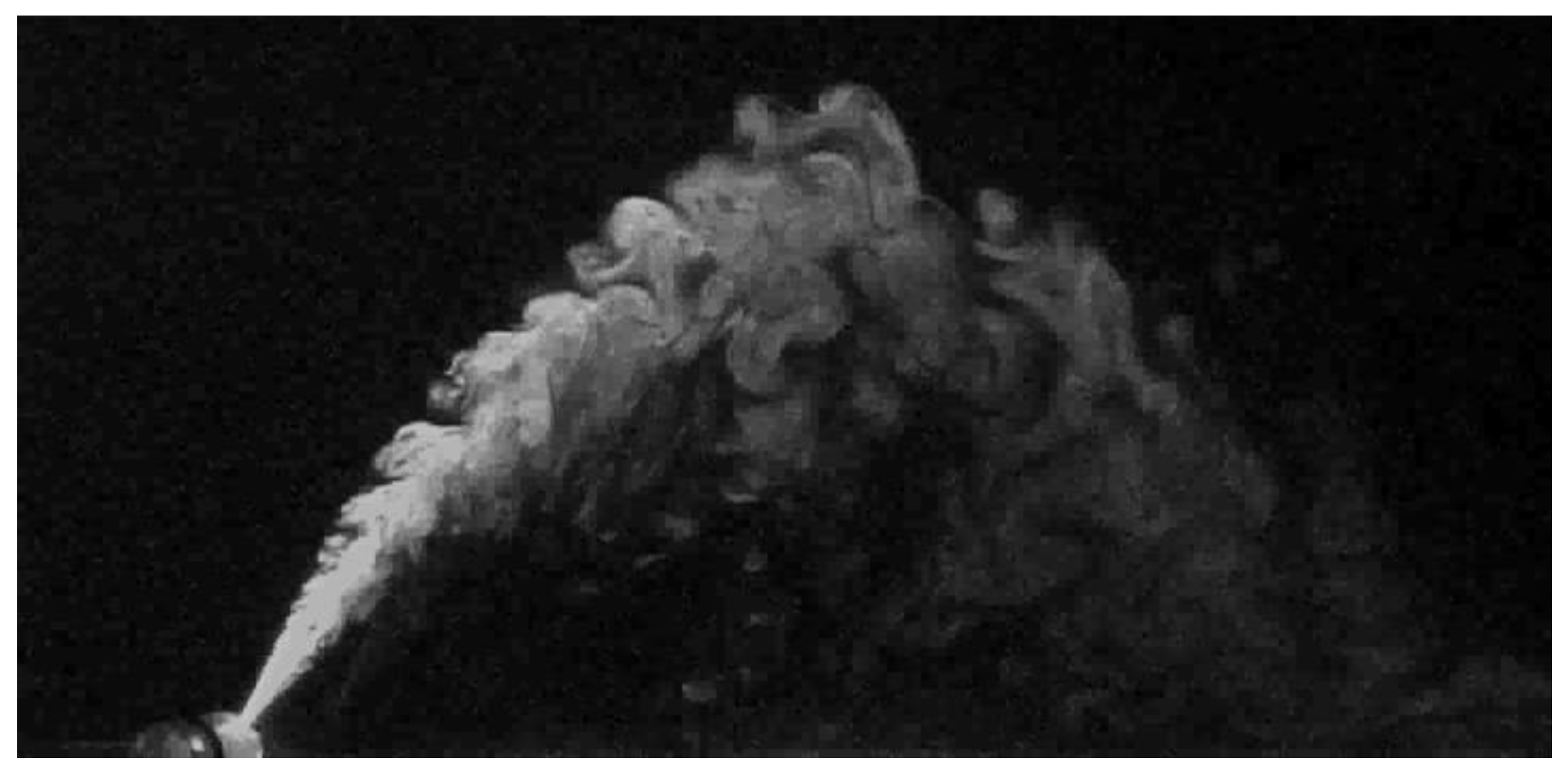
In
Figure 2 and
Figure 3, two instantaneous visualizations of an inclined negatively buoyant jet with
Fr = 28.0, released respectively in a stagnant and in a wavy environment with
T = 1.00 s and
A = 12.5 mm, are shown. High concentrations are indicated by pale grey, low concentrations by dark grey.
Figure 2 shows that an inclined NBJ released in a stagnant environment has an ascent region (where the initial momentum prevails on the negative buoyancy) followed by a descent region (where the negative buoyancy prevails). Moreover, the jet luminosity close to the outlet is high (as indicated by the pale grey color) and it tends to reduce along the jet path, pointing out the dilution caused by the entrainment of external fluid into the jet. As a matter of fact, the external fluid has null concentration, so its color is black. Few seconds of this experiment are shown in the movie “Run7_Ferrari_et_al.mp4”, available as
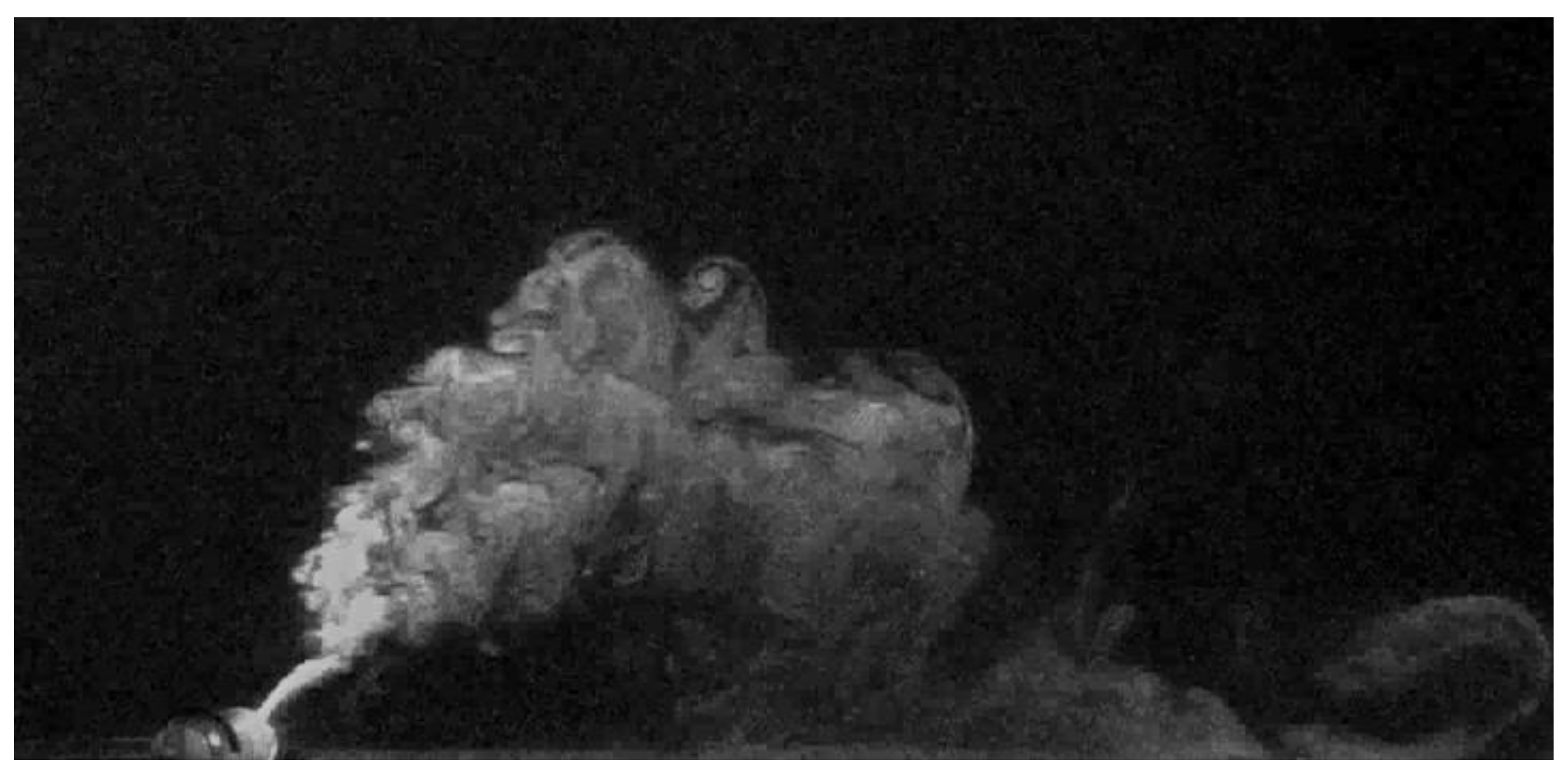
Supplementary Material.
Figure 3 shows the modifications induced on the NBJ (the same of
Figure 2) by the waves: Even if these modifications will be discussed in depth in
Section 3, it is apparent that this jet, even though it still has an ascent and a descent region, has a different shape and is lower and shorter than the one released in the stagnant environment. Few seconds of this experiment are shown in the movie “Run10_Ferrari_et_al.mp4”, available as
Supplementary Material.
An image of the background was obtained by recording, before each run, 100 images without the NBJ and computing their point-by-point average. This image of the background was then subtracted from each image with the NBJ, and the resulting images (field of light intensity) were normalized by the grey level measured at the outlet, corresponding to the initial concentration
C0. The subtraction of the background from the images with the jet allows us to remove sources of light not linked to the discharged fluid concentration. The subtraction of the background explains why the cylindrical pipe with the outlet on its wall is visible in
Figure 2 and
Figure 3 (before the background removal) and not visible in
Figure 4,
Figure 5 and
Figure 6, Figure 10 and Figure 11 (after the background removal). Under the assumption of ergodicity, the non-dimensional fields of the mean concentration
C/C0 were obtained by time averaging the measured values of
C/C0 on each pixel. The value of
C/C0 is reported in false colors in
Figure 4,
Figure 5 and
Figure 6, Figures 10 and 11, according to the color bar shown on the left of each Figure (dark red is linked to the highest concentrations, dark blue to the lowest ones). As a consequence,
C/C0 is a measure of the reduction of the mean concentration compared to the outlet concentration
C0: For instance,
C/C0 = 1 (dark red) means that the concentration
C in that point is the same as
C0 (no dilution),
C/C0 = 0.5 (green) means that the concentration
C in that point is one half of
C0,
C/C0 = 0 (dark blue) means that the concentration
C in that point is zero (external fluid not reached by the jet). The
x-axis and
y-axis are non-dimensionalised by the outlet diameter
D, with the origin on the outlet.
The jet axis was assumed as the locus of the concentration maxima on the jet cross-sections (on the non-dimensional mean concentration fields) and it was computed via the iterative procedure described in Ferrari and Querzoli [
1]. The stagnant case jet axis was determined on the non-dimensional mean concentration fields shown in Figure 10a for
Fr = 18.0 and in
Figure 4 and Figure 11a for
Fr = 28.0. This stagnant case jet axis is drawn as a white line in
Figure 4,
Figure 5 and
Figure 6, Figures 10 and 11 for comparison with the features of the NBJ with the same
Fr released into a receiving body affected by regular waves. Moving along the jet axis, the color change from dark red to blue (i.e., from high concentrations to low concentration) highlights the dilution due to the entrainment. As shown in
Figure 2 and
Figure 4, an inclined NBJ has an ascent and a descent region, so its axis will have a non-symmetrical parabolic-like shape, with the origin coinciding with the outlet (green star in
Figure 4, with
X/D = 0,
Y/D = 0), a point of maximum height (defined as the highest point reached by the jet axis, with coordinates
X/D =
Xh/D,
Y/D =
Yh/D) and an impact point (defined as the point where the jet axis reaches again the outlet height, with coordinates
X/D =
Xd/D,
Y/D = 0). The point of maximum height and the impact point for the stagnant case are drawn, respectively, as a white circle and a white asterisk in
Figure 4,
Figure 5 and
Figure 6, Figures 10 and 11. The vertical distance between the jet origin and the point of maximum height is defined as the maximum height (vertical orange line in
Figure 4) and the horizontal distance between the jet origin and the impact point is defined as the impact distance (horizontal orange line in
Figure 4).
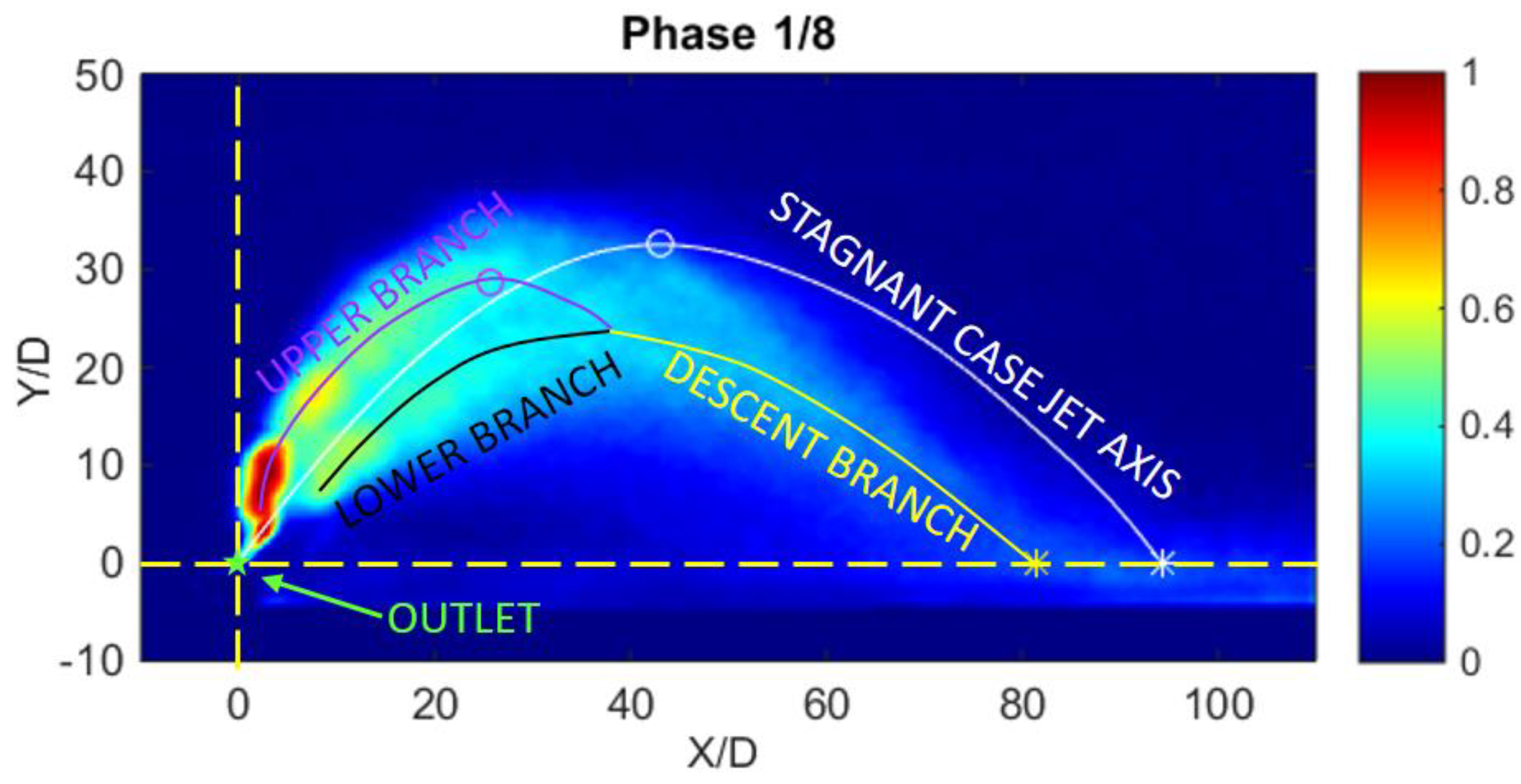
The runs in a wavy environment were also analyzed by dividing the wave period in 8 phases equally spaced in time by a Δ
T =
T/8: phase 1 is taken when the wave trough is above the outlet, phase 5 corresponds approximately to the moment when the wave crest is above the outlet. In
Figure 5 the phase averaged
C/C0 field for phase 1/8 is shown. For the NBjs released into a wave environment, the impact point was measured as the point of maximum height of
C/C0 on the horizontal line
Y/D = 0 for
X/D >
Xh/D (i.e., beyond the horizontal coordinate of the point of maximum height; yellow asterisk in
Figure 5 and
Figure 6), while the point of maximum height for the jet undergoing a bifurcation (see
Section 3.1.1 for the phenomenological discussion) was measured in the upper branch of the two branches caused by the bifurcation. In
Figure 5 and
Figure 6, the point of maximum height is drawn as a magenta circle. In
Figure 5, the jet axis of the upper branch as a magenta line, the jet axis of the lower branch as a black line and the jet axis of the descent branch as a yellow line.
See Ferrari and Querzoli, 2010 [
1], for more details on the experimental configuration simulating the discharge of inclined NBJs and data elaboration; see Ferrari and Querzoli, 2015 [
35] and Ferrari et al., 2016 [
40] for more details on the wavemaker system.
3. Results
This section is organized as follows: In
Section 3.1, the focus is on the temporal evolution of the phenomenon, so, for each of the eight phases, the mean concentration fields (3.1.1), the maximum height and impact point (3.1.2), and the concentration profiles (3.1.3) are shown; in
Section 3.2 the overall mean concentration fields, computed performing the time average on all the images for each run, are presented; eventually, the measured dilutions are reported in
Section 3.3.
3.1. Temporal Evolution
3.1.1. Mean Concentration Fields
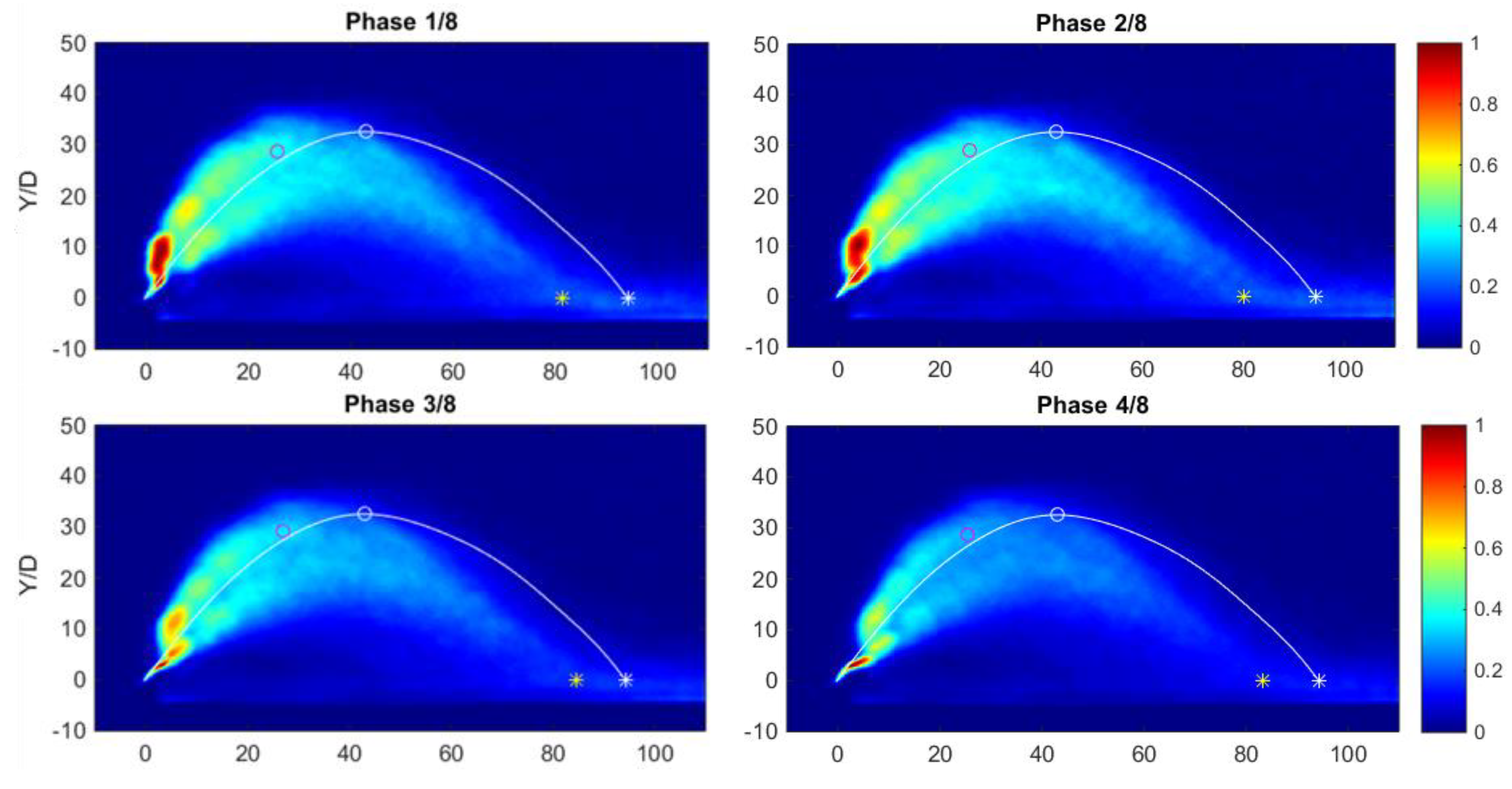
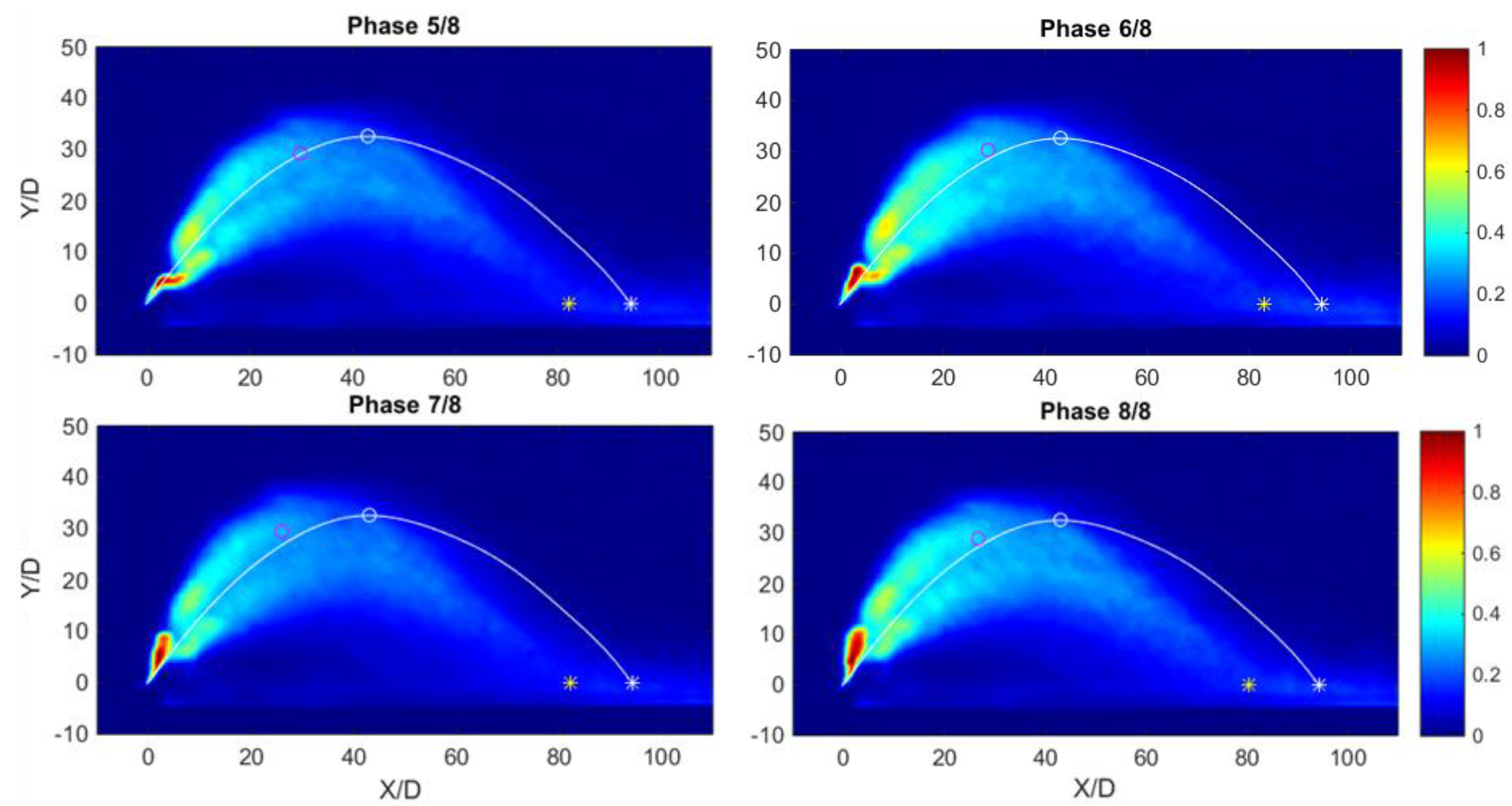
To better highlight the temporal behaviour of a negatively buoyant jet released upwards with a certain angle to the horizontal when a wave is passing through, in
Figure 6 the non-dimensional mean concentration field of an NBJ with
Fr = 28.0 subjected to regular waves with
T = 1.00 s and
A = 12.5 mm has been divided into 8 phases; in addition, to ease the comparison with the stationary case (shown in
Figure 4), on each image the stagnant case jet axis (white line) is superimposed. The images of
Figure 6 are shown as a movie in “Run10_mean_phase_Ferrari_et_al.mp4”, available as
Supplementary Material. To highlight the differences between the stationary and the wave case, a white circle and a white asterisk indicate, respectively, the point of maximum height and the impact point for the stationary case, whilst a magenta circle and a yellow asterisk indicate, for each phase, the wave case maximum height point and impact point.
Close to the outlet (
X/D = 0,
Y/D = 0), the NBJ is deflected upwards or downwards, so it oscillates around the stationary position (pointed out by the white line, i.e., the stationary case jet axis): So in this region the NBJ tends to resist the wave because it tends to preserve its initial direction, as it still retains most of its initial momentum. This behavior is similar to the simple jet one and this region can be identified as the jet deflection region, in agreement with the findings of Chyan and Hwung (1993, [
33]) and Mossa (2004 [
32]). This oscillation is linked to the position of the wave above the jet which, in turn, is linked to the phase: In phase 1 the wave trough is above the outlet, so there is the largest leftward deflection, while when the wave crest is above the outlet (phase 5), the jet experiences the largest rightward deflection. It is interesting to note that this oscillation is larger upwards than downwards; this is presumably due to the velocity field generated by the interaction between the wave motion (mostly horizontal in that region) and the cylindrical pipe simulating the pipe (visible in
Figure 2 and
Figure 3). Velocities tend to be higher and directed upwards close to the outlet, whilst they tend to be lower and horizontal in the lower zone. Consequently, the deflection which pushes the jet upwards tends to carry it towards regions with higher velocity and this causes this larger displacement upward.
Coming back to the observation of
Figure 5 and
Figure 6, and moving along the jet axis, it is noticeable how, after the jet deflection region, if the wave is intense enough (i.e., with
T and
A high enough), the NBJ bifurcates; this is the transition region. The jet, slowed down by the enhanced entrainment of low-momentum fluid, is divided into two branches, one mainly higher (magenta line in
Figure 5) and one lower (black line in
Figure 5) than the stationary jet axis (white line in
Figure 5). Eventually, the two branches merge to build up again a single jet flow in the descent branch (yellow line in
Figure 5); this is the developed jet region. This bifurcation is sharpened by the fact that the change in the direction is not gradual but, instead, the NBJ in the jet deflection region tends to abruptly move from one extreme to the other.
3.1.2. Geometrical Features
The point of maximum height of the NBJ released into a wavy environment is in the upper branch of the bifurcated jet (magenta asterisk in
Figure 5 and
Figure 6) and tends to be lower than the same point of the stagnant case jet (white circle in
Figure 5 and
Figure 6); a similar consideration stands for the impact point (compare the yellow asterisk, i.e., the wave case impact point, with the white asterisk, i.e., the stagnant case impact point, in
Figure 5 and
Figure 6). For this reason, in
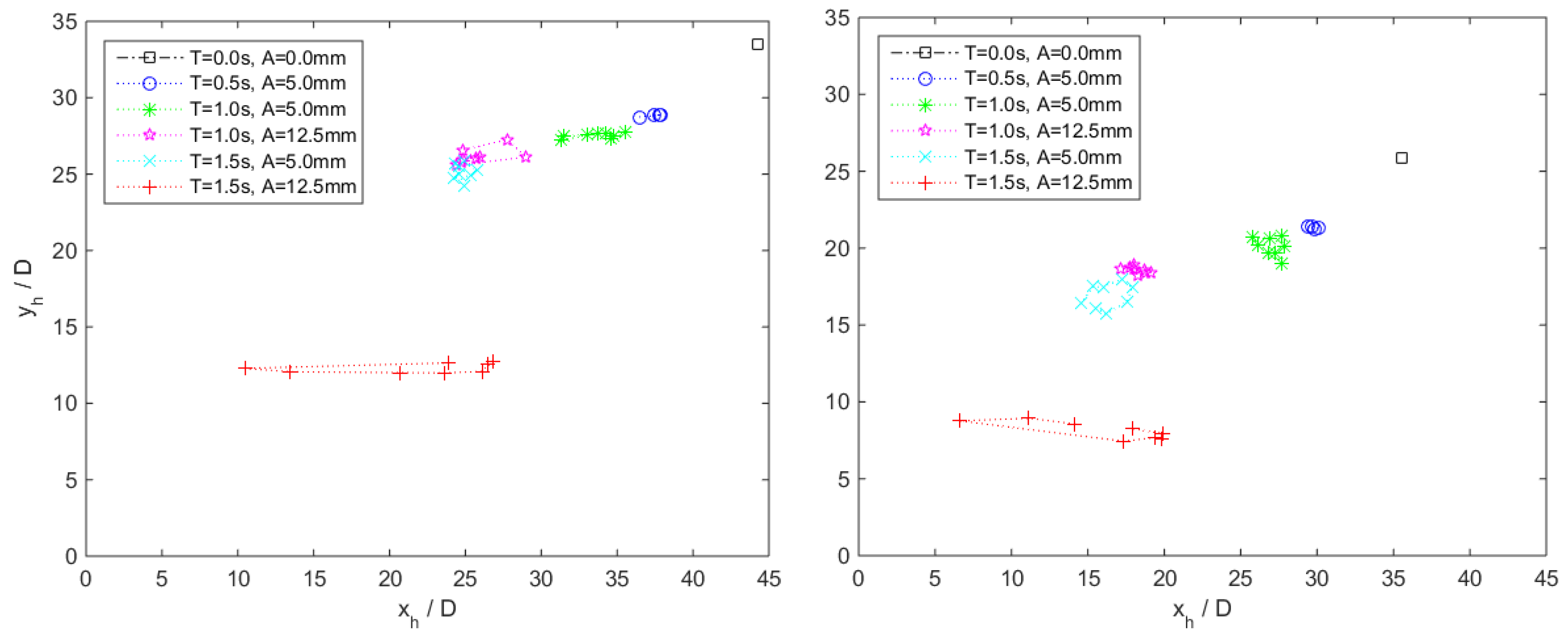
Figure 7 the trajectories followed by the points of maximum height for the wave cases (colored lines: blue circles for
T = 0.5 s and
A = 5.0 mm, green asterisks for
T = 1.0 s and
A = 5.0 mm, magenta stars for
T = 1.0 s and
A = 12.5 mm, cyan xs for
T = 1.5 s and
A = 5.0 mm and red +s for
T = 1.5 s and
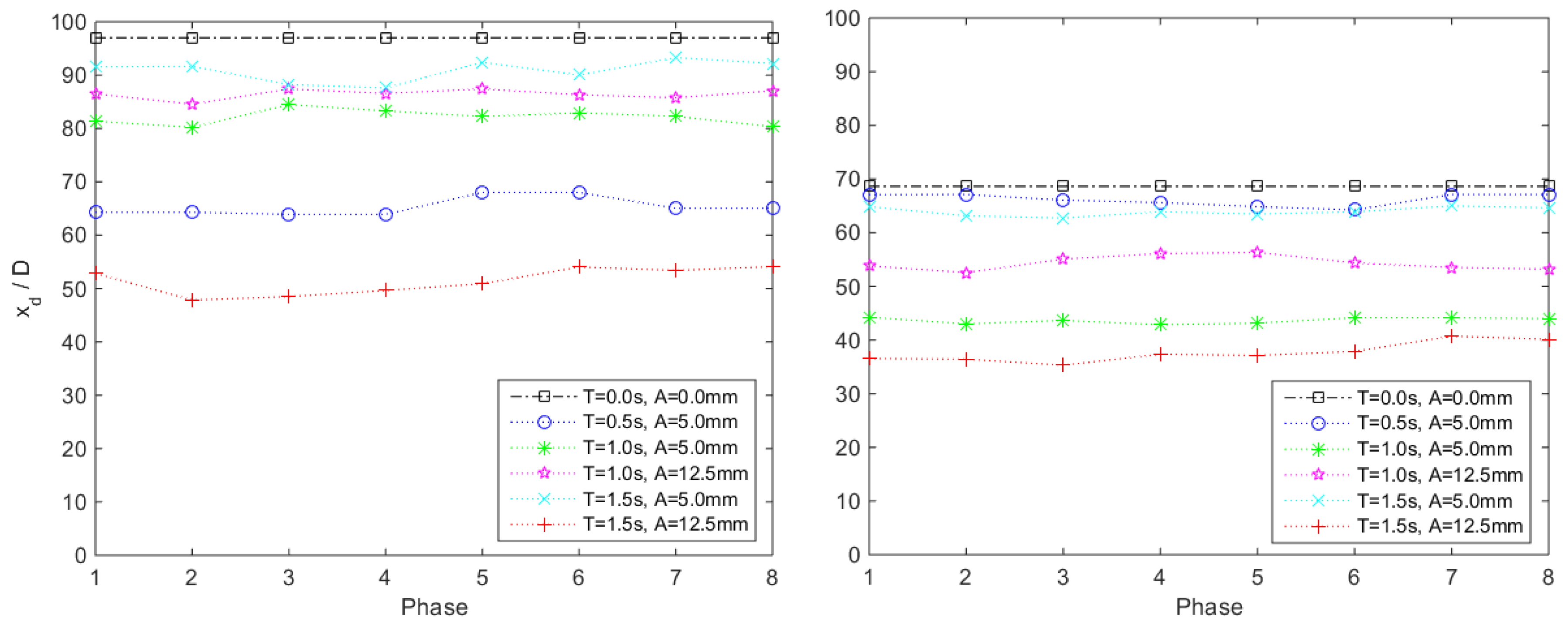
A = 12.5 mm) are compared with the coordinates of the maximum height point for the stagnant case (a single black square, as it does not move in the stagnant case). Similarly, in
Figure 8 the oscillation of the impact distances for the wave cases in the various wave phases (colored lines, the same as in
Figure 7) are compared with the constant impact distance for the stationary case (black line). In both
Figure 7 and
Figure 8, the left subfigure refers to the NBJ with
Fr = 28 and the right subfigure to the NBJ with
Fr = 18.
By looking at
Figure 7 and
Figure 8, it is possible to note the peculiar behavior of an NBJ released into a wavy environment: The maximum height and the impact distance of the NBJs released in wavy environment are shorter than those of the stationary case for all the different waves tested here. In particular, the ratio between the maximum height for the wave cases and the stagnant case varies from a maximum value of about 0.86 (
T = 0.5 s,
A = 5.0 mm) to a minimum of about 0.36 (
T = 1.5 s,
A = 12.5 mm) for
Fr = 28.0, and from a maximum of about 0.83 (
T = 0.5 s,
A = 5.0 mm) to a minimum of about 0.32 (
T = 1.5 s,
A = 12.5 mm) for
Fr = 18.0.
Moreover, by looking at
Figure 7 it is noticeable that the trajectories of the point of maximum height tend to be rotations around a fixed point, even if, in some cases, the closed trajectories are quite flattened. The point of maximum height tends to be lower and closer to the outlet when the wave parameters change: When the wave period
T and amplitude
A increase, the distance from the stationary position increases. If, on one hand, it is clear that the strongest waves (red +,
T = 1.5 s and
A = 12.5 mm) have the strongest impact on this phenomenon, on the other the wave period
T seems to have the biggest role on the decrease of the maximum height; as a matter of fact, the curves in
Figure 7 are sorted by increasing wave period
T.
The impact point (
Figure 8) oscillates around a fixed point which is different from the stationary impact point. Different to the point of maximum height, the impact point seems more influenced by the wave amplitude
A; as a matter of fact, in
Figure 8, the curves relative to
A = 5.0 mm are generally closer to the stationary position than the ones with
A = 12.5 mm. The only exception to this rule is the case of
T = 0.5 s and
A = 5.0 mm for
Fr = 28.0 (blue circles on the left of
Figure 8); an explanation for this will be given in the
Section 3.2. Similar to the maximum height, also the impact distance of the wave cases shows a reduction in size with respect to the stagnant one. In particular, the ratio between the impact distance for the wave cases and the stagnant case varies from a maximum value of about 0.94 (
T = 1.5 s,
A = 5.0 mm) to a minimum of about 0.51 (
T = 1.5 s,
A = 12.5 mm) for
Fr = 28.0, and from a maximum of about 0.97 (
T = 0.5 s,
A = 5.0 mm) to a minimum of about 0.54 (
T = 1.5 s,
A = 12.5 mm) for
Fr = 18.0.
In summary, close to the outlet, the NBJ oscillates around the stationary position, as the simple jets; conversely, the NBJ maximum height point rotates around a different position from the stationary maximum height point and the NBJ impact point oscillates around a different position from the stationary impact point.
The reduction of the maximum height and impact distance in the wave cases showed in
Figure 7 and
Figure 8 confirms the contraction of NBJs when discharged into a wavy environment. This contraction is probably due to the periodic oscillation of the initial direction of the NBJ that causes its bifurcation and a consequent increase of the entrainment; the larger amount of low-momentum external fluid trapped into the NBJ causes a premature slowdown (when compared to the stagnant case).
3.1.3. Concentration Profiles
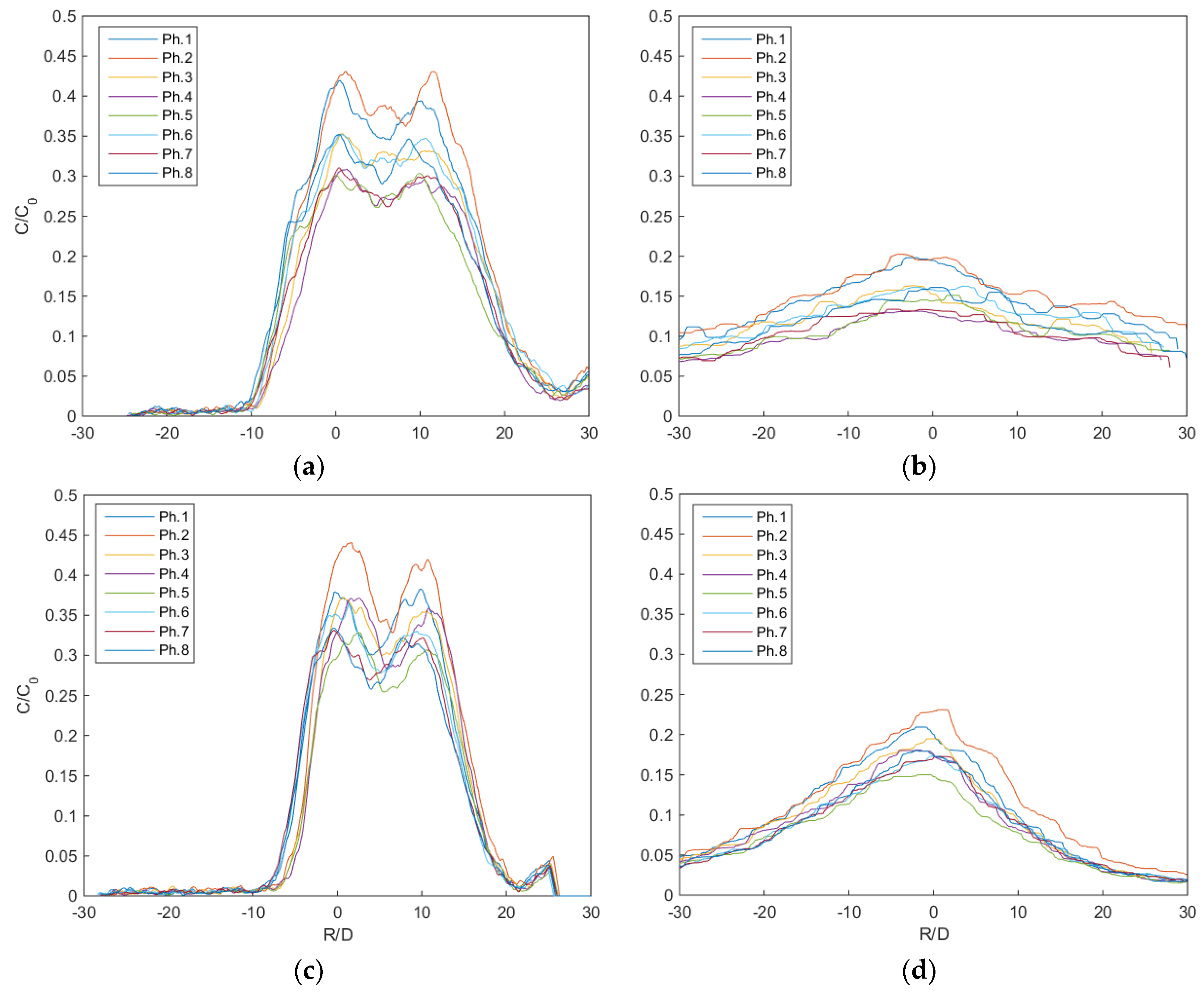
In
Figure 9, the cross-sectional profiles of the non-dimensional mean concentration
C/C0 measured on the point of maximum height (a and c, vertical profiles) and on the impact point (b and d, horizontal profiles), in eight different phases of the wave cycle, are shown, for two NBJs with
Fr = 28.0 (a and b) and
Fr = 18.0 (c and d) released into a receiving body affected by a wave motion with
T = 1.00 s and
A = 12.5 mm. The different colors highlight the different phases the profiles are measured in. The bimodal distribution of the concentration maxima in
Figure 7c and
Figure 9a confirms what was previously stated about the bifurcation of NBJs released in a wave environment.
In the impact point, the various profiles have a single peak because here the NBJ is in the developed jet region, where it tends to merge again in a single entity (the yellow line in
Figure 5).
The differences among the concentration values in the various phases highlight the different concentration dilutions achieved by the NBJ in the different phases.
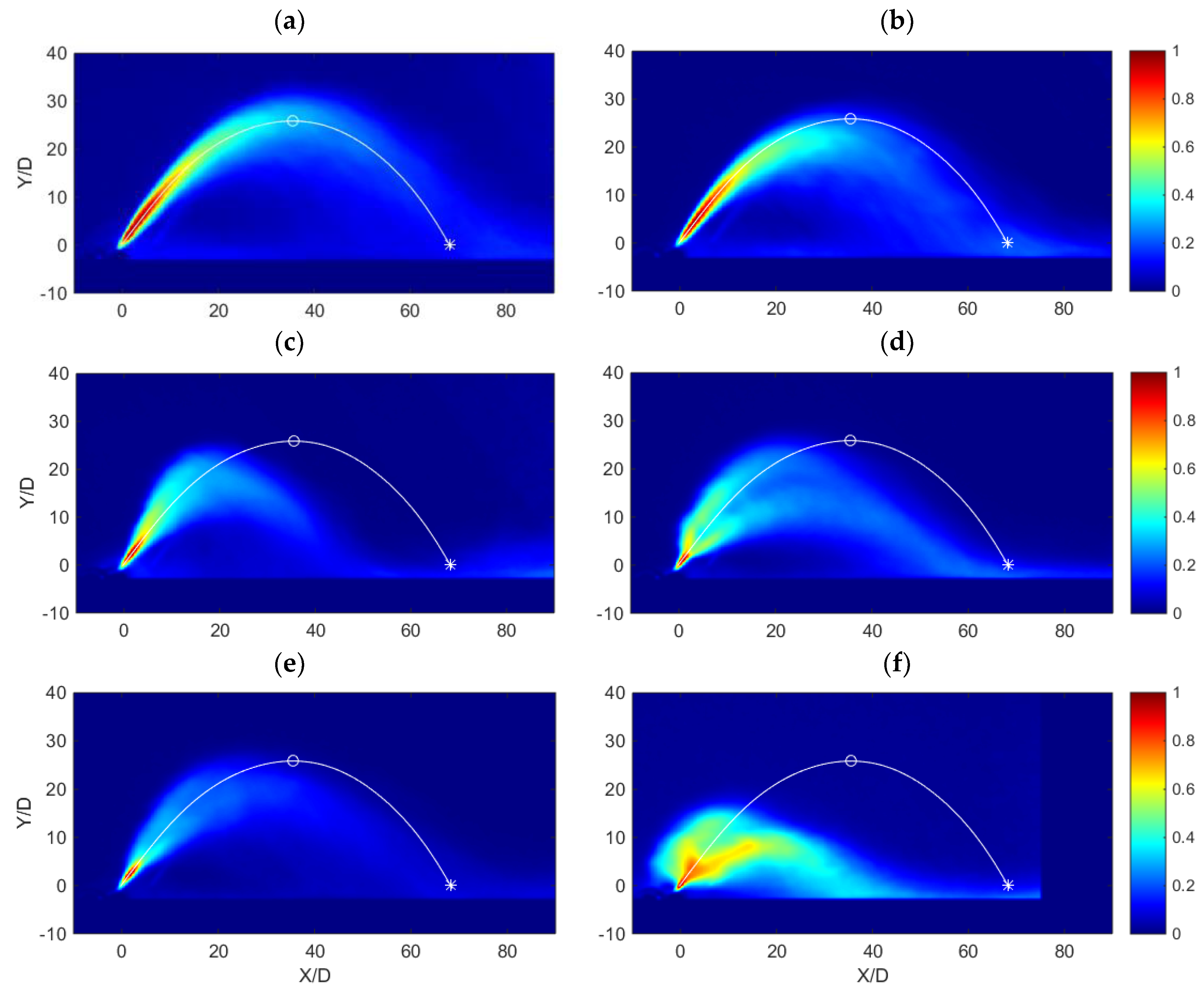
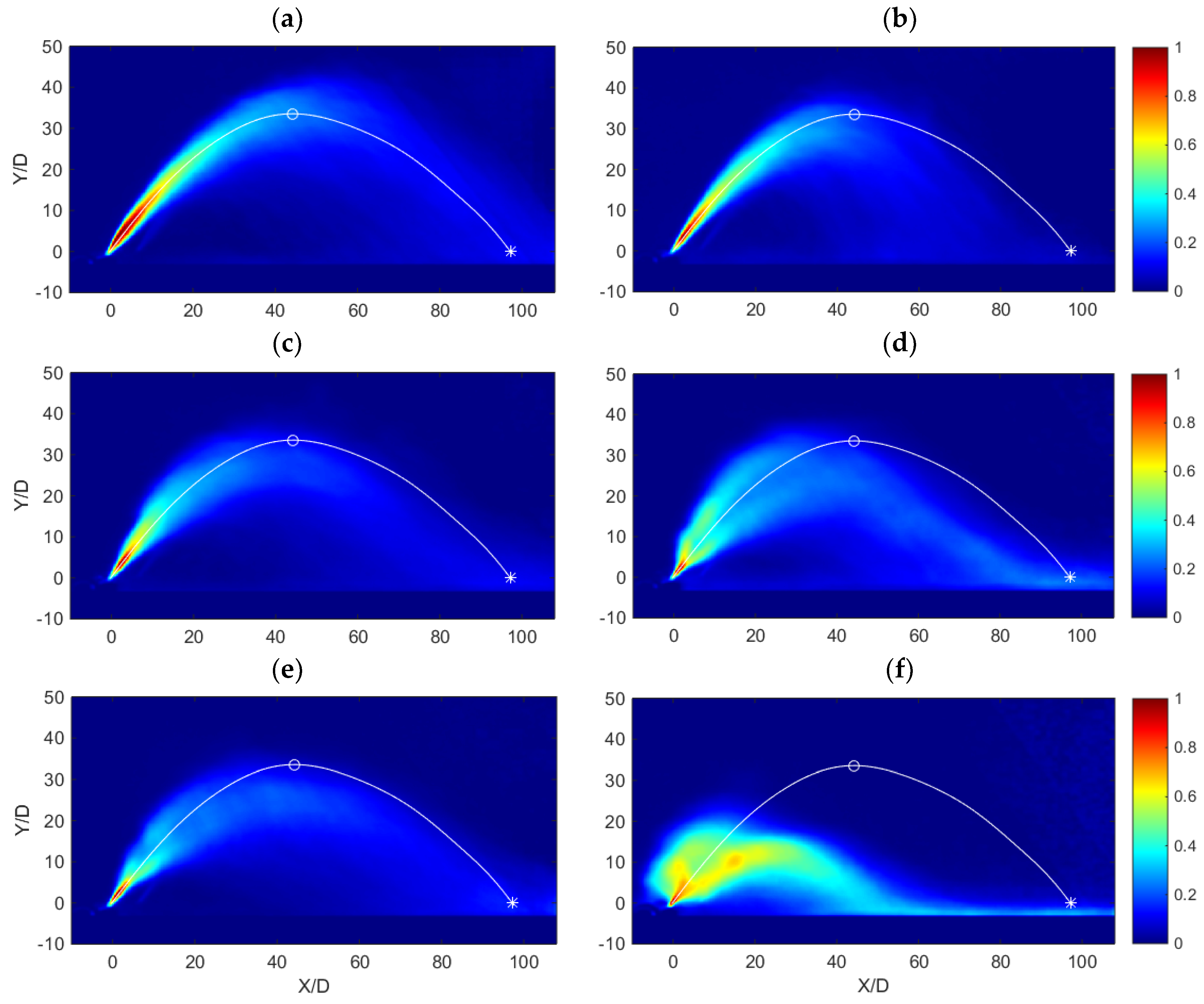
3.2. Overall Time Averaged Concentration Fields
In
Figure 10 and
Figure 11, the mean concentration fields, computed performing the time average over all the images recorded on each experiment and not divided by phases, are shown:
Figure 10 concerns the inclined negatively buoyant jets with
Fr = 18.0, while
Figure 11 concerns the ones with
Fr = 28.0. In particular, the
Figure 10a and
Figure 11a show the inclined NBJs released into a stagnant receiving body, whilst the others (
Figure 10b–f and
Figure 11b–f) show the inclined NBJs released into a wavy environment.
By comparing the concentration field of the NBJ released into a stagnant environment with those of the NBJs released into a wavy environment, it is apparent how the interaction with the waves causes a contraction of the jet, which tends to be less high and shorter (with a decrease of the maximum height and of the impact distance compared to the stagnant cases, as stated before). This contraction tends to increase as the wave period T and amplitude A increase.
Moreover, for the highest
T and
A (
Figure 10d–f and
Figure 11d–f), the distribution of the concentration is bimodal, confirming a bifurcation of the NBJ into two branches, one higher and one lower than the stationary position. These two branches tend to behave as two NBJs released with different angles to the horizontal, to eventually merge when the higher branch falls down on the lower one, causing an increase in the concentration in the lower branch, which is clearly visible in
Figure 10f and
Figure 11f at
X/D ≈ 15 and
Y/D ≈ 10. This bifurcation, caused by the oscillation of the initial region of the NBJ around the stationary position, becomes more pronounced when the wave amplitude
A increases, as it is possible to see from a comparison of the
Figure 10d,f (or
Figure 11d,f, with
A = 12.5 mm) with
Figure 10b,c,e (or
Figure 11b,c,e, with
A = 5.0 mm). If in the first two Figures the bifurcation is more evident, in the other three it is almost absent or very weak. As a matter of fact, in
Figure 10b and
Figure 11b the effect of the wave begins to be noticeable only very close to the point of maximum height, where the initial momentum of the NBJ has been almost completely spent. In
Figure 10c and
Figure 11c, concerning a wave with
T = 1.00 s and
A = 5.0 mm, the oscillation of the initial region of the NBJ caused by the wave is still present, because the jet widens more than in the stationary case, but it is not sufficient to create the bifurcation. This could suggest that the bifurcation is more linked to high-amplitude waves.
The reduction of the maximum height of the NBJ is mainly caused by the bifurcation. As a matter of fact, because of the strong deflection upwards and downwards imposed by the bifurcation (see
Figure 10f and
Figure 11f), the jet uses a portion of its initial momentum to return to the initial direction and, consequently, it cannot reach the same height of the stagnant case. When the wave deflects the jet downwards, the trajectory is similar to the one of a NBJ released with a lower angle to the horizontal, i.e., the jet tends to reach a lower maximum height (see Ferrari and Querzoli, 2010, [
1]).
The reduction of the impact distance is mainly caused by a combination of the bifurcation and of the rotation of the maximum height point.; the fluid in the lower branch finds the opposition of the oscillating fluid trapped between the bottom and the jet itself, while the fluid in the upper branch, as stated before, falls down on the lower branch, causing an additional mixing and a slowing down of the NBJ.
In
Figure 11b, the effect of the wave with
T = 0.5 s and
A = 5.0 mm on the impact point (compare with
Figure 8) can be explained. The wave is too weak to slow down the NBJ enough, so, when the NBJ comes close to the point of maximum height, it has covered a distance long enough to consume most of its initial momentum and, consequently, it undergoes the rotatory movement imposed by the waves, with an additional stirring that lets the jet fall down almost vertically, with a consequent strong reduction of the impact distance.
In summary, the main effect of the wave amplitude A is the bifurcation of the NBJ, while the one of the wave period T is more linked to the additional stirring, with a rotatory motion, imposed to the transition region of the NBJ. Both these phenomena contribute to consume the initial momentum of the NBJ and to decrease the size of the sea region interested by the NBJ itself. An alternative explanation of these effects of the waves on NBJs could be linked to the Stokes drift. For this reason, we have planned to perform Lagrangian velocity measurements in the future.
3.3. Dilution
In order to study the effect of waves on the dilution of inclined negatively buoyant jets, we can define the ratio of the dilution of jets under waves to the dilution of jets in a stagnant environment, if
RDIL: if
RDIL is higher than one, the waves increase the dilution and vice versa. In
Figure 12,
RDIL has been plotted versus
Fr for all the experiments. The horizontal dotted black line at
RDIL = 1 highlights the stagnant case, while, as in the previous Figures, colored lines highlight the wave cases (blue circles for
T = 0.5 s and
A = 5.0 mm, green asterisks for
T = 1.0 s and
A = 5.0 mm, magenta stars for
T = 1.0 s and
A = 12.5 mm, cyan xs for
T = 1.5 s and
A = 5.0 mm and red +s for
T = 1.5 s and
A = 12.5 mm). The dilution is measured, in all the cases, as the inverse of the maximum non-dimensional concentration at the impact point on the overall time-averaged fields, in order to avoid phase variations (see
Figure 9b,d).
Figure 12 shows that, differently from what was found by investigations on simple jets or positively buoyant jets, the dilution not always increases for NBJs released in a wavy environment. In particular, the waves with
A = 5.0 mm and
T = 0.5 s,
T = 1.0 s enhance the dilution (
RDIL = 1.81 for
A = 5.0 mm,
T = 0.5 s,
Fr = 18.0;
RDIL = 1.08 for
A = 5.0 mm,
T = 1.0 s,
Fr = 18.0;
RDIL = 1.26 for
A = 5.0 mm,
T = 0.5 s,
Fr = 28.0;
RDIL = 1.08 for
A = 5.0 mm,
T = 1.0 s,
Fr = 28.0), whilst the remaining waves (with higher values of
A and
T) reduce the dilution. The lowest values for R
DIL have been measured for the strongest wave (
A = 12.5 mm,
T = 1.0 s) for both the
Fr (
RDIL = 0.36 for
Fr = 28.0;
RDIL = 0.45 for
Fr = 18.0).
This result can be explained by two of the effects of the waves on the NBJ: The reduction in size of the sea region interested by the discharge and the bifurcation.
Because of the contraction, the NBJ is forced by the waves to remain in a smaller region compared to the stagnant case, so the path available for mixing is decreased and this can reduce (or even cancel) the additional stirring caused by the rotation. Moreover, if the NBJ is forced into a smaller region, it will tend to re-entrain some jet fluid instead of entraining external fluid.
The bifurcation has a conflicting role: On one hand, it increases the surface available for entrainment, but, on the other hand, the lower boundary of the upper branch and the upper boundary of the lower branch tend to exchange jet fluid between themselves and not to entrain external fluid, reducing the dilution. Moreover, as shown in the previous subsections, the upper branch tends to fall down over the lower one, causing an increase in concentration along the path of the wave case NBJ.
The authors cited in the introduction found that discharging a horizontal NBJ or a simple jet in the opposite direction to the wave propagation increases in size the region occupied by the jet and, as a consequence, its dilution. In the present case, an inclined NBJ (in particular with the strongest waves) experiences, as previously seen, a reduction in size of the region occupied by the jet in comparison with the stagnant case which, consequently, leads to a lower dilution.
For these reasons, the waves that cause the worst dilutions are the ones with A = 12.5 mm. On the contrary, the two waves with A = 5.0 mm and T = 0.5 s, T = 1.0 s enhance the dilution, because the rotation imposed by the waves on the NBJs is intense enough to compensate their contraction (which, anyway, is smaller than in the other cases).
In summary, the peculiar nature of inclined NBJs, which tend to behave in a limited region of space and cannot reach an asymptotic state like some simple or positively buoyant jets, leads to the conclusion that the wave motion not always enhances their dilution. In particular, the strongest waves tested in the present work tend to reduce the dilution, whilst the weakest ones tend to enhance it.